Multi-Objective Real-Time Tuning of SVC Used in Electrified Traction Systems
Abstract
:1. Introduction
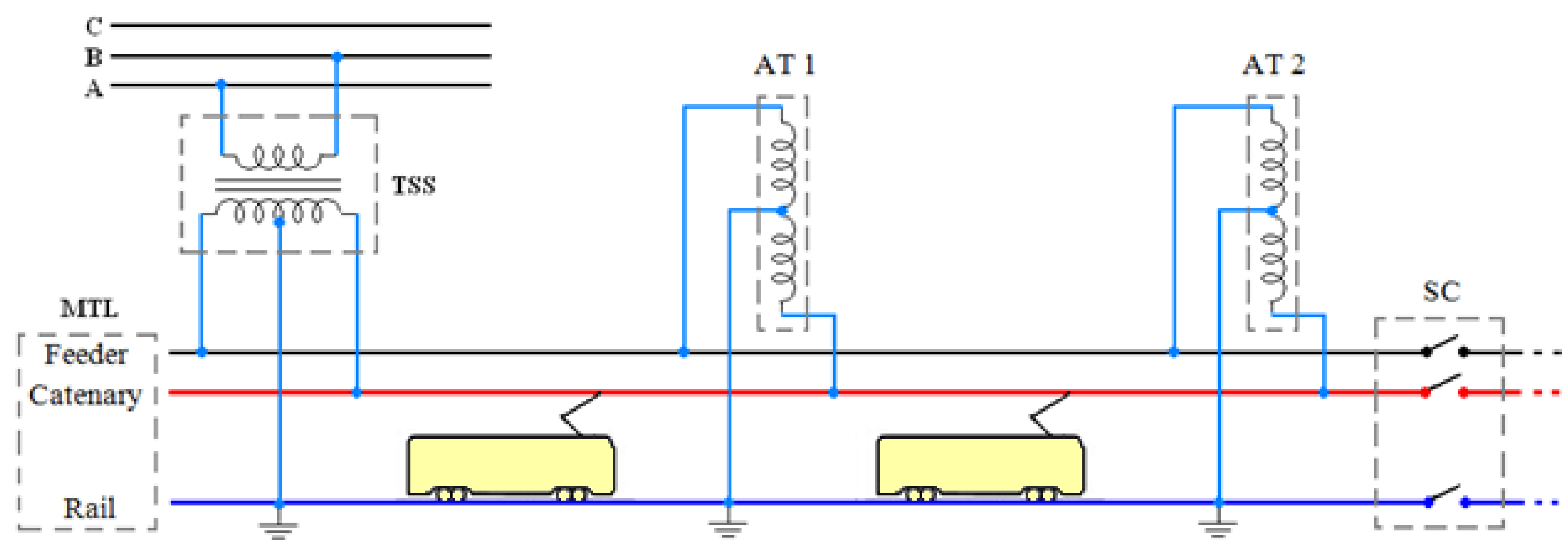
2. Arrangement of AC Traction System (2 × 25 kV)
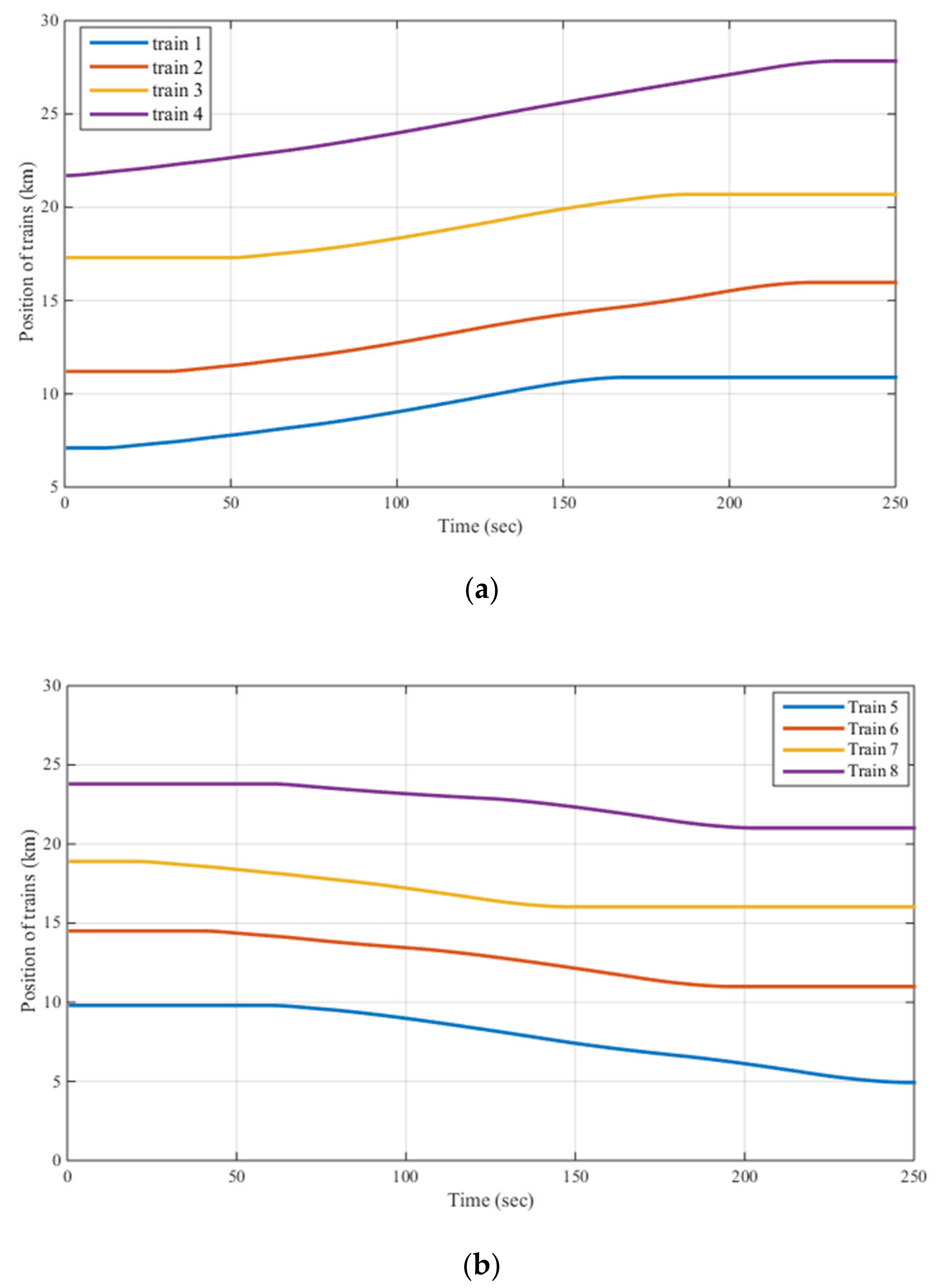
2.1. Train Modeling
| Control mode of train; | |
| Tractive effort (N·m); | |
| Speed of train (m/s); | |
| Factor of efficiency; | |
| Voltage of catenary (V); | |
| Current and voltage phase difference; | |
| Mechanical power (Watt); | |
| Electrical power (Watt); | |
| Train’s mass (effective) (kg); | |
| Resistance of train (N); | |
| Gravity force (N); | |
| track slope; | |
| Train’s position (m); | |
| Track resistance (N). |
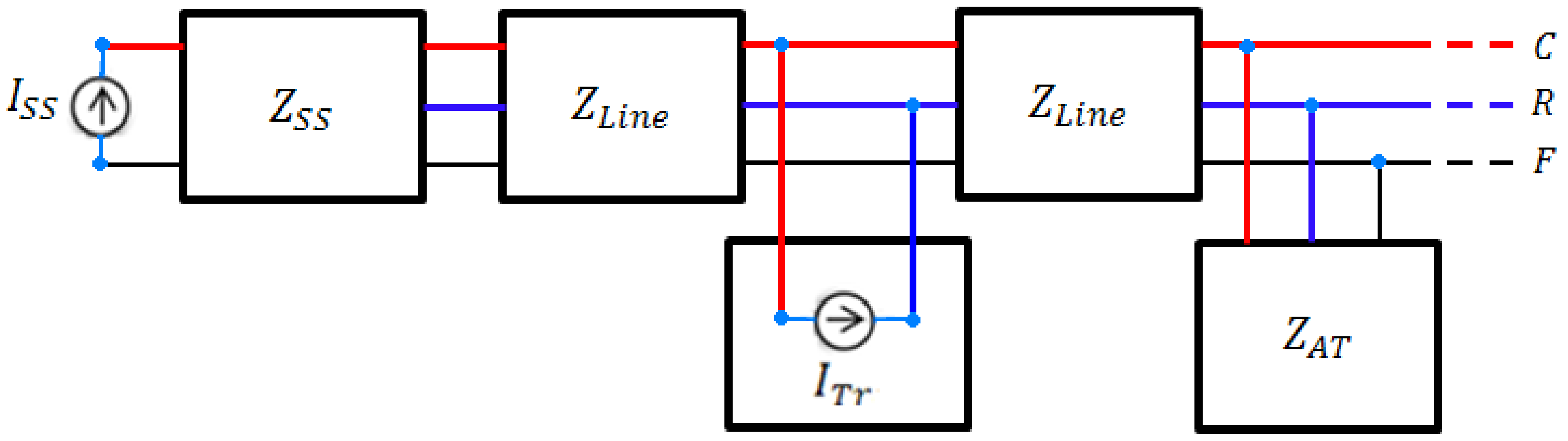
2.2. Multi-Transmission Line (MTL) Modeling
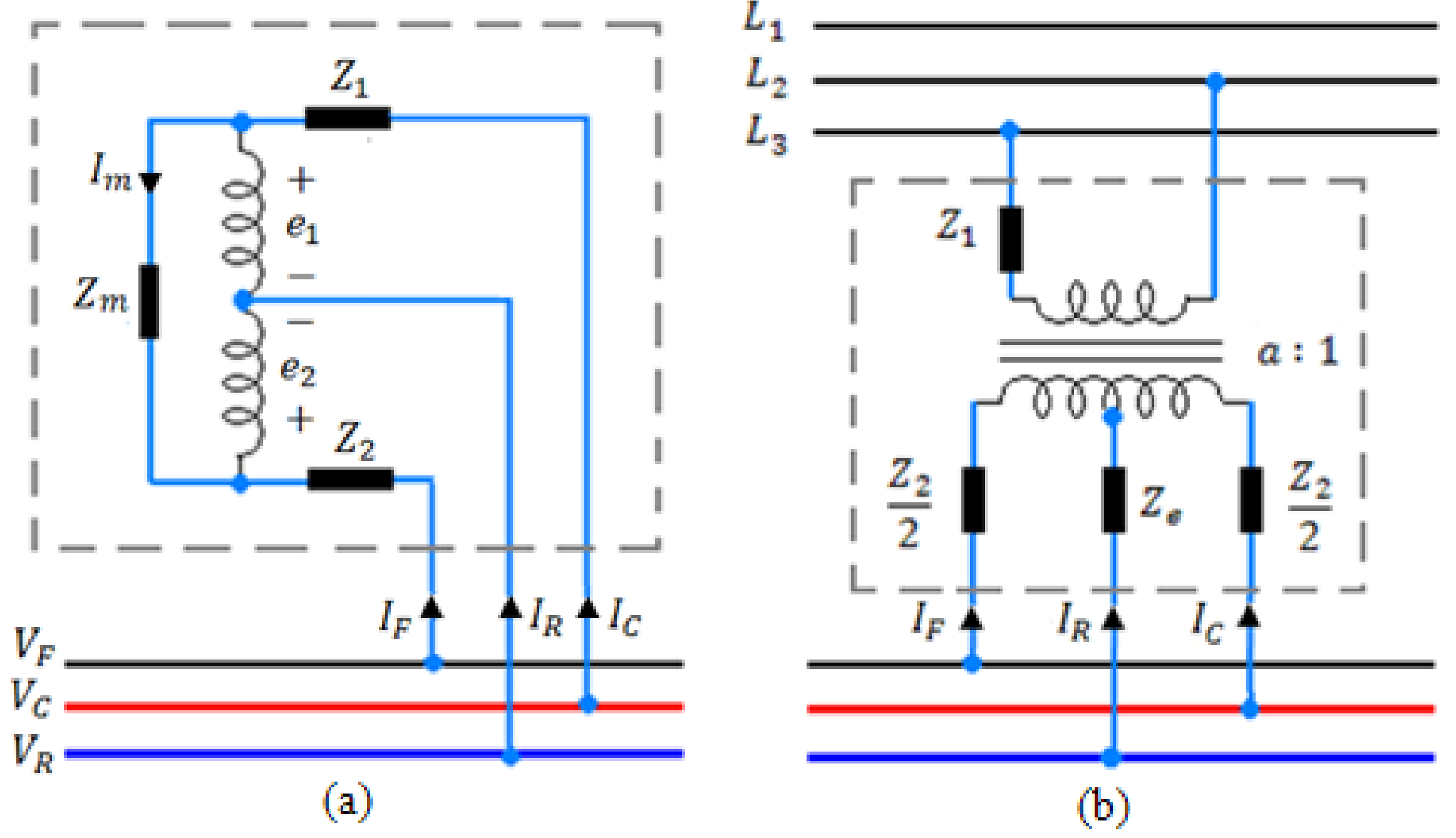
2.3. Modeling of Autotransformer (AT) Substations
2.4. Modeling of Traction Substations (TSS)
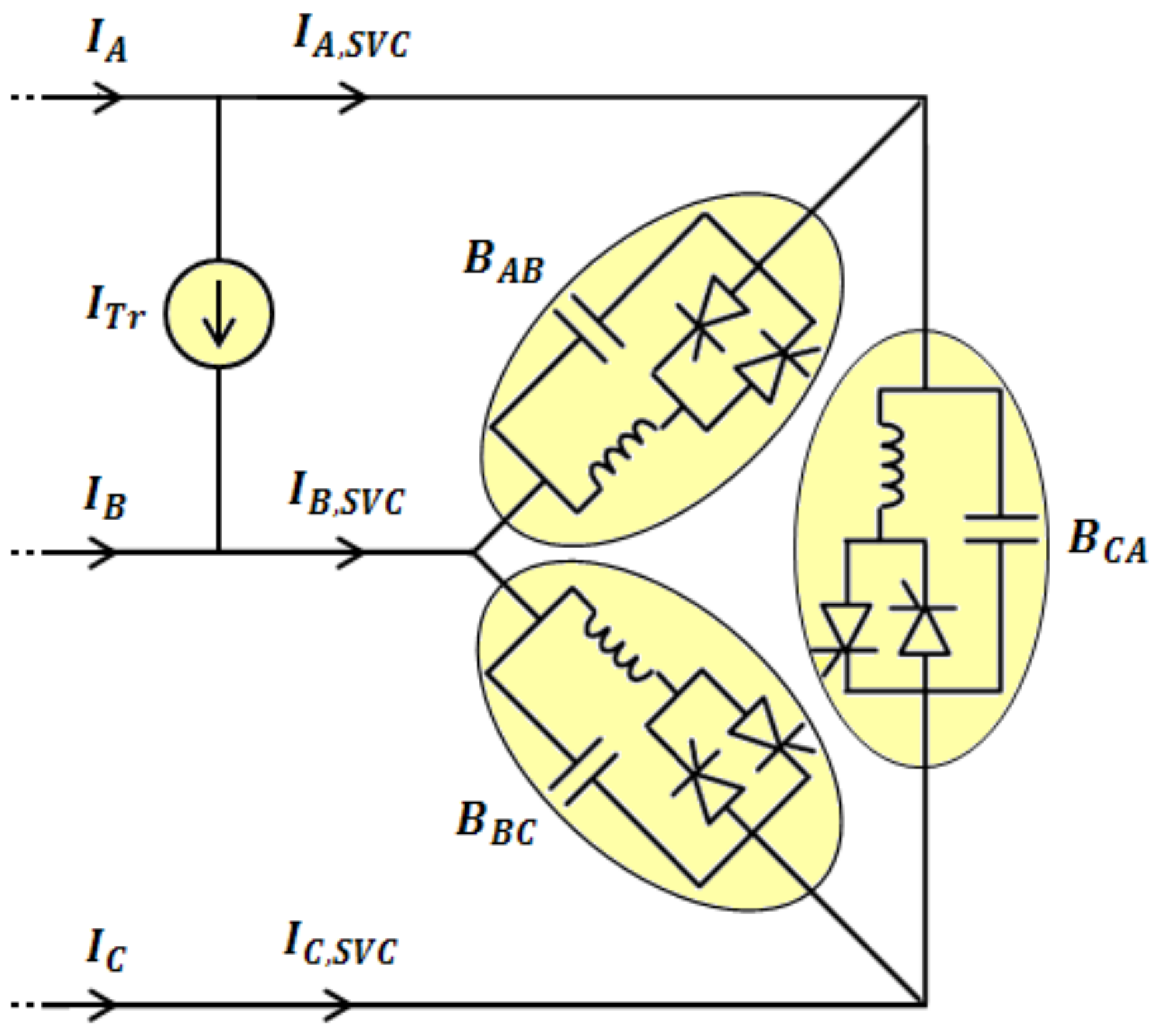
3. SVC Implementation
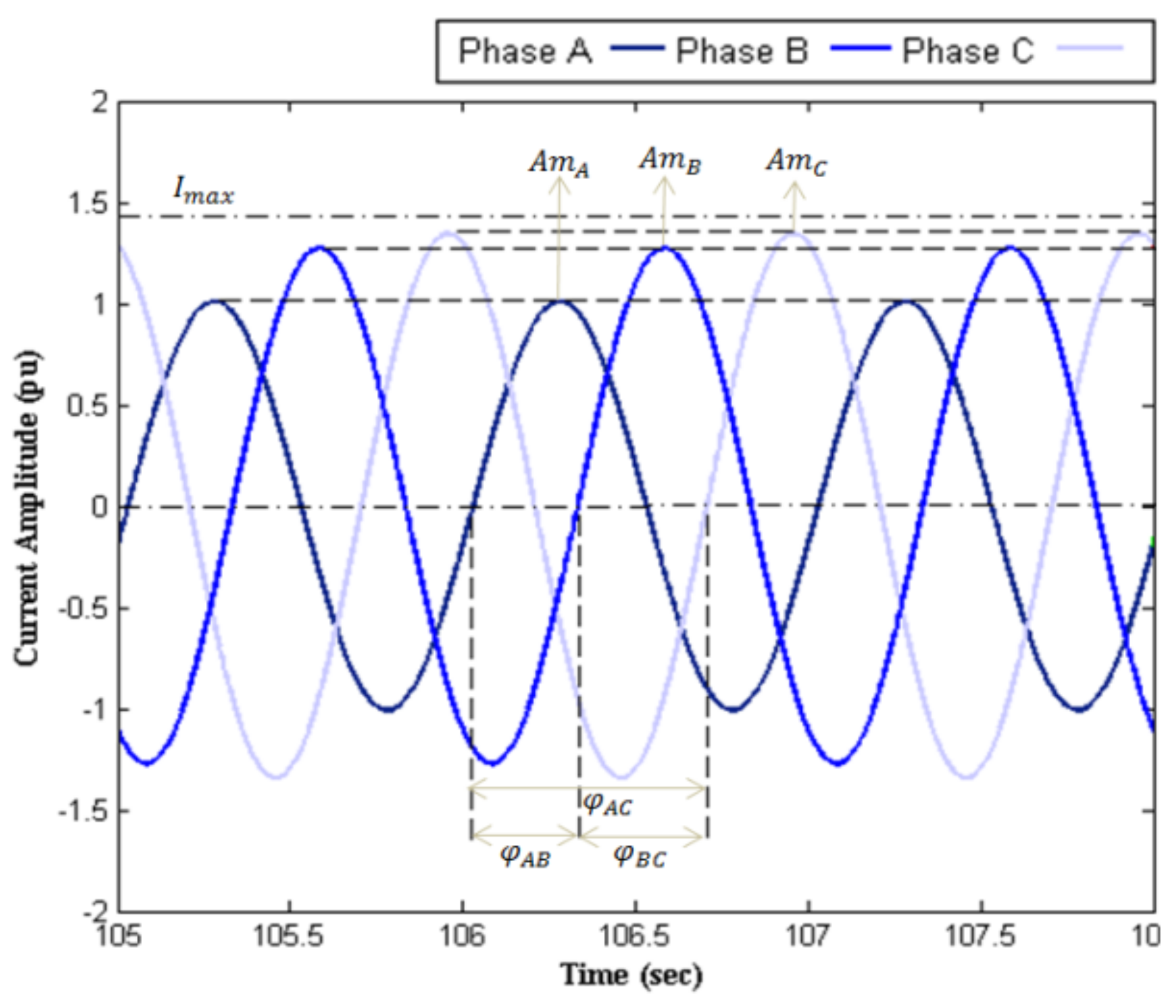
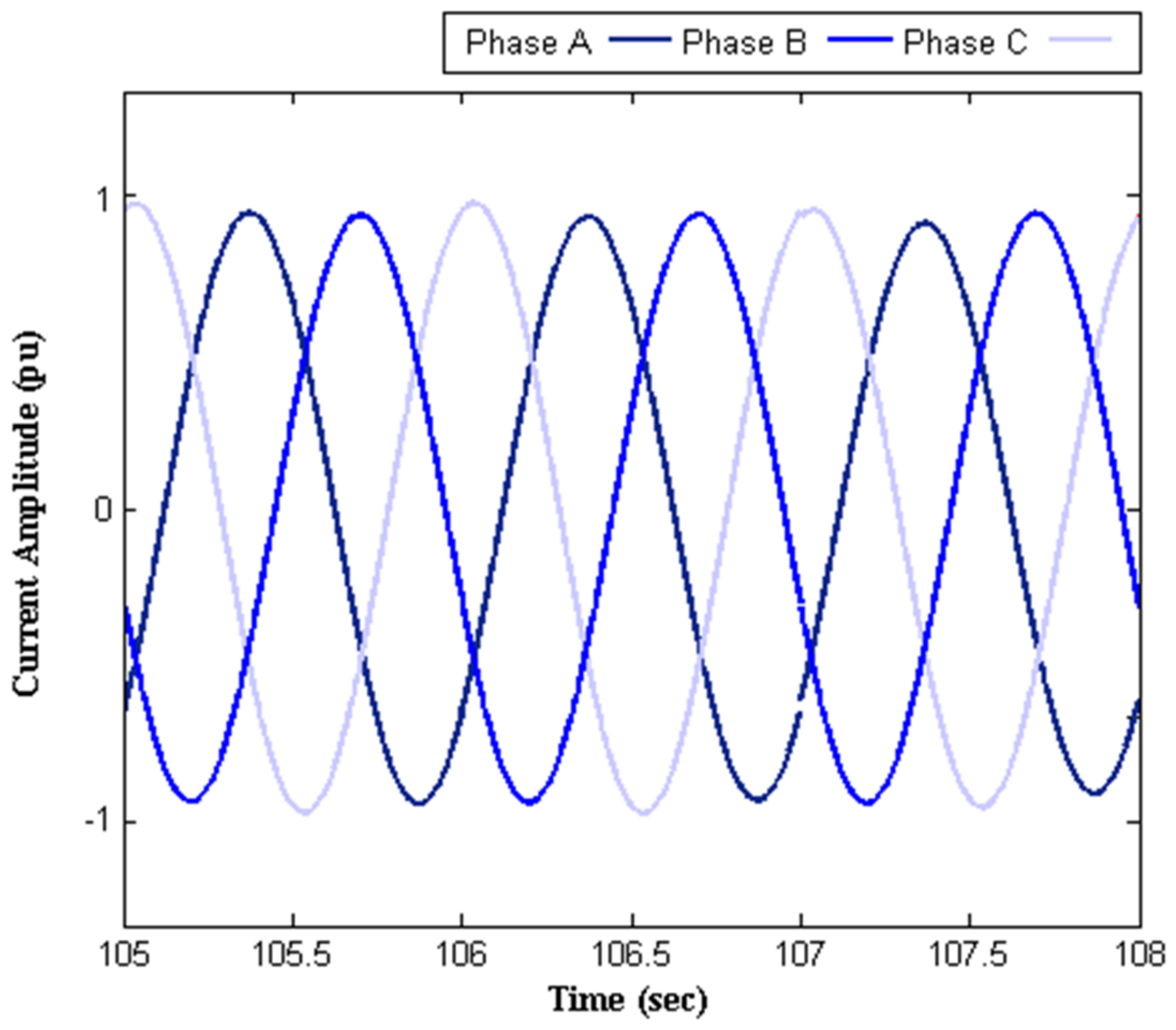
3.1. Network Current Balancing
3.2. Reactive Power Compensation
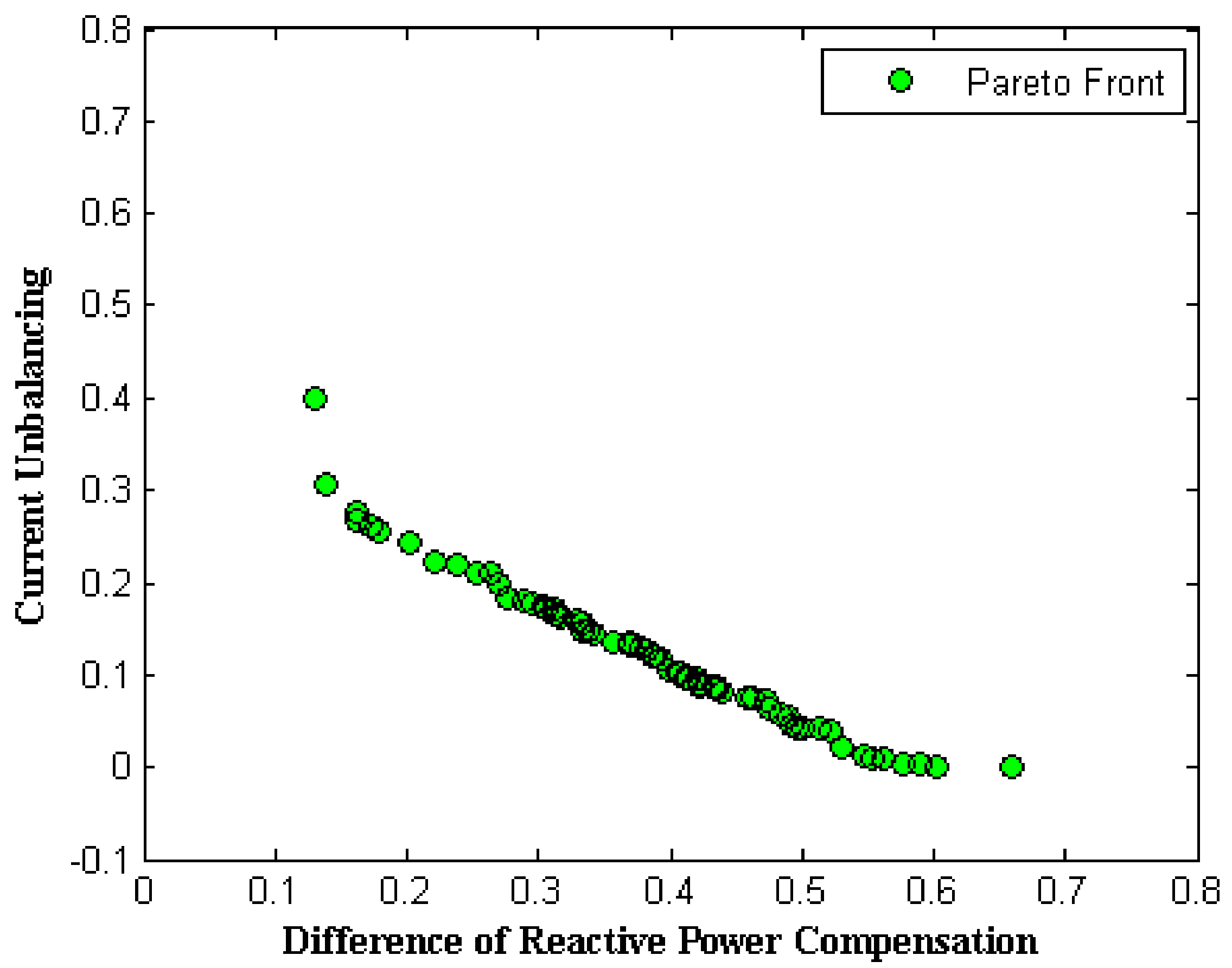
4. Multi-Objective Optimization
4.1. Problem Definition
4.2. Non-Dominated Sorting Genetic Algorithm
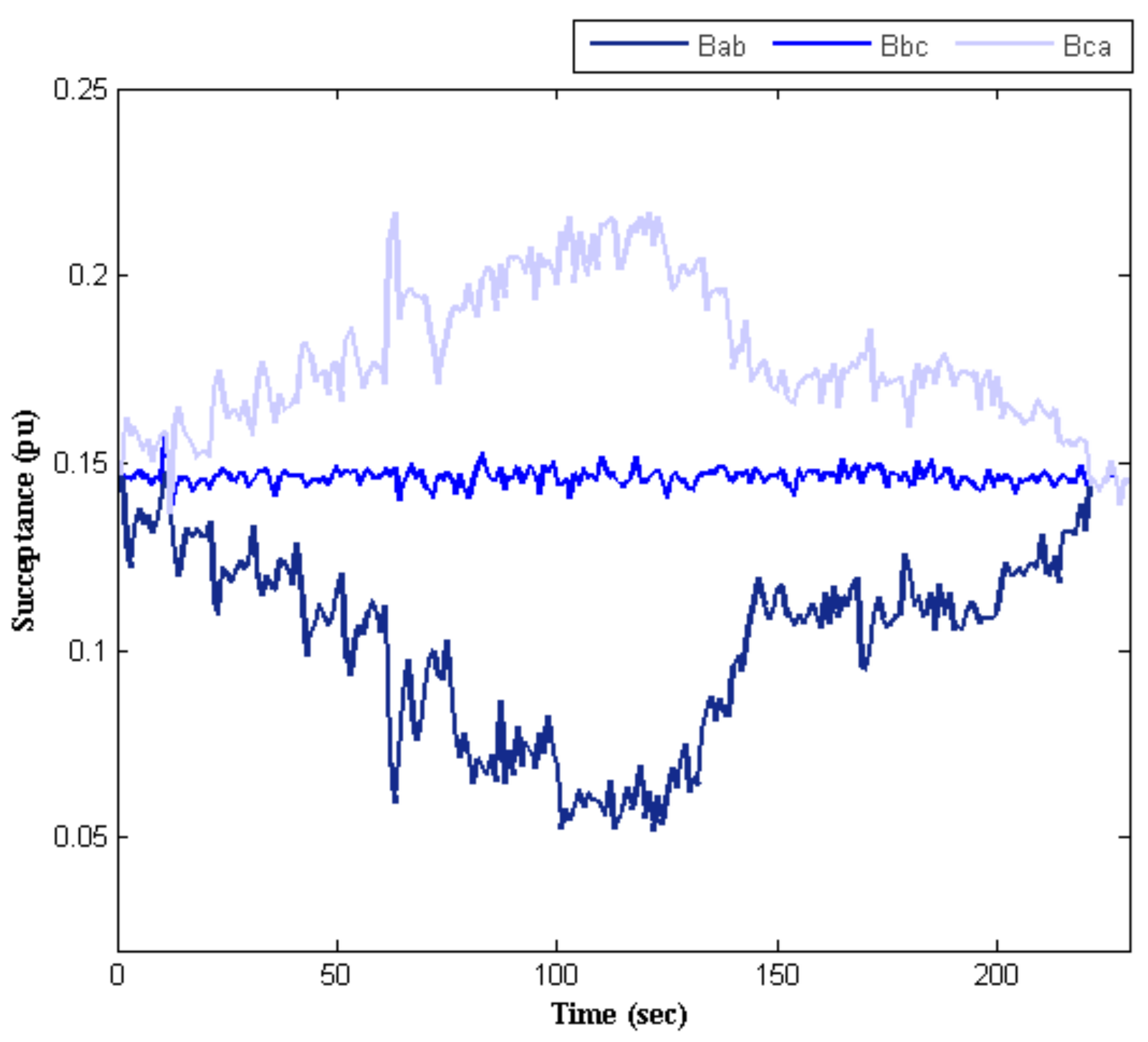
5. Simulation Results
6. Conclusions
Appendix A

Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Givoni, M. Development and impact of the modern high-speed train: A review. Transp. Rev. 2006, 26, 593–611. [Google Scholar] [CrossRef]
- He, Z.; Zheng, Z.; Hu, H. Power quality in high-speed railway systems. Int. J. Rail Transp. 2016, 4, 71–97. [Google Scholar] [CrossRef] [Green Version]
- Milešević, B.; Uglešić, I.; Filipović-Grčić, B. Power quality analysis in electric traction system with three-phase induction motors. Electr. Power Syst. Res. 2016, 138, 172–179. [Google Scholar] [CrossRef]
- Ciccarelli, F.; Fantauzzi, M.; Lauria, D.; Rizzo, R. Special transformers arrangement for AC railway systems. In Proceedings of the 2012 Electrical Systems for Aircraft, Railway and Ship Propulsion, Bologna, Italy, 16–18 October 2012. [Google Scholar]
- Terciyanli, A.; Acik, A.; Cetin, A.; Ermis, M.; Cadirci, I.; Ermis, C.; Demirci, T.; Bilgin, H.F. Power quality solutions for light rail public transportation systems fed by medium-voltage underground cables. IEEE Trans. Ind. Appl. 2012, 48, 1017–1029. [Google Scholar] [CrossRef]
- Zhao, T.; Peng, X. The AC traction power supply system for urban rail transit based on negative sequence current compensator. In Proceedings of the 2018 International Power Electronics Conference (IPEC-Niigata 2018-ECCE Asia), Niigata, Japan, 20–24 May 2018. [Google Scholar]
- Barros, L.A.M.; Tanta, M.; Martins, A.P.; Afonso, J.L.; Pinto, J.G. STATCOM evaluation in electrified railway using V/V and Scott power transformers. In Proceedings of the International Conference on Sustainable Energy for Smart Cities, Braga, Portugal, 4–6 December 2019. [Google Scholar]
- Roudsari, H.M.; Jalilian, A.; Jamali, S. Flexible fractional compensating mode for railway static power conditioner in a V/v traction power supply system. IEEE Trans. Ind. Electron. 2018, 65, 7963–7974. [Google Scholar] [CrossRef]
- Tanta, M.; Pinto, J.G.; Monteiro, V.; Martins, A.P.; Carvalho, A.S.; Afonso, J.L. A Comprehensive Comparison of Rail Power Conditioners Based on Two-Level Converters and a V/V Power Transformer in Railway Traction Power Systems. In Proceedings of the 7th Transport Research Arena Conference, Vienna, Austria, 16–19 April 2018; pp. 1–10. [Google Scholar]
- Tümay, M.; Demirdelen, T.; Bal, S.; Kayaalp, R.I.; Doğru, B.; Aksoy, M. A review of magnetically controlled shunt reactor for power quality improvement with renewable energy applications. Renew. Sustain. Energy Rev. 2017, 77, 215–228. [Google Scholar] [CrossRef]
- Pavleka, J.; Nikolovski, S.; Marušić, A. Using a FACTS Device as a Power Conditioner Suitable for Dynamic Reactive Power Compensation in Railway Application. Teh. Vjesn. 2019, 26, 1686–1693. [Google Scholar]
- Xiao, D.; Chen, M.; Chen, Y. Negative sequence current and reactive power comprehensive compensation for freight railway considering the impact of DFIGs. CPSS Trans. Power Electron. Appl. 2021, 6, 235–241. [Google Scholar] [CrossRef]
- Guiping, Z.; Jianye, C.; Xiaoyu, L. Compensation for the negative-sequence currents of electric railway based on SVC. In Proceedings of the 2008 3rd IEEE Conference on Industrial Electronics and Applications, Singapore, Singapore, 3–5 June 2008. [Google Scholar]
- Meidan, C.; Mingli, W. The switching transient simulation of SVC used in electric railway traction substation. In Proceedings of the 2009 International Conference on Sustainable Power Generation and Supply, Nanjing, China, 6–7 April 2009. [Google Scholar]
- Chen, S.-L.; Li, R.-J.; Hsi, P.-H. Traction system unbalance problem-analysis methodologies. IEEE Trans. Power Deliv. 2004, 19, 1877–1883. [Google Scholar] [CrossRef]
- Martinez, J.; Ramos, G. Reactive power and harmonic distortion control in electric traction systems. In Proceedings of the 2010 IEEE/PES Transmission and Distribution Conference and Exposition: Latin America (T&D-LA), São Paulo, Brazil, 8–10 November 2010. [Google Scholar]
- Jianzong, M.; Mingli, W.; Shaobing, Y. The application of SVC for the power quality control of electric railways. In Proceedings of the 2009 International Conference on Sustainable Power Generation and Supply, Nanjing, China, 6–7 April 2009. [Google Scholar]
- Wang, H.; Liu, Y.; Yan, K.; Fu, Y.; Zhang, C. Analysis of static VAr compensators installed in different positions in electric railways. IET Electr. Syst. Transp. 2015, 5, 129–134. [Google Scholar] [CrossRef]
- Habibolahzadeh, M.; Roudsari, H.M.; Jalilian, A.; Jamali, S. Hybrid SVC-HPQC scheme with partial compensation technique in co-phase electric railway system. In Proceedings of the 2019 27th Iranian Conference on Electrical Engineering (ICEE), Yazd, Iran, 30 April–2 May 2019. [Google Scholar]
- Chen, B.; Zhang, C.; Zeng, W.; Xue, G.; Tian, C.; Yuan, J. Electrical magnetic hybrid power quality compensation system for V/V traction power supply system. IET Power Electron. 2016, 9, 62–70. [Google Scholar] [CrossRef]
- Bai, X.; Peng, J.; He, X. Design of Comprehensive Compensation System for Railway Power Distribution System. In Proceedings of the 2020 IEEE 9th International Power Electronics and Motion Control Conference (IPEMC2020-ECCE Asia), Nanjing, China, 31 May–3 June 2020. [Google Scholar]
- Amira, C.R.; Ramdane, B.; Hamza, B.; Meriem, A.; Imen, M. Genetic Algorithm Approach of HB-RPC for Adaptive Power Quality Improvement in Railway Traction Chain. In Proceedings of the 2021 International Conference on Electrical, Communication, and Computer Engineering (ICECCE), Kuala Lumpur, Malaysia, 12–13 June 2021. [Google Scholar]
- Fang, L.; Xu, X.; Fang, H.; Xiao, Y. Negative-sequence current compensation of power quality compensator for high-speed electric railway. In Proceedings of the 2014 IEEE Conference and Expo Transportation Electrification Asia-Pacific (ITEC Asia-Pacific), Beijing, China, 31 August–3 September 2014. [Google Scholar]
- Sekhar, G.C.; Kale, V.; Krishna, G.V. Application of DVR to improve voltage profile of indian railway traction system. In Proceedings of the 2014 6th IEEE Power India International Conference (PIICON), Delhi, India, 5–7 December 2014. [Google Scholar]
- Liu, L.; Dai, N.; Lao, K.W.; Song, Y. Nonuniform Power Factor Partial Compensation for Compensating Current Reduction Using Particle Swarm Optimization in Traction Power Supply System. IEEE Trans. Ind. Electron. 2021, 69, 6140–6151. [Google Scholar] [CrossRef]
- Andrusca, M.; Adam, M.; Dragomir, A.; Lunca, E. Innovative Integrated Solution for Monitoring and Protection of Power Supply System from Railway Infrastructure. Sensors 2021, 21, 7858. [Google Scholar] [CrossRef]
- Raygani, S.; Tahavorgar, A.; Fazel, S.; Moaveni, B. Load flow analysis and future development study for an AC electric railway. IET Electr. Syst. Transp. 2012, 2, 139–147. [Google Scholar] [CrossRef]
- Bigharaz, M.H.; Hosseinian, S.H.; Afshar, A.; Suratgar, A.A.; Dehcheshmeh, M.A. A comprehensive simulator of AC autotransformer electrified traction system. Int. J. Power Energy Convers. 2019, 10, 129–147. [Google Scholar] [CrossRef]
- Dehcheshmeh, M.A.; Hosseinian, S.H.; Bigharaz, M.H.; Mohseni, K. Analysis of lightning transient in 2× 25 kV AC autotransformer traction system. Int. J. Power Energy Convers. 2018, 9, 89–103. [Google Scholar] [CrossRef]
- Mariscotti, A.; Pozzobon, P.; Vanti, M. Simplified Modeling of 2x25-kV AT Railway System for the Solution of Low Frequency and Large-Scale Problems. IEEE Trans. Power Deliv. 2007, 22, 296–301. [Google Scholar] [CrossRef]
- Thomas, R. Reactive power compensation in electrical traction Using Active impedance concepts. In Proceedings of the 2013 International Conference on Circuits, Power and Computing Technologies (ICCPCT), Nagercoil, India, 20–21 March 2013. [Google Scholar]
- Saini, D.K.; Venkatasubramanian, B.V.; Yadav, M. Effect of Unaccounted Parameters on Reactive Power Compensation in Indian Electric Traction Line. IEEE Access 2020, 8, 182679–182692. [Google Scholar] [CrossRef]
- Chu, W.-S.; Gu, J.-C. A new hybrid SVC scheme with Scott transformer for balance improvement. In Proceedings of the American Society of Mechanical Engineers (ASME)/IEEE Joint Rail Conference, Atlanta, GA, USA, 4–6 April 2006. [Google Scholar]
- Lee, G.-S.; Hwang, P.-I.; Lee, B.-G.; Moon, S.-I. Loss Minimization of Electrified Railway Traction Systems Using SVC Based on Particle Swarm Optimization. IEEE Access 2020, 8, 219680–219689. [Google Scholar] [CrossRef]
- Lao, K.W.; Wong, M.C.; Santoso, S. Recent advances of FACTS devices for power quality compensation in railway traction power supply. In Proceedings of the 2018 IEEE/PES Transmission and Distribution Conference and Exposition (T&D), Denver, CO, USA, 16–19 April 2018. [Google Scholar]
- Vedam, R.S.; Sarma, M.S. Control of static Var compensators. In Power quality: Var Compensation in Power Systems, 1th ed.; CRC press: Boca Raton, FL, USA, 2008. [Google Scholar]
- Morais, V.A.; Afonso, J.L.; Carvalho, A.S.; Martins, A.P. New Reactive Power Compensation Strategies for Railway Infrastructure Capacity Increasing. Energies 2020, 13, 4379. [Google Scholar] [CrossRef]
- Wang, D.; Wang, J.; Yang, C.; Zhang, X.; Li, G. Research on Application of TCR+ FC Typed SVC in Power Quality Integrated Management for Power Traction System. In Proceedings of the International Conference on Sustainable Power Generation and Supply (SUPERGEN), Hangzhou, China, 8–9 September 2012. [Google Scholar]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef] [Green Version]
- Li, Y.; Wang, S.; Duan, X.; Liu, S.; Liu, J.; Hu, S. Multi-objective energy management for Atkinson cycle engine and series hybrid electric vehicle based on evolutionary NSGA-II algorithm using digital twins. Energy Convers. Manag. 2021, 230, 113788. [Google Scholar] [CrossRef]
- Xing, C.; Li, K.; Zhang, L.; Li, W. Optimal compensation control of railway co-phase traction power supply integrated with renewable energy based on NSGA-II. IET Renew. Power Gener. 2020, 14, 3668–3678. [Google Scholar] [CrossRef]





| TSS | AT | Train | |||
|---|---|---|---|---|---|
| Primary voltage | 230 kV | Rated Voltage | 25 kV | Rated Power | 4 MVA |
| Secondary voltage | 25 kV | Leakage Impedances | 0.1564 + j0.0997 Ω | Power Factor | 0.7 |
| Rated Power | 16.5 MVA | Rated Power | 5 MVA | Mass | 200 tons |
| Sol. | Objective Space | Decision Space | Running Time | |||
| Obj. I | Obj. II | 0.893 sec (in time interval (910) sec of simulator running) | ||||
| 1 | 0.050135 | 0.309336 | 0.147019 | 0.194459 | 0.228315 | |
| 2 | 0.245369 | 0.182319 | 0.182085 | 0.197768 | 0.214491 | |
| 3 | 0.127370 | 0.258360 | 0.160946 | 0.196607 | 0.222621 | |
| 4 | 0.252364 | 0.177715 | 0.185536 | 0.197619 | 0.216171 | |
| 5 | 0.054233 | 0.306107 | 0.149850 | 0.196143 | 0.229902 | |
| 6 | 0.312023 | 0.139873 | 0.201127 | 0.197404 | 0.217196 | |
| 7 | 0.320461 | 0.134344 | 0.199656 | 0.198789 | 0.213597 | |
| 8 | 0.465730 | 0.039019 | 0.223266 | 0.199745 | 0.200516 | |
| 9 | 0.339299 | 0.121827 | 0.194002 | 0.199469 | 0.203125 | |
| 10 | 0.271779 | 0.165950 | 0.193625 | 0.197261 | 0.219731 | |
| Without SVC | Amplitude Deviation | −23% | |
| −9.9% | |||
| −4.8% | |||
| Phase Deviation | −8.5% | ||
| +11.6% | |||
| + 4.1% | |||
| With SVC | Amplitude Deviation | −1.8% | |
| −0.2% | |||
| +0.9% | |||
| Phase Deviation | +1% | ||
| −0.5% | |||
| +1.5% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bigharaz, M.H.; Dehcheshmeh, M.A.; Givi, H.; Hubálovský, Š. Multi-Objective Real-Time Tuning of SVC Used in Electrified Traction Systems. Sensors 2022, 22, 1584. https://doi.org/10.3390/s22041584
Bigharaz MH, Dehcheshmeh MA, Givi H, Hubálovský Š. Multi-Objective Real-Time Tuning of SVC Used in Electrified Traction Systems. Sensors. 2022; 22(4):1584. https://doi.org/10.3390/s22041584
Chicago/Turabian StyleBigharaz, Mohammad Hossein, Mehdi Amiri Dehcheshmeh, Hadi Givi, and Štěpán Hubálovský. 2022. "Multi-Objective Real-Time Tuning of SVC Used in Electrified Traction Systems" Sensors 22, no. 4: 1584. https://doi.org/10.3390/s22041584
APA StyleBigharaz, M. H., Dehcheshmeh, M. A., Givi, H., & Hubálovský, Š. (2022). Multi-Objective Real-Time Tuning of SVC Used in Electrified Traction Systems. Sensors, 22(4), 1584. https://doi.org/10.3390/s22041584






