An Optical Fiber Sensor for Axial Strain, Curvature, and Temperature Measurement Based on Single-Core Six-Hole Optical Fiber
Abstract
:1. Introduction
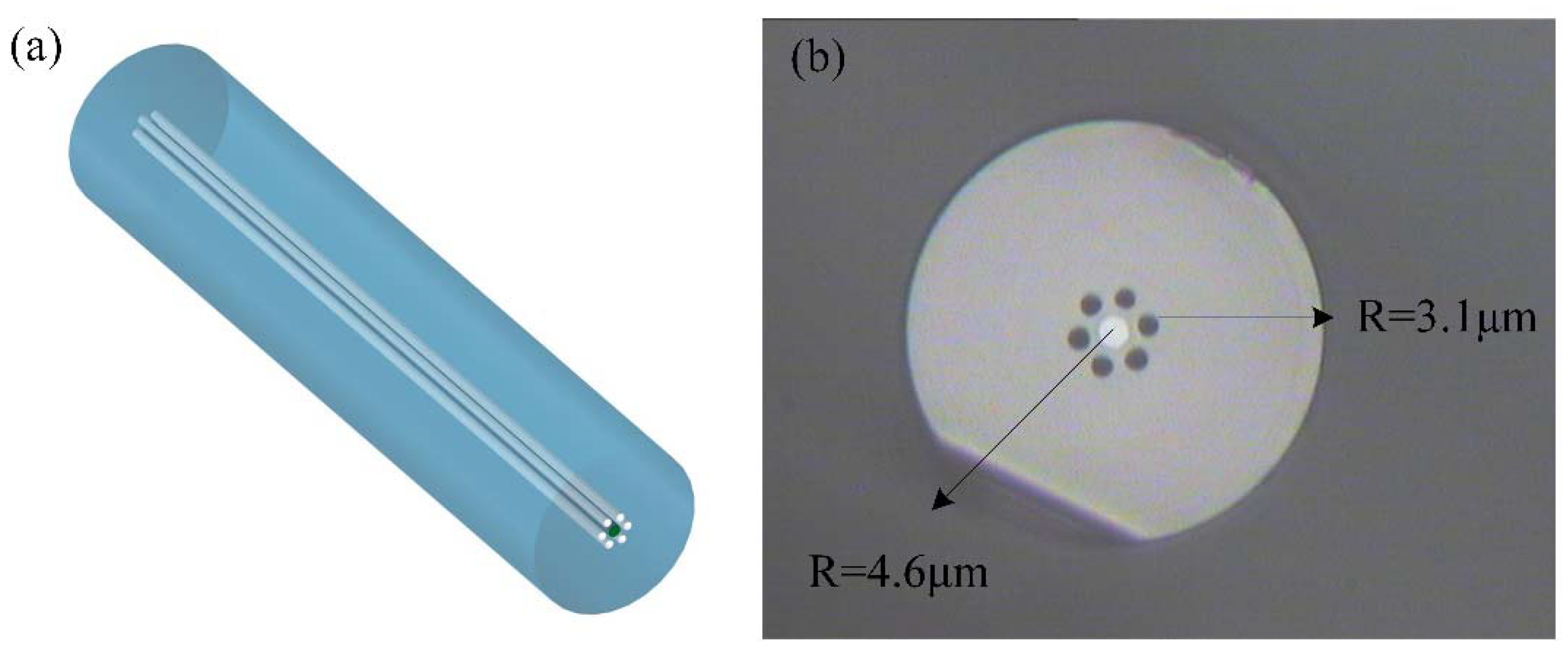
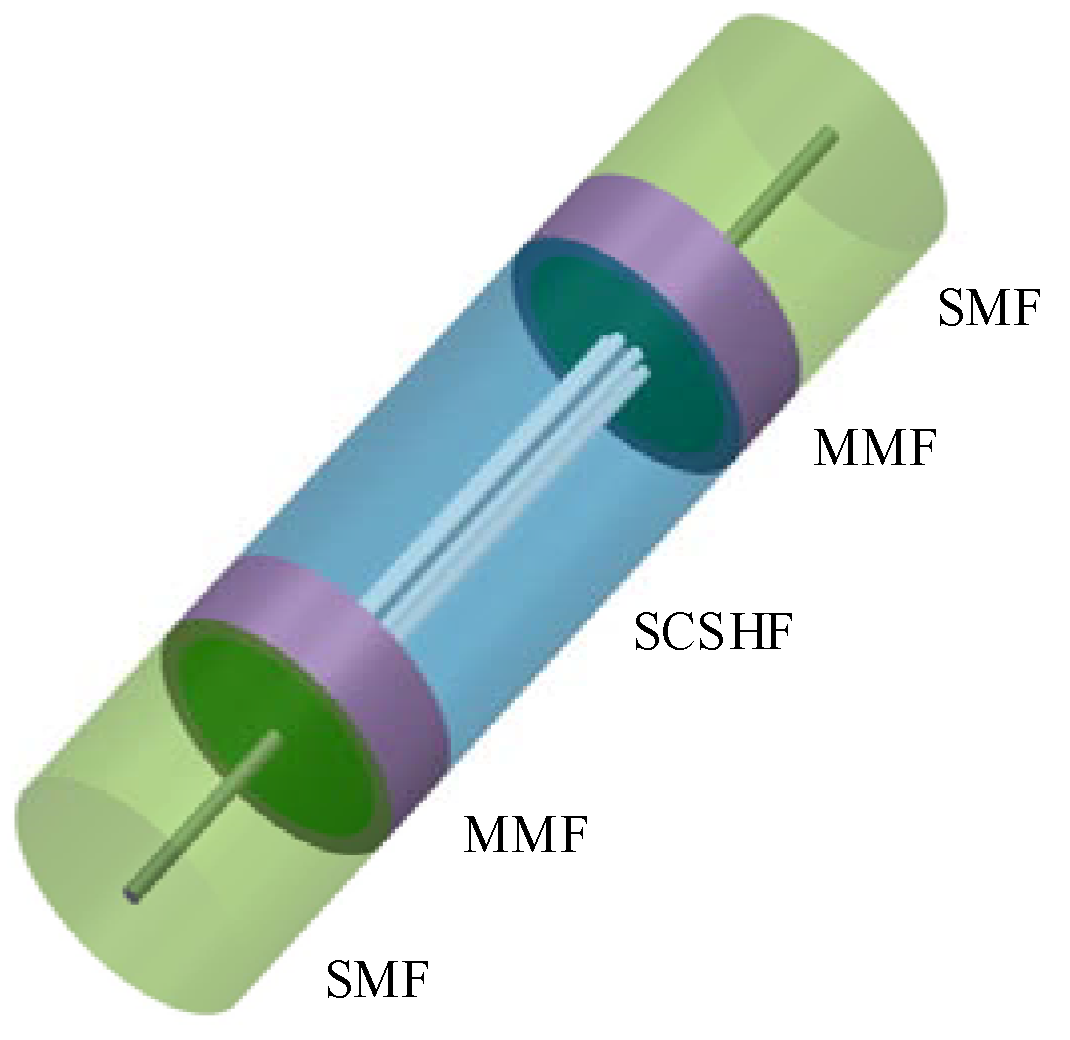
2. Fabrication and Principles
2.1. Fabrication
2.2. Principles
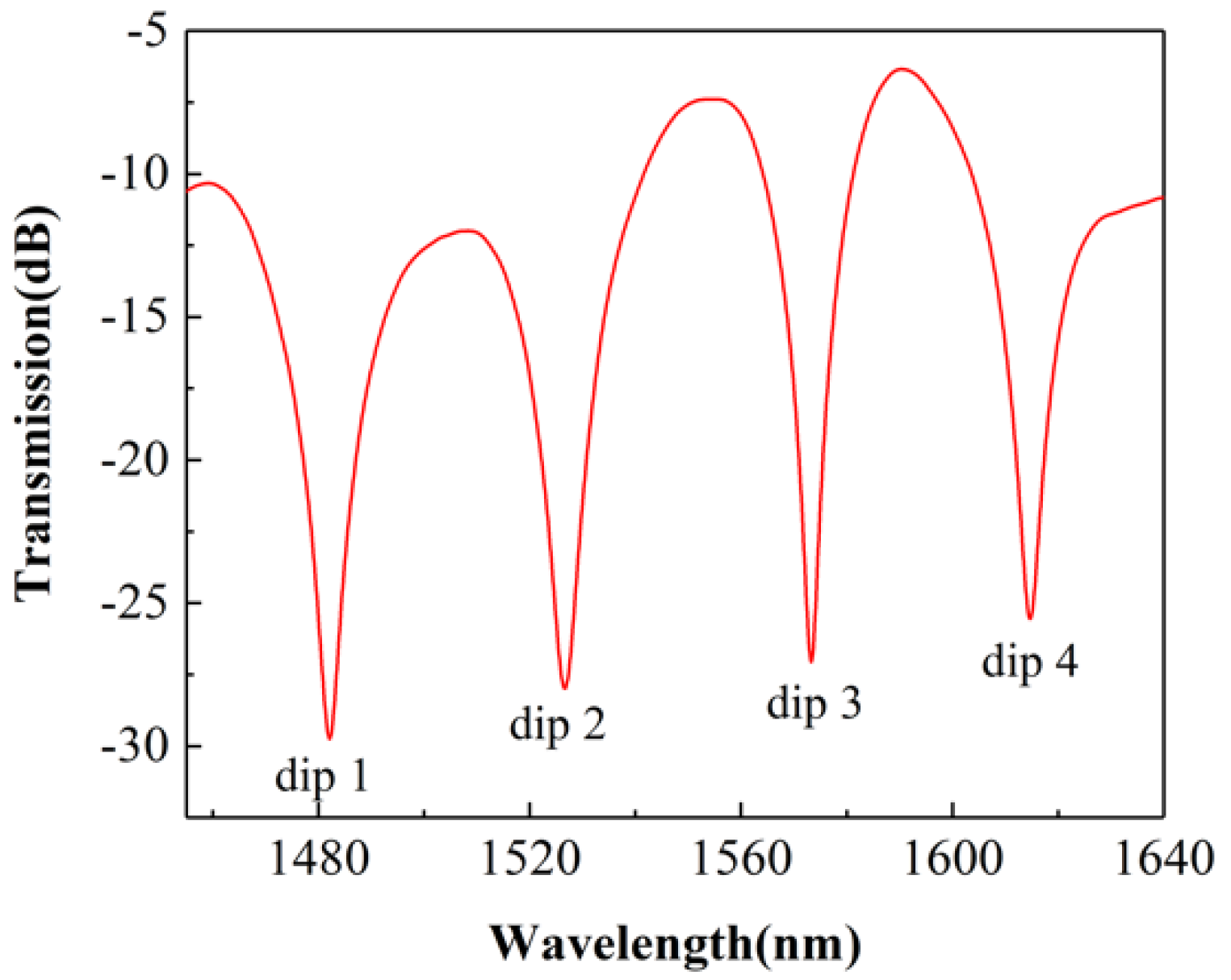
3. Experimental Results
3.1. Strain Sensing Experiment
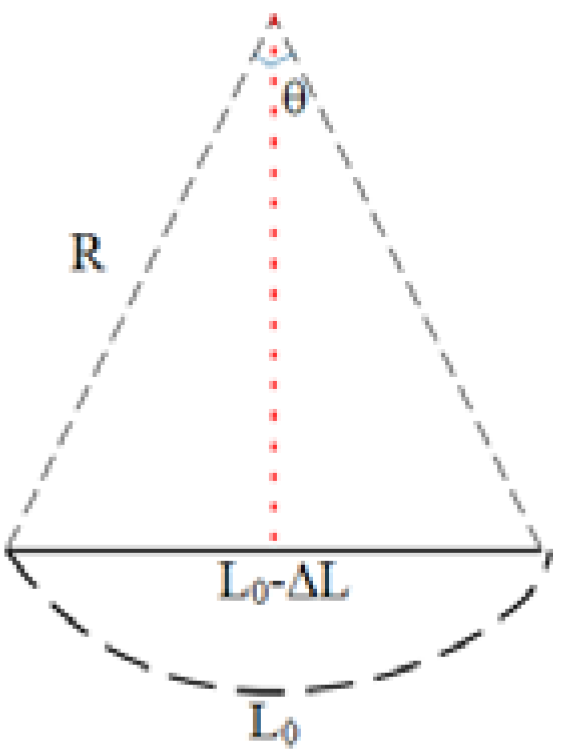
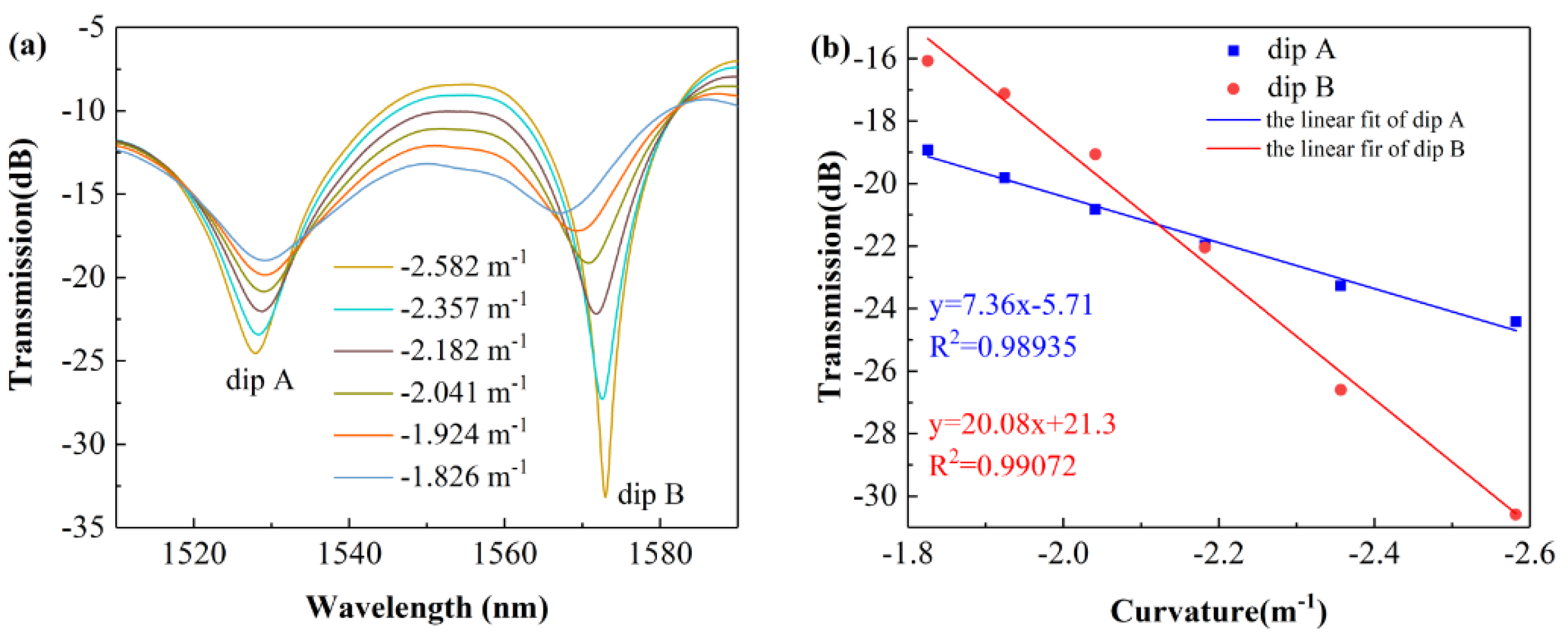
3.2. Curvature Sensing Experiment
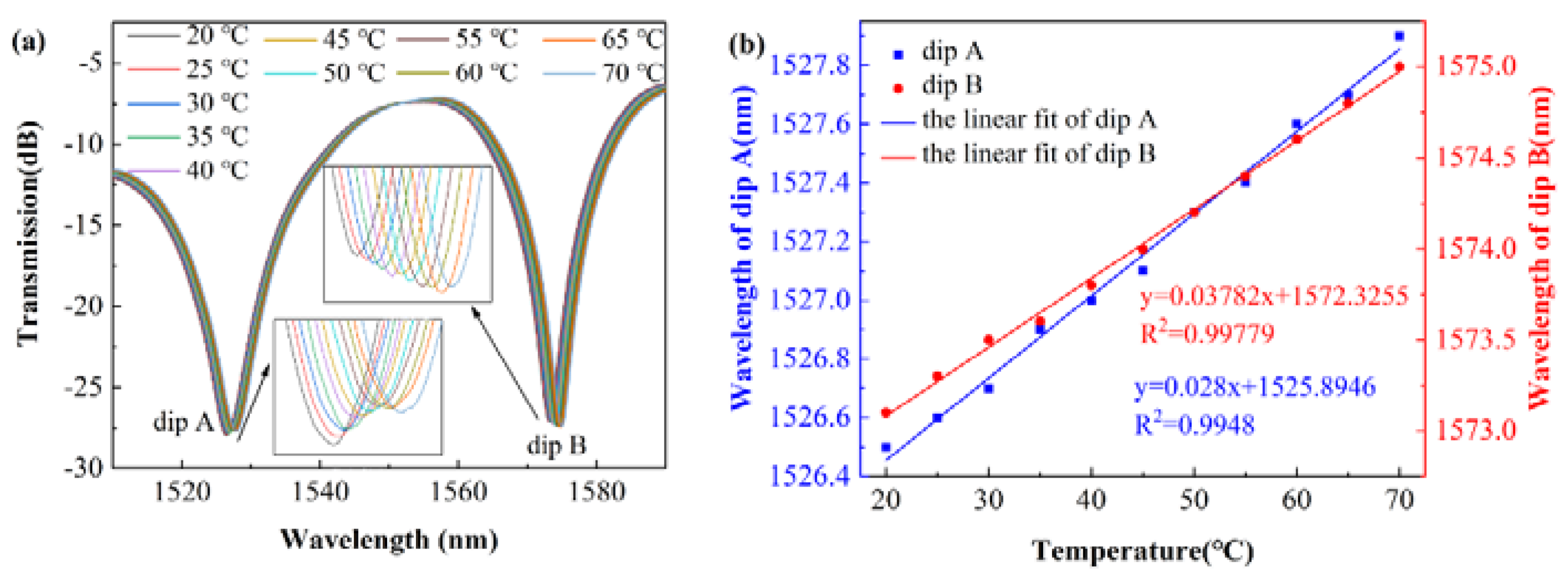
3.3. Temperature Sensing Experiment
3.4. Theoretical Analysis of Simultaneous Measurement
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Tang, J.L.; Wang, J.N. Chemical sensing sensitivity of long-period grating sensor enhanced by colloidal gold nanoparticles. Sensors 2008, 8, 171–184. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Campanella, C.E.; Giorgini, A.; Avino, S.; Malara, P.; Zullo, R.; Gagliardi, G.; De, N.P. Localized strain sensing with fiber Bragg-grating ring cavities. Opt. Express 2013, 21, 29435–29441. [Google Scholar] [CrossRef] [PubMed]
- Lim, J.H.; Jang, H.S.; Lee, K.S.; Kim, J.C.; Lee, B.H. Mach-Zehnder interferometer formed in a photonic crystal fiber based on a pair of long-period fiber gratings. Opt. Lett. 2004, 29, 346–348. [Google Scholar] [CrossRef] [PubMed]
- Villatoro, J.; Finazzi, V.; Minkovich, V.P.; Pruneri, V.; Badenes, G. Temperature-insensitive photonic crystal fiber interferometer for absolute strain sensing. Appl. Phys. Lett. 2007, 91, 091109. [Google Scholar] [CrossRef]
- Chen, G.; Liu, L.; Jia, H.; Yu, J.; Lei, X.; Wang, W. Simultaneous strain and temperature measurements with fiber Bragg grating written in novel Hi-Bi optical fiber. IEEE Photon. Technol. Lett. 2004, 16, 221–223. [Google Scholar] [CrossRef]
- Zhang, S.; Deng, S.; Geng, T.; Sun, C.; Niu, H.; Li, X.; Wang, Z.; Li, X.; Ma, Y.; Yang, W.; et al. A miniature ultra-long period fiber grating for simultaneous measurement of axial strain and temperature. Opt. Laser Technol. 2020, 126, 106121. [Google Scholar] [CrossRef]
- Song, M.I.; Yin, S.; Ruffin, P.B. Fiber Bragg grating strain sensor demodulation with quadrature sampling of a Mach-Zehnder interferometer. Appl. Opt. 2000, 39, 1106–1111. [Google Scholar] [CrossRef]
- Xia, P.; Tan, Y.; Yang, C.; Zhou, Z.; Yun, K. A Composite Fabry-Perot Interferometric Sensor with the Dual-Cavity Structure for Simultaneous Measurement of High Temperature and Strain. Sensors 2021, 21, 4989. [Google Scholar] [CrossRef]
- Liu, Y.; Liu, B.; Miao, Y.; Zhang, H.; Liu, J. Effect of bending and orientation on the fiber modal Mach-Zehnder interferometer. Microwave Opt. Technol. Lett. 2011, 54, 136–139. [Google Scholar] [CrossRef]
- Zhang, J.; Zhang, W.; Zhang, Y.; Wang, B.; Xue, Y.; Yan, T.; Chen, L.; Wang, L. Bending vector sensor based on Mach-Zehnder interferometer using S type fibre taper and lateral-offset. J. Mod. Opt. 2016, 63, 2146–2150. [Google Scholar] [CrossRef]
- Broadway, C.; Min, R.; Leal-Junior, A.G.; Marques, C.; Caucheteur, C. Toward commercial polymer fiber Bragg grating sensors: Review and applications. J. Lightwave Technol. 2019, 37, 2605–2615. [Google Scholar] [CrossRef]
- Yao, K.; Lin, Q.; Jiang, Z.; Zhao, N.; Peng, G.-D.; Tian, B.; Jia, W.; Yang, P. Design and Analysis of a Combined Strain–Vibration–Temperature Sensor with Two Fiber Bragg Gratings and a Trapezoidal Beam. Sensors 2019, 19, 3571. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Li, R.; Chen, Y.; Tan, Y.; Zhou, Z.; Li, T.; Mao, J. Sensitivity Enhancement of FBG-Based Strain Sensor. Sensors 2018, 18, 1607. [Google Scholar] [CrossRef] [Green Version]
- Zhou, W.; Wong, W.C.; Chan, C.C.; Shao, L.-Y.; Dong, X. Highly sensitive fiber loop ringdown strain sensor using photonic crystal fiber interferometer. Appl. Opt. 2011, 50, 3087–3092. [Google Scholar] [CrossRef]
- Dong, X.; Du, H.; Sun, X.; Luo, Z.; Duan, J.A. A novel strain sensor with large measurement range based on all fiber mach-zehnder interferometer. Sensors 2018, 18, 1549. [Google Scholar] [CrossRef] [Green Version]
- Zhang, H.; Wu, Z.; Shum, P.; Din, X.; Low, C.; Xu, Z.; Wang, R.; Shao, X.; Fu, S.; Tong, W.; et al. Highly sensitive strain sensor based on helical structure combined with Mach-Zehnder interferometer in multicore fiber. Sci. Rep. 2017, 7, 46633. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhang, C.; Ning, T.; Li, J.; Zheng, J.; Gao, X.; Pei, L. Refractive index and strain sensor based on twin-core fiber with a novel T-shaped taper. Opt. Fiber Technol. 2018, 102, 12–16. [Google Scholar] [CrossRef]
- Leal-Junior, A.G.; Frizera, A.; Marques, C.; Sánchez, M.R.A.; Santos, W.M.d.; Siqueira, A.A.G.; Segatto, M.V.; Pontes, M.J.; Pontes, M.J. Polymer Optical Fiber for Angle and Torque Measurements of a Series Elastic Actuator’s Spring. J. Lightwave Technol. 2018, 36, 1698–1705. [Google Scholar] [CrossRef]
- Dong, L.; Gang, T.; Bian, C.; Tong, R.; Wang, J.; Hu, M. A high sensitivity optical fiber strain sensor based on hollow core tapering. Opt. Fiber Technol. 2020, 56, 102179. [Google Scholar] [CrossRef]
- Liu, S.; Yang, K.; Wang, Y.; Qu, J.; Liao, C.; He, J.; Li, Z.; Yin, G.; Sun, B.; Zhou, J. High-sensitivity strain sensor based on an in-fiber rectangular air bubble. Sci. Rep. 2015, 5, 1–7. [Google Scholar] [CrossRef] [Green Version]
- Fan, R.; Li, L.; Zhuo, Y.; Lv, X.; Ren, Z.; Shen, J.; Peng, B. Practical research on photonic crystal fiber micro-strain sensor. Opt. Fiber Technol. 2019, 52, 101959. [Google Scholar] [CrossRef]
- Leal-Junior, A.; Frizera, A.; Marques, C.; Pontes, M.J. Polymer-optical-fiber-based sensor system for simultaneous measurement of angle and temperature. Appl. Opt. 2018, 57, 1717–1723. [Google Scholar] [CrossRef] [PubMed]
- Ni, W.; Lu, P.; Fu, X.; Wang, S.; Sun, Y.; Liu, D.; Zhang, J. Highly Sensitive Optical Fiber Curvature and Acoustic Sensor Based on Thin Core Ultralong Period Fiber Grating. IEEE Photonics J. 2017, 9, 1–9. [Google Scholar] [CrossRef]
- Liu, Z.; Shen, C.; Xiao, Y.; Gong, J.; Wang, Y.; Lang, T.; Zhang, Y.; Xu, W.; Jing, Z.; Jin, Y.; et al. Sensitivity-Enhanced Strain Sensor Based on Thin-Core Fiber Modal Interferometer Interacted With Tilted Fiber Bragg Grating. IEEE Sens. J. 2019, 19, 1802–1806. [Google Scholar] [CrossRef]
- Qureshi, K.K.; Liu, Z.; Tam, H.w.; Zia, M.F. A strain sensor based on in-line fiber Mach–Zehnder interferometer in twin-core photonic crystal fiber. Opt. Commun. 2013, 309, 68–70. [Google Scholar] [CrossRef]
- Jasim, A.A.; Hayashi, N.; Harun, S.W.; Ahmad, H.; Penny, R.; Mizuno, Y.; Nakamura, K. Refractive index and strain sensing using inline Mach–Zehnder interferometer comprising perfluorinated graded-index plastic optical fiber. Sens. Actuator A Phys. 2014, 219, 94–99. [Google Scholar] [CrossRef]
- Yang, H.Z.; Qiao, X.G.; Wang, Y.P.; Ali, M.M.; Lai, M.H.; Lim, K.S.; Ahmad, H. In-fiber gratings for simultaneous monitoring temperature and strain in ultrahigh temperature. IEEE Photon. Technol. Lett. 2014, 27, 58–61. [Google Scholar] [CrossRef]
- Huang, T.; Fu, S.; Ke, C.; Shum, P.P.; Liu, D. Characterization of fiber Bragg grating inscribed in few-mode silica-germanate fiber. IEEE Photonics Technol. Lett. 2014, 26, 1908–1911. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, W.; Zhang, Y.; Wang, S.; Yu, L.; Yan, Y. Simultaneous measurement of curvature and temperature based on LP 11 mode Bragg grating in seven-core fiber. Meas. Sci. Technol. 2017, 28, 055101. [Google Scholar] [CrossRef]
- Ni, K.; Li, T.; Hu, L.; Qian, W.; Zhang, Q.; Jin, S. Temperature-independent curvature sensor based on tapered photonic crystal fiber interferometer. Opt. Commun. 2014, 24, 5148–5150. [Google Scholar] [CrossRef]
- Cui, W.; Si, J.; Chen, T.; Hou, X. Compact bending sensor based on a fiber Bragg grating in an abrupt biconical taper. Opt. Express 2015, 23, 11031–11036. [Google Scholar] [CrossRef] [PubMed]







| SMF | MMF | |
|---|---|---|
| Core diameter | 9.2 μm | 105 μm |
| Cladding diameter | 125 μm | 125 μm |
| EFI of core | 1.4509 | 1.4509 |
| EFI of cladding | 1.444 | 1.444 |
| Wavelength | 1.55 μm | 1.55 μm |
| SMF | MMF | SCSHF | |
|---|---|---|---|
| Core diameter | 9.2 μm | 105 μm | 9.2 μm |
| Cladding diameter | 125 μm | 125 μm | 125 μm |
| EFI of core | 1.4509 | 1.4509 | 1.4509 |
| EFI of cladding | 1.444 | 1.444 | 1.444 |
| Distance between air hole and core | - | - | 10 μm |
| Length | 50 μm | 400 μm | 1 cm |
| Wavelength | 1.55 μm | 1.55 μm | 1.55 μm |
| Structure | Strain Sensitivity (pm/με) | Temperature Sensitivity (pm/°C) | Curvature Sensitivity (dB/m−1) | Temperature Cross Sensitivity | Reference |
|---|---|---|---|---|---|
| FBG-MMF | 0.12 | 9 | low | [24] | |
| TCF-TFBG | 0.67 | 33 | low | [25] | |
| TC-PCF | 0.31 | 6.68 | low | [26] | |
| HCPCF | −0.81 | - | high | [27] | |
| FMF-FBG | 0.91 | 11.5 | low | [28] | |
| 7CF-FBG | 12 | −7.28 | [29] | ||
| SMF-PCF | 8.35 | low | [30] | ||
| Taper-FBG | 10 | 0.1196 | [31] | ||
| SCSHF | −1.05 | 37.82 | 20.08 | low | This work |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Y.; Yu, C.; Lu, P. An Optical Fiber Sensor for Axial Strain, Curvature, and Temperature Measurement Based on Single-Core Six-Hole Optical Fiber. Sensors 2022, 22, 1666. https://doi.org/10.3390/s22041666
Li Y, Yu C, Lu P. An Optical Fiber Sensor for Axial Strain, Curvature, and Temperature Measurement Based on Single-Core Six-Hole Optical Fiber. Sensors. 2022; 22(4):1666. https://doi.org/10.3390/s22041666
Chicago/Turabian StyleLi, Yujian, Changyuan Yu, and Ping Lu. 2022. "An Optical Fiber Sensor for Axial Strain, Curvature, and Temperature Measurement Based on Single-Core Six-Hole Optical Fiber" Sensors 22, no. 4: 1666. https://doi.org/10.3390/s22041666
APA StyleLi, Y., Yu, C., & Lu, P. (2022). An Optical Fiber Sensor for Axial Strain, Curvature, and Temperature Measurement Based on Single-Core Six-Hole Optical Fiber. Sensors, 22(4), 1666. https://doi.org/10.3390/s22041666








