Experimental Investigation of Vibration Analysis on Implant Stability for a Novel Implant Design
Abstract
:1. Introduction
2. Materials and Methods
2.1. Specimens
2.2. Experimental Setup
3. Results
3.1. Determination of Upper Frequency Bound
3.2. Triangular–Shaped Implant
3.2.1. Colormap of Magnitude
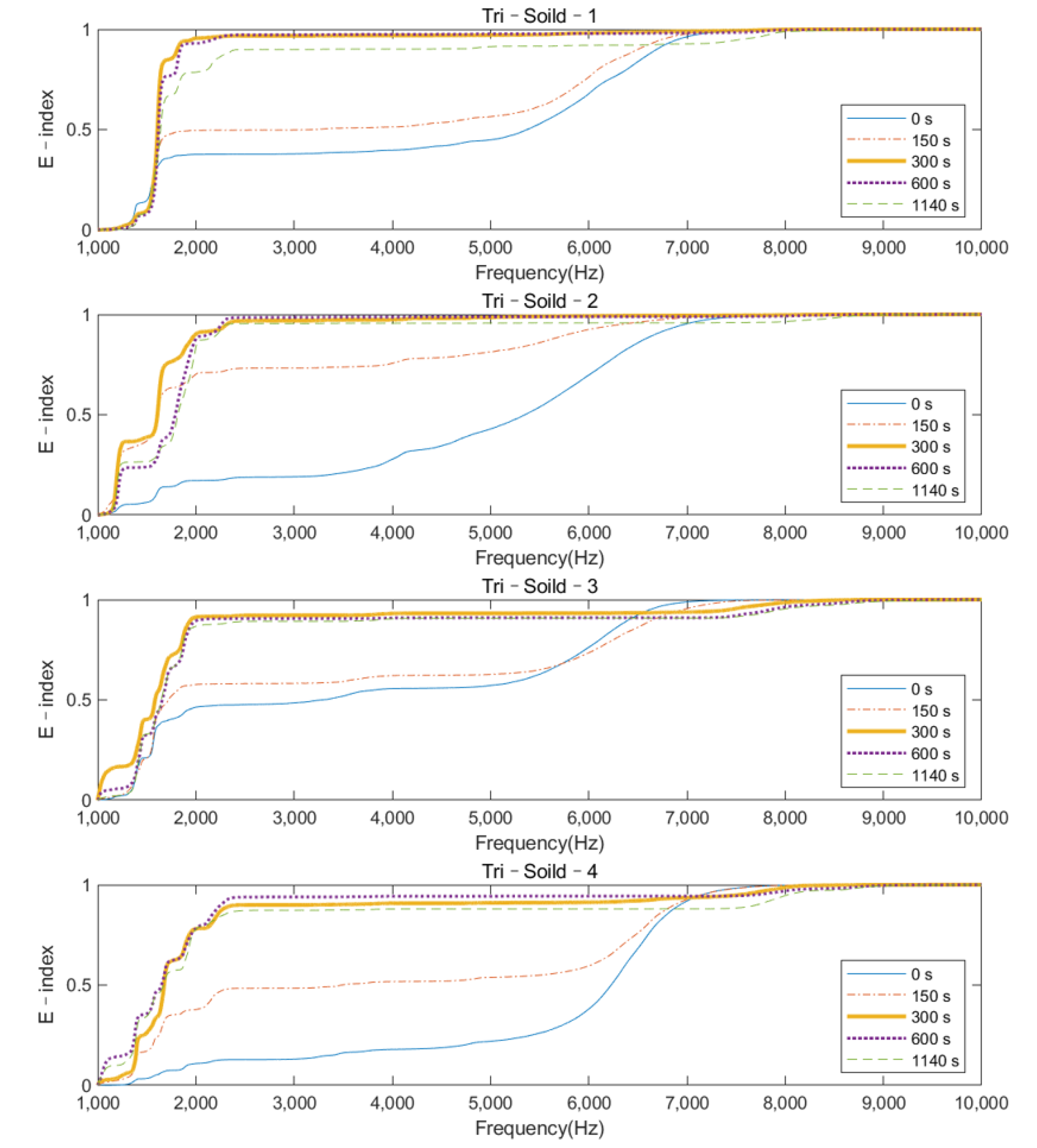
3.2.2. E–Index against Frequency
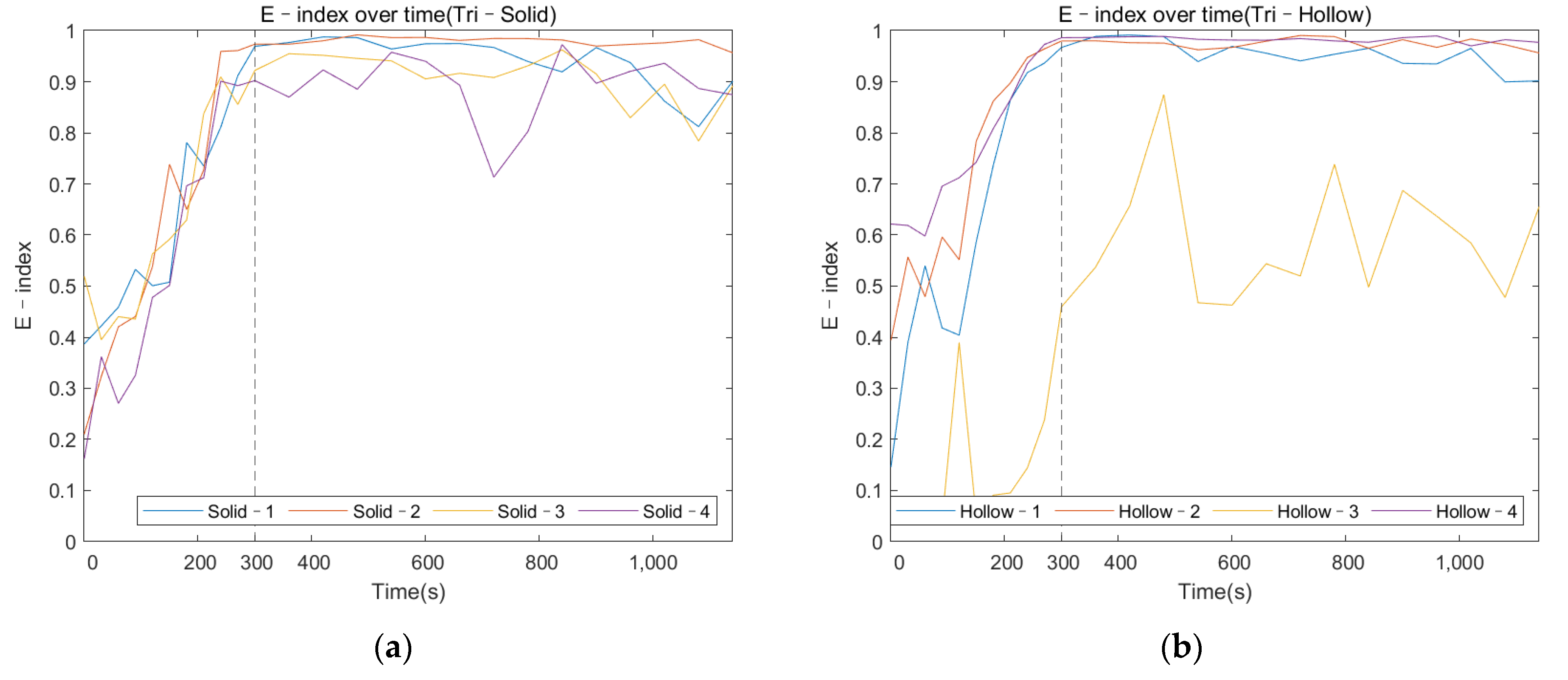
3.2.3. E–Index against Cure Time
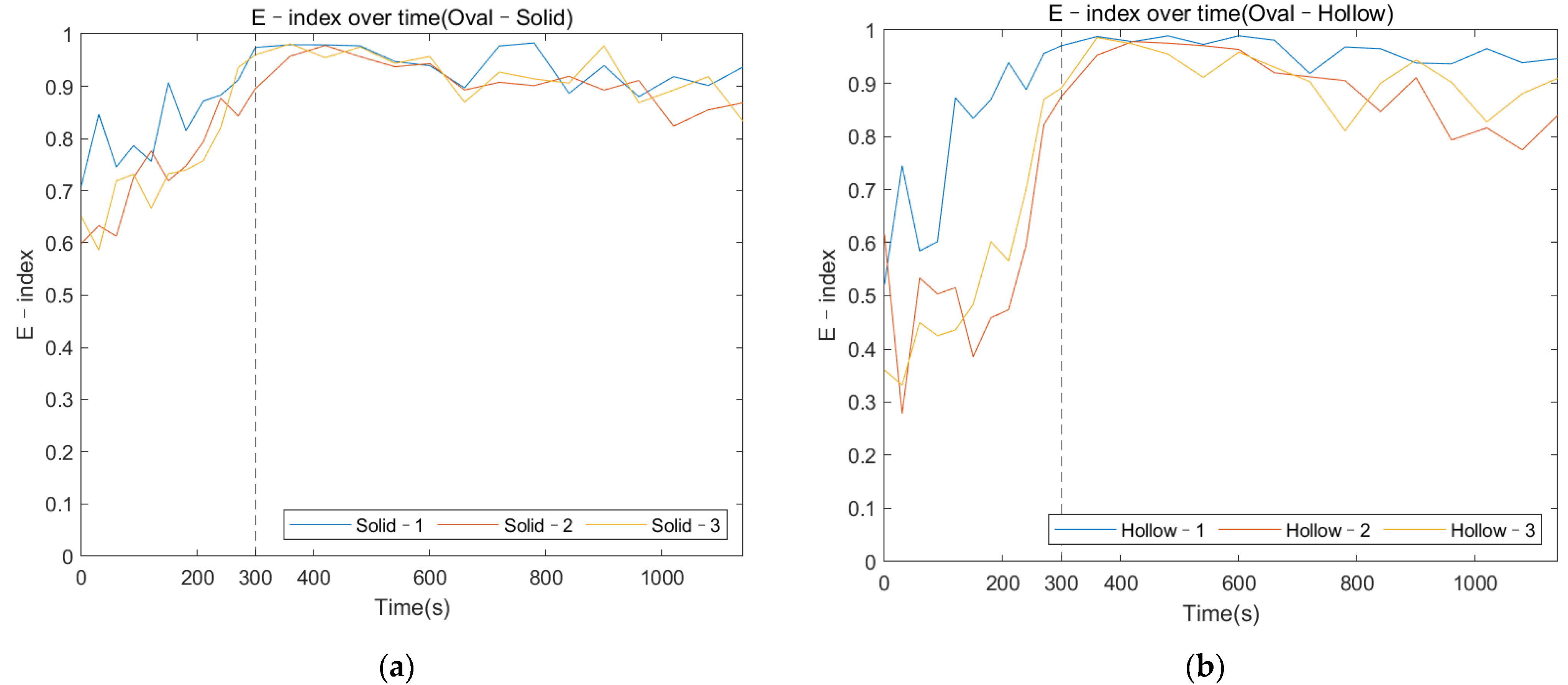
3.3. Oval–Shaped Implant
3.3.1. Colormap of Magnitude
3.3.2. E–Index against Cure Time
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Wang, W.; Lynch, J.P. IWSHM 2017: Application of guided wave methods to quantitatively assess healing in osseointegrated prostheses. Struct. Health Monit. 2018, 17, 1377–1392. [Google Scholar] [CrossRef] [Green Version]
- Shao, F.; Xu, W.; Crocombe, A.; Ewins, D. Natural frequency analysis of osseointegration for trans-femoral implant. Ann. Biomed. Eng. 2007, 35, 817–824. [Google Scholar] [CrossRef] [PubMed]
- Lee, W.C.; Frossard, L.A.; Hagberg, K.; Haggstrom, E.; Brånemark, R.; Evans, J.H.; Pearcy, M.J. Kinetics of transfemoral amputees with osseointegrated fixation performing common activities of daily living. Clin. Biomech. 2007, 22, 665–673. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Webster, J.B.; Bachus, K.N.; Beck, J.P.; Jeyapalina, S.; Drew, A.J.; Bloebaum, R.D. Osseointegration research. In Full Stride; Springer: Berlin/Heidelberg, Germany, 2017; pp. 167–193. [Google Scholar]
- Hebert, J.S.; Rehani, M.; Stiegelmar, R. Osseointegration for lower-limb amputation: A systematic review of clinical outcomes. JBJS Rev. 2017, 5, e10. [Google Scholar] [CrossRef]
- Brånemark, R.; Brånemark, P.I.; Rydevik, B.; Myers, R.R. Osseointegration in skeletal reconstruction and rehabilitation: A review. J. Rehabil. Res. Dev. 2001, 38, 175. [Google Scholar] [PubMed]
- Hagberg, K.; Brånemark, R. Consequences of non-vascular trans-femoral amputation: A survey of quality of life, prosthetic use and problems. Prosthet. Orthot. Int. 2001, 25, 186–194. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Tomaszewski, P.K. Osseointegrated System for Fixation of Upper Leg Prostheses; Rijksuniversiteit: Groningen, The Netherlands, 2012. [Google Scholar]
- Thesleff, A.; Håkansson, B.; Ortiz-Catalan, M. Biomechanical Characterisation of Bone-anchored Implant Systems for Amputation Limb Prostheses: A Systematic Review. Ann. Biomed. Eng. 2018, 46, 377–391. [Google Scholar] [CrossRef] [Green Version]
- Tomaszewski, P.; Verdonschot, N.; Bulstra, S.; Verkerke, G.J. A comparative finite-element analysis of bone failure and load transfer of osseointegrated prostheses fixations. Ann. Biomed. Eng. 2010, 38, 2418–2427. [Google Scholar] [CrossRef] [Green Version]
- Isaacson, B.M.; Jeyapalina, S. Osseointegration: A review of the fundamentals for assuring cementless skeletal fixation. Orthop. Res. Rev. 2014, 6, 55–65. [Google Scholar] [CrossRef] [Green Version]
- Agarwal, R.; García, A.J. Biomaterial strategies for engineering implants for enhanced osseointegration and bone repair. Adv. Drug Deliv. Rev. 2015, 94, 53–62. [Google Scholar] [CrossRef] [Green Version]
- Lu, S.; Vien, B.; Russ, M.; Fitzgerald, M.; Chiu, W. Non-radiative healing assessment techniques for fractured long bones and osseointegrated implant. Biomed. Eng. Lett. 2020, 10, 63–81. [Google Scholar] [CrossRef] [PubMed]
- Ward, D.; Robinson, K. Osseointegration for the skeletal fixation of limb prostheses in amputations at the trans-femoral level. The Osseointegration Book: From Calvarium to Calcaneus; Quintessence: Berlin, Germany, 2005; pp. 463–476. [Google Scholar]
- Hagberg, K.; Häggström, E.; Jönsson, S.; Rydevik, B.; Brånemark, R. Osseoperception and osseointegrated prosthetic limbs. In Psychoprosthetics; Springer: Berlin/Heidelberg, Germany, 2008; pp. 131–140. [Google Scholar]
- Al Muderis, M.; Lu, W.; Tetsworth, K.; Bosley, B.; Li, J.J. Single-stage osseointegrated reconstruction and rehabilitation of lower limb amputees: The Osseointegration Group of Australia Accelerated Protocol-2 (OGAAP-2) for a prospective cohort study. BMJ Open 2017, 7, e013508. [Google Scholar] [CrossRef] [PubMed]
- Isaacson, B.M.; Vance, R.E.; Chou, T.G.R.; Bloebaum, R.D.; Bachus, K.N.; Webster, J.B. Effectiveness of resonance frequency in predicting orthopedic implant strength and stability in an in vitro osseointegration model. Resonance 2009, 37, 43–60. [Google Scholar] [CrossRef] [PubMed]
- Petersen, R.C. Titanium implant osseointegration problems with alternate solutions using epoxy/carbon-fiber-reinforced composite. Metals 2014, 4, 549–569. [Google Scholar] [CrossRef] [PubMed]
- Hickok, N.J.; Shapiro, I.M. Immobilized antibiotics to prevent orthopaedic implant infections. Adv. Drug Deliv. Rev. 2012, 64, 1165–1176. [Google Scholar] [CrossRef] [Green Version]
- Cairns, N.J.; Pearcy, M.J.; Smeathers, J.; Adam, C.J. Ability of modal analysis to detect osseointegration of implants in transfemoral amputees: A physical model study. Med. Biol. Eng. Comput. 2013, 51, 39–47. [Google Scholar] [CrossRef] [Green Version]
- Cairns, N.J.; Adam, C.J.; Pearcy, M.J.; Smeathers, J. Evaluation of modal analysis techniques using physical models to detect osseointegration of implants in transfemoral amputees. In Proceedings of the Annual International Conference of the IEEE Engineering in Medicine and Biology Society, Boston, MA, USA, 30 August–3 September 2011; pp. 1600–1603. [Google Scholar]
- Vayron, R.; Nguyen, V.H.; Lecuelle, B.; Haiat, G. Evaluation of dental implant stability in bone phantoms: Comparison between a quantitative ultrasound technique and resonance frequency analysis. Clin. Implant Dent. Relat. Res. 2018, 20, 470–478. [Google Scholar] [CrossRef] [Green Version]
- Chiu, W.K.; Vien, B.S.; Russ, M.; Fitzgerald, M. Healing assessment of fractured femur treated with an intramedullary nail. Struct. Health Monit. 2019, 20, 1475921718816781. [Google Scholar] [CrossRef]
- Vien, B.S.; Chiu, W.; Russ, M.; Fitzgerald, M. A Quantitative Approach for the Bone-implant Osseointegration Assessment Based on Ultrasonic Elastic Guided Waves. Sensors 2019, 19, 454. [Google Scholar] [CrossRef] [Green Version]
- Alshuhri, A.A.; Holsgrove, T.P.; Miles, A.W.; Cunningham, J.L. Development of a non-invasive diagnostic technique for acetabular component loosening in total hip replacements. Med. Eng. Phys. 2015, 37, 739–745. [Google Scholar] [CrossRef] [Green Version]
- Huang, H.-M.; Chiu, C.-L.; Yeh, C.-Y.; Lee, S.-Y. Factors influencing the resonance frequency of dental implants. J. Oral Maxillofac. Surg. 2003, 61, 1184–1188. [Google Scholar] [CrossRef]
- Varini, E.; Bialoblocka-Juszczyk, E.; Lannocca, M.; Cappello, A.; Cristofolini, L. Assessment of implant stability of cementless hip prostheses through the frequency response function of the stem–bone system. Sens. Actuators A Phys. 2010, 163, 526–532. [Google Scholar] [CrossRef]
- Li, P.; Jones, N.; Gregg, P. Vibration analysis in the detection of total hip prosthetic loosening. Med. Eng. Phys. 1996, 18, 596–600. [Google Scholar] [CrossRef]
- Jaecques, S.V.; Pastrav, C.; Van der Perre, G. Analysis of the Fixation Quality of Total Hip Replacements Using a Vibrational Technique. In Proceedings of the ASME 7th Biennial Conference on Engineering Systems Design and Analysis, Manchester, UK, 19–22 July 2004; American Society of Mechanical Engineers: New York, NY, USA, 2004; pp. 579–588. [Google Scholar]
- Qi, G.; Paul Mouchon, W.; Tan, T.E. How much can a vibrational diagnostic tool reveal in total hip arthroplasty loosening? Clin. Biomech. 2003, 18, 444–458. [Google Scholar] [CrossRef]
- Lannocca, M.; Varini, E.; Cappello, A.; Cristofolini, L.; Bialoblocka, E. Intra-operative evaluation of cementless hip implant stability: A prototype device based on vibration analysis. Med. Eng. Phys. 2007, 29, 886–894. [Google Scholar] [CrossRef]
- Lu, S.; Vien, B.; Russ, M.; Fitzgerald, M.; Kong, W. Quantitative Monitoring of Osseointegrated Implant Stability Using Vibration Analysis. Mater. Res. Proc. 2021, 18, 87. [Google Scholar]
- Xu, D.; Crocombe, A.; Xu, W. Numerical evaluation of bone remodelling associated with trans-femoral osseointegration implant–A 68 month follow-up study. J. Biomech. 2016, 49, 488–492. [Google Scholar] [CrossRef] [Green Version]
- Rizzo, P. A review on the latest advancements in the non-invasive evaluation/monitoring of dental and trans-femoral implants. Biomed. Eng. Lett. 2020, 10, 83–102. [Google Scholar] [CrossRef]
- Huang, H.M.; Chiu, C.L.; Yeh, C.Y.; Lin, C.T.; Lin, L.H.; Lee, S.Y. Early detection of implant healing process using resonance frequency analysis. Clin. Oral Implant. Res. 2003, 14, 437–443. [Google Scholar] [CrossRef]
- Feng, S.-W.; Ho, K.-N.; Chan, Y.-H.; Chang, K.-J.; Lai, W.-Y.; Huang, H.-M. Damping factor as a diagnostic parameter for assessment of osseointegration during the dental implant healing process: An experimental study in rabbits. Ann. Biomed. Eng. 2016, 44, 3668–3678. [Google Scholar] [CrossRef]
- Atieh, M.A.; Alsabeeha, N.H.; Payne, A.G.; de Silva, R.K.; Schwass, D.S.; Duncan, W.J. The prognostic accuracy of resonance frequency analysis in predicting failure risk of immediately restored implants. Clin. Oral Implant. Res. 2014, 25, 29–35. [Google Scholar] [CrossRef] [PubMed]
- Michael Norton, B. Primary stability versus viable constraint—A need to redefine. Int. J. Oral Maxillofac. Implant. 2013, 28, 19–21. [Google Scholar]
- Mistry, G.; Shetty, O.; Shetty, S.; Singh, R.D. Measuring implant stability: A review of different methods. J. Dent. Implant. 2014, 4, 165. [Google Scholar] [CrossRef]
- Manresa, C.; Bosch, M.; Echeverría, J.J. The comparison between implant stability quotient and bone-implant contact revisited: An experiment in B eagle dog. Clin. Oral Implant. Res. 2014, 25, 1213–1221. [Google Scholar] [CrossRef]
- Russ, M.; Chiu, W.K.; Ong, W.H.; Tran, T.; Russ, M.; Fitzgerald, M. Development of a Novel Osseointegrated Endoprosthesis, Combing Orthopaedic and Engineering Design Principles, and Structural Health Monitoring Conc. Struct. Health Monit. 2017 2017, 87–94. [Google Scholar] [CrossRef]
- Chiu, W.K.; Vien, B.S.; Russ, M.; Fitzgerald, M. Vibration-based healing assessment of an internally fixated femur. J. Nondestruct. Eval. Diagn. Progn. Eng. Syst. 2019, 2, 021003. [Google Scholar] [CrossRef]
- Wade, R.; Moorcroft, C.; Thomas, P. Fracture stiffness as a guide to the management of tibial fractures. Bone Jt. J. 2001, 83, 533–535. [Google Scholar] [CrossRef]
- Claes, E.L.; Cunningham, L.J. Monitoring the Mechanical Properties of Healing Bone. Clin. Orthop. Relat. Res. 2009, 467, 1964–1971. [Google Scholar] [CrossRef] [Green Version]
- Eriksson, C.; Ohlson, K.; Richter, K.; Billerdahl, N.; Johansson, M.; Nygren, H. Callus formation and remodeling at titanium implants. J. Biomed. Mater. Res. Part A Off. J. Soc. Biomater. Jpn. Soc. Biomater. Aust. Soc. Biomater. Korean Soc. Biomater. 2007, 83, 1062–1069. [Google Scholar] [CrossRef]
- Chiu, W.K.; Vien, B.S.; Russ, M.; Fitzgerald, M. Healing assessment of an internally fixated femur using vibration analysis. In Proceedings of the 7th Asia-Pacific Workshop on Structural Health Monitoring, Hong Kong, China, 12–15 November 2018; Volume 19, p. 857. [Google Scholar]
- Chiu, W.K.; Vien, B.S.; Russ, M.; Fitzgerald, M. Towards a Non-Invasive Technique for Healing Assessment of Internally Fixated Femur. Sensors 2019, 19, 857. [Google Scholar] [CrossRef] [Green Version]
- Ong, W.; Chiu, W.; Russ, M.; Chiu, Z. Extending structural health monitoring concepts for bone healing assessment. Fatigue Fract. Eng. Mater. Struct. 2016, 39, 491–501. [Google Scholar] [CrossRef]
- Ong, W.; Chiu, W.; Russ, M.; Chiu, Z. Integrating sensing elements on external fixators for healing assessment of fractured femur. Struct. Control. Health Monit. 2016, 23, 1388–1404. [Google Scholar] [CrossRef]
- Vien, B.S.; Chiu, W.K.; Russ, M.; Fitzgerald, M. A stress wave-based health monitoring concept on a novel osseointegrated endoprosthesis design. In Proceedings of the 7th Asia-Pacific Workshop on Structural Health Monitoring (APWSHM), Hong Kong, China, 12–15 November 2018. [Google Scholar]
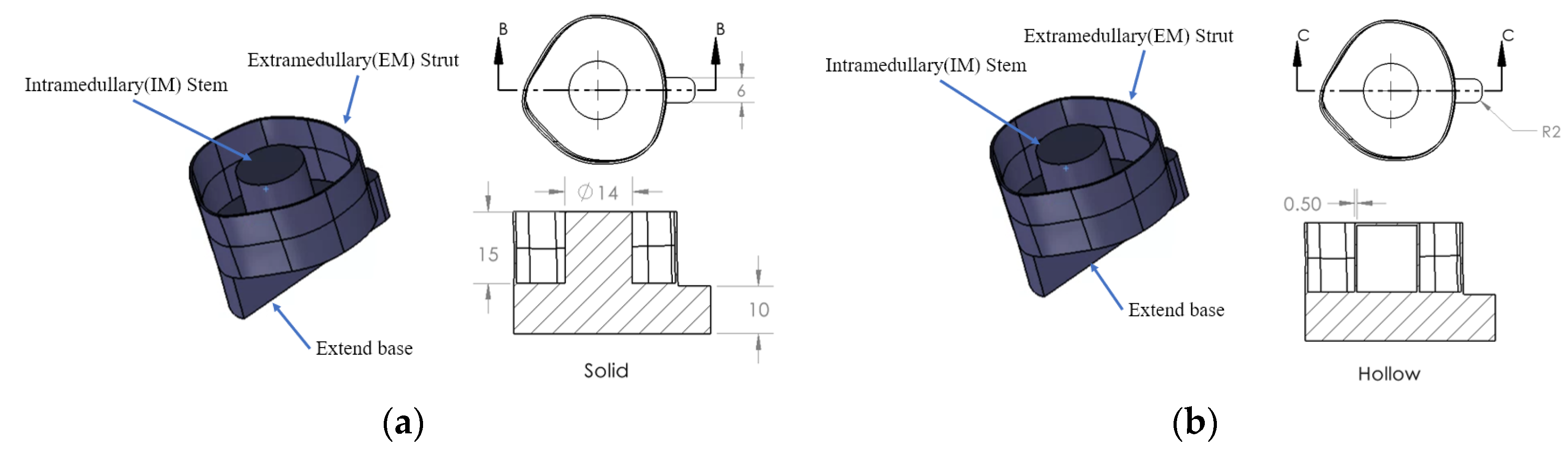
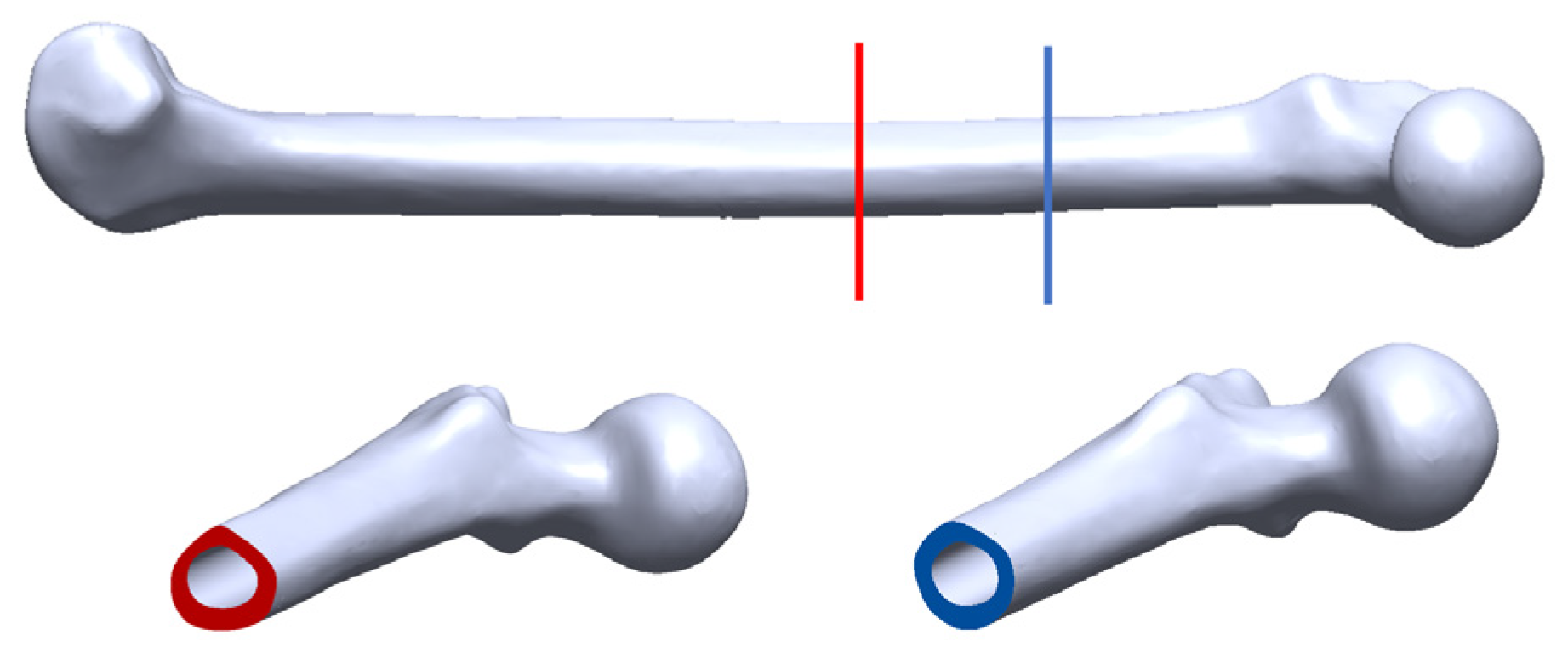
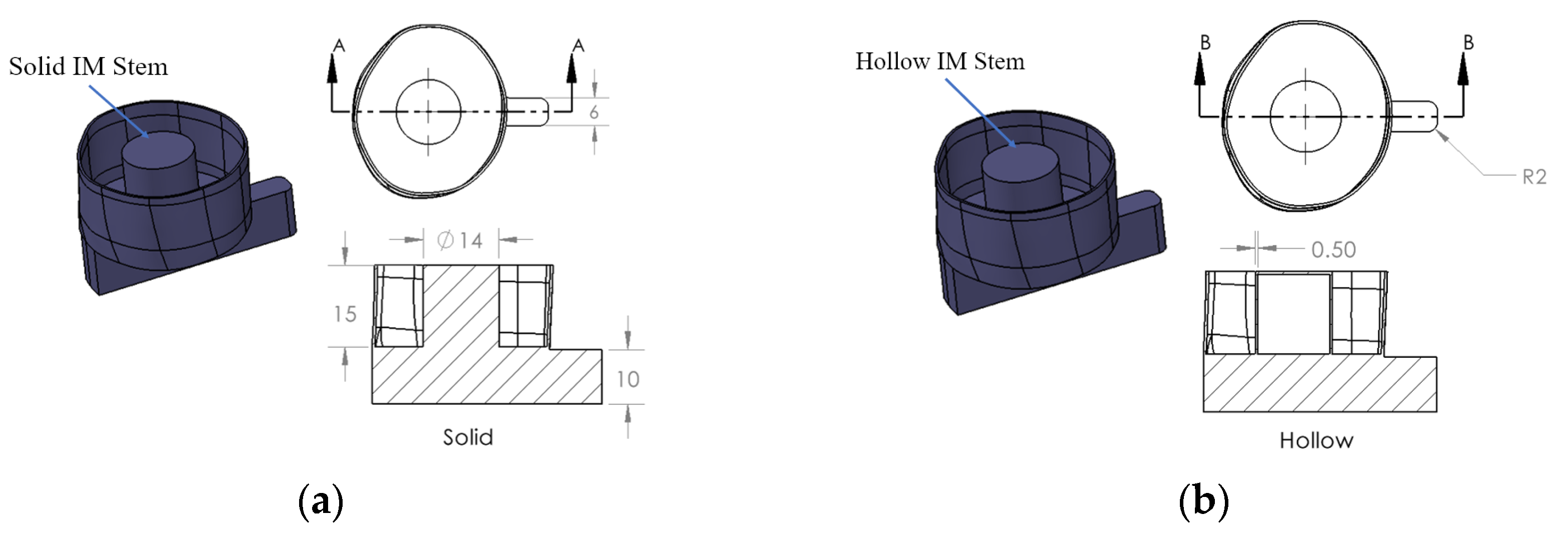
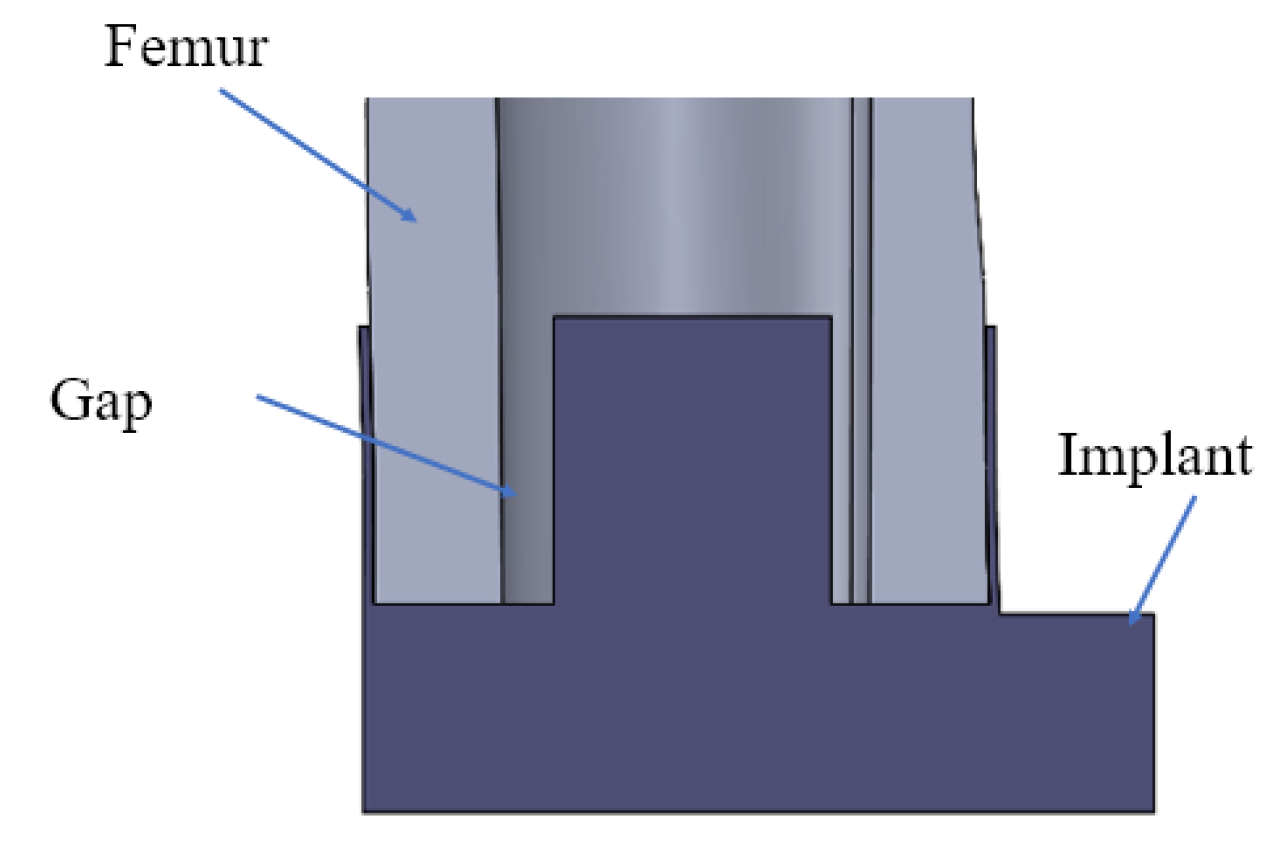

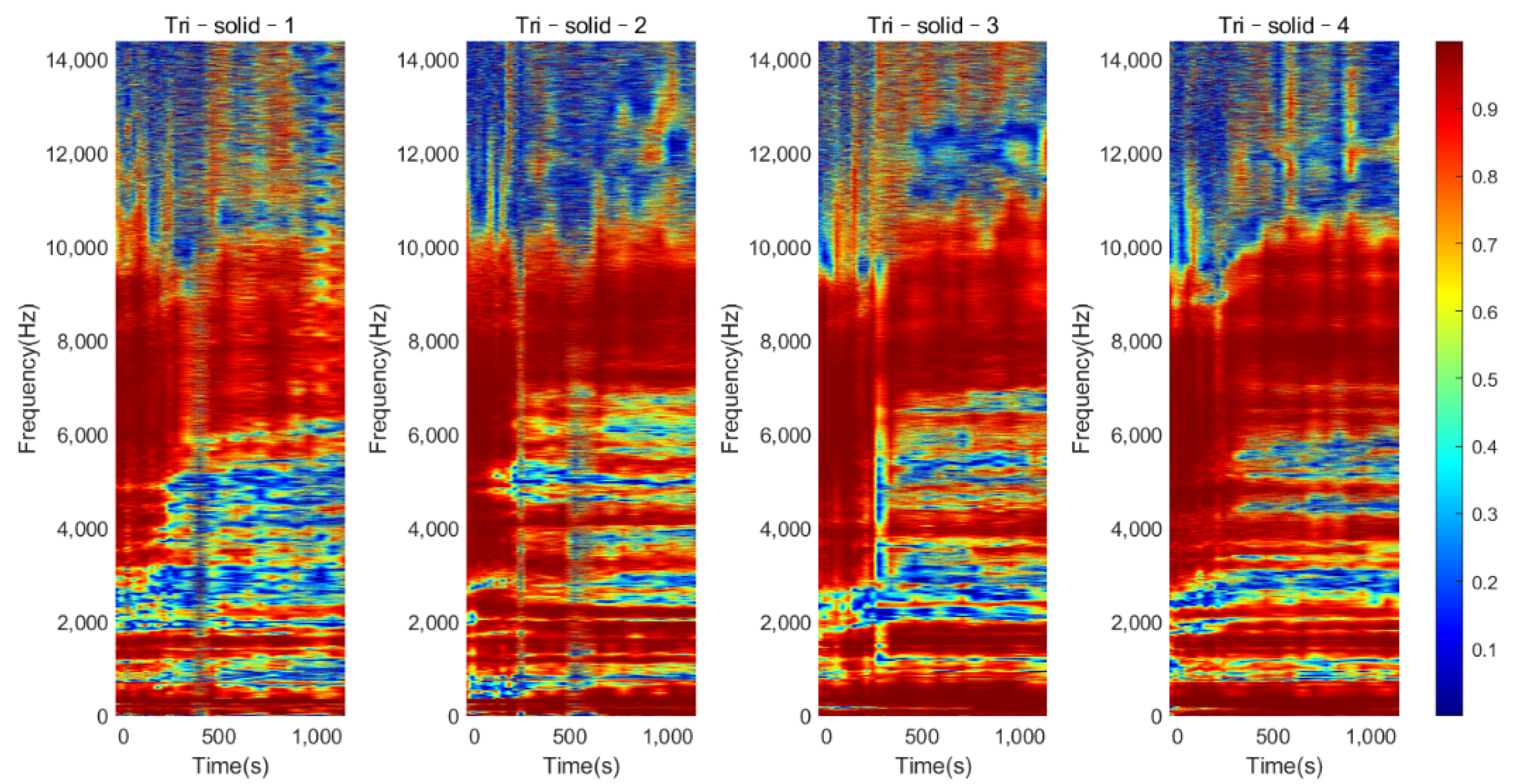

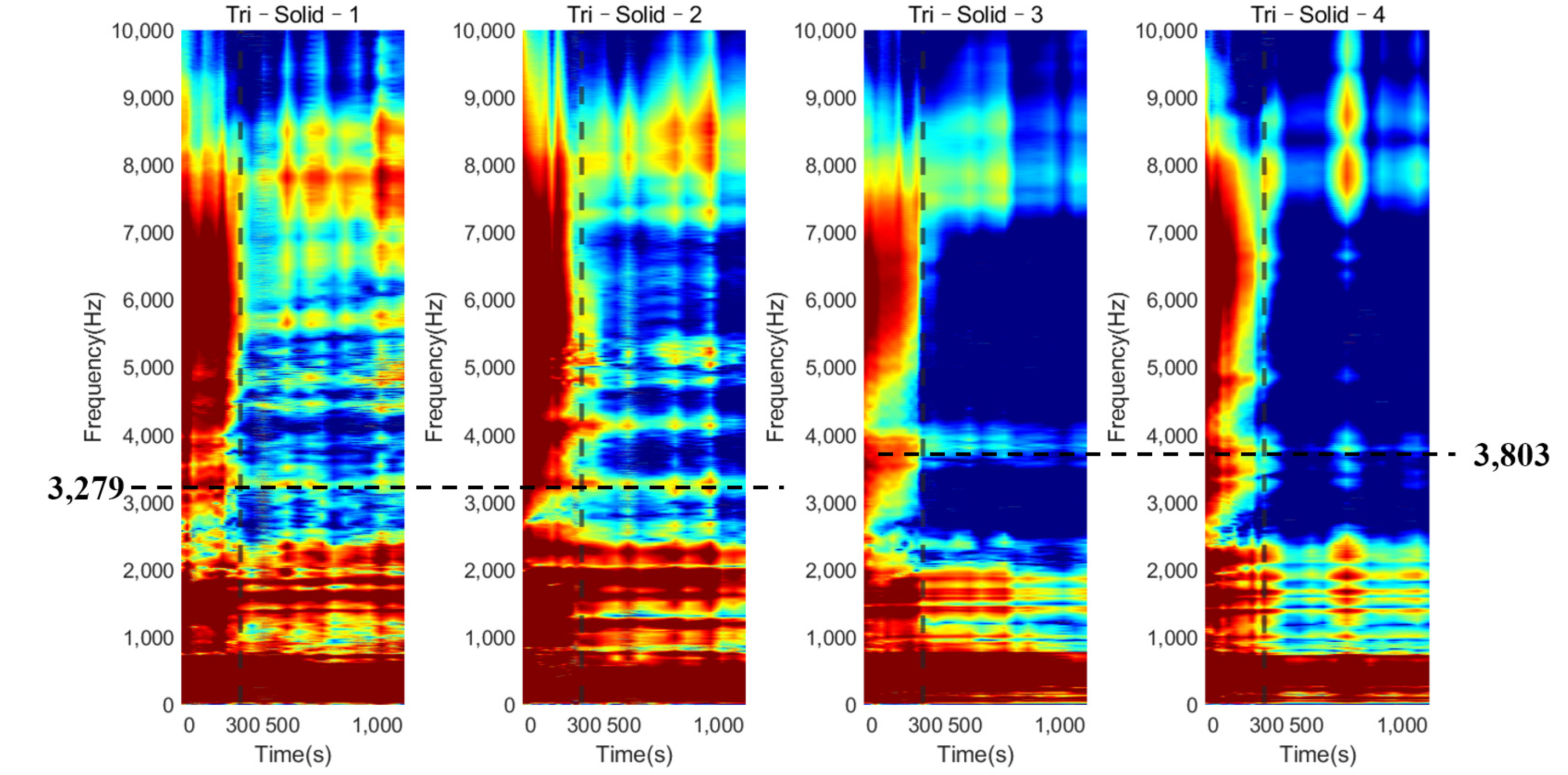





| Frequency (Hz) | 0 s | 150 s | 300 s | 600 s | 1140 s | Change in dB (Relative to 0 s) |
|---|---|---|---|---|---|---|
| 3279 | −6.010 | −7.425 | −7.965 | −9.623 | −10.074 | −4.064 |
| 4124 | −5.195 | −6.684 | −7.610 | −9.391 | −11.135 | −5.940 |
| Test | Difference (%) | |
|---|---|---|
| Solid | Hollow | |
| 1 | 132.82 | 516.53 |
| 2 | 354.55 | 142.80 |
| 3 | 71.81 | 713.73 |
| 4 | 439.45 | 57.17 |
| Averaged | 249.66 | 355.04 |
| Test | Difference (%) | |
| Solid | Hollow | |
| 1 | 32.05 | 81.53 |
| 2 | 44.93 | 36.46 |
| 3 | 28.11 | 152.37 |
| Averaged | 35.03 | 90.12 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lu, S.; Vien, B.S.; Russ, M.; Fitzgerald, M.; Chiu, W.K. Experimental Investigation of Vibration Analysis on Implant Stability for a Novel Implant Design. Sensors 2022, 22, 1685. https://doi.org/10.3390/s22041685
Lu S, Vien BS, Russ M, Fitzgerald M, Chiu WK. Experimental Investigation of Vibration Analysis on Implant Stability for a Novel Implant Design. Sensors. 2022; 22(4):1685. https://doi.org/10.3390/s22041685
Chicago/Turabian StyleLu, Shouxun, Benjamin Steven Vien, Matthias Russ, Mark Fitzgerald, and Wing Kong Chiu. 2022. "Experimental Investigation of Vibration Analysis on Implant Stability for a Novel Implant Design" Sensors 22, no. 4: 1685. https://doi.org/10.3390/s22041685
APA StyleLu, S., Vien, B. S., Russ, M., Fitzgerald, M., & Chiu, W. K. (2022). Experimental Investigation of Vibration Analysis on Implant Stability for a Novel Implant Design. Sensors, 22(4), 1685. https://doi.org/10.3390/s22041685







