A Novel Unified Framework for Energy-Based Spectrum Sensing Analysis in the Presence of Fading
Abstract
:1. Introduction
- For the unification of the wide range of existing channel models, a new moment-generating function model (i.e., the factorized power-type (FPT) representation) was introduced. It is demonstrated that such a generalization can easily handle non-line-of-sight and shadowed line-of-sight models widely applied in communication theory.
- Under this assumption, applying the contour-integral transformation technique, closed-form analytic expressions for the average probability of detection and area under the receiver operating characteristic curve are derived, and their simple interconnections are established.
- Based on the high signal-to-noise ratio assumption, asymptotic expressions for the FTP models’ APD and AUC, useful for numeric computation, are derived.
- Capitalizing on the obtained results, the novel closed-form representations of the aforementioned detection quality metrics and their asymptotic versions for the Fluctuating Beckmann and the Beaulieu-Xie shadowed models were evaluated. Lastly, the validating numeric simulation was executed to establish the dependencies of the sensing performance from the channel parameters and identify the ranges of their asymptotic behavior.
2. Preliminaries
3. Derived Results
3.1. Channel Model with FPT MGF
3.2. Special Simplified Cases of the FPT MGF Model. Models’ Connections
- Rayleigh. The Rayleigh fading channel model is the classical one and is among the most frequently used in cases of NLoS situations. In can be seen that to be in full compliance with the Rayleigh MGF, defined, for instance, as in [4], one has to perform the following set of substitutions in (4): , , , , .
- Nakagami-m. The Nakagami-m fading channel is usually assumed to be more versatile than the Rayleigh model, including scenarios with fading that is heavier and lighter than Rayleigh. Following the same procedure as before and matching the definition of the Nakagami-m MGF (given, for example, in [4]) with (4), the substitutions will look like: , , , , .
- Hoyt. The Hoyt fading channel model distribution is typically employed to model the enriched multipath fading [17] (for instance, in cases of strong ionospheric scintillation in satellite links or mobile satellite channels being simulated in the form of a two-state process). Contrary to Rayleigh and Nakagami-m, the application of the Hoyt MGF definition given in [4] leads to , , and other parameters will be , , , .
- shadowed. The shadowed fading channel model, that has recently drawn much attention [27], was first presented in [28], and defines a generalized model accounting for the most of the abovementioned cases (with the exception of the Hoyt model, see [6]) combined with the shadowed LoS situation. The parameters , defined as in [28] and connected with (4), are as follows: , , , , , , .
- Mixture-Gamma. Amidst the existing channel models, Mixture-Gamma stands out and is regarded as having paramount importance, since it can successively approximate a wide a range of the existing models, including the aforementioned ones and their generalizations (see [11]). The principal difference between (4) and the Mixture-Gamma MGF (defined in [11] in terms of parameters ) is that the latter can be viewed as a linear combination of versions of (4) with a specific treatment of normalization constants (i.e., ). For each of the summands, the substitutions are as follows: , , , , . Moreover, ref. [29] states Mixture-Gamma as an approximation model for such composite fading channels as , and , thus expanding the applicability of the proposed FPT MGF model.
3.3. General Results
3.4. Application of the Derived Results
3.4.1. Exact and Asymptotic APD and AUC for the Fluctuating Beckmann Channel Model
3.4.2. Exact and Asymptotic APD and AUC for the Beaulieu-Xie Shadowed Channel Model
3.5. Models’ Connections
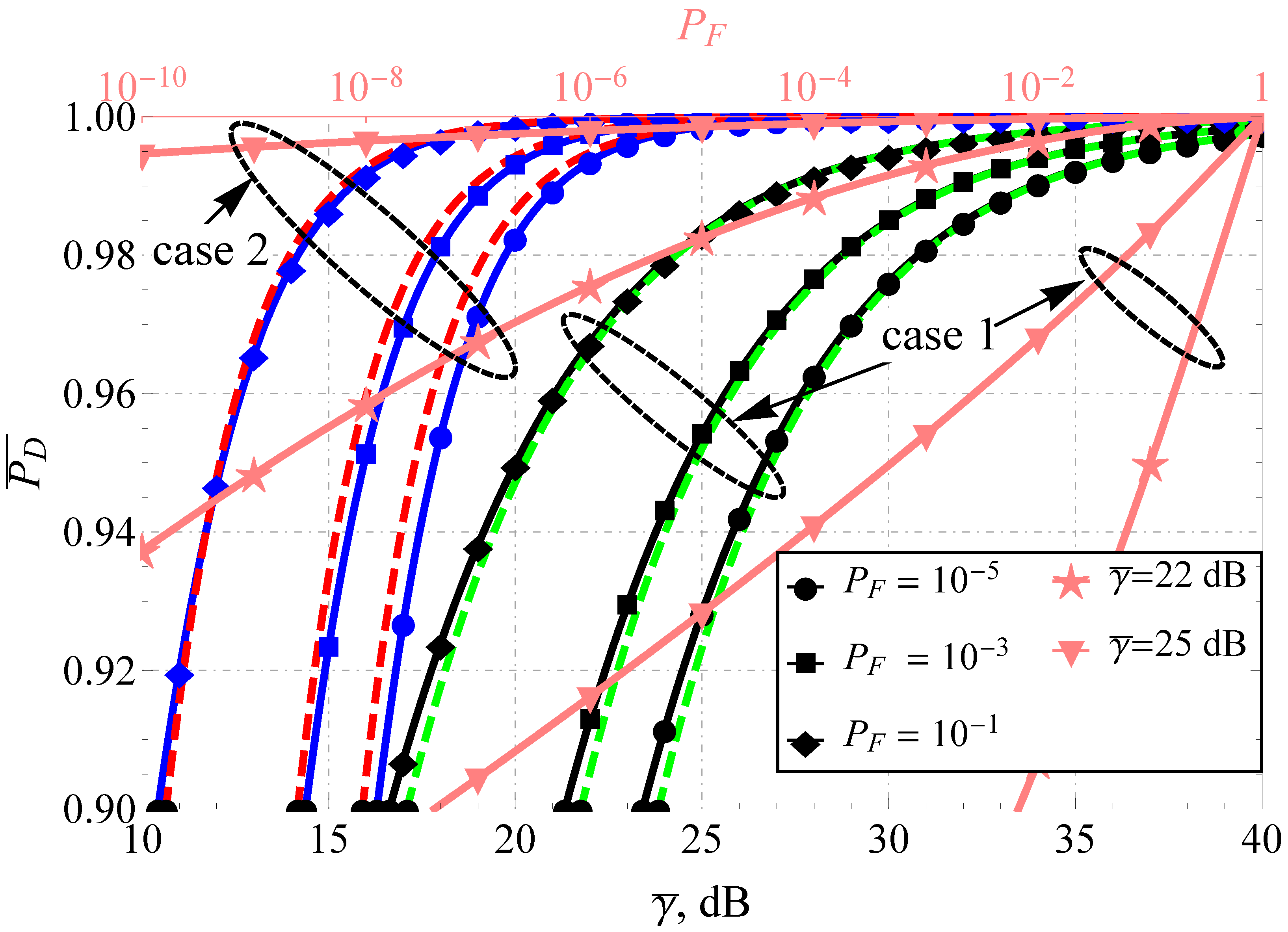
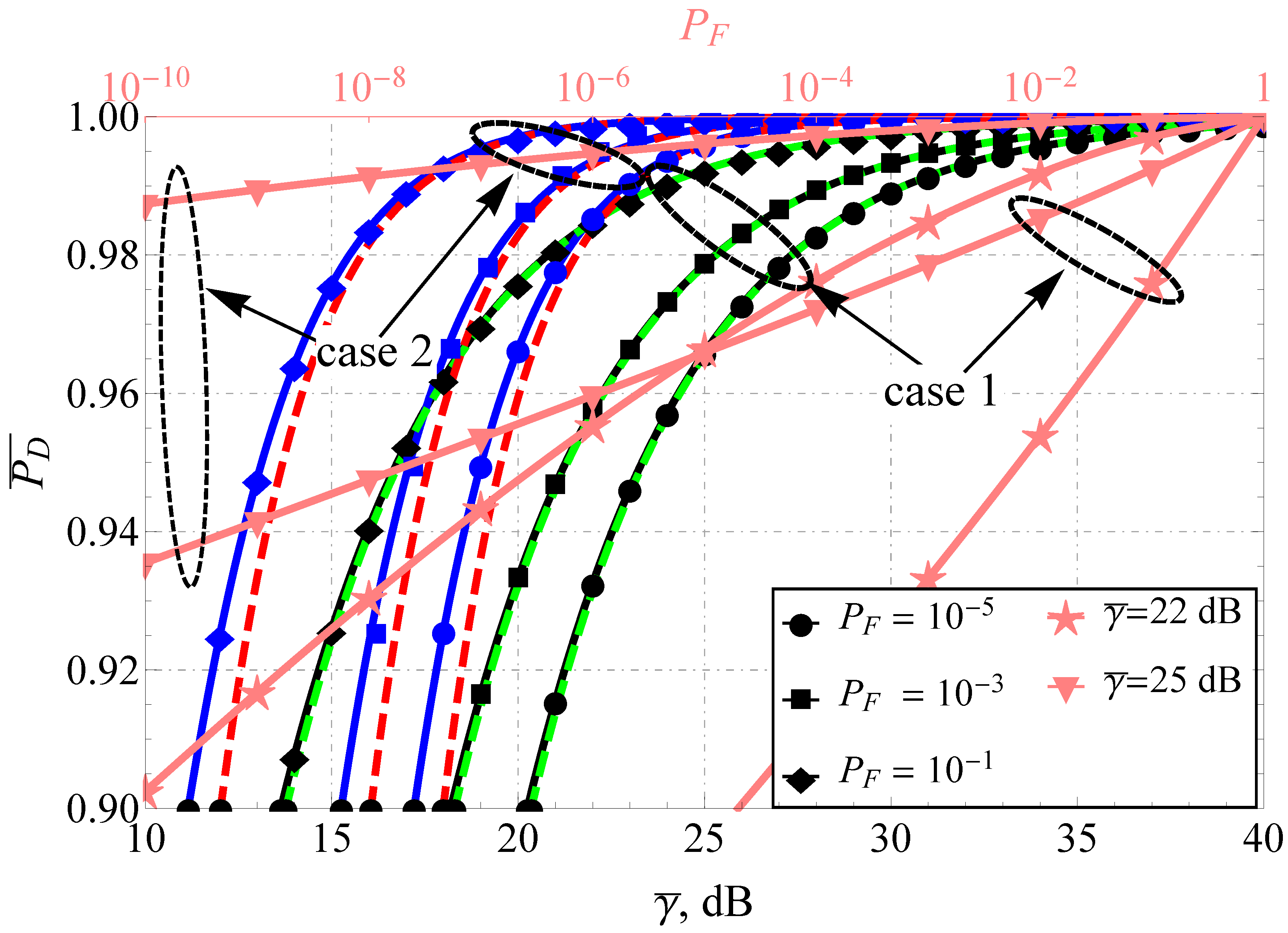
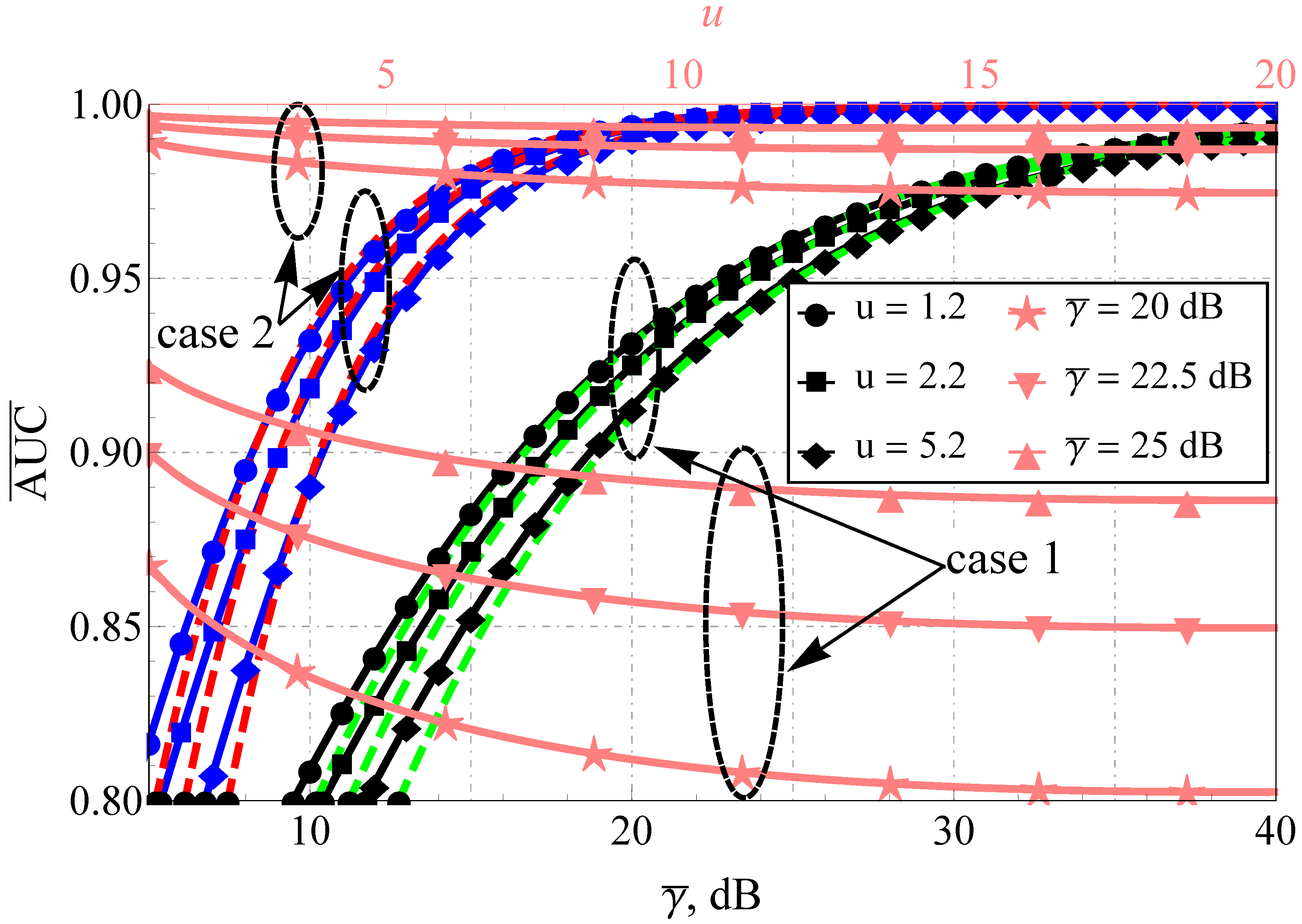
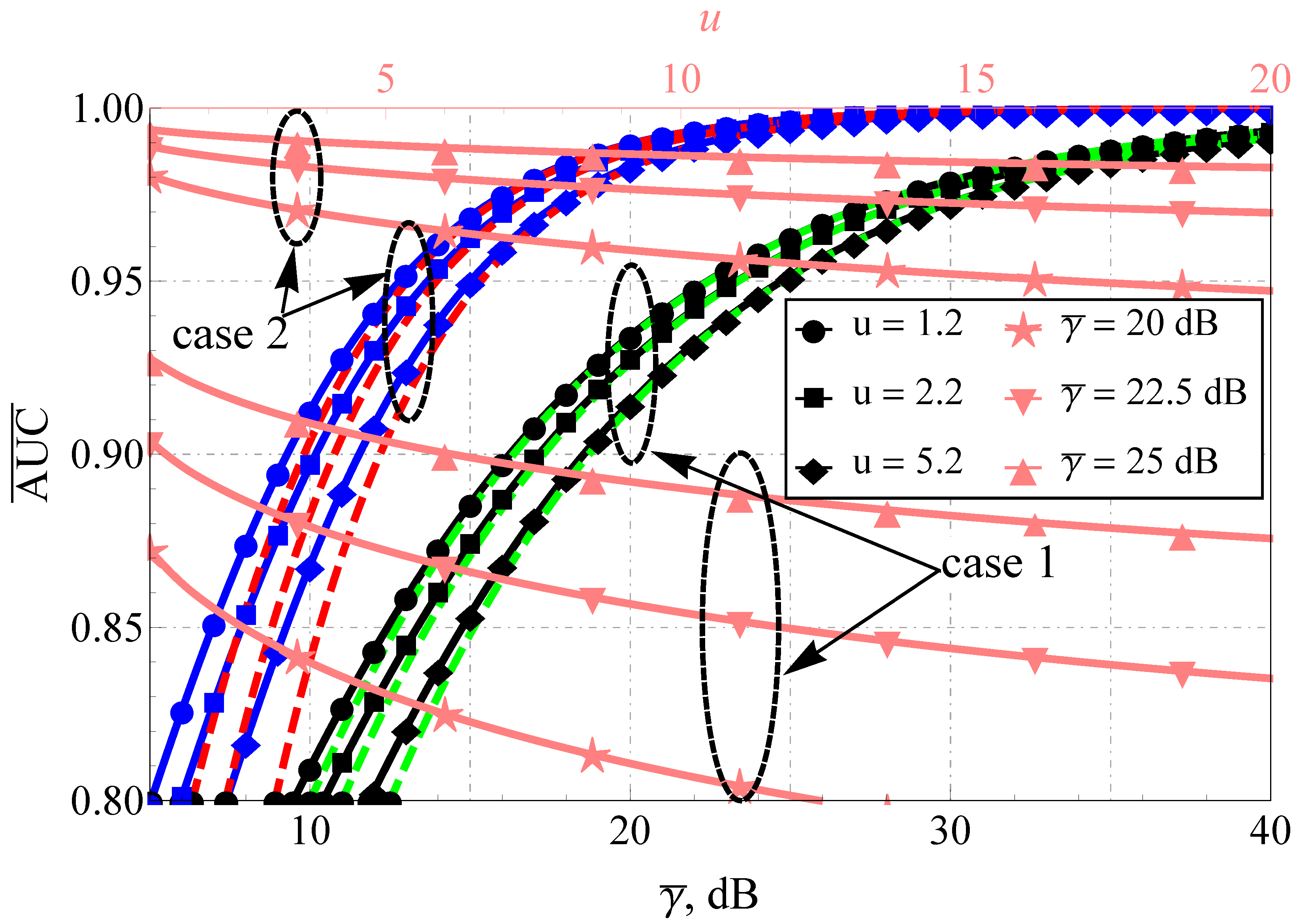
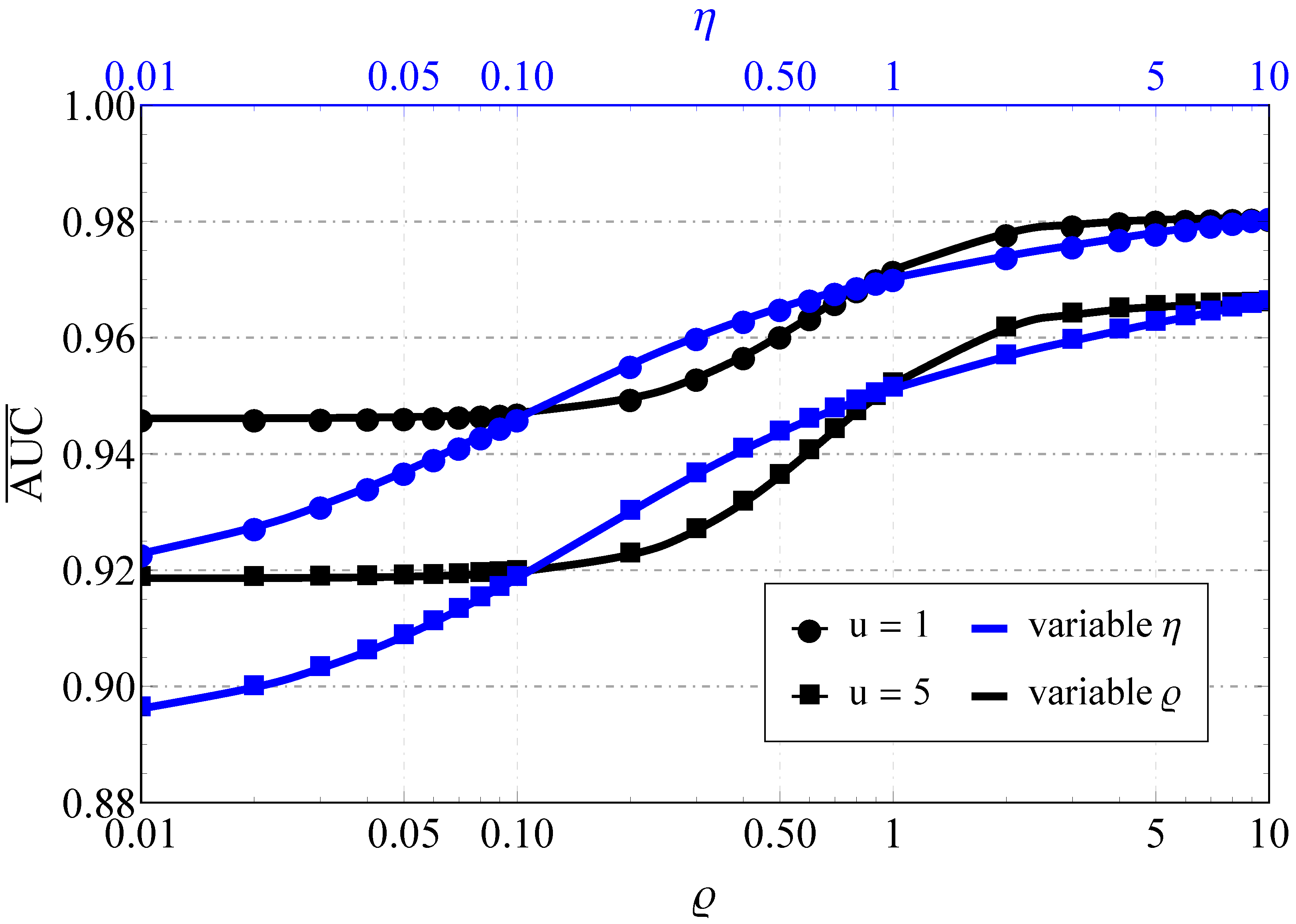
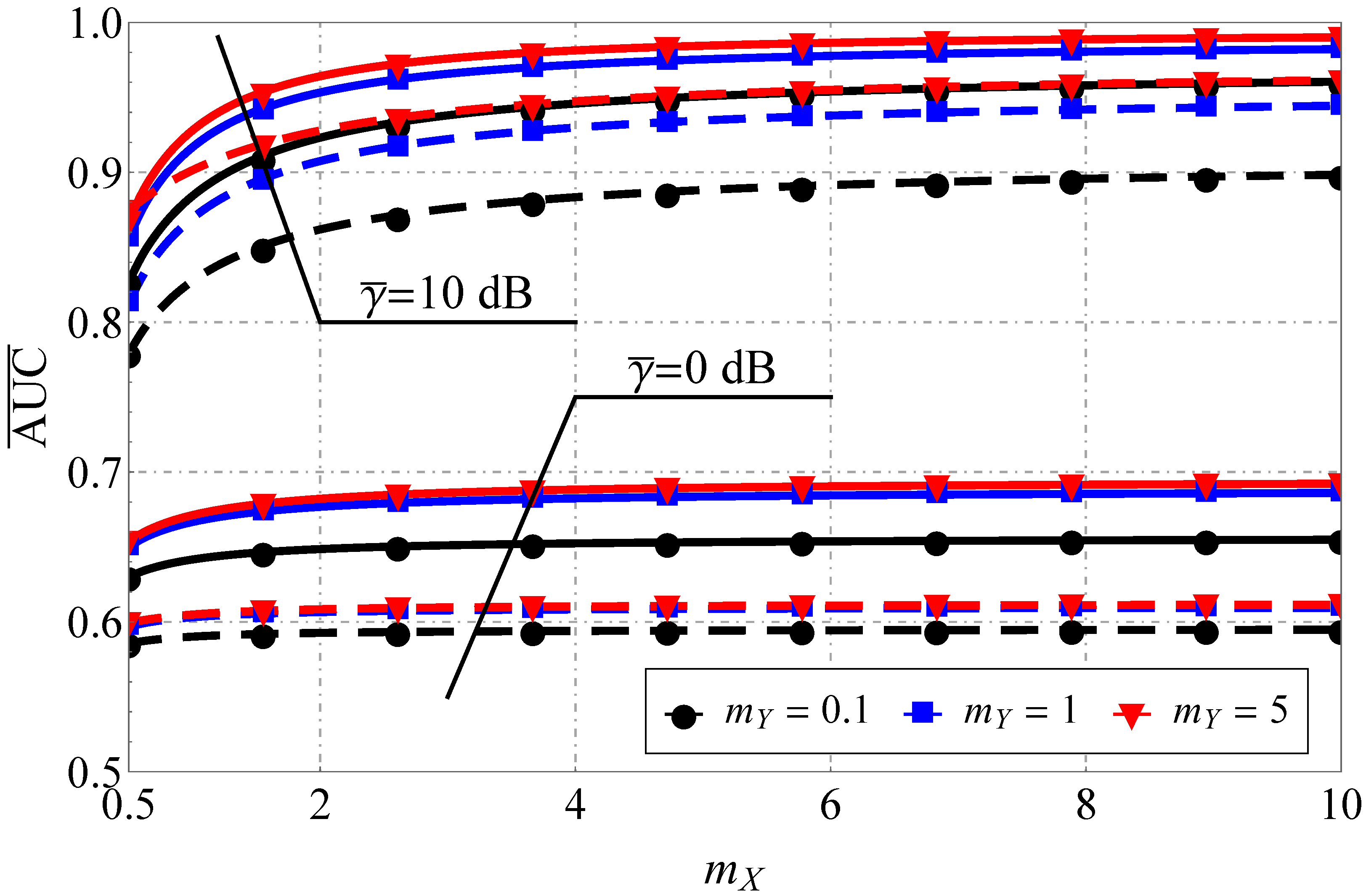
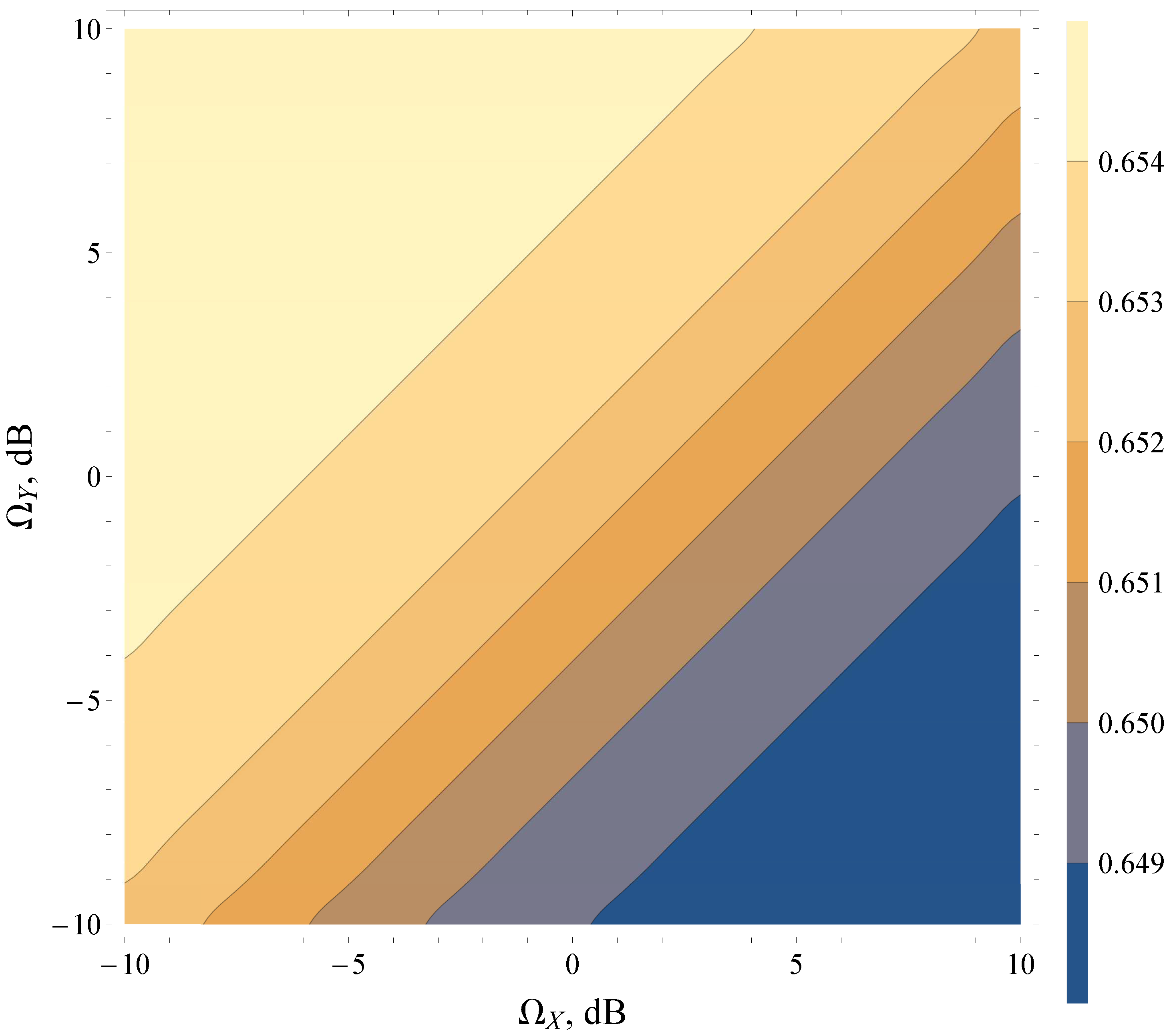
4. Simulation and Results
5. Discussion and Further Generalization
6. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A. Proof of Theorem 1
Appendix B. Proof of Theorem 2
References
- Atapattu, S.; Tellambura, C.; Jiang, H. Energy Detection for Spectrum Sensing in Cognitive Radio; Springer Briefs in Computer Science; Springer: New York, NY, USA, 2014. [Google Scholar] [CrossRef]
- Axell, E.; Leus, G.; Larsson, E.; Poor, H. Spectrum Sensing for Cognitive Radio: State-of-the-Art and Recent Advances. IEEE Signal Process. Mag. 2012, 29, 101–116. [Google Scholar] [CrossRef] [Green Version]
- Urkowitz, H. Energy detection of unknown deterministic signals. Proc. IEEE 1967, 55, 523–531. [Google Scholar] [CrossRef]
- Simon, M.K.; Alouini, M.S. Digital Communication over Fading Channels; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2005. [Google Scholar] [CrossRef]
- Peppas, K.; Nistazakis, H.; Tombras, G. An Overview of the Physical Insight and the Various Performance Metrics of Fading Channels in Wireless Communication Systems. In Advanced Trends in Wireless Communications; InTech: London, UK, 2011. [Google Scholar] [CrossRef] [Green Version]
- Paris, J.F. Advances in the Statistical Characterization of Fading: From 2005 to Present. Int. J. Antennas Propag. 2014, 2014, 258308. [Google Scholar] [CrossRef]
- Shankar, P.M. Fading and Shadowing in Wireless Systems; Springer International Publishing: Berlin/Heidelberg, Germany, 2017. [Google Scholar]
- Digham, F.F.; Alouini, M.S.; Simon, M.K. On the Energy Detection of Unknown Signals Over Fading Channels. IEEE Trans. Commun. 2007, 55, 21–24. [Google Scholar] [CrossRef]
- Atapattu, S.; Tellambura, C.; Jiang, H. Energy detection of primary signals over η − μ fading channels. In Proceedings of the 2009 International Conference on Industrial and Information Systems (ICIIS), Peradeniya, Sri Lanka, 28–31 December 2009. [Google Scholar] [CrossRef]
- Alam, S.; Olabiyi, O.; Odejide, O.; Annamalai, A. Energy detector’s performance evaluation in a relay based cognitive radio network: Area under the ROC curve (AUC) approach. In Proceedings of the 2011 IEEE GLOBECOM Workshops (GC Wkshps), Houston, TX, USA, 5–9 December 2011. [Google Scholar] [CrossRef]
- Atapattu, S.; Tellambura, C.; Jiang, H. A Mixture Gamma Distribution to Model the SNR of Wireless Channels. IEEE Trans. Wirel. Commun. 2011, 10, 4193–4203. [Google Scholar] [CrossRef]
- Atapattu, S.; Tellambura, C.; Jiang, H. MGF Based Analysis of Area under the ROC Curve in Energy Detection. IEEE Commun. Lett. 2011, 15, 1301–1303. [Google Scholar] [CrossRef] [Green Version]
- Annamalai, A.; Olaluwe, A. Energy detection of unknown deterministic signals in κ − μ and η − μ generalized fading channels with diversity receivers. In Proceedings of the 2014 International Conference on Computing, Networking and Communications (ICNC), Honolulu, HI, USA, 3–6 February 2014. [Google Scholar] [CrossRef]
- Aloqlah, M. Performance analysis of energy detection-based spectrum sensing in κ − μ shadowed fading. Electron. Lett. 2014, 50, 1944–1946. [Google Scholar] [CrossRef]
- Peppas, K.P.; Efthymoglou, G.; Aalo, V.A.; Alwakeel, M.; Alwakeel, S. Energy detection of unknown signals in Gamma-shadowed Rician fading environments with diversity reception. IET Commun. 2015, 9, 196–210. [Google Scholar] [CrossRef]
- Gvozdarev, A.S. Partial order generalized Marcum Q-function contour integral representation. Integral Transform. Spec. Funct. 2017, 28, 876–887. [Google Scholar] [CrossRef]
- Bagheri, A.; Sofotasios, P.C.; Tsiftsis, T.A.; Ho-Van, K.; Loupis, M.I.; Freear, S.; Valkama, M. Energy detection based spectrum sensing over enriched multipath fading channels. In Proceedings of the 2016 IEEE Wireless Communications and Networking Conference, Doha, Qatar, 3–6 April 2016. [Google Scholar] [CrossRef] [Green Version]
- Chandrasekaran, G.; Kalyani, S. Performance Analysis of Cooperative Spectrum Sensing Over κ − μ Shadowed Fading. IEEE Wirel. Commun. Lett. 2015, 4, 553–556. [Google Scholar] [CrossRef]
- Aloqlah, M.S.; Alzubaidi, R.A. Energy-Detection performance for SIMO Cognitive Radio Systems with Selection Combining over κ − μ Shadowed Fading Channels. In Proceedings of the 2018 28th International Telecommunication Networks and Applications Conference (ITNAC), Sydney, NSW, Australia, 21–23 November 2018. [Google Scholar] [CrossRef]
- Lopez-Martinez, F.J.; Paris, J.F.; Romero-Jerez, J.M. The κ − μ Shadowed Fading Model With Integer Fading Parameters. IEEE Trans. Veh. Technol. 2017, 66, 7653–7662. [Google Scholar] [CrossRef] [Green Version]
- Adebola, E.; Annamalai, A. Unified analysis of diversity average energy detectors over generalized fading channels. In Proceedings of the 2013 International Conference on Connected Vehicles and Expo (ICCVE), Las Vegas, NV, USA, 2–6 December 2013. [Google Scholar] [CrossRef]
- Adebola, E.; Annamalai, A. Unified analysis of energy detectors with diversity reception in generalised fading channels. IET Commun. 2014, 8, 3095–3104. [Google Scholar] [CrossRef]
- Wang, Y.; Zhang, M.; Shi, Q. Unified approach to performance analysis of energy detection in generalised fading channels. Electron. Lett. 2014, 50, 837–839. [Google Scholar] [CrossRef]
- Ayadi, M.M.E.; Ismail, M.H.; Alhennawi, H.R. Unified approach for probability of detection evaluation over generalised fading channels. IET Commun. 2016, 10, 1532–1541. [Google Scholar] [CrossRef]
- Olver, F.W.J. NIST Handbook of Mathematical Functions; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar]
- Paris, J.F. Unified Analysis of the Average Gaussian Error Probability for a Class of Fading Channels. arXiv 2011, arXiv:1103.0502. [Google Scholar]
- Simmons, N.; Silva, C.R.N.D.; Cotton, S.L.; Sofotasios, P.C.; Yoo, S.K.; Yacoub, M.D. On Shadowing the κ − μ Fading Model. IEEE Access 2020, 8, 120513–120536. [Google Scholar] [CrossRef]
- Paris, J.F. Statistical Characterization of κ − μ Shadowed Fading. IEEE Trans. Veh. Technol. 2014, 63, 518–526. [Google Scholar] [CrossRef] [Green Version]
- Al-Hmood, H.; Al-Raweshidy, H.S. Unified Modeling of Composite κ -μ /Gamma, η -μ/Gamma, and α -μ/Gamma Fading Channels Using a Mixture Gamma Distribution With Applications to Energy Detection. IEEE Antennas Wirel. Propag. Lett. 2017, 16, 104–108. [Google Scholar] [CrossRef]
- Al-Hmood, H. Performance of Cognitive Radio Systems over κ − μ Shadowed with Integer μ and Fisher-Snedecor F Fading Channels. In Proceedings of the 2018 International Conference on Engineering Technology and their Applications (IICETA), Al-Najaf, Iraq, 8–9 May 2018. [Google Scholar] [CrossRef]
- Gvozdarev, A.S. Average quality description of energy detection for generalised multipath shadowed κ − μ fading channels. J. Electromagn. Waves Appl. 2021, 35, 2163–2175. [Google Scholar] [CrossRef]
- Ramirez-Espinosa, P.; Lopez-Martinez, F.J.; Paris, J.F.; Yacoub, M.D.; Martos-Naya, E. An Extension of the κ − μ Shadowed Fading Model: Statistical Characterization and Applications. IEEE Trans. Veh. Technol. 2018, 67, 3826–3837. [Google Scholar] [CrossRef] [Green Version]
- Shi, Z.; Zhang, H.; Zhong, S.; Yang, G.; Ye, X.; Ma, S. On the Performance of Variable-Rate HARQ-IR over Beckmann Fading Channels. In Proceedings of the 2018 10th International Conference on Wireless Communications and Signal Processing (WCSP), Hangzhou, China, 18–20 October 2018. [Google Scholar] [CrossRef]
- Chen, J.; Yuan, C. Coverage and Rate Analysis in Downlink L-Tier HetNets With Fluctuating Beckmann Fading. IEEE Wirel. Commun. Lett. 2019, 8, 1489–1492. [Google Scholar] [CrossRef]
- Al-Hmood, H.; Al-Raweshidy, H. Performance Analysis of Physical-Layer Security Over Fluctuating Beckmann Fading Channels. IEEE Access 2019, 7, 119541–119556. [Google Scholar] [CrossRef]
- Devarakonda, S.J.S.; Pamula, V.K. Error Rate Analysis of MPSK Signals over Fluctuating Beckmann Fading Channel. In Proceedings of the 2019 International Conference on Wireless Communications Signal Processing and Networking (WiSPNET), Chennai, India, 21–23 March 2019. [Google Scholar] [CrossRef]
- Olutayo, A.; Ma, H.; Cheng, J.; Holzman, J.F. Level Crossing Rate and Average Fade Duration for the Beaulieu-Xie Fading Model. IEEE Wirel. Commun. Lett. 2017, 6, 326–329. [Google Scholar] [CrossRef]
- Kansal, V.; Singh, S. Analysis of Average Symbol Error Probability of MDPSK, MFSK and MPSK in the Beaulieu-Xie Fading. In Proceedings of the 2018 6th Edition of International Conference on Wireless Networks & Embedded Systems (WECON), Rajpura, India, 16–17 November 2018. [Google Scholar] [CrossRef]
- Olutayo, A.; Cheng, J.; Holzman, J.F. A New Statistical Channel Model for Emerging Wireless Communication Systems. IEEE Open J. Commun. Soc. 2020, 1, 916–926. [Google Scholar] [CrossRef]
- Kansal, V.; Singh, S. Average Bit Error Rate Analysis of Selection Combining over Beaulieu-Xie Fading Model. In Proceedings of the 2020 6th International Conference on Signal Processing and Communication (ICSC), Noida, India, 5–7 March 2020. [Google Scholar] [CrossRef]
- Gvozdarev, A.S. The Generalized MGF Approach to Closed-Form Average Symbol Error Rate Calculation. IEEE Commun. Lett. 2021, 25, 1124–1128. [Google Scholar] [CrossRef]
- Bhatnagar, M.R. On the Sum of Correlated Squared κ − μ Shadowed Random Variables and Its Application to Performance Analysis of MRC. IEEE Trans. Veh. Technol. 2015, 64, 2678–2684. [Google Scholar] [CrossRef] [Green Version]
- Alouini, M.S.; Abdi, A.; Kaveh, M. Sum of gamma variates and performance of wireless communication systems over Nakagami-fading channels. IEEE Trans. Veh. Technol. 2001, 50, 1471–1480. [Google Scholar] [CrossRef]
- Zhang, J.; Chen, X.; Peppas, K.P.; Li, X.; Liu, Y. On High-Order Capacity Statistics of Spectrum Aggregation Systems Over κ − μ and κ − μ Shadowed Fading Channels. IEEE Trans. Commun. 2017, 65, 935–944. [Google Scholar] [CrossRef] [Green Version]
- Atapattu, S.; Tellambura, C.; Jiang, H. Energy Detection Based Cooperative Spectrum Sensing in Cognitive Radio Networks. IEEE Trans. Wirel. Commun. 2011, 10, 1232–1241. [Google Scholar] [CrossRef]
- Alhussein, O.; Hammadi, A.A.; Sofotasios, P.C.; Muhaidat, S.; Liang, J.; Al-Qutayri, M.; Karagiannidis, G.K. Performance analysis of energy detection over mixture gamma based fading channels with diversity reception. In Proceedings of the 2015 IEEE 11th International Conference on Wireless and Mobile Computing, Networking and Communications (WiMob), Abu Dhabi, United Arab Emirates, 19–21 October 2015. [Google Scholar] [CrossRef] [Green Version]
- van Laarhoven, P.J.; Kalker, T.A. On the computation of Lauricella functions of the fourth kind. J. Comput. Appl. Math. 1988, 21, 369–375. [Google Scholar] [CrossRef] [Green Version]
- Abate, J.; Whitt, W. Numerical Inversion of Laplace Transforms of Probability Distributions. ORSA J. Comput. 1995, 7, 36–43. [Google Scholar] [CrossRef] [Green Version]
- Cohen, A.M. Numerical Methods for Laplace Transform Inversion; Numerical Methods and Algorithms; Springer: New York, NY, USA, 2007; Volume 5. [Google Scholar] [CrossRef]
- Brychkov, Y.A.; Saad, N. Some formulas for the Appell F1(a, b, b’; c; w, z). Integral Transform. Spec. Funct. 2011, 23, 793–802. [Google Scholar] [CrossRef]
- Kumar, S.; Kalyani, S. Outage Probability and Rate for κ − μ Shadowed Fading in Interference Limited Scenario. IEEE Trans. Wirel. Commun. 2017, 16, 8289–8304. [Google Scholar] [CrossRef] [Green Version]
- Bouhlel, N.; Dziri, A. Kullback-Leibler Divergence Between Multivariate Generalized Gaussian Distributions. IEEE Signal Process. Lett. 2019, 26, 1021–1025. [Google Scholar] [CrossRef]
- Srivastava, H.; Karlsson, P. Multiple Gaussian Hypergeometric Series; Ellis Horwood Series in Mathematics and Its Applications; E. Horwood: Chichester, West Sussex, UK; Halsted Press: New York, NY, USA, 1985. [Google Scholar]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gvozdarev, A.S. A Novel Unified Framework for Energy-Based Spectrum Sensing Analysis in the Presence of Fading. Sensors 2022, 22, 1742. https://doi.org/10.3390/s22051742
Gvozdarev AS. A Novel Unified Framework for Energy-Based Spectrum Sensing Analysis in the Presence of Fading. Sensors. 2022; 22(5):1742. https://doi.org/10.3390/s22051742
Chicago/Turabian StyleGvozdarev, Aleksey S. 2022. "A Novel Unified Framework for Energy-Based Spectrum Sensing Analysis in the Presence of Fading" Sensors 22, no. 5: 1742. https://doi.org/10.3390/s22051742
APA StyleGvozdarev, A. S. (2022). A Novel Unified Framework for Energy-Based Spectrum Sensing Analysis in the Presence of Fading. Sensors, 22(5), 1742. https://doi.org/10.3390/s22051742




