Measurement of Corona Discharges under Variable Geometry, Frequency and Pressure Environment
Abstract
:1. Introduction
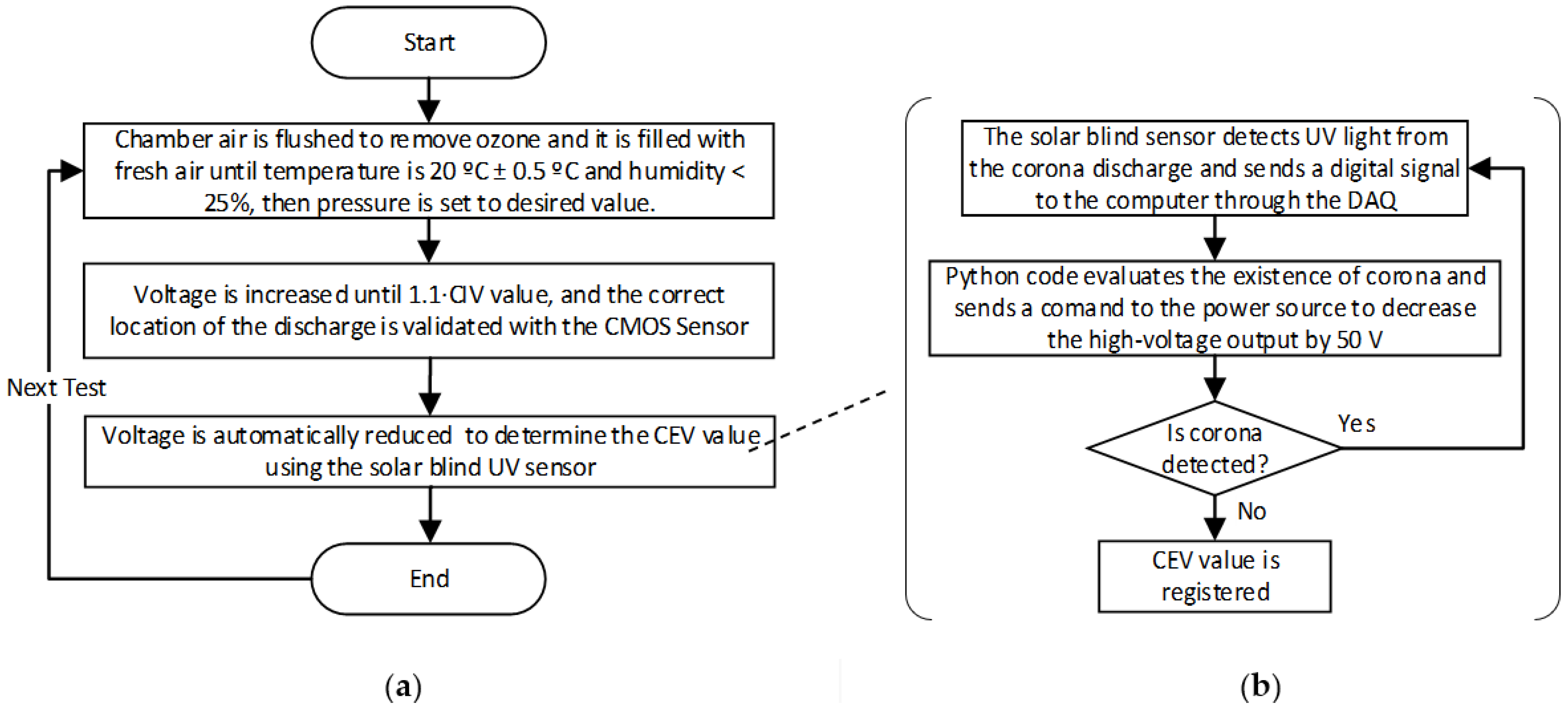
2. Procedure Applied to Detect the Corona Extinction Voltage (CEV)
3. Finite Element Method to Determine the Electric Field Strength
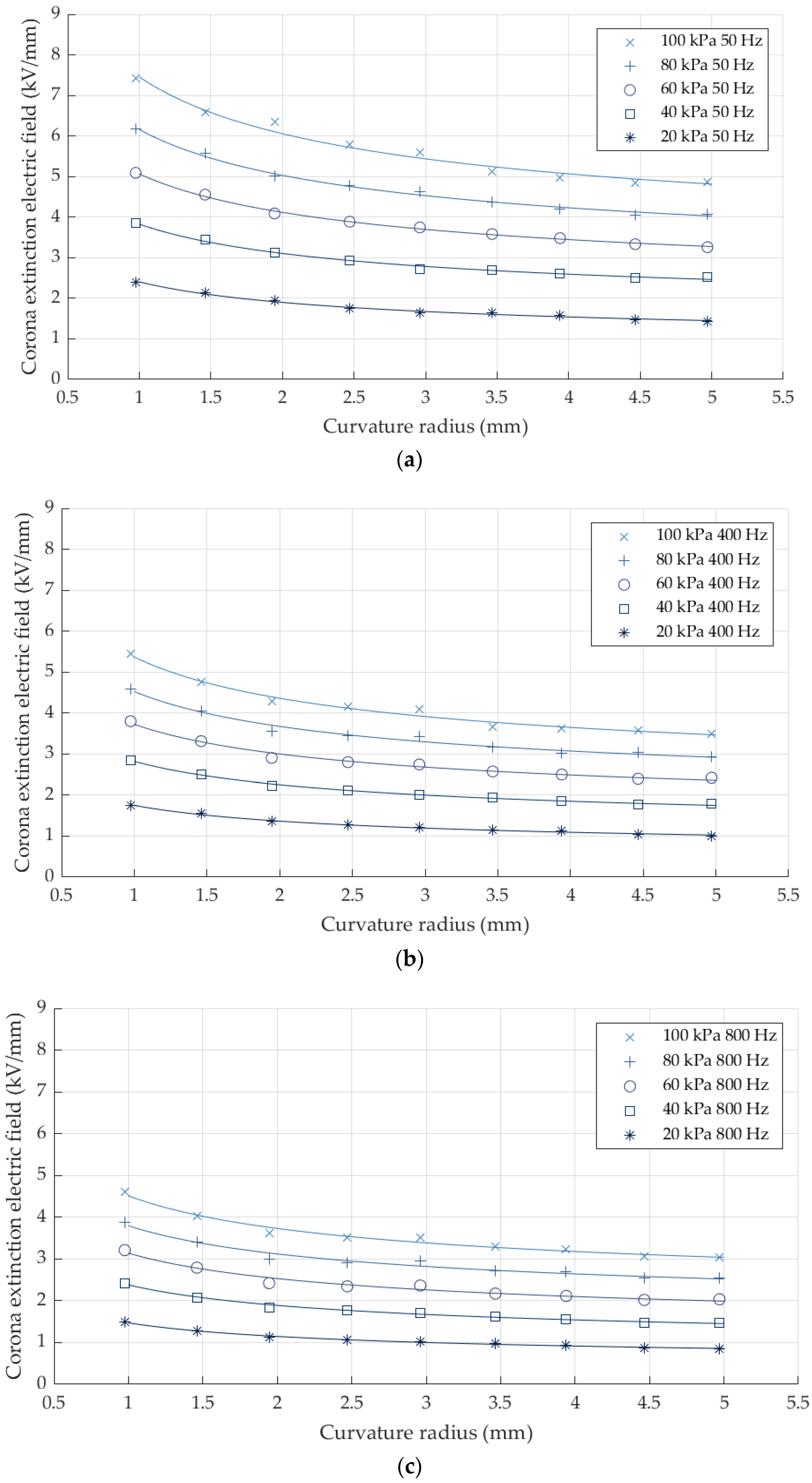
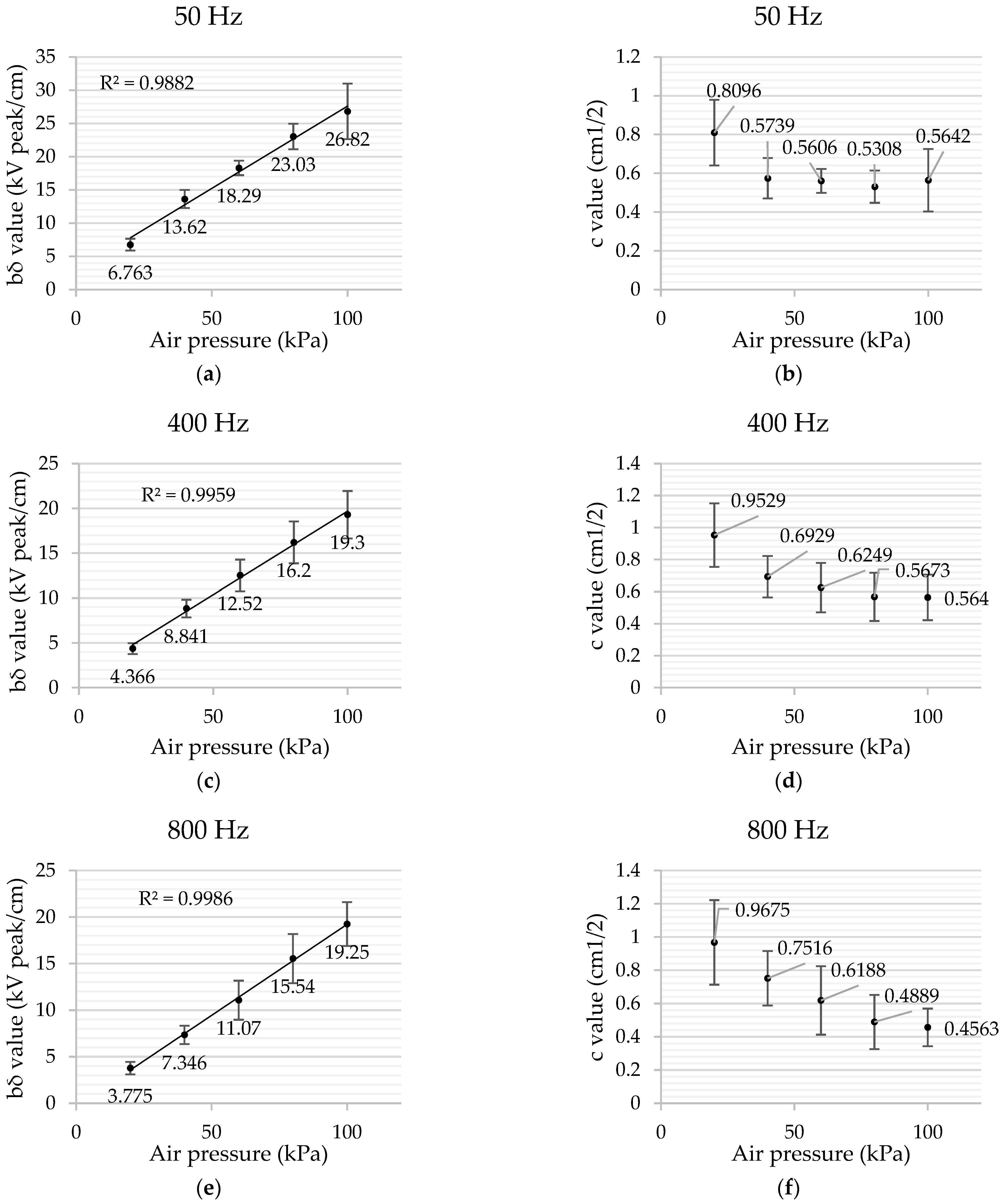
4. The Generalized Peek’s Law for Sphere-to-Plane Electrodes
5. Experimental Setup
6. Experimental Results
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Ramin, R.; Montanari, G.C.; Yang, Q. Designing the Insulation System for Motors in Electrified Aircraft: Optimization, Partial Discharge Issues and Use of Advanced Materials. Materials 2021, 14, 7555. [Google Scholar] [CrossRef] [PubMed]
- Bas-Calopa, P.; Riba, J.R.; Moreno-Eguilaz, M. Corona Discharge Characteristics under Variable Frequency and Pressure Environments. Sensors 2021, 21, 6676. [Google Scholar] [CrossRef] [PubMed]
- Riba, J.-R.; Gomez-Pau, A.; Moreno-Eguilaz, M. Sensor Comparison for Corona Discharge Detection Under Low Pressure Conditions. IEEE Sens. J. 2020, 20, 11698–11706. [Google Scholar] [CrossRef]
- Riba, J.-R.; Gómez-Pau, Á.; Moreno-Eguilaz, M. Experimental Study of Visual Corona under Aeronautic Pressure Conditions Using Low-Cost Imaging Sensors. Sensors 2020, 20, 411. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kuffel, J.; Zaengl, W.S.; Kuffel, P. High Voltage Engineering Fundamentals, 2nd ed.; Newnes: Oxford, UK, 2000; ISBN 978-0-7506-3634-6. [Google Scholar]
- Ravi, L.; Hu, J.; Zhao, X.; Dong, D.; Burgos, R.; Chandrasekaran, S.; Alipour, S.; Eddins, R. Electrical Insulation Design and Qualification of a SiC-based Generator-Rectifier Unit (GRU) for High-Altitude Operation. In Proceedings of the IEEE Energy Conversion Congress and Exposition (ECCE), Vancouver, BC, Canada, 10–14 October 2021; Institute of Electrical and Electronics Engineers (IEEE): Vancouver, BC, Canada, 2021; pp. 1514–1520. [Google Scholar]
- Landfried, R.; Savi, L.; Leblanc, T.; Teste, P. Parametric study of electric arcs in aeronautical condition of pressure. EPJ Appl. Phys. 2014, 67, 20802. [Google Scholar] [CrossRef]
- Hongkun, Z.; Tao, C.; Wenjun, L. Arc fault signatures detection on aircraft wiring system. In Proceedings of the World Congress on Intelligent Control and Automation (WCICA), Dalian, China, 21–23 June 2006; Volume 2, pp. 5548–5552. [Google Scholar]
- Riba, J.-R.; Moreno-Eguilaz, M.; Ortega, J.A. Arc Fault Protections for Aeronautic Applications: A Review Identifying the Effects, Detection Methods, Current Progress, Limitations, Future Challenges, and Research Needs. IEEE Trans. Instrum. Meas. 2022, 1. [Google Scholar] [CrossRef]
- Esfahani, A.N.; Shahabi, S.; Stone, G.; Kordi, B. Investigation of Corona Partial Discharge Characteristics Under Variable Frequency and Air Pressure. In Proceedings of the 2018 IEEE Electrical Insulation Conference (EIC), San Antonio, TX, USA, 17–20 June 2018; pp. 31–34. [Google Scholar]
- Rui, R.; Cotton, I. Impact of low pressure aerospace environment on machine winding insulation. In Proceedings of the 2010 IEEE International Symposium on Electrical Insulation, San Diego, CA, USA, 6–9 June 2010; pp. 1–5. [Google Scholar]
- Riba, J.-R.; Abomailek, C.; Casals-Torrens, P.; Capelli, F. Simplification and cost reduction of visual corona tests. IET Gener. Transm. Distrib. 2018, 12, 834–841. [Google Scholar] [CrossRef] [Green Version]
- Becan, M.; Babuder, M.; Vizintin, S.; Kobal, I. Corona performance of 400 kV bundle conductors and insulator strings. In Proceedings of the Cigré Session 2014, Paris, France, 24–29 August 2014; pp. 1–9. [Google Scholar]
- Riba, J.-R.; Moreno-Eguilaz, M.; Boizieau, M.; Ibrayemov, T. Performance Evaluation of Solar-Blind Gas-Filled Sensors to Detect Electrical Discharges for Low-Pressure Aircraft Applications. Sensors 2022, 22, 492. [Google Scholar] [CrossRef]
- Ilkhechi, H.D.; Samimi, M.H. Applications of the Acoustic Method in Partial Discharge Measurement: A Review. IEEE Trans. Dielectr. Electr. Insul. 2021, 28, 42–51. [Google Scholar] [CrossRef]
- Song, J.; Zhang, J.; Fan, X. Device for online monitoring of insulation faults in high-voltage switchgears. Int. J. Distrib. Sens. Netw. 2021, 17, 2021. [Google Scholar] [CrossRef]
- Chen, L.; MacAlpine, J.M.K.; Bian, X.; Wang, L.; Guan, Z. Comparison of methods for determining corona inception voltages of transmission line conductors. J. Electrostat. 2013, 71, 269–275. [Google Scholar] [CrossRef]
- Souza, A.L.; Lopes, I.J.S. Experimental investigation of corona onset in contaminated polymer surfaces. IEEE Trans. Dielectr. Electr. Insul. 2015, 22, 1321–1331. [Google Scholar] [CrossRef]
- Wais, S.I.; Giliyana, D.D. Sphere-to-Plane Electrodes Configuration of Positive and Negative Plasma Corona Discharge. Am. J. Mod. Phys. 2013, 2, 46–52. [Google Scholar] [CrossRef] [Green Version]
- Riba, J.-R.; Morosini, A.; Capelli, F.; Riba, J.-R.; Morosini, A.; Capelli, F. Comparative Study of AC and Positive and Negative DC Visual Corona for Sphere-Plane Gaps in Atmospheric Air. Energies 2018, 11, 2671. [Google Scholar] [CrossRef] [Green Version]
- Qiu, Z.; Zhang, L.; Liu, Y.; Liu, J.; Hou, H.; Zhu, X. Electrostatic Field Feature Selection Technique for Breakdown Voltage Prediction of Sphere Gaps Using Support Vector Regression. IEEE Trans. Magn. 2021, 57, 1–4. [Google Scholar] [CrossRef]
- Diaz, O.; Arevalo, L. Streamer-to-leader transition in a sphere-to-plane air gap tested with switching impulses. In Proceedings of the 2021 35th International Conference on Lightning Protection (ICLP) and XVI International Symposium on Lightning Protection (SIPDA), Colombo, Sri Lanka, 20–26 September 2021; pp. 1–4. [Google Scholar] [CrossRef]
- Afrouzi, H.N.; Hassan, A.; Tay Ye Chee, D.; Mehranzamir, K.; Abdul Malek, Z.; Mashak, S.V.; Ahmed, J. In-depth exploration of partial discharge modelling methods within insulations. Clean. Eng. Technol. 2022, 6, 100390. [Google Scholar] [CrossRef]
- Turner, J.; Igoe, D.; Parisi, A.V.; McGonigle, A.J.; Amar, A.; Wainwright, L. A review on the ability of smartphones to detect ultraviolet (UV) radiation and their potential to be used in UV research and for public education purposes. Sci. Total Environ. 2020, 706, 135873. [Google Scholar] [CrossRef] [PubMed]
- Wu, H.; Wang, J.; Liu, P.; Peng, Z.; Deng, Z.; Wei, X. Research on corona inception electric-field strength and critical electric-field values for valve hall fittings. In Proceedings of the 2014 IEEE Conference on Electrical Insulation and Dielectric Phenomena (CEIDP), Des Moines, IA, USA, 19–22 October 2014; pp. 308–311. [Google Scholar]
- Linder, W.; Steele, H. Estimating voltage breakdown performance of high-altitude antennas. In Proceedings of the WESCON/59 Conference Record, San Francisco, CA, USA, 18–21 August 1959; Volume 3, pp. 9–16. [Google Scholar]
- Peek, F.W. The law of corona and the dielectric strength of air. Proc. Am. Inst. Electr. Eng. 1911, 30, 1485–1561. [Google Scholar] [CrossRef]



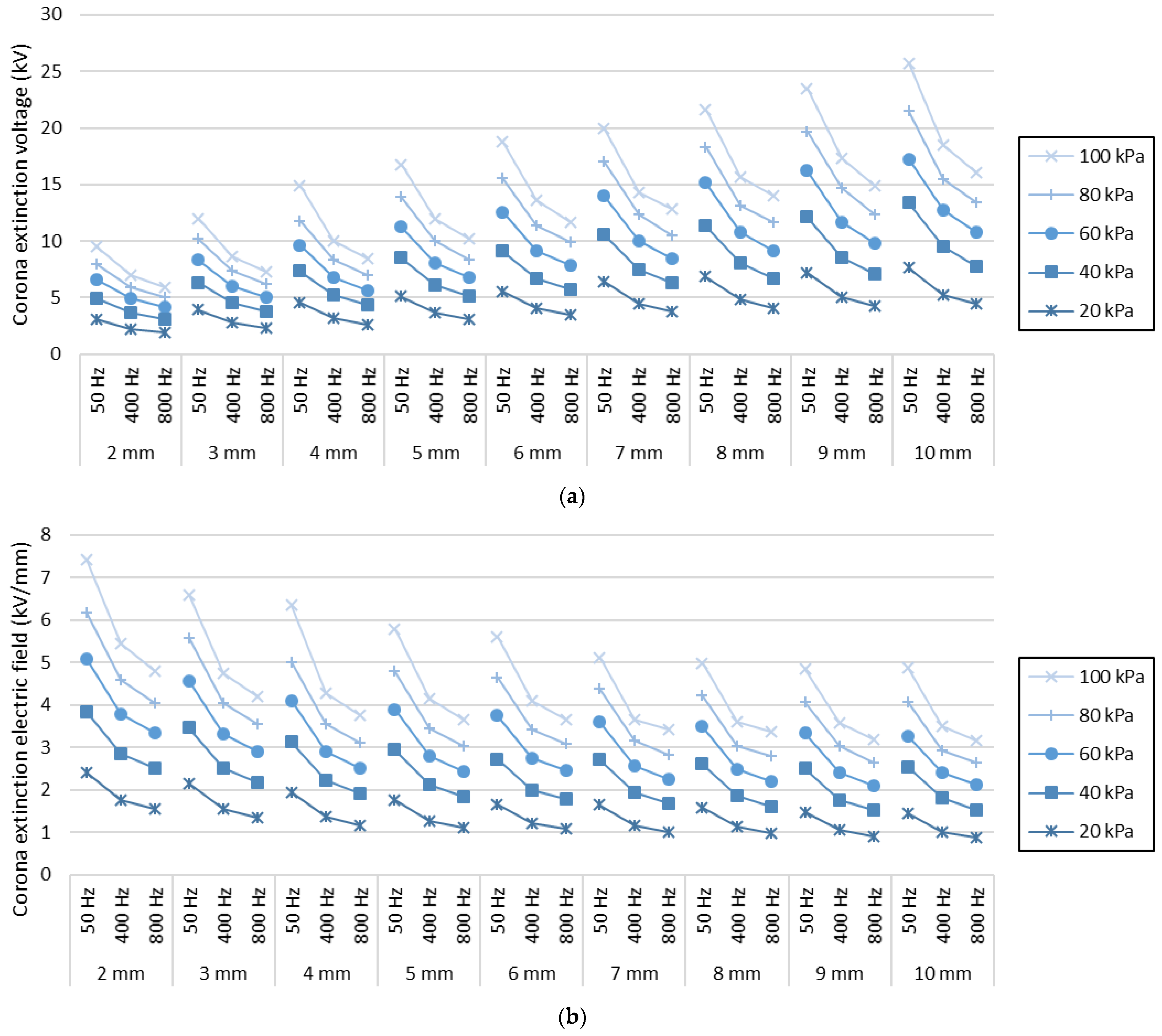
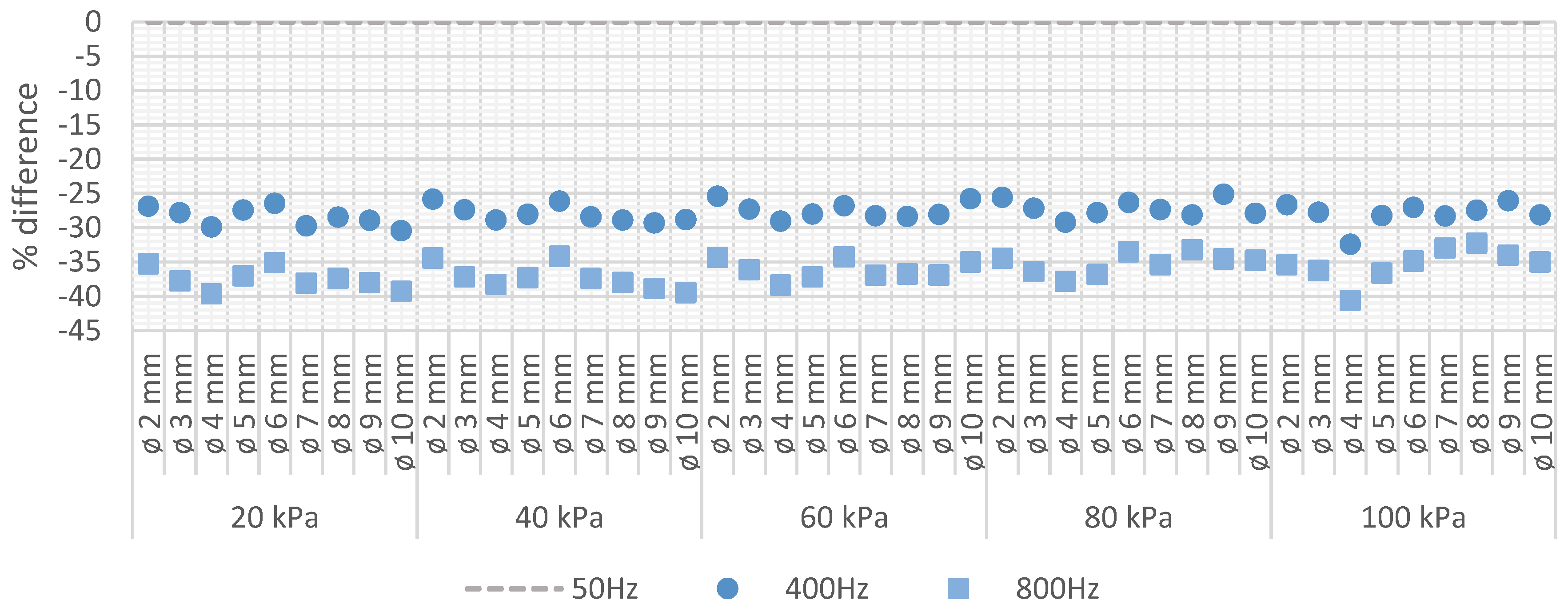
| Air Pressure (kPa) | Sphere Diameter (mm) | CEV (Corona Extinction Voltage) (kVpeak) | Corona Extinction Electric Field Strength (kVpeak/mm) | ||||
|---|---|---|---|---|---|---|---|
| 50 Hz | 400 Hz | 800 Hz | 50 Hz | 400 Hz | 800 Hz | ||
| 20 kPa | 2 mm | 3.099 | 2.265 | 1.927 | 2.403 | 1.757 | 1.555 |
| 3 mm | 3.901 | 2.815 | 2.333 | 2.148 | 1.550 | 1.336 | |
| 4 mm | 4.542 | 3.185 | 2.634 | 1.939 | 1.359 | 1.170 | |
| 5 mm | 5.055 | 3.668 | 3.059 | 1.750 | 1.270 | 1.102 | |
| 6 mm | 5.522 | 4.061 | 3.444 | 1.655 | 1.217 | 1.074 | |
| 7 mm | 6.371 | 4.477 | 3.791 | 1.638 | 1.151 | 1.014 | |
| 8 mm | 6.829 | 4.884 | 4.107 | 1.574 | 1.125 | 0.985 | |
| 9 mm | 7.154 | 5.084 | 4.261 | 1.475 | 1.049 | 0.914 | |
| 10 mm | 7.600 | 5.285 | 4.434 | 1.439 | 1.001 | 0.874 | |
| 40 kPa | 2 mm | 4.967 | 3.683 | 3.129 | 3.852 | 2.857 | 2.525 |
| 3 mm | 6.280 | 4.560 | 3.790 | 3.457 | 2.510 | 2.171 | |
| 4 mm | 7.307 | 5.196 | 4.334 | 3.119 | 2.218 | 1.925 | |
| 5 mm | 8.508 | 6.122 | 5.128 | 2.946 | 2.120 | 1.848 | |
| 6 mm | 9.071 | 6.700 | 5.738 | 2.719 | 2.008 | 1.790 | |
| 7 mm | 10.519 | 7.528 | 6.328 | 2.704 | 1.935 | 1.693 | |
| 8 mm | 11.312 | 8.045 | 6.740 | 2.607 | 1.854 | 1.616 | |
| 9 mm | 12.117 | 8.564 | 7.117 | 2.499 | 1.766 | 1.527 | |
| 10 mm | 13.381 | 9.525 | 7.782 | 2.534 | 1.804 | 1.534 | |
| 60 kPa | 2 mm | 6.574 | 4.902 | 4.149 | 5.099 | 3.802 | 3.348 |
| 3 mm | 8.285 | 6.021 | 5.082 | 4.561 | 3.315 | 2.912 | |
| 4 mm | 9.596 | 6.806 | 5.683 | 4.096 | 2.905 | 2.524 | |
| 5 mm | 11.241 | 8.092 | 6.786 | 3.892 | 2.802 | 2.445 | |
| 6 mm | 12.516 | 9.159 | 7.904 | 3.751 | 2.745 | 2.465 | |
| 7 mm | 13.961 | 10.011 | 8.463 | 3.589 | 2.574 | 2.264 | |
| 8 mm | 15.134 | 10.841 | 9.195 | 3.487 | 2.498 | 2.205 | |
| 9 mm | 16.180 | 11.635 | 9.810 | 3.337 | 2.399 | 2.105 | |
| 10 mm | 17.232 | 12.791 | 10.763 | 3.263 | 2.422 | 2.121 | |
| 80 kPa | 2 mm | 7.962 | 5.925 | 5.013 | 6.175 | 4.595 | 4.046 |
| 3 mm | 10.129 | 7.377 | 6.188 | 5.576 | 4.061 | 3.545 | |
| 4 mm | 11.748 | 8.316 | 7.017 | 5.015 | 3.549 | 3.117 | |
| 5 mm | 13.843 | 9.992 | 8.404 | 4.793 | 3.460 | 3.028 | |
| 6 mm | 15.495 | 11.414 | 9.897 | 4.645 | 3.421 | 3.087 | |
| 7 mm | 17.001 | 12.348 | 10.551 | 4.370 | 3.174 | 2.823 | |
| 8 mm | 18.288 | 13.141 | 11.732 | 4.214 | 3.028 | 2.813 | |
| 9 mm | 19.665 | 14.721 | 12.363 | 4.055 | 3.036 | 2.653 | |
| 10 mm | 21.487 | 15.485 | 13.473 | 4.069 | 2.932 | 2.655 | |
| 100 kPa | 2 mm | 9.576 | 7.023 | 5.944 | 7.427 | 5.446 | 4.797 |
| 3 mm | 11.972 | 8.648 | 7.333 | 6.591 | 4.761 | 4.201 | |
| 4 mm | 14.880 | 10.053 | 8.488 | 6.351 | 4.291 | 3.770 | |
| 5 mm | 16.731 | 12.004 | 10.189 | 5.793 | 4.156 | 3.671 | |
| 6 mm | 18.717 | 13.654 | 11.711 | 5.610 | 4.093 | 3.653 | |
| 7 mm | 19.913 | 14.278 | 12.823 | 5.119 | 3.671 | 3.431 | |
| 8 mm | 21.630 | 15.687 | 14.080 | 4.984 | 3.615 | 3.376 | |
| 9 mm | 23.467 | 17.349 | 14.884 | 4.839 | 3.578 | 3.194 | |
| 10 mm | 25.731 | 18.485 | 16.067 | 4.873 | 3.501 | 3.166 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bas-Calopa, P.; Riba, J.-R.; Moreno-Eguilaz, M. Measurement of Corona Discharges under Variable Geometry, Frequency and Pressure Environment. Sensors 2022, 22, 1856. https://doi.org/10.3390/s22051856
Bas-Calopa P, Riba J-R, Moreno-Eguilaz M. Measurement of Corona Discharges under Variable Geometry, Frequency and Pressure Environment. Sensors. 2022; 22(5):1856. https://doi.org/10.3390/s22051856
Chicago/Turabian StyleBas-Calopa, Pau, Jordi-Roger Riba, and Manuel Moreno-Eguilaz. 2022. "Measurement of Corona Discharges under Variable Geometry, Frequency and Pressure Environment" Sensors 22, no. 5: 1856. https://doi.org/10.3390/s22051856
APA StyleBas-Calopa, P., Riba, J.-R., & Moreno-Eguilaz, M. (2022). Measurement of Corona Discharges under Variable Geometry, Frequency and Pressure Environment. Sensors, 22(5), 1856. https://doi.org/10.3390/s22051856








