Dual-Wavelength Polarization-Dependent Bifocal Metalens for Achromatic Optical Imaging Based on Holographic Principle
Abstract
:1. Introduction
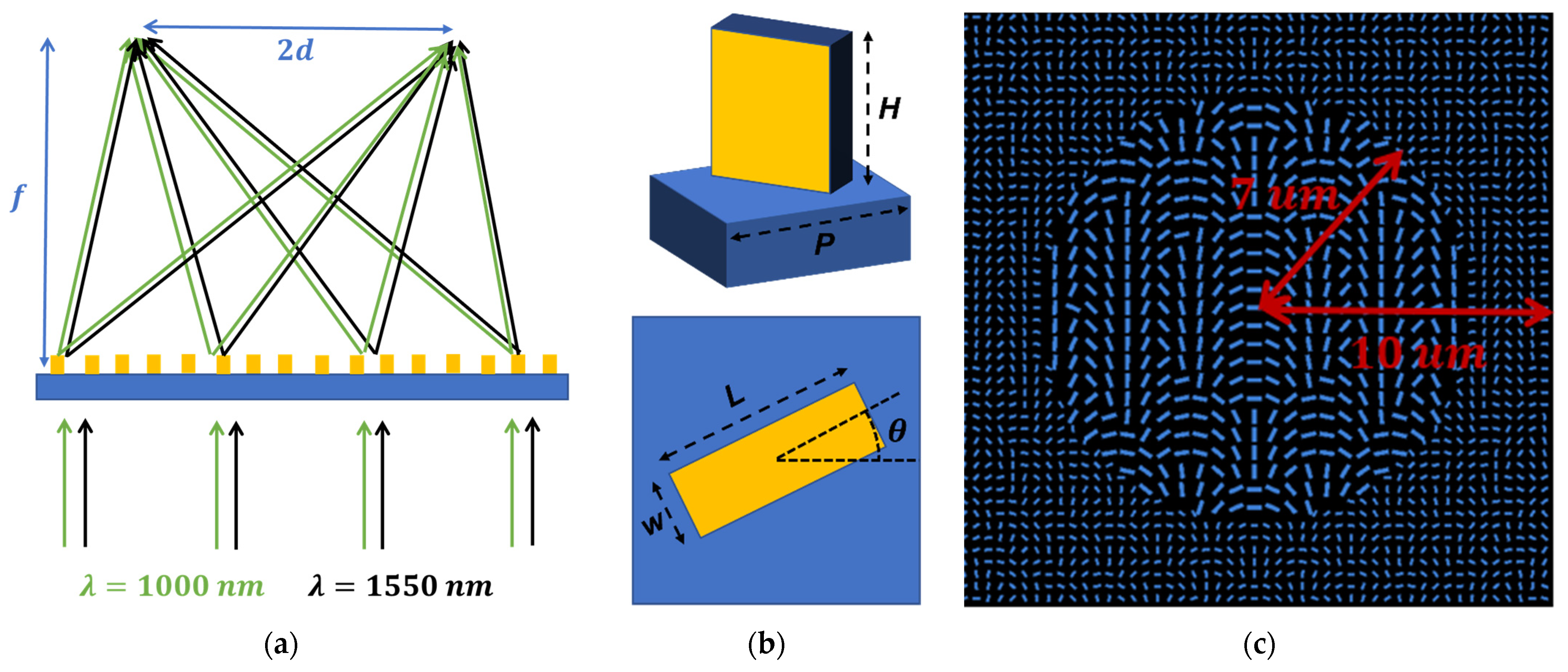
2. Designs and Structures
3. Results and Discussions
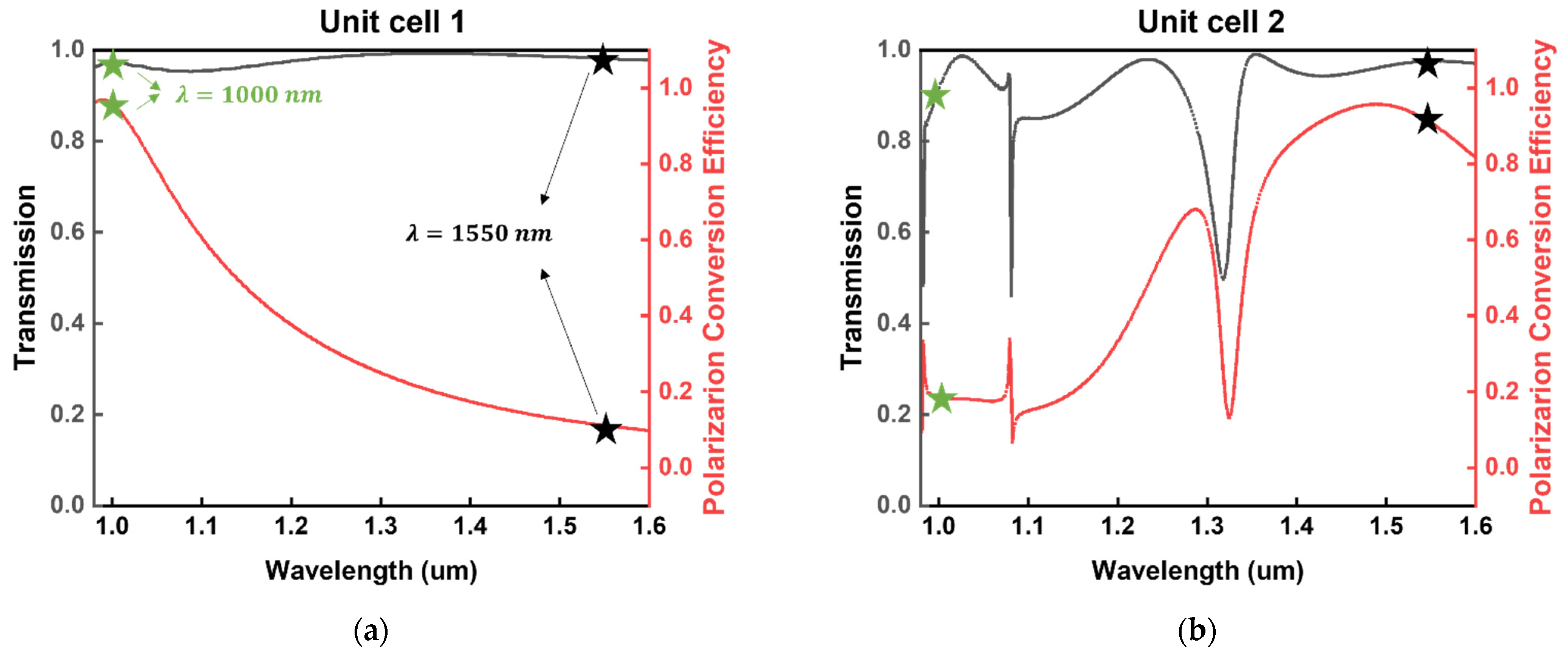
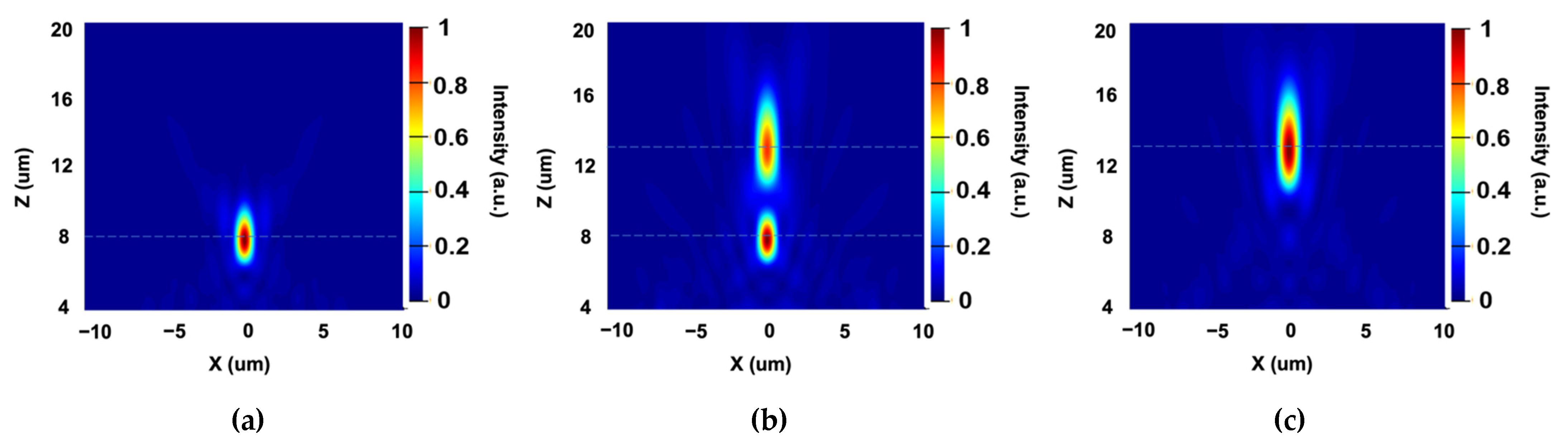
3.1. Dual-Wavelength Achromatic Metalens
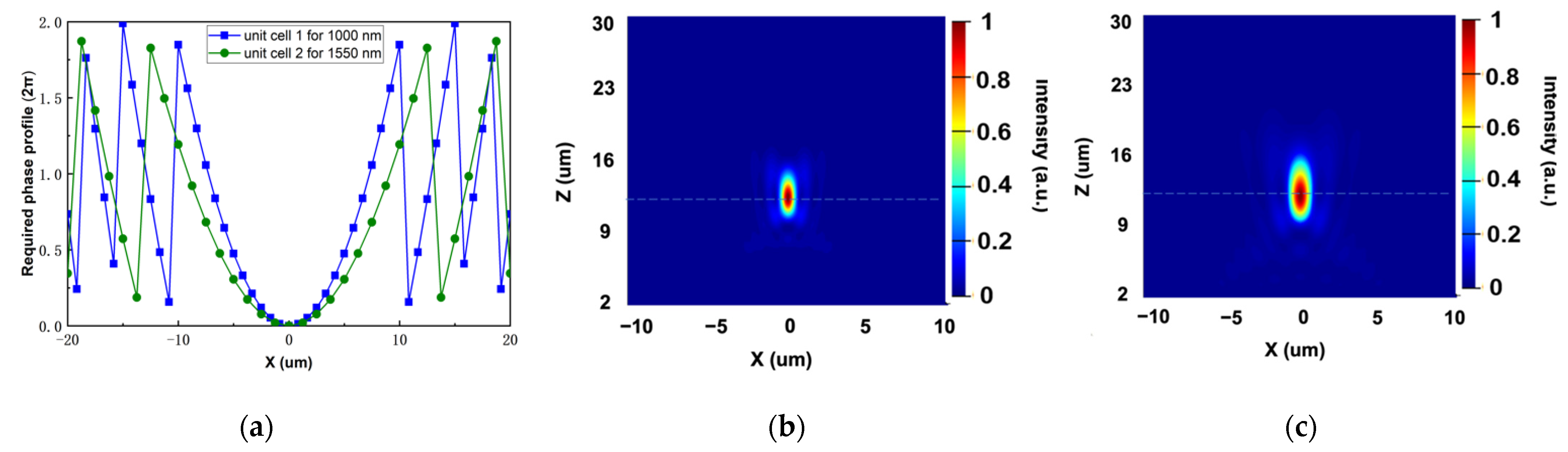
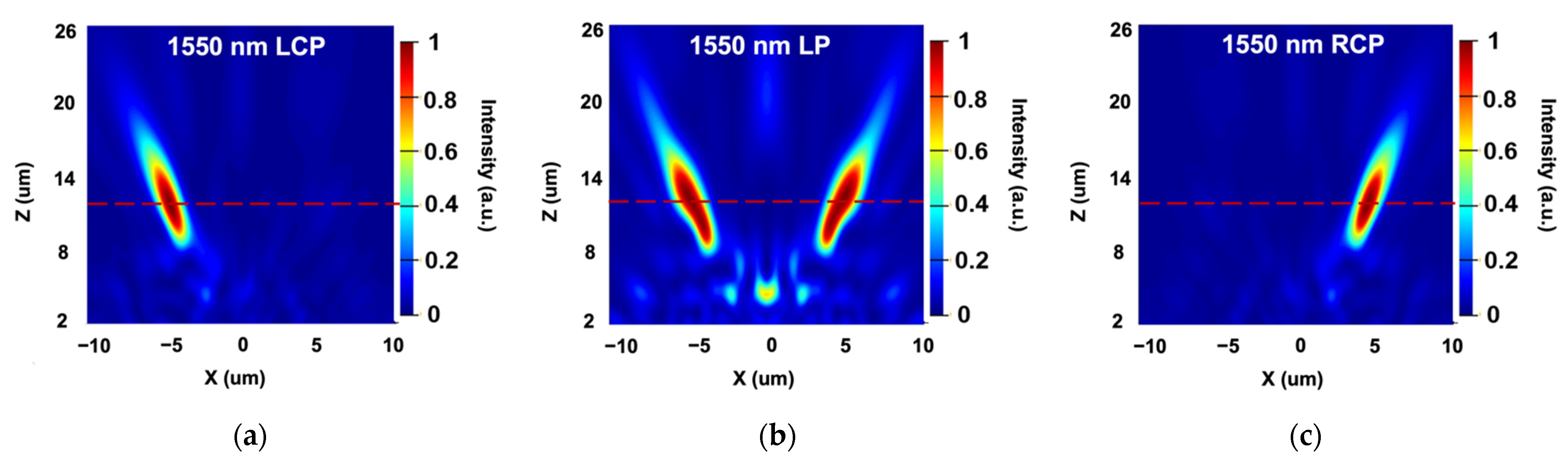
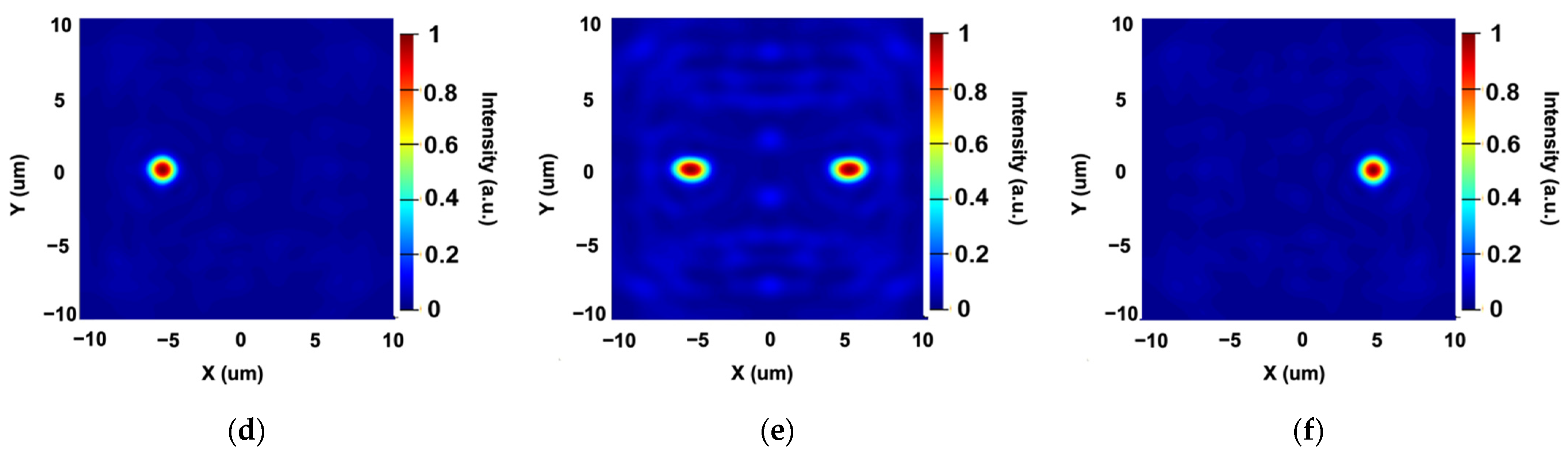
3.2. Polarization-Dependent Bifocal Metalens Using the Holographic Principle
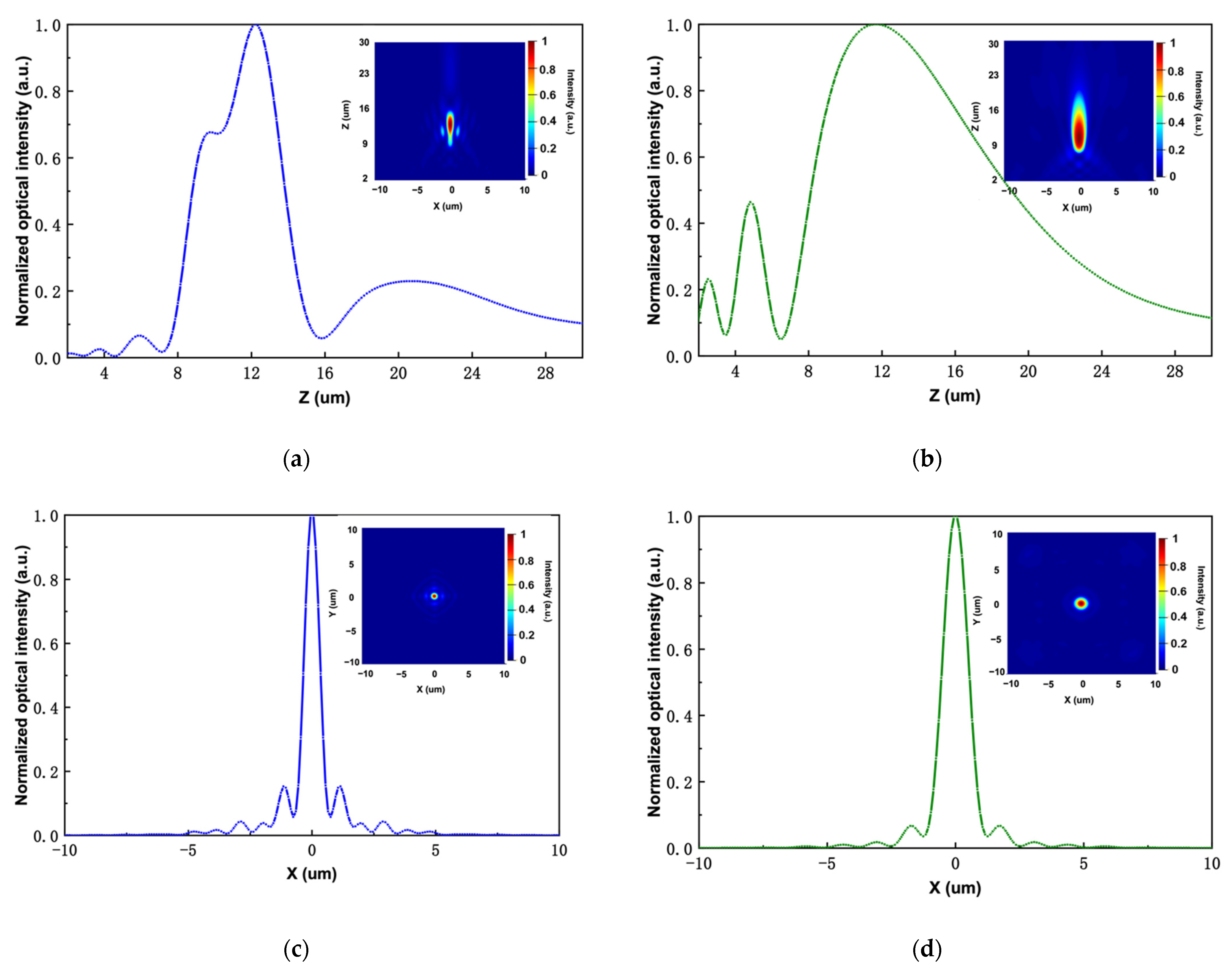
3.3. Performance of the Proposed Metalens
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Yu, N.; Genevet, P.; Kats, M.A.; Aieta, F.; Tetienne, J.-P.; Capasso, F.; Gaburro, Z. Light Propagation with Phase Discontinuities: Generalized Laws of Reflection and Refraction. Science 2011, 334, 333–337. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yu, N.; Capasso, F. Flat Optics with Designer Metasurfaces. Nat. Mater. 2014, 13, 139–150. [Google Scholar] [CrossRef] [PubMed]
- Arbabi, A.; Horie, Y.; Bagheri, M.; Faraon, A. Dielectric Metasurfaces for Complete Control of Phase and Polarization with Subwavelength Spatial Resolution and High Transmission. Nat. Nanotechnol. 2015, 10, 937–943. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhang, M.; Pu, M.; Zhang, F.; Guo, Y.; He, Q.; Ma, X.; Huang, Y.; Li, X.; Yu, H.; Luo, X. Plasmonic Metasurfaces for Switchable Photonic Spin-orbit Interactions based on Phase Change Materials. Adv. Sci. 2018, 5, 1800835. [Google Scholar] [CrossRef] [PubMed]
- Sun, S.; Yang, K.Y.; Wang, C.M.; Juan, T.K.; Chen, W.T.; Liao, C.Y.; He, Q.; Xiao, S.; Kung, W.-T.; Guo, G.-Y.; et al. High-Efficiency Broadband Anomalous Reflection by Gradient Meta-Surfaces. Nano Lett. 2012, 12, 6223–6229. [Google Scholar] [CrossRef] [PubMed]
- Huang, Y.W.; Chen, W.T.; Tsai, W.-Y.; Wu, P.C.; Wang, C.M.; Sun, G.; Tsai, D.P. Aluminum Plasmonic Multicolor Meta-Hologram. Nano Lett. 2015, 15, 3122–3127. [Google Scholar] [CrossRef] [PubMed]
- Khorasaninejad, M.; Ambrosio, A.; Kanhaiya, P.; Capasso, F. Broadband and chiral binary dielectric meta-holograms. Sci. Adv. 2016, 2, e1501258. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kim, I.; Kim, W.-S.; Kim, K.; Ansari, M.A.; Mehmood, M.Q.; Badloe, T.; Kim, Y.; Gwak, J.; Lee, H.; Kim, Y.-K.; et al. Holographic metasurface gas sensors for instantaneous visual alarms. Sci. Adv. 2021, 7, eabe9943. [Google Scholar] [CrossRef] [PubMed]
- Principe, M.; Consales, M.; Micco, A.; Crescitelli, A.; Castaldi, G.; Esposito, E.; La Ferrara, V.; Cutolo, A.; Galdi, V.; Cusano, A. Optical fiber meta-tips. Light Sci. Appl. 2016, 6, e16226. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Xie, J.; Guo, H.; Zhuang, S.; Hu, J. Polarization-controllable perfect vortex beam by a dielectric metasurface. Opt. Express 2021, 29, 3081–3089. [Google Scholar] [CrossRef]
- Li, S.; Li, X.; Zhang, L.; Wang, G.; Zhang, L.; Liu, M.; Zeng, C.; Wang, L.; Sun, Q.; Zhao, W.; et al. Efficient optical angular momentum manipulation for compact multiplexing and demultiplexing using a dielectric metasurface. Adv. Opt. Mater. 2020, 8, 1901666. [Google Scholar] [CrossRef]
- Zhang, S.; Huo, P.; Zhu, W.; Zhang, C.; Chen, P.; Liu, M.; Chen, L.; Lezec, H.J.; Agrawal, A.; Lu, Y.; et al. Broadband detection of multiple spin and orbital angular momenta via dielectric metasurface. Laser Photonics Rev. 2020, 14, 2000062. [Google Scholar] [CrossRef]
- Wu, P.C.; Tsai, W.Y.; Chen, W.T.; Huang, Y.W.; Chen, T.Y.; Chen, J.-W.; Liao, C.Y.; Chu, C.H.; Sun, G.; Tsai, D.P. Versatile Polarization Generation with an Aluminum Plasmonic Metasurface. Nano Lett. 2017, 17, 445–452. [Google Scholar] [CrossRef] [PubMed]
- Khorasaninejad, M.; Chen, W.T.; Devlin, R.C.; Oh, J.; Zhu, A.Y.; Capasso, F. Metalenses at Visible Wavelengths: Diffraction-Limited Focusing and Subwavelength Resolution Imaging. Science 2016, 352, 1190–1194. [Google Scholar] [CrossRef] [Green Version]
- Khorasaninejad, M.; Zhu, A.Y.; Roques-Carmes, C.; Chen, W.T.; Oh, J.; Mishra, I.; Devlin, R.C.; Capasso, F. Polarization-insensitive metalenses at visible wavelengths. Nano Lett. 2016, 16, 7229–7234. [Google Scholar] [CrossRef]
- Chen, W.T.; Zhu, A.Y.; Sanjeev, V.; Khorasaninejad, M.; Shi, Z.; Lee, E.; Capasso, F. A broadband achromatic metalens for focusing and imaging in the visible. Nat. Nanotechnol. 2018, 13, 220–226. [Google Scholar] [CrossRef] [Green Version]
- Pahlevaninezhad, H.; Khorasaninejad, M.; Huang, Y.W.; Shi, Z.; Hariri, L.P.; Adams, D.C.; Ding, V.; Zhu, A.; Qiu, C.W.; Capasso, F.; et al. Nano-optic endoscope for high-resolution optical coherence tomography in vivo. Nat. Photonics 2018, 12, 540–547. [Google Scholar] [CrossRef] [PubMed]
- Yang, J.; Ghimire, I.; Wu, P.C.; Gurung, S.; Arndt, C.; Tsai, D.P.; Lee, H.W. Photonic Crystal Fiber Metalens. Nanophotonics 2019, 8, 443–449. [Google Scholar] [CrossRef]
- Qu, J.; Zhao, Q.; Yu, C. Single-Mode Fiber Metalenses Based on Dielectric Nanopillars. In Proceedings of the 26th Optoelectronics and Communications Conference, Hong Kong, 3–7 July 2021. [Google Scholar]
- Zhao, Q.; Qu, J.; Peng, G.; Yu, C. Endless single-mode Photonics Crystal Fiber Metalens for broadband and efficient focusing in near-infrared range. Micromachines 2021, 12, 219. [Google Scholar] [CrossRef]
- Chen, X.; Chen, M.; Mehmood, M.Q.; Wen, D.; Yue, F.; Qiu, C.-W.; Zhang, S. Longitudinal multifoci metalens for circularly polarized light. Adv. Opt. Mater. 2015, 3, 1201–1206. [Google Scholar] [CrossRef]
- Gao, S.; Park, C.; Zhou, C.; Lee, S.; Choi, D. Twofold Polarization-Selective All-Dielectric Trifoci Metalens for Linearly Polarized Visible Light. Adv. Opt. Mater. 2019, 7, 1900883. [Google Scholar] [CrossRef]
- Khorasaninejad, M.; Chen, W.T.; Zhu, A.Y.; Oh, J.; Devlin, R.C.; Rousso, D.; Capasso, F. Multispectral chiral imaging with a metalens. Nano Lett. 2016, 16, 4595–4600. [Google Scholar] [CrossRef] [PubMed]
- Chen, C.; Gao, S.; Song, W.; Li, H.; Zhu, S.N.; Li, T. Metasurfaces with planar chiral meta-atoms for spin light manipulation. Nano Lett. 2021, 21, 1815–1821. [Google Scholar] [CrossRef] [PubMed]
- Shen, Z.; Zhou, S.; Ge, S.; Duan, W.; Ma, L.; Lu, Y.; Hu, W. Liquid crystal tunable terahertz lens with spin-selected focusing property. Opt. Express 2019, 27, 8800. [Google Scholar] [CrossRef] [PubMed]
- Wang, W.; Guo, Z.; Zhou, K.; Sun, Y.; Shen, F.; Li, Y.; Qu, S.; Liu, S. Polarization-independent longitudinal multi-focusing metalens. Opt. Express 2015, 23, 29855–29866. [Google Scholar] [CrossRef]
- Lv, H.; Lu, X.; Han, Y.; Mou, Z.; Teng, S. Multifocal metalens with a controllable intensity ratio. Opt. Lett. 2019, 44, 2518–2521. [Google Scholar] [CrossRef]
- Tian, S.; Guo, H.; Hu, J.; Zhuang, S. Dielectric longitudinal bifocal metalens with adjustable intensity and high focusing efficiency. Opt. Express 2019, 27, 680–688. [Google Scholar] [CrossRef]
- Chen, D.; Wang, J.; Wang, S.; Zhao, S.; Qi, Y.; Sun, X. The bifocal metalenses for independent focusing of orthogonally circularly polarized light. J. Phys. D 2020, 54, 075103. [Google Scholar] [CrossRef]
- Zhou, Y.; Yuan, Y.; Zeng, T.; Wang, X.; Tang, D.; Fan, F.; Wen, S. Liquid crystal bifocal lens with adjustable intensities through polarization controls. Opt. Lett. 2020, 2020 45, 5716. [Google Scholar] [CrossRef]
- Tang, L.; Jin, R.; Cao, Y.; Li, J.; Wang, J.; Dong, Z.G. Spin-dependent dual-wavelength multiplexing metalens. Opt. Lett. 2020, 45, 5258–5261. [Google Scholar] [CrossRef]
- Ding, J.; An, S.; Zheng, B.; Zhang, H. Multiwavelength metasurfaces based on single-layer dual-wavelength meta-atoms: Toward complete phase and amplitude modulations at two wavelengths. Adv. Opt. Mater. 2017, 5, 1700079. [Google Scholar] [CrossRef]
- Lin, R.; Li, X. Multifocal metalens based on multi-layer Pancharatnam-Berry phase elements architecture. Opt. Lett. 2019, 44, 2819–2822. [Google Scholar] [CrossRef]
- Groever, B.; Chen, W.T.; Capasso, F. Meta-lens doublet in the visible region. Nano Lett. 2017, 17, 4902–4907. [Google Scholar] [CrossRef] [PubMed]
- Yang, H.; Li, G.; Cao, G.; Yu, F.; Zhao, Z.; Ou, K.; Chen, X.; Lu, W. High efficiency dual-wavelength achromatic metalens via cascaded dielectric metasurfaces. Opt. Mater. Express 2018, 8, 1940–1950. [Google Scholar] [CrossRef]
- Avayu, O.; Almeida, E.; Prior, Y.; Ellenbogen, T. Composite functional metasurfaces for multispectral achromatic optics. Nat. Commun. 2017, 8, 1–7. [Google Scholar] [CrossRef]
- Lin, D.; Holsteen, A.L.; Maguid, E.; Wetzstein, G.; Kik, P.G.; Hasman, E.; Brongersma, M.L. Photonic multitasking interleaved si nanoantenna phased array. Nano Lett. 2016, 16, 7671–7676. [Google Scholar] [CrossRef]
- Pang, H.; Gao, H.; Deng, Q.; Yin, S.; Qiu, Q.; Du, C. Multi-focus plasmonic lens design based on Holography. Opt. Express 2013, 21, 18689–18696. [Google Scholar] [CrossRef] [PubMed]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qu, J.; Luo, H.; Yu, C. Dual-Wavelength Polarization-Dependent Bifocal Metalens for Achromatic Optical Imaging Based on Holographic Principle. Sensors 2022, 22, 1889. https://doi.org/10.3390/s22051889
Qu J, Luo H, Yu C. Dual-Wavelength Polarization-Dependent Bifocal Metalens for Achromatic Optical Imaging Based on Holographic Principle. Sensors. 2022; 22(5):1889. https://doi.org/10.3390/s22051889
Chicago/Turabian StyleQu, Jiaqi, Huaijian Luo, and Changyuan Yu. 2022. "Dual-Wavelength Polarization-Dependent Bifocal Metalens for Achromatic Optical Imaging Based on Holographic Principle" Sensors 22, no. 5: 1889. https://doi.org/10.3390/s22051889
APA StyleQu, J., Luo, H., & Yu, C. (2022). Dual-Wavelength Polarization-Dependent Bifocal Metalens for Achromatic Optical Imaging Based on Holographic Principle. Sensors, 22(5), 1889. https://doi.org/10.3390/s22051889







