Development and Validation of a Weigh-in-Motion Methodology for Railway Tracks
Abstract
:1. Introduction
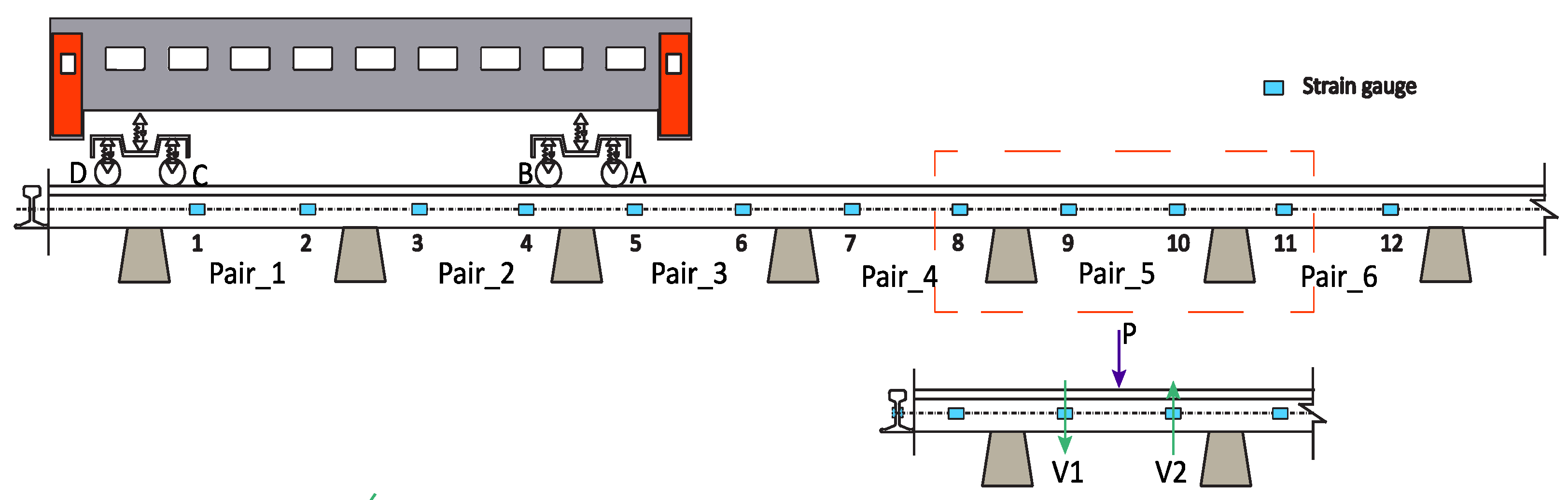
2. Layout Scheme of the WIM System
3. Description of the Train–Track Coupling Model
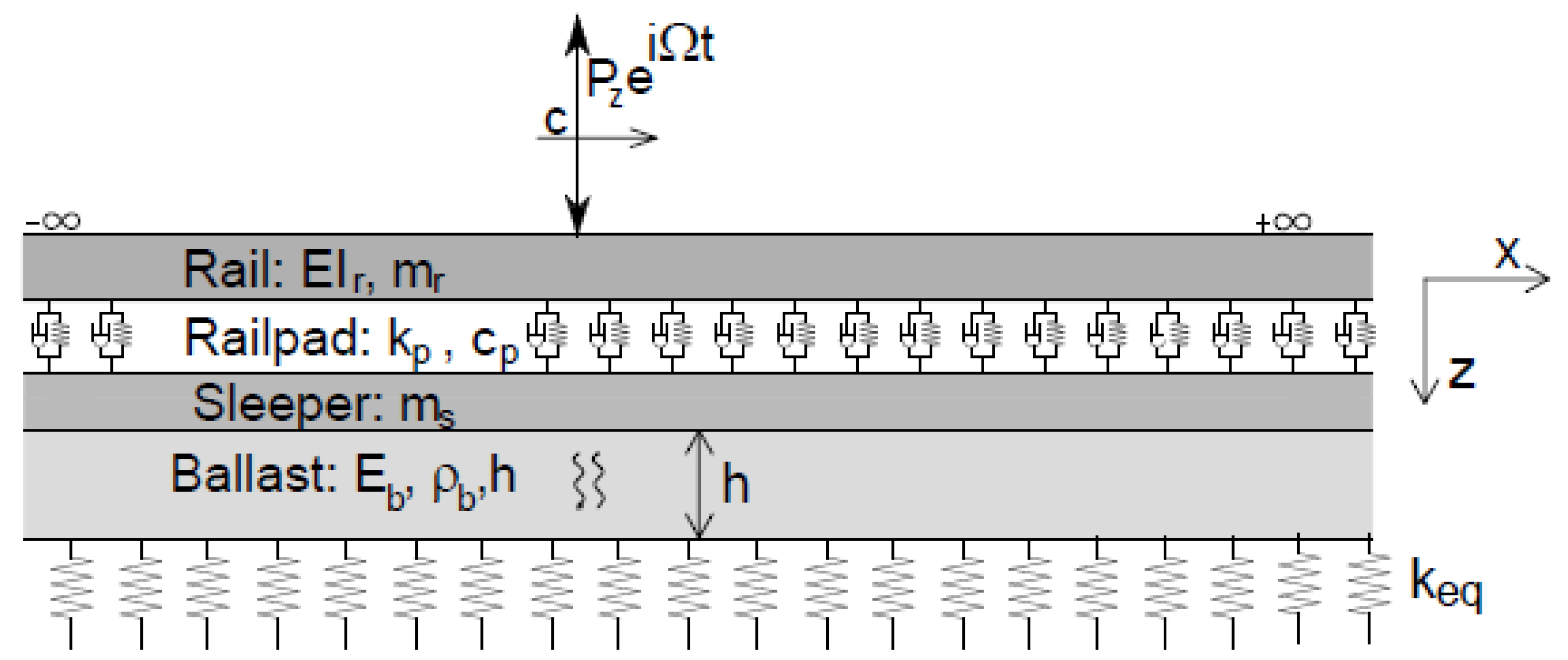
3.1. Track Model
3.2. Train Model
3.3. Train–Track Interaction
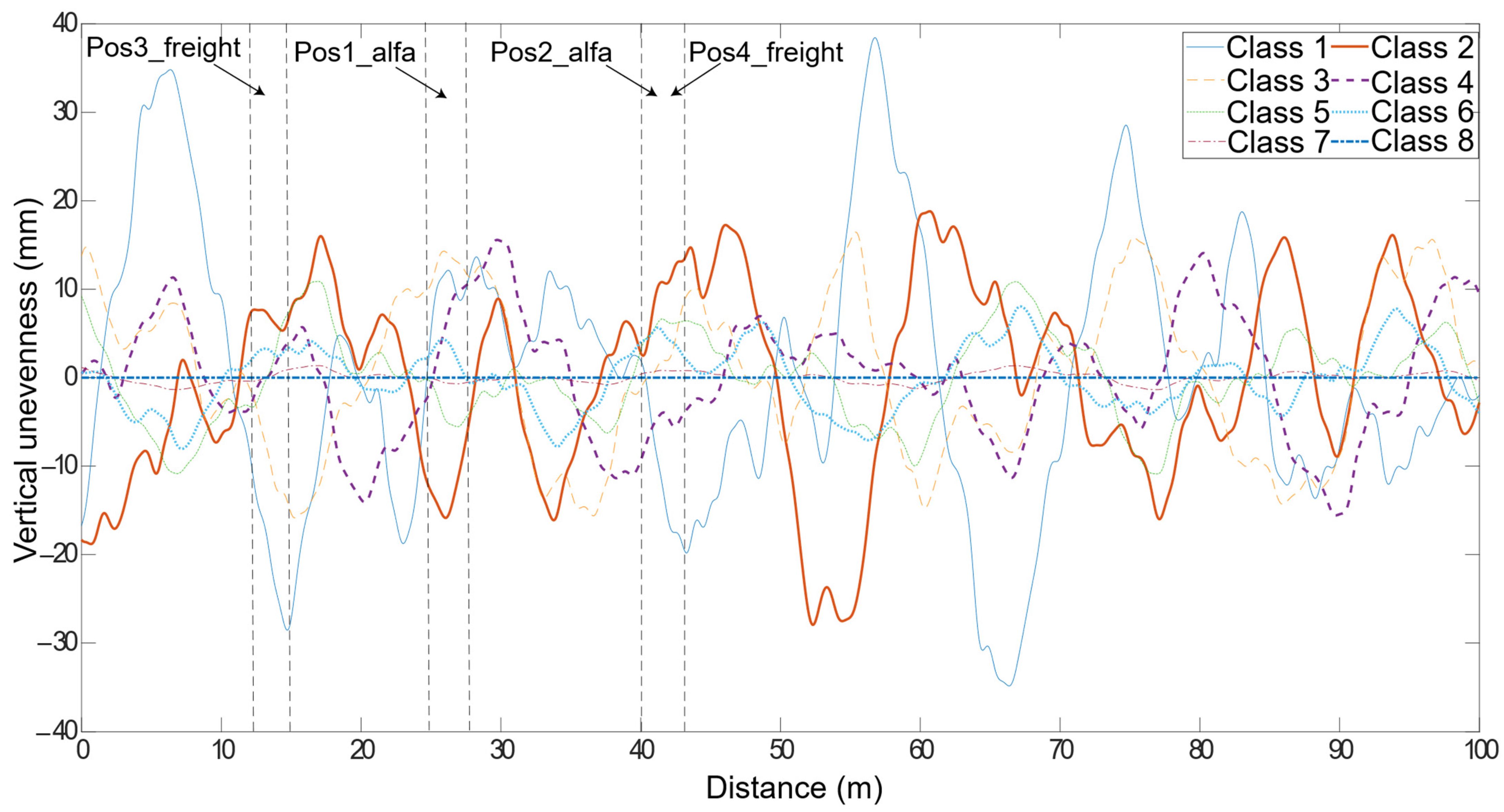
3.4. Unevenness Profile
3.5. Methodology for the Dynamic Load Assessment
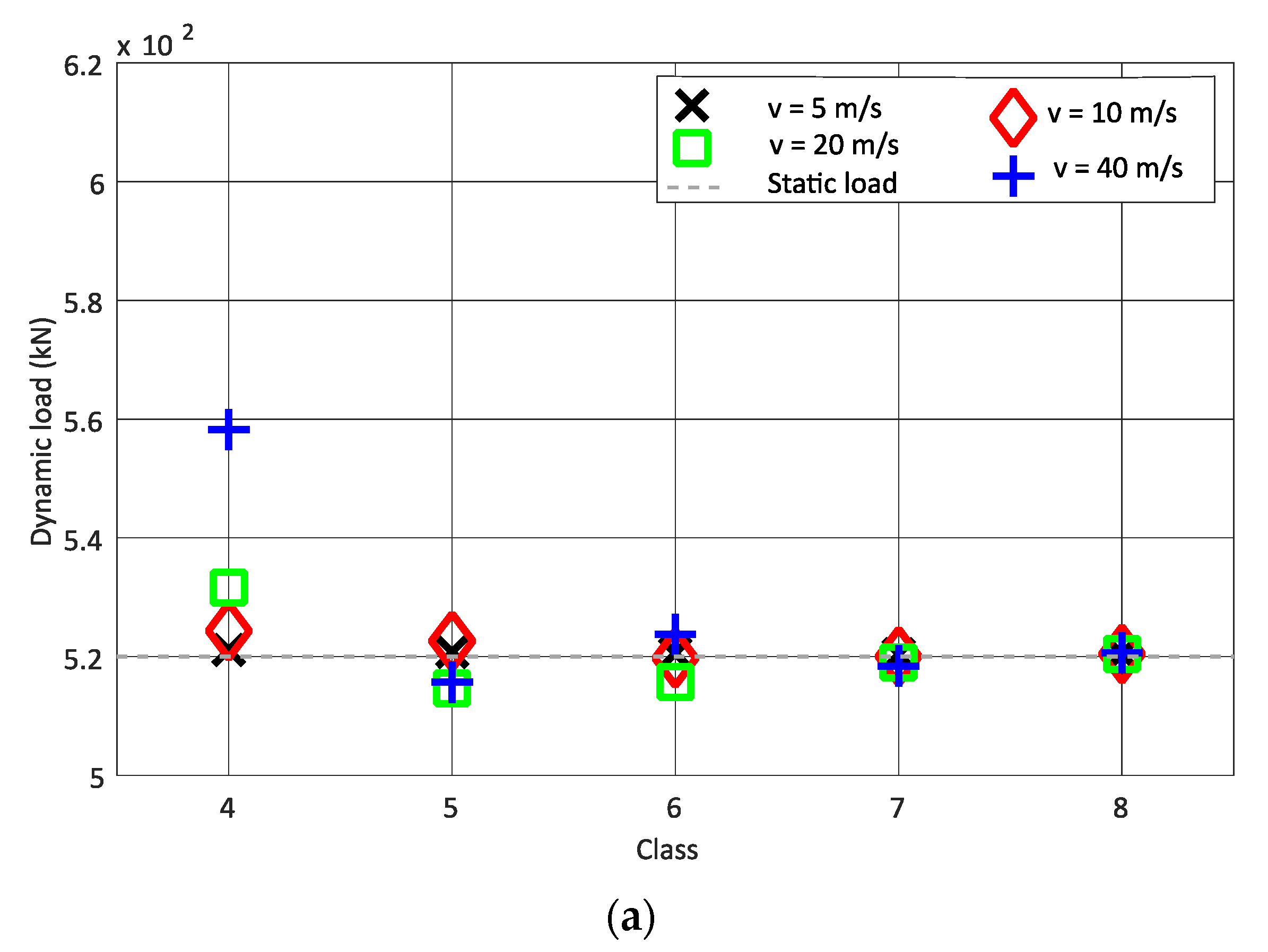
4. Sensitivity Analysis Regarding the Axle Dynamic Loads
5. Evaluation of Static Loads through a WIM System
5.1. Methodology
5.2. Numerical Study
6. Validation of the Proposed Methodology
7. Conclusions
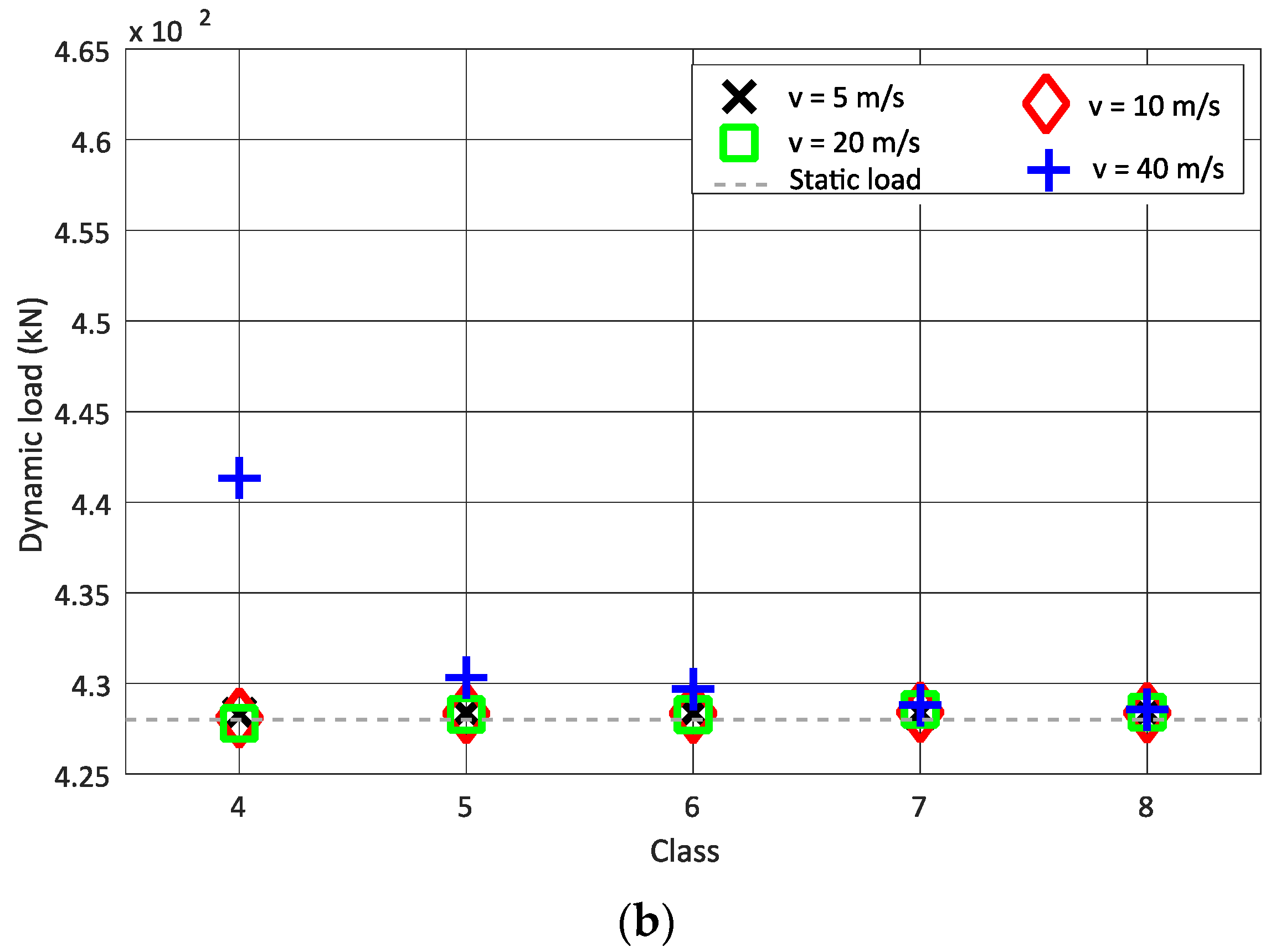
- The dynamic load has a strong correlation with the type of train, which means that the dynamic properties of the train significantly influence the predicted dynamic load;
- The dynamic load also has a strong correlation with the contact stiffness; however, the contact linearisation in the track–vehicle interaction modelling is acceptable for the vehicle speeds and track profiles in the analysis;
- For the same speed, as the track quality improves (the class type increases from 4 to 8), the mean dynamic load value obtained from six positions of strain gauges is closer to the static load;
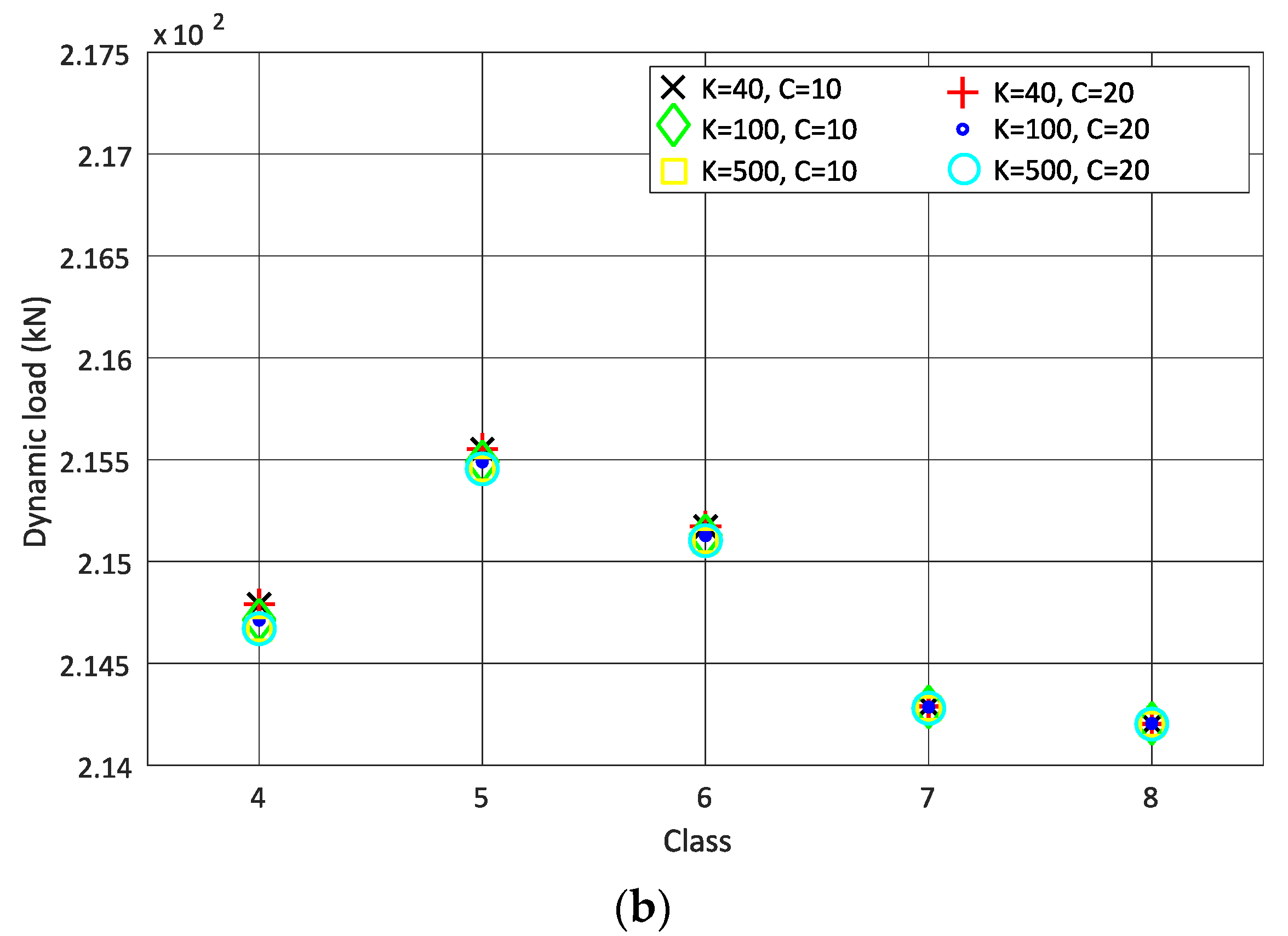
- The variation of stiffness and damping for rail pads does not have a significant influence of the calculation of the dynamic load;
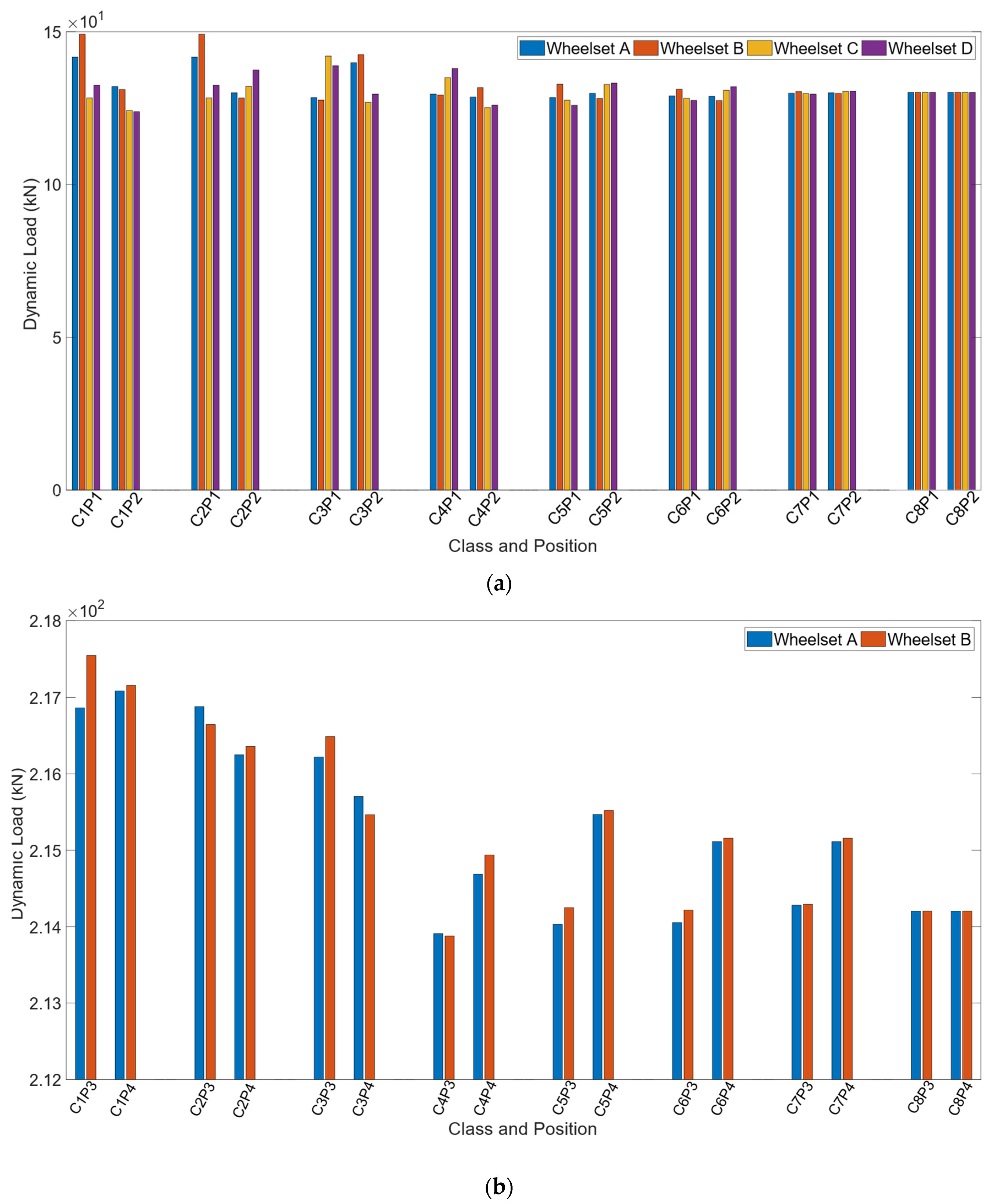
- The dynamic load may be sensitive to the position of the monitoring system in tracks. These differences in the obtained dynamic load may be due to the fact that the unevenness profile of the track is different and the evaluated dynamic load from one position is different to the dynamic load obtained at the other position.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Mayer, R.; Poulikakos, L.; Lees, A.R.; Heutschi, K.; Kalivoda, M.; Soltic, P. Reducing the environmental impact of road and rail vehicles. Environ. Impact Assess. Rev. 2012, 32, 25–32. [Google Scholar] [CrossRef]
- Molodova, M.; Li, Z.; Núñez, A.; Dollevoet, R. Automatic Detection of Squats in Railway Infrastructure. IEEE Trans. Intell. Transp. Syst. 2014, 15, 1980–1990. [Google Scholar] [CrossRef] [Green Version]
- Mosleh, A.; Costa, P.; Calçada, R. Development of a Low-Cost Trackside System for Weighing in Motion and Wheel Defects Detection. Int. J. Railw. Res. 2020, 7, 1–9. [Google Scholar] [CrossRef]
- Chen, S.; Feng, D.; Sun, Z. Reliability-based vehicle weight limit determination for urban bridge network subjected to stochastic traffic flow considering vehicle-bridge coupling. Eng. Struct. 2021, 247, 113166. [Google Scholar] [CrossRef]
- Xu, L.; Zhai, W. Train–track coupled dynamics analysis: System spatial variation on geometry, physics and mechanics. Railw. Eng. Sci. 2020, 28, 36–53. [Google Scholar] [CrossRef] [Green Version]
- Vale, C. Wheel Flats in the Dynamic Behavior of Ballasted and Slab Railway Tracks. Appl. Sci. 2021, 11, 7127. [Google Scholar] [CrossRef]
- Bosso, N.; Gugliotta, A.; Zampieri, N. Wheel flat detection algorithm for onboard diagnostic. Measurement 2018, 123, 193–202. [Google Scholar] [CrossRef]
- Mosleh, A.; Meixedo, A.; Costa, P.; Calçada, R. Trackside Monitoring Solution for Weighing in Motion of Rolling Stock. In Proceedings of the TESTE2019—2nd Conference on Testing and Experimentations in Civil Engineering—Proceedings, Porto, Portugal, 19–21 February 2019. [Google Scholar]
- Bernal, E.; Spiryagin, M.; Cole, C. Onboard Condition Monitoring Sensors, Systems and Techniques for Freight Railway Vehicles: A Review. IEEE Sens. J. 2019, 19, 4–24. [Google Scholar] [CrossRef]
- Kanehara, H.; Fujioka, T. Measuring rail/wheel contact points of running railway vehicles. Wear 2002, 253, 275–283. [Google Scholar] [CrossRef]
- Uhl, T. The inverse identification problem and its technical application. Arch. Appl. Mech. 2007, 77, 325–337. [Google Scholar] [CrossRef]
- Neto, J.; Montenegro, P.A.; Vale, C.; Calçada, R. Evaluation of the train running safety under crosswinds—A numerical study on the influence of the wind speed and orientation considering the normative Chinese Hat Model. Int. J. Rail Transp. 2020, 9, 204–231. [Google Scholar] [CrossRef]
- Vale, C.; Bonifácio, C.; Seabra, J.; Calçada, R.; Mazzino, N.; Elisa, M.; Terribile, S.; Anguita, D.; Fumeo, E.; Saborido, C.; et al. Novel Efficient Technologies in Europe for Axle Bearing Condition Monitoring—The MAXBE Project. Transp. Res. Procedia 2016, 14, 635–644. [Google Scholar] [CrossRef] [Green Version]
- Carraro, F.; Gonçalves, M.S.; Lopez, R.H.; Miguel, L.F.F.; Valente, A.M. Weight estimation on static B-WIM algorithms: A comparative study. Eng. Struct. 2019, 198, 109463. [Google Scholar] [CrossRef]
- Pimentel, R.; Ribeiro, D.; Matos, L.; Mosleh, A.; Calçada, R. Bridge Weigh-in-Motion system for the identification of train loads using fiber-optic technology. Structures 2021, 30, 1056–1070. [Google Scholar] [CrossRef]
- Sun, Z.; Siringoringo, D.; Fujino, Y. Load-carrying capacity evaluation of girder bridge using moving vehicle. Eng. Struct. 2021, 229, 111645. [Google Scholar] [CrossRef]
- Hajializadeh, D.; Žnidarič, A.; Kalin, J.; OBrien, E.J. Development and Testing of a Railway Bridge Weigh-in-Motion System. Appl. Sci. 2020, 10, 4708. [Google Scholar] [CrossRef]
- Allotta, B.; Adamio, P.D.; Marini, L.; Meli, E.; Pugi, L.; Rindi, A. A New Strategy for Dynamic Weighing in Motion of Railway Vehicles. IEEE Trans. Intell. Transp. Syst. 2015, 16, 3520–3533. [Google Scholar] [CrossRef]
- Onat, A.; Kayaalp, B.T. A Novel Methodology for Dynamic Weigh in Motion System for Railway Vehicles With Traction. IEEE Trans. Veh. Technol. 2019, 68, 10545–10558. [Google Scholar] [CrossRef]
- Costa, B.; Martins, R.; Santos, M.; Felgueiras, C.; Calçada, R. Weighing-in-motion wireless system for sustainable railway transport. Energy Procedia 2017, 136, 408–413. [Google Scholar] [CrossRef]
- Zhou, W.; Abdulhakeem, S.; Fang, C.; Han, T.; Li, G.; Wu, Y.; Faisal, Y. A new wayside method for measuring and evaluating wheel-rail contact forces and positions. Measurement 2020, 166, 108244. [Google Scholar] [CrossRef]
- Bracciali, A.; Ciuffi, R.; Piccioli, F.; Knothe, K. Progetto e validazione di un sensore estensimetrico multifunzionale per il binario ferroviario. In the Proceedings of XXX Congresso AIAS, Alghero, Italy, 12–15 September 2001. [Google Scholar]
- Delprete, C.; Rosso, C. An easy instrument and a methodology for the monitoring and the diagnosis of a rail. Mech. Syst. Signal Process. 2009, 23, 940–956. [Google Scholar] [CrossRef]
- Sekuła, K.; Kołakowski, P. Piezo-based weigh-in-motion system for the railway transport. Struct. Control. Health Monit. 2012, 19, 199–215. [Google Scholar] [CrossRef]
- Kouroussis, G.; Kinet, D.; Moeyaert, V.; Dupuy, J.; Caucheteur, C. Railway structure monitoring solutions using fibre Bragg grating sensors. Int. J. Rail Transp. 2016, 4, 135–150. [Google Scholar] [CrossRef]
- Mosleh, A.; Costa, P.; Calçada, R. A new strategy to estimate static loads for the dynamic weighing in motion of railway vehicles. Inst. Mech. Eng. Part F J. Rail Rapid Transit 2020, 234, 183–200. [Google Scholar] [CrossRef]
- Mohammadi, M.; Mosleh, A.; Razzaghi, M.; Costa, P.; Calçada, R. Stochastic analysis of railway embankment with uncertain soil parameters using polynomial chaos expansion. Struct. Infrastruct. Eng. 2022. [Google Scholar] [CrossRef]
- Costa, P.M.B.A. Vibrações do Sistema via-Maciço Induzidas por Tráfego Ferroviário: Modelação Numérica e Validação Experimental; Porto University: Porto, Portugal, 2011. [Google Scholar]
- Costa, P.A.; Calçada, R.; Silva Cardoso, A. Track–ground vibrations induced by railway traffic: In-situ measurements and validation of a 2.5D FEM-BEM model. Soil Dyn. Earthq. Eng. 2012, 32, 111–128. [Google Scholar] [CrossRef]
- Dahlberg, T. Some railroad settlement models—A critical review. Proc. Inst. Mech. Eng. Part F J. Rail Rapid Transit 2001, 215, 289–300. [Google Scholar] [CrossRef]
- Vale, C.; Calçada, R. A dynamic vehicle-track interaction model for predicting the track degradation process. J. Infrastruct. Syst. 2014, 20, 04014016. [Google Scholar] [CrossRef]
- Dieterman, H.A.; Metrikine, A. Equivalent stiffness of a half-space interacting with a beam. Critical velocities of a moving load along the beam. Eur. J. Mech. A-Solids 1996, 15, 67–90. [Google Scholar]
- Sheng, X.; Jones, C.J.C.; Thompson, D. A theoretical model for ground vibration from trains generated by vertical track irregularities. J. Sound Vib. 2004, 272, 937–965. [Google Scholar] [CrossRef]
- Steenbergen, M.J.M.M.; Metrikine, A.V. The effect of the interface conditions on the dynamic response of a beam on a half-space to a moving load. Eur. J. Mech. A-Solids 2007, 26, 33–54. [Google Scholar] [CrossRef]
- Thompson, D.; Kouroussis, G.; Ntotsios, E. Modelling, simulation and evaluation of ground vibration caused by rail vehicles. Veh. Syst. Dyn. 2019, 57, 936–983. [Google Scholar] [CrossRef]
- Lombaert, G.; Degrande, G.; François, S.; Thompson, D. Ground-Borne Vibration due to Railway Traffic: A Review of Excitation Mechanisms, Prediction Methods and Mitigation Measures. Notes Numer. Fluid Mech. Multidiscip. Des. 2015, 126, 253–287. [Google Scholar] [CrossRef]
- Song, Y.; Wang, Z.; Liu, Z.; Wang, R. A spatial coupling model to study dynamic performance of pantograph-catenary with vehicle-track excitation. Mech. Syst. Signal Process. 2021, 151, 107336. [Google Scholar] [CrossRef]
- Luo, R. Anti-sliding control simulation of railway vehicle braking. J. Mech. Eng. 2008, 33, 35–40. [Google Scholar] [CrossRef]
- Zhai, W.; Cai, Z. Dynamic interaction between a lumped mass vehicle and a discretely supported continuous rail track. Comput. Struct. 1997, 63, 987–997. [Google Scholar] [CrossRef]
- Mosleh, A.; Montenegro, P.A.; Costa, P.A.; Calçada, R. Railway Vehicle Wheel Flat Detection with Multiple Records Using Spectral Kurtosis Analysis. Appl. Sci. 2021, 11, 4002. [Google Scholar] [CrossRef]
- Hertz, H. Ueber die Berührung fester elastischer Körper [On the contact of elastic solids]. J. Für Die Reine Und Angew. Math. 1882, 92, 156–171. [Google Scholar]
- Fries, R.H.; Coffey, B.M. A State-Space Approach to the Synthesis of Random Vertical and Crosslevel Rail Irregularities. J. Dyn. Syst. Meas. Control. 1990, 112, 83–87. [Google Scholar] [CrossRef]
- Hamid, A.; Yang, T.L. Analytical Description of Track Geometry Variations; Transportation Research Board: Washington, DC, USA, 1981; pp. 19–26. [Google Scholar]
- Mosleh, A.; Montenegro, P.; Alves Costa, P.; Calçada, R. An approach for wheel flat detection of railway train wheels using envelope spectrum analysis. Struct. Infrastruct. Eng. 2020, 17, 1710–1729. [Google Scholar] [CrossRef]








| Rail (UIC-60) | |||||
| ) | ) | ) | ν (−) | ) | |
| 0.01534 | 7850 | 6.11 × 10−5 | 0.3 | 2 × 108 | |
| Railpads | Sleepers | Ballast | Foundation | ||
| (kN s/m) | (kN/m) | ρ (kg/m) | ) | G (MPa) | ) |
| 30 | 2 × 105 | 525 | 1550 | 20 | 1900 |
| Properties | Alfa Pendular Vehicle | Freight Wagon | |
|---|---|---|---|
| Box | Mass—Mc (kg) | 35,640 | 41,100 |
| Pitch moment of inertia—Ic (kg·m2) | 1,475,000 | 673,322.46 | |
| Secondary suspension | Stiffness—k2 (kN/m) | 734,832 | 0 |
| Damping—c2 (kN·s/m) | 35 | 0 | |
| Bogie | Mass—Mb (kg) | 2829 | 16,739 |
| Pitch moment of inertia—Ib (kg·m2) | 1931.49 | 0 | |
| Primary suspension | Stiffness—k1 (kN/m) | 1,652,820 | 1,860,000 |
| Damping—c1 (Ns/m) | 16,739 | 16,739 | |
| Axle | Mass—Mr (kg) | 1711 | 1246.52 |
| Static load per axle—Q (kN) | 130 | 214 | |
| Dimensions | Longitudinal distance between wheelsets—a2 (m) | 2.7 | - |
| Longitudinal distance between bogies—a1 (m) | 19 | 6 | |
| Class | 1 | 2 | 3 | 4 | 5 | 6 |
| ) | 660.079 | 376.229 | 208.841 | 116.856 | 65.929 | 37.505 |
| Alfa Pendular | Freight Train | ||||
|---|---|---|---|---|---|
| Class | Kh | kN/m | Class | Kh | kN/m |
| Class 1 | 1.282 × 106 | Class 1 | 1.442 × 106 | ||
| 1.182 × 106 | 1.438 × 106 | ||||
| Class 2 | 1.288 × 106 | Class 2 | 1.417 × 106 | ||
| 1.227 × 106 | 1.414 × 106 | ||||
| Class 3 | 1.232 × 106 | Class 3 | 1.419 × 106 | ||
| 1.205 × 106 | 1.417 × 106 | ||||
| Class 4 | 1.224 × 106 | Class 4 | 1.396 × 106 | ||
| 1.208 × 106 | 1.396 × 106 | ||||
| Class 5 | 1.197 × 106 | Class 5 | 1.404 × 106 | ||
| 1.177 × 106 | 1.402 × 106 | ||||
| Class 6 | 1.209 × 106 | Class 6 | 1.403 × 106 | ||
| 1.176 × 106 | 1.402 × 106 | ||||
| Class 7 | 1.187 × 106 | Class 7 | 1.402 × 106 | ||
| 1.185 × 106 | 1.402 × 106 | ||||
| V | C | T | CS | kp | cp | DL | |
| V | 1 | ||||||
| C | −5.37 × 10−2 | 1 | |||||
| T | −9.87 × 10−17 | −3.34 × 10−17 | 1 | ||||
| CS | 4.15 × 10−2 | −2.48 × 10−2 | 9.99 × 10−2 | 1 | |||
| kp | −1.11 × 10−2 | −1.53 × 10−3 | −1.65 × 10−17 | −1.11 × 10−3 | 1 | ||
| cp | −2.19 × 10−1 | −3.04 × 10−2 | 2.50 × 10−17 | 2.34 × 10−2 | −4.11 × 10−2 | 1 | |
| DL | 1.45 × 10−1 | −1.18 × 10−1 | 9.46 × 10−1 | −9.17 × 10−1 | −5.05 × 10−3 | 7.99 × 10−2 | 1 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pintão, B.; Mosleh, A.; Vale, C.; Montenegro, P.; Costa, P. Development and Validation of a Weigh-in-Motion Methodology for Railway Tracks. Sensors 2022, 22, 1976. https://doi.org/10.3390/s22051976
Pintão B, Mosleh A, Vale C, Montenegro P, Costa P. Development and Validation of a Weigh-in-Motion Methodology for Railway Tracks. Sensors. 2022; 22(5):1976. https://doi.org/10.3390/s22051976
Chicago/Turabian StylePintão, Bruno, Araliya Mosleh, Cecilia Vale, Pedro Montenegro, and Pedro Costa. 2022. "Development and Validation of a Weigh-in-Motion Methodology for Railway Tracks" Sensors 22, no. 5: 1976. https://doi.org/10.3390/s22051976
APA StylePintão, B., Mosleh, A., Vale, C., Montenegro, P., & Costa, P. (2022). Development and Validation of a Weigh-in-Motion Methodology for Railway Tracks. Sensors, 22(5), 1976. https://doi.org/10.3390/s22051976








