Intelligent Diagnosis of Rolling Element Bearing Based on Refined Composite Multiscale Reverse Dispersion Entropy and Random Forest
Abstract
:1. Introduction
- (1)
- RCMRDE is proposed for the first time, and its advantages in fault diagnosis are explored. Simulation and experimental results indicate that RCMRDE exhibits outstanding performance compared with several existing entropy.
- (2)
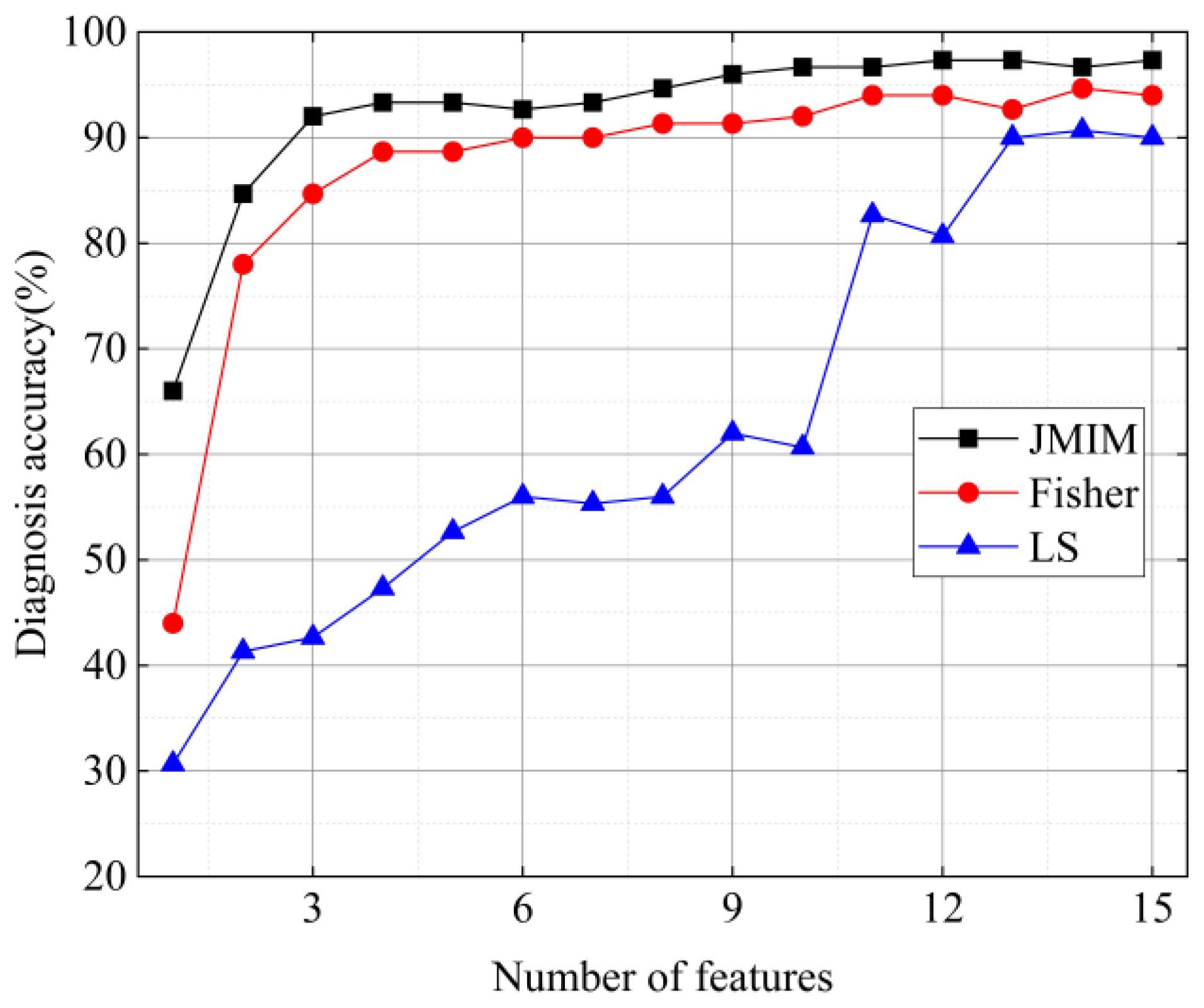
- There are few studies based on VMD and JMIM feature selection. JMIM feature selection can effectively calculate the resolution of each feature and select RCMRDE with high sensitivity to construct fault feature set. In this study, through JMIM feature selection, the original RCMRDE set is reduced by 91.4%, and the recognition accuracy is still 97.33%.
2. Refined Composite Multiscale Reverse Dispersion Entropy
2.1. Reverse Dispersion Entropy
- (1)
- Mapping by the normal distribution function.
- (2)
- Using a linear algorithm to map each to integers in [1,].
2.2. Refined Composite Multiscale Reverse Dispersion Entropy
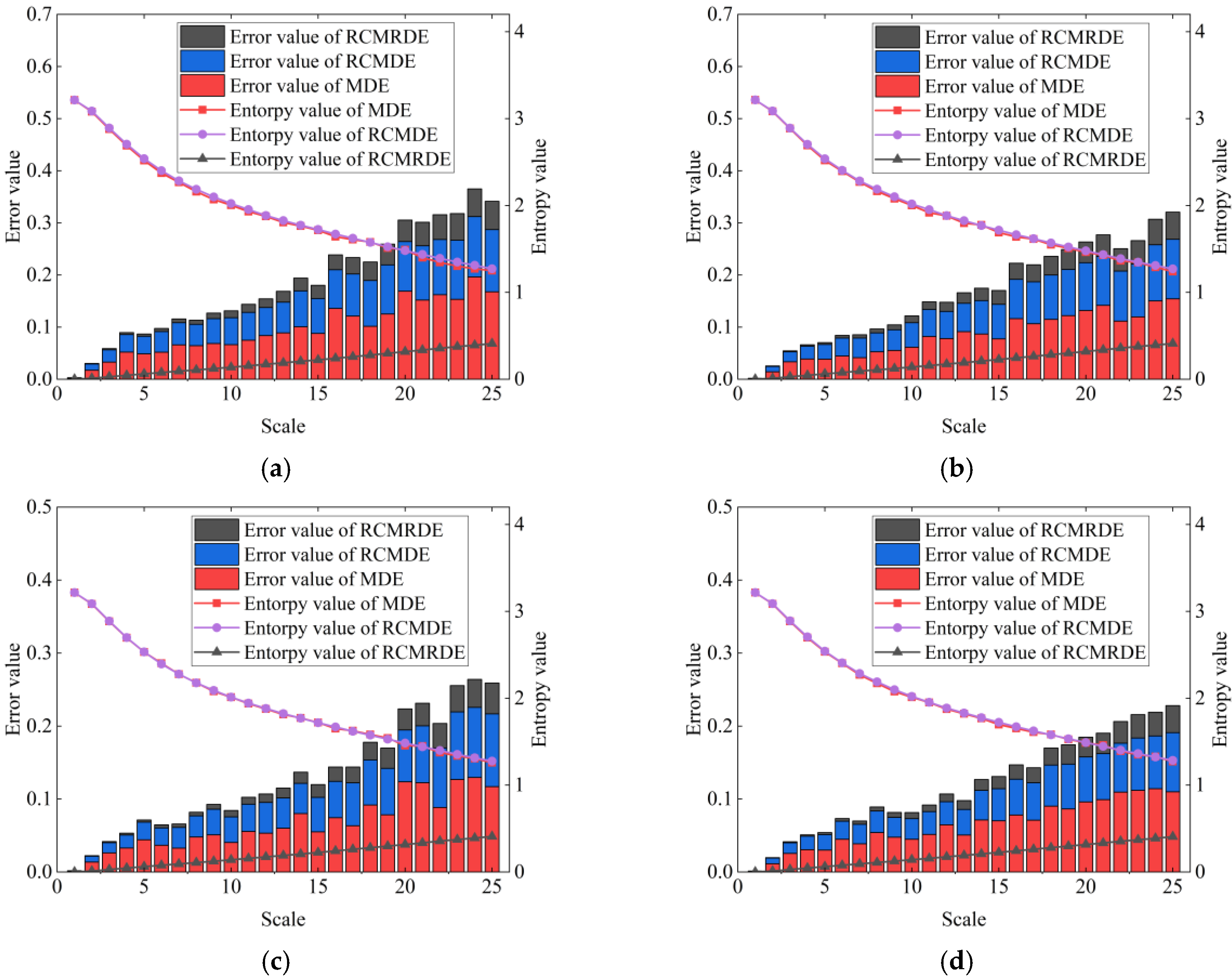
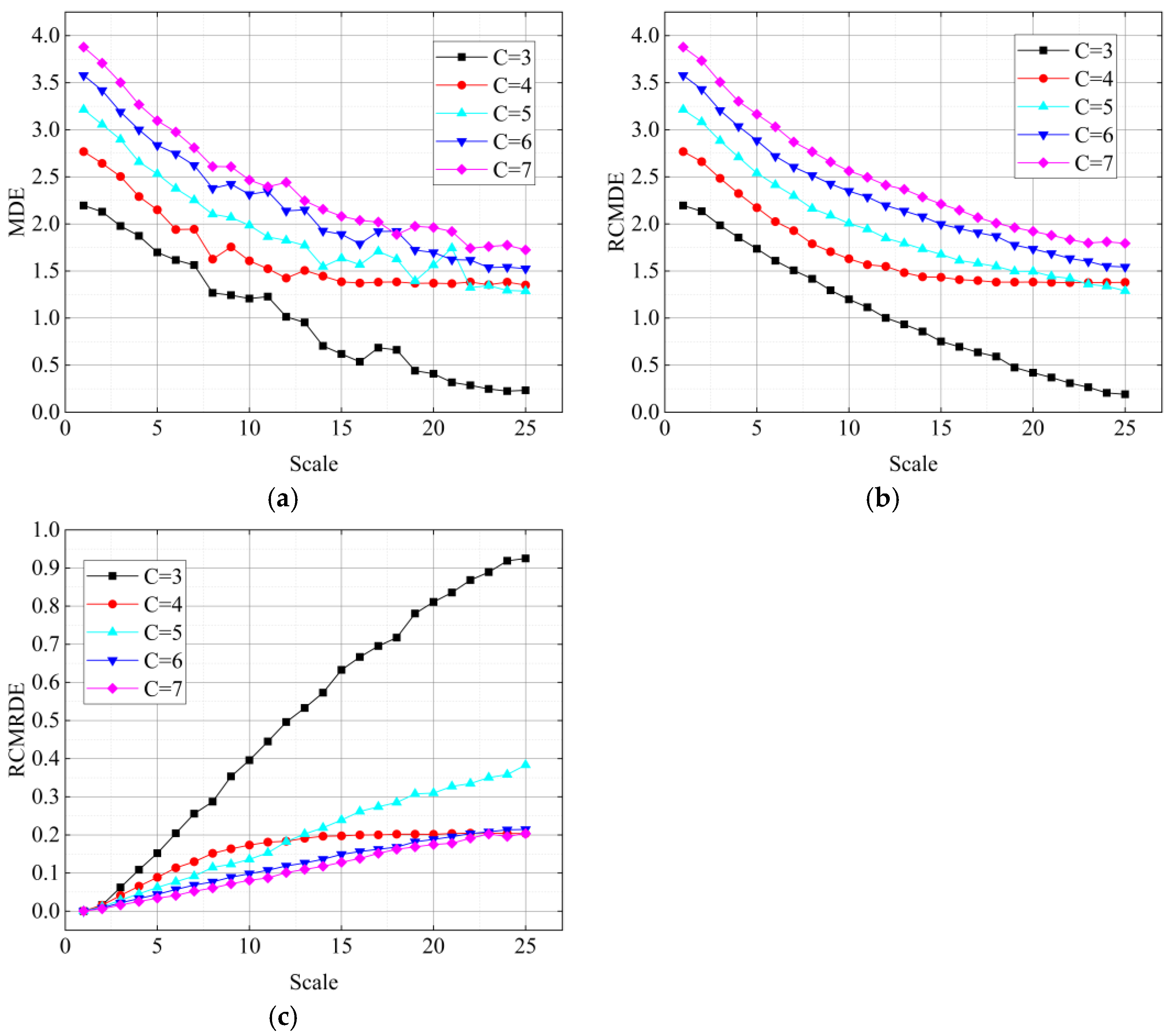
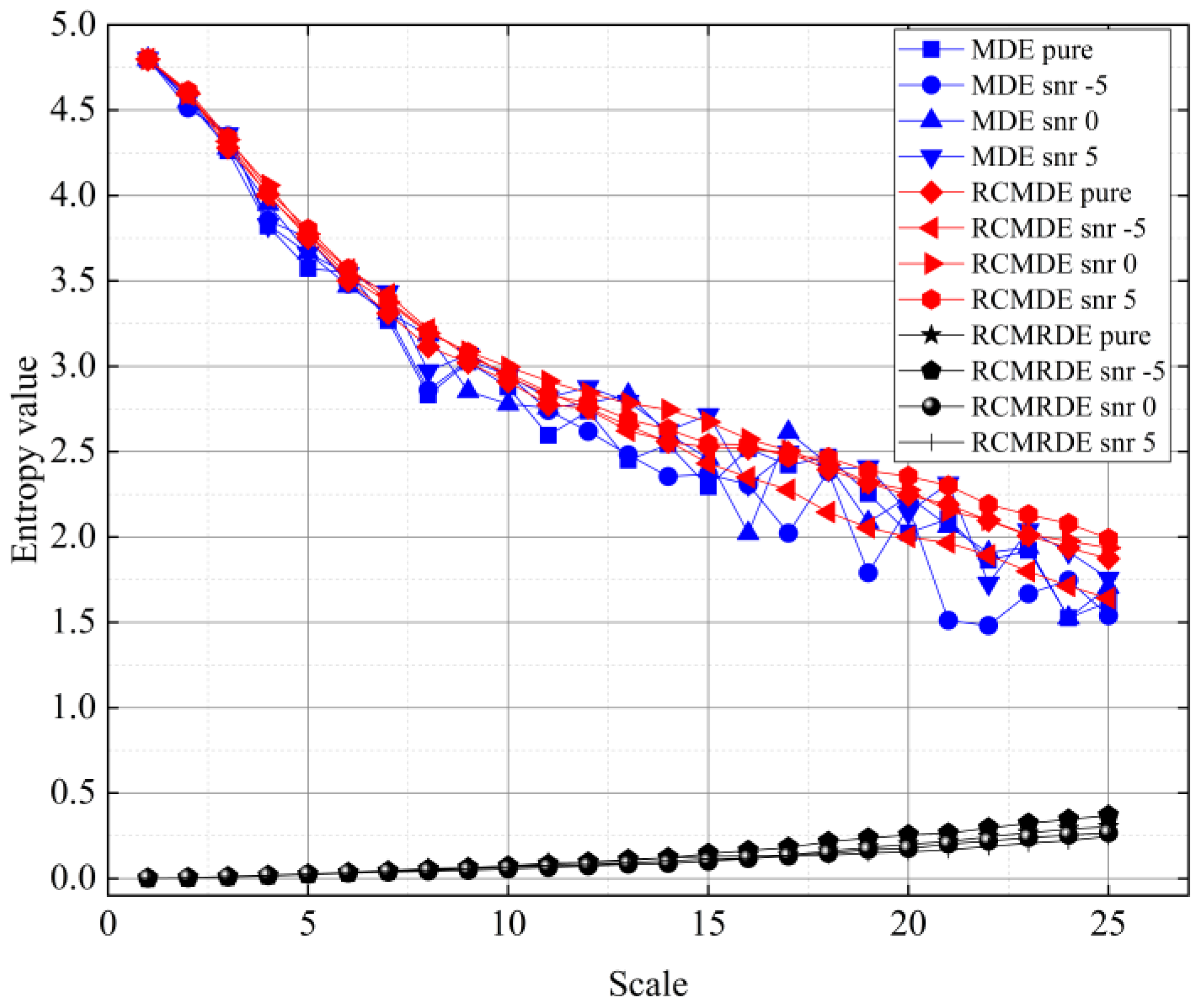
2.3. Comparison between MDE, RCMDE, and RCMRDE Using Simulation Signals
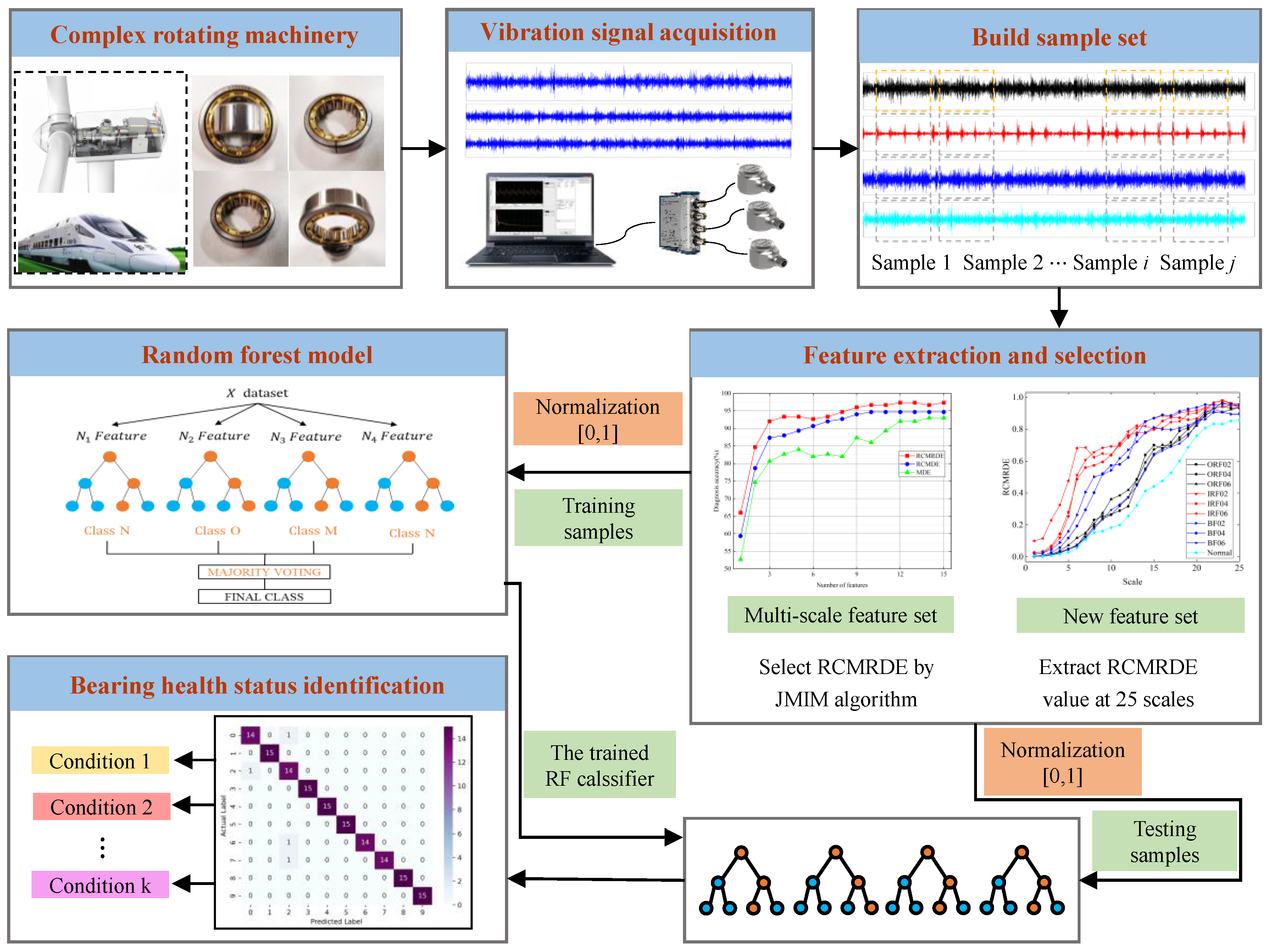
3. The Proposed Fault Diagnosis Method
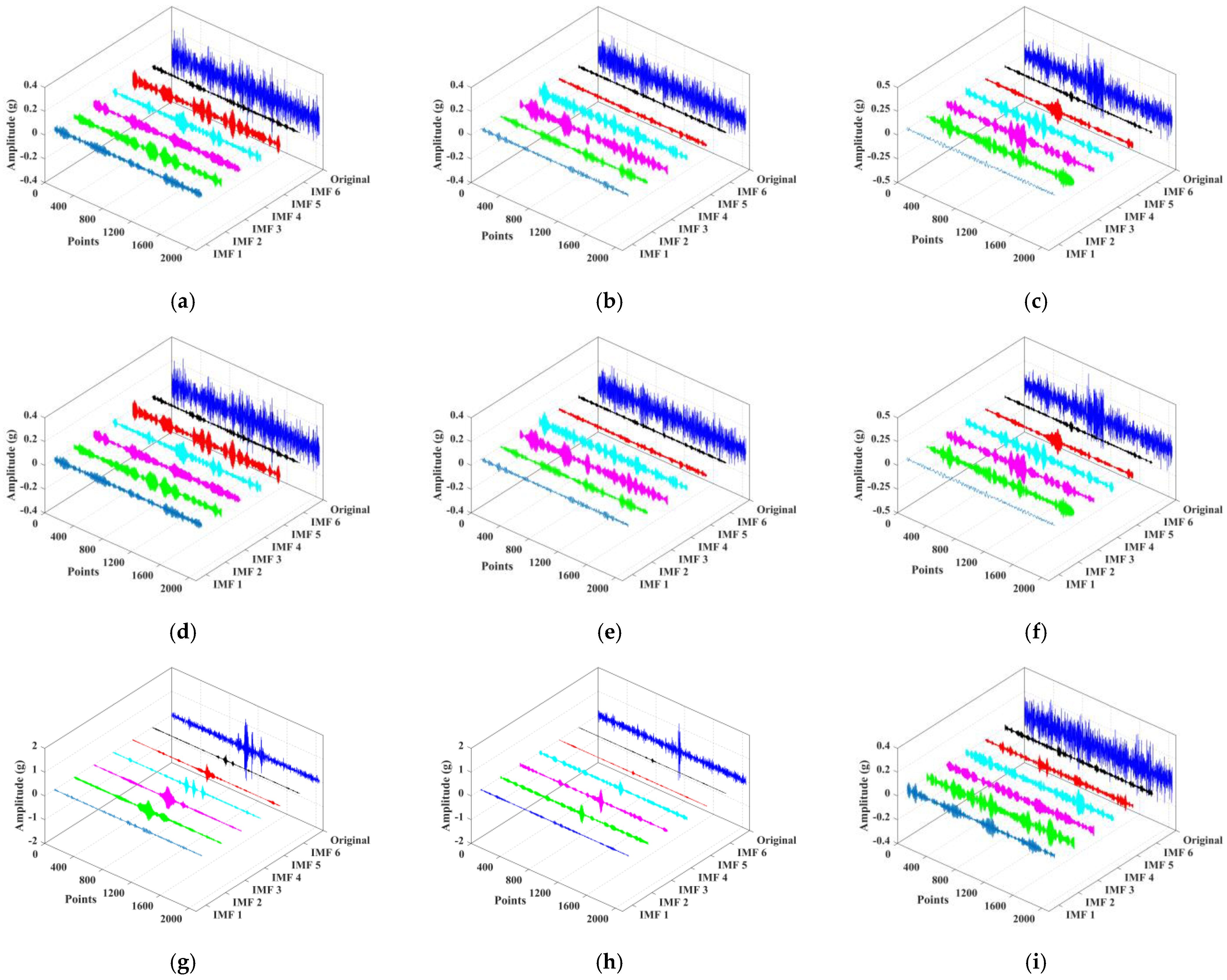
3.1. Variational Mode Decomposition
3.2. Feature Selection Based on JMIM
3.3. Random Forest
3.4. Proposed Fault Diagnostic Framework
- (1)
- VMD is applied to decompose the original signal into several modal components. The modal number is based on the decomposition criterion that the frequency center frequency of each component is not overlapping.
- (2)
- Based on the original signal and VMD decomposed components, RCMRDE at 25 scales is calculated as the initial feature set. The high-dimensional features contain redundant information. Subsequently, JMIM is employed to select sensitive features, thereby removing redundant information and reducing the dimension of feature set data.
- (3)
- Input sensitive features selected in steps (2) into the RF model to identify bearing health status. The presented method performance is checked by the rolling bearing vibration signals under different conditions.
4. Experiments and Data Analysis
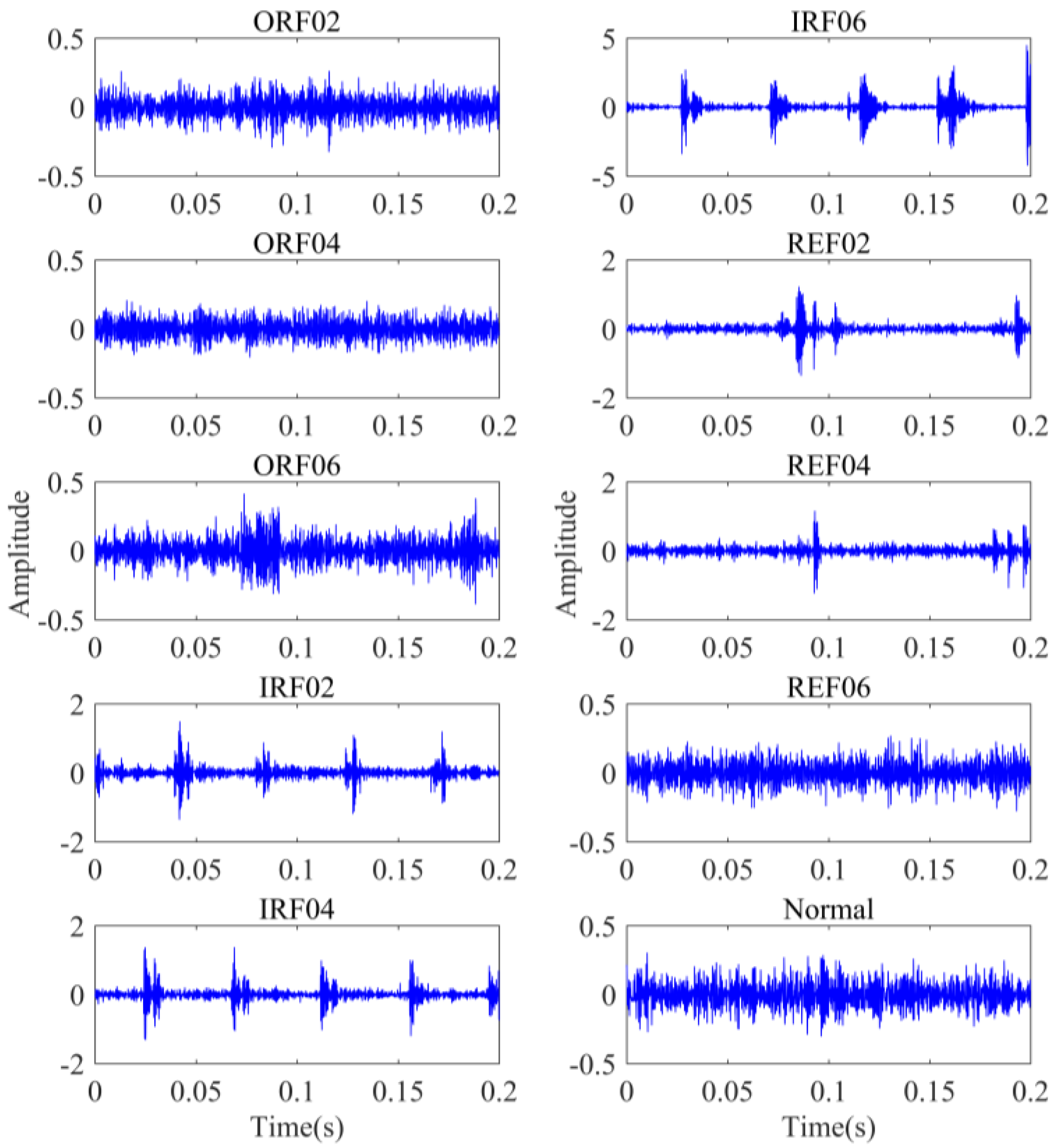
4.1. Experimental Setup and Data Acquisition
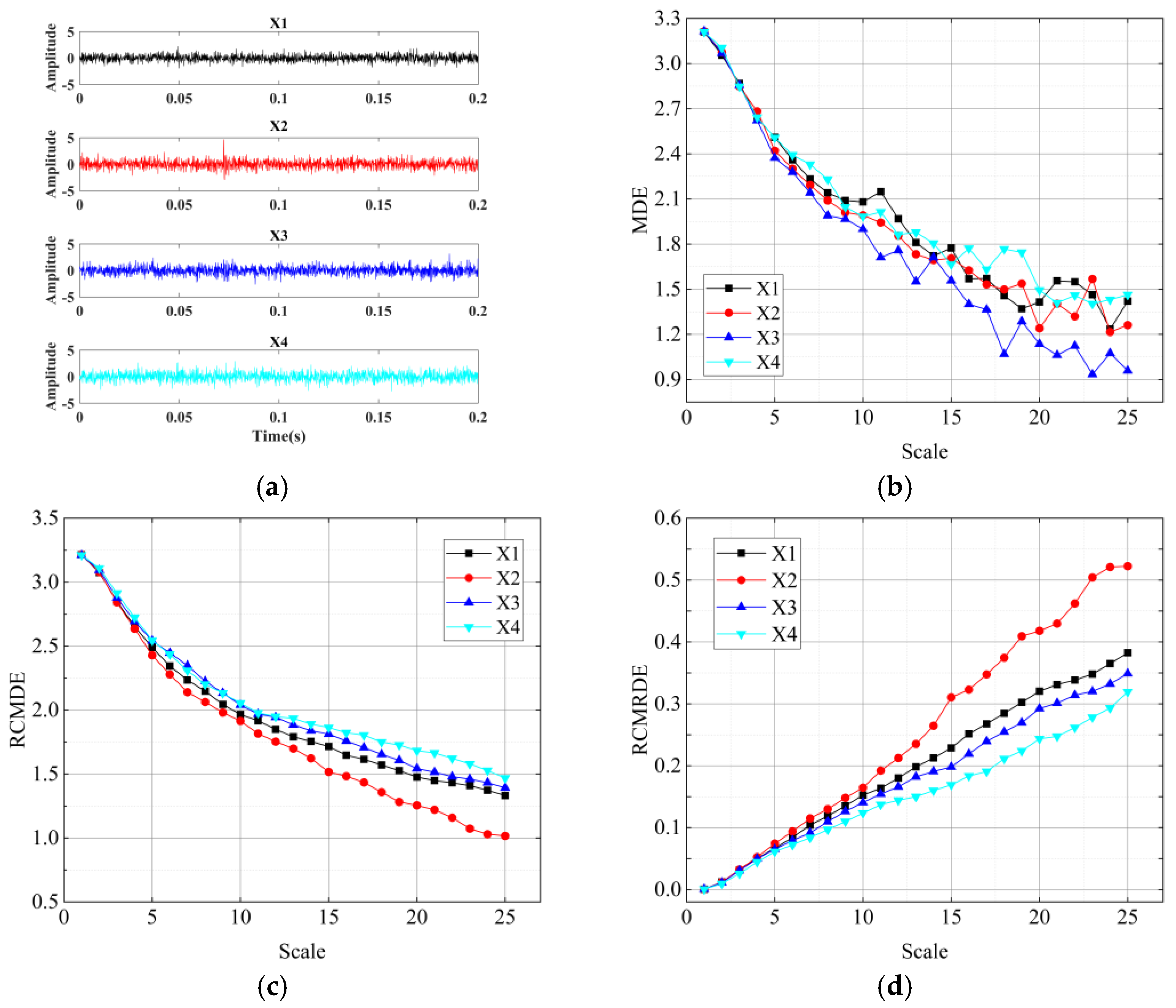
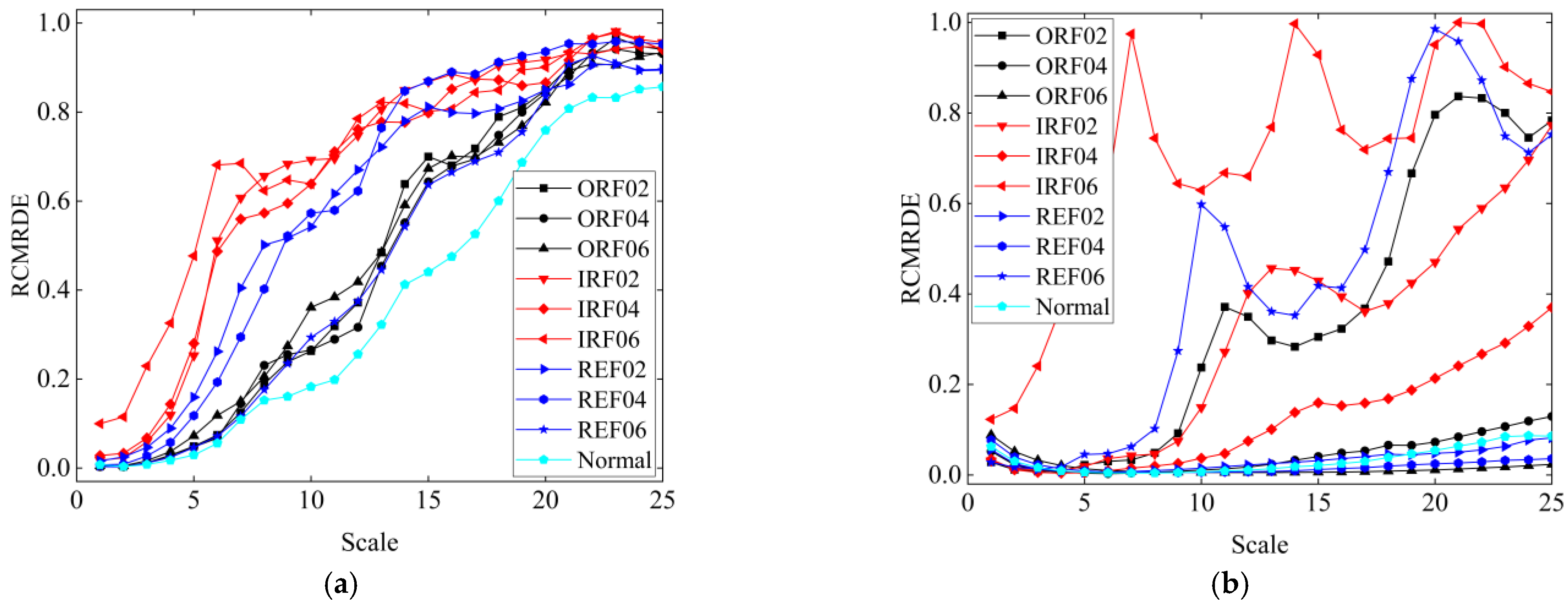
4.2. Feature Extraction by VMD-Based RCMRDE
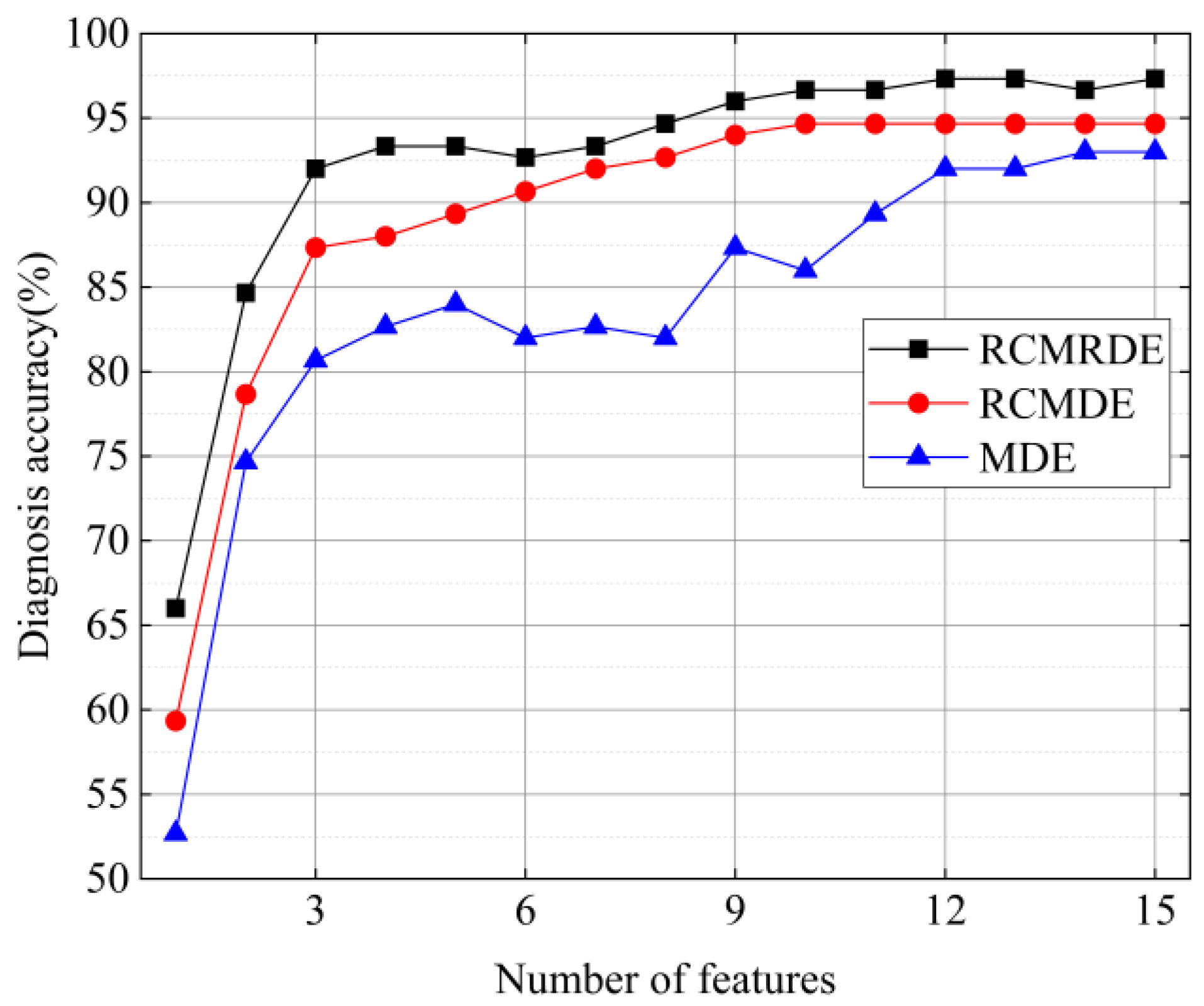
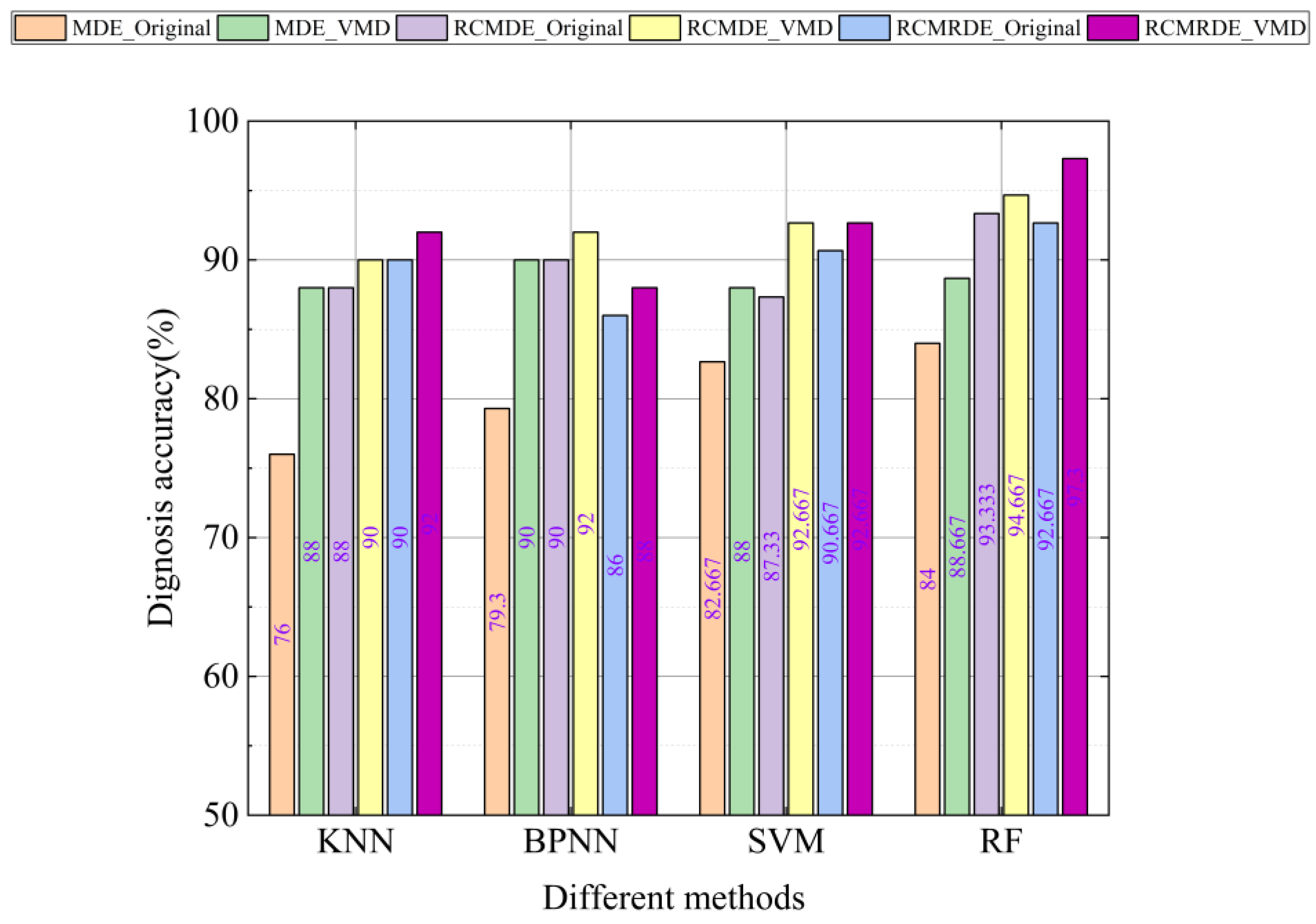
4.3. Diagnosis Results and Analysis
4.4. Comparison with Other Methods
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Yan, X.; Jia, M. Intelligent fault diagnosis of rotating machinery using improved multiscale dispersion entropy and mRMR feature selection. Knowl.-Based Syst. 2019, 163, 450–471. [Google Scholar] [CrossRef]
- Chen, Z.; Mauricio, A.; Li, W.; Gryllias, K. A deep learning method for bearing fault diagnosis based on Cyclic Spectral Coherence and Convolutional Neural Networks. Mech. Syst. Signal Process. 2020, 140, 106683. [Google Scholar] [CrossRef]
- Kaplan, K.; Lmaz, K.Y.; Melih, K.; Recep, M.N.M.; Metin, E.H. An improved feature extraction method using texture analysis with LBP for bearing fault diagnosis. Appl. Soft Comput. 2020, 87, 106019. [Google Scholar] [CrossRef]
- Wang, Z.; Yao, L.; Cai, Y. Rolling bearing fault diagnosis using generalized refined composite multiscale sample entropy and optimized support vector machine. Measurement 2020, 156, 107574. [Google Scholar] [CrossRef]
- Prasannamoorthy, V.; Devarajan, N. Fault Detection and Classification in Power Electronic Circuits Using Wavelet Transform and Neural Network. J. Comput. Sci. 2011, 7, 95–100. [Google Scholar] [CrossRef] [Green Version]
- Wang, C.; Li, H.; Ou, J.; Hu, R.; Hu, S.; Liu, A. Identification of planetary gearbox weak compound fault based on parallel dual-parameter optimized resonance sparse decomposition and improved MOMEDA. Measurement 2020, 165, 108079. [Google Scholar] [CrossRef]
- Tuncer, E.; Bolat, E.D. Classification of epileptic seizures from electroencephalogram (EEG) data using bidirectional short-term memory (Bi-LSTM) network architecture. Biomed. Signal Process. Control 2021, 73, 103462. [Google Scholar] [CrossRef]
- Li, R.; Ran, C.; Zhang, B.; Han, L.; Feng, S. Rolling Bearings Fault Diagnosis Based on Improved Complete Ensemble Empirical Mode Decomposition with Adaptive Noise, Nonlinear Entropy, and Ensemble SVM. Appl. Sci. 2020, 16, 5542. [Google Scholar] [CrossRef]
- Li, Z.; Chen, J.; Zi, Y.; Pan, J. Independence-oriented VMD to identify fault feature for wheel set bearing fault diagnosis of high speed locomotive. Mech. Syst. Signal Process. 2017, 85, 512–529. [Google Scholar] [CrossRef]
- Shaomin, Z.; Hong, X.; Binsen, P.; Enrico, Z.; Zhichao, W.; Yingying, J. Feature extraction for early fault detection in rotating machinery of nuclear power plants based on adaptive VMD and Teager energy operator. Ann. Nucl. Energy 2021, 160, 108392. [Google Scholar]
- Huang, Y.; Yan, C.J.; Xu, Q. On the difference between empirical mode decomposition and Hilbert vibration decomposition for earthquake motion records. In Proceedings of the 15th World Conference on Earthquake Engineering, Lisbon, Portugal, 24–28 September 2012. [Google Scholar]
- Dragomiretskiy, K.; Zosso, D. Variational Mode Decomposition. IEEE Trans. Signal Process. 2014, 62, 531–544. [Google Scholar] [CrossRef]
- Civera, M.; Surace, C.A. Comparative Analysis of Signal Decomposition Techniques for Structural Health Monitoring on an Experimental Benchmark. Sensors 2021, 21, 1825. [Google Scholar] [CrossRef] [PubMed]
- Yang, W.; Peng, Z.; Wei, K.; Shi, P.; Tian, W. Superiorities of variational mode decomposition over empirical mode decomposition particularly in time–frequency feature extraction and wind turbine condition monitoring. IET Renew. Power Gener. 2017, 11, 443–452. [Google Scholar] [CrossRef] [Green Version]
- Chen, X.; Yang, Y.; Cui, Z.; Shen, J. Vibration fault diagnosis of wind turbines based on variational mode decomposition and energy entropy. Energy 2019, 174, 1100–1109. [Google Scholar] [CrossRef]
- Kumar, A.; Zhou, Y.; Xiang, J. Optimization of VMD using kernel-based mutual information for the extraction of weak features to detect bearing defects. Measurement 2021, 168, 108402. [Google Scholar] [CrossRef]
- Chang, L.; Gang, C.; Xihui, C.; Yusong, P. Planetary Gears Feature Extraction and Fault Diagnosis Method Based on VMD and CNN. Sensors 2018, 5, 1523. [Google Scholar]
- Liang, Z.; Cao, J.; Ji, X.; Wei, P. Fault severity assessment of rolling bearings method based on improved VMD and LSTM. J. Vibroeng. 2020, 6, 1338–1356. [Google Scholar]
- Gai, J.; Shen, J.; Hu, Y.; Wang, H. An integrated method based on hybrid grey wolf optimizer improved variational mode decomposition and deep neural network for fault diagnosis of rolling bearing. Measurement 2020, 162, 107901. [Google Scholar] [CrossRef]
- Xu, F.; Tse, P.W. A method combining refined composite multiscale fuzzy entropy with PSO-SVM for roller bearing fault diagnosis. J. Cent. South Univ. 2019, 9, 2404–2417. [Google Scholar] [CrossRef]
- Richman, J.S.; Moorman, J.R. Physiological time-series analysis using approximate entropy and sample entropy. American journal of physiology. Am. J. Physiol.-Heart Circ. Physiol. 2000, 6, 2039–2049. [Google Scholar] [CrossRef] [Green Version]
- Tylová, L.; Kukal, J.; Hubata-Vacek, V.; Vyšata, O. Unbiased estimation of permutation entropy in EEG analysis for Alzheimer’s disease classification. Biomed. Signal Process. Control 2018, 39, 424–430. [Google Scholar] [CrossRef]
- Zair, M.; Rahmoune, C.; Benazzouz, D. Multi-fault diagnosis of rolling bearing using fuzzy entropy of empirical mode decomposition, principal component analysis, and SOM neural network. Proc. Inst. Mech. Eng. Part C 2019, 233, 3317–3328. [Google Scholar] [CrossRef]
- Yin, Y.; Sun, K.; He, S. Multiscale permutation Rényi entropy and its application for EEG signals. PLoS ONE 2018, 13, 0202558. [Google Scholar] [CrossRef]
- Ceravolo, R.; Civera, M.; Lenticchia, E.; Miraglia, G.; Surace, C. Detection and Localization of Multiple Damages through Entropy in Information Theory. Appl. Sci. 2021, 13, 5773. [Google Scholar] [CrossRef]
- Civera, M.; Surace, C. An Application of Instantaneous Spectral Entropy for the Condition Monitoring of Wind Turbines. Appl. Sci. 2022, 3, 1059. [Google Scholar] [CrossRef]
- Rostaghi, M.; Ashory, M.R.; Azami, H. Application of dispersion entropy to status characterization of rotary machines. J. Sound Vib. 2019, 438, 291–308. [Google Scholar] [CrossRef]
- Jinde, Z.; Junsheng, C.; Yu, Y. A rolling bearing fault diagnosis approach based on LCD and fuzzy entropy. Mech. Mach. Theory 2013, 70, 441–453. [Google Scholar]
- Zhenya, W.; Ligang, Y.; Gang, C.; Jiaxin, D. Modified multiscale weighted permutation entropy and optimized support vector machine method for rolling bearing fault diagnosis with complex signals. ISA Trans. 2021, 114, 470–480. [Google Scholar]
- Jinde, Z.; Haiyang, P.; Jinyu, T.; Qingyun, L. Generalized refined composite multiscale fuzzy entropy and multi-cluster feature selection based intelligent fault diagnosis of rolling bearing. ISA Trans. 2021. [Google Scholar] [CrossRef]
- Yongjian, L.; Hao, S.; Bingrong, M.; Weihua, Z.; Qing, X. Improved multiscale weighted-dispersion entropy and its application in fault diagnosis of train bearing. Meas. Sci Technol. 2021, 32, 075002. [Google Scholar]
- Costa, M.; Goldberger, A.L.; Peng, C.-K. Multiscale entropy analysis of complex physiologic time series. Phys. Rev. Lett. 2002, 6, 137–140. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wu, S.; Wu, C.; Lin, S.; Wang, C.; Lee, K. Time Series Analysis Using Composite Multiscale Entropy. Entropy 2013, 3, 1369–1374. [Google Scholar] [CrossRef] [Green Version]
- Gituku, E.W.; Kimotho, J.K.; Njiri, J.G. Cross-domain bearing fault diagnosis with refined composite multiscale fuzzy entropy and the self organizing fuzzy classifier. Eng. Rep. 2021, 3, 12307. [Google Scholar] [CrossRef]
- Songrong, L.; Wenxian, Y.; Youxin, L. Fault Diagnosis of a Rolling Bearing Based on Adaptive Sparest Narrow-Band Decomposition and RefinedComposite Multiscale Dispersion Entropy. Entropy 2020, 22, 375. [Google Scholar]
- Li, Y.; Gao, X.; Wang, L. Reverse Dispersion Entropy: A New Complexity Measure for Sensor Signal. Sensors 2019, 19, 5023. [Google Scholar] [CrossRef] [Green Version]
- Ding, S.; Zhao, H.; Zhang, Y.; Xu, X.; Nie, R. Extreme learning machine: Algorithm, theory and applications. Artif. Intell. Rev. 2015, 44, 103–115. [Google Scholar] [CrossRef]
- GuangBin, H.; Hongming, Z.; Xiaojian, D.; Rui, Z. Extreme learning machine for regression and multiclass classification. IEEE Trans. Syst. Man Cybern. 2012, 42, 513–529. [Google Scholar] [CrossRef] [Green Version]
- Maglogiannis, I.; Karpouzis, K.; Wallace, M.; Soldatos, J.; Kotsiantis, S.B. Supervised Machine Learning: A Review of Classification Techniques. Emerg. Artif. Intell. Appl. Comput. Eng. 2007, 160, 249–268. [Google Scholar]
- Svetnik, V.; Liaw, A.; Tong, C.; Culberson, J.C.; Sheridan, R.P.; Feuston, B.P. Random Forest: A Classification and Regression Tool for Compound Classification and QSAR Modeling. J. Chem. Inf. Comput. Sci. 2003, 43, 1947–1958. [Google Scholar] [CrossRef]
- Wei, Y.; Yang, Y.; Xu, M.; Huang, W. Intelligent fault diagnosis of planetary gearbox based on refined composite hierarchical fuzzy entropy and random forest. ISA Trans. 2021, 109, 340–351. [Google Scholar] [CrossRef]
- Fezai, R.; Dhibi, K.; Mansouri, M.; Trabelsi, M.; Hajji, M.; Bouzrara, K.; Nounou, H.; Nounou, M. Effective Random Forest-Based Fault Detection and Diagnosis for Wind Energy Conversion Systems. IEEE Sens. J. 2021, 21, 6914–6921. [Google Scholar] [CrossRef]
- Liu, W.; Cao, S.; Wang, Z. Application of variational mode decomposition to seismic random noise reduction. J. Geophys. Eng. 2017, 14, 888–898. [Google Scholar]
- Xi, C.; Yang, G.; Liu, L.; Jiang, H.; Chen, X. A Refined Composite Multivariate Multiscale Fluctuation Dispersion Entropy and Its Application to Multivariate Signal of Rotating Machinery. Entropy 2021, 23, 128. [Google Scholar] [CrossRef] [PubMed]
- Bennasar, M.; Hicks, Y.; Setchi, R. Feature selection using Joint Mutual Information Maximisation. Expert Syst. Appl. 2015, 42, 8520–8532. [Google Scholar] [CrossRef] [Green Version]
- Cabrera, D.; Sancho, F.; Sánchez, R.; Zurita, G.; Cerrada, M.; Li, C.; Vásquez, R.E. Fault diagnosis of spur gearbox based on random forest and wavelet packet decomposition. Front. Mech. Eng. 2015, 10, 277–286. [Google Scholar] [CrossRef]
- Qin, X.; Li, Q.; Dong, X.; Lv, S. The Fault Diagnosis of Rolling Bearing Based on Ensemble Empirical Mode Decomposition and Random Forest. Shock. Vib. 2017, 2017, 2623081. [Google Scholar] [CrossRef]
- LI, Y.; Zhang, J.; Lin, Y. Combining Fisher Criterion and Deep Learning for Patterned Fabric Defect Inspection. IEICE Trans. Inf. Syst. 2016, 11, 2840–2842. [Google Scholar] [CrossRef] [Green Version]
- Tsapparellas, G.; Jin, N.; Dai, X.; Fehringer, G. Laplacian Scores-Based Feature Reduction in IoT Systems for Agricultural Monitoring and Decision-Making Support. Sensors 2020, 20, 5107. [Google Scholar] [CrossRef]




| Methods | Data Length | |||
|---|---|---|---|---|
| 2048 | 3072 | 4096 | 5120 | |
| MDE | 0.1059 s | 0.1148 s | 0.1235 s | 0.1335 s |
| RCMDE | 0.2061 s | 0.2867 s | 0.3704 s | 0.4490 s |
| RCMRDE | 0.1997 s | 0.2818 s | 0.3637 s | 0.4431 s |
| Parameter | Value | Parameter | Value | Parameter | Value |
|---|---|---|---|---|---|
| 73 | 3 | 2 | |||
| 0.025 | N (2, 5, 1) | 0.025 | |||
| 0.5, 0.6, 0.7, 0.8 | 10 | ||||
| 2600 | 1700 | 20 | |||
| 0 | 0 | ||||
| 1000 | 800 |
| Type | Inner Diameter (mm) | Outer Diameter (mm) | Rolling Element Diameter (mm) | Pitch Circle Diameter (mm) | Number of Rolling Element | Characteristic |
|---|---|---|---|---|---|---|
| 25 | 52 | 7.5 | 39 | 13 | Detachable outer ring | |
| 25 | 52 | 7.5 | 39 | 13 | Detachable inner ring |
| Bearing State | Fault Size (mm) | Abbreviation | Label | Training Data | Test Data |
|---|---|---|---|---|---|
| Outer race fault | 0.2 | ORF02 | 0 | 35 | 15 |
| Outer race fault | 0.4 | ORF04 | 1 | 35 | 15 |
| Outer race fault | 0.6 | ORF06 | 2 | 35 | 15 |
| Inner race fault | 0.2 | IRF02 | 3 | 35 | 15 |
| Inner race fault | 0.4 | IRF04 | 4 | 35 | 15 |
| Inner race fault | 0.6 | IRF06 | 5 | 35 | 15 |
| Rolling element fault | 0.2 | REF02 | 6 | 35 | 15 |
| Rolling element fault | 0.4 | REF04 | 7 | 35 | 15 |
| Rolling element fault | 0.6 | REF06 | 8 | 35 | 15 |
| Normal | - | Normal | 9 | 35 | 15 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, A.; Yang, Z.; Li, H.; Wang, C.; Liu, X. Intelligent Diagnosis of Rolling Element Bearing Based on Refined Composite Multiscale Reverse Dispersion Entropy and Random Forest. Sensors 2022, 22, 2046. https://doi.org/10.3390/s22052046
Liu A, Yang Z, Li H, Wang C, Liu X. Intelligent Diagnosis of Rolling Element Bearing Based on Refined Composite Multiscale Reverse Dispersion Entropy and Random Forest. Sensors. 2022; 22(5):2046. https://doi.org/10.3390/s22052046
Chicago/Turabian StyleLiu, Aiqiang, Zuye Yang, Hongkun Li, Chaoge Wang, and Xuejun Liu. 2022. "Intelligent Diagnosis of Rolling Element Bearing Based on Refined Composite Multiscale Reverse Dispersion Entropy and Random Forest" Sensors 22, no. 5: 2046. https://doi.org/10.3390/s22052046
APA StyleLiu, A., Yang, Z., Li, H., Wang, C., & Liu, X. (2022). Intelligent Diagnosis of Rolling Element Bearing Based on Refined Composite Multiscale Reverse Dispersion Entropy and Random Forest. Sensors, 22(5), 2046. https://doi.org/10.3390/s22052046







