Multi-Unit Serial Polynomial Multiplier to Accelerate NTRU-Based Cryptographic Schemes in IoT Embedded Systems
Abstract
:1. Introduction
- The design of a highly configurable intellectual property (IP) module to implement a multi-unit serial polynomial multiplier and accelerate NTRU operations;
- The proposal of different interconnection schemes that optimize the bandwidth of communication infrastructures provided by device manufacturers;
- The possibility of choosing the number of arithmetic units in the multiplier, as well as selecting the interconnection scheme to be used, which allows establishing an adequate cost/performance/security level trade-off based on the intended application for the embedded system.
2. The NTRU Cryptographic Scheme
3. Implementation of NTRU on Embedded Systems
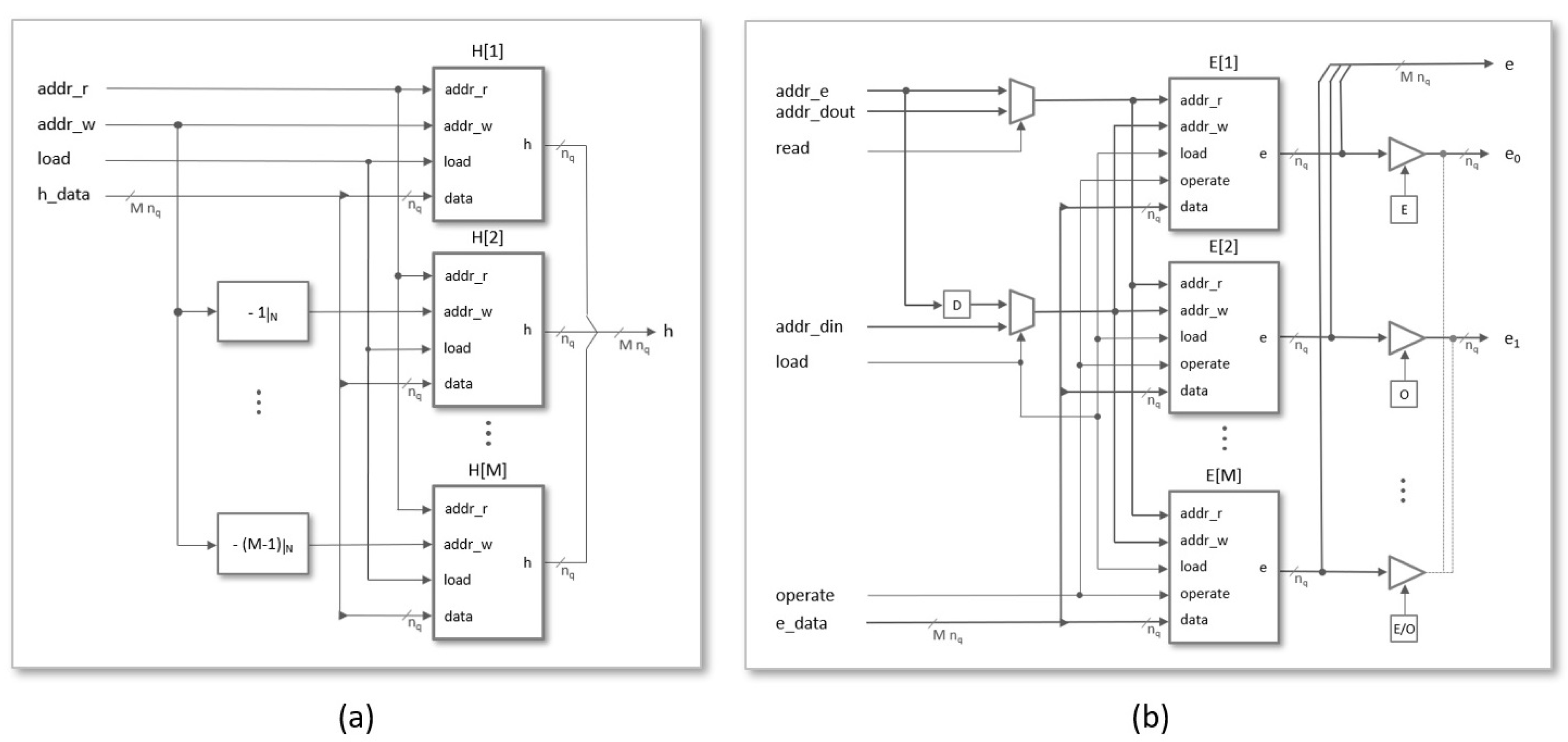
4. Multi-Unit Serial Polynomial Multiplier
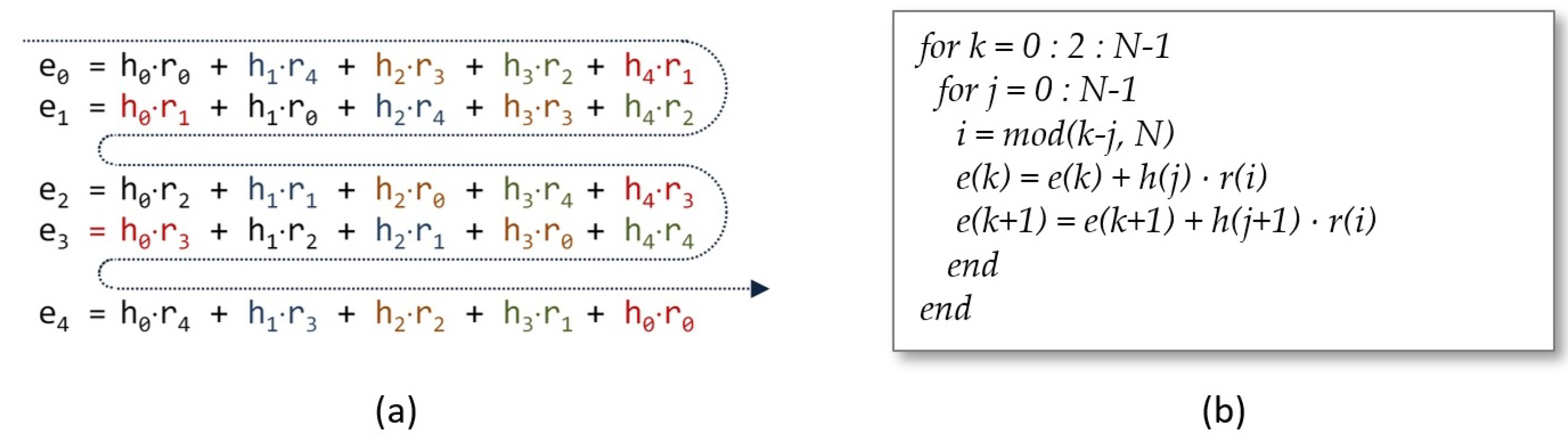
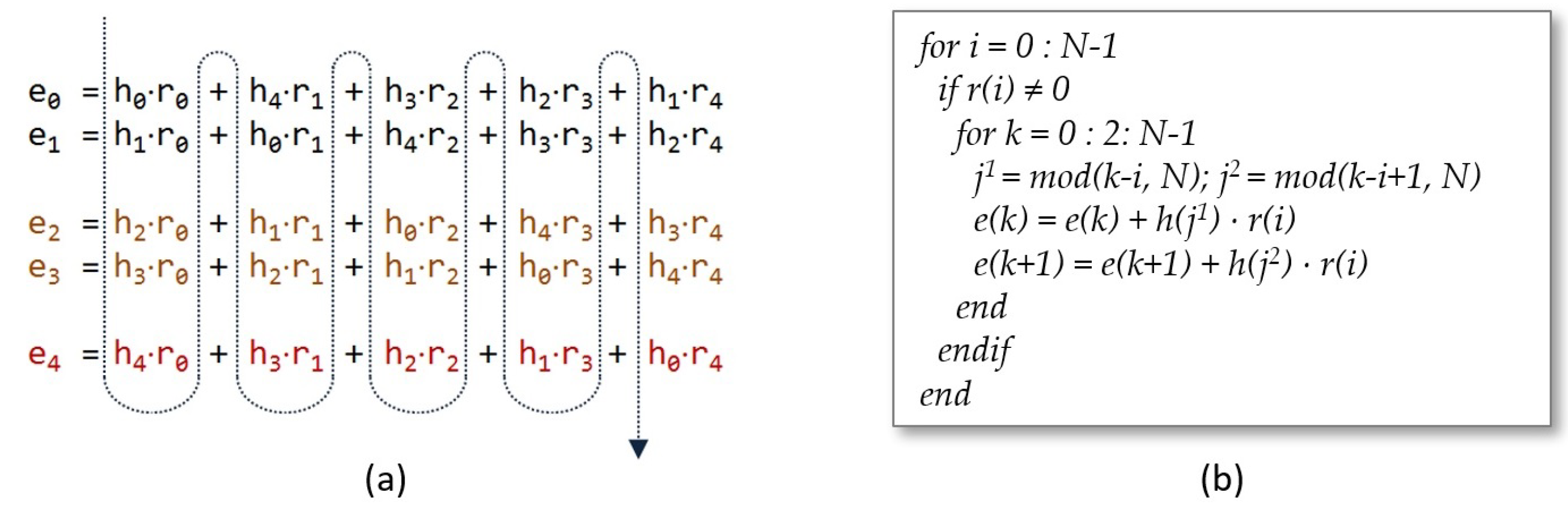
4.1. Core Design of the Polynomial Multiplier
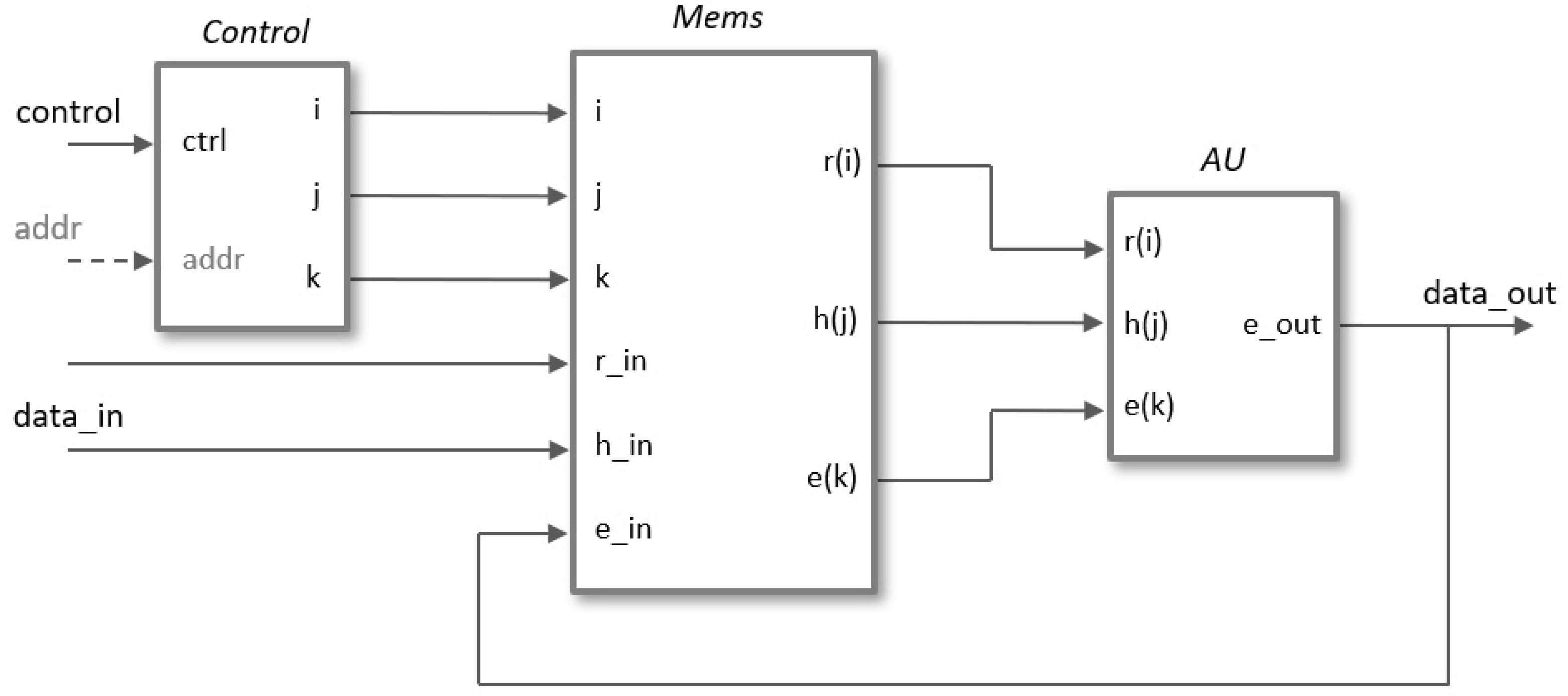
4.2. Interface Design and IP-Module Encapsulation
4.2.1. AXI4-Lite Option
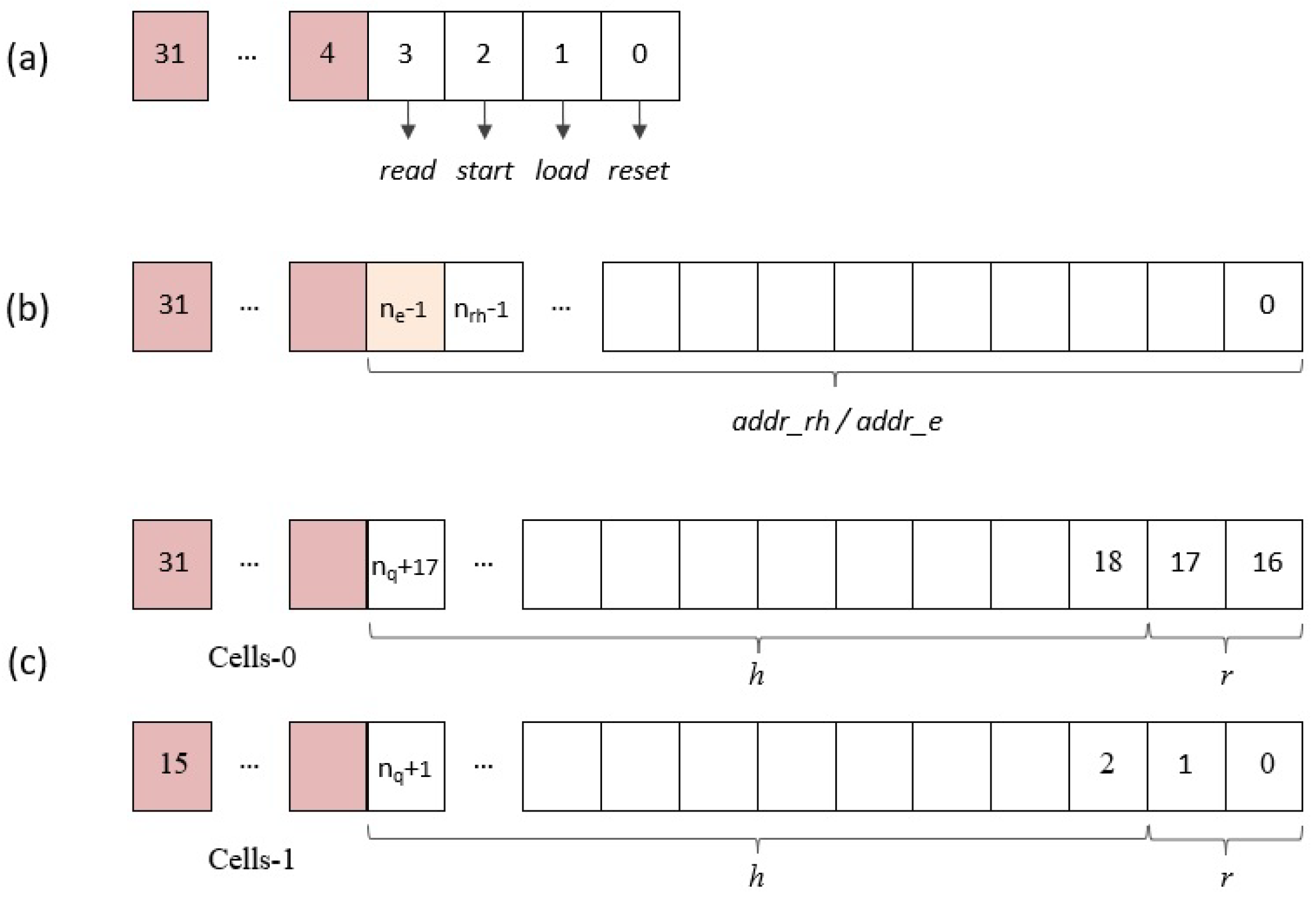
- register: The four least significant bits of this input register, as shown in Figure 10a, are used from the software to supply the module reset signal () and the enable signals for initialization and coefficient loading (), operation start (), and reading of results ().
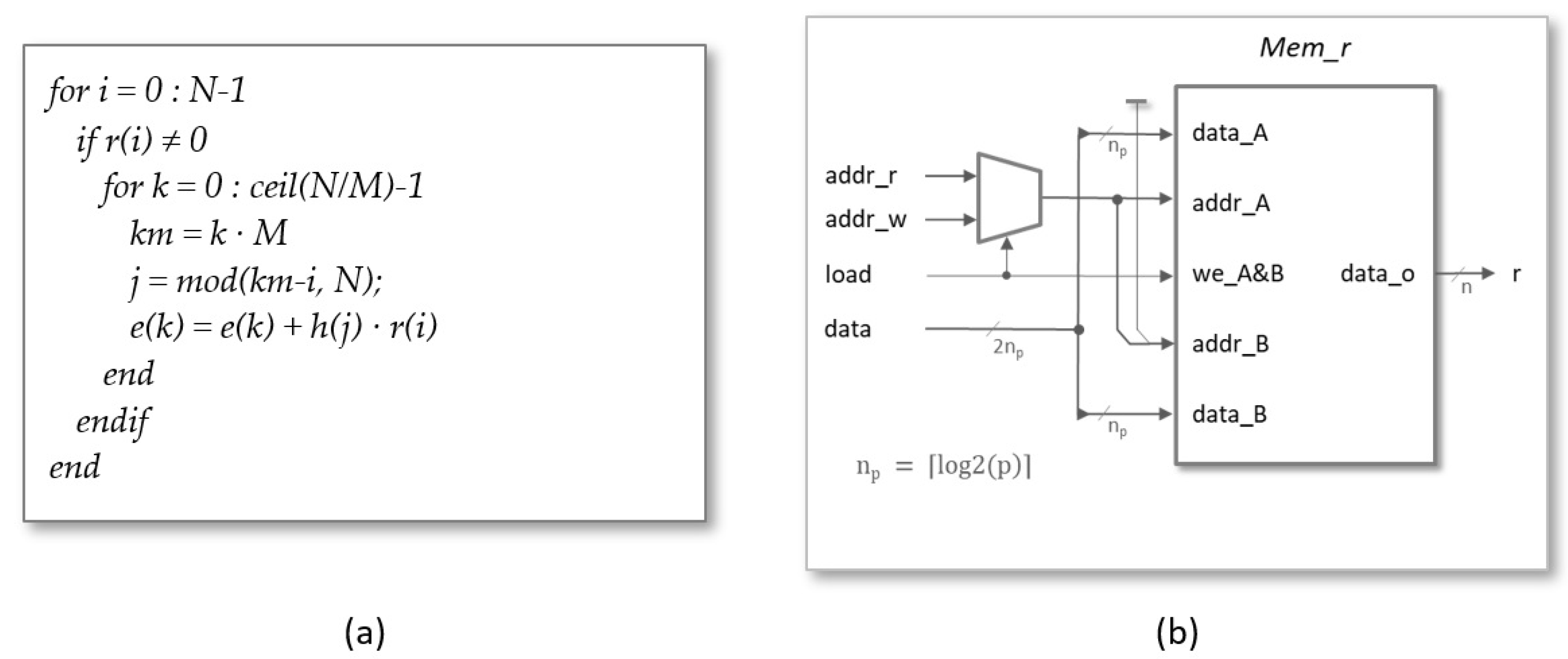
- register: During the load phase, the register shown in Figure 10b is used to indicate the indices of the coefficients and , whose values are provided through the register. The number of bits required to encode the memory addresses depends on the implemented parameter set . On the other hand, in the read phase, the content of this register points to the memory address of the coefficient , whose value is output through the register. As a consequence of the simplified addressing scheme used in the design, the number of bits needed to encode the memory addresses is, in this case, a function not only of N but also of the degree of multiplicity of the polynomial multiplier . (When M is different from 1, it is necessary to generate the enable signals of the M memories used to calculate the result of the operation. The solution adopted in this case to simplify the generation of these signals is to generate the memory addresses externally).
- Data input () register: Considering that all the parameter sets defined by the IEEE standard use values of p and q equal to 3 and 2048, respectively, 2 pairs of coefficients and can be transmitted simultaneously in each AXI4 transfer using the bit distribution shown in Figure 10c, where bits in the upper and lower half of the 32-bit register are used for each pair of coefficients.
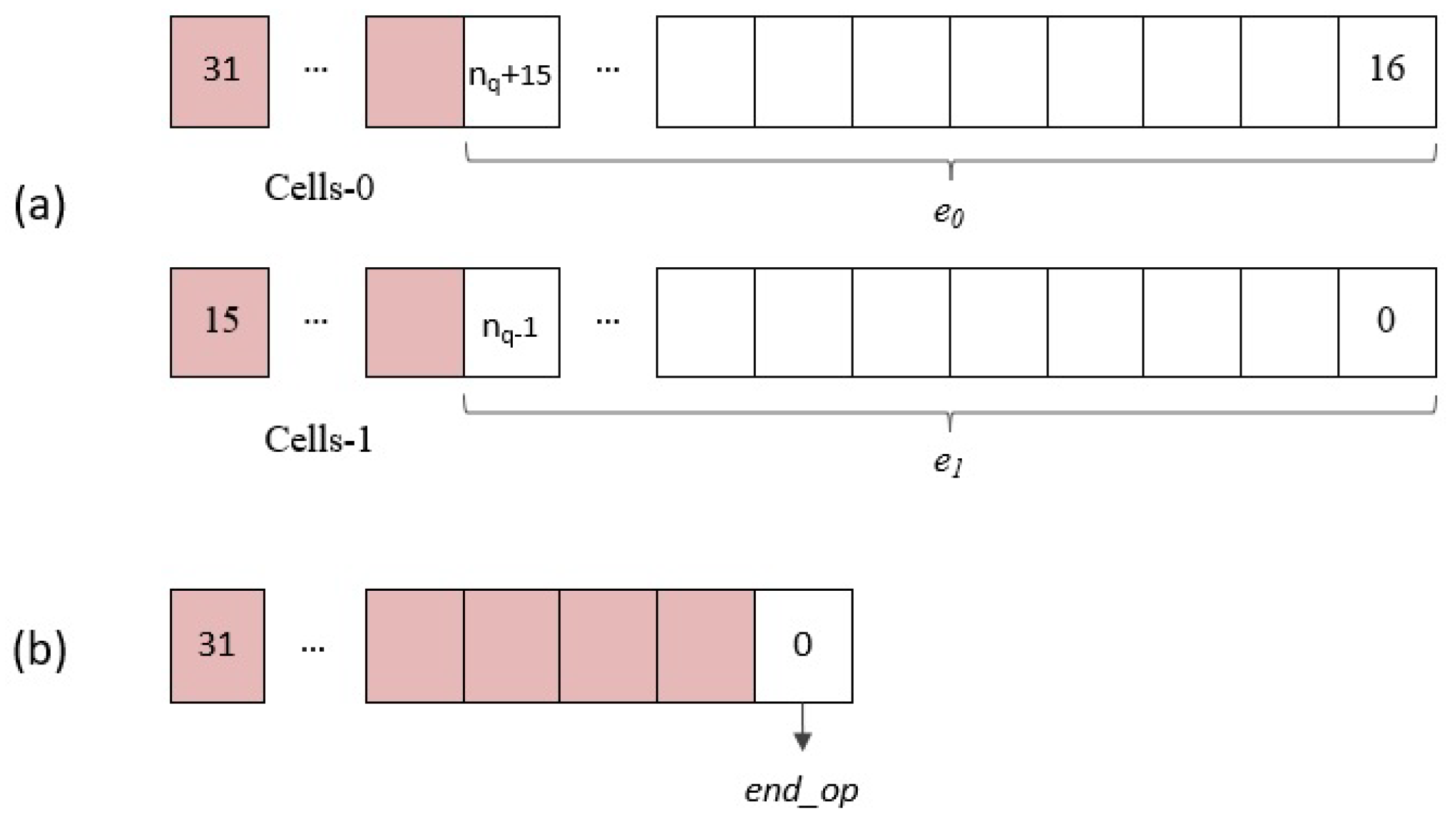
- Data output () register: As in the case of input polynomials, two coefficients of the multiplier result can be retrieved in each read access to this register through the AXI4 interface. As shown in Figure 11a, bits are used in the upper and lower half of the 32-bit register.
- End operation () register: The least significant bit (LSB) of the register shown in Figure 11b gives access to the status signal of the same name, which will be used by the general-purpose processor to determine when the polynomial multiplier has finished its operation and start the results reading phase.
4.2.2. AXI4-Stream Option
5. Implementation Results
6. Embedded System Integration
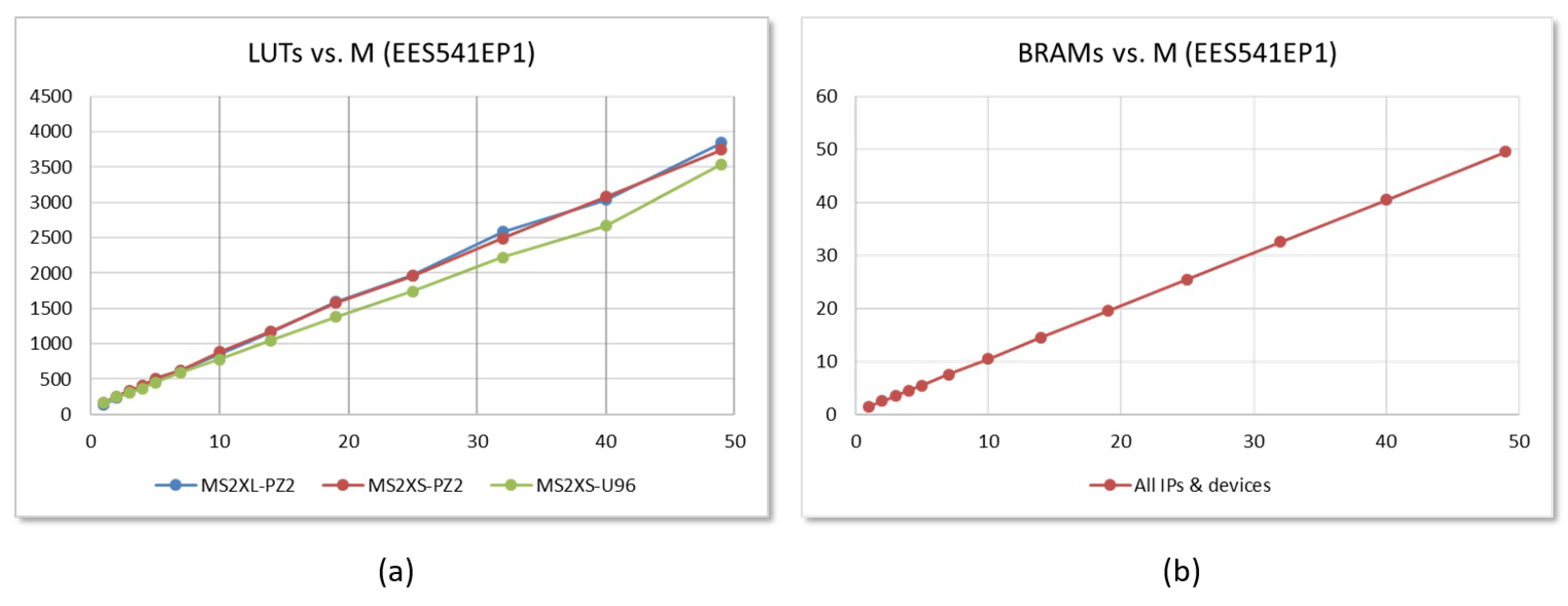
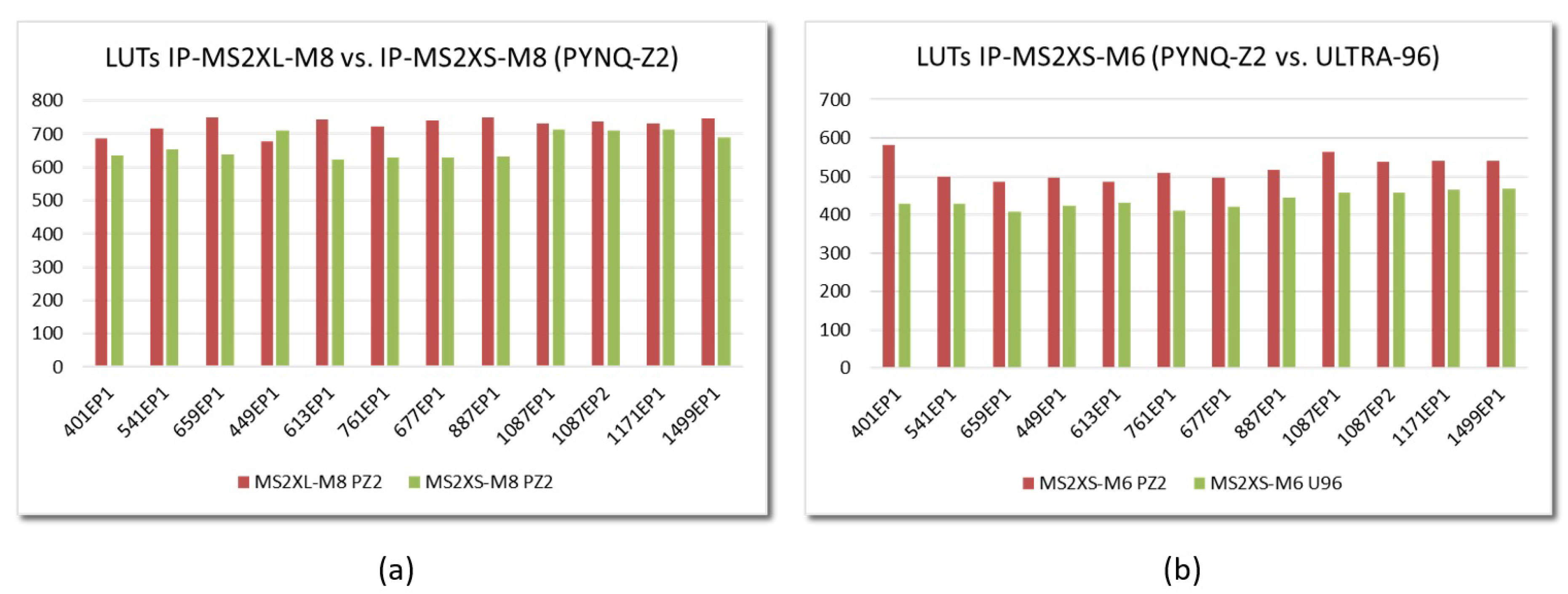
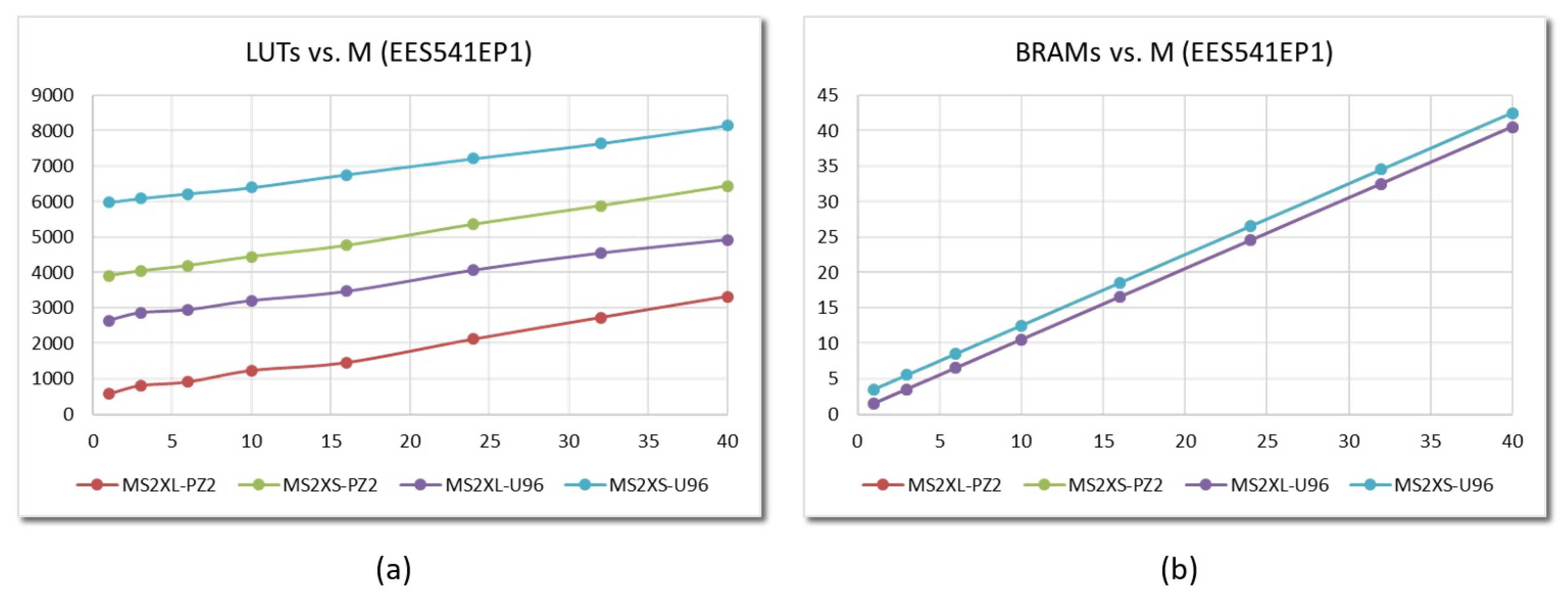
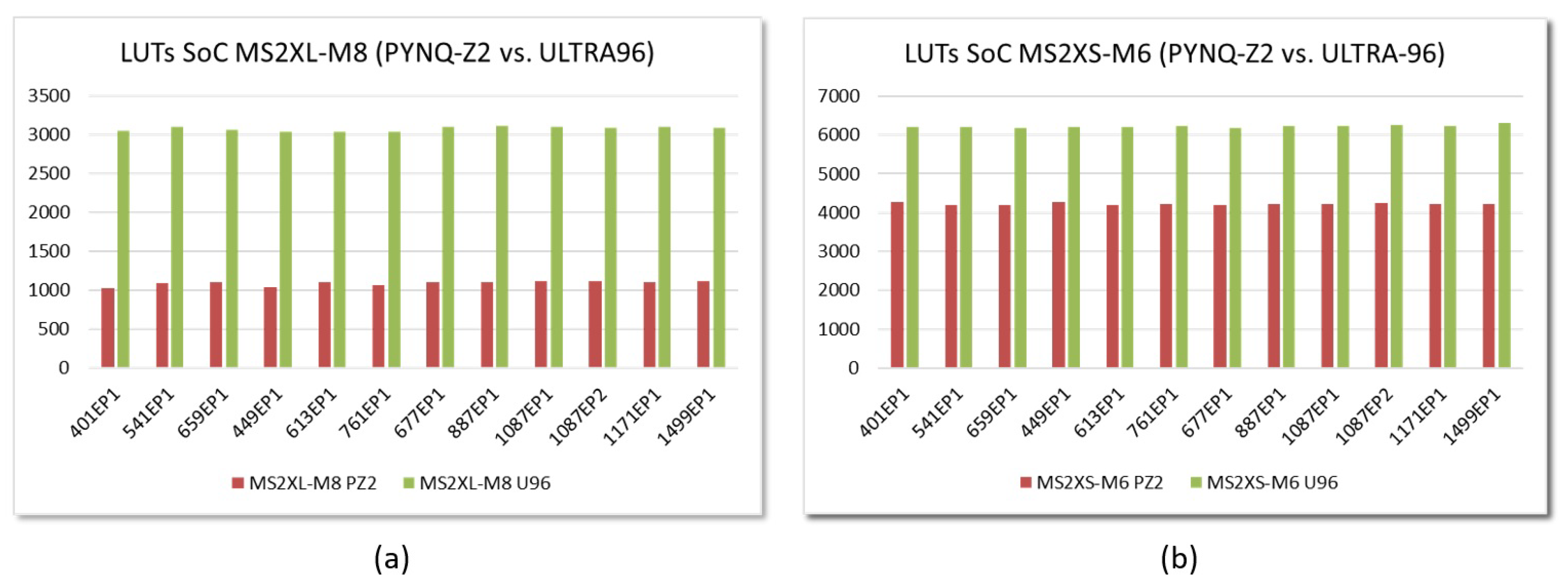
6.1. Resource Consumption
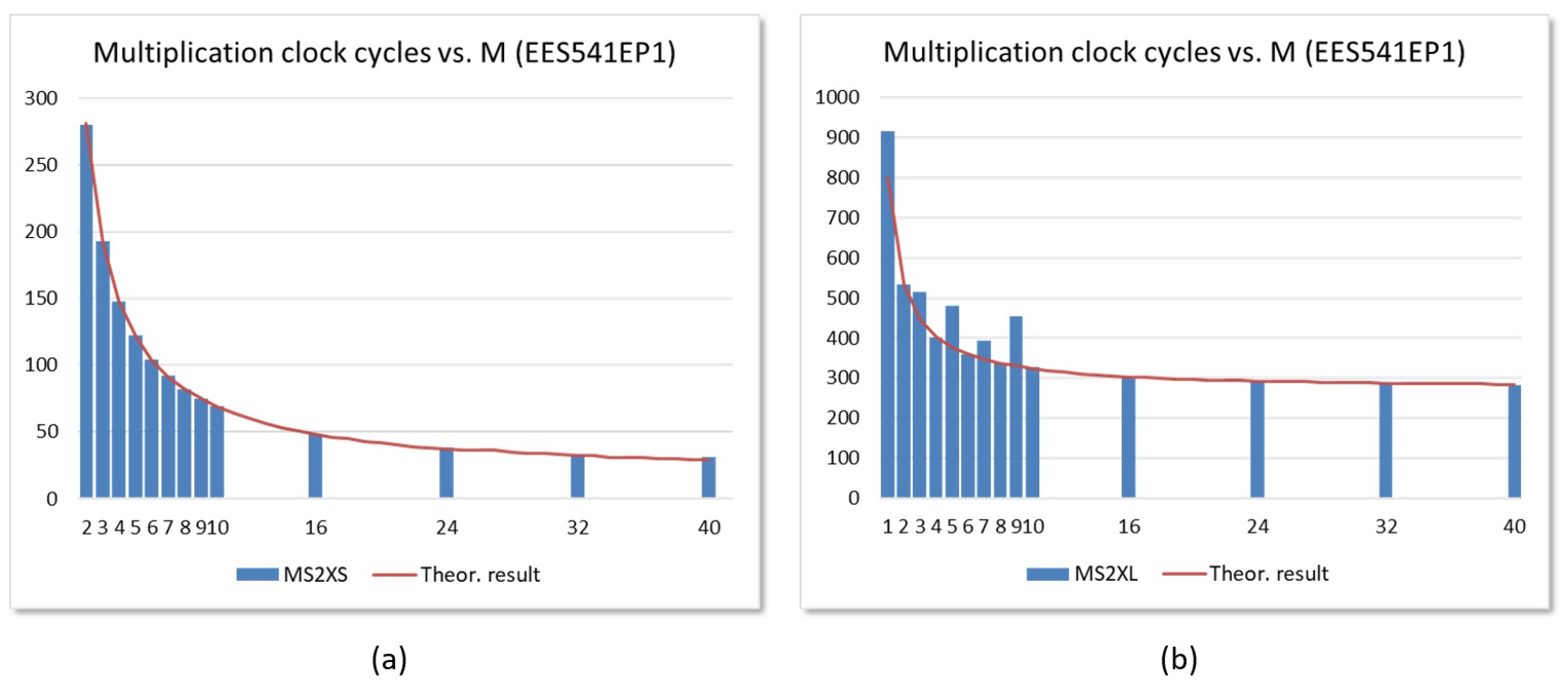
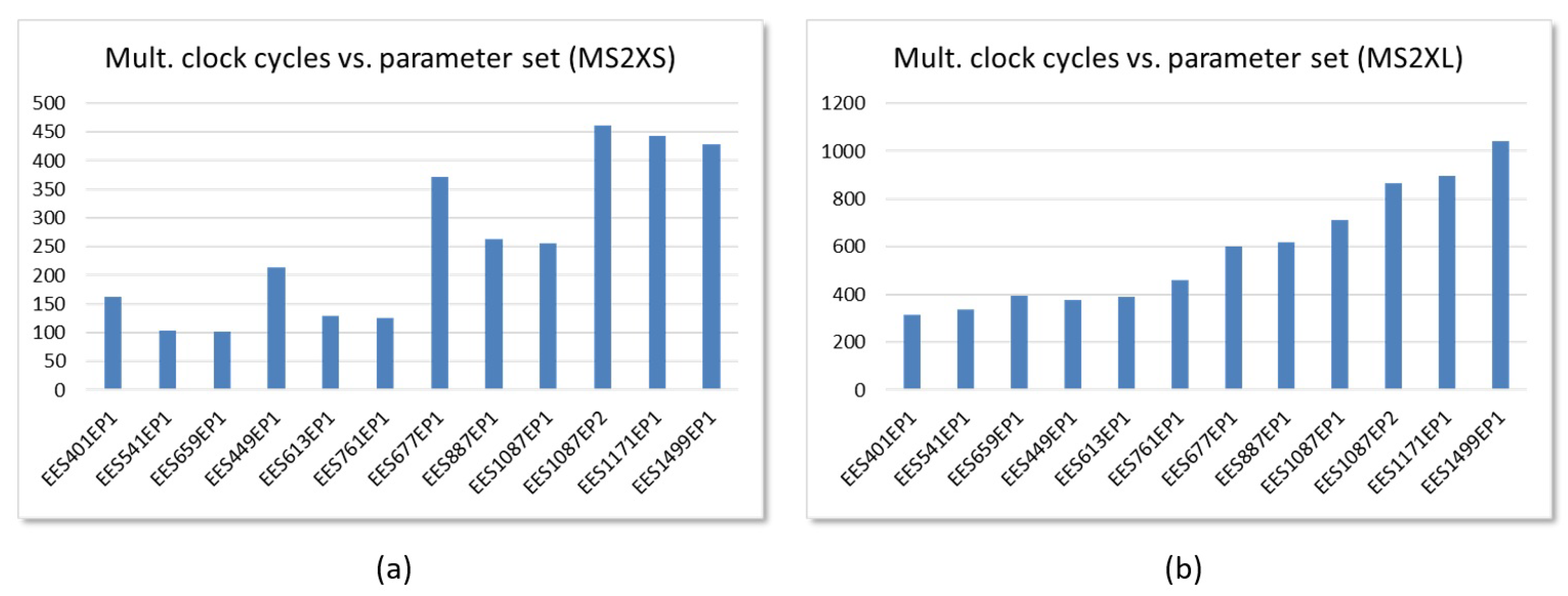
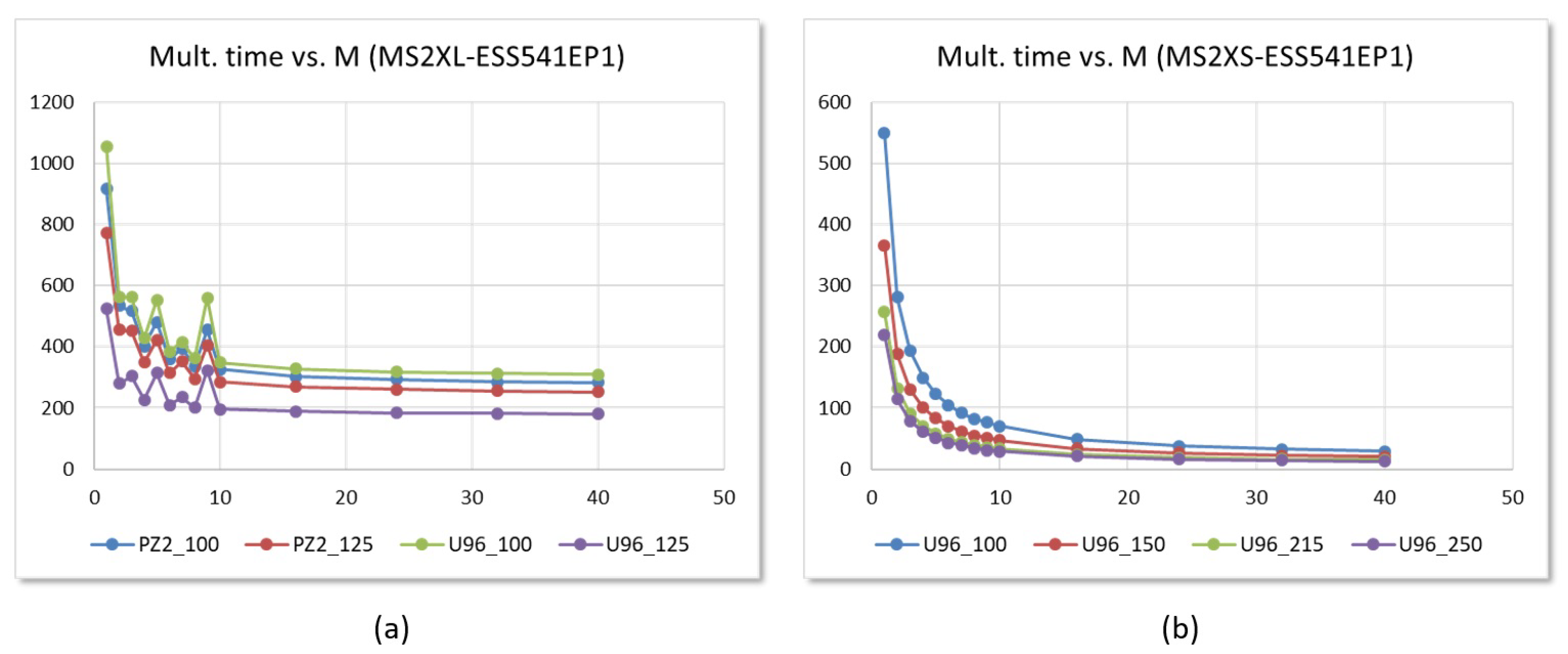
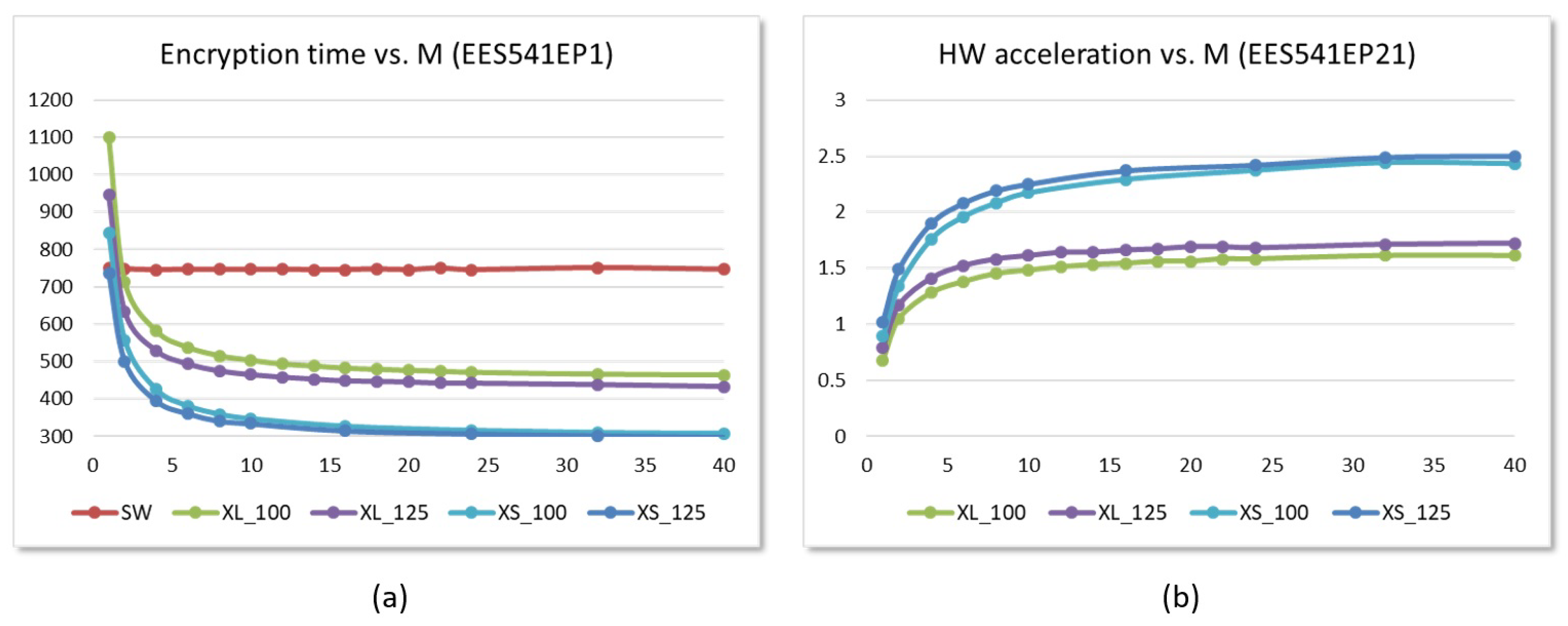
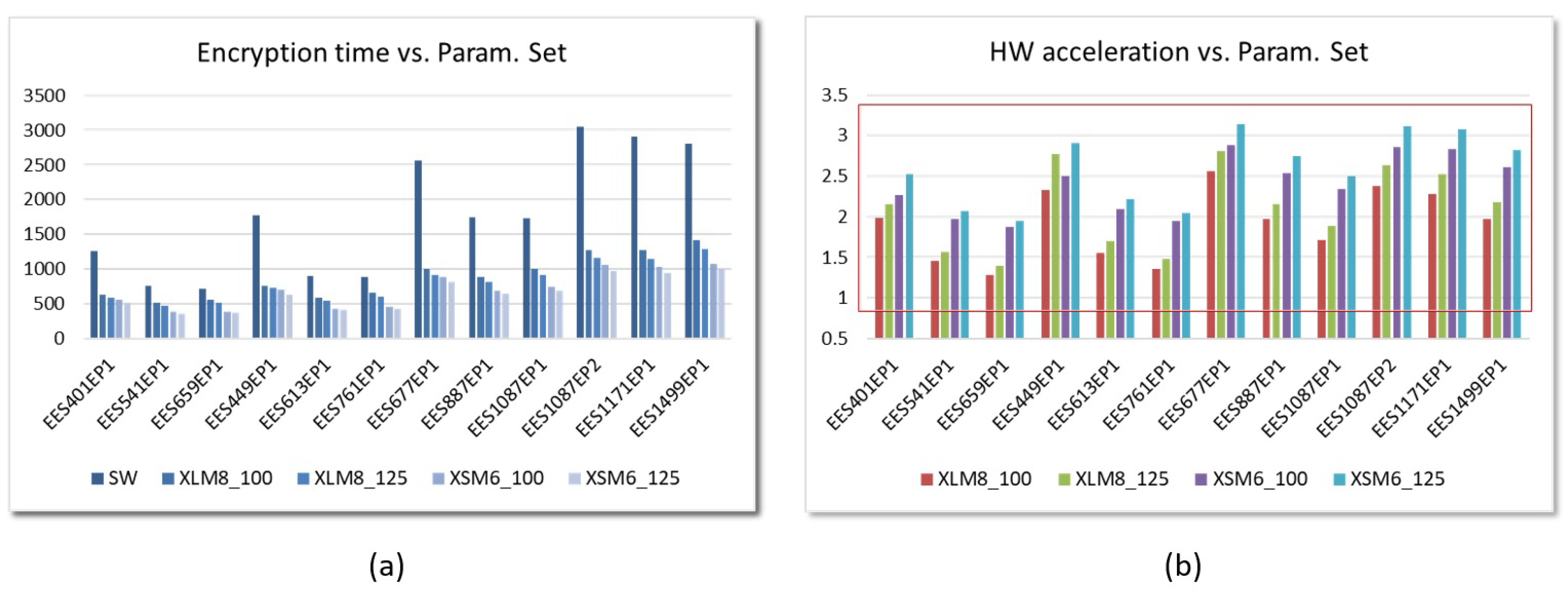
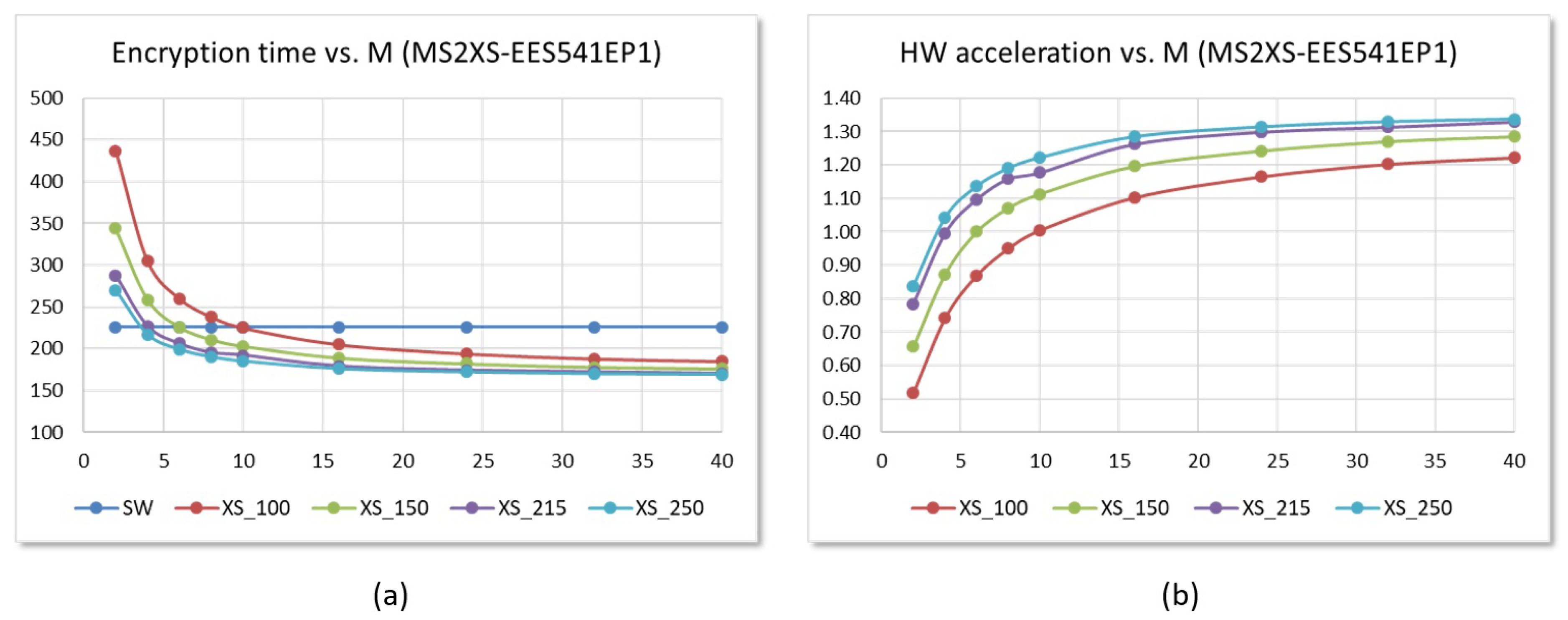
6.2. Performance Evaluation
7. Integration of HW Accelerators into LibNTRU
8. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Atzori, L.; Iera, A.; Morabito, G. The Internet of Things: A survey. Comput. Netw. 2010, 54, 2787–2805. [Google Scholar] [CrossRef]
- Li, S.; Xu, L.; Zhao, S. The internet of things: A survey. Inf. Syst. Front. 2014, 17, 243–259. [Google Scholar] [CrossRef]
- Narayanan, K. Addressing the challenges facing IoT adoption. Microw. J. 2017, 60, 110–118. [Google Scholar]
- Mehta, R.; Sahni, J.; Khanna, K. Internet of Things: Vision, Applications and Challenges. Procedia Comput. Sci. 2018, 132, 1263–1269. [Google Scholar] [CrossRef]
- Chegini, H.; Naha, R.K.; Mahanti, A.; Thulasiraman, P. Process Automation in an IoT–Fog–Cloud Ecosystem: A Survey and Taxonomy. IoT 2021, 2, 92–118. [Google Scholar] [CrossRef]
- Gilchrist, A. Introducing Industry 4.0. In Industry 4.0: The Industrial Internet of Things; Apress: Berkeley, CA, USA, 2016; pp. 195–215. [Google Scholar] [CrossRef]
- Öztemel, E.; Gursev, S. Literature review of Industry 4.0 and related technologies. J. Intell. Manuf. 2020, 31, 127–182. [Google Scholar] [CrossRef]
- Yang, F.; Gu, S. Industry 4.0, a revolution that requires technology and national strategies. Complex Intell. Syst. 2021, 7, 1311–1325. [Google Scholar] [CrossRef]
- Cheng, G.J.; Liu, L.T.; Qiang, X.; Liu, Y. Industry 4.0 Development and Application of Intelligent Manufacturing. In Proceedings of the 2016 International Conference on Information System and Artificial Intelligence (ISAI), Hong Kong, China, 24–26 June 2016; pp. 407–410. [Google Scholar] [CrossRef]
- Xu, L.D.; Xu, E.L.; Li, L. Industry 4.0: State of the art and future trends. Int. J. Prod. Res. 2018, 56, 2941–2962. [Google Scholar] [CrossRef] [Green Version]
- Alcácer, V.; Cruz-Machado, V. Scanning the Industry 4.0: A Literature Review on Technologies for Manufacturing Systems. Eng. Sci. Technol. Int. J. 2019, 22, 899–919. [Google Scholar] [CrossRef]
- Xu, T.; Wendt, J.B.; Potkonjak, M. Security of IoT systems: Design challenges and opportunities. In Proceedings of the 2014 IEEE/ACM International Conference on Computer-Aided Design (ICCAD), San Jose, CA, USA, 2–6 November 2014; pp. 417–423. [Google Scholar] [CrossRef]
- Patwary, A.A.N.; Naha, R.K.; Garg, S.; Battula, S.K.; Patwary, M.A.K.; Aghasian, E.; Amin, M.B.; Mahanti, A.; Gong, M. Towards Secure Fog Computing: A Survey on Trust Management, Privacy, Authentication, Threats and Access Control. Electronics 2021, 10, 1171. [Google Scholar] [CrossRef]
- Dhirani, L.L.; Armstrong, E.; Newe, T. Industrial IoT, Cyber Threats, and Standards Landscape: Evaluation and Roadmap. Sensors 2021, 21, 3901. [Google Scholar] [CrossRef]
- Crowder, R. 11—Cyber Physical systems and security. In Electric Drives and Electromechanical Systems, 2nd ed.; Crowder, R., Ed.; Butterworth-Heinemann: Oxford, UK, 2020; pp. 271–289. [Google Scholar] [CrossRef]
- Malina, L.; Hajny, J.; Fujdiak, R.; Hosek, J. On perspective of security and privacy-preserving solutions in the internet of things. Comput. Netw. 2016, 102, 83–95. [Google Scholar] [CrossRef]
- Rajendran, S.; Mary Lourde, R. Security Threats of Embedded Systems in IoT Environment. In Inventive Communication and Computational Technologies; Ranganathan, G., Chen, J., Rocha, Á., Eds.; Springer: Singapore, 2020; pp. 745–754. [Google Scholar] [CrossRef]
- Lezzi, M.; Lazoi, M.; Corallo, A. Cybersecurity for Industry 4.0 in the current literature: A reference framework. Comput. Ind. 2018, 103, 97–110. [Google Scholar] [CrossRef]
- Gebremichael, T.; Ledwaba, L.; Eldefrawy, M.; Hancke, G.; Pereira, N.; Gidlund, M.; Akerberg, J. Security and Privacy in the Industrial Internet of Things: Current Standards and Future Challenges. IEEE Access 2020, 8, 152351–152366. [Google Scholar] [CrossRef]
- Tsiknas, K.; Taketzis, D.; Demertzis, K.; Skianis, C. Cyber Threats to Industrial IoT: A Survey on Attacks and Countermeasures. IoT 2021, 2, 163–186. [Google Scholar] [CrossRef]
- Pal, S.; Hitchens, M.; Rabehaja, T.; Mukhopadhyay, S. Security Requirements for the Internet of Things: A Systematic Approach. Sensors 2020, 20, 5897. [Google Scholar] [CrossRef]
- Hodgson, R. Solving the security challenges of IoT with public key cryptography. Netw. Secur. 2019, 2019, 17–19. [Google Scholar] [CrossRef]
- Höglund, J.; Lindemer, S.; Furuhed, M.; Raza, S. PKI4IoT: Towards public key infrastructure for the Internet of Things. Comput. Secur. 2020, 89, 101658. [Google Scholar] [CrossRef]
- Profentzas, C.; Günes, M.; Nikolakopoulos, Y.; Landsiedel, O.; Almgren, M. Performance of Secure Boot in Embedded Systems. In Proceedings of the 2019 15th International Conference on Distributed Computing in Sensor Systems (DCOSS), Santorini, Greece, 29–31 May 2019; pp. 198–204. [Google Scholar] [CrossRef] [Green Version]
- Mavroeidis, V.; Vishi, K.; Zych, M.D.; Jøsang, A. The Impact of Quantum Computing on Present Cryptography. Int. J. Adv. Comput. Sci. Appl. 2018, 9. [Google Scholar] [CrossRef] [Green Version]
- Shor, P. Algorithms for quantum computation: Discrete logarithms and factoring. In Proceedings of the 35th Annual Symposium on Foundations of Computer Science, Santa Fe, NM, USA, 20–22 November 1994; pp. 124–134. [Google Scholar] [CrossRef]
- Bernstein, D.J.; Lange, T. Post-quantum cryptography. Nature 2017, 549, 188–194. [Google Scholar] [CrossRef]
- Marzougui, S.; Krämer, J. Post-Quantum Cryptography in Embedded Systems. In Proceedings of the 14th International Conference on Availability, Reliability and Security (ARES’19), Canterbury, UK, 26–29 August 2019; pp. 1–7. [Google Scholar] [CrossRef] [Green Version]
- NIST. Post-Quantum Cryptography Standardization. Available online: https://csrc.nist.gov/news/2016/public-key-post-quantum-cryptographic-algorithms (accessed on 20 February 2022).
- NIST. Post-Quantum Cryptography—Round 3 Submissions. Available online: https://csrc.nist.gov/projects/post-quantum-cryptography/round-3-submissions (accessed on 20 February 2022).
- NIST. Third PQC Standardization Conference. Available online: https://csrc.nist.gov/Events/2021/third-pqc-standardization-conference (accessed on 20 February 2022).
- Hoffstein, J.; Pipher, J.; Silverman, J.H. NTRU: A ring-based public key cryptosystem. In Algorithmic Number Theory; Buhler, J.P., Ed.; Springer: Berlin/ Heidelberg, Germany, 1998; pp. 267–288. [Google Scholar] [CrossRef]
- IEEE Std 1363.1-2008; IEEE Standard Specification for Public Key Cryptographic Techniques Based on Hard Problems over Lattices. IEEE: New York, NY, USA, 2009; pp. 1–81. [CrossRef]
- Lattice-Based Polynomial Public Key Establishment Algorithm for the Financial Services Industry. ANSI X9.98-2010. 2011. Available online: https://webstore.ansi.org/standards/ascx9/ansix9982010r2017 (accessed on 20 February 2022).
- Hoffstein, J.; Silverman, J. Optimizations for NTRU. In Public-Key Cryptography and Computational Number Theory; De Gruyter: Berlin, Geramny; New York, NY, USA, 2001; pp. 77–88. [Google Scholar] [CrossRef] [Green Version]
- Howgrave-Graham, N.; Silverman, J.; Whyte, W. Choosing parameter sets for NTRUEncrypt with NAEP and SVES-3. IACR Cryptol. EPrint Arch. 2005, 2005, 45. [Google Scholar] [CrossRef] [Green Version]
- Hirschhorn, P.S.; Hoffstein, J.; Howgrave-Graham, N.; Whyte, W. Choosing NTRUEncrypt Parameters in Light of Combined Lattice Reduction and MITM Approaches. In Applied Cryptography and Network Security; Abdalla, M., Pointcheval, D., Fouque, P.A., Vergnaud, D., Eds.; Springer: Berlin/Heidelberg, Germany, 2009; pp. 437–455. [Google Scholar] [CrossRef]
- Hoffstein, J.; Howgrave-Graham, N.; Pipher, J.; Whyte, W. Practical lattice-based cryptography: NTRUEncrypt and NTRUSign. In The LLL Algorithm; Springer: Berlin/Heidelberg, Germany, 2009; pp. 349–390. [Google Scholar] [CrossRef]
- Hoffstein, J.; Pipher, J.; Schanck, J.M.; Silverman, J.H.; Whyte, W.; Zhang, Z. Choosing Parameters for NTRUEncrypt. Cryptology ePrint Archive, Report 2015/708. 2015. Available online: https://ia.cr/2015/708 (accessed on 20 February 2022).
- Gaithuru, J.; Salleh, M.; Bakhtiari, M. Identification of influential parameters for NTRU decryption failure and recommendation of extended parameter selection criteria for elimination of decryption failure. IAENG Int. J. Comput. Sci. 2017, 44, 358–367. [Google Scholar]
- Chen, C.; Hoffstein, J.; Whyte, W.; Zhenfei, Z. NIST PQ Submission: NTRUEncrypt, a Lattice Based Encryption Algorithm, tech. rep., NIST PQC Standardization, Round 1. 2017. Available online: https://csrc.nist.gov/projects/post-quantum-cryptography/round-1-submissions (accessed on 20 February 2022).
- Hülsing, A.; Rijneveld, J.; Schanck, J.; Schwabe, P. High-Speed Key Encapsulation from NTRU. In Cryptographic Hardware and Embedded Systems—CHES 2017; Fischer, W., Homma, N., Eds.; Springer International Publishing: Cham, Switzerlamd, 2017; pp. 232–252. [Google Scholar] [CrossRef] [Green Version]
- Bernstein, D.J.; Chuengsatiansup, C.; Lange, T.; van Vredendaal, C. NTRU Prime: Reducing Attack Surface at Low Cost. Cryptology ePrint Archive, Report 2016/461. 2016. Available online: https://ia.cr/2016/461 (accessed on 20 February 2022).
- Hoffstein, J.; Howgrave-Graham, N.; Pipher, J.; Silverman, J.H.; Whyte, W. NTRUSign: Digital Signatures Using the NTRU Lattice. In Topics in Cryptology—CT-RSA 2003; Joye, M., Ed.; Springer: Berlin/Heidelberg, Germany, 2003; pp. 122–140. [Google Scholar] [CrossRef]
- Chen, C.; Danba, O.; Hoffstein, J.; Rijneveld, A.H.J.; Schanck, J.M.; Schwabe, P.; Whyte, W.; Zhenfei, Z. NIST PQ Submission: NTRU, Algorithm Specifications And Supporting Documentation, tech. rep., NIST PQC Standardization, Round 2. 2019. Available online: https://ntru.org/f/ntru-20190330.pdf (accessed on 20 February 2022).
- Guillen, O.M.; Pöppelmann, T.; Bermudo Mera, J.M.; Bongenaar, E.F.; Sigl, G.; Sepulveda, J. Towards post-quantum security for IoT endpoints with NTRU. In Proceedings of the Design, Automation & Test in Europe Conference Exhibition (DATE), Lausanne, Switzerland, 27–31 March 2017; pp. 698–703. [Google Scholar] [CrossRef]
- Bailey, D.V.; Coffin, D.; Elbirt, A.; Silverman, J.H.; Woodbury, A.D. NTRU in Constrained Devices. In Cryptographic Hardware and Embedded Systems—CHES 2001; Koç, Ç.K., Naccache, D., Paar, C., Eds.; Springer: Berlin/Heidelberg, Germany, 2001; pp. 262–272. [Google Scholar] [CrossRef] [Green Version]
- Malina, L.; Popelova, L.; Dzurenda, P.; Hajny, J.; Martinasek, Z. On Feasibility of Post-Quantum Cryptography on Small Devices. IFAC-PapersOnLine 2018, 51, 462–467. [Google Scholar] [CrossRef]
- Basu, K.; Soni, D.; Nabeel, M.; Karri, R. NIST Post-Quantum Cryptography—A Hardware Evaluation Study. Cryptology ePrint Archive, Report 2019/047. 2019. Available online: https://ia.cr/2019/047 (accessed on 20 February 2022).
- Imran, M.; Abideen, Z.U.; Pagliarini, S. An Experimental Study of Building Blocks of Lattice-Based NIST Post-Quantum Cryptographic Algorithms. Electronics 2020, 9, 1953. [Google Scholar] [CrossRef]
- Farahmand, F.; Sharif, M.U.; Briggs, K.; Gaj, K. A High-Speed Constant-Time Hardware Implementation of NTRUEncrypt SVES. In Proceedings of the 2018 International Conference on Field-Programmable Technology (FPT), Naha, Japan, 10–14 December 2018; pp. 190–197. [Google Scholar] [CrossRef]
- Atici, A.C.; Batina, L.; Fan, J.; Verbauwhede, I.; Berna Ors Yalcin, S. Low-cost implementations of NTRU for pervasive security. In Proceedings of the 2008 International Conference on Application-Specific Systems, Architectures and Processors, Leuven, Belgium, 2–4 July 2008; pp. 79–84. [Google Scholar] [CrossRef] [Green Version]
- Hoffstein, J.; Silverman, J.H. Random small Hamming weight products with applications to cryptography. Discret. Appl. Math. 2003, 130, 37–49. [Google Scholar] [CrossRef] [Green Version]
- Zhan, X.; Zhang, R.; Xiong, Z.; Zheng, Z.; Liu, Z. Efficient Implementations of NTRU in Wireless Network. Commun. Netw. 2013, 5, 485–492. [Google Scholar] [CrossRef]
- O’Rourke, C. Efficient NTRU Implementations. Master’s Thesis, Worcester Polytechnic Institute, Worcester, MA, USA, 2002. [Google Scholar]
- Kaps, J.P. Cryptography for Ultra-Low Power Devices. Ph.D. Thesis, Worcester Polytechnic Institute, Worcester, MA, USA, 2006. [Google Scholar]
- Kamal, A.A.; Youssef, A.M. Strengthening hardware implementations of NTRUEncrypt against fault analysis attacks. J. Cryptogr. Eng. 2013, 3, 227–240. [Google Scholar] [CrossRef]
- Kamal, A.A.; Youssef, A.M. An FPGA implementation of the NTRUEncrypt cryptosystem. In Proceedings of the 2009 International Conference on Microelectronics—ICM, Marrakech, Morocco, 9–22 December 2009; pp. 209–212. [Google Scholar] [CrossRef]
- Liu, B.; Wu, H. Efficient architecture and implementation for NTRUEncrypt system. In Proceedings of the 58th IEEE International Midwest Symposium on Circuits and Systems (MWSCAS), Fort Collins, CO, USA, 2–5 August 2015; pp. 1–4. [Google Scholar] [CrossRef]
- Liu, B.; Wu, H. Efficient multiplication architecture over truncated polynomial ring for NTRUEncrypt system. In Proceedings of the 2016 IEEE International Symposium on Circuits and Systems (ISCAS), Montreal, QC, Canada, 22–25 May 2016; pp. 1174–1177. [Google Scholar] [CrossRef]
- Braun, K.; Fritzmann, T.; Maringer, G.; Schamberger, T.; Sepúlveda, J. Secure and Compact Full NTRU Hardware Implementation. In Proceedings of the 2018 IFIP/IEEE International Conference on Very Large Scale Integration (VLSI-SoC), Verona, Italy, 8–10 October 2018; pp. 89–94. [Google Scholar] [CrossRef]
- Camacho-Ruiz, E.; Martínez-Rodríguez, M.C.; Sánchez-Solano, S.; Brox, P. Accelerating the Development of NTRU Algorithm on Embedded Systems. In Proceedings of the 2020 XXXV Conference on Design of Circuits and Integrated Systems (DCIS), Segovia, Spain, 18–20 November 2020; pp. 1–6. [Google Scholar] [CrossRef]
- Camacho-Ruiz, E.; Sánchez-Solano, S.; Brox, P.; Martínez-Rodríguez, M.C. Timing-Optimized Hardware Implementation to Accelerate Polynomial Multiplication in the NTRU Algorithm. J. Emerg. Technol. Comput. Syst. 2021, 17. [Google Scholar] [CrossRef]
- Qin, Z.; Tong, R.; Wu, X.; Bai, G.; Wu, L.; Su, L. A Compact Full Hardware Implementation of PQC Algorithm NTRU. In Proceedings of the 2021 International Conference on Communications, Information System and Computer Engineering (CISCE), Beijing, China, 14–16 May 2021; pp. 792–797. [Google Scholar] [CrossRef]
- Farahmand, F.; Dang, V.B.; Nguyen, D.T.; Gaj, K. Evaluating the Potential for Hardware Acceleration of Four NTRU-Based Key Encapsulation Mechanisms Using Software/Hardware Codesign. In Post-Quantum Cryptography; Ding, J., Steinwandt, R., Eds.; Springer International Publishing: Cham, Switzerland, 2019; pp. 23–43. [Google Scholar] [CrossRef]
- Dang, V.B.; Farahmand, F.; Andrzejczak, M.; Gaj, K. Implementing and Benchmarking Three Lattice-Based Post-Quantum Cryptography Algorithms Using Software/Hardware Codesign. In Proceedings of the 2019 International Conference on Field-Programmable Technology (ICFPT), Tianjin, China, 9–13 December 2019; pp. 206–214. [Google Scholar] [CrossRef]
- Dang, V.B.; Farahmand, F.; Andrzejczak, M.; Mohajerani, K.; Nguyen, D.T.; Gaj, K. Implementation and Benchmarking of Round 2 Candidates in the NIST Post-Quantum Cryptography Standardization Process Using Hardware and Software/Hardware Co-design Approaches. Cryptology ePrint Archive, Report 2020/795. 2020. Available online: https://ia.cr/2020/795 (accessed on 20 February 2022).
- Xie, J.; Basu, K.; Gaj, K.; Guin, U. Special Session: The Recent Advance in Hardware Implementation of Post-Quantum Cryptography. In Proceedings of the 2020 IEEE 38th VLSI Test Symposium (VTS), San Diego, CA, USA, 5–8 April 2020; pp. 1–10. [Google Scholar] [CrossRef]
- Farahmand, F.; Nguyen, D.T.; Dang, V.B.; Ferozpuri, A.; Gaj, K. Software/Hardware Codesign of the Post Quantum Cryptography Algorithm NTRUEncrypt Using High-Level Synthesis and Register-Transfer Level Design Methodologies. In Proceedings of the 29th International Conference on Field Programmable Logic and Applications (FPL), Barcelona, Spain, 8–12 September 2019; pp. 225–231. [Google Scholar] [CrossRef]
- PYNQ—Python Productivity for Zynq. Available online: http://www.pynq.io (accessed on 20 February 2022).
- Brown, N. PYNQ API: C API for PYNQ FPGA Board. Available online: https://github.com/mesham/pynq_api (accessed on 20 February 2022).
- LibNTRU: C Implementation of NTRUEncrypt. Available online: https://github.com/tbuktu/libntru (accessed on 20 February 2022).






| Parameter Set | Recommended Security Level | N | p | q | |||
|---|---|---|---|---|---|---|---|
| EES401EP1 | 112 | 401 | 3 | 2048 | 113 | 133 | 113 |
| EES541EP1 | 112 | 541 | 3 | 2048 | 49 | 180 | 49 |
| EES659EP1 | 112 | 659 | 3 | 2048 | 38 | 219 | 38 |
| EES449EP1 | 128 | 449 | 3 | 2048 | 134 | 149 | 134 |
| EES613EP1 | 128 | 613 | 3 | 2048 | 55 | 204 | 55 |
| EES761EP1 | 128 | 761 | 3 | 2048 | 42 | 253 | 42 |
| EES677EP1 | 192 | 677 | 3 | 2048 | 157 | 225 | 157 |
| EES887EP1 | 192 | 887 | 3 | 2048 | 81 | 295 | 81 |
| EES1087EP1 | 192 | 1087 | 3 | 2048 | 63 | 362 | 63 |
| EES1087EP2 | 256 | 1087 | 3 | 2048 | 120 | 367 | 120 |
| EES1171EP1 | 256 | 1171 | 3 | 2048 | 106 | 390 | 106 |
| EES1499EP1 | 256 | 1499 | 3 | 2048 | 79 | 499 | 79 |
| Zynq-7000 | Slice LUTs (53,200) | Slice Registers (106,400) | Slice(13,300) | LUT as Logic (53,200) | LUT as Mem. (17,400) | Block RAM Tile (140) |
|---|---|---|---|---|---|---|
| MS2XL-M8 IP | 743 | 195 | 267 | 743 | 0 | 8.5 |
| MS2XS-M8 IP | 603 | 90 | 209 | 603 | 0 | 8.5 |
| MS2XL-M8 SoC | 1094 | 652 | 409 | 1034 | 60 | 8.5 |
| MS2XS-M8 So) | 4346 | 5388 | 2811 | 3728 | 618 | 10.5 |
| Zynq UltraScale+ | CLB LUTs (70,560) | CLB Registers (141,120) | CLB (8820) | LUT as Logic (70,560) | LUT as Mem. (28,800) | Block RAM Tile (216) |
| MS2XL-M8 IP | 637 | 194 | 145 | 637 | 0 | 8.5 |
| MS2XS-M8 IP | 517 | 90 | 116 | 517 | 0 | 8.5 |
| MS2XL-M8 SoC | 3094 | 2879 | 644 | 2891 | 203 | 8.5 |
| MS2XS-M8 SoC | 6343 | 8108 | 1262 | 5409 | 934 | 10.5 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sánchez-Solano, S.; Camacho-Ruiz, E.; Martínez-Rodríguez, M.C.; Brox, P. Multi-Unit Serial Polynomial Multiplier to Accelerate NTRU-Based Cryptographic Schemes in IoT Embedded Systems. Sensors 2022, 22, 2057. https://doi.org/10.3390/s22052057
Sánchez-Solano S, Camacho-Ruiz E, Martínez-Rodríguez MC, Brox P. Multi-Unit Serial Polynomial Multiplier to Accelerate NTRU-Based Cryptographic Schemes in IoT Embedded Systems. Sensors. 2022; 22(5):2057. https://doi.org/10.3390/s22052057
Chicago/Turabian StyleSánchez-Solano, Santiago, Eros Camacho-Ruiz, Macarena C. Martínez-Rodríguez, and Piedad Brox. 2022. "Multi-Unit Serial Polynomial Multiplier to Accelerate NTRU-Based Cryptographic Schemes in IoT Embedded Systems" Sensors 22, no. 5: 2057. https://doi.org/10.3390/s22052057
APA StyleSánchez-Solano, S., Camacho-Ruiz, E., Martínez-Rodríguez, M. C., & Brox, P. (2022). Multi-Unit Serial Polynomial Multiplier to Accelerate NTRU-Based Cryptographic Schemes in IoT Embedded Systems. Sensors, 22(5), 2057. https://doi.org/10.3390/s22052057







