Introducing a Novel Model-Free Multivariable Adaptive Neural Network Controller for Square MIMO Systems
Abstract
:1. Introduction
- During the weight training process of the neural networks, the controlled systems can become unstable;
- It is not always clear when to stop the weight training process;
- A long training time for the weights can be unsatisfactory for the speed of the control systems;
- The traditional activation functions employed in the neural networks may not be suitable for control purposes;
- The common error back-propagation learning algorithm uses only the last two consecutive samples of the outputs in discrete derivative functions and does not comply with the requirement of a proper model-free approach in which a full history of inputs and outputs must be used in order to generate an effective control action.
- By constantly observing the accumulated errors and comparing them with their desired values, the controller can decide to stop the learning algorithm and lock the neural network weights at an optimal point; this ensures the convergence of the controller weight adjustments and provides a clear optimal number for the weight training steps;
- By choosing proper initial learning rates and dynamically changing them during the learning process according to the system stability criteria, the weight training speed can be significantly increased; this forms a clear comparison with and improvement over the traditional static learning rates [15,18,47,62,63];
- By designing specific activation functions that utilize typical proportional, integral, and derivative operations in the neural network structure of the controller, the proposed controller is simple and straightforward in its configuration; this makes the controller a potential candidate suitable for replacing classical PID controllers in industrial applications;
- By applying accumulated gradients in the error back-propagation algorithm and using new partial derivative estimations, the proposed method fully uses the history of the system outputs together with the current weights to produce the outputs of the controller (the inputs of the system) for the next step. This new learning method significantly reduces the overshoot and settling time of the system by minimizing the summation of errors of the system outputs in each step rather than using only the last two consecutive samples of the system outputs as its traditional counterparts do [61,64,65,66,67], and allows for the closed-loop system to achieve its best control performance with a minimum number of weight training steps.
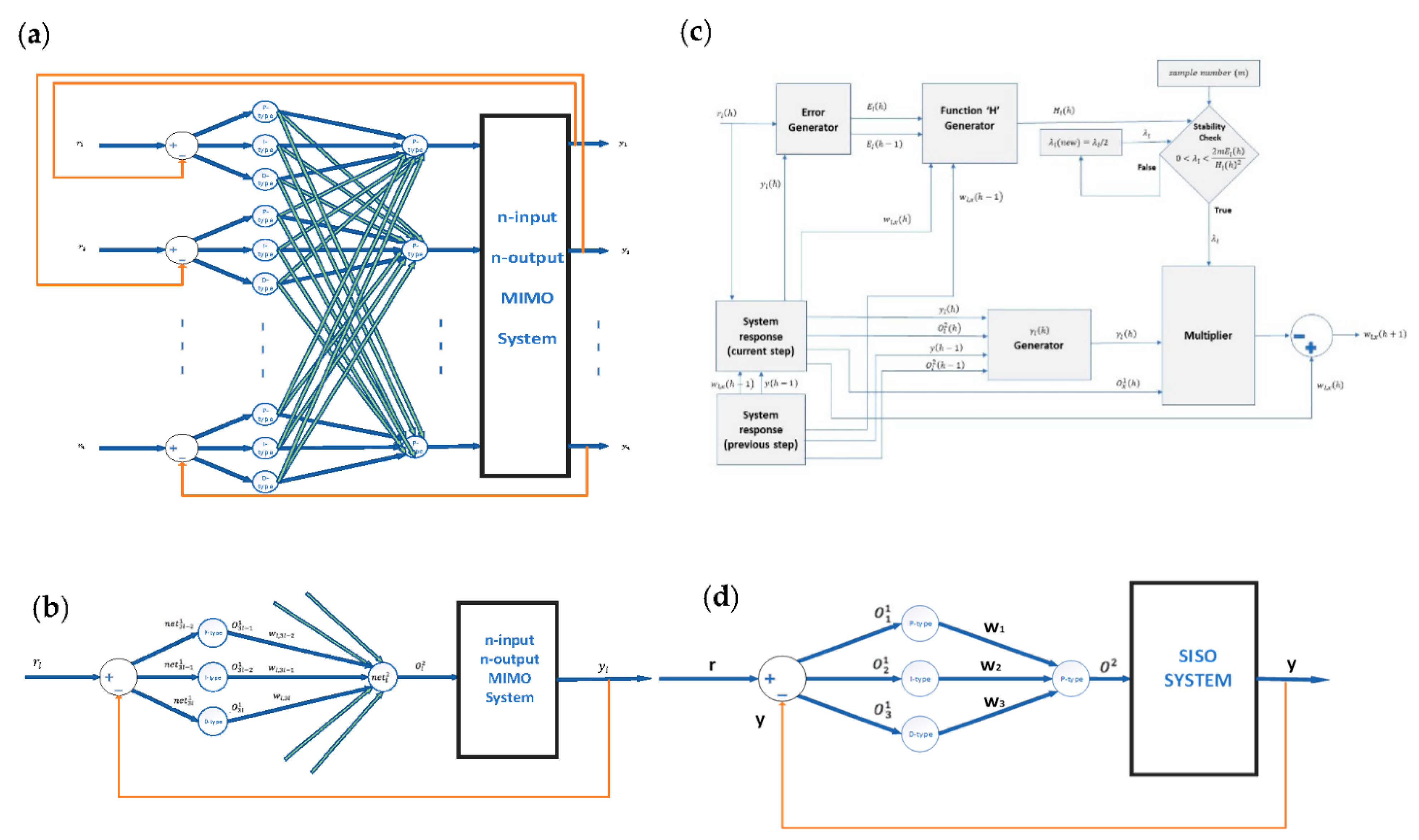
2. Multivariable Adaptive Neural Network Controller
2.1. Closed-Loop Structure of MANNC
2.2. Structure of Sub-MANNC (S-MANNC)
2.3. Matrix Representation
3. Learning Algorithm
4. Stability Analysis
- (i)
- (ii)
- (For all , (i.e., V is positive definite)
- (iii)
- For all ,
5. Specifying MANNC to Control SISO Systems
6. Simulation Results
6.1. Case 1: Application of MANNC on a Time-Invariant Nonlinear Square MIMO System
- −
- where is the standard unit step function.
- −
- where is the standard unit ramp function.
6.2. Case 2: Application of MANNC on a Time-Variant Nonlinear MIMO System
6.3. Case 3: Application of MANNC on a Hybrid System
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zhou, Q.; Shi, P.; Tian, Y.; Wang, M. Approximation-based adaptive tracking control for MIMO nonlinear systems with input saturation. IEEE Trans. Cybern. 2015, 45, 2119–2128. [Google Scholar] [CrossRef] [PubMed]
- Patino, H.; Liu, D. Neural network-based model reference adaptive control system. IEEE Trans. Syst. Man Cybern. Part B 2000, 30, 198–204. [Google Scholar] [CrossRef] [PubMed]
- Liu, M. Delayed standard neural network models for control systems. IEEE Trans. Neural Netw. 2007, 18, 1376–1391. [Google Scholar] [CrossRef] [PubMed]
- Meng, D.; Jia, Y.; Du, J.; Yu, F. Data-driven control for relative degree systems via iterative learning. IEEE Trans. Neural Netw. 2011, 22, 2213–2225. [Google Scholar] [CrossRef]
- Oomen, T.; van der Maas, R.; Rojas, C.R.; Hjalmarsson, H. Iterative data-driven H∞ norm estimation of multivariable systems with application to robust active vibration isolation. IEEE Trans. Contol Syst. Technol. 2014, 22, 2247–2260. [Google Scholar] [CrossRef]
- Zhang, M.; Gan, M.-G. Data-driven adaptive optimal control for linear systems with structured time-varying uncertainty. IEEE Access 2019, 7, 9215–9224. [Google Scholar] [CrossRef]
- Hay, M.; Miklau, G.; Jensen, D.; Towsley, D.; Weis, P. Resisting structural re-identification in anonymized social networks. Proc. VLDB Endow. 2008, 1, 102–114. [Google Scholar] [CrossRef] [Green Version]
- Donald, C.; Charles, K.A.; Ronald, K.J. Control Systems; McGraw-Hill Education: New York, NY, USA, 2005. [Google Scholar]
- Fliess, M.; Join, C. Model-free control. Int. J. Control 2013, 86, 2228–2252. [Google Scholar] [CrossRef] [Green Version]
- Lafont, F.; Balmat, J.-F.; Pessel, N.; Fliess, M. A model-free control strategy for an experimental greenhouse with an application to fault accommodation. Comput. Electron. Agric. 2015, 110, 139–149. [Google Scholar] [CrossRef] [Green Version]
- Madadi, E.; Söffker, D. Model-free approaches applied to the control of nonlinear systems: A brief survey with special attention to intelligent PID iterative learning control. In Proceedings of the ASME 2015 Dynamic Systems and Control Conference, Columbus, OH, USA, 28–30 October 2015. [Google Scholar] [CrossRef]
- Radac, M.-B.; Precup, R.-E.; Petriu, E.M. Model-free primitive-based iterative learning control approach to trajectory tracking of MIMO systems with experimental validation. IEEE Trans. Neural Netw. Learn. Syst. 2015, 26, 2925–2938. [Google Scholar] [CrossRef]
- Hou, Z.; Liu, S.; Tian, T. Lazy-learning-based data-driven model-free adaptive predictive control for a class of discrete-time nonlinear systems. IEEE Trans. Neural Netw. Learn. Syst. 2016, 28, 1914–1928. [Google Scholar] [CrossRef] [PubMed]
- Lu, W.; Zhu, P.; Ferrari, S. A hybrid-adaptive dynamic programming approach for the model-free control of nonlinear switched systems. IEEE Trans. Autom. Control 2015, 61, 3203–3208. [Google Scholar] [CrossRef]
- Wang, Z.; Liu, L.; Zhang, H. Neural network-based model-free adaptive fault-tolerant control for discrete-time nonlinear systems with sensor fault. IEEE Trans. Syst. Man Cybern. Syst. 2017, 47, 2351–2362. [Google Scholar] [CrossRef]
- Gao, B.; Cao, R.; Hou, Z.; Zhou, H. Model-free adaptive MIMO control algorithm application in polishing robot. In Proceedings of the 6th Data Driven Control and Learning Systems Conference (DDCLS), Chongqing, China, 26–27 May 2017. [Google Scholar] [CrossRef]
- Luo, B.; Liu, D.; Wu, H.-N.; Wang, D.; Lewis, F.L. Policy gradient adaptive dynamic programming for data-based optimal control. IEEE Trans. Cybern. 2016, 47, 3341–3354. [Google Scholar] [CrossRef]
- Mehrafrooz, A.; He, F. Introducing a model-free adaptive neural network auto-tuned control method for nonlinear SISO systems. In Proceedings of the 2018 IEEE International Conference on Information and Automation, Wuyishan, China, 11–13 August 2018. [Google Scholar] [CrossRef]
- Safaei, A.; Mahyuddin, M.N. Adaptive model-free control based on an ultra-local model with model-free parameter estimations for a generic SISO system. IEEE Access 2018, 6, 4266–4275. [Google Scholar] [CrossRef]
- Roshani, G.H.; Nazemi, E.; Feghhi, S.A.H.; Setayeshi, S. Flow regime identification and void fraction prediction in two-phase flows based on gamma ray attenuation. Measurement 2015, 62, 25–32. [Google Scholar] [CrossRef]
- Roshani, G.; Nazemi, E.; Roshani, M. Intelligent recognition of gas-oil-water three-phase flow regime and determination of volume fraction using radial basis function. Flow Meas. Instrum. 2017, 54, 39–45. [Google Scholar] [CrossRef]
- Roshani, G.; Nazemi, E. Intelligent densitometry of petroleum products in stratified regime of two phase flows using gamma ray and neural network. Flow Meas. Instrum. 2017, 58, 6–11. [Google Scholar] [CrossRef]
- Roshani, G.; Nazemi, E.; Feghhi, S. Investigation of using 60 Co source and one detector for determining the flow regime and void fraction in gas–liquid two-phase flows. Flow Meas. Instrum. 2016, 50, 73–79. [Google Scholar] [CrossRef]
- Jamshidi, M.B.; Lalbakhsh, A.; Alibeigi, N.; Soheyli, M.R.; Oryani, B.; Rabbani, N. Socialization of industrial robots: An innovative solution to improve productivity. In Proceedings of the 2018 IEEE 9th Annual Information Technology, Electronics and Mobile Communication Conference (IEMCON), Vancouver, BC, Canada, 1–3 November 2018. [Google Scholar] [CrossRef]
- Jamshidi, M.B.; Alibeigi, N.; Lalbakhsh, A.; Roshani, S. An ANFIS approach to modeling a small satellite power source of NASA. In Proceedings of the 2019 IEEE 16th International Conference on Networking, Sensing and Control, Banff, AB, Canada, 9–11 May 2019. [Google Scholar] [CrossRef]
- Jamshidi, M.B.; Lalbakhsh, A.; Mohamadzade, B.; Siahkamari, H.; Mousavi, S.M.H. A novel neural-based approach for design of microstrip filters. AEU-Int. J. Electron. Commun. 2019, 110, 152847. [Google Scholar] [CrossRef]
- Jamshidi, M.; Lalbakhsh, A.; Lotfi, S.; Siahkamari, H.; Mohamadzade, B.; Jalilian, J. A neuro-based approach to designing a Wilkinson power divider. Int. J. RF Microwav. Comput.-Aided Eng. 2020, 30, e22091. [Google Scholar] [CrossRef]
- Sattari, M.A.; Roshani, G.H.; Hanus, R.; Nazemi, E. Applicability of time-domain feature extraction methods and artificial intelligence in two-phase flow meters based on gamma-ray absorption technique. Measurement 2021, 168, 108474. [Google Scholar] [CrossRef]
- Roshani, G.; Hanus, R.; Khazaei, A.; Zych, M.; Nazemi, E.; Mosorov, V. Density and velocity determination for single-phase flow based on radiotracer technique and neural networks. Flow Meas. Instrum. 2018, 61, 9–14. [Google Scholar] [CrossRef]
- Roshani, M.; Sattari, M.A.; Ali, P.J.M.; Roshani, G.H.; Nazemi, B.; Corniani, E.; Nazemi, E. Application of GMDH neural network technique to improve measuring precision of a simplified photon attenuation based two-phase flowmeter. Flow Meas. Instrum. 2020, 75, 101804. [Google Scholar] [CrossRef]
- Roshani, M.; Phan, G.; Roshani, G.H.; Hanus, R.; Nazemi, B.; Corniani, E.; Nazemi, E. Combination of X-ray tube and GMDH neural network as a nondestructive and potential technique for measuring characteristics of gas-oil–water three phase flows. Measurement 2021, 168, 108427. [Google Scholar] [CrossRef]
- Roshani, G.; Feghhi, S.; Mahmoudi-Aznaveh, A.; Nazemi, E.; Adineh-Vand, A. Precise volume fraction prediction in oil–water–gas multiphase flows by means of gamma-ray attenuation and artificial neural networks using one detector. Measurement 2014, 51, 34–41. [Google Scholar] [CrossRef]
- Roshani, M.; Phan, G.T.; Ali, P.J.M.; Roshani, G.H.; Hanus, R.; Duong, T.; Corniani, E.; Nazemi, E.; Kalmoun, E.M. Evaluation of flow pattern recognition and void fraction measurement in two phase flow independent of oil pipeline’s scale layer thickness. Alex. Eng. J. 2021, 60, 1955–1966. [Google Scholar] [CrossRef]
- Lalbakhsh, A.; Afzal, M.U.; Esselle, K.P. Multiobjective particle swarm optimization to design a time-delay equalizer metasurface for an electromagnetic band-gap resonator antenna. IEEE Antennas Wirel. Propag. Lett. 2016, 16, 912–915. [Google Scholar] [CrossRef]
- Lalbakhsh, A.; Afzal, M.U.; Esselle, K.P.; Smith, S.L. A fast design procedure for quadrature reflection phase. In Proceedings of the 2017 IEEE Progress in Electromagnetics Research Symposium-Fall (PIERS-FALL), Singapore, 19–22 November 2017. [Google Scholar]
- Lalbakhsh, A.; Afzal, M.U.; Esselle, K.P.; Smith, S. Design of an artificial magnetic conductor surface using an evolutionary algorithm. In Proceedings of the 2017 IEEE International Conference on Electromagnetics in Advanced Applications (ICEAA), Verona, Italy, 11–15 September 2017. [Google Scholar]
- Roshani, G.; Nazemi, E.; Roshani, M. Usage of two transmitted detectors with optimized orientation in order to three phase flow metering. Measurement 2017, 100, 122–130. [Google Scholar] [CrossRef]
- Nazemi, E.; Roshani, G.H.; Feghhi, S.A.H.; Setayeshi, S.; Zadeh, E.E.; Fatehi, A. Optimization of a method for identifying the flow regime and measuring void fraction in a broad beam gamma-ray attenuation technique. Int. J. Hydrog. Energy 2016, 41, 7438–7444. [Google Scholar] [CrossRef]
- Karami, A.; Roshani, G.H.; Nazemi, E.; Roshani, S. Enhancing the performance of a dual-energy gamma ray based three-phase flow meter with the help of grey wolf optimization algorithm. Flow Meas. Instrum. 2018, 64, 164–172. [Google Scholar] [CrossRef]
- Karambasti, B.M.; Ghodrat, M.; Ghorbani, G.; Lalbakhsh, A.; Behnia, M. Design methodology and multi-objective optimization of small-scale power-water production based on integration of Stirling engine and multi-effect evaporation desalination system. Desalination 2022, 526, 115542. [Google Scholar] [CrossRef]
- Lalbakhsh, P.; Zaeri, B.; Lalbakhsh, A. An improved model of ant colony optimization using a novel pheromone update strategy. IEICE Trans. Inf. Syst. 2013, 96, 2309–2318. [Google Scholar] [CrossRef] [Green Version]
- Wang, Y.; Zhang, Y.; Fu, Y.; Chai, T.; Fu, J. Adaptive decoupling switching control based on generalised predictive control. IET Control Theory Appl. 2012, 6, 1828–1841. [Google Scholar] [CrossRef]
- Peng, K.; Fan, D.; Yang, F.; Gou, L.; Lv, W. A frequency domain decoupling method and multivariable controller design for turbofan engines. IEEE Access 2017, 5, 27757–27766. [Google Scholar] [CrossRef]
- Nguyen, T.N.; Su, S.; Nguyen, H.T. Neural network based diagonal decoupling control of powered wheelchair systems. IEEE Trans. Neural Syst. Rehabil. Eng. 2013, 22, 371–378. [Google Scholar] [CrossRef]
- Cong, S.; Liang, Y. PID-like neural network nonlinear adaptive control for uncertain multivariable motion control systems. IEEE Trans. Ind. Electron. 2009, 56, 3872–3879. [Google Scholar] [CrossRef]
- Hwang, C.-L.; Jan, C. Recurrent-neural-network-based multivariable adaptive control for a class of nonlinear dynamic systems with time-varying delay. IEEE Trans. Neural Netw. Learn. Syst. 2015, 27, 388–401. [Google Scholar] [CrossRef]
- Scott, G.; Shavlik, J.; Ray, W. Refining PID controllers using neural networks. Adv. Neural Inf. Process. Syst. 1991, 4, 555–565. [Google Scholar] [CrossRef]
- Merabet, A.; Tanvir, A.A.; Beddek, K. Speed control of sensorless induction generator by artificial neural network in wind energy conversion system. IET Renew. Power Gener. 2016, 10, 1597–1606. [Google Scholar] [CrossRef]
- Yang, B.-J.; Calise, A.J. Adaptive control of a class of nonaffine systems using neural networks. IEEE Trans. Neural Netw. 2007, 18, 1149–1159. [Google Scholar] [CrossRef] [PubMed]
- Tee, K.P.; Ge, S.S.; Tay, F.E.H. Adaptive neural network control for helicopters in vertical flight. IEEE Trans. Control Syst. Technol. 2008, 16, 753–762. [Google Scholar] [CrossRef]
- Park, J.-H.; Kim, S.-H.; Moon, C.-J. Adaptive neural control for strict-feedback nonlinear systems without backstepping. IEEE Trans. Neural Netw. 2009, 20, 1204–1209. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.-J.; Tong, S.-C.; Wang, D.; Li, T.-S.; Chen, C.L.P. Adaptive neural output feedback controller design with reduced-order observer for a class of uncertain nonlinear SISO systems. IEEE Trans. Neural Netw. 2011, 22, 1328–1334. [Google Scholar] [CrossRef]
- Zhang, J.; Ge, S.S.; Lee, T.H. Output feedback control of a class of discrete MIMO nonlinear systems with triangular form inputs. IEEE Trans. Neural Netw. 2005, 16, 1491–1503. [Google Scholar] [CrossRef] [PubMed]
- Zhang, T.; Ge, S.S. Adaptive neural network tracking control of MIMO nonlinear systems with unknown dead zones and control directions. IEEE Trans. Neural Netw. 2009, 20, 483–497. [Google Scholar] [CrossRef]
- Chen, M.; Ge, S.S.; How, B.V.E. Robust adaptive neural network control for a class of uncertain MIMO nonlinear systems with input nonlinearities. IEEE Trans. Neural Netw. 2010, 21, 796–812. [Google Scholar] [CrossRef]
- Yang, Q.; Yang, Z.; Sun, Y. Universal neural network control of MIMO uncertain nonlinear systems. IEEE Trans. Neural Netw. Learn. Syst. 2012, 23, 1163–1169. [Google Scholar] [CrossRef]
- Chen, Z.; Ge, S.S.; Zhang, Y.; Li, Y. Adaptive neural control of MIMO nonlinear systems with a block-triangular pure-feedback control structure. IEEE Trans. Neural Netw. Learn. Syst. 2014, 25, 2017–2029. [Google Scholar] [CrossRef] [Green Version]
- Meng, W.; Yang, Q.; Sun, Y. Adaptive neural control of nonlinear MIMO systems with time-varying output constraints. IEEE Trans. Neural Netw. Learn. Syst. 2014, 26, 1074–1085. [Google Scholar] [CrossRef]
- Yang, Q.; Jagannathan, S.; Sun, Y. Robust integral of neural network and error sign control of MIMO nonlinear systems. IEEE Trans. Neural Netw. Learn. Syst. 2015, 26, 3278–3286. [Google Scholar] [CrossRef] [PubMed]
- Ronald, J. Neural network applications. In Electronic Engine Control Technologies; SAE: Warrendale, PA, USA, 2004; p. 661. [Google Scholar]
- Yong, Z.; Hai-Bo, Z.; Tian-Qi, L. PIDNN decoupling control of boiler combustion system based on MCS. In Proceedings of the 2017 29th Chinese Control and Decision Conference (CCDC), Chongqing, China, 28–30 May 2017. [Google Scholar] [CrossRef]
- Hernandez-Alvarado, R.; Garcia-Valdovinos, L.G.; Salgado-Jimenez, T.; Gomez-Espinosa, A.; Navarro, F.F. Self-tuned PID control based on backpropagation Neural Networks for underwater vehicles. In Proceedings of the OCEANS 2016 MTS/IEEE Monterey Conference, Monterey, CA, USA, 19–23 September 2016. [Google Scholar] [CrossRef]
- Jing, X.; Cheng, L. An optimal PID control algorithm for training feedforward neural networks. IEEE Trans. Ind. Electron. 2012, 60, 2273–2283. [Google Scholar] [CrossRef]
- Shu, H.; Xu, Y.-K. Application of additional momentum in PID neural network. In Proceedings of the 2014 4th IEEE International Conference on Information Science and Technology, Shenzhen, China, 26–28 April 2014. [Google Scholar]
- Meng, L.; Zou, Z.-Y.; Wang, Z.-Z.; Gui, X.-J.; Yu, M. Design of an improved PID neural network controller based on particle swarm optimazation. In Proceedings of the 2015 IEEE Chinese Automation Congress (CAC), Wuhan, China, 27–29 November 2015. [Google Scholar] [CrossRef]
- Teng, W.-F.; Pan, H.-P.; Ren, J. Neural network PID decoupling control based on chaos particle swarm optimization. In Proceedings of the 33rd IEEE Chinese Control Conference, Nanjing, China, 28–30 July 2014. [Google Scholar] [CrossRef]
- Tian, Z.; Guo, H.; Ding, X.; He, X. A PID neural network control for position servo system with gear box at variable load. In Proceedings of the 2016 IEEE Vehicle Power and Propulsion Conference (VPPC), Hangzhou, China, 17–20 October 2016. [Google Scholar] [CrossRef]
- Bahri, N.; Atig, A.; Abdennour, R.B.; Druaux, F.; Lefebvre, D. Multivariable adaptive neural control based on multimodel emulator for nonlinear square MIMO systems. In Proceedings of the 2014 IEEE 11th International Multi-Conference on Systems, Signals & Devices (SSD14), Barcelona, Spain, 11–14 February 2014. [Google Scholar]
- Saerens, M.; Soquet, A. Neural controller based on back-propagation algorithm. IEE Proc. F Radar Signal Process. 1991, 138, 55–62. [Google Scholar] [CrossRef]
- Goodfellow, I.; Bengio, Y.; Courville, A. 6.5 Back-propagation and other differentiation algorithms. In Deep Learning; MIT Press: Cambridge, MA, USA, 2016. [Google Scholar]
- Cilimkovic, M. Neural Networks and Back Propagation Algorithm; Institute of Technology Blanchardstown: Dublin, Ireland, 2015; Volume 15. [Google Scholar]
- Merayo, N.; Juárez, D.; Aguado, J.C.; De Miguel, I.; Durán, R.J.; Fernández, P.; Lorenzo, R.M.; Abril, E.J. PID controller based on a self-adaptive neural network to ensure QoS bandwidth requirements in passive optical networks. J. Opt. Commun. Netw. 2017, 9, 433–445. [Google Scholar] [CrossRef] [Green Version]
- Parandin, F. Ultra-compact terahertz all-optical logic comparator on GaAs photonic crystal platform. Opt. Laser Technol. 2021, 144, 107399. [Google Scholar] [CrossRef]
- Parandin, F.; Heidari, F.; Rahimi, Z.; Olyaee, S. Two-dimensional photonic crystal Biosensors: A review. Opt. Laser Technol. 2021, 144, 107397. [Google Scholar] [CrossRef]
- Abdollahi, M.; Parandin, F. A novel structure for realization of an all-optical, one-bit half-adder based on 2D photonic crystals. J. Comput. Electron. 2019, 18, 1416–1422. [Google Scholar] [CrossRef]
- Saghaei, H.; Zahedi, A.; Karimzadeh, R.; Parandin, F. Line defects on As2Se3-chalcogenide photonic crystals for the design of all-optical power splitters and digital logic gates. Superlattices Microstruct. 2017, 110, 133–138. [Google Scholar] [CrossRef]
- Karkhanehchi, M.M.; Parandin, F.; Zahedi, A. Design of an all optical half-adder based on 2D photonic crystals. Photon-Netw. Commun. 2017, 33, 159–165. [Google Scholar] [CrossRef]
- Vahdati, A.; Parandin, F. Antenna patch design using a photonic crystal substrate at a frequency of 1.6 THz. Wirel. Pers. Commun. 2019, 109, 2213–2219. [Google Scholar] [CrossRef]
- Dehghani, K.; Karimi, G.; Lalbakhsh, A.; Maki, S. Design of lowpass filter using novel stepped impedance resonator. Electron. Lett. 2014, 50, 37–39. [Google Scholar] [CrossRef]
- Lalbakhsh, A.; Mohamadpour, G.; Roshani, S.; Ami, M.; Roshani, S.; Sayem, A.S.M.; Alibakhshikenari, M.; Koziel, S. Design of a compact planar transmission line for miniaturized rat-race coupler with harmonics suppression. IEEE Access 2021, 9, 129207–129217. [Google Scholar] [CrossRef]
- Roshani, S. A compact microstrip low-pass filter with ultra wide stopband using compact microstrip resonant cells. Int. J. Microw. Wirel. Technol. 2017, 9, 1023–1027. [Google Scholar] [CrossRef]
- Heshmati, H.; Roshani, S. A miniaturized lowpass bandpass diplexer with high isolation. AEU-Int. J. Electron. Commun. 2018, 87, 87–94. [Google Scholar] [CrossRef]
- Pirasteh, A.; Roshani, S.; Roshani, S. A modified class-F power amplifier with miniaturized harmonic control circuit. AEU-Int. J. Electron. Commun. 2018, 97, 202–209. [Google Scholar] [CrossRef]
- Roshani, S.; Dehghani, K.; Roshani, S. A Lowpass Filter Design Using Curved and Fountain Shaped Resonators. Frequenz 2019, 73, 267–272. [Google Scholar] [CrossRef]
- Lotfi, S.; Roshani, S.; Roshani, S. Design of a miniaturized planar microstrip Wilkinson power divider with harmonic cancellation. Turk. J. Electr. Eng. Comput. Sci. 2020, 28, 3126–3136. [Google Scholar]
- Bavandpour, S.K.; Roshani, S.; Pirasteh, A.; Roshani, S.; Seyedi, H. A compact lowpass-dual bandpass diplexer with high output ports isolation. AEU-Int. J. Electron. Commun. 2021, 135, 153748. [Google Scholar] [CrossRef]
- Moloudian, G.; Bahrami, S.; Hashmi, R.M. A microstrip lowpass filter with wide tuning range and sharp roll-off response. IEEE Trans. Circuits Syst. II Express Briefs 2020, 67, 2953–2957. [Google Scholar] [CrossRef]
- Lalbakhsh, A.; Afzal, M.U.; Esselle, K.P.; Smith, S.L. All-metal wideband frequency-selective surface bandpass filter for TE and TM polarizations. IEEE Trans. Antennas Propag. 2021, 70, 1. [Google Scholar] [CrossRef]
- Parandin, F.; Moayed, M. Designing and simulation of 3-input majority gate based on two-dimensional photonic crystals. Optik 2020, 216, 164930. [Google Scholar] [CrossRef]
- Parandin, F.; Kamarian, R.; Jomour, M. A novel design of all optical half-subtractor using a square lattice photonic crystals. Opt. Quantum Electron. 2021, 53, 114. [Google Scholar] [CrossRef]
- Paul, G.S.; Mandal, K.; Lalbakhsh, A. Single-layer ultra-wide stop-band frequency selective surface using interconnected square rings. AEU-Int. J. Electron. Commun. 2021, 132, 153630. [Google Scholar] [CrossRef]
- Roshani, S.; Roshani, S. Design of a high efficiency class-F power amplifier with large signal and small signal measurements. Measurement 2020, 149, 106991. [Google Scholar] [CrossRef]
- Parandin, F.; Mahtabi, N. Design of an ultra-compact and high-contrast ratio all-optical NOR gate. Opt. Quantum Electron. 2021, 53, 666. [Google Scholar] [CrossRef]
- Bahrami, S.; Moloudian, G.; Miri-Rostami, S.R.; Bjorninen, T. Compact microstrip antennas with enhanced bandwidth for the implanted and external subsystems of a wireless retinal prosthesi. IEEE Trans. Antennas Propag. 2020, 69, 2969–2974. [Google Scholar] [CrossRef]
- Roshani, G.H.; Roshani, S.; Nazemi, E.; Roshani, S. Online measuring density of oil products in annular regime of gas-liquid two phase flows. Measurement 2018, 129, 296–301. [Google Scholar] [CrossRef]
- Roshani, M.; Phan, G.; Faraj, R.H.; Phan, N.-H.; Roshani, G.H.; Nazemi, B.; Corniani, E.; Nazemi, E. Proposing a gamma radiation based intelligent system for simultaneous analyzing and detecting type and amount of petroleum by-products. Nucl. Eng. Technol. 2021, 53, 1277–1283. [Google Scholar] [CrossRef]
- Roman, R.-C.; Rădac, M.-B.; Precup, R.-E.; Stinean, A.-I. Two data-driven control algorithms for a MIMO aerodynamic system with experimental validation. In Proceedings of the 2015 19th International Conference on System Theory, Control and Computing (ICSTCC), Cheile Gradistei, Romania, 14–16 October 2015. [Google Scholar] [CrossRef]
- Kalpana, D.; Thyagarajan, T.; Gokulraj, N. Modeling and control of non-square MIMO system using relay feedback. ISA Trans. 2015, 59, 408–417. [Google Scholar] [CrossRef]
- Phillips, S.F.; Seborg, D.E. Conditions that guarantee no overshoot for linear systems. Int. J. Control 1988, 47, 1043–1059. [Google Scholar] [CrossRef]





| System’s outputs | System’s desired outputs | System’s inputs | System’s transfer matrix |
| Output layer’s inputs | Neural Network Weights | Neurons’ outputs | Activation functions |
| Hidden layer’s inputs | Triple desired outputs | Triple system’s outputs | Triple unit |
| 10.23 | 0.33 | 6.93 | −2.23 | −2.13 | −2.10 | |
| −1.35 | 3.59 | 1.36 | 3.22 | 3.24 | 1.94 |
| Controller | Number of Trainings | Time of Training | Output 1 Overshoot | Output 1 Maximum Error Less than 5% | Output 1 Maximum Error Less than 2% | Output 2 Maximum Error Less than 5% | Output 2 Maximum Error Less than 2% |
|---|---|---|---|---|---|---|---|
| MANNC | 20 | 1.48 s | 0% | 8 s.t. * | 10 s.t. | 9 s.t. | 14 s.t. |
| PIDNN | 20 | 3.67 s | 22% | 15 s.t. | 20 s.t. | 17 s.t. | 22 s.t. |
| 3.34 | 2.43 | 4.73 | −5.12 | −8.13 | −2.19 | |
| −11.30 | −4.44 | −7.74 | 6.32 | 3.55 | 3.82 |
| Controller | Number of Trainings | Time of Training | Output 1 Overshoot | Output 1 Maximum Error Less than 5% | Output 2 Maximum Error Less than 5% |
|---|---|---|---|---|---|
| MANNC | 50 | 2.39 s | 0% | 0.01 s | 0.05 s |
| PIDNN | 50 | 3.99 s | 22% | 0.03 s | 0.08 s |
| 3.1 | 1.21 | 2.43 | −1.68 | −4.34 | −5.2 | |
| −0.13 | −1.58 | 4.28 | 0.88 | 2.06 | 3.41 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mehrafrooz, A.; He, F.; Lalbakhsh, A. Introducing a Novel Model-Free Multivariable Adaptive Neural Network Controller for Square MIMO Systems. Sensors 2022, 22, 2089. https://doi.org/10.3390/s22062089
Mehrafrooz A, He F, Lalbakhsh A. Introducing a Novel Model-Free Multivariable Adaptive Neural Network Controller for Square MIMO Systems. Sensors. 2022; 22(6):2089. https://doi.org/10.3390/s22062089
Chicago/Turabian StyleMehrafrooz, Arash, Fangpo He, and Ali Lalbakhsh. 2022. "Introducing a Novel Model-Free Multivariable Adaptive Neural Network Controller for Square MIMO Systems" Sensors 22, no. 6: 2089. https://doi.org/10.3390/s22062089






