Intelligent Tracking of Mechanically Thrown Objects by Industrial Catching Robot for Automated In-Plant Logistics 4.0
Abstract
:1. Introduction
- Fast transportation
- Productivity increase
- Flexibility
- Optimized utilization of facilities
- Improved safety
2. Related Work
- Mechanically throwing or shooting of objects;
- Tracking of the catching device;
- Catching mechanically thrown objects;
- Detecting thrown object on its trajectory
2.1. Mechanically Throwing or Shooting of Objects
2.2. Tracking of the Catching Device
2.3. Catching Mechanically Thrown Objects
2.4. Detecting Mechanically Thrown Object on Its Trajectory
2.5. Limitations in Existing Work of Mechanically Thrown Objects Tracking
3. Proposed Methodology
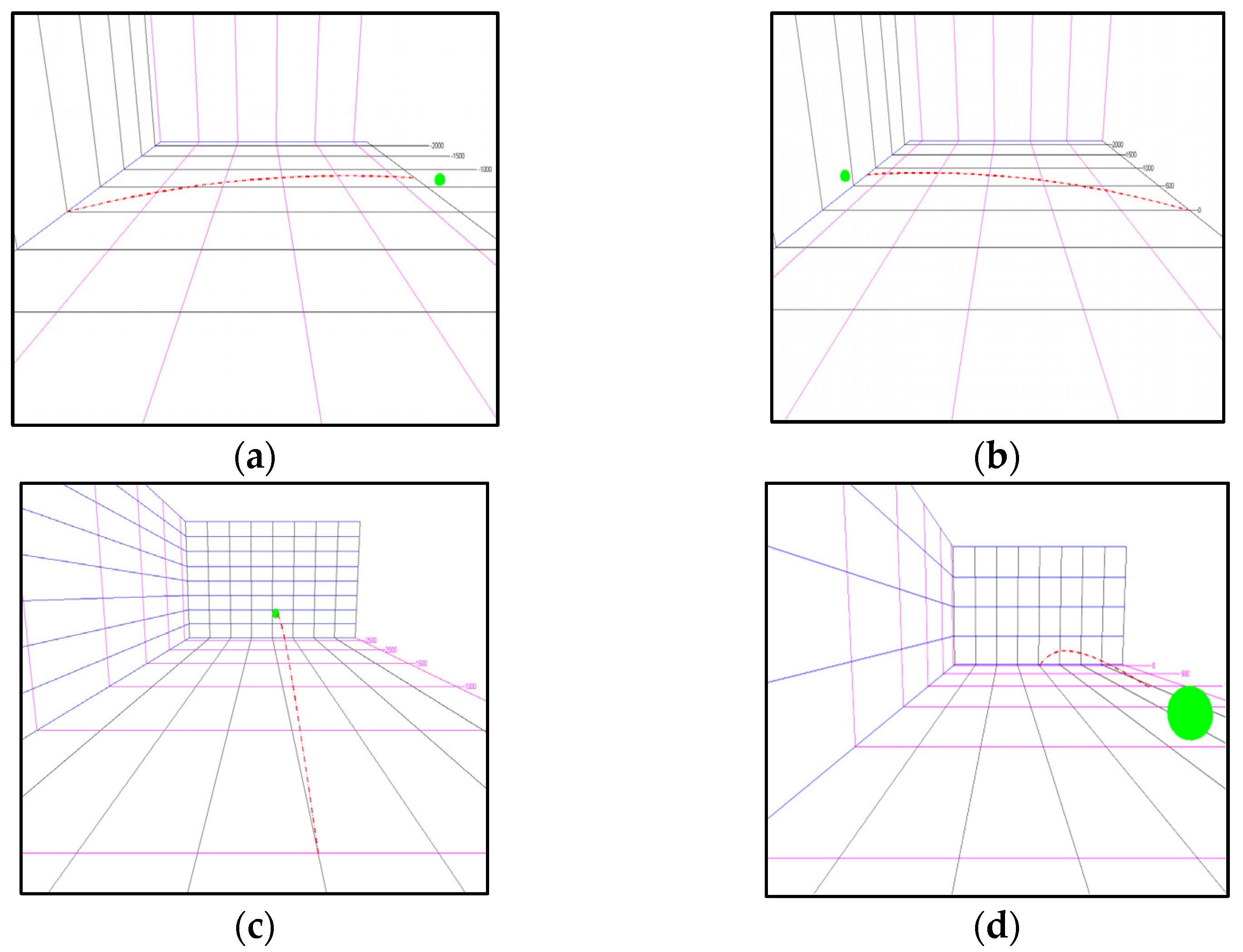
3.1. Simulation
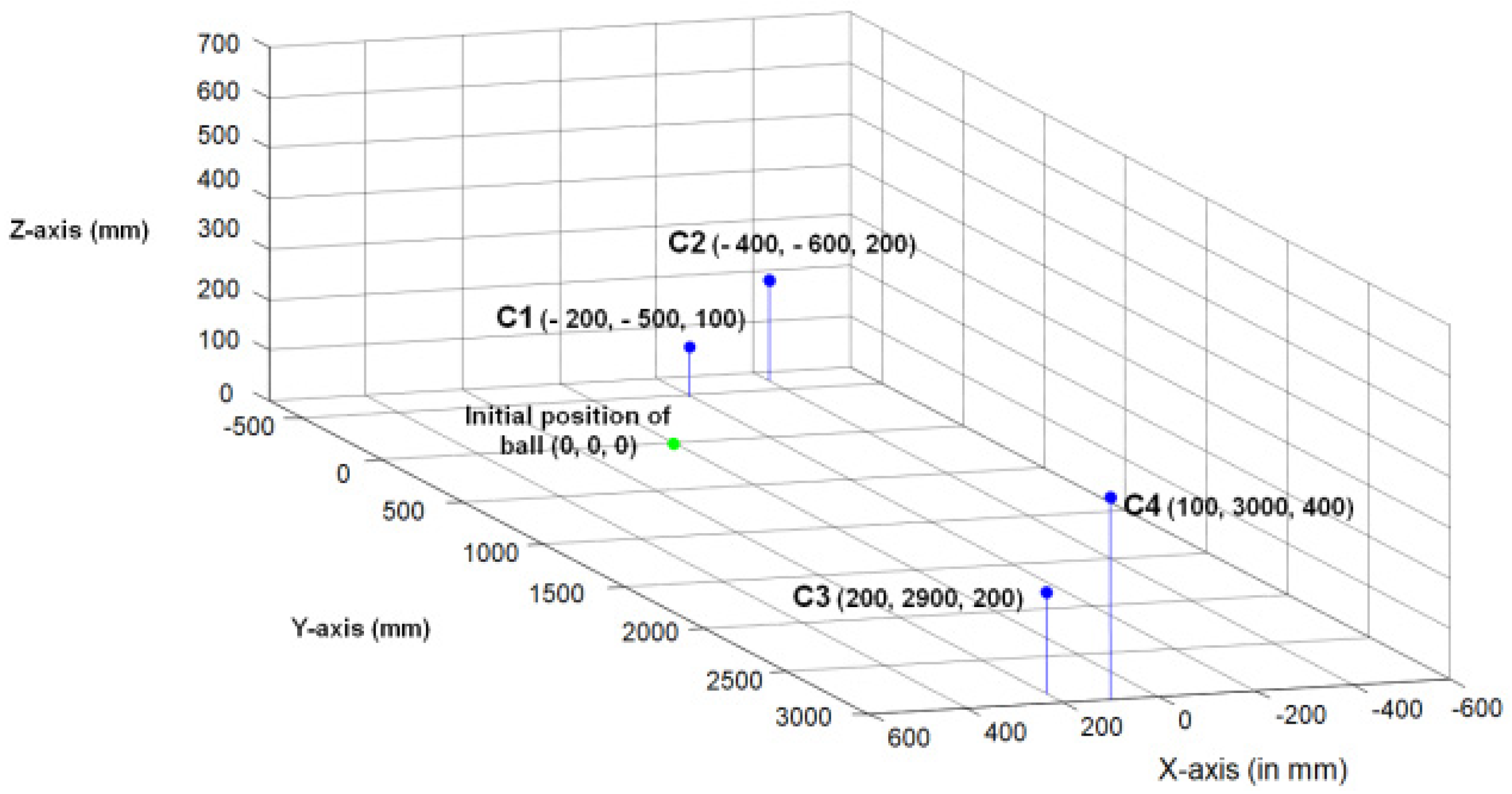
3.2. Experimental Setup and Simulation Testing
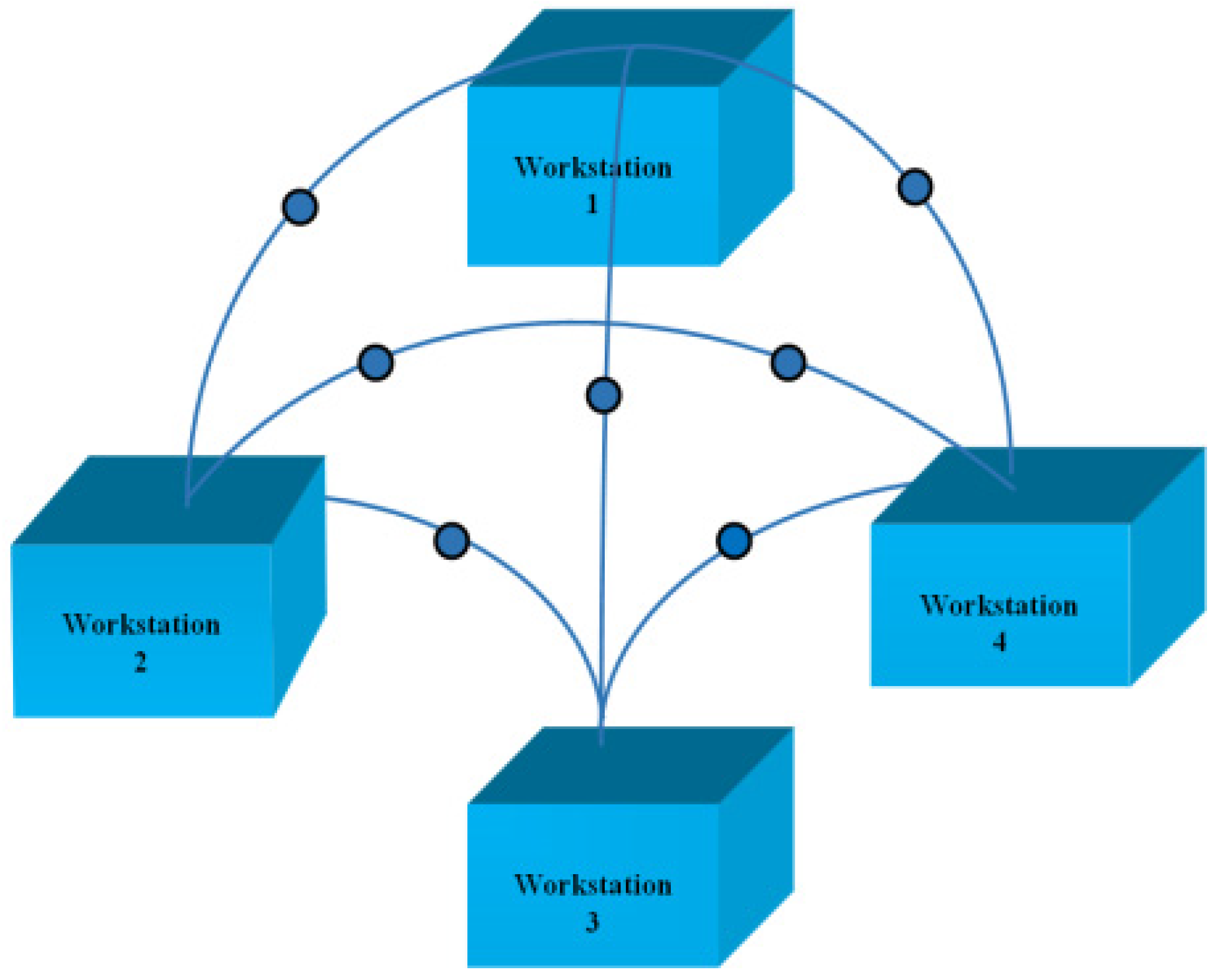
3.3. Best Multicamera Setup Derivation
3.4. Preparing Throws Datasets and Training Intelligent Tracking Models
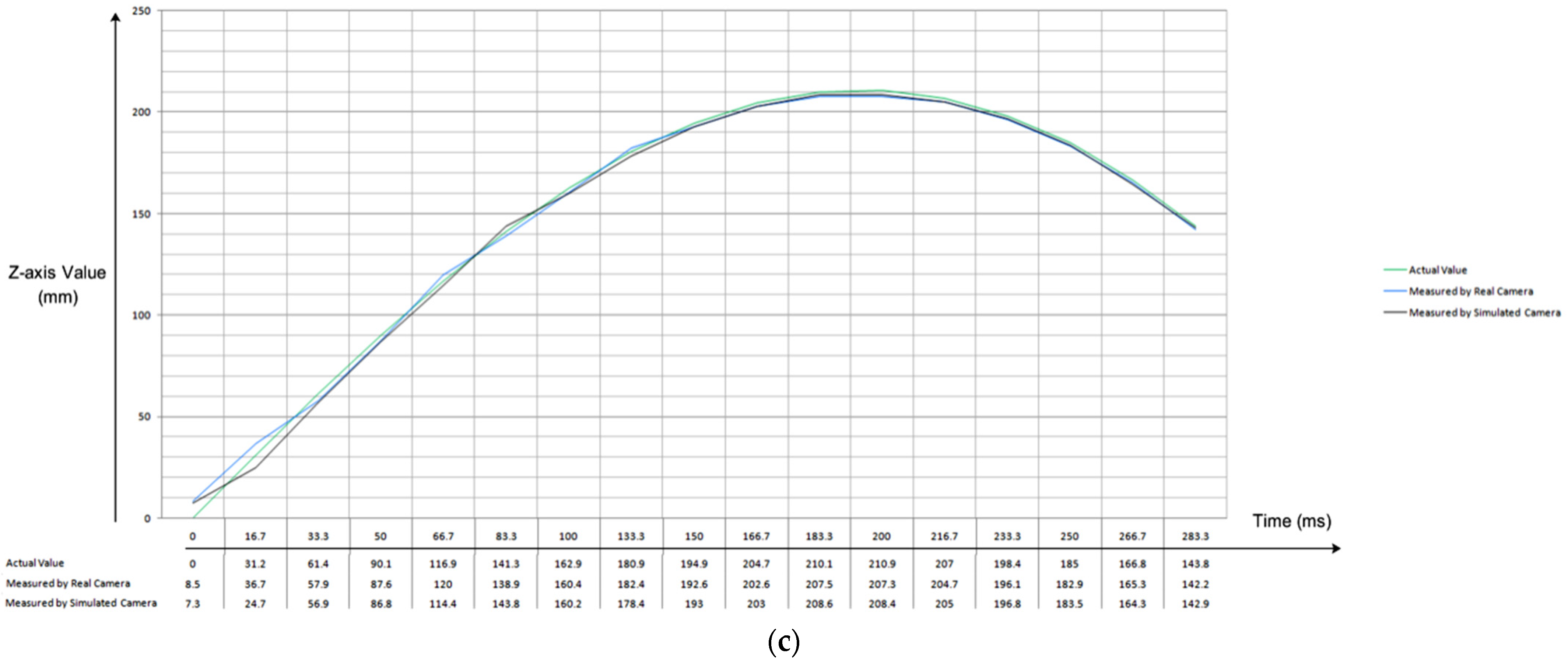
4. Results and Discussion
5. Conclusions and Future Work
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Black, J.T.; Kohser, R.A. DeGarmo’s Materials and Processes in Manufacturing; John Wiley & Sons: Hoboken, NJ, USA, 2020. [Google Scholar]
- Groover, M.P. Fundamentals of Modern Manufacturing: Materials, Processes and Systems; John Wiley & Sons: Hoboken, NJ, USA, 2020. [Google Scholar]
- Shirai, Y. Three-Dimensional Computer Vision; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Ghazal, R.; Malik, A.K.; Qadeer, N.; Raza, B.; Shahid, A.R.; Alquhayz, H. Intelligent Role-Based Access Control and Framework Using Semantic Business Roles in Multi-Domain Environments. IEEE Access 2020, 8, 12253–12267. [Google Scholar] [CrossRef]
- Ghazal, R.; Malik, A.K.; Raza, B.; Qadeer, N.; Qamar, N.; Bhatia, S. Agent-Based Semantic Role Mining for Intelligent Access Control in Multi-Domain Collaborative Applications of Smart Cities. Sensors 2021, 21, 4253. [Google Scholar] [CrossRef] [PubMed]
- Shi, Z.; Xu, M.; Pan, Q.; Yan, B.; Zhang, H. LSTM-Based Flight Trajectory Prediction. In Proceedings of the 2018 International Joint Conference on Neural Networks (IJCNN), Rio de Janeiro, Brazil, 8–13 July 2018; pp. 1–8. [Google Scholar]
- Zhao, Y.; Yang, R.; Chevalier, G.; Shah, R.C.; Romijnders, R. Applying Deep Bidirectional LSTM and Mixture Density Network for Basketball Trajectory Prediction. Optik 2018, 158, 266–272. [Google Scholar] [CrossRef] [Green Version]
- Frank, H.; Wellerdick-Wojtasik, N.; Hagebeuker, B.; Novak, G.; Mahlknecht, S. Throwing Objects—A Bio-Inspired Approach for the Transportation of Parts. In Proceedings of the 2006 IEEE International Conference on Robotics and Biomimetics, Kunming, China, 17–20 December 2006; pp. 91–96. [Google Scholar]
- Frank, H.; Barteit, D.; Kupzog, F. Throwing or Shooting-a New Technology for Logistic Chains within Production System. In Proceedings of the 2008 IEEE International Conference on Technologies for Practical Robot Applications, Woburn, MA, USA, 10–11 November 2008; pp. 62–67. [Google Scholar]
- Frank, H. Design and Simulation of a Numerical Controlled Throwing Devic. In Proceedings of the 2008 Second Asia International Conference on Modelling & Simulation (AMS), Kuala Lumpur, Malaysia, 13–15 May 2008; pp. 777–782. [Google Scholar]
- Smith, C.; Christensen, H.I. Using COTS to Construct a High Performance Robot Arm. In Proceedings of the Proceedings 2007 IEEE International Conference on Robotics and Automation, Rome, Italy, 10–14 April 2007; pp. 4056–4063. [Google Scholar]
- Frank, H.; Mittnacht, A.; Scheiermann, J. Throwing of Cylinder-Shaped Objects. In Proceedings of the 2009 IEEE/ASME International Conference on Advanced Intelligent Mechatronics, Singapore, 14–17 July 2009; pp. 59–64. [Google Scholar]
- Frank, H.; Barteit, D.; Meyer, M.; Mittnacht, A.; Novak, G.; Mahlknecht, S. Optimized Control Methods for Capturing Flying Objects with a Cartesian Robo. In Proceedings of the 2008 IEEE Conference on Robotics, Automation and Mechatronics, Chengdu, China, 21–24 September 2008; pp. 160–165. [Google Scholar]
- Frank, H.; Barteit, D.; Wellerdick-Wojtasik, N.; Frank, T.; Novak, G.; Mahlknecht, S. Autonomous Mechanical Controlled Grippers for Capturing Flying Object. In Proceedings of the 2007 5th IEEE International Conference on Industrial Informatics, Vienna, Austria, 23–27 June 2007; pp. 431–436. [Google Scholar]
- Kim, S.; Shukla, A.; Billard, A. Catching Objects in Flight. IEEE Trans. Robot. 2014, 30, 1049–1065. [Google Scholar] [CrossRef]
- Kamble, P.; Keskar, A.; Bhurchandi, K. A Deep Learning Ball Tracking System in Soccer Videos. Opto-Electron. Rev. 2019, 27, 58–69. [Google Scholar] [CrossRef]
- Najeeb, H.D.; Ghani, R.F. Tracking Ball in Soccer Game Video Using Extended KalmanFilte. In Proceedings of the 2020 International Conference on Computer Science and Software Engineering (CSASE), Duhok, Iraq, 16–18 April 2020; pp. 78–82. [Google Scholar]
- Desai, U.B.; Merchant, S.N.; Zaveri, M.; Ajishna, G.; Purohit, M.; Phanish, H. Small Object Detection and Tracking: Algorithm, Analysis and Applicatio. In Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2005; pp. 108–117. [Google Scholar]
- Velammal, B.; Kumar, P.A. An Efficient Ball Detection Framework for Cricket. Int. J. Comput. Sci. Issues 2010, 7, 30. [Google Scholar]
- Chen, H.-T.; Tien, M.-C.; Chen, Y.-W.; Tsai, W.-J.; Lee, S.-Y. Physics-Based Ball Tracking and 3D Trajectory Reconstruction with Applications to Shooting Location Estimation in Basketball Video. J. Vis. Commun. Image Represent. 2009, 20, 204–216. [Google Scholar] [CrossRef]
- Zhou, X.; Xie, L.; Huang, Q.; Cox, S.J.; Zhang, Y. Tennis Ball Tracking Using a Two-Layered Data Association Approach. IEEE Trans. Multimed. 2014, 17, 145–156. [Google Scholar] [CrossRef]
- Lin, H.-I.; Yu, Z.; Huang, Y.-C. Ball Tracking and Trajectory Prediction for Table-Tennis Robots. Sensors 2020, 20, 333. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Gomez Gonzalez, S. Real Time Probabilistic Models for Robot Trajectories. Ph.D. Thesis, Technische Universität Darmstadt, Darmstadt, Germany, 2020. [Google Scholar]
- Gomez-Gonzalez, S.; Prokudin, S.; Schölkopf, B.; Peters, J. Real Time Trajectory Prediction Using Deep Conditional Generative Models. IEEE Robot. Autom. Lett. 2020, 5, 970–976. [Google Scholar] [CrossRef] [Green Version]
- Gomez-Gonzalez, S.; Nemmour, Y.; Schölkopf, B.; Peters, J. Reliable Real-Time Ball Tracking for Robot Table Tennis. Robotics 2019, 8, 90. [Google Scholar] [CrossRef] [Green Version]
- Birbach, O.; Frese, U.; Bäuml, B. Realtime Perception for Catching a Flying Ball with a Mobile Humanoid. In Proceedings of the 2011 IEEE International Conference on Robotics and Automation, Shanghai, China, 9–13 May 2011; pp. 5955–5962. [Google Scholar]
- Cigliano, P.; Lippiello, V.; Ruggiero, F.; Siciliano, B. Robotic Ball Catching with an Eye-in-Hand Single-Camera System. IEEE Trans. Control Syst. Technol. 2015, 23, 1657–1671. [Google Scholar] [CrossRef] [Green Version]
- Möller, T.; Kraft, H.; Frey, J.; Albrecht, M.; Lange, R. Robust 3D Measurement with PMD Sensors. Range Imaging Day 2005, 7, 8. [Google Scholar]
- Barteit, D.; Frank, H.; Kupzog, F. Accurate Prediction of Interception Positions for Catching Thrown Objects in Production Systems. In Proceedings of the 2008 6th IEEE International Conference on Industrial Informatics, Daejeon, Korea, 13–16 July 2008; pp. 893–898. [Google Scholar]
- Barteit, D.; Frank, H.; Pongratz, M.; Kupzog, F. Measuring the Intersection of a Thrown Object with a Vertical Plane. In Proceedings of the 2009 7th IEEE International Conference on Industrial Informatics, Cardiff, UK, 23–26 June 2009; pp. 680–685. [Google Scholar]
- Barteit, D.F. Tracking of Thrown Objects: Catching of Mechanically Thrown Parts for Transport in Manufacturing. Ph.D. Thesis, Technische Universität Wien, Vienna, Austria, 2010. [Google Scholar]
- Mironov, K.; Pongratz, M. Fast kNN-Based Prediction for the Trajectory of a Thrown Body. In Proceedings of the 2016 24th Mediterranean Conference on Control and Automation (MED), Athens, Greece, 21–26 June 2016; pp. 512–517. [Google Scholar]
- Mironov, K.; Vladimirova, I.; Pongratz, M. Processing and Forecasting the Trajectory of a Thrown Object Measured by the Stereo Vision System. IFAC-PapersOnLine 2015, 48, 28–35. [Google Scholar] [CrossRef]
- Mironov, K.; Pongratz, M. Applying Neural Networks for Prediction of Flying Objects Trajectory. Bull. Ufa State Aviat. Tech. Univ. 2013, 17, 33–37. [Google Scholar]
- Gayanov, R.; Mironov, K.; Kurennov, D. Estimating the Trajectory of a Thrown Object from Video Signal with Use of Genetic Programmin. In Proceedings of the 2017 IEEE International Symposium on Signal Processing and Information Technology (ISSPIT), Bilbao, Spain, 18–20 December 2017; pp. 134–138. [Google Scholar]
- Gayanov, R.; Mironov, K.; Mukhametshin, R.; Vokhmintsev, A.; Kurennov, D. Transportation of Small Objects by Robotic Throwing and Catching: Applying Genetic Programming for Trajectory Estimation. IFAC-PapersOnLine 2018, 51, 533–537. [Google Scholar] [CrossRef]
- Mironov, K.; Gayanov, R.; Kurennov, D. Observing and Forecasting the Trajectory of the Thrown Body with Use of Genetic Programming. Adv. Sci. Technol. Eng. Syst. 2019, 1, 248–257. [Google Scholar] [CrossRef] [Green Version]
- Mironov, K. Transport by Robotic Throwing and Catching: Accurate Stereo Tracking of the Spherical Object. In Proceedings of the 2017 International Conference on Industrial Engineering, Applications and Manufacturing (ICIEAM), St. Petersburg, Russia, 16–19 May 2017; pp. 1–6. [Google Scholar]
- Mehta, R.; Alam, F.; Subic, A. Review of Tennis Ball Aerodynamics. Sports Technol. 2008, 1, 7–16. [Google Scholar] [CrossRef]
- Alam, F.; Tio, W.; Watkins, S.; Subic, A.; Naser, J. Effects of Spin on Tennis Ball Aerodynamics: An Experimental and Computational Study. In Proceedings of the 16th Australasian Fluid Mechanics Conference Crown Plaza, Gold Coast, Australia, 2–7 December 2007. [Google Scholar]





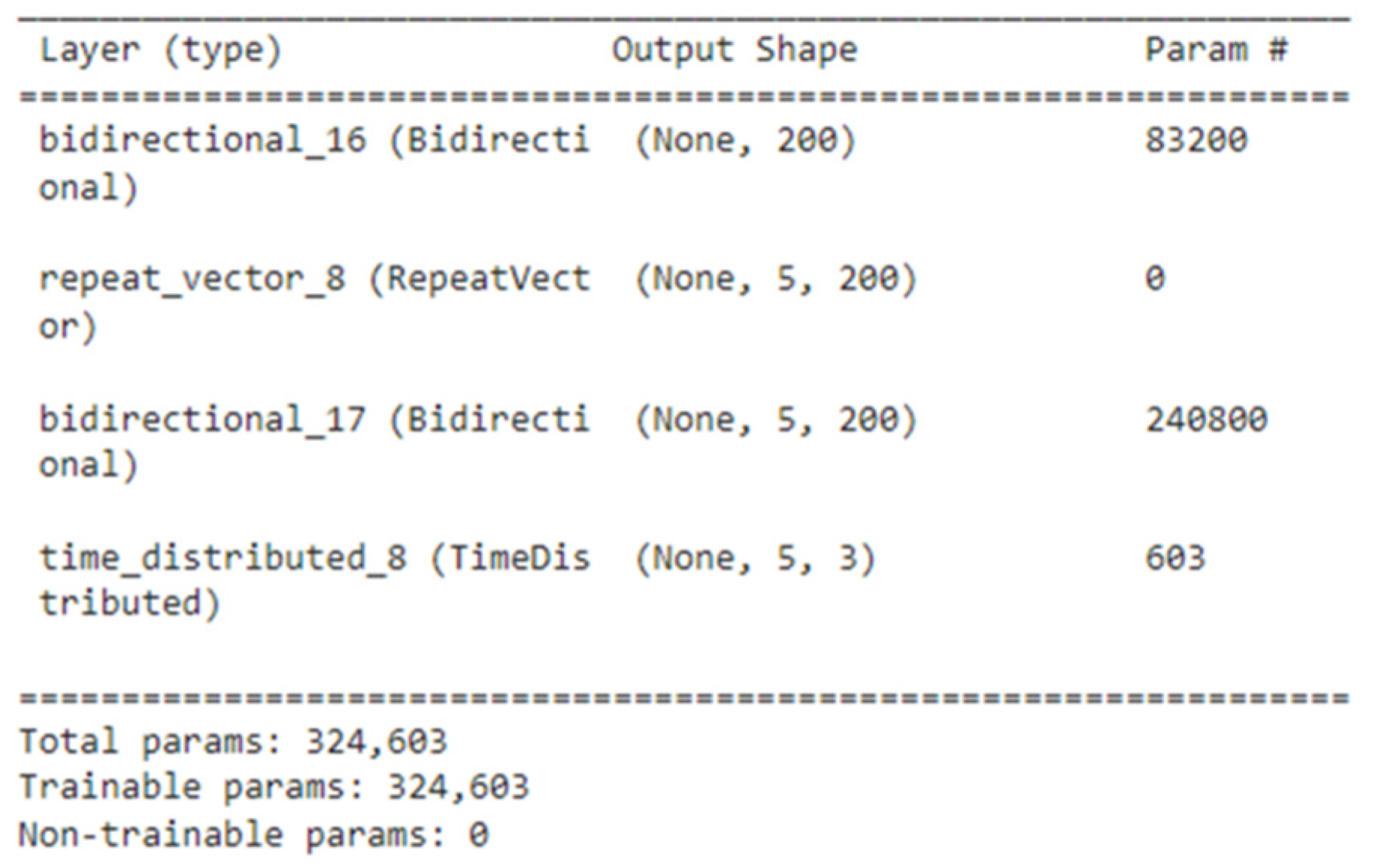

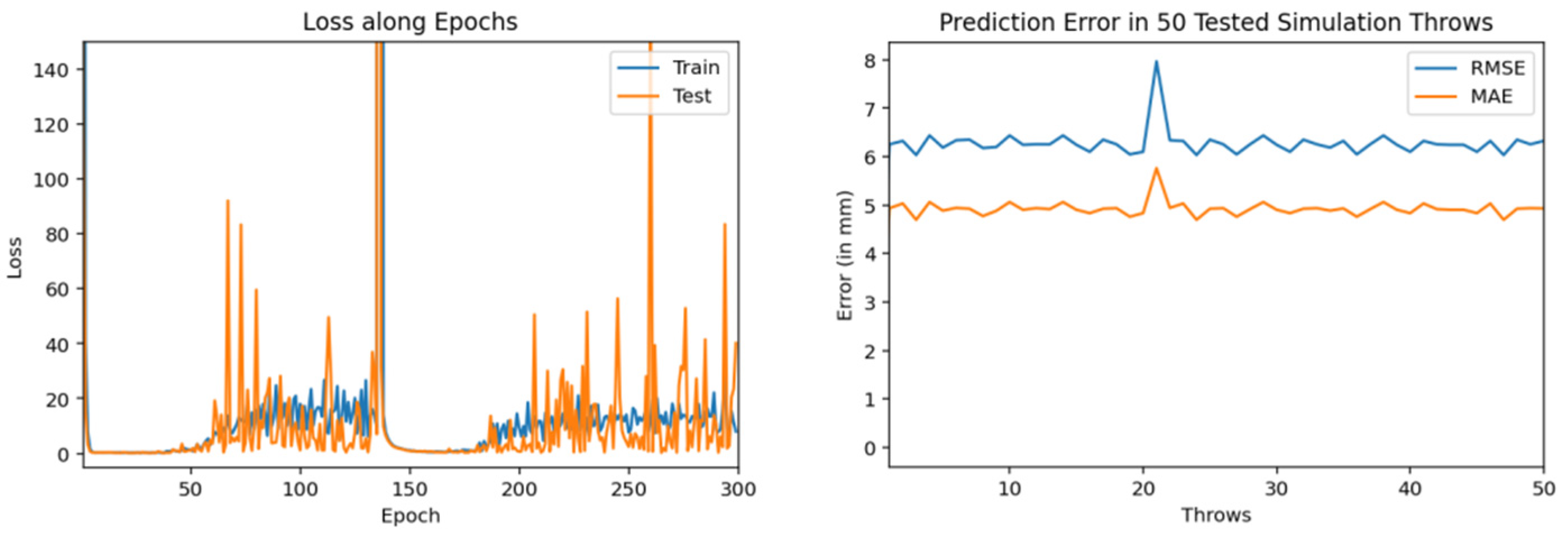
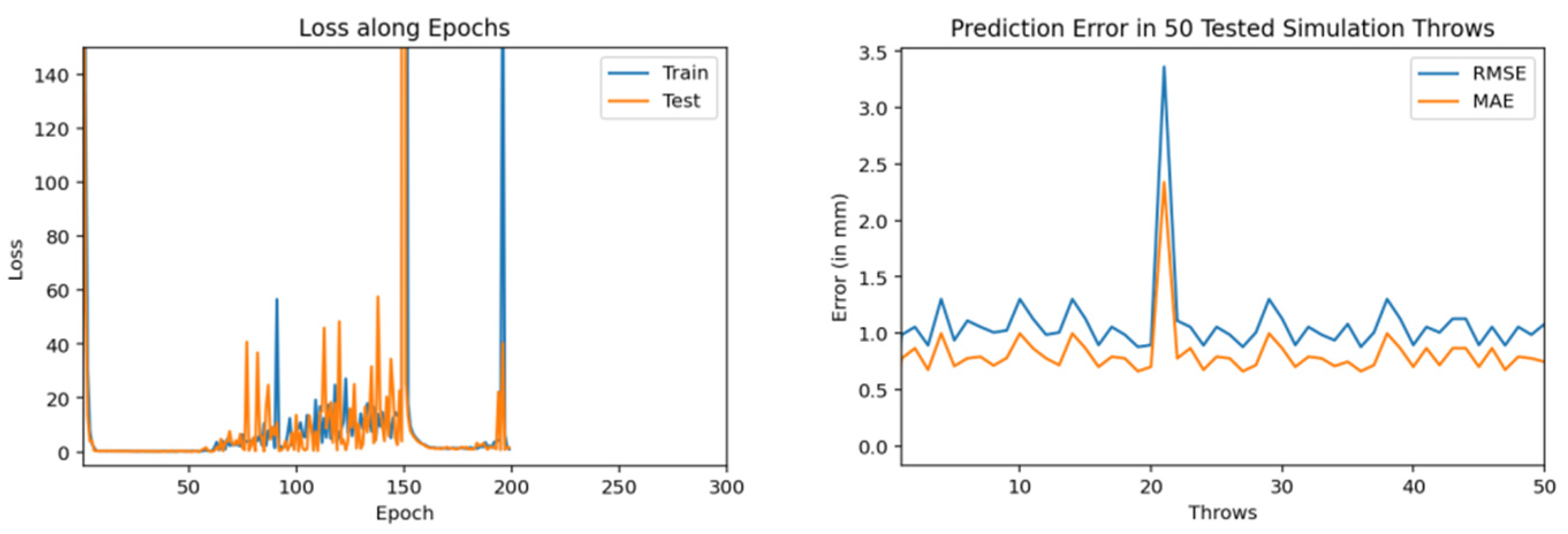
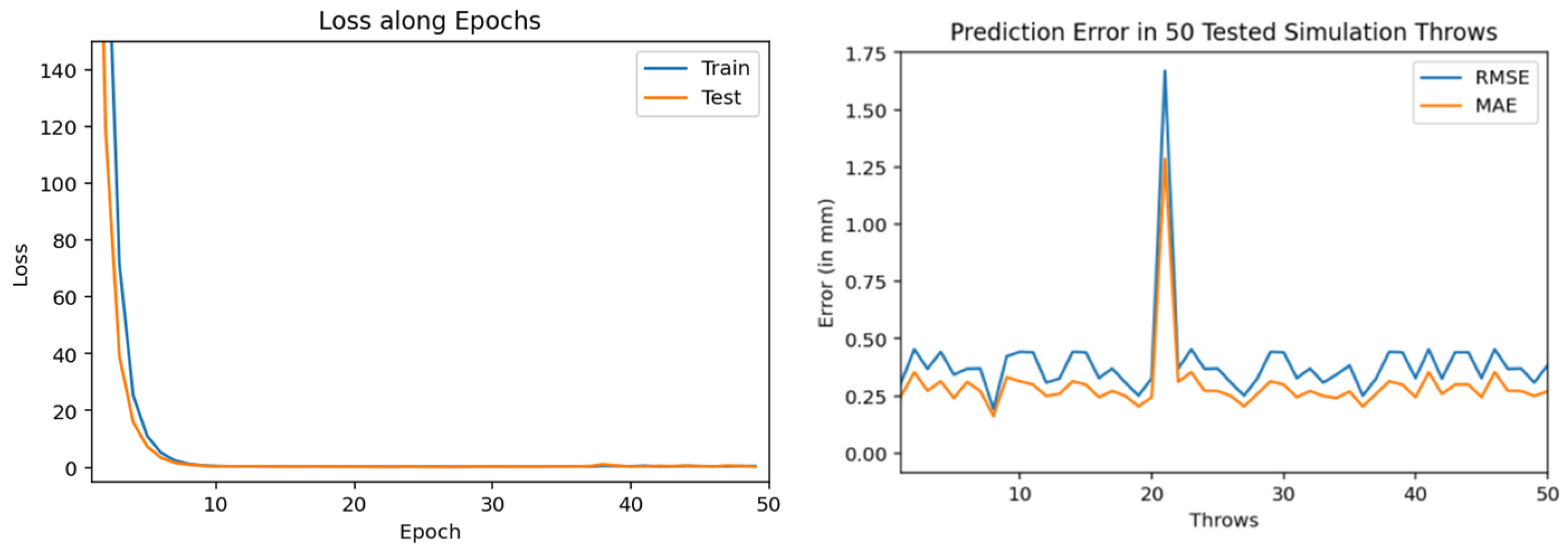
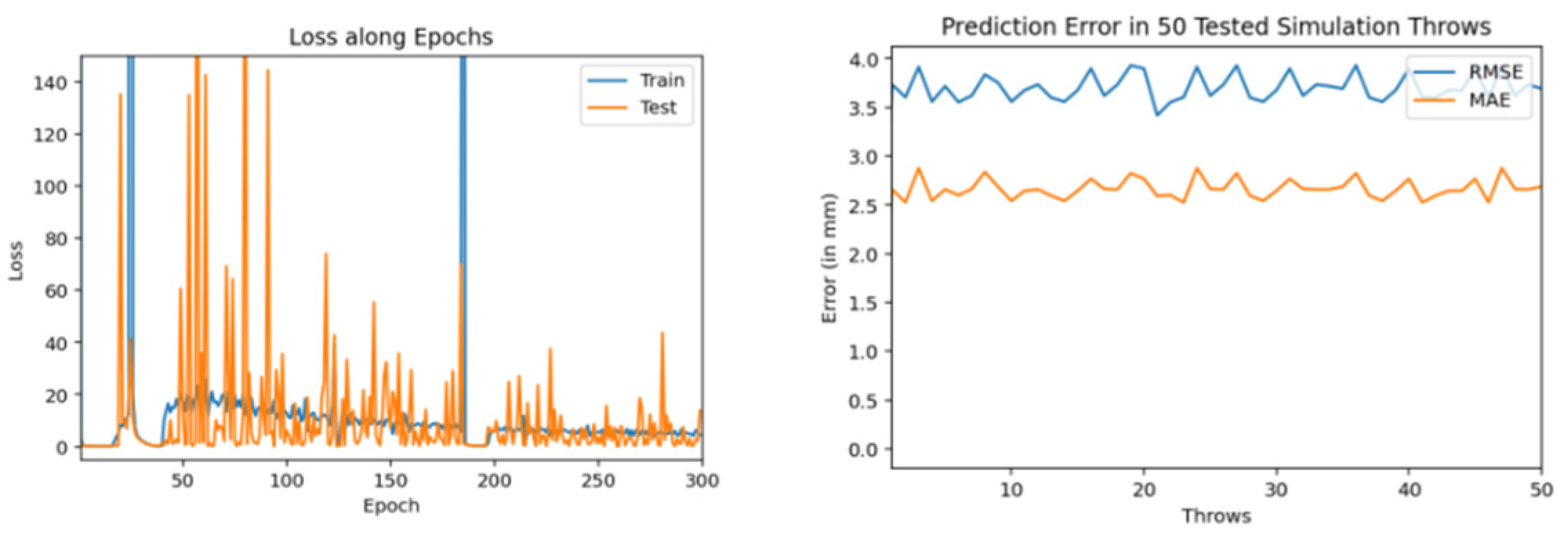

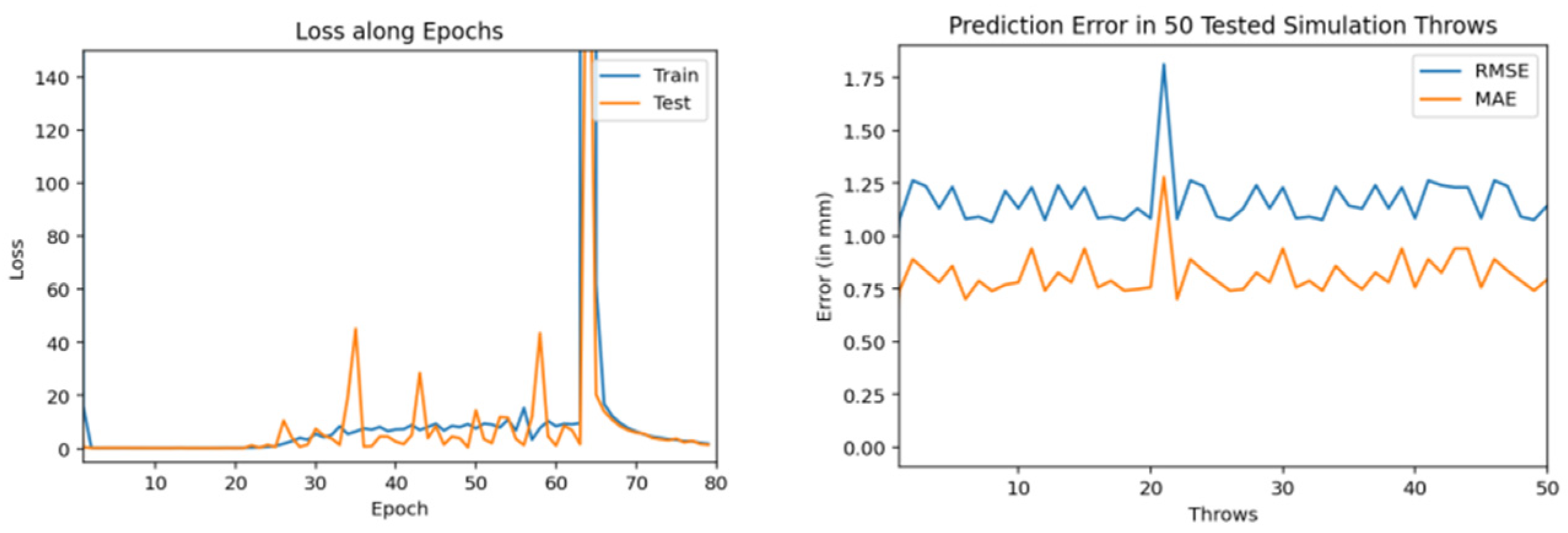
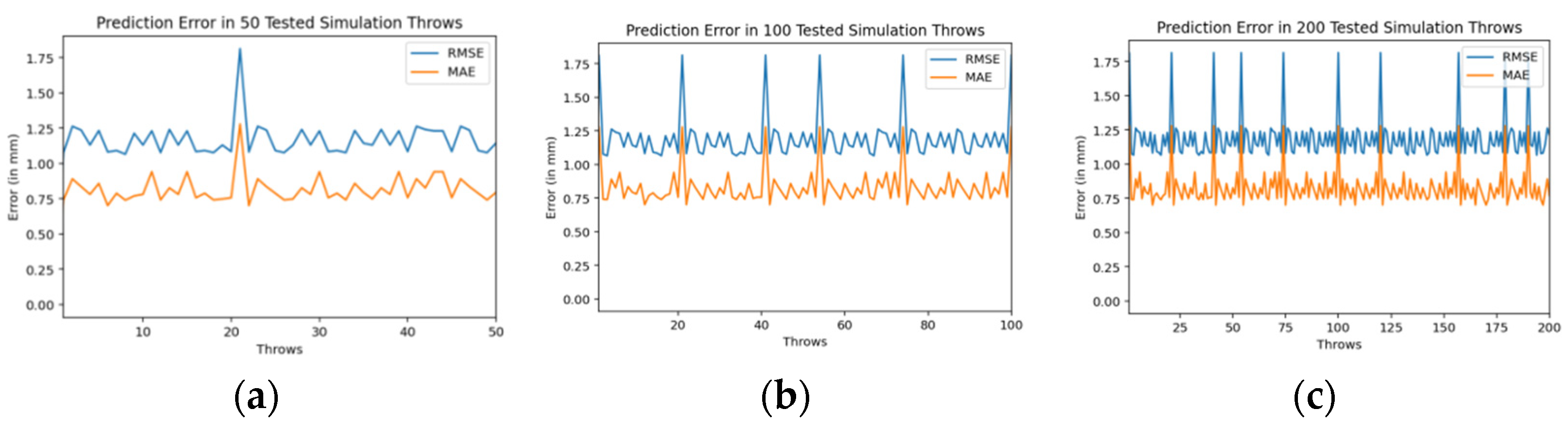
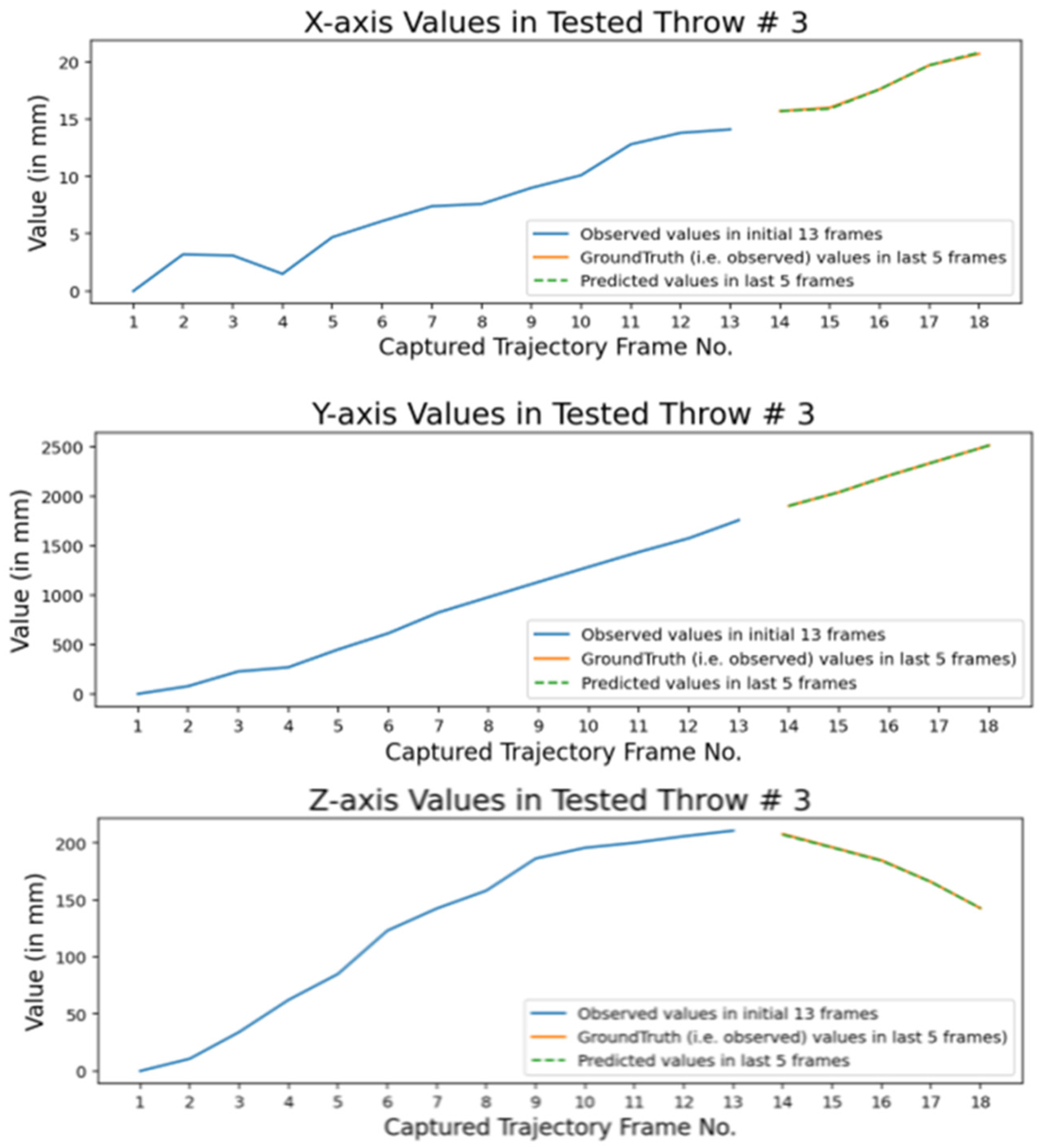
| Ref. | Year | Trajectory Type | Prediction Algorithm | Results (Accuracy) | Limitation(s) |
|---|---|---|---|---|---|
| [22] | 2020 | Mechanical ball throws using ping-pong playing robot. Observe its flight through 3 cameras (right, left and auxiliary) of speed 169 FPS | Dual Neural Network | 300 trajectories for the training set and 30 trajectories for the test set. The test results in absolute mean error of 36.6 mm and standard deviation of 18.8 mm | Limited training and testing |
| [23] | 2020 | Mechanical ball throw using ping-pong playing robot and observe its flight (0.8 to 1.2 s) through 4 RGB cameras of speed 180 FPS (Frames Per Second) attached at ceiling | Variational auto-encoder deep NN | 614 trajectories for the training set (90% training and 10% for validation) and 35 trajectories for the test set. Prediction’s absolute mean error converges to nearly 40–60 mm based upon observations in first 40–50 frames of flight trajectory. | Error is high but could be improved with more training trajectories |
| [24] | 2019 | ||||
| [25] | 2020 | ||||
| [29] | 2010 | Ball throws using mechanical device. Observe its actual positions in flight with the help of photoelectric sensors. Flight is also captured by single camera of 87 FPS speed. | Observations of ball positions through photoelectric sensors and Size based Tracking of ball through 2D coordinates in image plane are further passed to EKF for prediction of final 2D impact point on DST-Touch screen | The accuracy was measured in 17 test throws only and for final 2D impact position (on a DST-Touch kit) only. The average error deviation of final impact position was 1.20 mm to 3.98 mm. |
|
| [30] | 2009 | ||||
| [31] | 2008 | ||||
| [32] | 2016 | Ball throws using mechanical device. Observe its flight trajectory through stereo vision of 2 cameras (left and right) of spatial resolution 2048 × 2048 and speed was not specified in their articles. | kNN (k-Nearest Neighbor) Regression | 2048 real-world trajectories were saved in the database and then testing were performed on 150 trajectories. First 40 frames ball positions were used during testing and after applying KNN the prediction was within 30 mm for 92% of trajectories. | Error is high but could be improved with:
|
| [33] | 2015 | ||||
| [34] | 2013 | The mechanical throws were simulated using physical motion model. Each sample trajectory was obtained in nearly 2.5 m long flight of tennis ball. | Neural Network with one hidden layer was used to train 15 simulated trajectory sets whereas each set had 10 sample trajectories | The mean error was nearly 24 to 26 mm between measured values and prediction results in simulated environment. | Being results in simulated environment, this error is high. Also very limited training and testing |
| [35] | 2017 | Ball throws using mechanical device. Observe its flight trajectory through stereo vision of 2 cameras (left and right) of spatial resolution 2048 × 2048 and speed was not specified in their articles. | Deterministic motion model further governed by genetic programming algorithm | Their algorithm was tested through MSE (Mean Square Error) in chosen frames 60 to 80 only and in only 20 test trajectories. The average mean square error (MSE) in 20 trajectories was 5.4 mm | Average MSE was good but it was based upon just 20 testing trajectories as well as the error was calculated within selected frames (60 to 80) and it does not reflect the error of whole flight trajectory |
| [36] | 2018 | ||||
| [37] | 2019 | ||||
| [38] | 2017 |
| Multicamera Setups | Final 3D Interception Position Error (Average Error—in mm) | ||
|---|---|---|---|
| X-Axis | Y-Axis | Z-Axis | |
| C2 + C4 | 2.5 | 1.7 | 5.4 |
| C1 + C4 | 1.9 | 5.2 | 2.0 |
| C2 + C3 | 2.5 | 6.5 | 3.1 |
| C1 + C3 | 2.8 | 4.5 | 1.5 |
| C1 + C2 + C4 | 1.5 | 5.0 | 1.9 |
| C1 + C2 + C3 | 2.3 | 4.5 | 1.7 |
| C2 + C3 + C4 | 1.1 | 2.0 | 1.4 |
| C1 + C3 + C4 | 0.9 | 1.8 | 1.6 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qadeer, N.; Shah, J.H.; Sharif, M.; Khan, M.A.; Muhammad, G.; Zhang, Y.-D. Intelligent Tracking of Mechanically Thrown Objects by Industrial Catching Robot for Automated In-Plant Logistics 4.0. Sensors 2022, 22, 2113. https://doi.org/10.3390/s22062113
Qadeer N, Shah JH, Sharif M, Khan MA, Muhammad G, Zhang Y-D. Intelligent Tracking of Mechanically Thrown Objects by Industrial Catching Robot for Automated In-Plant Logistics 4.0. Sensors. 2022; 22(6):2113. https://doi.org/10.3390/s22062113
Chicago/Turabian StyleQadeer, Nauman, Jamal Hussain Shah, Muhammad Sharif, Muhammad Attique Khan, Ghulam Muhammad, and Yu-Dong Zhang. 2022. "Intelligent Tracking of Mechanically Thrown Objects by Industrial Catching Robot for Automated In-Plant Logistics 4.0" Sensors 22, no. 6: 2113. https://doi.org/10.3390/s22062113
APA StyleQadeer, N., Shah, J. H., Sharif, M., Khan, M. A., Muhammad, G., & Zhang, Y. -D. (2022). Intelligent Tracking of Mechanically Thrown Objects by Industrial Catching Robot for Automated In-Plant Logistics 4.0. Sensors, 22(6), 2113. https://doi.org/10.3390/s22062113








