Feature Extraction of the Brain’s Dynamic Complex Network Based on EEG and a Framework for Discrimination of Pediatric Epilepsy
Abstract
:1. Introduction
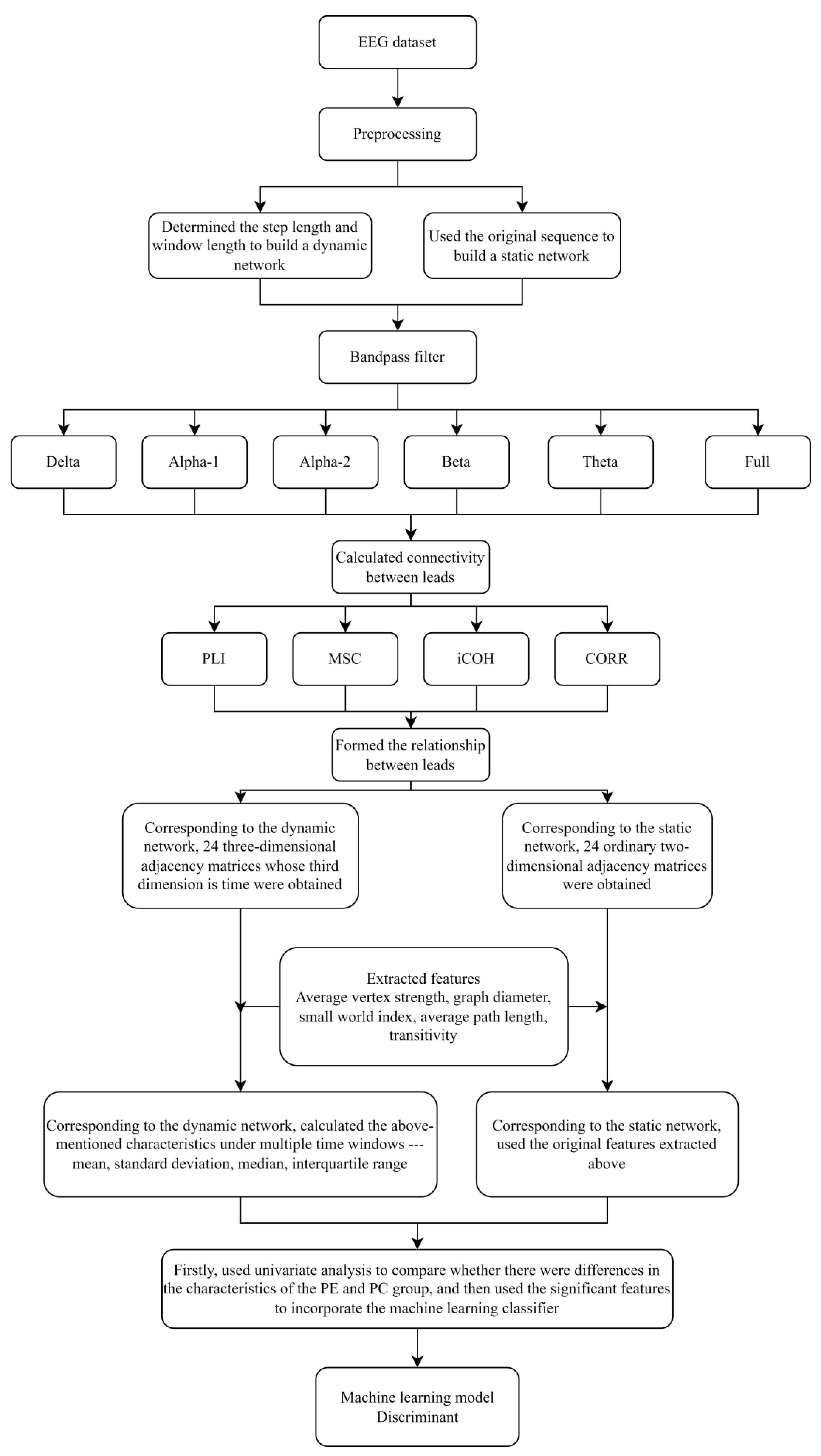
2. Materials and Methods
2.1. Research Participants
2.2. EEG Signals and Preprocessing
2.3. The Construction of the Brain’s Static and Dynamic Complex Networks
2.3.1. Constructing the Original EEG Dataset and the Split-Fragment EEG Dataset
2.3.2. Frequency Filtering
2.3.3. The Calculation of the Connectivity and Connectivity Strength between EEG Leads
2.3.4. The Construction of the Brain’s Static Complex Network
2.3.5. The Construction of the Brain’s Dynamic Complex Network
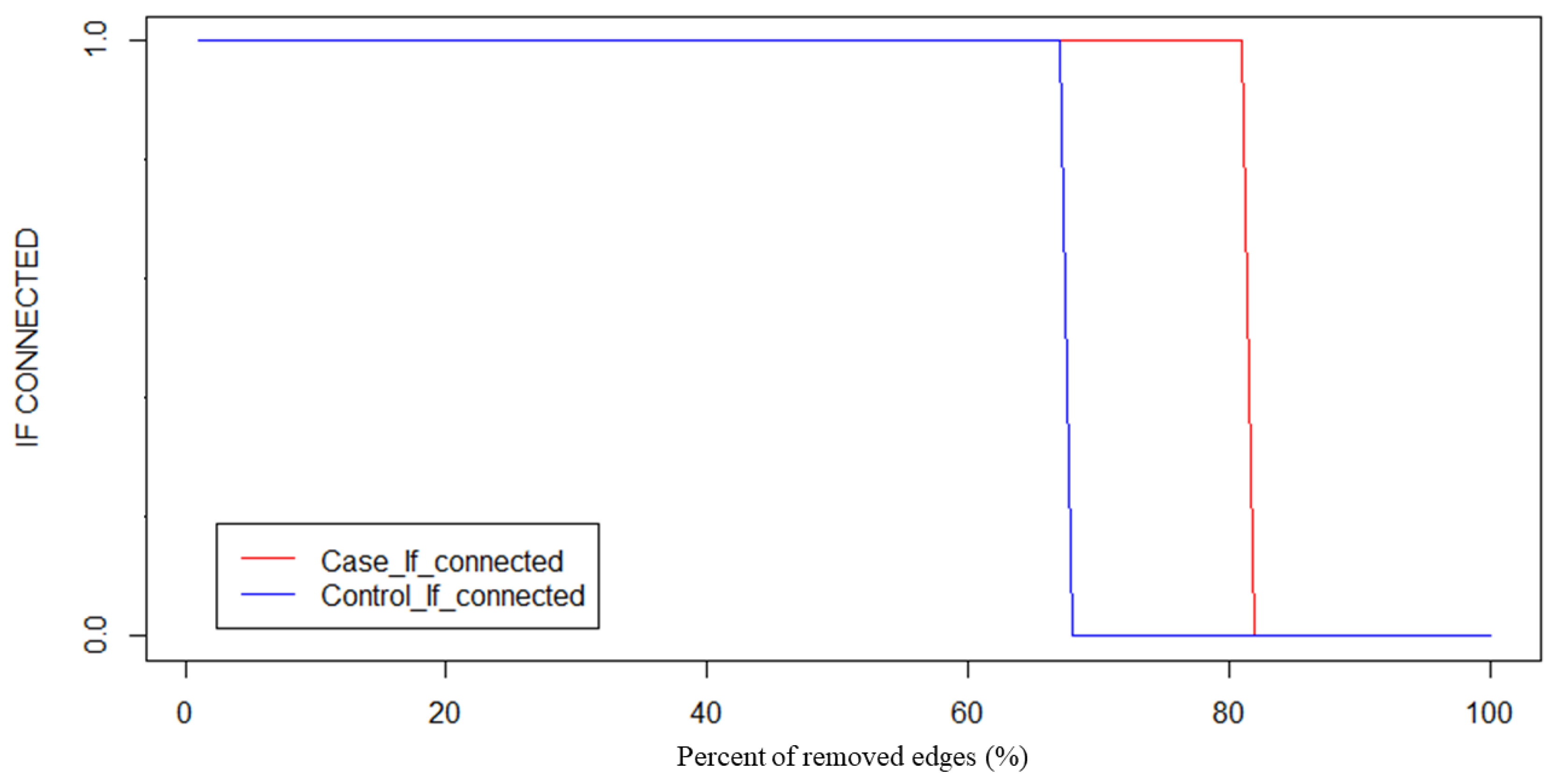
2.3.6. Selection of the Threshold in the Complex Network
2.4. Feature Extraction under the Brain’s Static and Dynamic Complex Network
2.4.1. Feature Extraction under the Brain’s Static Complex Network
2.4.2. Feature Extraction under the Brain’s Dynamic Complex Network
2.5. Feature Selection, Machine Learning Classifier and Evaluating
2.5.1. Feature Selection and Machine Learning Classifier
2.5.2. Evaluating the Classification Performances
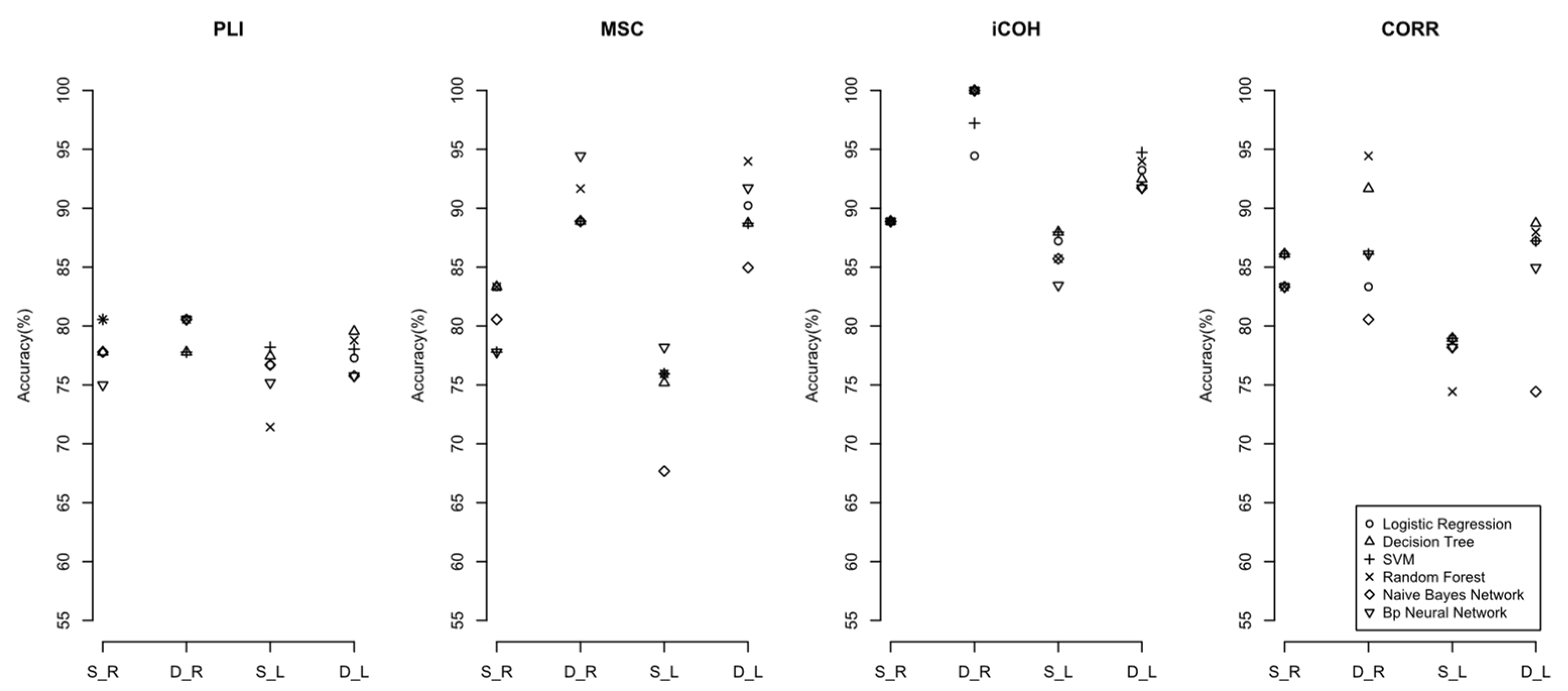
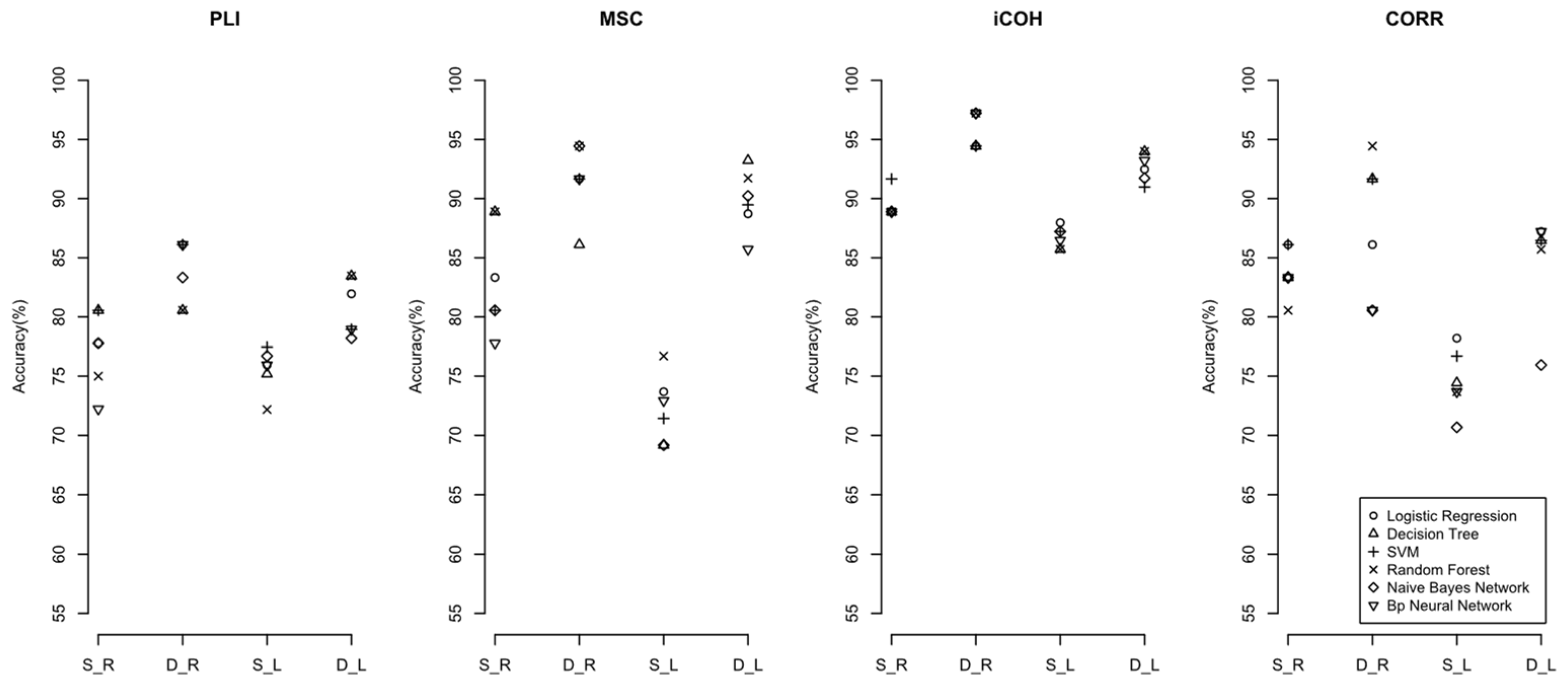
3. Results
3.1. Threshold Selection
3.2. Univariate Analysis Results
4. Discussion
4.1. Constructing the Brain’s Dynamic Complex Network and Extracting Its Characteristics Has a Better Performance than the Brain’s Static Complex Network
4.2. The Impact of EEG Frequency Band Splitting on the Discriminant Effect of Machine Learning Models
4.3. Changes in the Topological Characteristics of PE in the Brain Network
4.4. Shortage of This Research
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- WHO. Epilepsy: A Public Health Imperative; World Health Organization: Geneva, Switzerland, 2019. [Google Scholar]
- Fine, A.; Wirrell, E.C. Seizures in Children. Pediatrics Rev. 2020, 41, 321–347. [Google Scholar] [CrossRef] [PubMed]
- Aaberg, K.M.; Gunnes, N.; Bakken, I.J.; Lund Søraas, C.; Berntsen, A.; Magnus, P.; Lossius, M.I.; Stoltenberg, C.; Chin, R.; Surén, P. Incidence and Prevalence of Childhood Epilepsy: A Nationwide Cohort Study. Pediatrics 2017, 139, e20163908. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kwan, P.; Brodie, M.J. Early identification of refractory epilepsy. N. Engl. J. Med. 2000, 342, 314–319. [Google Scholar] [CrossRef] [PubMed]
- Cvetkovska, E.; Babunovska, M.; Kuzmanovski, I.; Boskovski, B.; Sazdova-Burneska, S.; Aleksovski, V.; Isjanovska, R. Patients’ attitude toward AED withdrawal: A survey among individuals who had been seizure-free for over 2 years. Epilepsy Behav. 2020, 104, 106881. [Google Scholar] [CrossRef] [PubMed]
- Raj Ghosh, G.; Nelson, A.L.A. Indications for epilepsy monitoring in pediatric and adolescent health care. Curr. Probl. Pediatr. Adolesc. Health Care 2020, 50, 100890. [Google Scholar] [CrossRef]
- Rosenow, F.; Klein, K.M.; Hamer, H.M. Non-invasive EEG evaluation in epilepsy diagnosis. Expert Rev. Neurother. 2015, 15, 425–444. [Google Scholar] [CrossRef]
- McKenna, T.M.; McMullen, T.A.; Shlesinger, M.F. The brain as a dynamic physical system. Neuroscience 1994, 60, 587–605. [Google Scholar] [CrossRef]
- Mesulam, M.M. From sensation to cognition. Brain 1998, 121 Pt 6, 1013–1052. [Google Scholar] [CrossRef]
- Wang, B.; Han, X.; Yang, S.; Zhao, P.; Li, M.; Zhao, Z.; Wang, N.; Ma, H.; Zhang, Y.; Zhao, T.; et al. An integrative prediction algorithm of drug-refractory epilepsy based on combined clinical-EEG functional connectivity features. J. Neurol. 2021, 269, 1501–1514. [Google Scholar] [CrossRef]
- Drenthen, G.S.; Jansen, J.F.A.; Gommer, E.; Gupta, L.; Hofman, P.A.M.; van Kranen-Mastenbroek, V.H.; Hilkman, D.M.; Vlooswijk, M.C.G.; Rouhl, R.P.W.; Backes, W.H. Predictive value of functional MRI and EEG in epilepsy diagnosis after a first seizure. Epilepsy Behav. 2021, 115, 107651. [Google Scholar] [CrossRef]
- Zhang, B.; Yan, G.; Yang, Z.; Su, Y.; Wang, J.; Lei, T. Brain Functional Networks Based on Resting-State EEG Data for Major Depressive Disorder Analysis and Classification. IEEE Trans. Neural Syst. Rehabil. Eng. 2021, 29, 215–229. [Google Scholar] [CrossRef] [PubMed]
- Diykh, M.; Li, Y.; Wen, P. Classify epileptic EEG signals using weighted complex networks based community structure detection. Expert Syst. Appl. 2017, 90, 87–100. [Google Scholar] [CrossRef]
- Zhang, Q.Z.; Hu, Y.J.; Potter, T.; Li, R.H.; Quach, M.; Zhang, Y.C. Establishing functional brain networks using a nonlinear partial directed coherence method to predict epileptic seizures. J. Neurosci. Methods 2020, 329, 108447. [Google Scholar] [CrossRef] [PubMed]
- Li, X.Z.; Mota, B.; Kondo, T.; Nasuto, S.; Hayashi, Y. EEG dynamical network analysis method reveals the neural signature of visual-motor coordination. PLoS ONE 2020, 15, e0231767. [Google Scholar] [CrossRef] [PubMed]
- Christiaen, E.; Goossens, M.G.; Descamps, B.; Larsen, L.E.; Boon, P.; Raedt, R.; Vanhove, C. Dynamic functional connectivity and graph theory metrics in a rat model of temporal lobe epilepsy reveal a preference for brain states with a lower functional connectivity, segregation and integration. Neurobiol. Dis. 2020, 139, 104808. [Google Scholar] [CrossRef] [PubMed]
- Fisher, R.S.; Acevedo, C.; Arzimanoglou, A.; Bogacz, A.; Cross, J.H.; Elger, C.E.; Engel, J., Jr.; Forsgren, L.; French, J.A.; Glynn, M.; et al. ILAE official report: A practical clinical definition of epilepsy. Epilepsia 2014, 55, 475–482. [Google Scholar] [CrossRef] [Green Version]
- Delorme, A.; Makeig, S. EEGLAB: An open source toolbox for analysis of single-trial EEG dynamics including independent component analysis. J. Neurosci. Methods 2004, 134, 9–21. [Google Scholar] [CrossRef] [Green Version]
- Niso, G.; Bruna, R.; Pereda, E.; Gutierrez, R.; Bajo, R.; Maestu, F.; del-Pozo, F. HERMES: Towards an Integrated Toolbox to Characterize Functional and Effective Brain Connectivity. Neuroinformatics 2013, 11, 405–434. [Google Scholar] [CrossRef] [Green Version]
- Nolte, G.; Bai, O.; Wheaton, L.; Mari, Z.; Vorbach, S.; Hallett, M. Identifying true brain interaction from EEG data using the imaginary part of coherency. Clin. Neurophysiol. 2004, 115, 2292–2307. [Google Scholar] [CrossRef]
- Stam, C.J.; Nolte, G.; Daffertshofer, A. Phase lag index: Assessment of functional connectivity from multi channel EEG and MEG with diminished bias from common sources. Hum. Brain Mapp. 2007, 28, 1178–1193. [Google Scholar] [CrossRef]
- Pezoulas, V.C.; Athanasiou, A.; Nolte, G.; Zervakis, M.; Fratini, A.; Fotiadis, D.I.; Klados, M.A. In FCLAB: An EEGLAB Module for Performing Functional Connectivity Analysis on Single-Subject EEG Data. In Proceedings of the 2018 IEEE EMBS International Conference on Biomedical & Health Informatics (BHI), Las Vegas, NV, USA, 4–7 March 2018; pp. 96–99. [Google Scholar]
- Lehnertz, K.; Geier, C.; Rings, T.; Stahn, K. Capturing time-varying brain dynamics. Epj Nonlinear Biomed. 2017, 5, 2. [Google Scholar] [CrossRef] [Green Version]
- Iakovidou, N.D. Graph Theory at the Service of Electroencephalograms. Brain Connect. 2017, 7, 137–151. [Google Scholar] [CrossRef] [PubMed]
- Tahaei, M.S.; Jalili, M.; Knyazeva, M.G. Synchronizability of EEG-Based Functional Networks in Early Alzheimer’s Disease. IEEE Trans. Neural Syst. Rehabil. Eng. 2012, 20, 636–641. [Google Scholar] [CrossRef] [PubMed]
- Watts, D.J.; Strogatz, S.H. Collective dynamics of ‘small-world’ networks. Nature 1998, 393, 440–442. [Google Scholar] [CrossRef]
- Sargolzaei, S.; Cabrerizo, M.; Goryawala, M.; Eddin, A.S.; Adjouadi, M. Scalp EEG brain functional connectivity networks in pediatric epilepsy. Comput. Biol. Med. 2015, 56, 158–166. [Google Scholar] [CrossRef]
- Van Diessen, E.; Otte, W.M.; Braun, K.P.J.; Stam, C.J.; Jansen, F.E. Improved Diagnosis in Children with Partial Epilepsy Using a Multivariable Prediction Model Based on EEG Network Characteristics. PLoS ONE 2013, 8, e59764. [Google Scholar] [CrossRef] [Green Version]
- Rodrigues, P.G.; Stefano, C.A.; Attux, R.; Castellano, G.; Soriano, D.C. Space-time recurrences for functional connectivity evaluation and feature extraction in motor imagery brain-computer interfaces. Med. Biol. Eng. Comput. 2019, 57, 1709–1725. [Google Scholar] [CrossRef]
- Lacasa, L.; Nicosia, V.; Latora, V. Network structure of multivariate time series. Sci. Rep. 2015, 5, 15508. [Google Scholar] [CrossRef] [Green Version]
- Arbabyazd, L.M.; Lombardo, D.; Blin, O.; Didic, M.; Battaglia, D.; Jirsa, V. Dynamic Functional Connectivity as a complex random walk: Definitions and the dFCwalk toolbox. Methodsx 2020, 7, 101168. [Google Scholar] [CrossRef]
- Lee, H.; Noh, G.J.; Joo, P.; Choi, B.M.; Silverstein, B.H.; Kim, M.; Wang, J.; Jung, W.S.; Kim, S. Diversity of Functional Connectivity Patterns is Reduced in Propofol-Induced Unconsciousness. Hum. Brain Mapp. 2017, 38, 4980–4995. [Google Scholar] [CrossRef] [Green Version]
- Van Diessen, E.; Numan, T.; van Dellen, E.; van der Kooi, A.W.; Boersma, M.; Hofman, D.; van Lutterveld, R.; van Dijk, B.W.; van Straaten, E.C.W.; Hillebrand, A.; et al. Opportunities and methodological challenges in EEG and MEG resting state functional brain network research. Clin. Neurophysiol. 2015, 126, 1468–1481. [Google Scholar] [CrossRef] [PubMed]
- Pegg, E.J.; Taylor, J.R.; Laiou, P.; Richardson, M.; Mohanraj, R. Interictal electroencephalographic functional network topology in drug-resistant and well-controlled idiopathic generalized epilepsy. Epilepsia 2021, 62, 492–503. [Google Scholar] [CrossRef] [PubMed]
- Chowdhury, F.A.; Woldman, W.; FitzGerald, T.H.; Elwes, R.D.; Nashef, L.; Terry, J.R.; Richardson, M.P. Revealing a brain network endophenotype in families with idiopathic generalised epilepsy. PLoS ONE 2014, 9, e110136. [Google Scholar] [CrossRef] [PubMed]
- Van Diessen, E.; Otte, W.M.; Stam, C.J.; Braun, K.P.; Jansen, F.E. Electroencephalography based functional networks in newly diagnosed childhood epilepsies. Clin. Neurophysiol. 2016, 127, 2325–2332. [Google Scholar] [CrossRef]
- Leitgeb, E.P.; Sterk, M.; Petrijan, T.; Gradisnik, P.; Gosak, M. The brain as a complex network: Assessment of EEG-based functional connectivity patterns in patients with childhood absence epilepsy. Epileptic Disord. 2020, 22, 519–530. [Google Scholar] [CrossRef]
- O’Neill, G.C.; Tewarie, P.; Vidaurre, D.; Liuzzi, L.; Woolrich, M.W.; Brookes, M.J. Dynamics of large-scale electrophysiological networks: A technical review. Neuroimage 2018, 180 Pt B, 559–576. [Google Scholar] [CrossRef] [Green Version]
- Preti, M.G.; Bolton, T.A.; Van De Ville, D. The dynamic functional connectome: State-of-the-art and perspectives. Neuroimage 2017, 160, 41–54. [Google Scholar] [CrossRef]


| Factor | PE | PC |
|---|---|---|
| Age (years) | 7.75 ± 4.92 | 7.05 ± 3.53 |
| Gender n (%) | ||
| Female | 6 (37.5) | 7 (35.0) |
| Male | 10 (62.5) | 13 (65.0) |
| Item | P50_PC | IQR_PC | P50_PE | IQR_PE | W | p |
|---|---|---|---|---|---|---|
| Small-world index | 1.21 | 0.21 | 1.33 | 0.28 | 106.0 | 0.089 |
| Average vertex strength | 0.59 | 0.16 | 1.03 | 0.62 | 53.0 | <0.001 * |
| Average path length | 1.63 | 0.04 | 1.64 | 0.05 | 136.0 | 0.453 |
| Transitivity | 0.44 | 0.04 | 0.47 | 0.07 | 111.0 | 0.124 |
| Diameter | 0.22 | 0.07 | 0.36 | 0.27 | 67.0 | 0.002 * |
| Item | P50_PC | IQR_PC | P50_PE | IQR_PE | W | p |
|---|---|---|---|---|---|---|
| Mean-Small-world index | 1.13 | 0.03 | 1.16 | 0.05 | 84.0 | 0.015 * |
| Standard Deviation-Small-world index | 0.18 | 0.02 | 0.18 | 0.01 | 117.0 | 0.178 |
| P50-Small-world index | 1.12 | 0.05 | 1.14 | 0.04 | 83.0 | 0.014 * |
| IQR-Small-world index | 0.24 | 0.05 | 0.25 | 0.05 | 132.0 | 0.386 |
| Mean-Average vertex strength | 2.60 | 0.23 | 2.91 | 0.33 | 65.0 | 0.002 * |
| Standard Deviation-Average vertex strength | 0.38 | 0.12 | 0.49 | 0.22 | 53.0 | <0.001 * |
| P50-Average vertex strength | 2.59 | 0.26 | 2.82 | 0.17 | 63.0 | 0.002 * |
| IQR-Average vertex strength | 0.51 | 0.18 | 0.66 | 0.30 | 43.0 | <0.001 * |
| Mean-Average path length | 1.64 | 0.01 | 1.64 | 0.01 | 75.0 | 0.006 * |
| Standard Deviation-Average path length | 0.03 | 0.01 | 0.04 | 0.01 | 84.0 | 0.015 * |
| P50-Average path length | 1.63 | 0.01 | 1.64 | 0.01 | 44.0 | <0.001 * |
| IQR-Average path length | 0.04 | 0.01 | 0.05 | 0.02 | 86.5 | 0.019 * |
| Mean-Transitivity | 0.44 | 0.01 | 0.45 | 0.02 | 60.0 | 0.001 * |
| Standard Deviation-Transitivity | 0.04 | 0.01 | 0.05 | 0.00 | 55.0 | 0.001 * |
| P50-Transitivity | 0.44 | 0.01 | 0.45 | 0.02 | 62.5 | 0.002 * |
| IQR-Transitivity | 0.06 | 0.01 | 0.07 | 0.01 | 71.0 | 0.004 * |
| Mean-Diameter | 0.96 | 0.09 | 1.09 | 0.14 | 57.0 | 0.001 * |
| Standard Deviation-Diameter | 0.19 | 0.05 | 0.26 | 0.10 | 60.0 | 0.001 * |
| P50-Diameter | 0.94 | 0.08 | 1.04 | 0.12 | 55.5 | 0.001 * |
| IQR-Diameter | 0.23 | 0.08 | 0.32 | 0.11 | 44.0 | <0.001 * |
| Item | P50_PC | IQR_PC | P50_PE | IQR_PE | W | p |
|---|---|---|---|---|---|---|
| Small-world index | 1.22 | 0.23 | 1.29 | 0.29 | 1977.0 | 0.324 |
| Average vertex strength | 0.64 | 0.24 | 0.97 | 0.72 | 912.0 | <0.001 * |
| Average path length | 1.64 | 0.04 | 1.64 | 0.05 | 2487.5 | 0.188 |
| Transitivity | 0.44 | 0.06 | 0.46 | 0.08 | 1864.0 | 0.134 |
| Diameter | 0.24 | 0.10 | 0.36 | 0.26 | 1031.5 | <0.001 * |
| Item | P50_PC | IQR_PC | P50_PE | IQR_PE | W | p |
|---|---|---|---|---|---|---|
| Mean-Small-world index | 1.14 | 0.03 | 1.15 | 0.05 | 1658.0 | 0.015 * |
| Standard Deviation-Small-world index | 0.17 | 0.02 | 0.18 | 0.03 | 1421.0 | <0.001 * |
| P50-Small-world index | 1.13 | 0.05 | 1.14 | 0.05 | 1642.0 | 0.012 * |
| IQR-Small-world index | 0.23 | 0.04 | 0.24 | 0.05 | 1638.0 | 0.012 * |
| Mean-Average vertex strength | 2.60 | 0.22 | 2.84 | 0.39 | 1008.0 | <0.001 * |
| Standard Deviation-Average vertex strength | 0.39 | 0.11 | 0.49 | 0.18 | 897.0 | <0.001 * |
| P50-Average vertex strength | 2.55 | 0.23 | 2.80 | 0.29 | 1030.5 | <0.001 * |
| IQR-Average vertex strength | 0.52 | 0.11 | 0.65 | 0.30 | 843.5 | <0.001 * |
| Mean-Average path length | 1.64 | 0.01 | 1.64 | 0.01 | 1751.0 | 0.045 * |
| Standard Deviation-Average path length | 0.04 | 0.01 | 0.04 | 0.01 | 1143.0 | <0.001 * |
| P50-Average path length | 1.63 | 0.01 | 1.64 | 0.01 | 1503.5 | 0.001 * |
| IQR-Average path length | 0.04 | 0.01 | 0.05 | 0.01 | 1540.0 | 0.003 * |
| Mean-Transitivity | 0.44 | 0.01 | 0.45 | 0.01 | 1072.0 | <0.001 * |
| Standard Deviation-Transitivity | 0.05 | 0.01 | 0.05 | 0.01 | 1354.0 | <0.001 * |
| P50-Transitivity | 0.44 | 0.01 | 0.45 | 0.01 | 1100.0 | <0.001 * |
| IQR-Transitivity | 0.06 | 0.01 | 0.06 | 0.01 | 1576.0 | 0.005 * |
| Mean-Diameter | 0.96 | 0.09 | 1.06 | 0.17 | 947.0 | <0.001 * |
| Standard Deviation-Diameter | 0.20 | 0.05 | 0.24 | 0.09 | 934.0 | <0.001 * |
| P50-Diameter | 0.93 | 0.09 | 1.03 | 0.14 | 903.5 | <0.001 * |
| IQR-Diameter | 0.25 | 0.07 | 0.31 | 0.11 | 898.0 | <0.001 * |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liang, Z.; Chen, S.; Zhang, J. Feature Extraction of the Brain’s Dynamic Complex Network Based on EEG and a Framework for Discrimination of Pediatric Epilepsy. Sensors 2022, 22, 2553. https://doi.org/10.3390/s22072553
Liang Z, Chen S, Zhang J. Feature Extraction of the Brain’s Dynamic Complex Network Based on EEG and a Framework for Discrimination of Pediatric Epilepsy. Sensors. 2022; 22(7):2553. https://doi.org/10.3390/s22072553
Chicago/Turabian StyleLiang, Zichao, Siyang Chen, and Jinxin Zhang. 2022. "Feature Extraction of the Brain’s Dynamic Complex Network Based on EEG and a Framework for Discrimination of Pediatric Epilepsy" Sensors 22, no. 7: 2553. https://doi.org/10.3390/s22072553
APA StyleLiang, Z., Chen, S., & Zhang, J. (2022). Feature Extraction of the Brain’s Dynamic Complex Network Based on EEG and a Framework for Discrimination of Pediatric Epilepsy. Sensors, 22(7), 2553. https://doi.org/10.3390/s22072553






