Feature Analysis and Extraction for Specific Emitter Identification Based on the Signal Generation Mechanisms of Radar Transmitters
Abstract
:1. Introduction
2. Theoretical Review
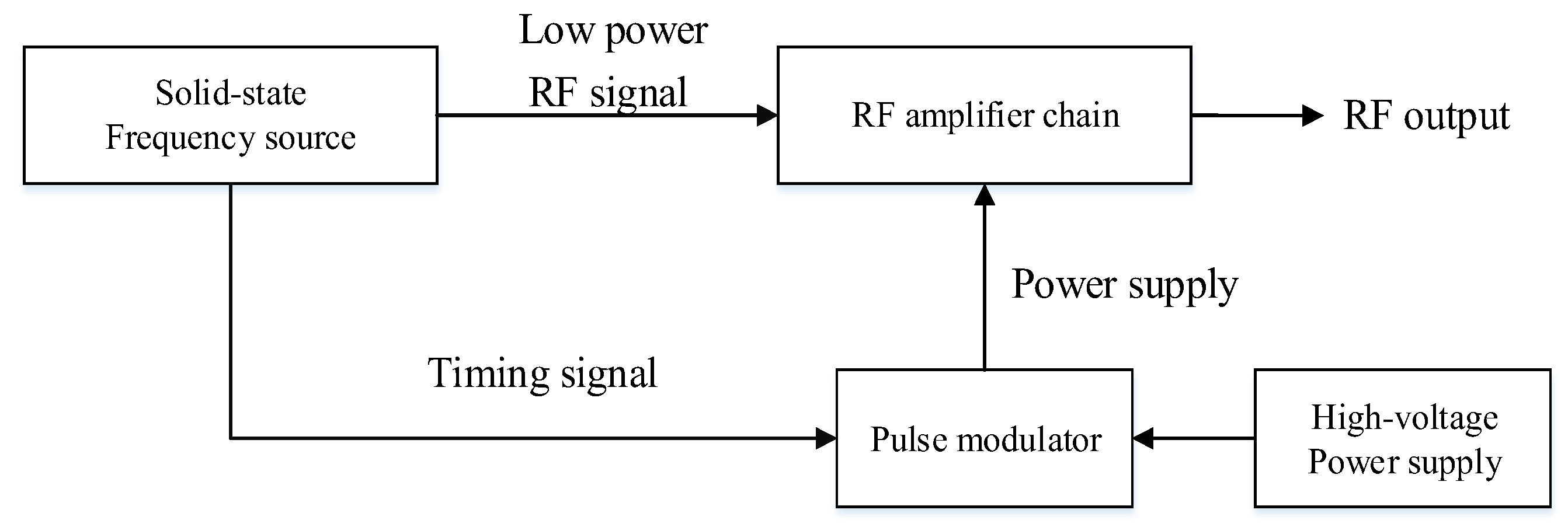
2.1. Structure of the MOPA Transmitter
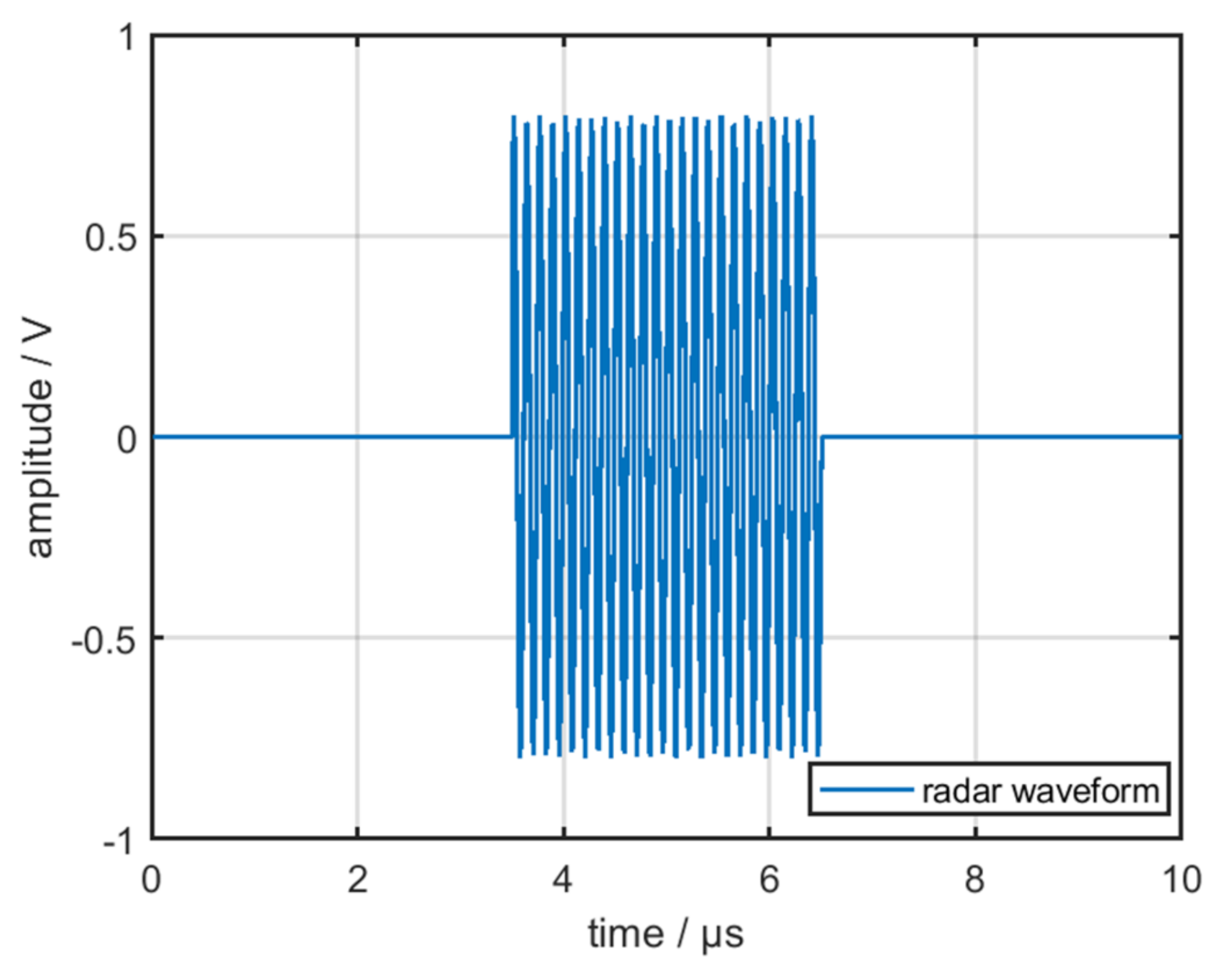
2.2. Model of the Typical Radar Signal
3. Feature Analysis and Extraction from the MOPA Transmitter
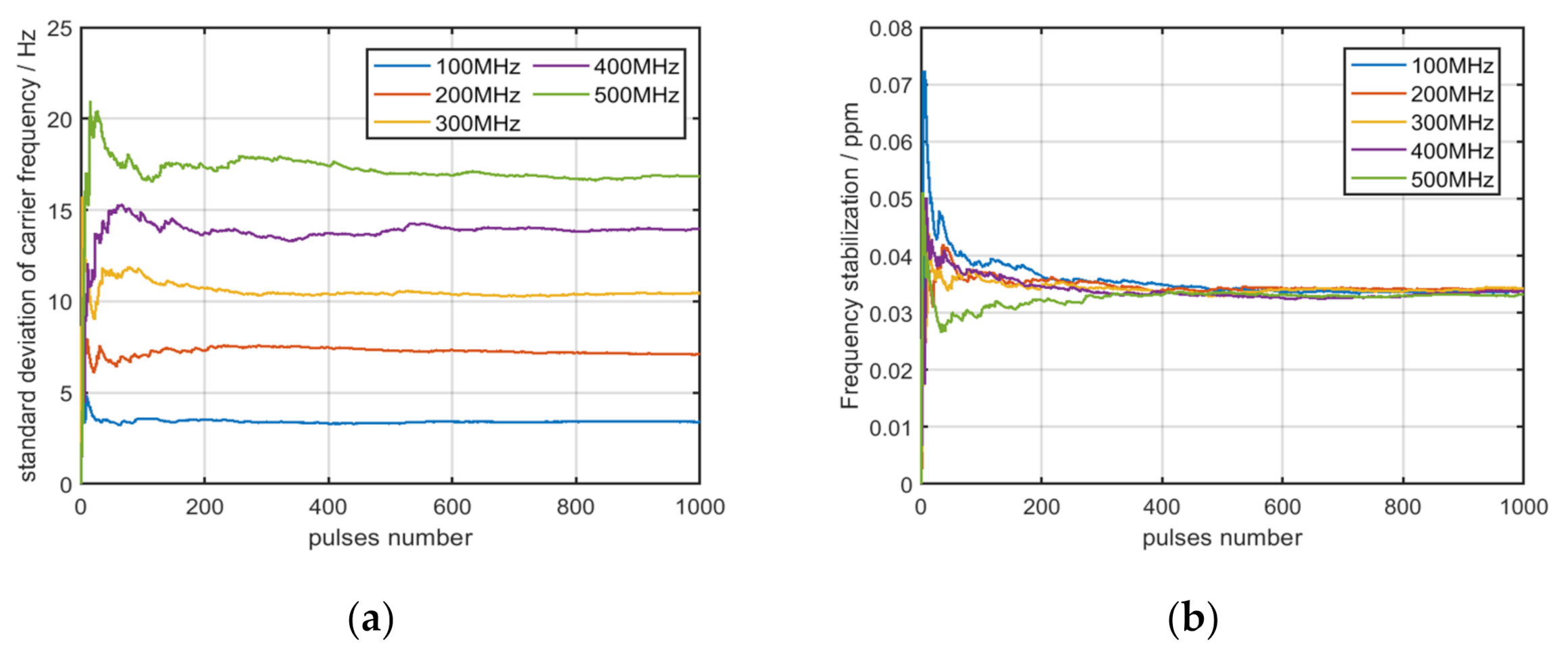
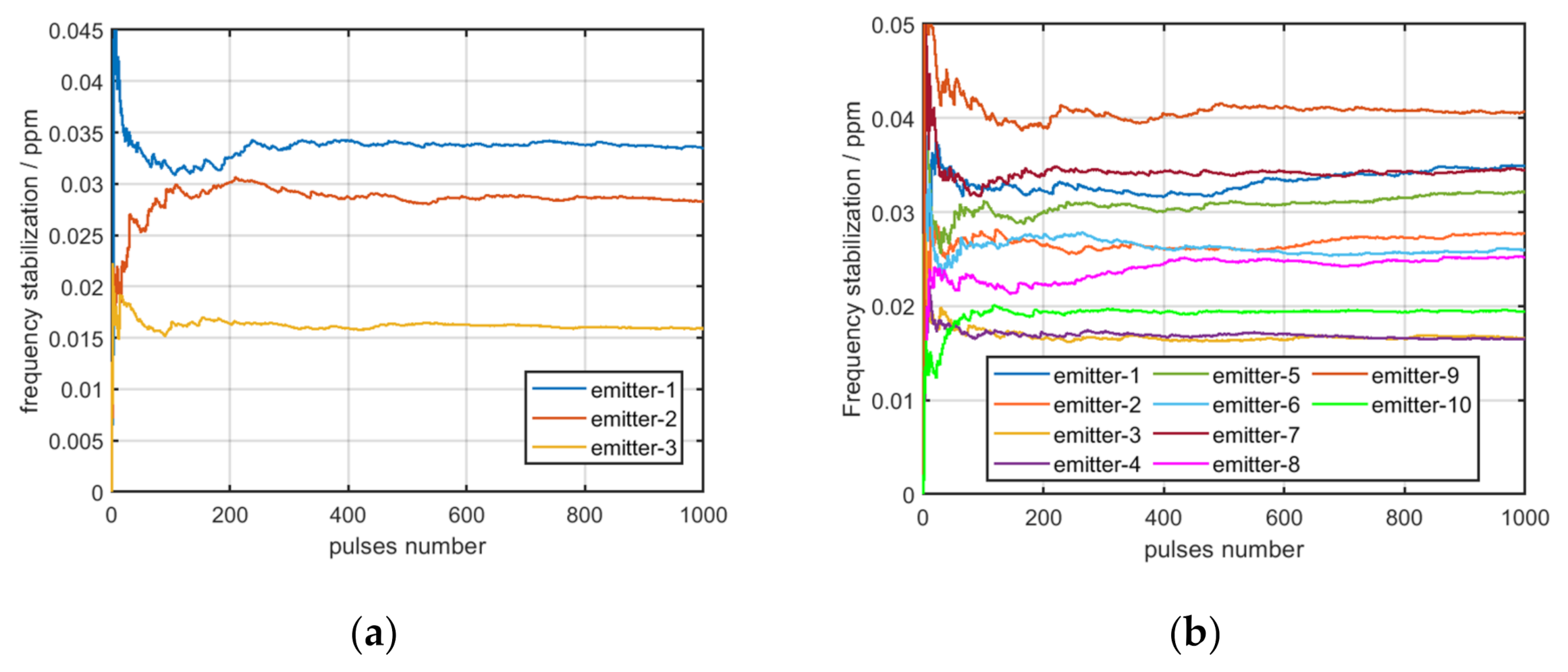
3.1. Analysis and Extraction of the Frequency Stabilization of the Solid-State Frequency Source
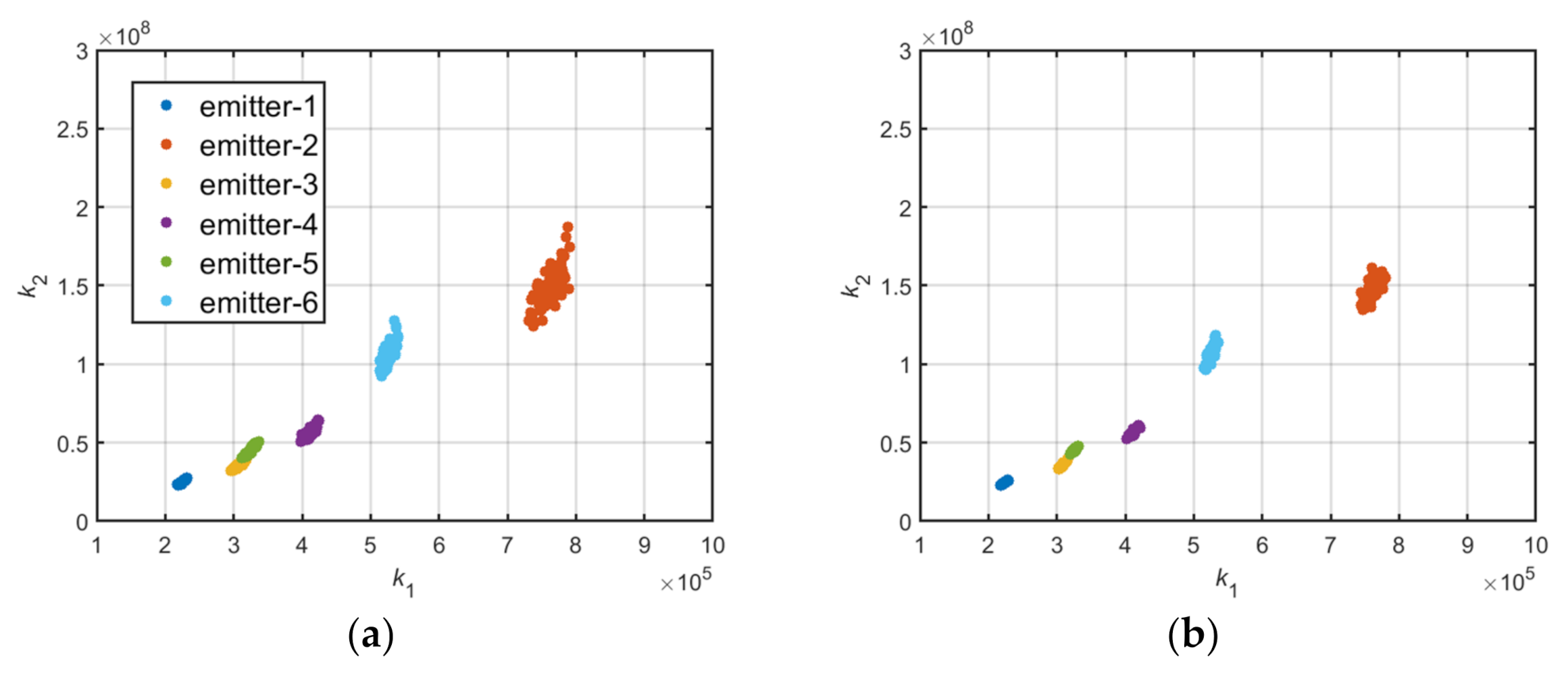
3.2. Analysis and Extraction of Total Harmonic Distortion of the RF Amplifier Chain
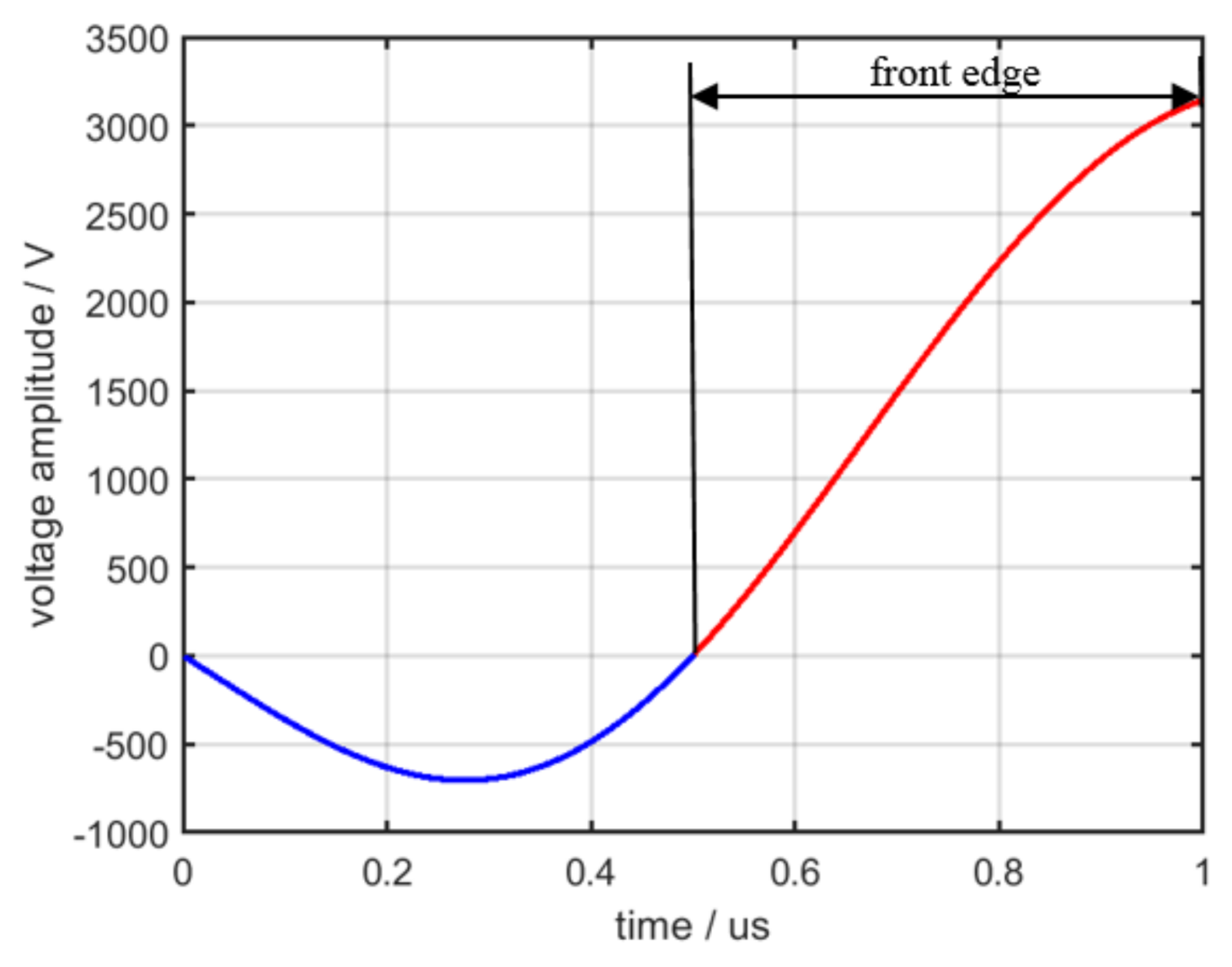
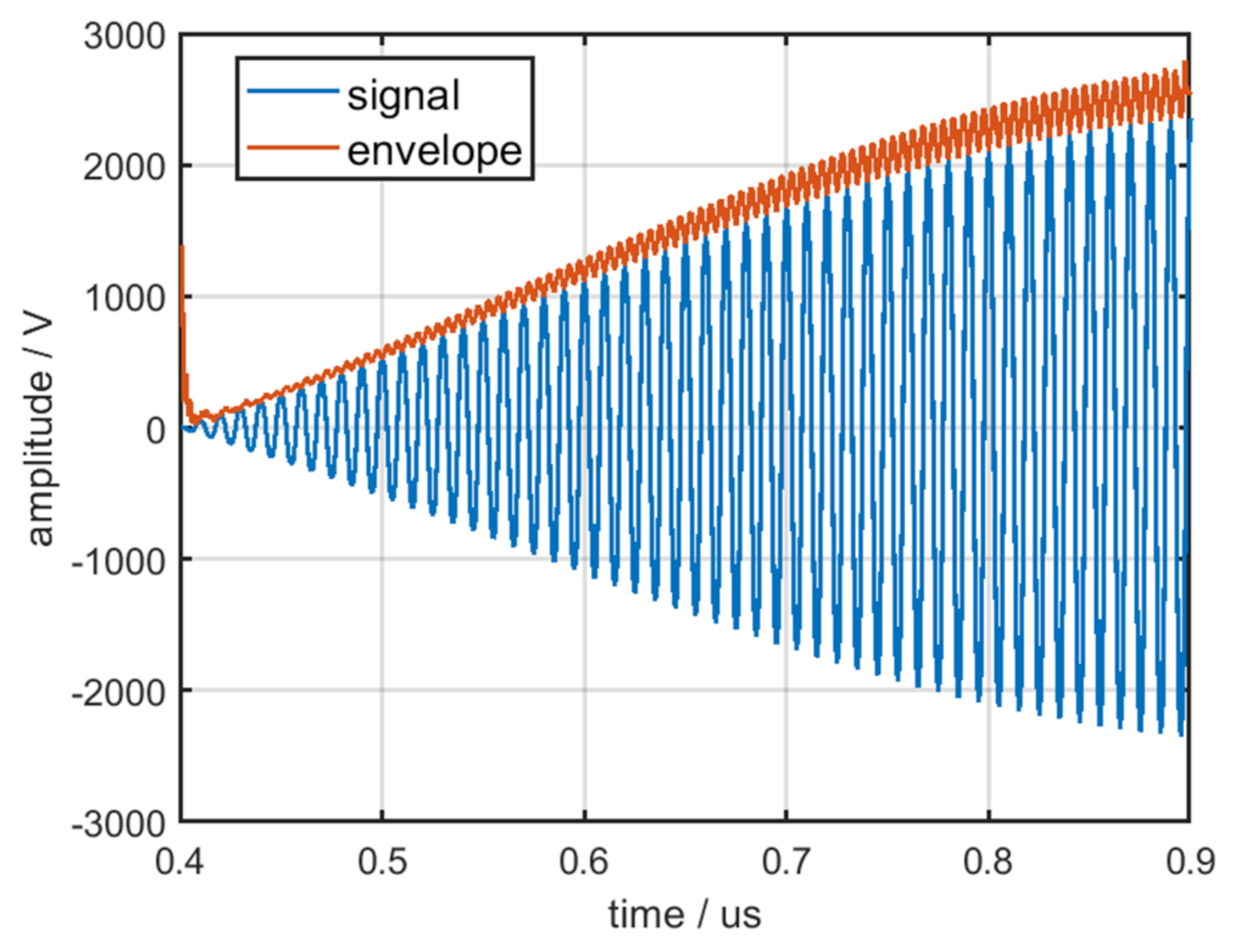
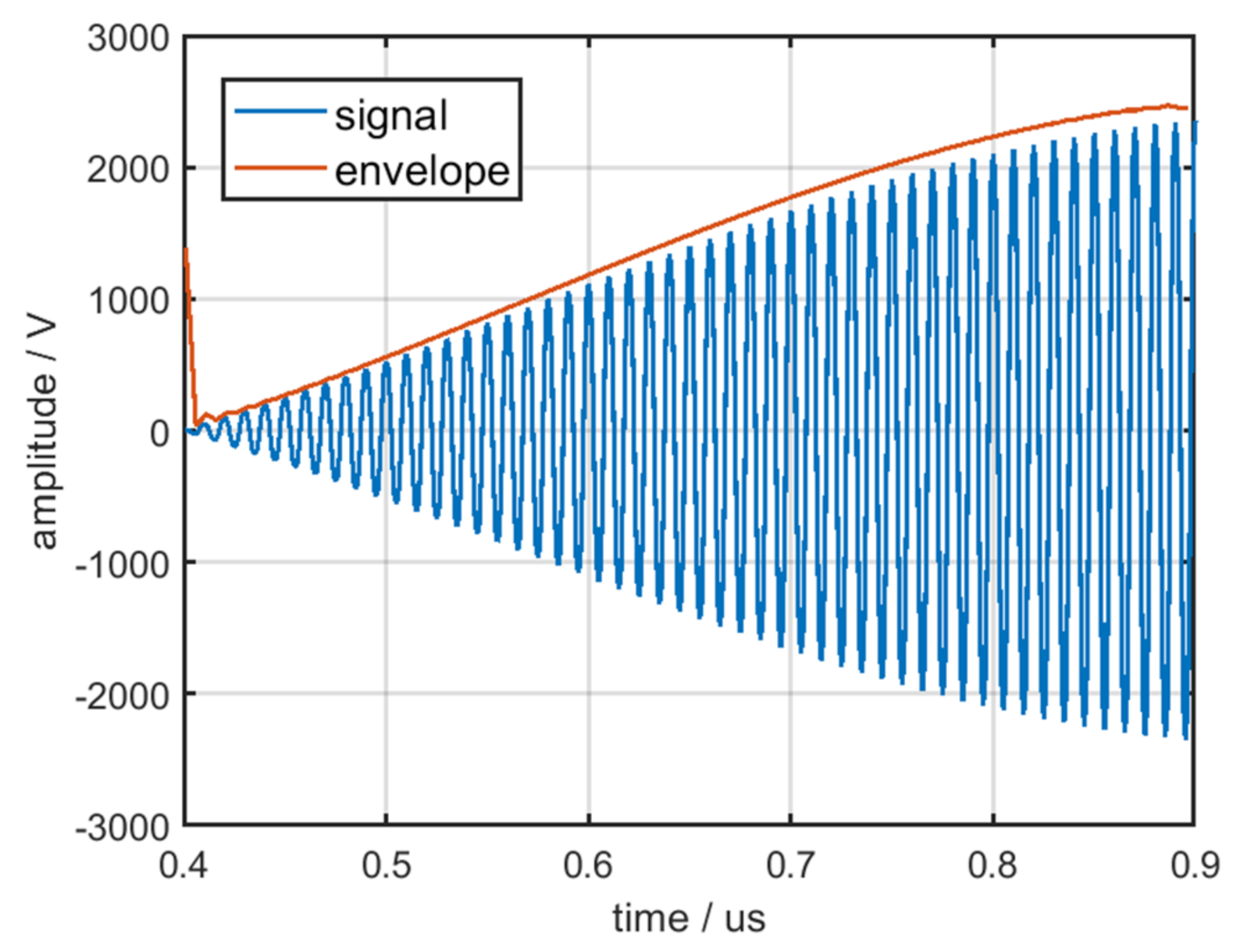
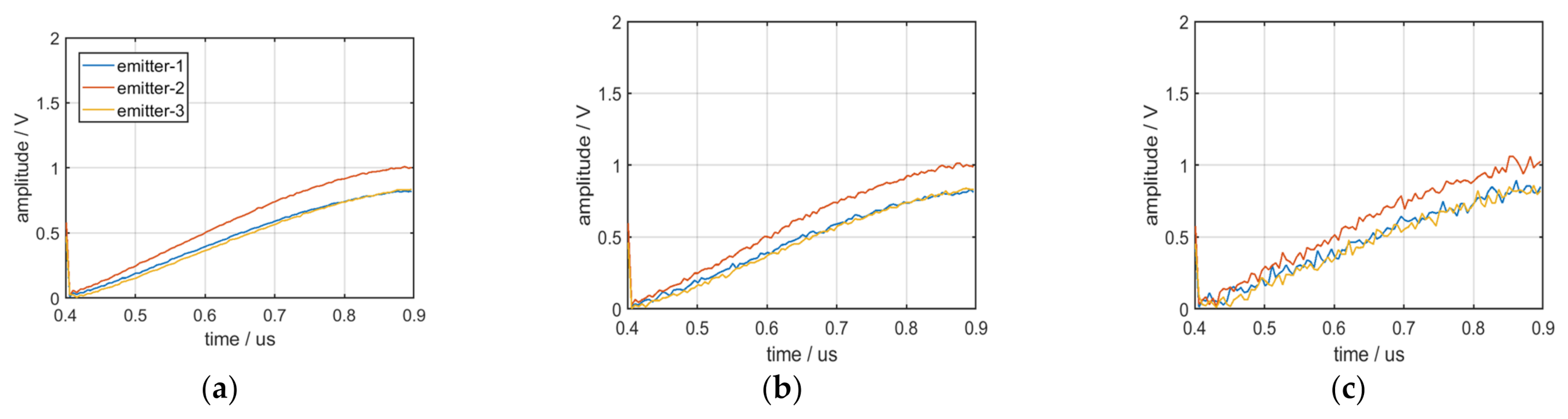
3.3. Analysis and Extraction of the Envelope Characteristic of the Pulse Front Edge
- (1)
- The mean curves of envelope characteristics exhibit excellent robustness.
- (2)
- Because of the many dimensions of the mean curves of the envelope characteristics, they can be distinguished by some algorithms when the number of emitters is large.
4. Analysis of the Simulation Experiment
4.1. Experimental Design
4.2. Experiment Result
5. Conclusions
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Wang, L. On Methods for Specific Radar Emitter Identification; Xidian University: Xi’an, China, 2016. [Google Scholar]
- Zhang, G. Research on Emitter Identification; National University of Defense Technology: Changsha, China, 2005. [Google Scholar]
- Yang, F. The Feature Extraction of Rader Source and Rader Individual Identification; Xidian University: Xi’an, China, 2017. [Google Scholar]
- Wan, T.; Fu, X.; Jiang, K.; Zhao, Y.; Tang, B. Radar Antenna Scan Pattern Intelligent Recognition Using Visibility Graph. IEEE Access 2019, 7, 175628–175641. [Google Scholar] [CrossRef]
- Guo, Q.; Yu, X.; Ruan, G. LPI Radar Waveform Recognition Based on Deep Convolutional Neural Network Transfer Learning. Symmetry 2019, 11, 540. [Google Scholar] [CrossRef] [Green Version]
- Ma, Z.; Huang, Z.; Lin, A.; Huang, G. LPI Radar Waveform Recognition Based on Features from Multiple Images. Sensors 2020, 20, 526. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Qu, Z.; Hou, C.; Hou, C.; Wang, W. Radar Signal Intra-Pulse Modulation Recognition Based on Convolutional Neural Network and Deep Q-Learning Network. IEEE Access 2020, 8, 49125–49136. [Google Scholar] [CrossRef]
- Gao, J.; Shen, L.; Gao, L. Modulation recognition for radar emitter signals based on convolutional neural network and fusion features. Trans. Emerg. Telecommun. Technol. 2019, 30, 12. [Google Scholar] [CrossRef]
- Barshan, B.; Eravci, B. Automatic Radar Antenna Scan Type Recognition in Electronic Warfare. IEEE Trans. Aerosp. Electron. Syst. 2012, 48, 4. [Google Scholar] [CrossRef]
- Liu, Y.; Tian, X.; Li, X. A Real-time Intra-pulse Recognition Method of Radar Signals Based on Restricted Boltzmann Machines. J. Phys. Conf. Series. 2019, 1237, 022064. [Google Scholar] [CrossRef]
- Wang, H.; Zhang, T.; Meng, F. Specific Emitter Identification Based on Time-Frequency Domain Characteristic. J. Inf. Eng. Univ. 2018, 19, 24–29. [Google Scholar]
- Hongwei, W.; Guoqing, Z.; Yujun, W. A specific emitter identification method based on front edge waveform of radar signal envelop. Aerosp. Electron. Warf. 2009, 25, 35–38. [Google Scholar]
- Yuan, Y.; Huang, Z.; Wu, H.; Wang, X. Specific emitter identification based on Hilbert–Huang transform-based time–frequency–energy distribution features. IET Commun. 2020, 8, 2404–2412. [Google Scholar] [CrossRef]
- Dan, X. Research on Mechanism and Methodology of Specific Emitter Identification. Ph.D. Thesis, National University of Defense Technology, Changsha, China, 2008. [Google Scholar]
- Zhang, L. Research on Technology of Specific Radar Emitter Identification Based on Deep Learning; Xidian University: Xi’an, China, 2020. [Google Scholar]
- Man, P.; Ding, C.; Ren, W.; Xu, G. A Nonlinear Fingerprint-Level Radar Simulation Modeling Method for Specific Emitter Identification. Electronics 2021, 10, 1030. [Google Scholar] [CrossRef]
- Levanon, N. Radar Principles; Christian Wolff: New York, NY, USA, 1988. [Google Scholar]
- Gok, G.; Alp, Y.K.; Arikan, O. A New Method for Specific Emitter Identification with Results on Real Radar Measurements. IEEE Trans. Inf. Forensics Secur. 2020, 15, 3335–3346. [Google Scholar] [CrossRef]
- Shin, J.; Shin, H. A 1.9–3.8 GHz ΔΣ Fractional-N PLL Frequency Synthesizer with Fast Auto-Calibration of Loop Bandwidth and VCO Frequency. IEEE J. Solid-State Circuits 2012, 47, 665–675. [Google Scholar] [CrossRef]
- Zhou, H.; Nicholls, C.; Kunz, T.; Schwartz, H. Frequency Accuracy & Stability Dependencies of Crystal Oscillators; Systems and Computer Engineering, Technical Report SCE; Carleton University: Ottawa, ON, Canada, 2008; Volume 8. [Google Scholar]
- Zhao, Y.; Li, Z.; Zhou, W.; Wu, H.; Bai, L.; Miao, M. Research on aging and frequency stability of crystal oscillator. J. Time Freq. 2018, 41, 267–275. [Google Scholar]
- Nussbaumer, H.J. The fast Fourier transform. In Fast Fourier Transform and Convolution Algorithms; Springer: Berlin/Heidelberg, Germany, 1981; pp. 80–111. [Google Scholar]
- Raab, F.H.; Asbeck, P.; Cripps, S.; Kenington, P.B.; Popovic, Z.B.; Pothecary, N.; Sevic, J.F.; Sokal, N.O. RF and microwave power amplifier and transmitter technologies-Part 1. High Freq. Electron. 2003, 2, 22–36. [Google Scholar]
- Zhang, J.; Wang, F.; Dobre, O.A.; Zhong, Z. Specific emitter identification via Hilbert–Huang transform in single-hop and relaying scenarios. IEEE Trans. Inf. Forensics Secur. 2016, 112, 1192–1205. [Google Scholar] [CrossRef]
- Setlur, P.; Amin, M.; Ahmad, F. Multipath model and exploitation in through-the-wall and urban radar sensing. IEEE Trans. Geosci. Remote Sens. 2011, 49, 4021–4034. [Google Scholar] [CrossRef]
- Scheer, J.; Holm, W.A. Principles of Modern Radar; Scitech Publishing: Raleigh, NC, USA, 2010. [Google Scholar]
- Kschischang, F.R. The Hilbert Transform; University of Toronto: Toronto, ON, Canada, 2006; Volume 83, p. 277. [Google Scholar]

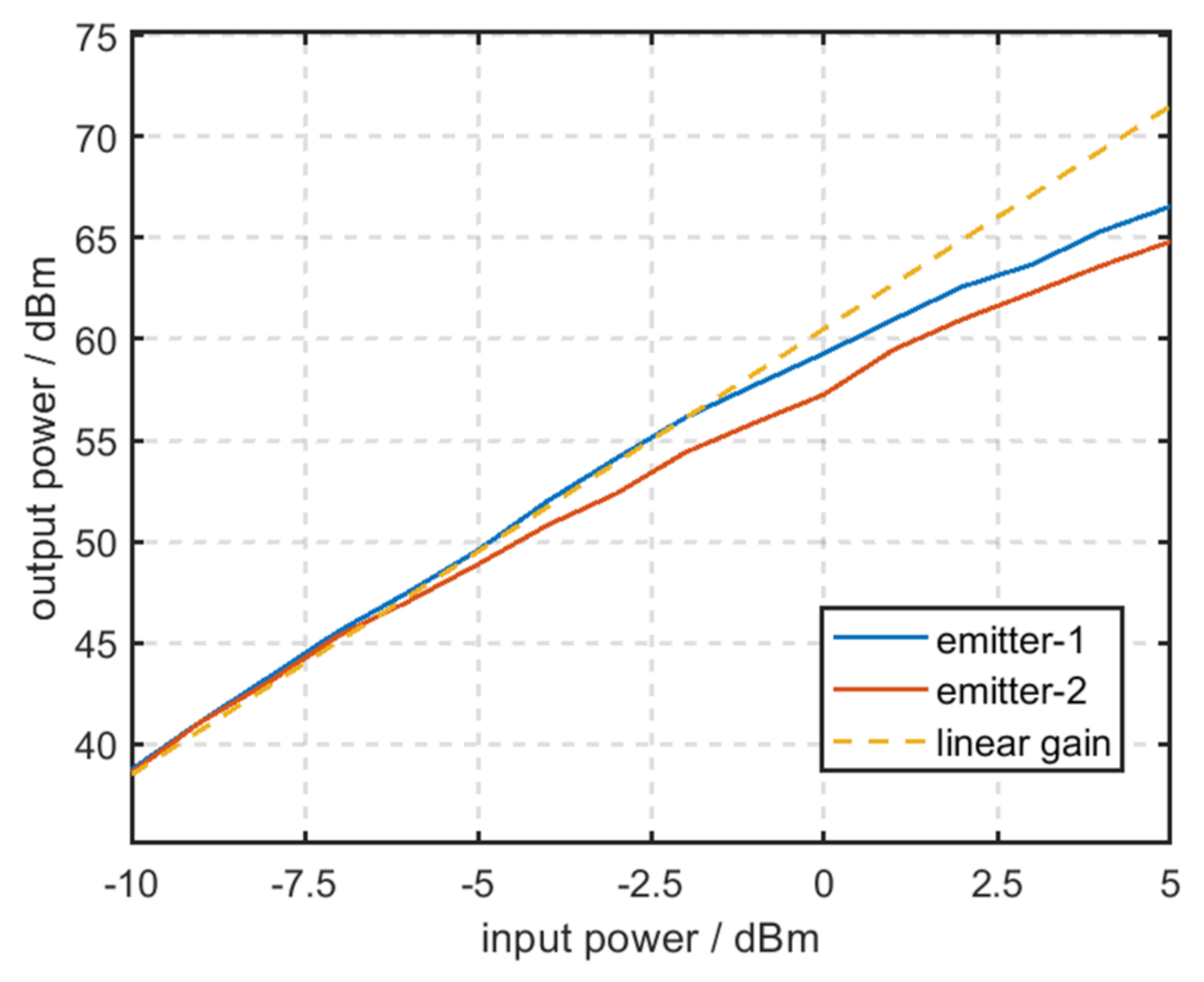
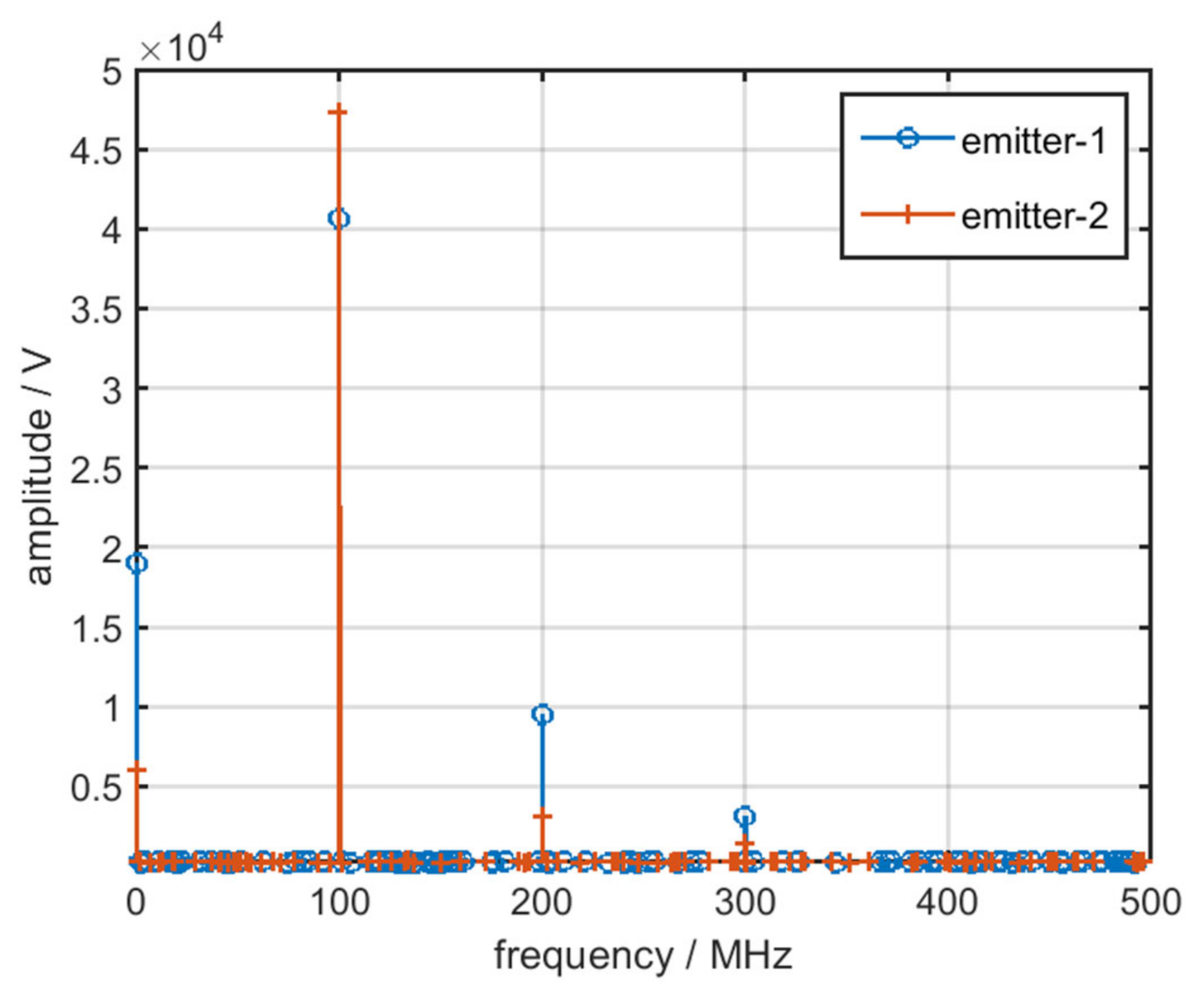
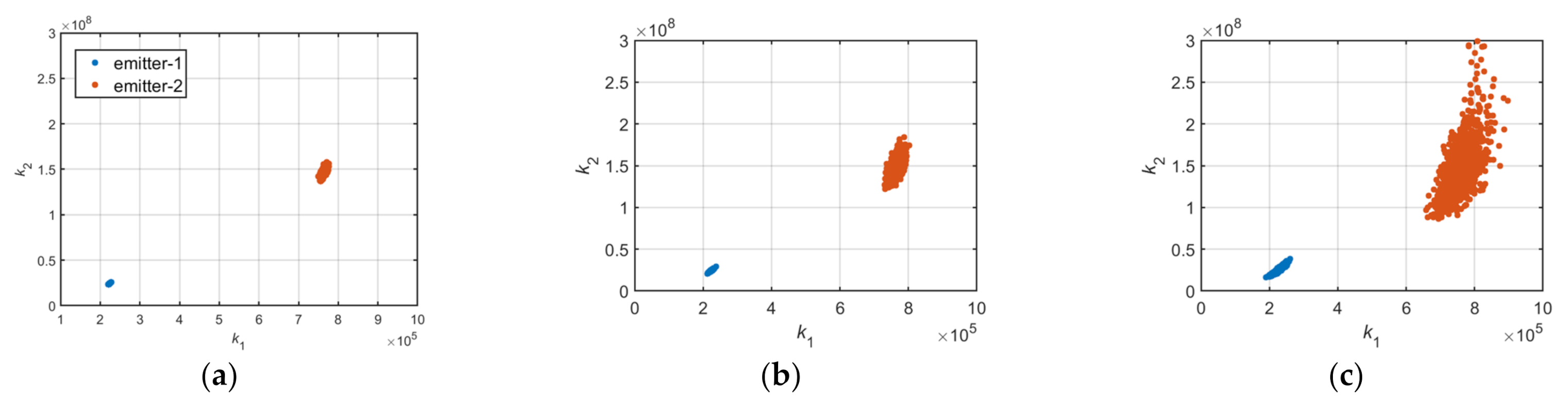
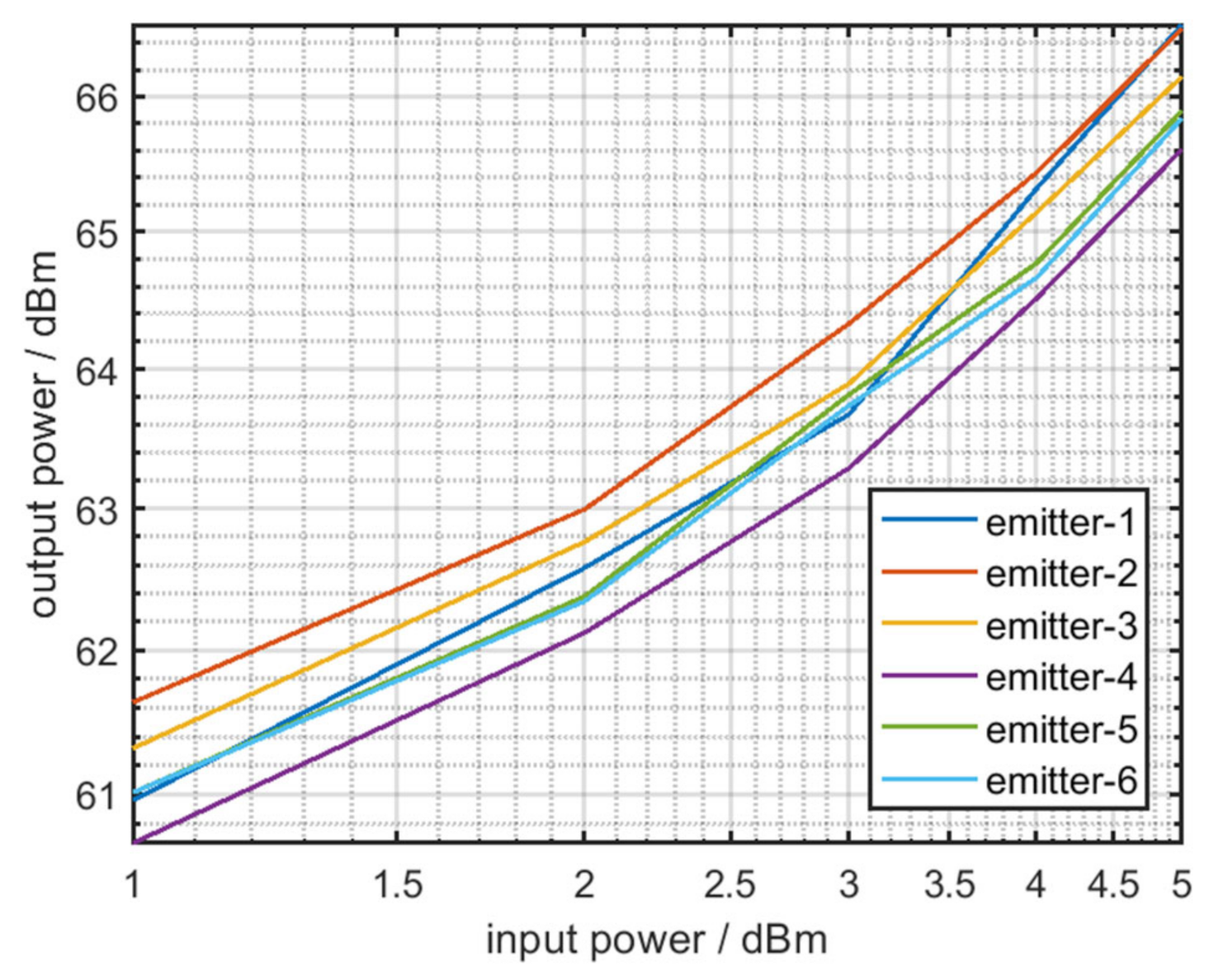






| Type | Serial Number | Nominal Frequency | Frequency Stability | Acceptable Value |
|---|---|---|---|---|
| KOS14D | 29 | 100.000 MHz | 0.034 ppm | 0.1 ppm |
| KOS14D | 31 | 100.000 MHz | 0.024 ppm | 0.1 ppm |
| KOS14D | 33 | 100.000 MHz | 0.030 ppm | 0.1 ppm |
| TCXO14 | 14 | 20.000 MHz | 0.39 ppm | 1 ppm |
| TCXO14 | 23 | 20.000 MHz | 0.54 ppm | 1 ppm |
| TCXO14 | 37 | 20.000 MHz | 0.42 ppm | 1 ppm |
| Emitter | Frequency Stabilization/ppm | Equivalent Circuit Parameters of Pulse Modulator | Nonlinear Coefficient of RF Amplifier Chain | ||||||
|---|---|---|---|---|---|---|---|---|---|
| /v | /Ω | /Ω | |||||||
| 1 | 0.034 | 12,000 | 50 | 10,000 | 100 | 900 | 1.00 | 0.38 | −0.25 |
| 2 | 0.024 | 12,050 | 50 | 10,000 | 95 | 920 | 1.03 | 0.12 | −0.11 |
| 3 | 0.030 | 12,080 | 50 | 9980 | 105 | 910 | 1.01 | 0.28 | −0.22 |
| 4 | 0.038 | 11,900 | 50 | 10,010 | 102 | 905 | 1.01 | 0.22 | −0.18 |
| 5 | 0.031 | 11,800 | 51 | 9990 | 90 | 890 | 1.01 | 0.30 | −0.20 |
| 6 | 0.025 | 12,100 | 49 | 9970 | 110 | 880 | 1.01 | 0.20 | −0.13 |
| 7 | 0.016 | 11,950 | 50 | 10,000 | 115 | 895 | 1.00 | 0.27 | −0.14 |
| 8 | 0.019 | 12,120 | 50 | 10,000 | 98 | 915 | 0.95 | 0.24 | −0.17 |
| 9 | 0.045 | 12,150 | 50 | 10,005 | 80 | 905 | 1.02 | 0.35 | −0.08 |
| 10 | 0.021 | 11,980 | 51 | 10,000 | 118 | 885 | 0.97 | 0.15 | −0.15 |
| SNR | All Features | Frequency Stabilization | Nonlinear Coefficients | Envelope of Pulse front Edge |
|---|---|---|---|---|
| 10 dB | 92.31% | 51.01% | 91.82% | 84.32% |
| 15 dB | 97.58% | 50.49% | 95.10% | 95.58% |
| 20 dB | 99.55% | 51.03% | 98.99% | 99.35% |
| 25 dB | 99.89% | 50.43% | 99.71% | 99.88% |
| 30 dB | 99.94% | 50.59% | 99.90% | 99.90% |
| SNR | 100 Pulses/Group | 50 Pulses/Group | 20 Pulses/Group | 10 Pulses/Group |
|---|---|---|---|---|
| 10 dB | 92.31% | 93.89% | 89.30% | 81.51% |
| 15 dB | 97.58% | 97.98% | 96.19% | 92.46% |
| 20 dB | 99.55% | 99.74% | 99.29% | 98.25% |
| 25 dB | 99.89% | 99.98% | 99.96% | 99.88% |
| 30 dB | 99.94% | 100.00% | 100.00% | 99.99% |
| SNR | Features Being Extracted + Random Forest | Time-Frequency Graph + LeNet | Envelope + SVM |
|---|---|---|---|
| 10 dB | 81.51% | 64.31% | 48.87% |
| 15 dB | 92.46% | 83.02% | 74.05% |
| 20 dB | 98.25% | 92.59% | 90.98% |
| 25 dB | 99.88% | 97.74% | 98.84% |
| 30 dB | 99.99% | 99.10% | 99.99% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Y.; Li, S.; Lin, X.; Gong, H.; Li, H. Feature Analysis and Extraction for Specific Emitter Identification Based on the Signal Generation Mechanisms of Radar Transmitters. Sensors 2022, 22, 2616. https://doi.org/10.3390/s22072616
Liu Y, Li S, Lin X, Gong H, Li H. Feature Analysis and Extraction for Specific Emitter Identification Based on the Signal Generation Mechanisms of Radar Transmitters. Sensors. 2022; 22(7):2616. https://doi.org/10.3390/s22072616
Chicago/Turabian StyleLiu, Yilin, Shengyong Li, Xiaohong Lin, Hui Gong, and Hongke Li. 2022. "Feature Analysis and Extraction for Specific Emitter Identification Based on the Signal Generation Mechanisms of Radar Transmitters" Sensors 22, no. 7: 2616. https://doi.org/10.3390/s22072616
APA StyleLiu, Y., Li, S., Lin, X., Gong, H., & Li, H. (2022). Feature Analysis and Extraction for Specific Emitter Identification Based on the Signal Generation Mechanisms of Radar Transmitters. Sensors, 22(7), 2616. https://doi.org/10.3390/s22072616





