A Novel Framework for Open-Set Authentication of Internet of Things Using Limited Devices
Abstract
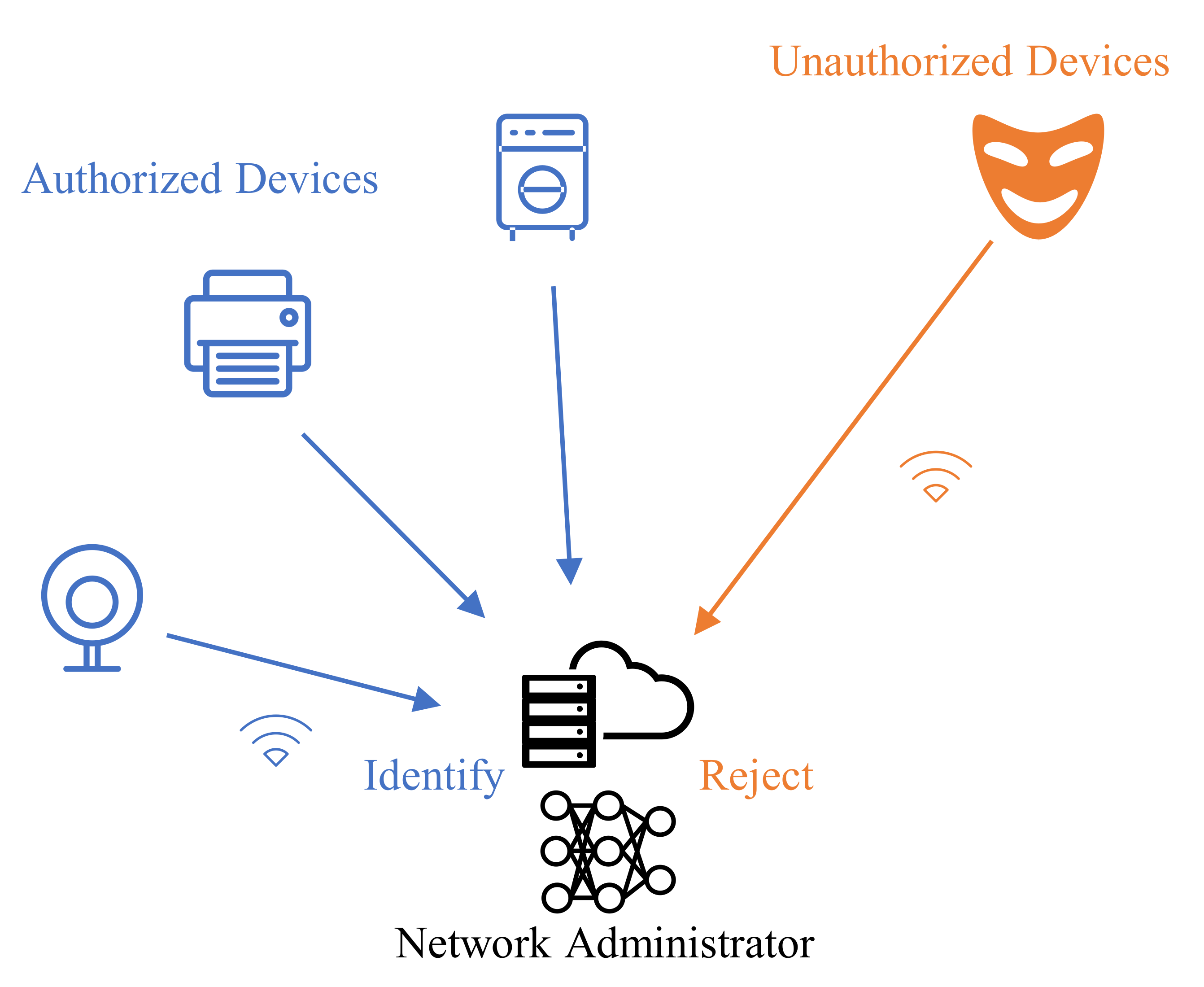
:1. Introduction
- We propose to adopt AAMSoftmax to enhance the discriminability of features that are learned by neural networks, so that the features of unseen devices are distributed away from those of authorized devices;
- We propose a modified OpenMAX method, namely adaptive class-wise OpenMAS, so that it can be combined with AAMSoftmax and unseen IoT devices can be distinguished adaptively based on the features that are learned by neural networks;
- We propose a framework that leverages the strengths of AAMSoftmax and OpenMAX for the open-set authentication of IoT devices. The evaluations of both simulated data and real ADS–B data show that the proposed framework was advantageous for open-set IoT authentication, especially when the number of devices for training was limited.
2. Related Works
2.1. Background
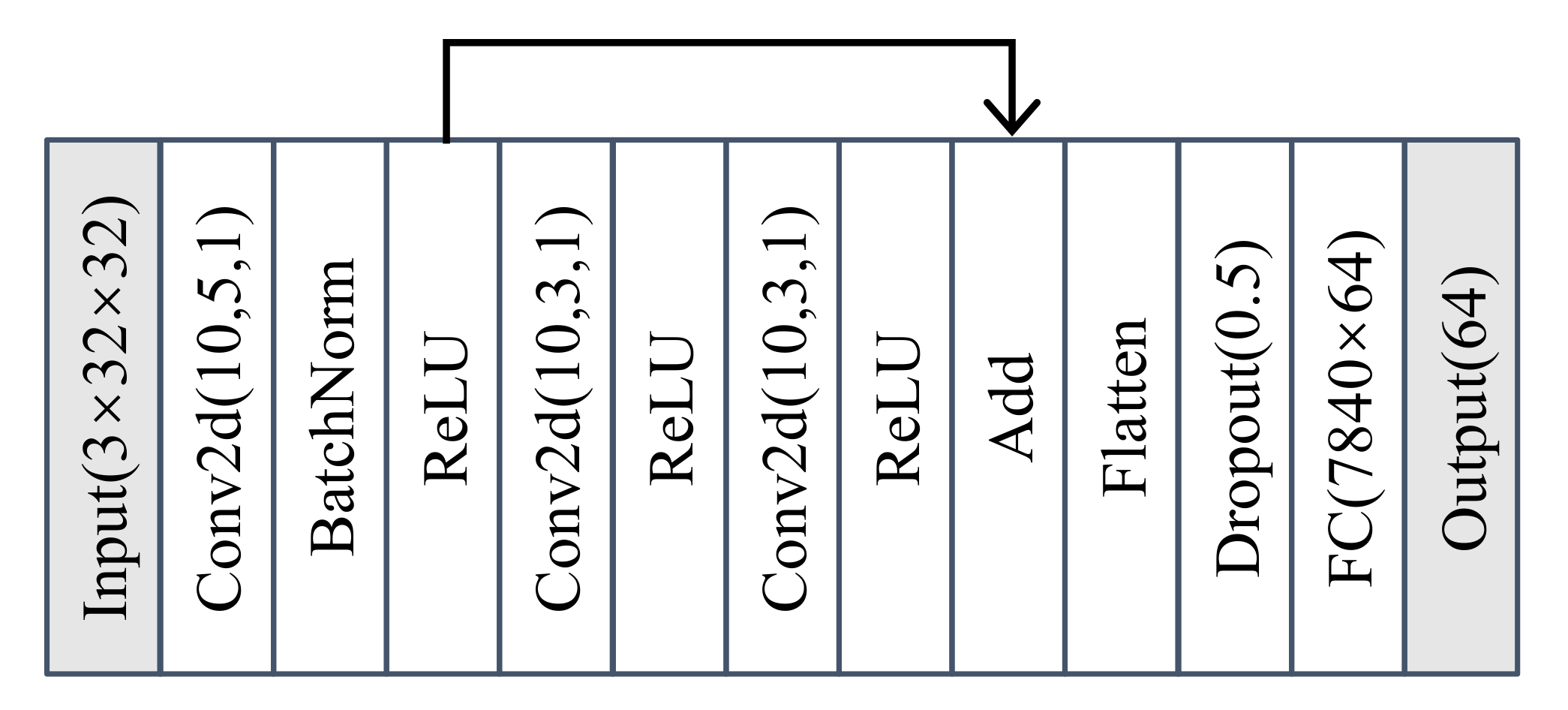
2.2. Feature Extractor
2.3. Open-Set Classifier
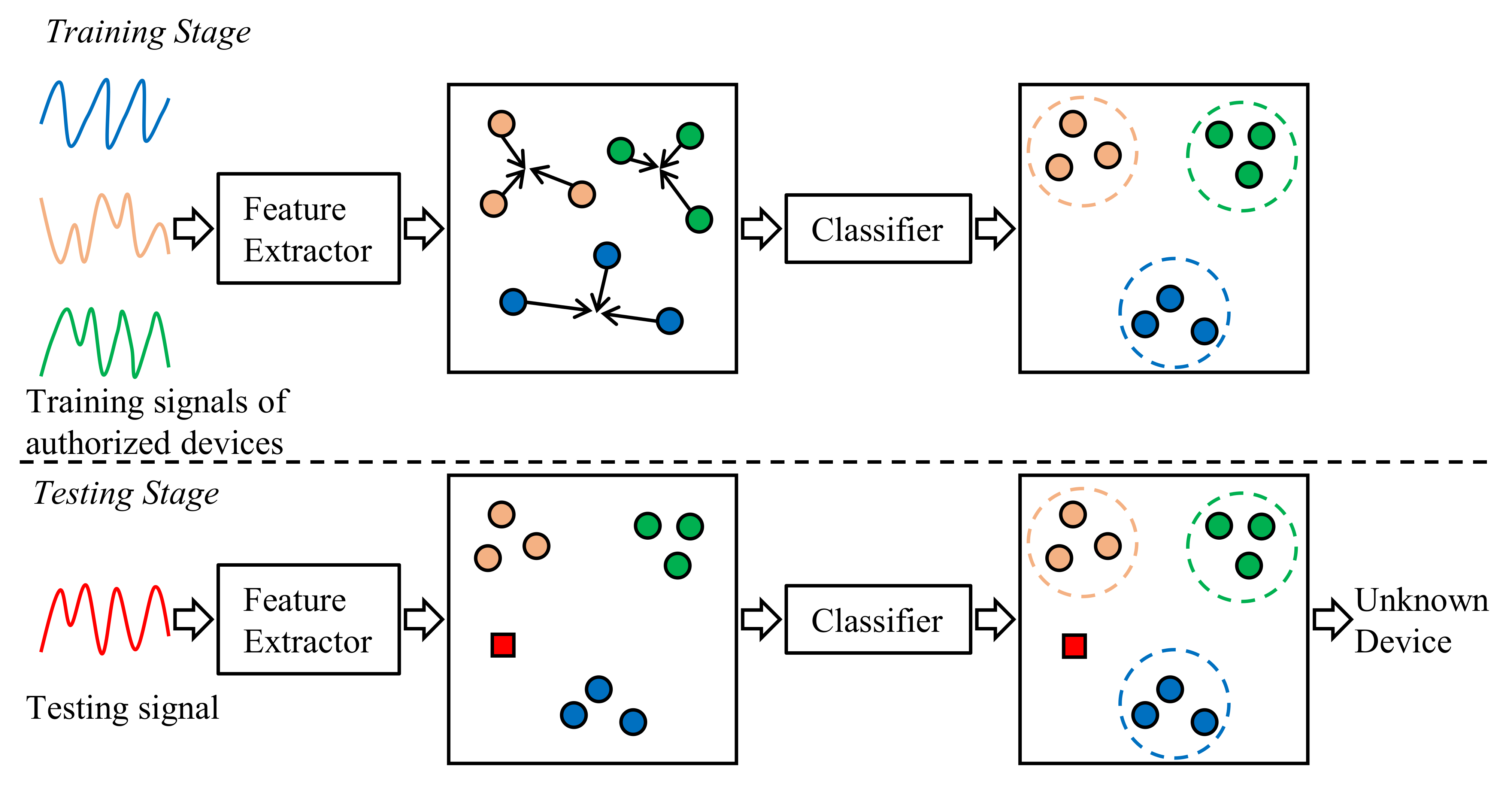
3. Problem Definition
4. Proposed Framework
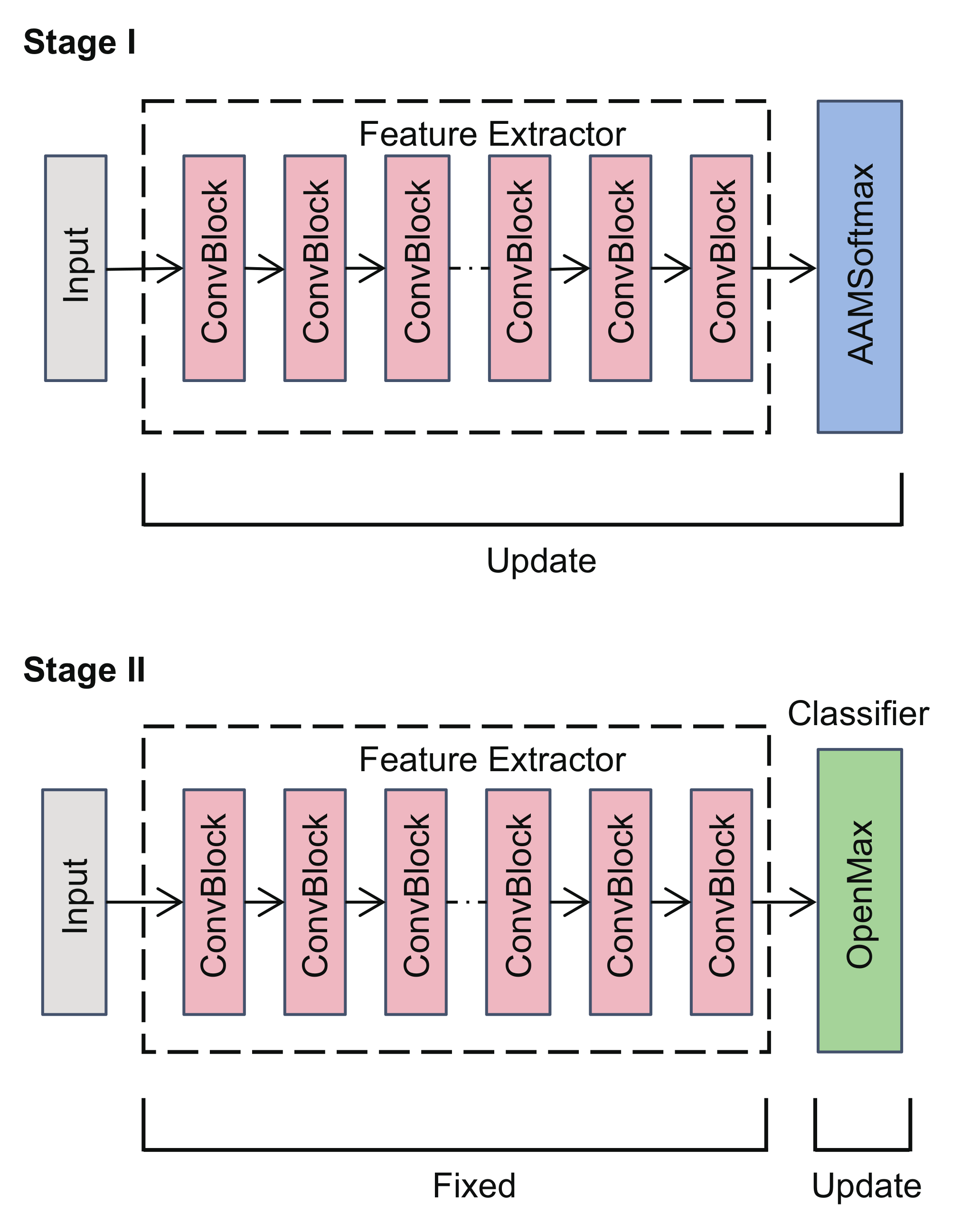
4.1. Feature Extractor with AAMSoftmax
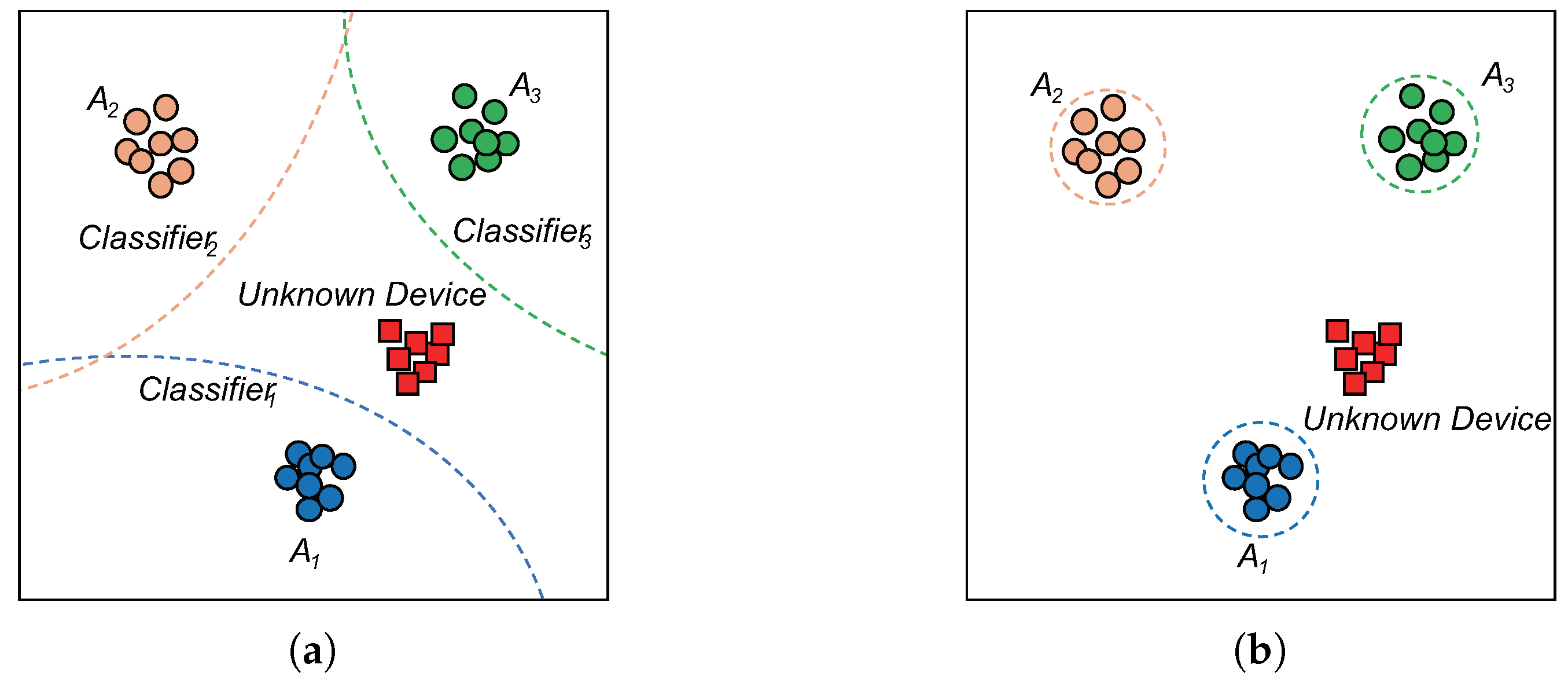
4.2. Classifier of Adaptive Class-Wise OpenMAX
| Algorithm 1 The training algorithm for adaptive class-wise OpenMAX. |
| Input: Set of extracted features and corresponding labels , with classes. |
| Output: mean feature vector of each class , Weibull model of each class . |
| 1: for to do |
| 2: Compute mean vector of class k, ; |
| 3: Find features belonging to class k, |
| ; |
| 4: Fit Weibull model of class k with adaptively chosen tail size , |
| ; |
| 5: end for |
| 6: Return means and models |
| Algorithm 2 The inference algorithm for adaptive class-wise OpenMAX. |
| Input: feature of the test sample. |
| Require: mean feature vector of each class , Weibull model of each class . |
| Output: , the prediction score of the test sample. |
| 1: Compute the closed-set prediction score ; |
| 2: Let , compute the probability the test sample is an outlier of class , ; |
| 3: Revise the prediction score as : |
| , for to and , |
| , |
| ; |
| 4: Return |
5. Performance Evaluation
5.1. Evaluation Dataset
5.1.1. Simulated Dataset
5.1.2. ADS–B Dataset
5.2. Evaluation Using the Simulated Dataset
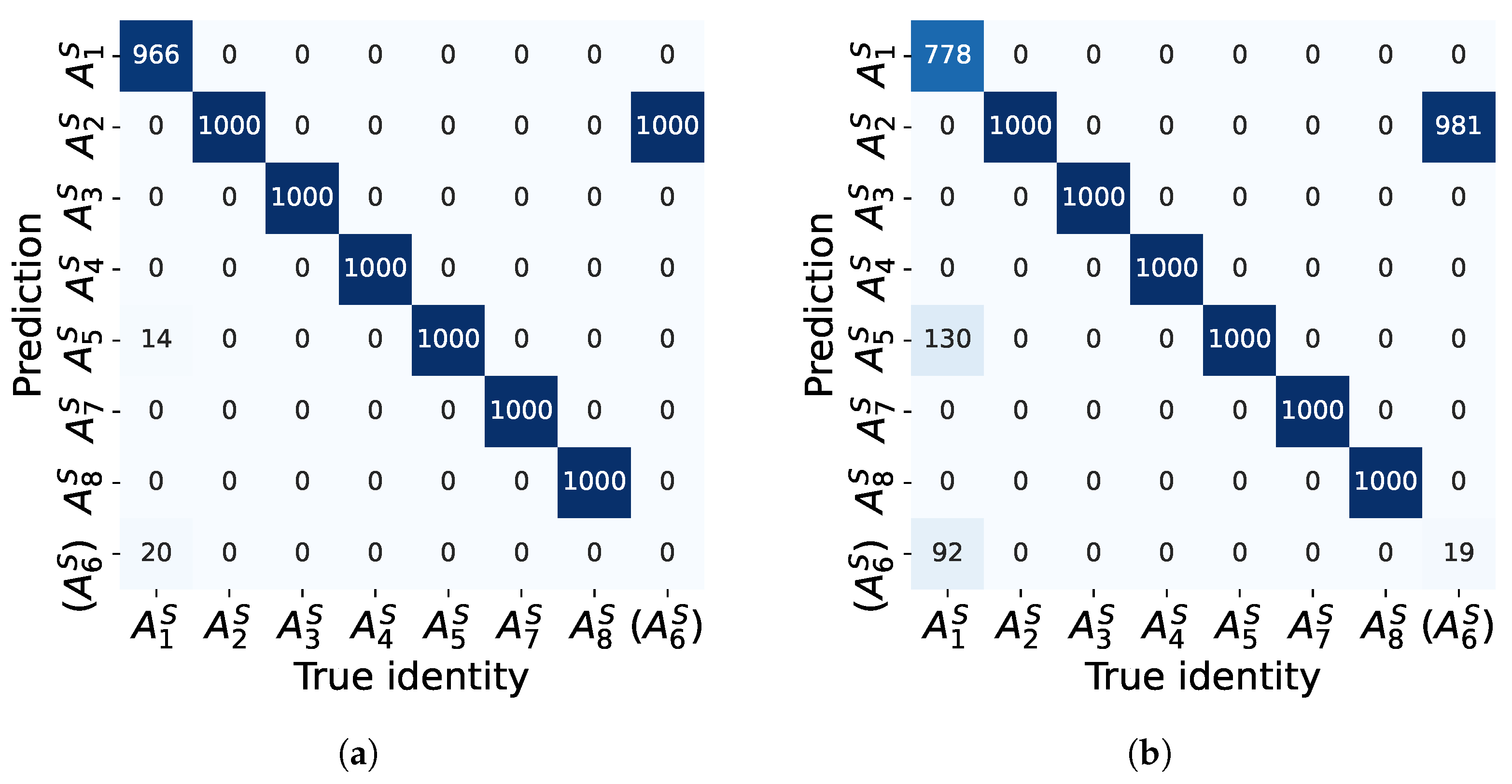
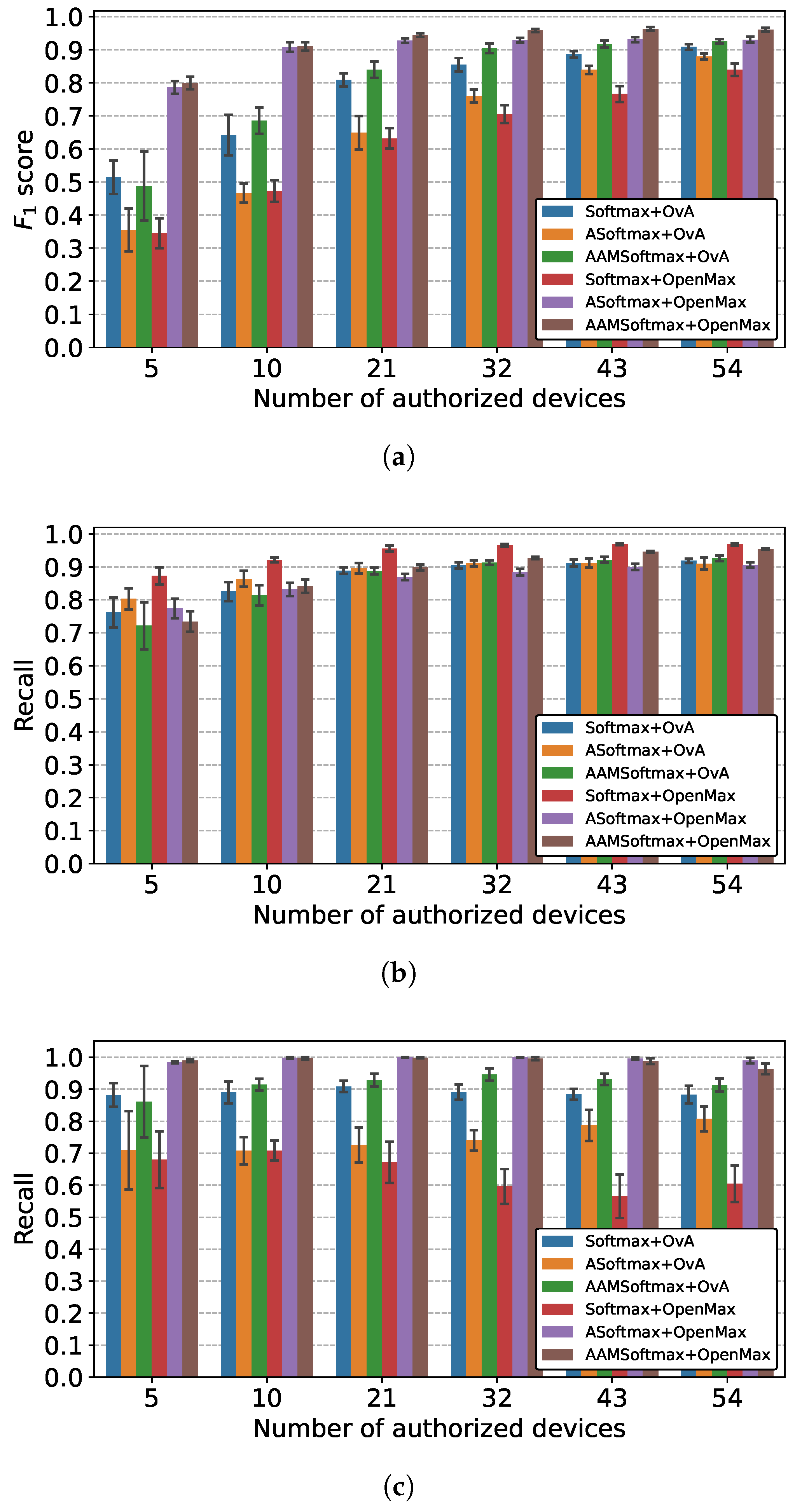
5.2.1. Comparison of Overall Performance
5.2.2. Comparison of Feature Extractors
5.2.3. Comparison of Classifiers
5.2.4. Comparison of Different Combinations
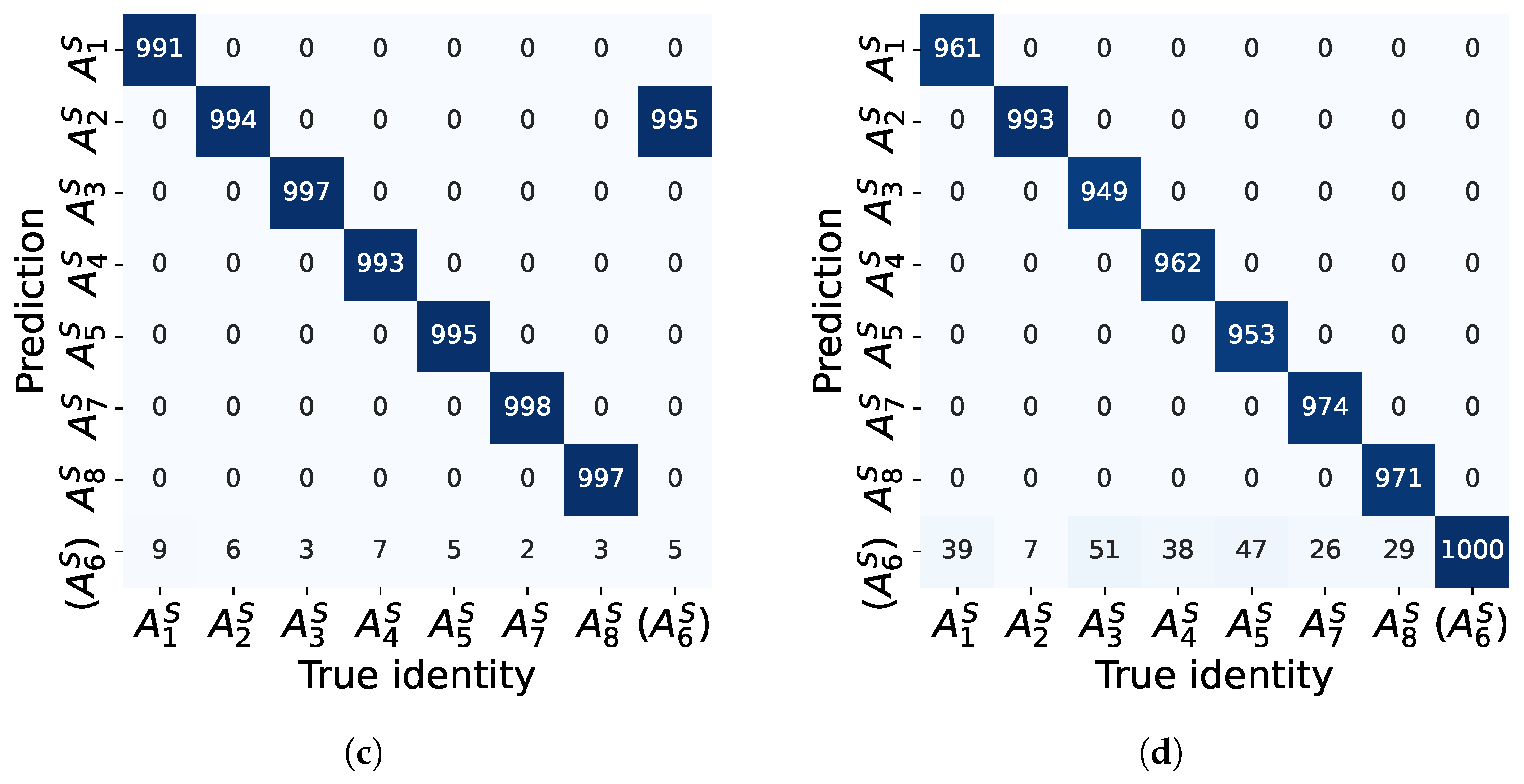
5.3. Evaluation Using the Real ADS–B Dataset
5.3.1. Performance Comparison
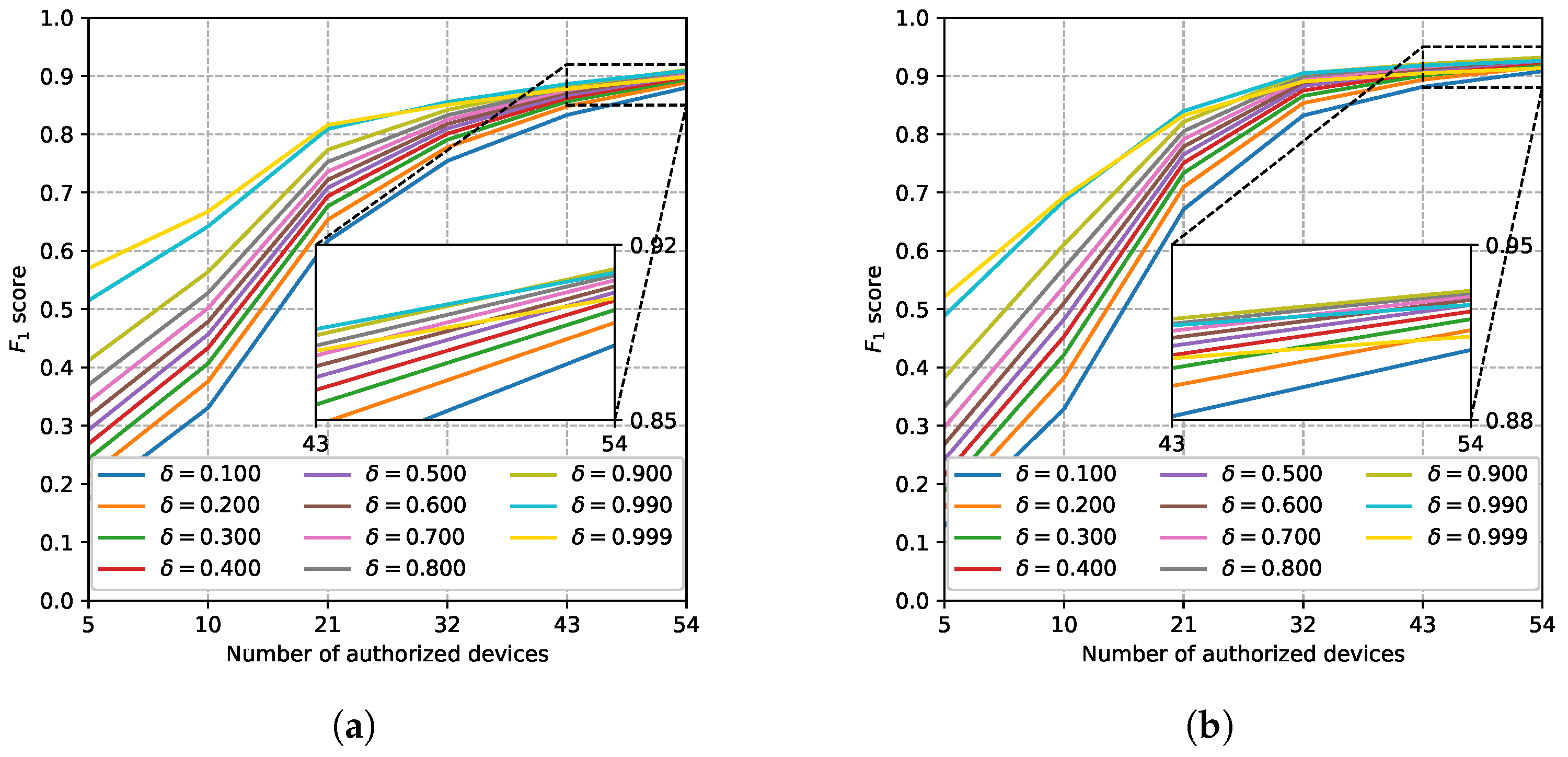
5.3.2. Effects of Hyperparameters
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ismail, B.; Patrik, Ö.; Houbing, S. Security of the Internet of Things: Vulnerabilities, attacks, and countermeasures. IEEE Commun. Surv. Tutor. 2019, 22, 616–644. [Google Scholar]
- Skarmeta, A.F.; Hernandez-Ramos, J.L.; Moreno, M.V. A decentralized approach for security and privacy challenges in the internet of things. In Proceedings of the 2014 IEEE World Forum on Internet of Things (WF-IoT), Seoul, Korea, 6–8 March 2014; IEEE: Piscataway, NJ, USA, 2014; pp. 67–72. [Google Scholar]
- Linda, S.; Marco, B.; Ennio, G. Statistical and machine learning-based decision techniques for physical layer authentication. In Proceedings of the 2019 IEEE Global Communications Conference (GLOBECOM), Waikoloa, HI, USA, 9–13 December 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 1–6. [Google Scholar]
- Yongxin, L.; Jian, W.; Jianqiang, L.; Shuteng, N.; Houbing, S. Machine learning for the detection and identification of internet of things (iot) devices: A survey. arXiv 2021, arXiv:2101.10181. [Google Scholar]
- Hansen, J.H.; Hasan, T. Speaker recognition by machines and humans: A tutorial review. IEEE Signal Process. Mag. 2015, 32, 74–99. [Google Scholar] [CrossRef]
- Vladimir, B.; Suman, B.; Marco, G.; Sangho, O. Wireless device identification with radiometric signatures. In Proceedings of the 14th ACM International Conference on Mobile Computing and Networking, San Francisco, CA, USA, 14–19 September 2008; pp. 116–127. [Google Scholar]
- Zhang, J.; Wang, F.; Dobre, O.A.; Zhong, Z. Specific emitter identification via Hilbert–Huang transform in single-hop and relaying scenarios. IEEE Trans. Inf. Forensics Secur. 2016, 11, 1192–1205. [Google Scholar] [CrossRef]
- Udit, S.; Nikita, T.; Gagarin, B.; Barathram, R. Specific emitter identification based on variational mode decomposition and spectral features in single hop and relaying scenarios. IEEE Trans. Inf. Forensics Secur. 2018, 14, 581–591. [Google Scholar]
- Jie, H.; Tao, Z.; Zhaoyang, Q.; Xiaoyu, Z. Communication emitter individual identification via 3D-Hilbert energy spectrum-based multiscale segmentation features. Int. J. Commun. Syst. 2019, 32, e3833. [Google Scholar]
- Dongfang, R.; Tao, Z. Specific emitter identification based on intrinsic time-scale-decomposition and image texture feature. In Proceedings of the 2017 IEEE 9th International Conference on Communication Software and Networks (ICCSN), Guangzhou, China, 6–8 May 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 1302–1307. [Google Scholar]
- Guangquan, H.; Yingjun, Y.; Xiang, W.; Zhitao, H. Specific emitter identification for communications transmitter using multi-measurements. Wirel. Pers. Commun. 2017, 94, 1523–1542. [Google Scholar]
- Yongqiang, J.; Shengli, Z.; Lu, G. Specific emitter identification based on the natural measure. Entropy 2017, 19, 117. [Google Scholar]
- Kevin, M.; Shauna, R.; George, S.; Bryan, N. Deep learning for RF device fingerprinting in cognitive communication networks. IEEE J. Sel. Top. Signal Process. 2018, 12, 160–167. [Google Scholar]
- Riyaz, S.; Sankhe, K.; Ioannidis, S.; Chowdhury, K. Deep learning convolutional neural networks for radio identification. IEEE Commun. Mag. 2018, 56, 146–152. [Google Scholar] [CrossRef]
- McGinthy, J.M.; Wong, L.J.; Michaels, A.J. Groundwork for neural network-based specific emitter identification authentication for IoT. IEEE Internet Things J. 2019, 6, 6429–6440. [Google Scholar] [CrossRef]
- Jiabao, Y.; Aiqun, H.; Guyue, L.; Linning, P. A robust RF fingerprinting approach using multisampling convolutional neural network. IEEE Internet Things J. 2019, 6, 6786–6799. [Google Scholar]
- Tong, J.; Costa, R.B.; Emmanuel, O.; Nasim, S.; Zifeng, W.; Kunal, S.; Andrey, G.; Jennifer, D.; Kaushik, C.; Stratis, I. Deep learning for RF fingerprinting: A massive experimental study. IEEE Internet Things Mag. 2020, 3, 50–57. [Google Scholar]
- Guanxiong, S.; Junqing, Z.; Alan, M.; Linning, P.; Xianbin, W. Radio Frequency Fingerprint Identification for LoRa Using Deep Learning. IEEE J. Sel. Areas Commun. 2021, 39, 2604–2616. [Google Scholar]
- Debashri, R.; Tathagata, M.; Mainak, C.; Erik, B.; Eduardo, P. Rfal: Adversarial learning for rf transmitter identification and classification. IEEE Trans. Cogn. Commun. Netw. 2019, 6, 783–801. [Google Scholar]
- Yongxin, L.; Jian, W.; Jianqiang, L.; Houbing, S.; Thomas, Y.; Shuteng, N.; Zhong, M. Zero-bias deep learning for accurate identification of Internet-of-Things (IoT) devices. IEEE Internet Things J. 2020, 8, 2627–2634. [Google Scholar]
- Andrey, G.; Zifeng, W.; Tong, J.; Jennifer, D.; Kaushik, C.; Stratis, I. Finding a ‘new’ needle in the haystack: Unseen radio detection in large populations using deep learning. In Proceedings of the 2019 IEEE International Symposium on Dynamic Spectrum Access Networks (DySPAN), Newark, NJ, USA, 11–14 November 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 1–10. [Google Scholar]
- Samer, H.; Samurdhi, K.; Danijela, C. Open set wireless transmitter authorization: Deep learning approaches and dataset considerations. IEEE Trans. Cogn. Commun. Netw. 2020, 7, 59–72. [Google Scholar]
- Renjie, X.; Wei, X.; Yanzhi, C.; Jiabao, Y.; Aiqun, H.; Kwan, N.D.W.; Lee, S.A. A Generalizable Model-and-Data Driven Approach for Open-Set RFF Authentication. IEEE Trans. Inf. Forensics Secur. 2021, 16, 4435–4450. [Google Scholar]
- Jiankang, D.; Jia, G.; Niannan, X.; Stefanos, Z. Arcface: Additive angular margin loss for deep face recognition. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 4690–4699. [Google Scholar]
- Bendale, A.; Boult, T.E. Towards open set deep networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 26 June–1 July 2016; pp. 1563–1572. [Google Scholar]
- Yandong, W.; Kaipeng, Z.; Zhifeng, L.; Yu, Q. A discriminative feature learning approach for deep face recognition. In Proceedings of the European Conference on Computer Vision, Amsterdam, The Netherlands, 8–16 October 2016; Springer: Berlin/Heidelberg, Germany, 2016; pp. 499–515. [Google Scholar]
- Zhongxin, B.; Xiao-Lei, Z. Speaker recognition based on deep learning: An overview. Neural Netw. 2021, 140, 65–99. [Google Scholar]
- Yuheng, W.; Junzhao, D.; Hui, L. Angular Margin Centroid Loss for Text-Independent Speaker Recognition. In Proceedings of the INTERSPEECH, Shanghai, China, 25–29 October 2020; pp. 3820–3824. [Google Scholar]
- Boxiang, H.; Fanggang, W. Cooperative Specific Emitter Identification via Multiple Distorted Receivers. IEEE Trans. Inf. Forensics Secur. 2020, 15, 3791–3806. [Google Scholar]
- Yongxin, L.; Jian, W.; Jianqiang, L.; Shuteng, N.; Houbing, S. Class-Incremental Learning for Wireless Device Identification in IoT. IEEE Internet Things J. 2021, 8, 17227–17235. [Google Scholar]
- Kaiming, H.; Xiangyu, Z.; Shaoqing, R.; Jian, S. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 26 June–1 July 2016; pp. 770–778. [Google Scholar]
- Juri, O.; Sebastian, B. Macro f1 and macro f1. arXiv 2019, arXiv:1911.03347. [Google Scholar]
- Van der Maaten, L.; Hinton, G. Visualizing data using t-SNE. J. Mach. Learn. Res. 2008, 9, 2579–2605. [Google Scholar]
- Sáez, T.D.; Li, M.; Margaret, H. Face recognition: From traditional to deep learning methods. arXiv 2018, arXiv:1811.00116. [Google Scholar]
- Restuccia, F.; D’Oro, S.; Al-Shawabka, A.; Belgiovine, M.; Angioloni, L.; Ioannidis, S.; Chowdhury, K.; Melodia, T. DeepRadioID: Real-time channel-resilient optimization of deep learning-based radio fingerprinting algorithms. In Proceedings of the Twentieth ACM International Symposium on Mobile Ad Hoc Networking and Computing, Catania, Italy, 2–5 July 2019; pp. 51–60. [Google Scholar]




| (Loss Function of) Feature Extractor | Classifier | |
|---|---|---|
| [19] | GAN | GAN |
| [20,23] | Angular Softmax | Distance-Based |
| [22] | Softmax | Disc, DClass, OvA, OpenMAX, Autoencoder |
| Our work | Additive Angular Margin Softmax | Adaptive Class-Wise OpenMAX |
| Devices | ||||||||
|---|---|---|---|---|---|---|---|---|
| G | 0.9608 | 1.0408 | 0.9608 | 1.0408 | 0.9802 | 1.0202 | 0.9608 | 1.0408 |
| 1 | 1 |
| Unknown Device | ||||||||
|---|---|---|---|---|---|---|---|---|
| Softmax + OvA | 0.8333 | 0.8333 | 0.8369 | 0.8552 | 0.7376 | 0.8303 | 0.8333 | 0.8331 |
| AAMSoftmax + OvA | 0.7842 | 0.8333 | 0.8438 | 0.9391 | 0.8315 | 0.8149 | 0.8326 | 0.8331 |
| Softmax + OpenMAX | 0.8766 | 0.7308 | 0.9628 | 0.9637 | 0.6010 | 0.8328 | 0.9451 | 0.9741 |
| AAMSoftmax + OpenMAX | 0.9695 | 0.9629 | 0.9688 | 0.9623 | 0.9654 | 0.9716 | 0.9658 | 0.9679 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, K.; Yang, J.; Hu, P.; Liu, H. A Novel Framework for Open-Set Authentication of Internet of Things Using Limited Devices. Sensors 2022, 22, 2662. https://doi.org/10.3390/s22072662
Huang K, Yang J, Hu P, Liu H. A Novel Framework for Open-Set Authentication of Internet of Things Using Limited Devices. Sensors. 2022; 22(7):2662. https://doi.org/10.3390/s22072662
Chicago/Turabian StyleHuang, Keju, Junan Yang, Pengjiang Hu, and Hui Liu. 2022. "A Novel Framework for Open-Set Authentication of Internet of Things Using Limited Devices" Sensors 22, no. 7: 2662. https://doi.org/10.3390/s22072662
APA StyleHuang, K., Yang, J., Hu, P., & Liu, H. (2022). A Novel Framework for Open-Set Authentication of Internet of Things Using Limited Devices. Sensors, 22(7), 2662. https://doi.org/10.3390/s22072662






