Robust Quantum State Tomography Method for Quantum Sensing
Abstract
:1. Introduction
2. Methods
- symmetric GGM
- antisymmetric GGM
- diagonal GGM
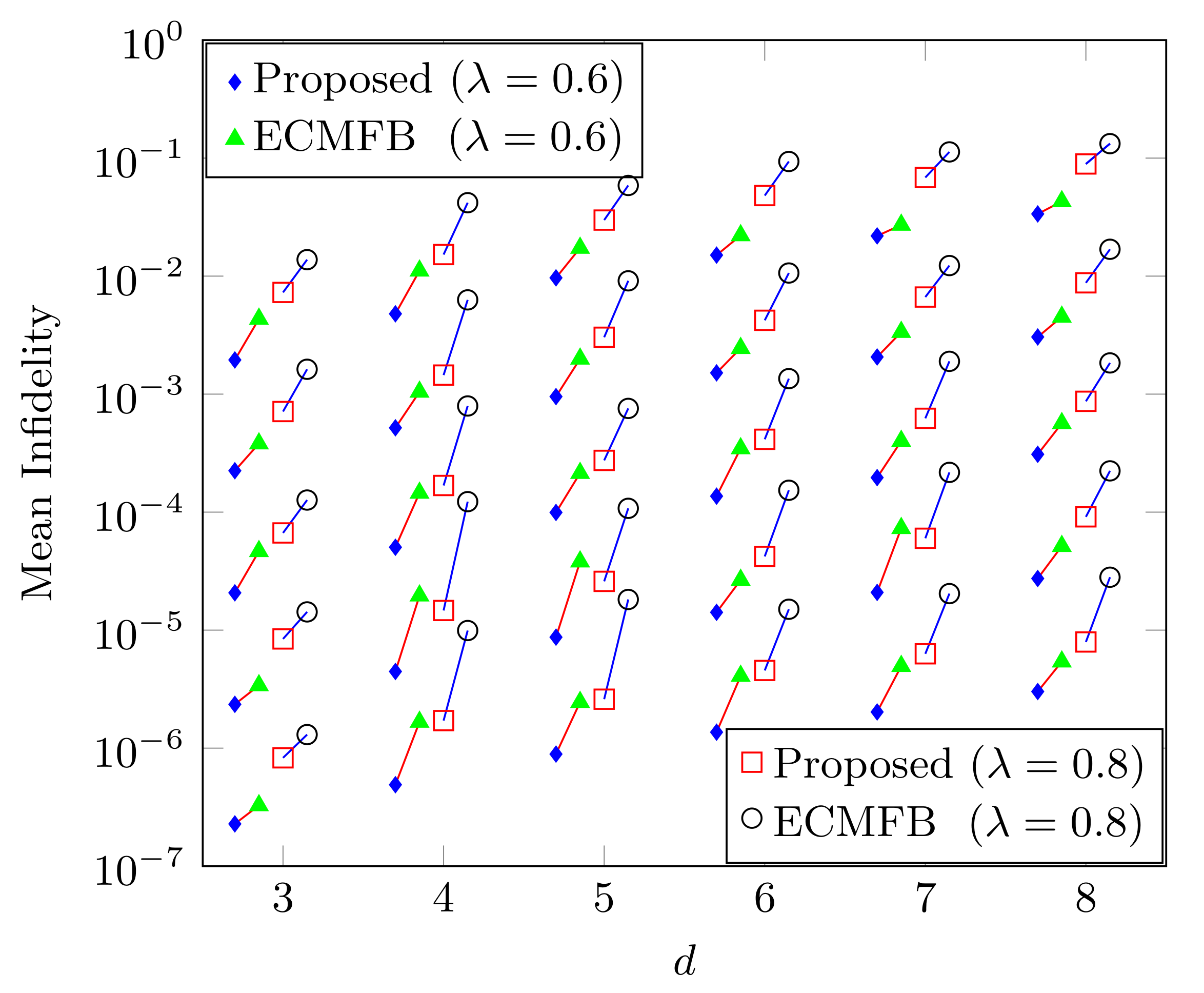
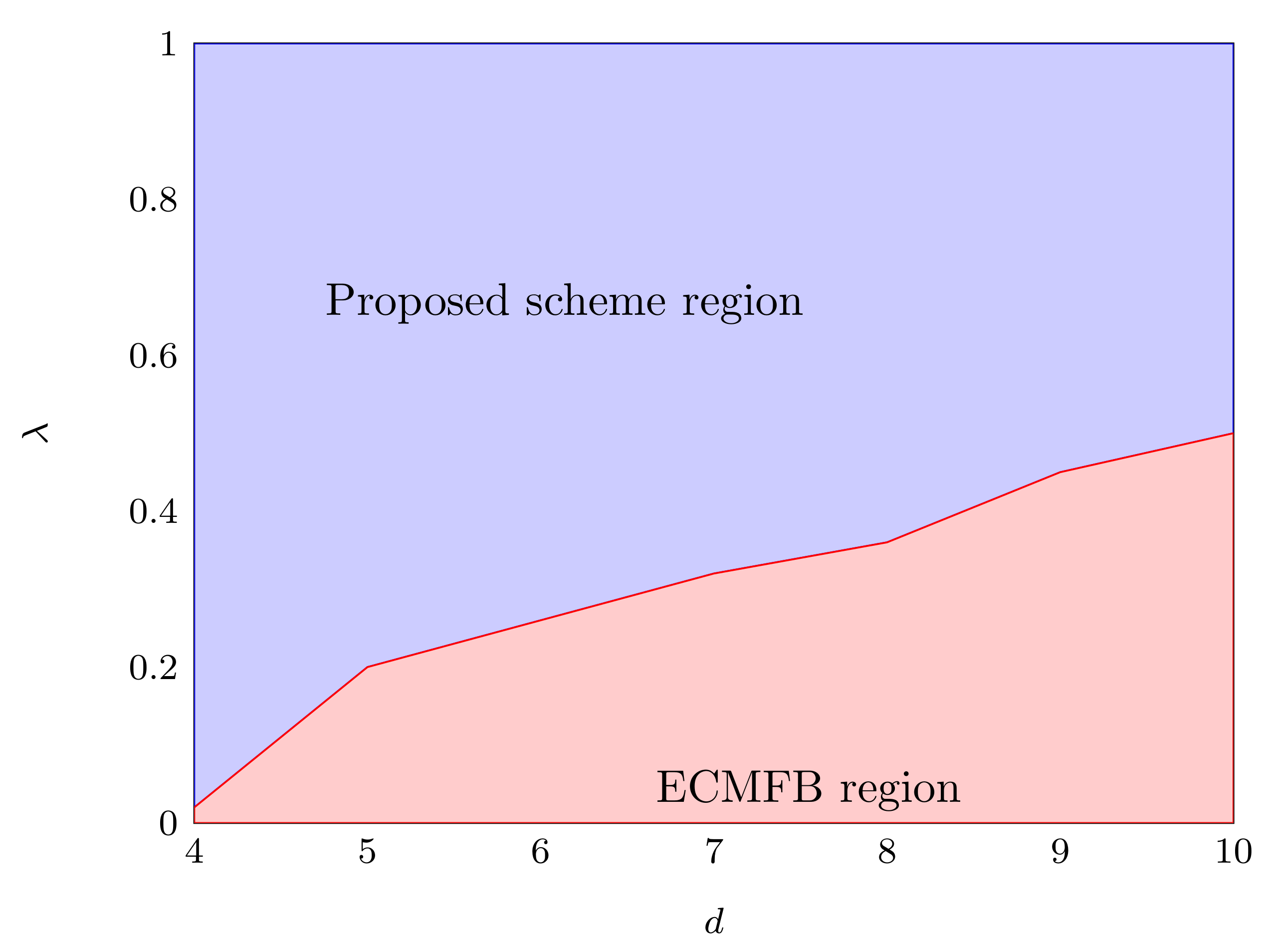
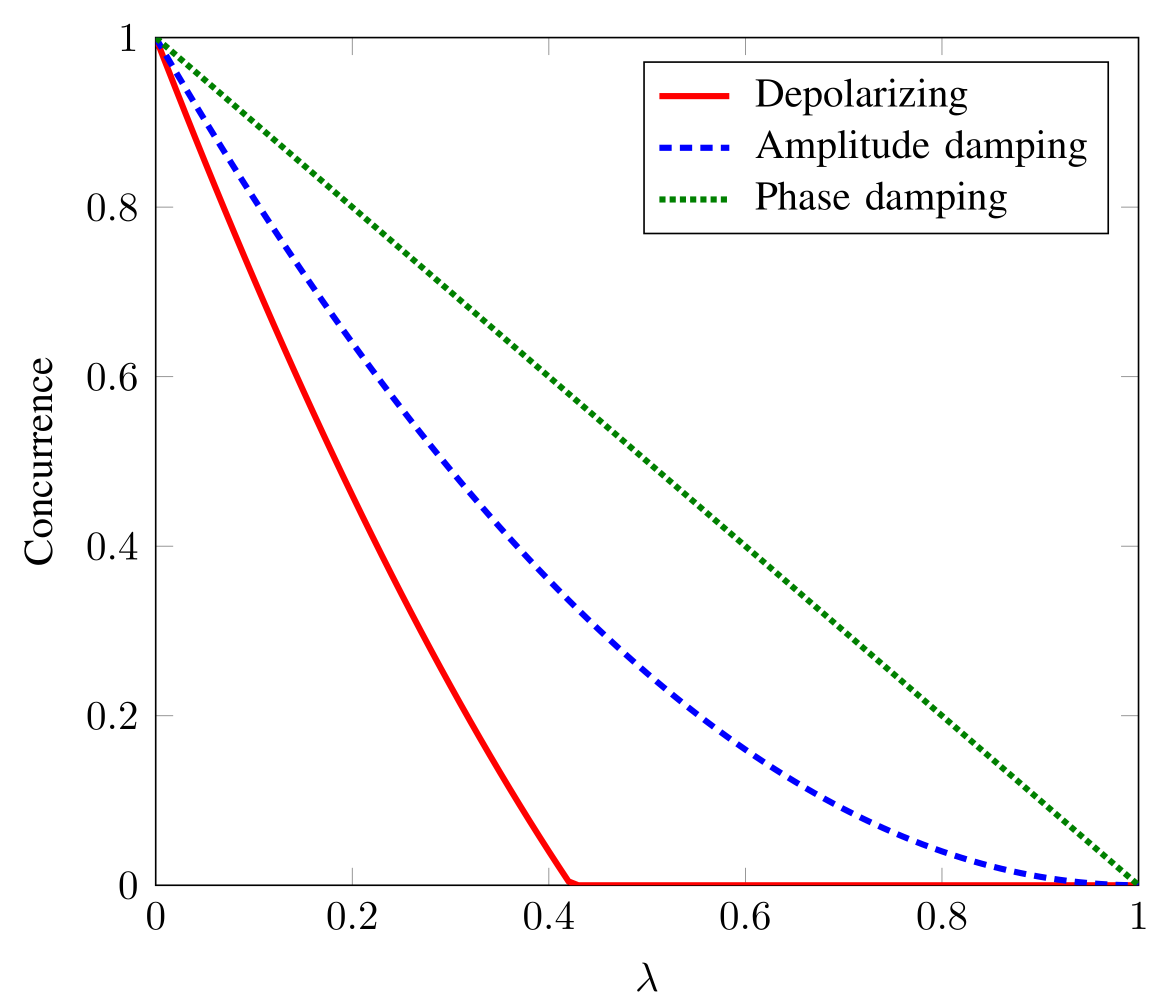
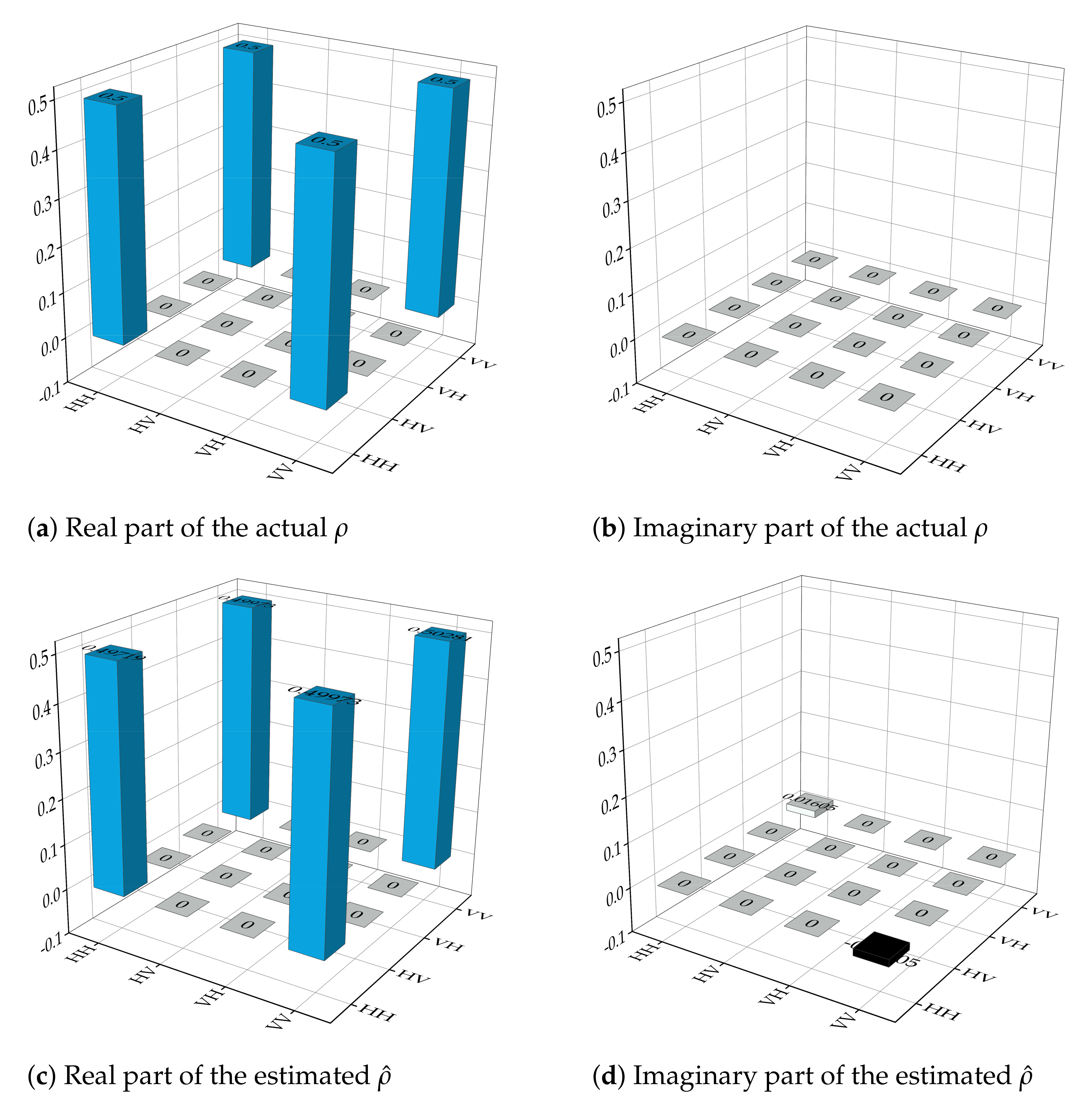
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| QST | quantum state tomography |
| ECMFB | error-corrected modified five bases |
| GGM | generalized Gell-Mann |
| MLE | maximum likelihood estimation |
| LRE | linear regression estimation |
References
- Erhard, M.; Fickler, R.; Krenn, M.; Zeilinger, A. Twisted Photons: New Quantum Perspectives in High Dimensions. Light. Sci. Appl. 2018, 7, 17146. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bechmann-Pasquinucci, H.; Tittel, W. Quantum Cryptography using Larger Alphabets. Phys. Rev. A 2000, 61, 062308. [Google Scholar] [CrossRef] [Green Version]
- Campbell, E.T.; Anwar, H.; Browne, D.E. Magic-State Distillation in All Prime Dimensions Using Quantum Reed-Muller Codes. Phys. Rev. X 2012, 2, 041021. [Google Scholar] [CrossRef] [Green Version]
- Khalid, U.; ur Rehman, J.; Shin, H. Metrologically Resourceful Multipartite Entanglement under Quantum Many-Body Effects. Quantum Sci. Technol. 2021, 6, 025007. [Google Scholar] [CrossRef]
- Degen, C.L.; Reinhard, F.; Cappellaro, P. Quantum sensing. Rev. Mod. Phys. 2017, 89, 1–39. [Google Scholar] [CrossRef] [Green Version]
- Torlai, G.; Mazzola, G.; Carrasquilla, J.; Troyer, M.; Melko, R.; Carleo, G. Neural-network quantum state tomography. Nat. Phys. 2018, 14, 447–450. [Google Scholar] [CrossRef] [Green Version]
- Neeley, M.; Ansmann, M.; Bialczak, R.C.; Hofheinz, M.; Lucero, E.; O’Connell, A.D.; Sank, D.; Wang, H.; Wenner, J.; Cleland, A.N.; et al. Emulation of a Quantum Spin with a Superconducting Phase Qudit. Science 2009, 325, 722–725. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Soltamov, V.; Kasper, C.; Poshakinskiy, A.; Anisimov, A.; Mokhov, E.; Sperlich, A.; Tarasenko, S.; Baranov, P.; Astakhov, G.; Dyakonov, V. Excitation and Coherent Control of Spin Qudit Modes in Silicon Carbide at Room Temperature. Nat. Commun. 2019, 10, 1–8. [Google Scholar] [CrossRef] [Green Version]
- Klimov, A.B.; Guzmán, R.; Retamal, J.C.; Saavedra, C. Qutrit Quantum Computer with Trapped Ions. Phys. Rev. A 2003, 67, 062313. [Google Scholar] [CrossRef]
- Abobeih, M.; Randall, J.; Bradley, C.; Bartling, H.; Bakker, M.; Degen, M.; Markham, M.; Twitchen, D.; Taminiau, T. Atomic-Scale Imaging of a 27-Nuclear-Spin Cluster using a Quantum Sensor. Nature 2019, 576, 411–415. [Google Scholar] [CrossRef] [Green Version]
- Banaszek, K.; D’Ariano, G.M.; Paris, M.G.A.; Sacchi, M.F. Maximum-Likelihood Estimation of the Density Matrix. Phys. Rev. A 1999, 61, 010304. [Google Scholar] [CrossRef] [Green Version]
- Opatrný, T.; Welsch, D.G.; Vogel, W. Least-Squares Inversion for Density-Matrix Reconstruction. Phys. Rev. A 1997, 56, 1788–1799. [Google Scholar] [CrossRef] [Green Version]
- Blume-Kohout, R. Optimal, Reliable Estimation of Quantum States. New J. Phys. 2010, 12, 043034. [Google Scholar] [CrossRef]
- Granade, C.; Ferrie, C.; Flammia, S.T. Practical adaptive quantum tomography. New J. Phys. 2017, 19, 113017. [Google Scholar] [CrossRef] [Green Version]
- Blume-Kohout, R. Hedged Maximum Likelihood Quantum State Estimation. Phys. Rev. Lett. 2010, 105, 200504. [Google Scholar] [CrossRef] [PubMed]
- Kazim, S.M.; Farooq, A.; ur Rehman, J.; Shin, H. Adaptive Quantum State Tomography with Iterative Particle Filtering. Quantum Inf. Process. 2021, 20, 348. [Google Scholar] [CrossRef]
- Shabani, A.; Kosut, R.L.; Mohseni, M.; Rabitz, H.; Broome, M.A.; Almeida, M.P.; Fedrizzi, A.; White, A.G. Efficient Measurement of Quantum Dynamics via Compressive Sensing. Phys. Rev. Lett. 2011, 106, 100401. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lloyd, S.; Mohseni, M.; Rebentrost, P. Quantum Principal Component Analysis. Nat. Phys. 2014, 10, 631–633. [Google Scholar] [CrossRef] [Green Version]
- Hou, Z.; Zhong, H.S.; Tian, Y.; Dong, D.; Qi, B.; Li, L.; Wang, Y.; Nori, F.; Xiang, G.Y.; Li, C.F.; et al. Full Reconstruction of a 14-Qubit State within Four Hours. New J. Phys. 2016, 18, 083036. [Google Scholar] [CrossRef]
- Qi, B.; Hou, Z.; Li, L.; Dongi, D.; Xiang, G.; Guo, G. Quantum State Tomography via Linear Regression Estimation. Sci. Rep. 2013, 3, 3496. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Qi, B.; Hou, Z.; Wang, Y.; Dong, D.; Zhong, H.S.; Li, L.; Xiang, G.Y.; Wiseman, H.M.; Li, C.F.; Guo, G.C. Adaptive Quantum State Tomography via Linear Regression Estimation: Theory and Two-Qubit Experiment. npj Quantum Inf. 2017, 3, 1–7. [Google Scholar] [CrossRef]
- Smolin, J.A.; Gambetta, J.M.; Smith, G. Efficient Method for Computing the Maximum-Likelihood Quantum State from Measurements with Additive Gaussian Noise. Phys. Rev. Lett. 2012, 108, 070502. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Rambach, M.; Qaryan, M.; Kewming, M.; Ferrie, C.; White, A.G.; Romero, J. Robust and Efficient High-Dimensional Quantum State Tomography. Phys. Rev. Lett. 2021, 126, 100402. [Google Scholar] [CrossRef]
- Steffens, A.; Riofrío, C.A.; McCutcheon, W.; Roth, I.; Bell, B.A.; McMillan, A.; Tame, M.S.; Rarity, J.G.; Eisert, J. Experimentally Exploring Compressed Sensing Quantum Tomography. Quantum Sci. Technol. 2017, 2, 025005. [Google Scholar] [CrossRef]
- Kueng, R.; Rauhut, H.; Terstiege, U. Low Rank Matrix Recovery from Rank One Measurements. Appl. Comput. Harmon. Anal. 2017, 42, 88–116. [Google Scholar] [CrossRef] [Green Version]
- Goyeneche, D.; Nas, G.C.; Etcheverry, S.; Gómez, E.S.; Xavier, G.B.; Lima, G.; Delgado, A. Five Measurement Bases Determine Pure Quantum States on Any Dimension. Phys. Rev. Lett. 2015, 115, 090401. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zambrano, L.; Pereira, L.; Martínez, D.; Nas, G.C.; Lima, G.; Delgado, A. Estimation of Pure States Using Three Measurement Bases. Phys. Rev. Appl. 2020, 14, 064004. [Google Scholar] [CrossRef]
- Zambrano, L.; Pereira, L.; Delgado, A. Improved Estimation Accuracy of the 5-Bases-Based Tomographic Method. Phys. Rev. A 2019, 100, 022340. [Google Scholar] [CrossRef]
- Torlai, G.; Melko, R.G. Latent Space Purification via Neural Density Operators. Phys. Rev. Lett. 2018, 120, 240503. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Nielsen, M.A.; Chuang, I. Quantum Computation and Quantum Information; Cambridge University Press: Cambridge, UK, 2002. [Google Scholar]
- Wilde, M.M. From Classical to Quantum Shannon Theory; Cambridge University Press: Cambridge, UK, 2013. [Google Scholar]
- Bertlmann, R.A.; Krammer, P. Bloch Vectors for Qudits. J. Phys. A Math. Theor. 2008, 41, 235303. [Google Scholar] [CrossRef]
- Khalid, U.; Jeong, Y.; Shin, H. Measurement-based quantum correlation in mixed-state quantum metrology. Quantum Inf. Process. 2018, 17, 343. [Google Scholar] [CrossRef]
- Im, D.G.; Kim, Y.H. Decoherence-Induced Sudden Death of Entanglement and Bell Nonlocality. Photonics 2022, 9, 58. [Google Scholar] [CrossRef]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Farooq, A.; Khalid, U.; ur Rehman, J.; Shin, H. Robust Quantum State Tomography Method for Quantum Sensing. Sensors 2022, 22, 2669. https://doi.org/10.3390/s22072669
Farooq A, Khalid U, ur Rehman J, Shin H. Robust Quantum State Tomography Method for Quantum Sensing. Sensors. 2022; 22(7):2669. https://doi.org/10.3390/s22072669
Chicago/Turabian StyleFarooq, Ahmad, Uman Khalid, Junaid ur Rehman, and Hyundong Shin. 2022. "Robust Quantum State Tomography Method for Quantum Sensing" Sensors 22, no. 7: 2669. https://doi.org/10.3390/s22072669
APA StyleFarooq, A., Khalid, U., ur Rehman, J., & Shin, H. (2022). Robust Quantum State Tomography Method for Quantum Sensing. Sensors, 22(7), 2669. https://doi.org/10.3390/s22072669





