Non-Singular Finite Time Tracking Control Approach Based on Disturbance Observers for Perturbed Quadrotor Unmanned Aerial Vehicles
Abstract
:1. Introduction
- -
- Design of a new disturbance observer combined with non-singular terminal sliding mode control for approximation of wind perturbation;
- -
- Proposition of a non-singular terminal sliding surface with fast convergence rate for position and attitude tracking control of quadrotors; and
- -
- Finite time reachability of the proposed sliding surface based on the Lyapunov stability theory.
2. Model Description of Quadrotor and Some Preliminaries
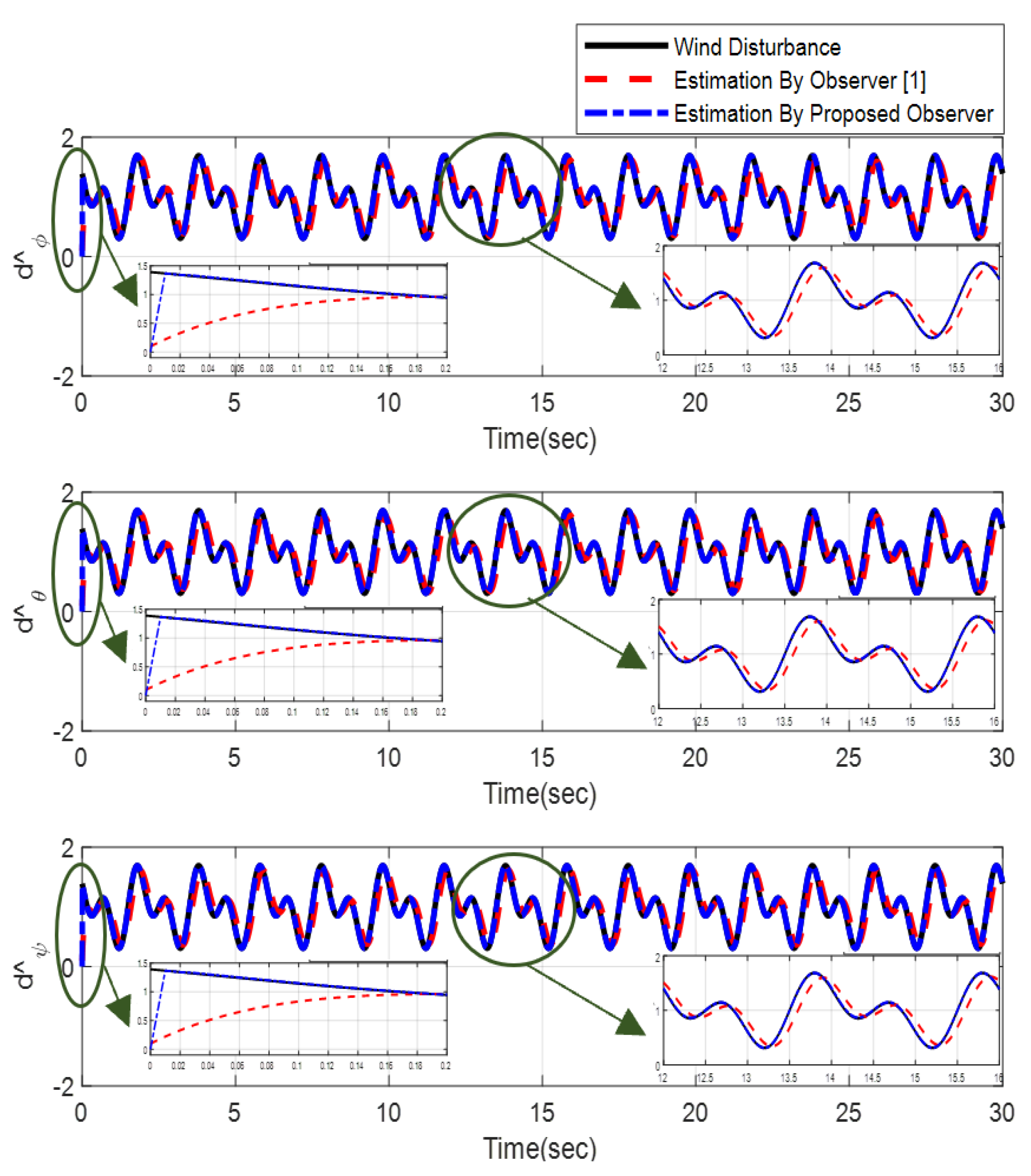
3. Disturbance Observer Design
4. Non-singular Terminal Sliding Mode Control
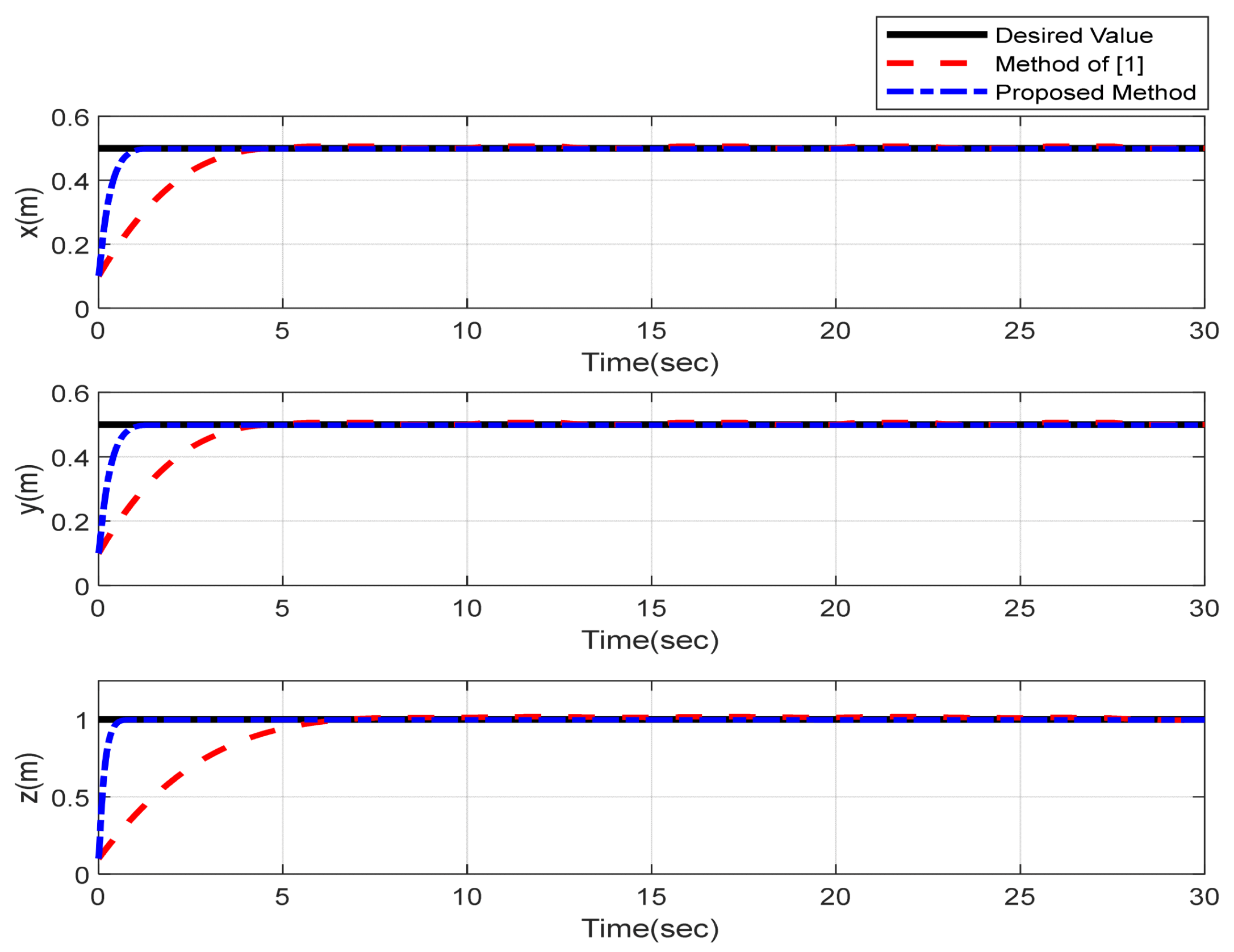
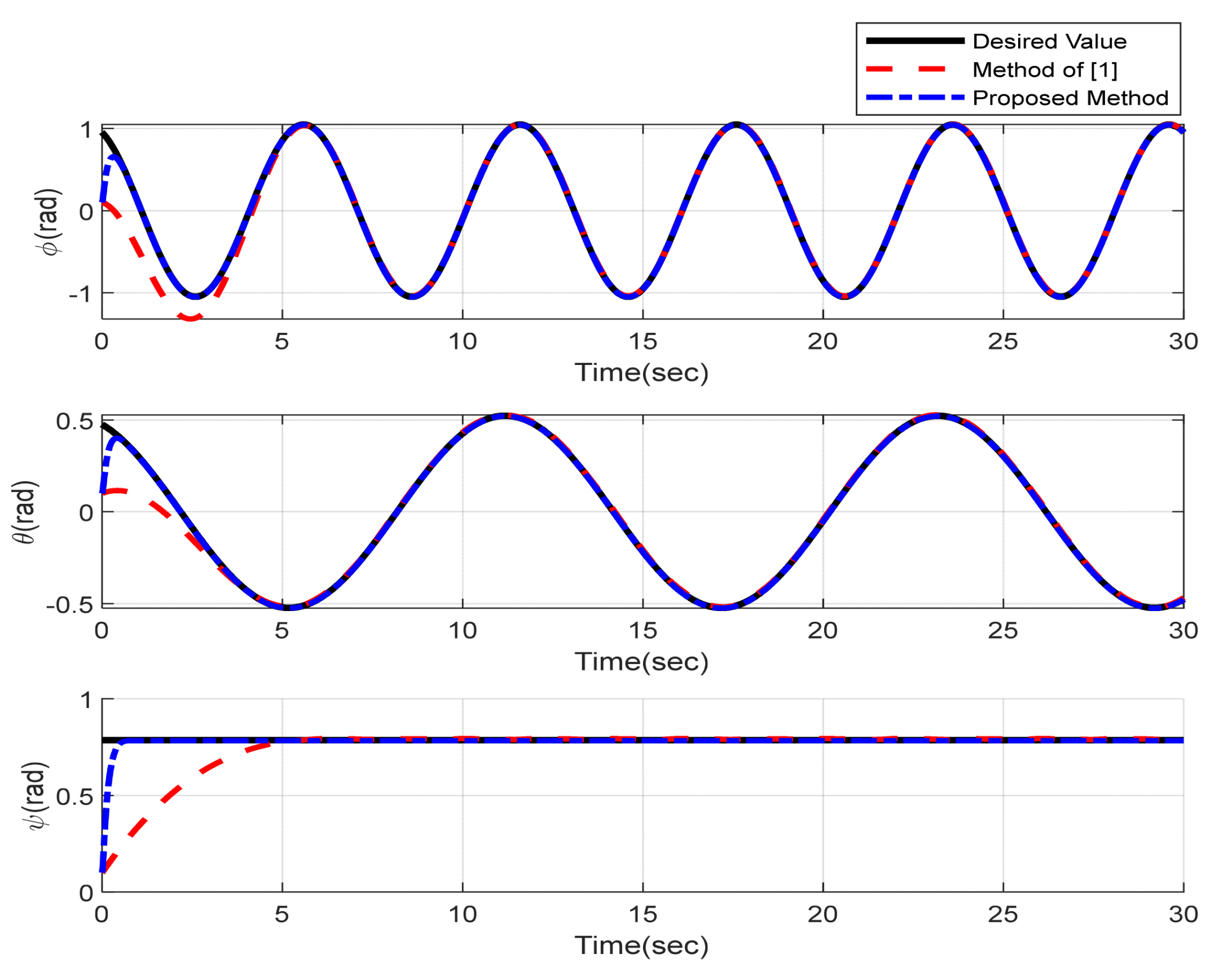
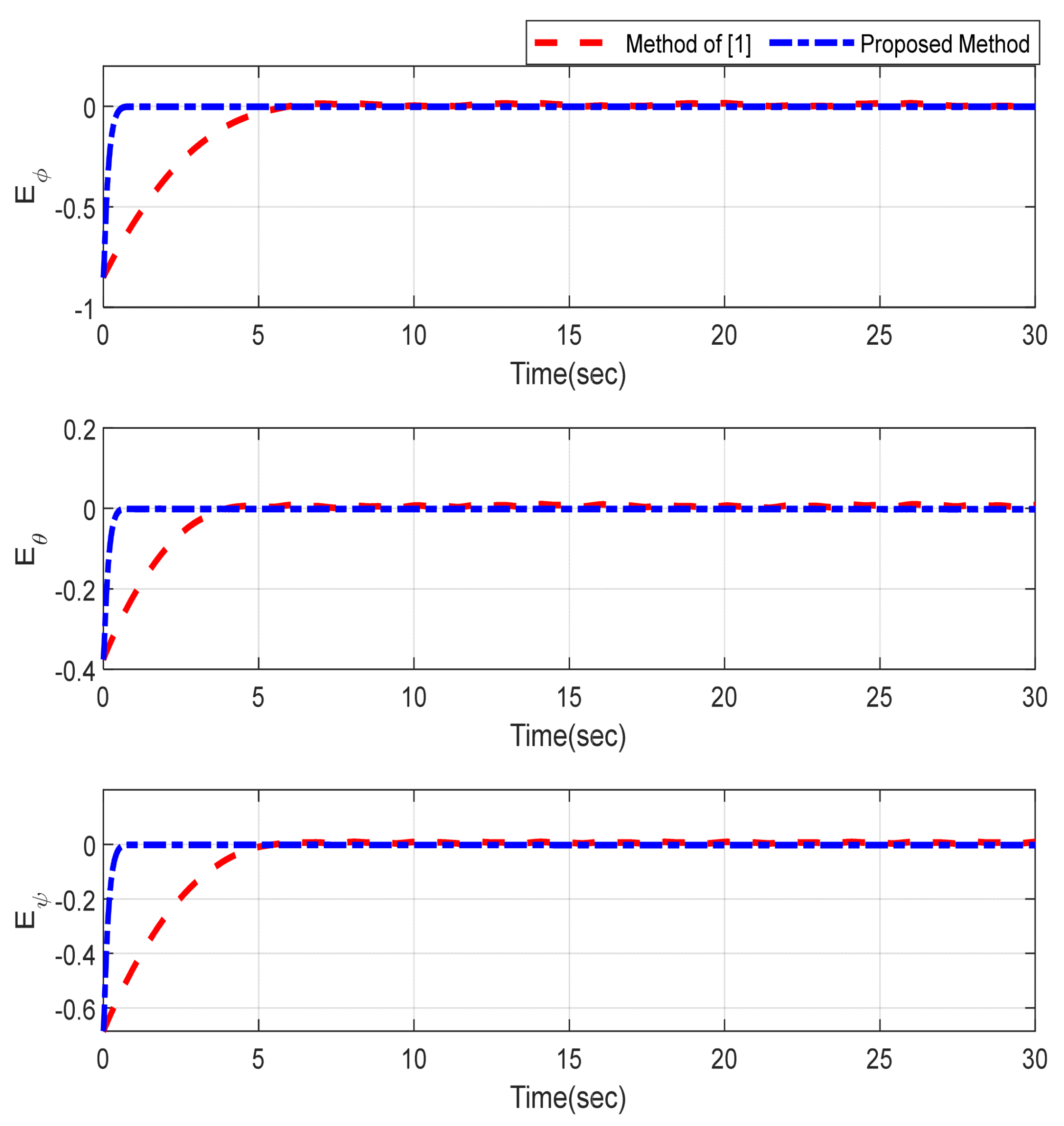
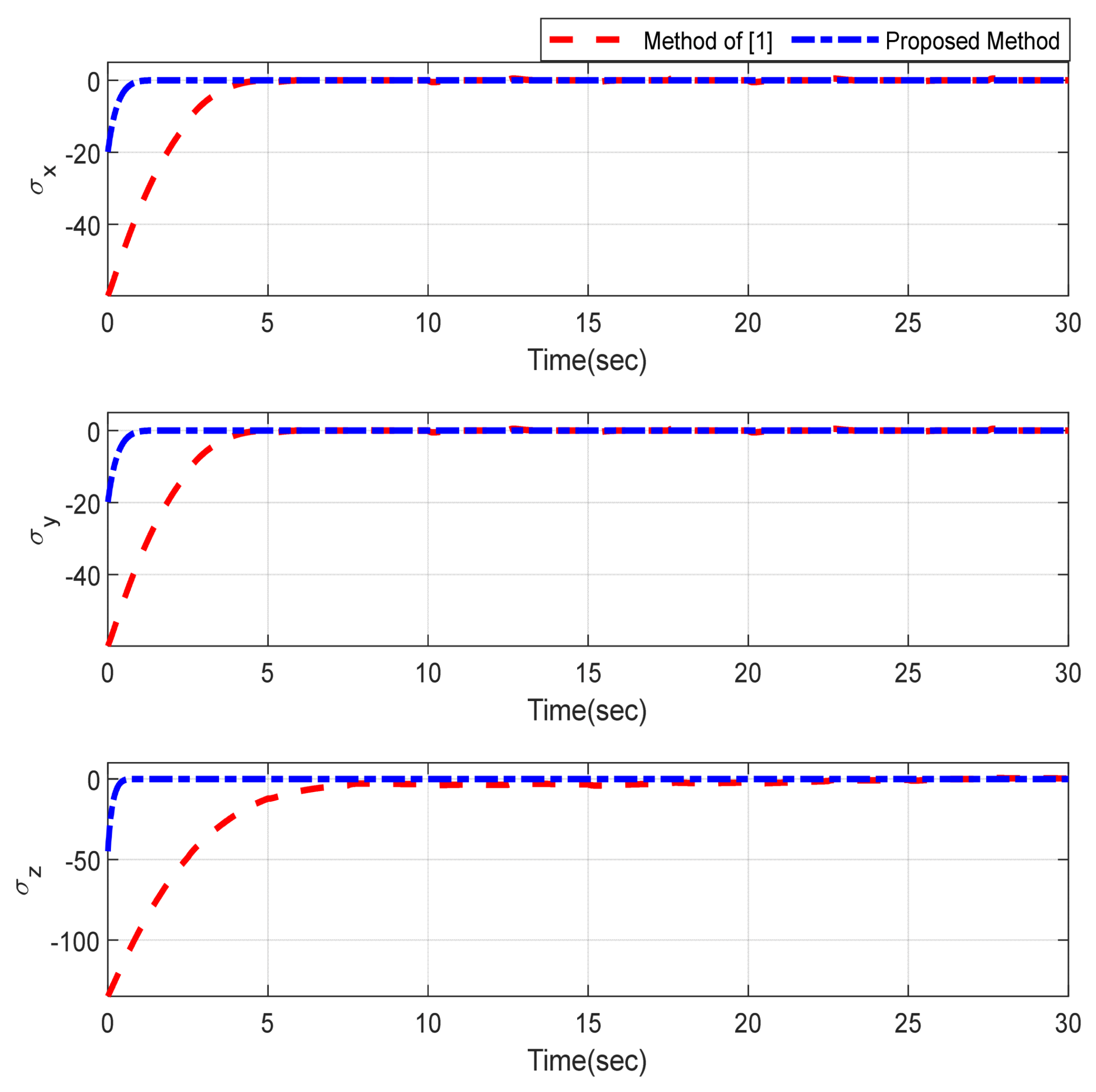
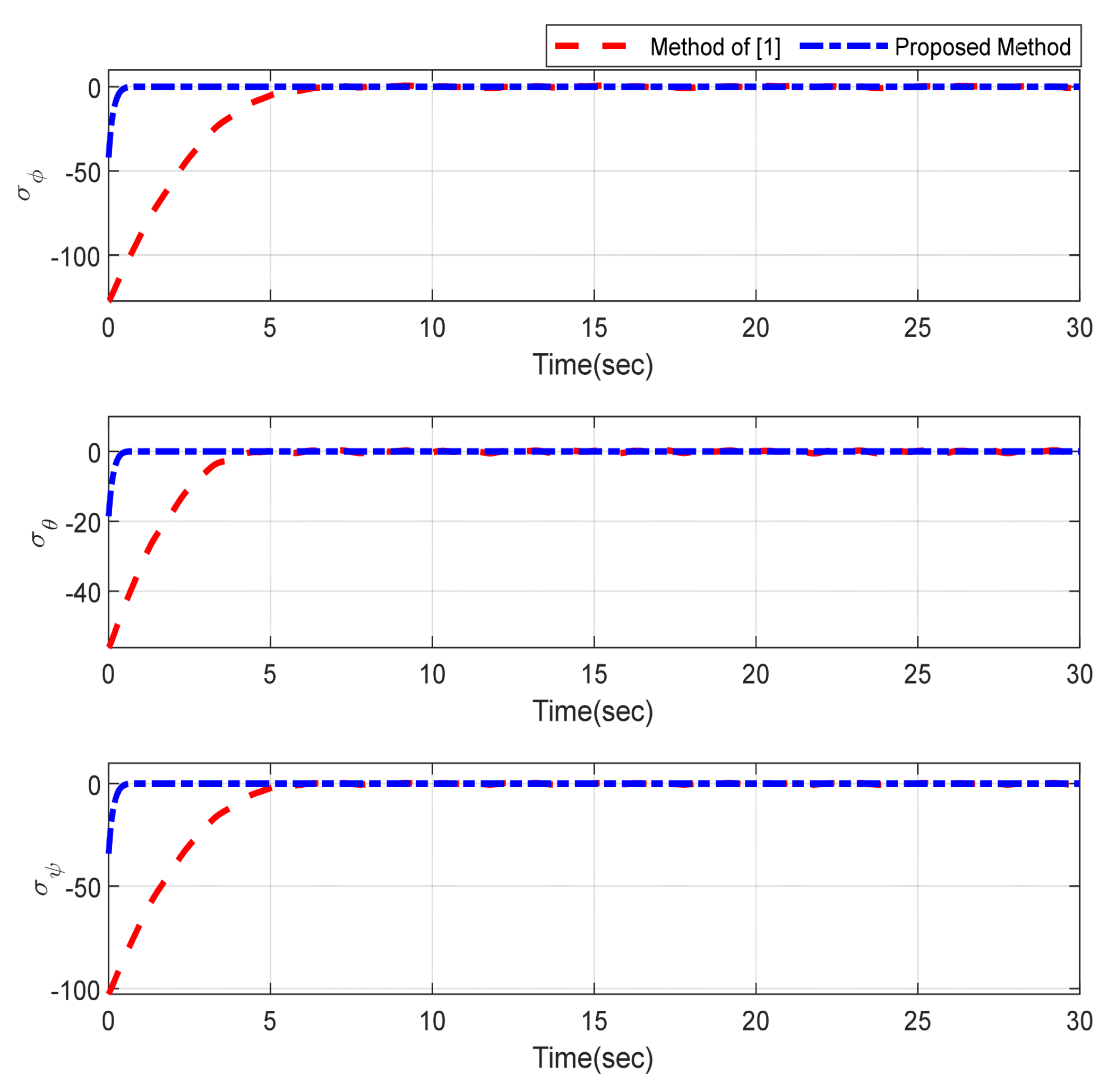
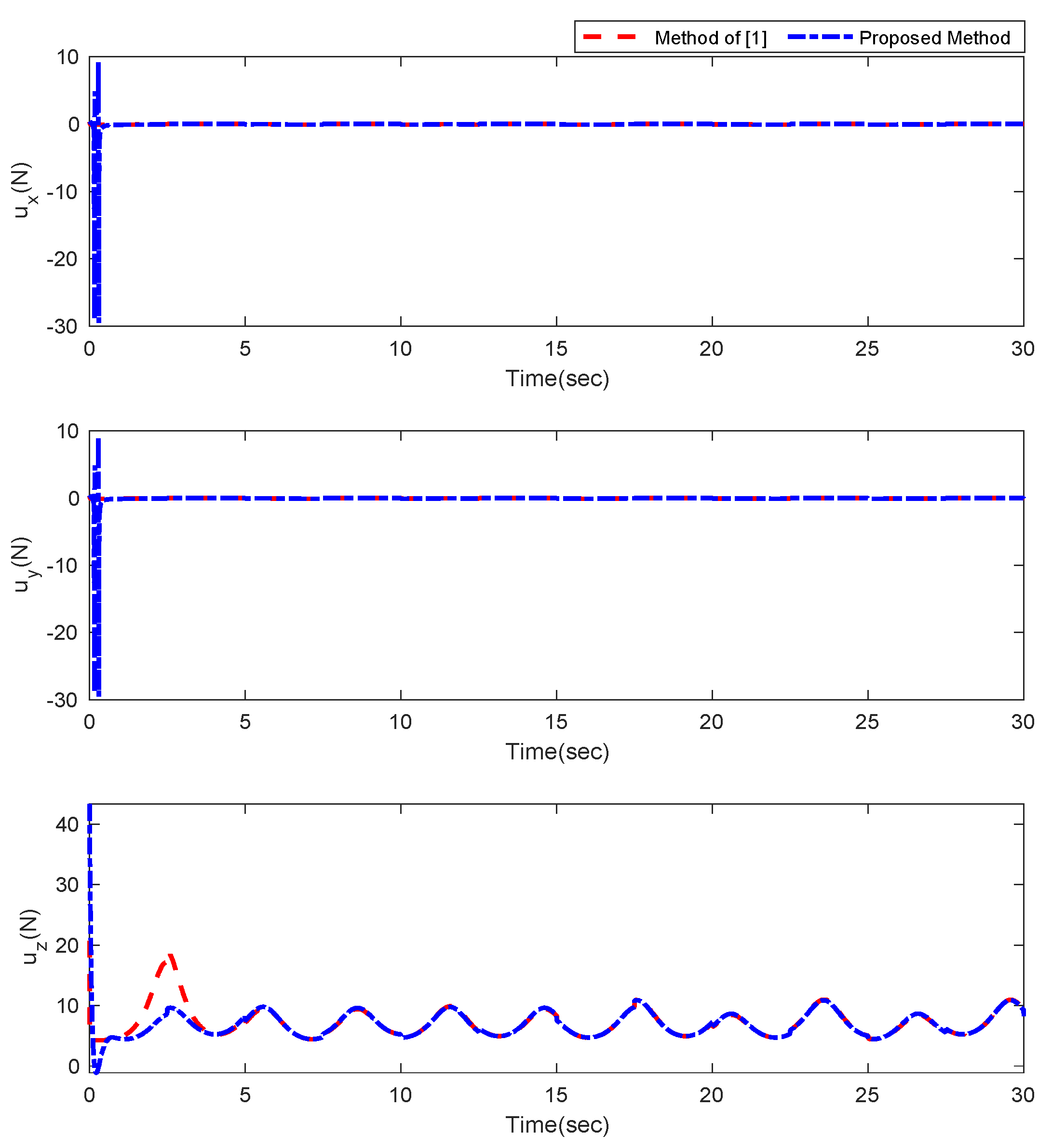
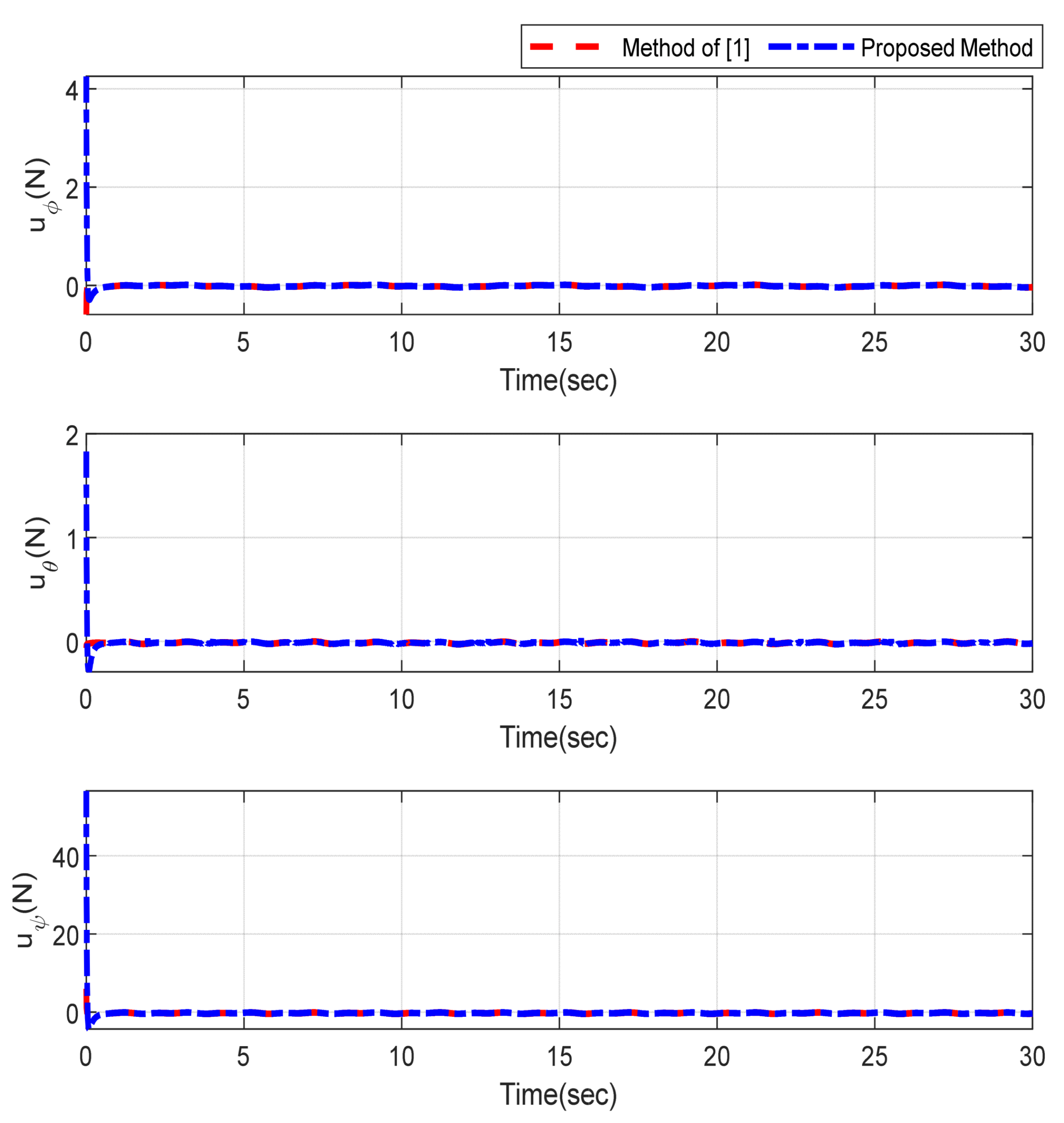
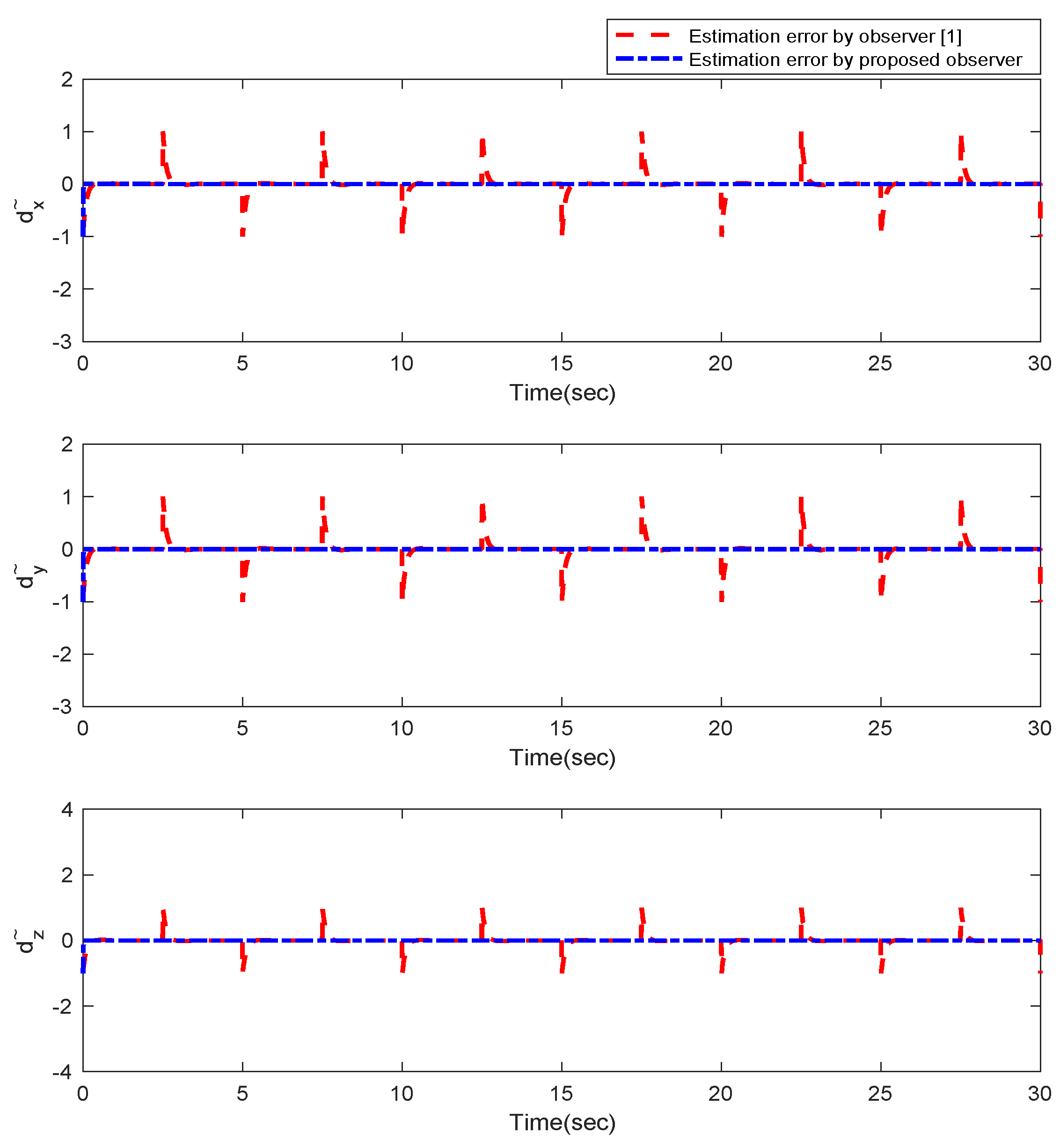
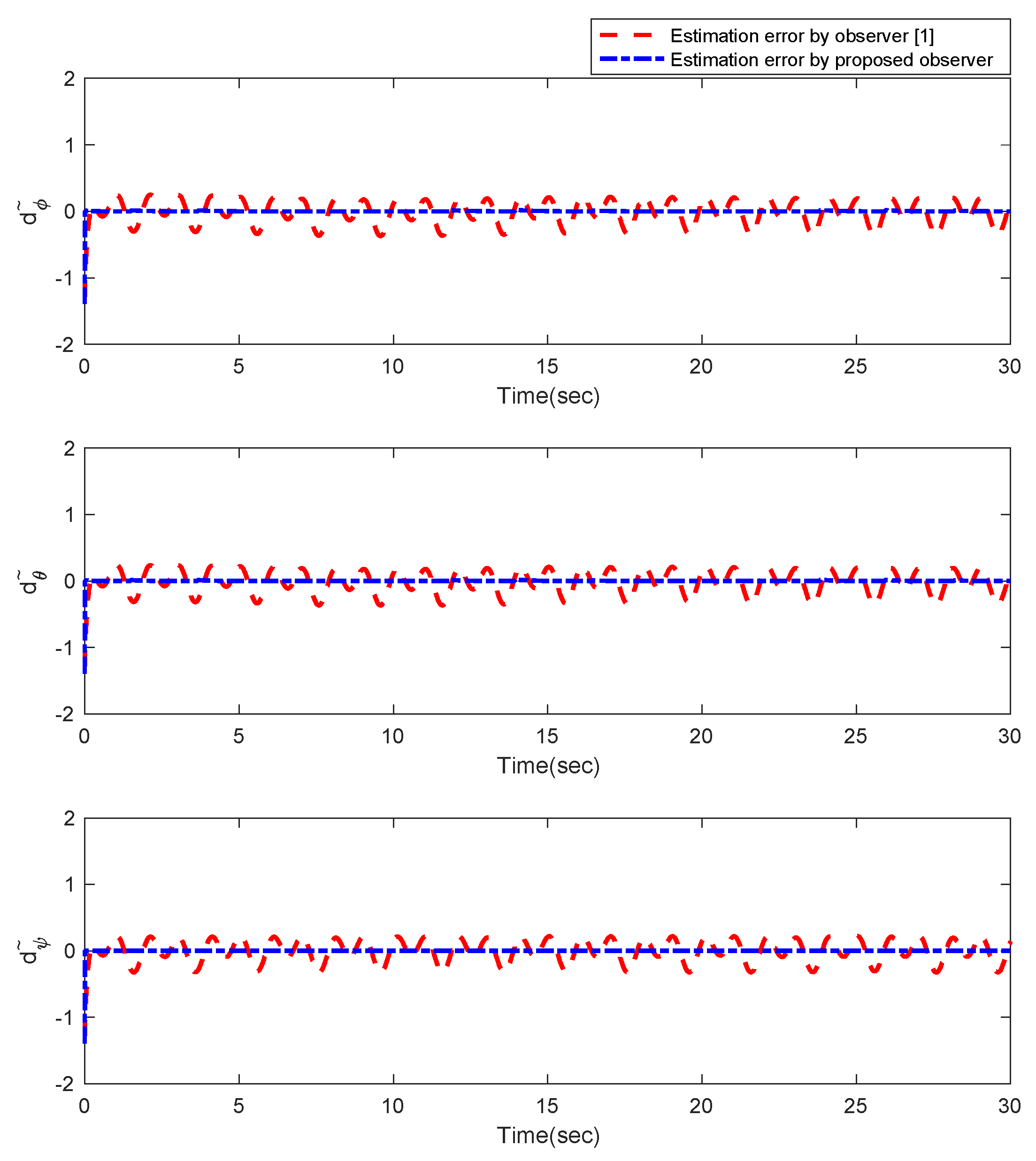
5. Simulation Results
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Tang, P.; Zhang, F.; Ye, J.; Lin, D. An integral TSMC-based adaptive fault-tolerant control for quadrotor with external disturbances and parametric uncertainties. Aerosp. Sci. Technol. 2021, 109, 106415. [Google Scholar] [CrossRef]
- Deng, X.; Guan, M.; Ma, Y.; Yang, X.; Xiang, T. Vehicle-Assisted UAV Delivery Scheme Considering Energy Consumption for Instant Delivery. Sensors 2022, 22, 2045. [Google Scholar] [CrossRef] [PubMed]
- Wei, L.; Chen, M.; Li, T. Disturbance-observer-based formation-containment control for UAVs via distributed adaptive event-triggered mechanisms. J. Frankl. Inst. 2021, 358, 5305–5333. [Google Scholar] [CrossRef]
- Huang, Y.; Liu, W.; Li, B.; Yang, Y.; Xiao, B. Finite-time formation tracking control with collision avoidance for quadrotor UAVs. J. Frankl. Inst. 2020, 357, 4034–4058. [Google Scholar] [CrossRef]
- Wang, D.; Pan, Q.; Shi, Y.; Hu, J. Efficient nonlinear model predictive control for quadrotor trajectory tracking: Algorithms and experiment. IEEE Trans. Cybern. 2021, 51, 5057–5068. [Google Scholar] [CrossRef] [PubMed]
- Zhang, J.; Zhang, P.; Yan, J. Distributed adaptive finite-time compensation control for UAV swarm with uncertain disturbances. IEEE Trans. Circuits Syst. I Regul. Pap. 2020, 68, 829–841. [Google Scholar] [CrossRef]
- Jiao, R.; Chou, W.; Rong, Y.; Dong, M. Anti-disturbance attitude control for quadrotor unmanned aerial vehicle manipulator via fuzzy adaptive sigmoid generalized super-twisting sliding mode observer. J. Vib. Control. 2021. [Google Scholar] [CrossRef]
- Wu, X.; Xu, K.; Lei, M.; He, X. Disturbance-Compensation-Based Continuous Sliding Mode Control for Overhead Cranes With Disturbances. IEEE Trans. Autom. Sci. Eng. 2020, 17, 2182–2189. [Google Scholar] [CrossRef]
- Sun, X.; Jin, Z.; Chen, L.; Yang, Z. Disturbance rejection based on iterative learning control with extended state observer for a four-degree-of-freedom hybrid magnetic bearing system. Mech. Syst. Signal Process. 2021, 153, 107465. [Google Scholar] [CrossRef]
- Xiao, B.; Yin, S. A new disturbance attenuation control scheme for quadrotor unmanned aerial vehicles. IEEE Trans. Ind. Inform. 2017, 13, 2922–2932. [Google Scholar] [CrossRef]
- Labbadi, M.; Boukal, Y.; Cherkaoui, M.; Djemai, M. Fractional-order global sliding mode controller for an uncertain quadrotor UAVs subjected to external disturbances. J. Frankl. Inst. 2021, 358, 4822–4847. [Google Scholar] [CrossRef]
- Nadda, S.; Swarup, A. On adaptive sliding mode control for improved quadrotor tracking. J. Vib. Control. 2018, 24, 3219–3230. [Google Scholar] [CrossRef]
- Zhang, Z.; Wang, F.; Guo, Y.; Hua, C. Multivariable sliding mode backstepping controller design for quadrotor UAV based on disturbance observer. Sci. China Inf. Sci. 2018, 61, 112207. [Google Scholar] [CrossRef]
- Shao, S.; Chen, M. Adaptive neural discrete-time fractional-order control for a UAV system with prescribed performance using disturbance observer. IEEE Trans. Syst. Man Cybern. Syst. 2018, 51, 742–754. [Google Scholar] [CrossRef]
- Smith, J.; Su, J.; Liu, C.; Chen, W.-H. Disturbance observer based control with anti-windup applied to a small fixed wing UAV for disturbance rejection. J. Intell. Robot. Syst. 2017, 88, 329–346. [Google Scholar] [CrossRef] [Green Version]
- Chen, J.; Sun, R.; Zhu, B. Disturbance observer-based control for small nonlinear UAV systems with transient performance constraint. Aerosp. Sci. Technol. 2020, 105, 106028. [Google Scholar] [CrossRef]
- Moeini, A.; Lynch, A.F.; Zhao, Q. Disturbance observer-based nonlinear control of a quadrotor UAV. Adv. Control. Appl. Eng. Ind. Syst. 2020, 2, e24. [Google Scholar] [CrossRef] [Green Version]
- Zhu, X.; Chen, J.; Zhu, Z.H. Adaptive learning observer for spacecraft attitude control with actuator fault. Aerosp. Sci. Technol. 2021, 108, 106389. [Google Scholar] [CrossRef]
- Azar, A.T.; Serrano, F.E.; Koubaa, A.; Ibrahim, H.A.; Kamal, N.A.; Khamis, A.; Ibraheem, I.K.; Humaidi, A.J.; Precup, R.-E. Robust fractional-order sliding mode control design for UAVs subjected to atmospheric disturbances. In Unmanned Aerial Systems; Elsevier: Amsterdam, The Netherlands, 2021; pp. 103–128. [Google Scholar]
- Najm, A.A.; Ibraheem, I.K.; Azar, A.T.; Humaidi, A.J. On the stabilization of 6-DOF UAV quadrotor system using modified active disturbance rejection control. In Unmanned Aerial Systems; Elsevier: Amsterdam, The Netherlands, 2021; pp. 257–287. [Google Scholar]
- Zhang, X.; Huang, W.; Wang, Q.-G. Robust H∞ Adaptive Sliding Mode Fault Tolerant Control for TS Fuzzy Fractional Order Systems With Mismatched Disturbances. IEEE Trans. Circuits Syst. I Regul. Pap. 2020, 68, 1297–1307. [Google Scholar] [CrossRef]
- Yang, Y.; Xu, D.; Ma, T.; Su, X. Adaptive cooperative terminal sliding mode control for distributed energy storage systems. IEEE Trans. Circuits Syst. I Regul. Pap. 2020, 68, 434–443. [Google Scholar] [CrossRef]
- Fei, J.; Chen, Y. Fuzzy double hidden layer recurrent neural terminal sliding mode control of single-phase active power filter. IEEE Trans. Fuzzy Syst. 2020, 29, 3067–3081. [Google Scholar] [CrossRef]
- Fei, J.; Chen, Y. Dynamic terminal sliding-mode control for single-phase active power filter using new feedback recurrent neural network. IEEE Trans. Power Electron. 2020, 35, 9906–9924. [Google Scholar] [CrossRef]
- Wang, Y.; Zhu, K.; Chen, B.; Jin, M. Model-free continuous nonsingular fast terminal sliding mode control for cable-driven manipulators. ISA Trans. 2020, 98, 483–495. [Google Scholar] [CrossRef] [PubMed]
- Guo, Y.; Xu, B.; Zhang, R. Terminal sliding mode control of mems gyroscopes with finite-time learning. IEEE Trans. Neural Netw. Learn. Syst. 2020, 32, 4490–4498. [Google Scholar] [CrossRef] [PubMed]
- Mao, J.; Yang, J.; Liu, X.; Li, S.; Li, Q. Modeling and robust continuous TSM control for an inertially stabilized platform with couplings. IEEE Trans. Control. Syst. Technol. 2020, 28, 2548–2555. [Google Scholar] [CrossRef]
- Gong, W.; Li, B.; Xiong, H.; Yang, Y.; Xiao, B. Observer based Appointed-finite-time Nonsingular Sliding Mode based Disturbance Attenuation Control for Quadrotor UAV. In Proceedings of the International Conference on Unmanned Aircraft Systems (ICUAS), Athens, Greece, 1–4 September 2020; pp. 1338–1343. [Google Scholar]
- Xiong, T.; Pu, Z.; Yi, J. Time-varying formation tracking control for multi-UAV systems with nonsingular fast terminal sliding mode. In Proceedings of the 32nd Youth Academic Annual Conference of Chinese Association of Automation (YAC), Hefei, China, 19–21 May 2017; pp. 937–942. [Google Scholar]
- Zhao, Z.; Li, T.; Cao, D. Trajectory Tracking Control for Quadrotor UAVs based on Composite Nonsingular Terminal Sliding Mode method. In Proceedings of the IECON The 46th Annual Conference of the IEEE Industrial Electronics Society, Singapore, 19–21 October 2020; pp. 5110–5115. [Google Scholar]
- Ranjbar, B.; Ranjbar Noiey, A.; Rezaie, B. Adaptive sliding mode observer–based decentralized control design for linear systems with unknown interconnections. J. Vib. Control. 2021, 27, 152–168. [Google Scholar] [CrossRef]
- Cheng, P.; Gao, Z.; Qian, M.; Lin, J. Active fault tolerant control design for UAV using nonsingular fast terminal sliding mode approach. In Proceedings of the Chinese Control And Decision Conference (CCDC), Shenyang, China, 9–11 June 2018; pp. 292–297. [Google Scholar]
- Mofid, O.; Mobayen, S. Adaptive sliding mode control for finite-time stability of quad-rotor UAVs with parametric uncertainties. ISA Trans. 2018, 72, 1–14. [Google Scholar] [CrossRef]



| Variable | Unit | Name | Variable | Unit | Name |
|---|---|---|---|---|---|
| (m) | Coordinate axes of quadrotor | (N·m/rad/s2) | Inertia to the axes | ||
| (Rad) | Pitch, Roll, Yaw angles | (N·m/rad/s) | Drag factors | ||
| (N/rad/s) | Drag coefficients | (N·m/rad/s2) | Motor inertia | ||
| (N/rad/s) | Aerodynamic fiction factors | (N·m/rad/s) | Lift power facto | ||
| (kg) | Mass of quadrotor | ,,, | (Rad/s) | Angular velocities | |
| (m) | Distance between rotation axes and center |
| Variable (Unit) | Quantity | Variable (Unit) | Quantity |
|---|---|---|---|
| m (kg) | 0.486 | 5.5670 × 10−4 | |
| d (m) | 0.25 | (N·m/rad/s2) | 3.8278 × 10−3 |
| Cd (N·m/rad/s) | 3.2320 × 10−2 | (N·m/rad/s2) | 3.8278 × 10−3 |
| (N·m/rad/s2) | 2.8385 × 10−5 | (N·m/rad/s2) | 7.6566 × 10−3 |
| 5.5670 × 10−4 | 6.3540 × 10−4 | ||
| 6.3540 × 10−4 | 2.9842 × 10−3 | ||
| 5.5670 × 10−4 | 5.5670 × 10−4 |
| Variable | Quantity | Variable | Quantity |
|---|---|---|---|
| 3/5 | |||
| Pulse generator(Pulse width: 50, period: 5, amplitude: 1) | |||
| 7/9 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
El-Sousy, F.F.M.; Alattas, K.A.; Mofid, O.; Mobayen, S.; Asad, J.H.; Skruch, P.; Assawinchaichote, W. Non-Singular Finite Time Tracking Control Approach Based on Disturbance Observers for Perturbed Quadrotor Unmanned Aerial Vehicles. Sensors 2022, 22, 2785. https://doi.org/10.3390/s22072785
El-Sousy FFM, Alattas KA, Mofid O, Mobayen S, Asad JH, Skruch P, Assawinchaichote W. Non-Singular Finite Time Tracking Control Approach Based on Disturbance Observers for Perturbed Quadrotor Unmanned Aerial Vehicles. Sensors. 2022; 22(7):2785. https://doi.org/10.3390/s22072785
Chicago/Turabian StyleEl-Sousy, Fayez F. M., Khalid A. Alattas, Omid Mofid, Saleh Mobayen, Jihad H. Asad, Paweł Skruch, and Wudhichai Assawinchaichote. 2022. "Non-Singular Finite Time Tracking Control Approach Based on Disturbance Observers for Perturbed Quadrotor Unmanned Aerial Vehicles" Sensors 22, no. 7: 2785. https://doi.org/10.3390/s22072785
APA StyleEl-Sousy, F. F. M., Alattas, K. A., Mofid, O., Mobayen, S., Asad, J. H., Skruch, P., & Assawinchaichote, W. (2022). Non-Singular Finite Time Tracking Control Approach Based on Disturbance Observers for Perturbed Quadrotor Unmanned Aerial Vehicles. Sensors, 22(7), 2785. https://doi.org/10.3390/s22072785









