A Combined Elevation Angle and C/N0 Weighting Method for GNSS PPP on Xiaomi MI8 Smartphones
Abstract
:1. Introduction
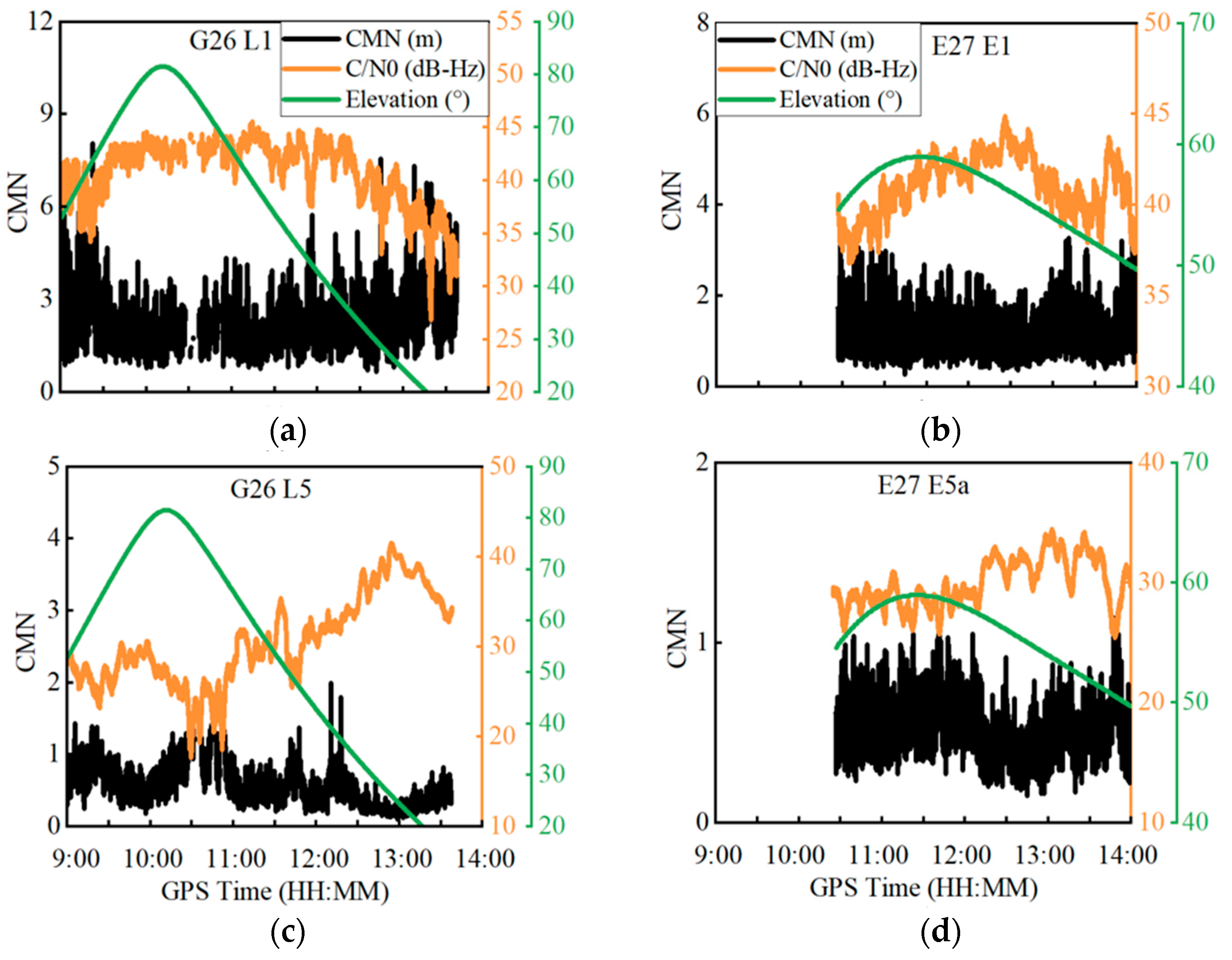
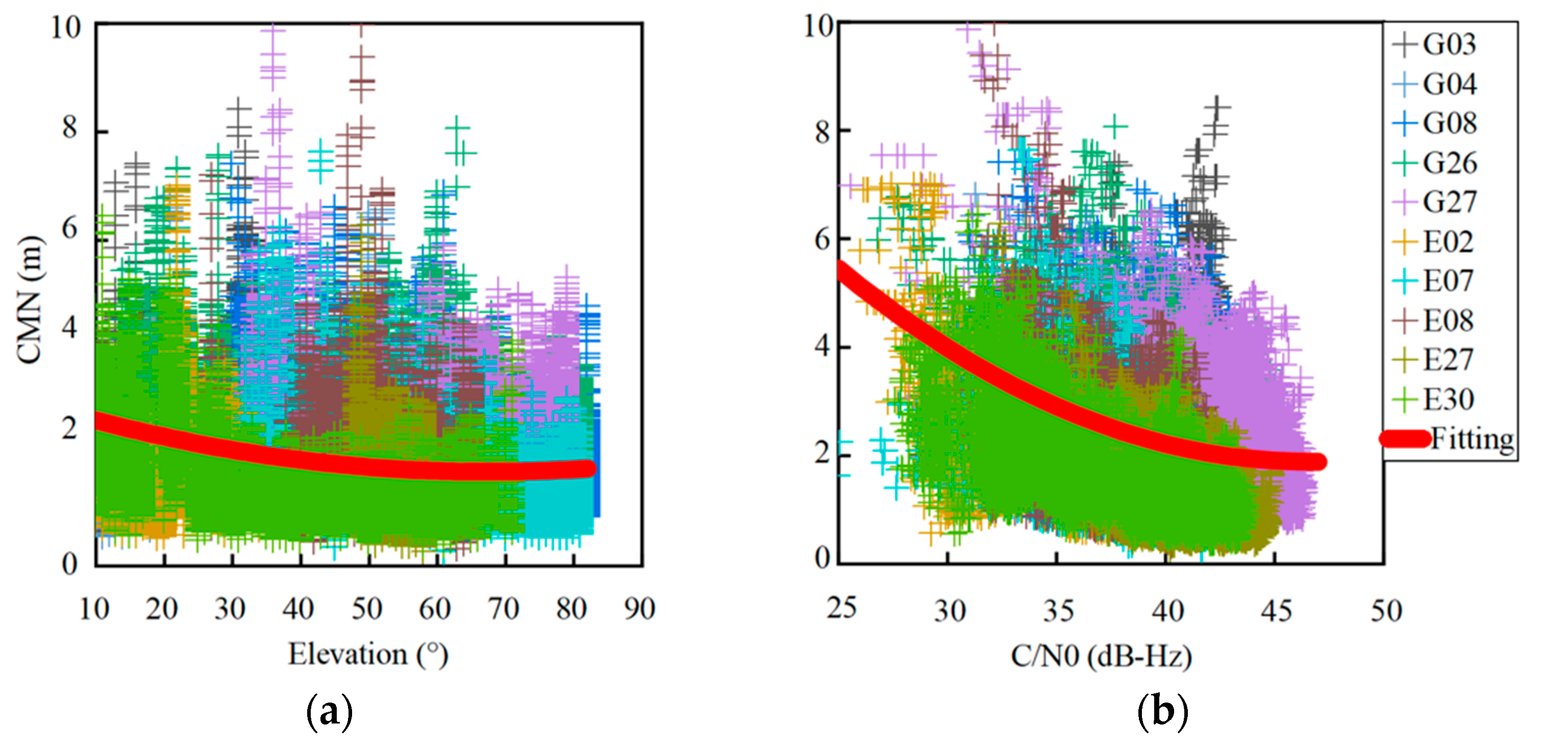
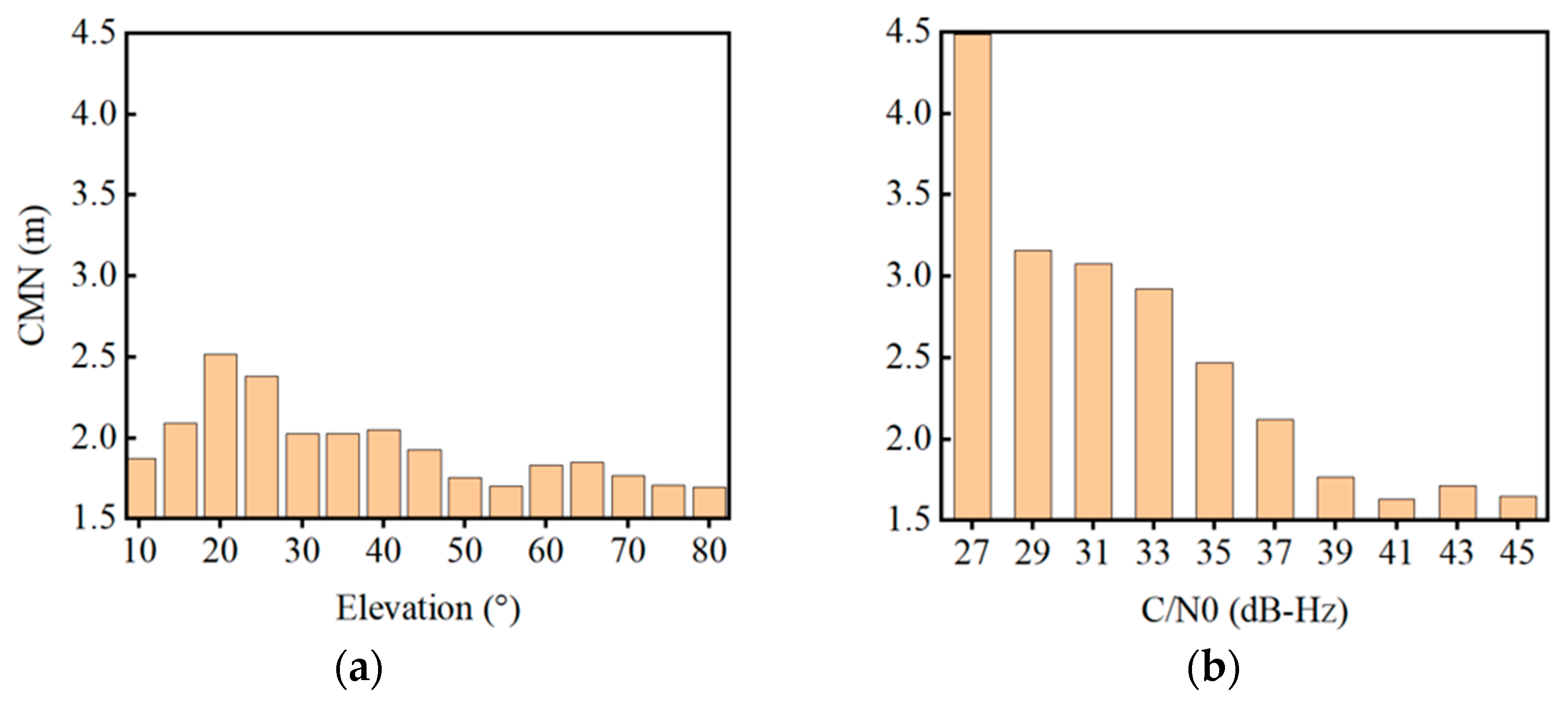
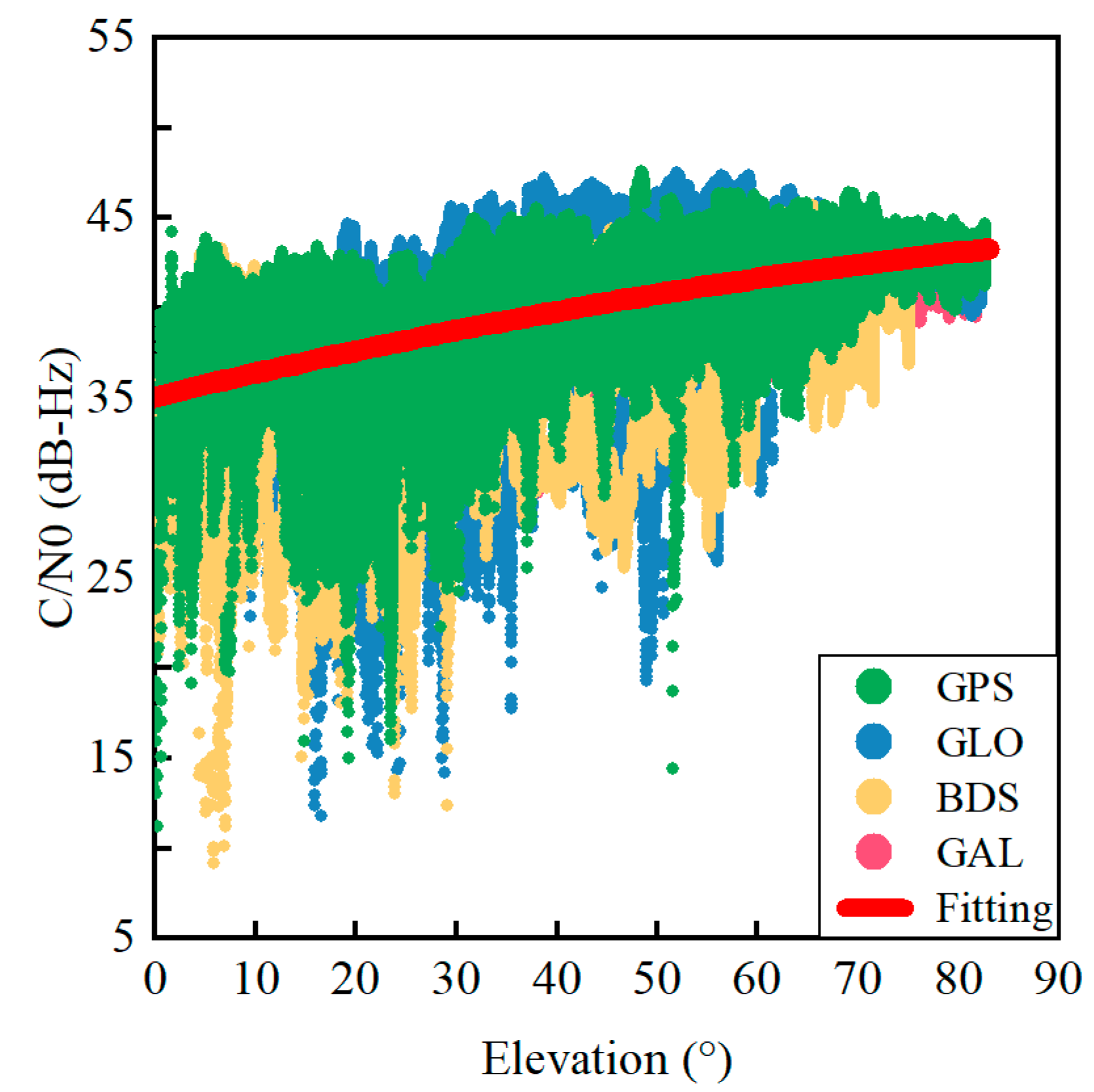
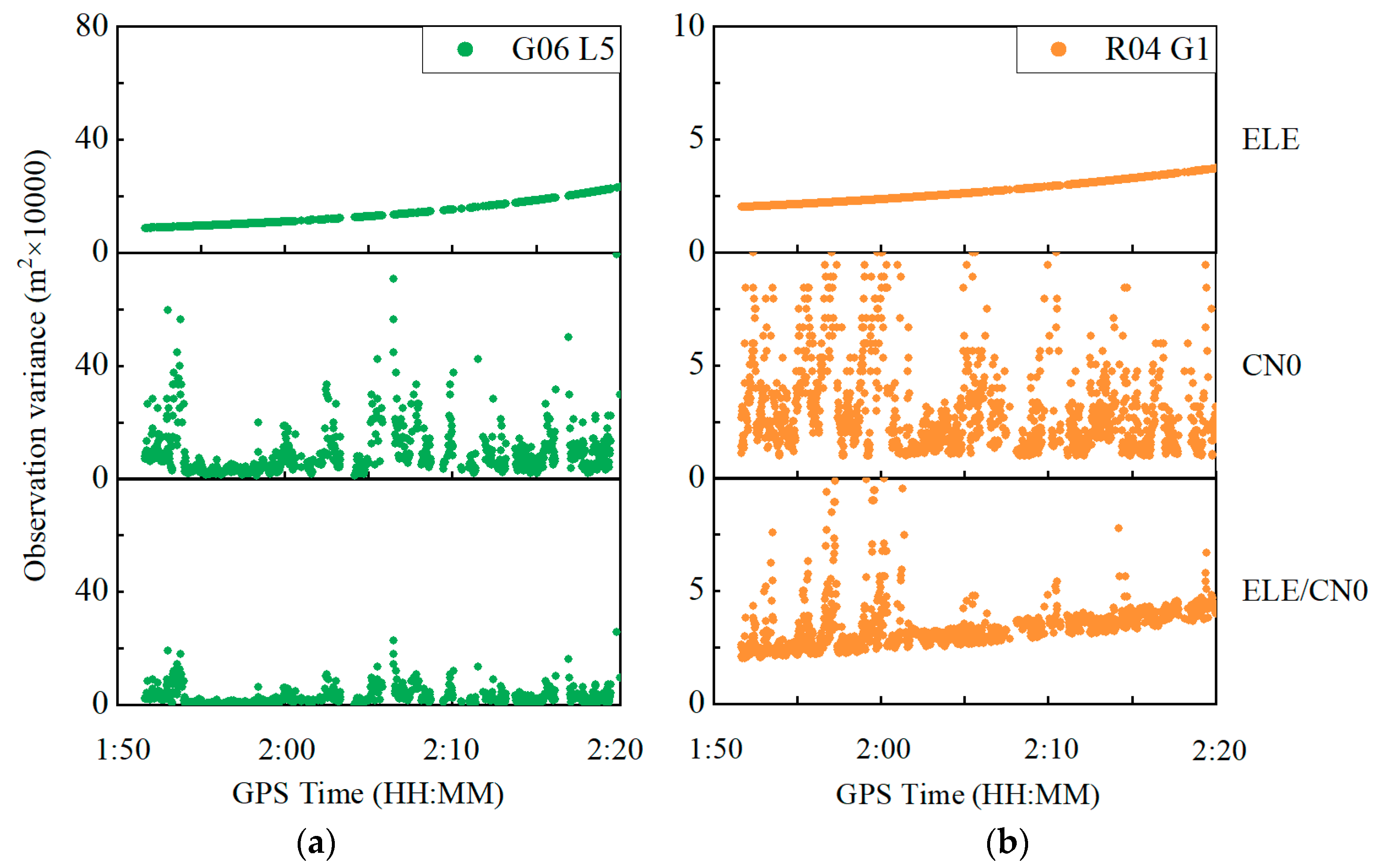
2. Correlation of CMN, Elevation Angle and C/N0
3. Combined Elevation Angle and C/N0 Weighting Method
4. Experimental Results and Discussion
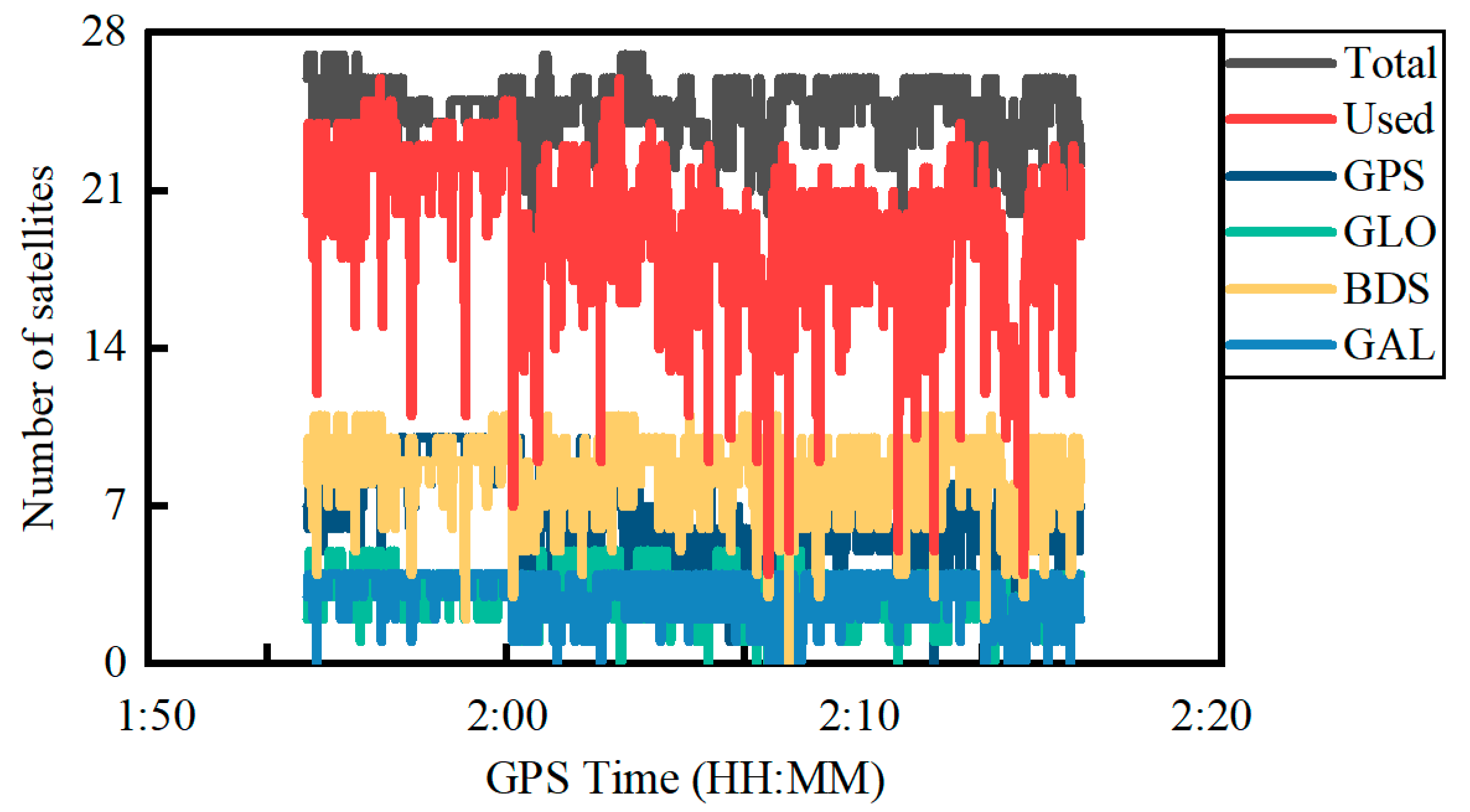
4.1. Quad-Constellation PPP Processing Strategy
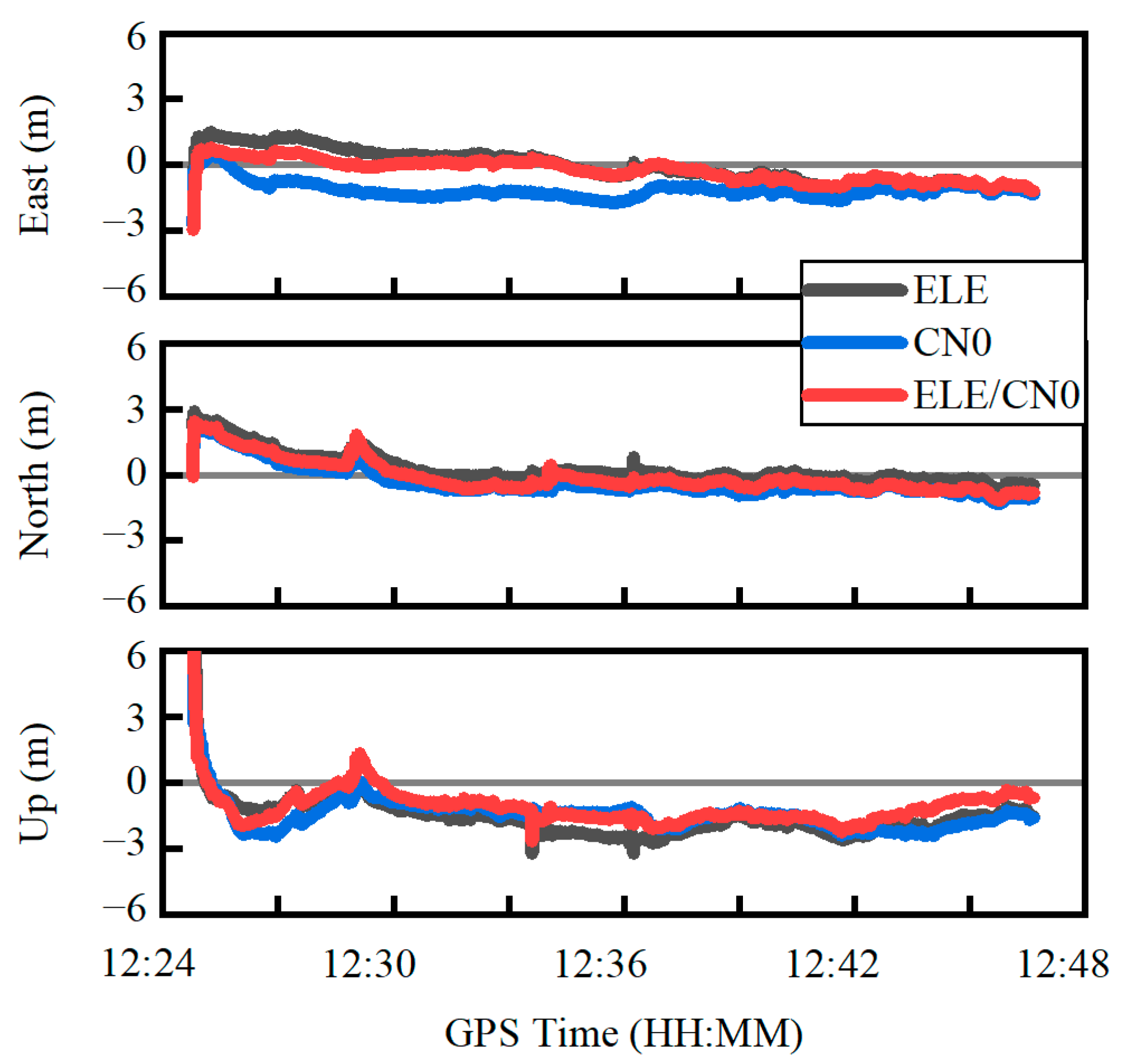
4.2. Kinematic Experiment in an Open Sky Environment
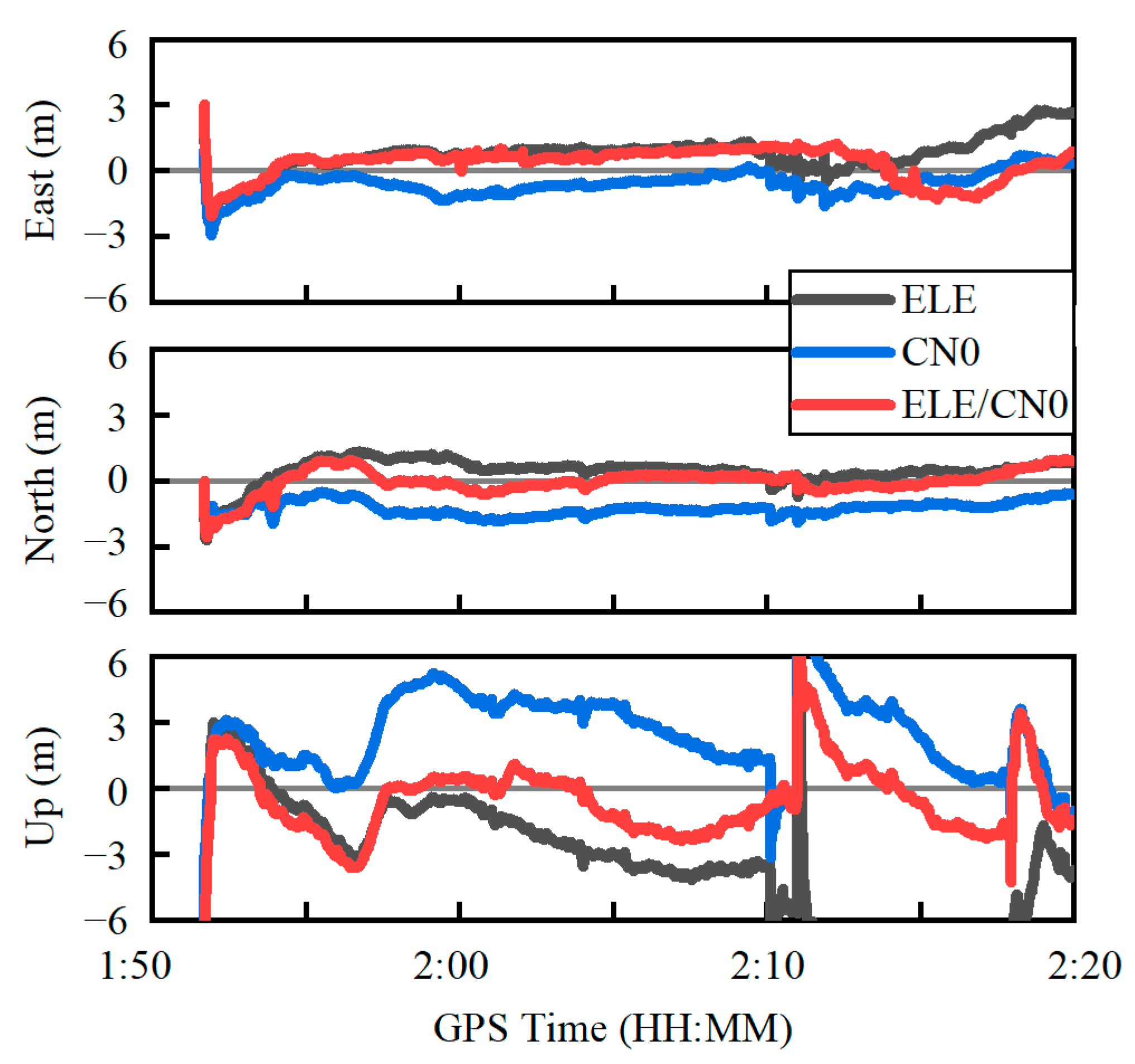
4.3. Kinematic Experiment in Constrained Visibility Environment
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Li, B.; Shen, Y.; Lou, L. Efficient Estimation of Variance and Covariance Components: A Case Study for GPS Stochastic Model Evaluation. IEEE Trans. Geosci. Remote Sens. 2010, 49, 203–210. [Google Scholar] [CrossRef]
- Li, B.; Lou, L.; Shen, Y. GNSS Elevation-Dependent Stochastic Modeling and Its Impacts on the Statistic Testing. J. Surv. Eng. 2016, 142, 04015012. [Google Scholar] [CrossRef]
- Robustelli, U.; Baiocchi, V.; Pugliano, G. Assessment of Dual Frequency GNSS Observations from a Xiaomi Mi 8 Android Smartphone and Positioning Performance Analysis. Electronics 2019, 8, 91. [Google Scholar] [CrossRef] [Green Version]
- Håkansson, M. Characterization of GNSS Observations from a Nexus 9 Android Tablet. GPS Solut. 2018, 23, 21. [Google Scholar] [CrossRef] [Green Version]
- Filho, V.C.L.; Moraes, A. Modeling Multifrequency GPS Multipath Fading in Land Vehicle Environments. GPS Solut. 2020, 25, 1–14. [Google Scholar] [CrossRef]
- Paziewski, J.; Sieradzki, R.; Baryla, R. Signal Characterization and Assessment of Code GNSS Positioning with Low-Power Consumption Smartphones. GPS Solut. 2019, 23, 1–12. [Google Scholar] [CrossRef] [Green Version]
- Zhang, X.; Tao, X.; Zhu, F.; Shi, X.; Wang, F. Quality Assessment of GNSS Observations from an Android N Smartphone and Positioning Performance Analysis using Time-Differenced Filtering Approach. GPS Solut. 2018, 22, 70. [Google Scholar] [CrossRef]
- Li, G.; Geng, J. Characteristics of Raw Multi-GNSS Measurement Error from Google Android Smart Devices. GPS Solut. 2019, 23, 90. [Google Scholar] [CrossRef]
- Chen, B.; Gao, C.; Liu, Y.; Sun, P. Real-time Precise Point Positioning with a Xiaomi MI 8 Android Smartphone. Sensors 2019, 19, 2835. [Google Scholar] [CrossRef] [Green Version]
- Wu, Q.; Sun, M.; Zhou, C.; Zhang, P. Precise Point Positioning Using Dual-Frequency GNSS Observations on Smartphone. Sensors 2019, 19, 2189. [Google Scholar] [CrossRef] [Green Version]
- Shinghal, G.; Bisnath, S. Conditioning and PPP Processing of Smartphone GNSS Measurements in Realistic Environments. Satell. Navig. 2021, 2, 1–17. [Google Scholar] [CrossRef] [PubMed]
- Zhu, H.; Xia, L.; Wu, D.; Xia, J.; Li, Q. Study on Multi-GNSS Precise Point Positioning Performance with Adverse Effects of Satellite Signals on Android Smartphone. Sensors 2020, 20, 6447. [Google Scholar] [CrossRef] [PubMed]
- Zangenehnejad, F.; Gao, Y. Application of UofC Model Based Multi-GNSS PPP to Smartphones GNSS Positioning. In Proceedings of the 34th International Technical Meeting of the Satellite Division of the Institute of Navigation (ION GNSS+ 2021), St. Louis, MO, USA, 20–24 September 2021; pp. 2986–3003. [Google Scholar]
- Geo++ RINEX Logger App. Available online: https://play.google.com/store/apps/details?id=de.geopp.rinexlogger (accessed on 10 January 2020).
- Estey, L.H.; Meertens, C.M. TEQC: The Multi-Purpose Toolkit for GPS/GLONASS Data. GPS Solut. 1999, 3, 42–49. [Google Scholar] [CrossRef]
- Cai, C.; He, C.; Santerre, R.; Pan, L.; Cui, X.; Zhu, J. A Comparative Analysis of Measurement Noise and Multipath for Four Constellations: GPS, BeiDou, GLONASS and Galileo. Surv. Rev. 2016, 48, 287–295. [Google Scholar] [CrossRef]
- Vaclavovic, P.; Dousa, J. G-Nut/Anubis: Open-Source Tool for Multi-GNSS Data Monitoring with a Multipath Detection for New Signals, Frequencies and Constellations. In IAG 150 Years; Springer: Cham, Switzerland, 2015; pp. 775–782. [Google Scholar] [CrossRef]
- Gill, M.; Bisnath, S.; Aggrey, J.; Seepersad, G. Precise Point Positioning (PPP) using Low-Cost and Ultra-Low-Cost GNSS Receivers. In Proceedings of the 30th International Technical Meeting of The Satellite Division of the Institute of Navigation (ION GNSS+ 2017), Portland, OR, USA, 25–29 September 2017; pp. 226–236. [Google Scholar]
- Takasu, T.; Yasuda, A. Development of the Low-Cost RTK-GPS Receiver with an Open Source Program Package RTKLIB. In Proceedings of the International Symposium on GPS/GNSS, Jeju, Korea, 4–6 November 2009. [Google Scholar]
- Zhang, Z.; Li, B.; Shen, Y.; Gao, Y.; Wang, M. Site-Specific Unmodeled Error Mitigation for GNSS Positioning in Urban Environments Using a Real-Time Adaptive Weighting Model. Remote Sens. 2018, 10, 1157. [Google Scholar] [CrossRef] [Green Version]
- King, R.; Bock, Y. Documentation for the GAMIT GPS Analysis Software; Massachusetts Institute of Technology: Cambridge, MA, USA, 2000; Available online: http://www-gpsg.mit.edu/~simon/gtgk/GAMIT.pdf (accessed on 19 January 2022).
- Dach, R.; Hugentobler, U.; Fridez, P.; Meindl, M. Bernese GPS Software, Version 5.0; Astronomical Institute, University of Bern: Bern, Switzerland, 2007. [Google Scholar]
- Wang, L.; Li, Z.; Wang, N.; Wang, Z. Real-time GNSS Precise Point Positioning for Low-Cost Smart Devices. GPS Solut. 2021, 25, 69. [Google Scholar] [CrossRef]
- Carcanague, S. Low Cost GPS/GLONASS Precise Positioning Algorithm in Constrained Environment. Ph.D. Thesis, Institut National Polytechnique de Toulouse-INP, Toulouse, France, 25 February 2014. [Google Scholar]
- Li, B.; Zang, N.; Ge, H.; Shen, Y. Single-frequency PPP Models: Analytical and Numerical Comparison. J. Geod. 2019, 93, 2499–2514. [Google Scholar] [CrossRef]
- Zhou, F.; Dong, D.; Li, P.; Li, X.; Schuh, H. Influence of Stochastic Modeling for Inter-System Biases on Multi-GNSS Undifferenced and Uncombined Precise Point Positioning. GPS Solut. 2019, 23, 59. [Google Scholar] [CrossRef]
- Liu, Q.; Hernández-Pajares, M.; Yang, H.; Monte-Moreno, E.; Roma-Dollase, D.; García-Rigo, A.; Li, Z.; Wang, N.; Laurichesse, D.; Blot, A.; et al. The Cooperative IGS RT-GIMs: A Reliable Estimation of the Global Ionospheric Electron Content Distribution in Real Time. Earth Syst. Sci. Data 2021, 13, 4567–4582. [Google Scholar] [CrossRef]
- Wang, G.; Bo, Y.; Yu, Q.; Li, M.; Yin, Z.; Chen, Y. Ionosphere-Constrained Single-Frequency PPP with an Android Smartphone and Assessment of GNSS Observations. Sensors 2020, 20, 5917. [Google Scholar] [CrossRef]
- Netthonglang, C.; Thongtan, T.; Satirapod, C. GNSS Precise Positioning Determinations using Smartphones. In Proceedings of the 2019 IEEE Asia Pacific Conference on Circuits and Systems (APCCAS), Bangkok, Thailand, 11–14 November 2019; pp. 401–404. [Google Scholar]
- Kazmierski, K.; Sośnica, K.; Hadas, T. Quality Assessment of Multi-GNSS Orbits and Clocks for Real-Time Precise Point Positioning. GPS Solut. 2017, 22, 11. [Google Scholar] [CrossRef] [Green Version]
- Saastamoinen, J. Atmospheric correction for the troposphere and stratosphere in radio ranging satellites. In The Use of Artificial Satellites for Geodesy; Geophysics Monograph Series; American Geophysical Union: Washington, DC, USA, 1972; pp. 247–251. [Google Scholar]
- Pirazzi, G.; Mazzoni, A.; Biagi, L.; Crespi, M. Preliminary Performance Analysis with a GPS+Galileo Enabled Chipset Embedded in a Smartphone. In Proceedings of the 30th International Technical Meeting of the Satellite Division of the Institute of Navigation (ION GNSS+ 2017), Portland, Oregon, 25–29 September 2017; pp. 101–115. [Google Scholar]

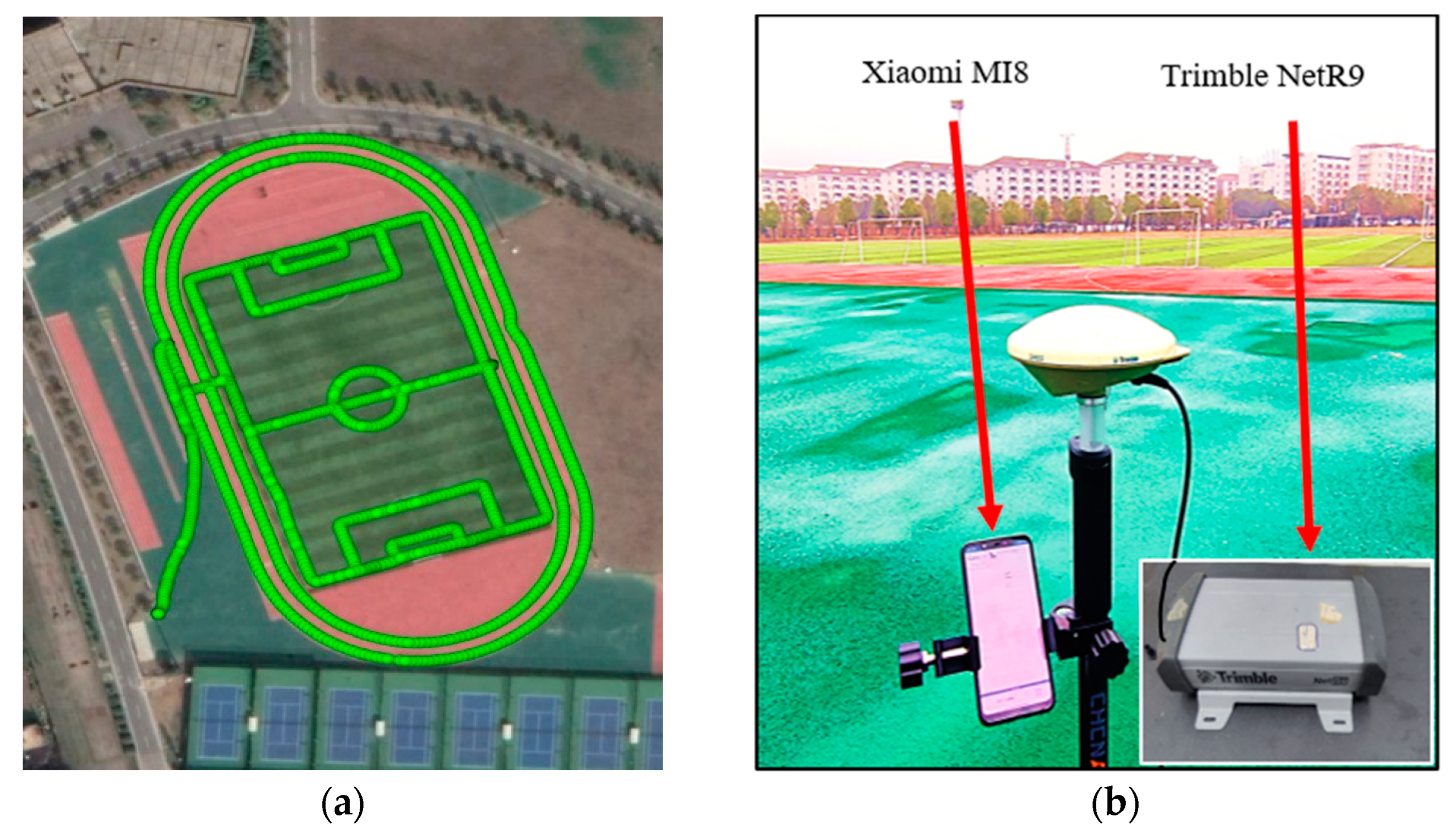
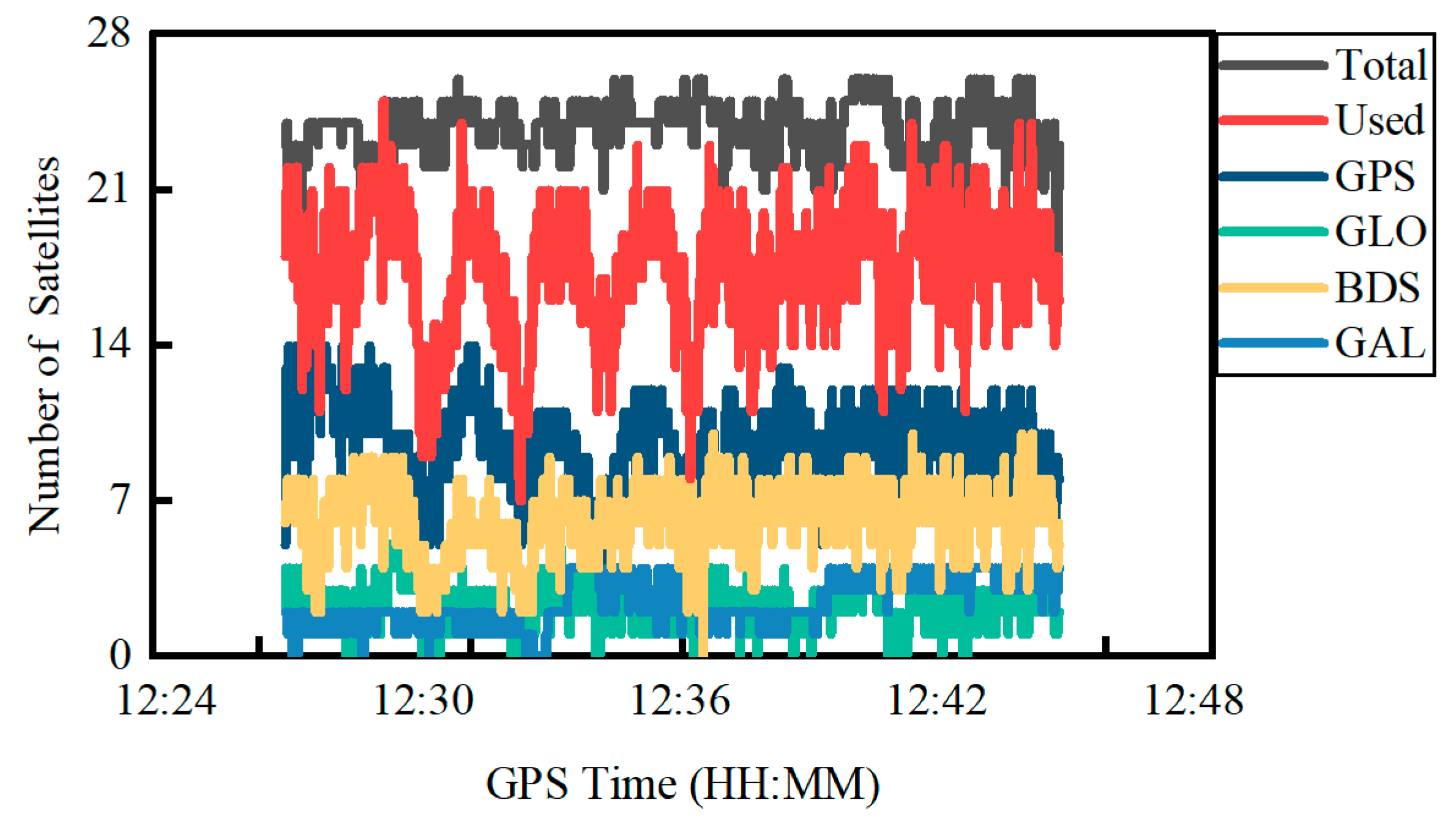
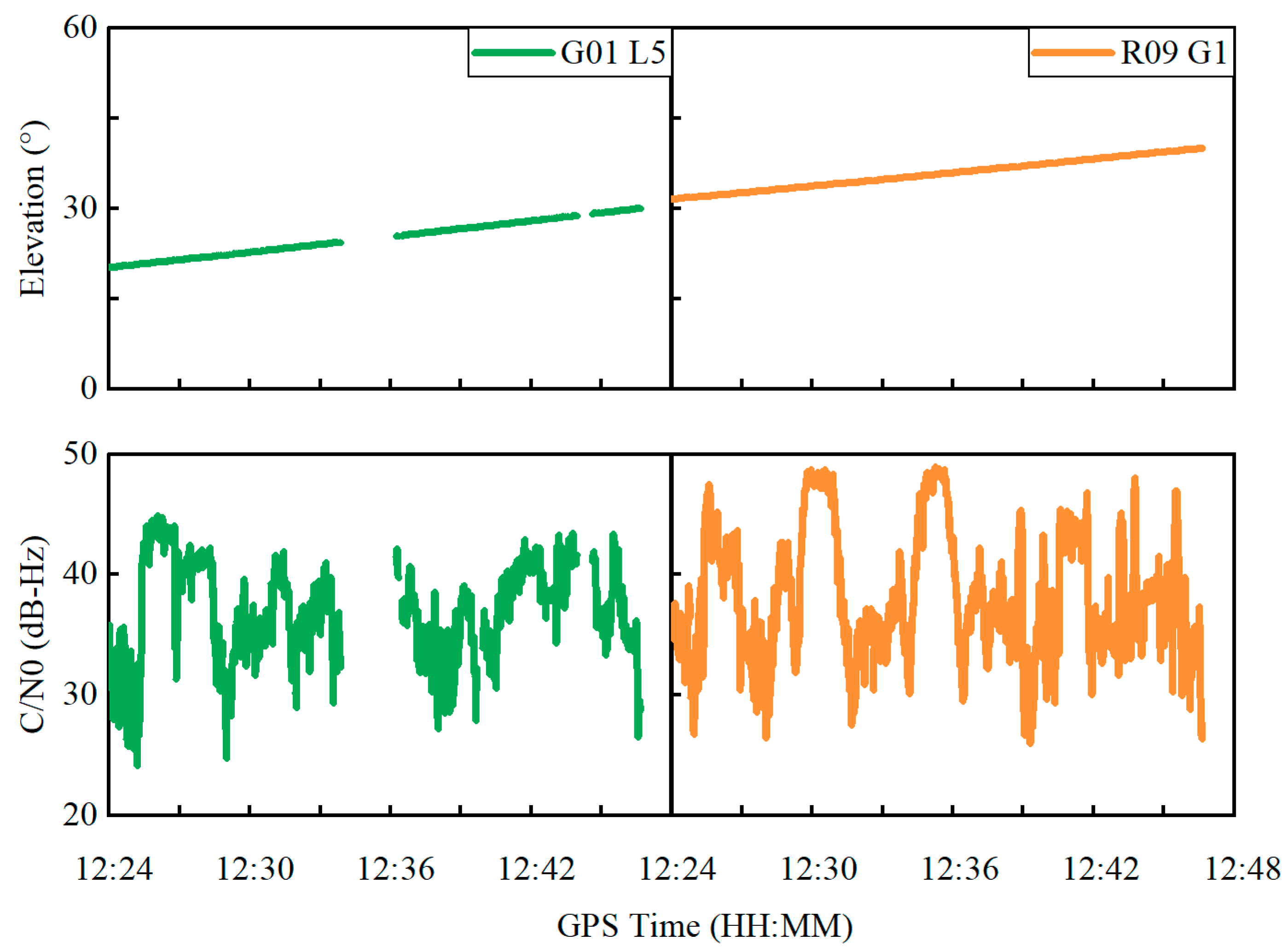
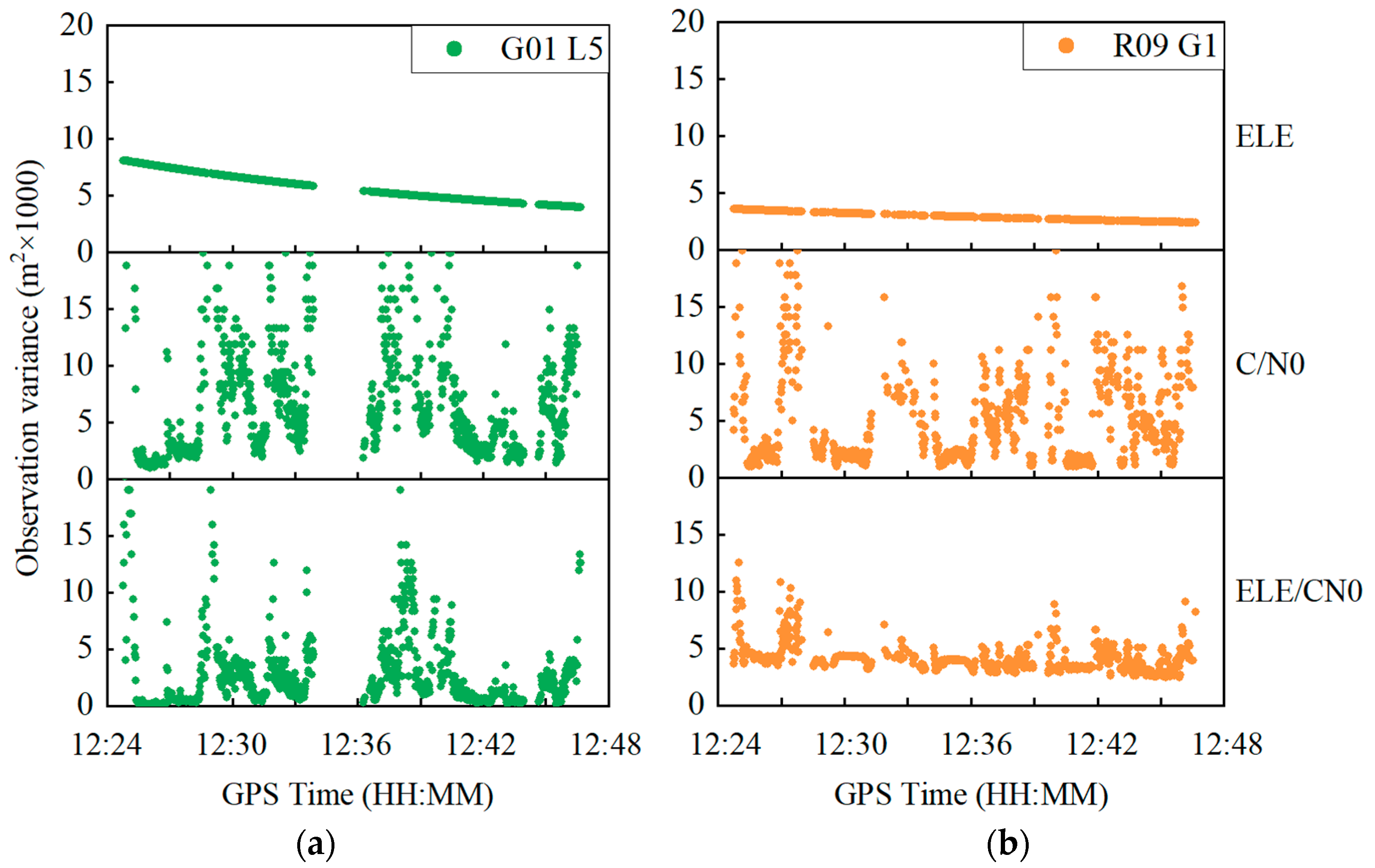

| Items | Processing Strategies |
|---|---|
| Estimation method | Kalman filter |
| Constellations | GPS (L1, L5)/GLONASS (G1)/BDS (B1)/Galileo (E1, E5a) |
| Weighting scheme | Combined elevation angle and C/N0 weighting method |
| Satellite orbit and clock | Real-time precise satellite orbit and clock products from Centre National d’Etudes Spatiales (CNES) [30] |
| Ionospheric delay | Estimated as random walk process and GIM products are used as pseudo-observations |
| Tropospheric delay | Hydrostatic delay uses Saastamoinen model correction [31], and zenith wet delay is estimated as random walk noise process |
| Receiver position | Estimated as random walk process |
| Receiver clock offset | Estimated as white noise |
| Inter-system bias | Estimated as white noise |
| Ambiguities | Estimated as constants |
| ELE | C/N0 | ELE/CN0 | |
|---|---|---|---|
| East (m) | 0.74 | 1.19 | 0.55 |
| North (m) | 0.75 | 0.77 | 0.73 |
| Up (m) | 1.83 | 1.62 | 1.35 |
| 3D (m) | 2.11 | 2.15 | 1.63 |
| ELE | CN0 | ELE/CN0 | |
|---|---|---|---|
| East (m) | 1.24 | 0.83 | 1.00 |
| North (m) | 0.71 | 1.28 | 0.62 |
| Up (m) | 5.03 | 3.03 | 2.22 |
| 3D (m) | 5.23 | 3.39 | 2.51 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Y.; Cai, C.; Xu, Z. A Combined Elevation Angle and C/N0 Weighting Method for GNSS PPP on Xiaomi MI8 Smartphones. Sensors 2022, 22, 2804. https://doi.org/10.3390/s22072804
Li Y, Cai C, Xu Z. A Combined Elevation Angle and C/N0 Weighting Method for GNSS PPP on Xiaomi MI8 Smartphones. Sensors. 2022; 22(7):2804. https://doi.org/10.3390/s22072804
Chicago/Turabian StyleLi, Yanjie, Changsheng Cai, and Zhenyu Xu. 2022. "A Combined Elevation Angle and C/N0 Weighting Method for GNSS PPP on Xiaomi MI8 Smartphones" Sensors 22, no. 7: 2804. https://doi.org/10.3390/s22072804
APA StyleLi, Y., Cai, C., & Xu, Z. (2022). A Combined Elevation Angle and C/N0 Weighting Method for GNSS PPP on Xiaomi MI8 Smartphones. Sensors, 22(7), 2804. https://doi.org/10.3390/s22072804





