Sparse Damage Detection with Complex Group Lasso and Adaptive Complex Group Lasso
Abstract
:1. Introduction
2. Signal Model
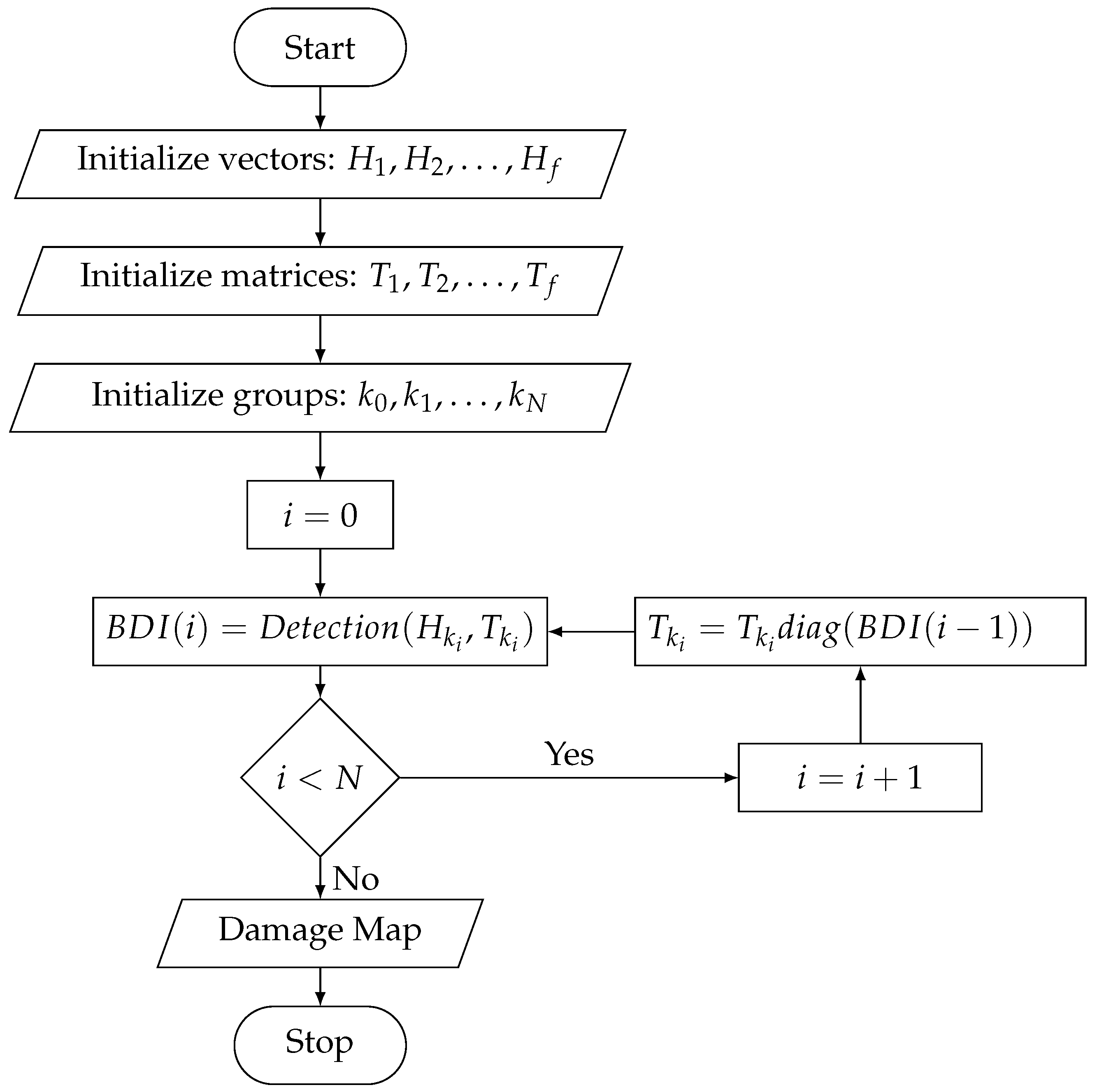
3. Sparse Damage Detection with Complex Group Lasso
3.1. Complex Group Lasso
| Algorithm 1:Complex Group Lasso For Damage Detection |
 |
3.2. Adaptive Complex Group Lasso
| Algorithm 2:Adaptive Complex Group Lasso For Damage Detection |
 |
4. Experimental Validation
4.1. Experimental Setup
- (i)
- : 1 point-like mass,
- (ii)
- : 4 point-like masses,
- (iii)
- : 1 extended mass oriented under 45° with respect to the edges of the plate.
4.2. Experiment
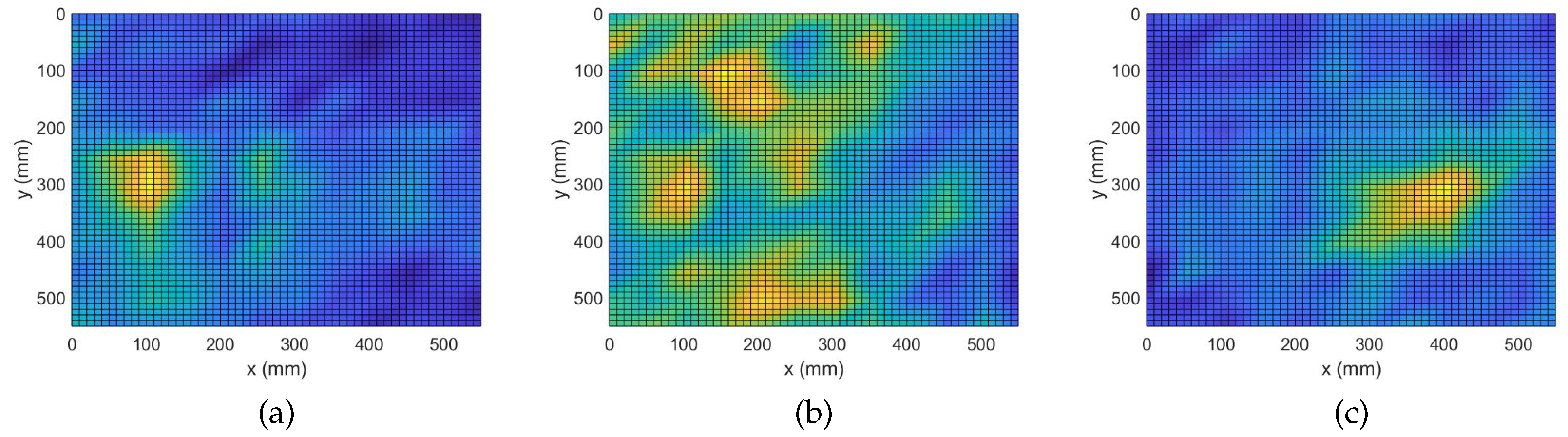
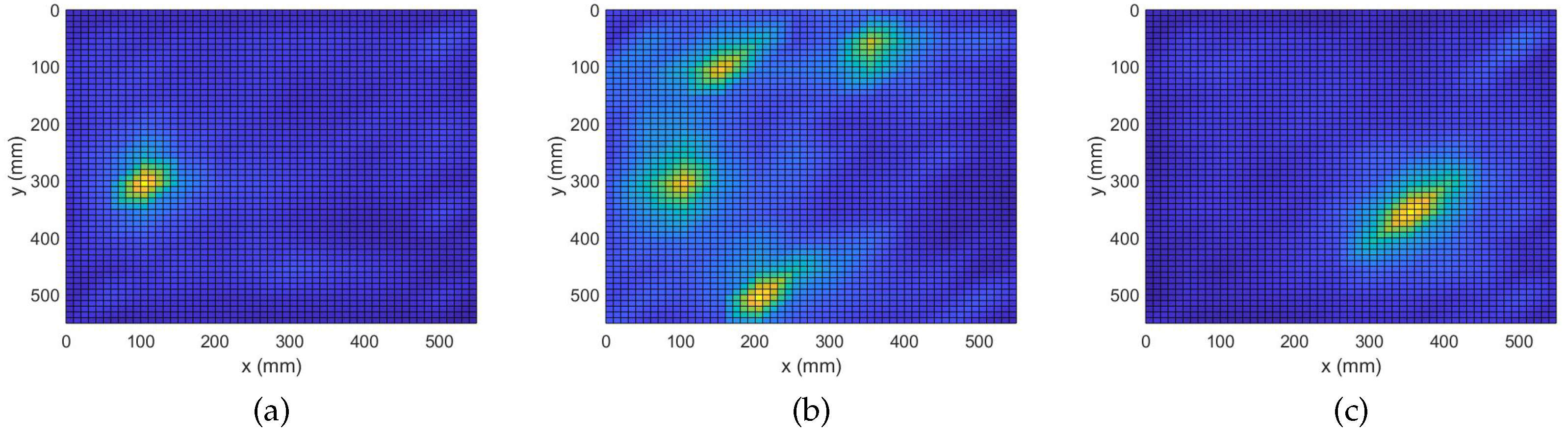
4.3. Damage Detection with Complex Group Lasso
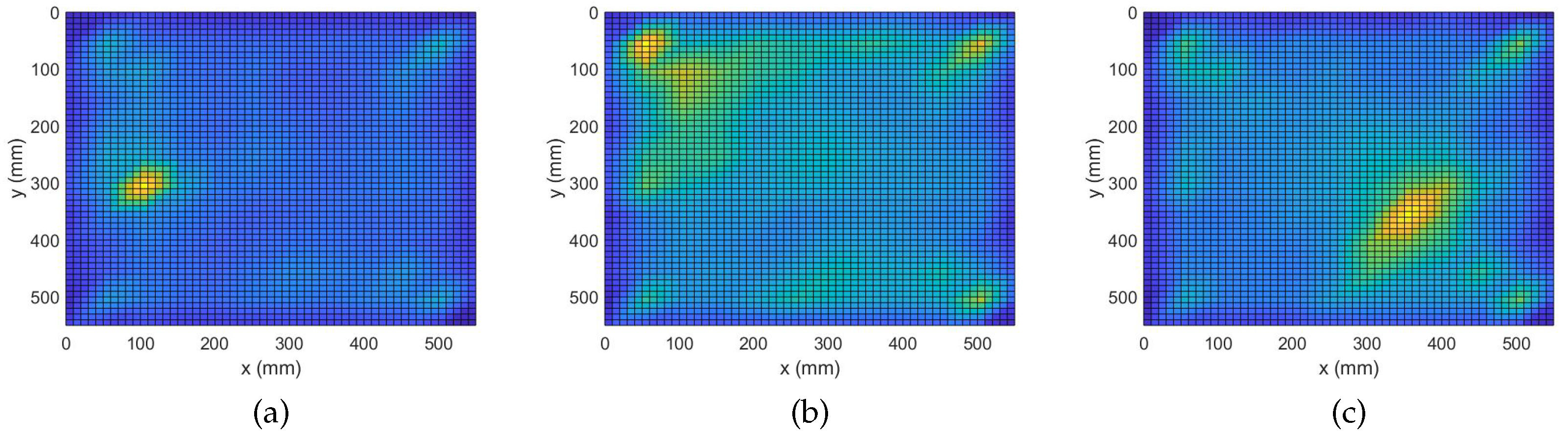
4.4. Damage Detection with Adaptive Complex Group Lasso
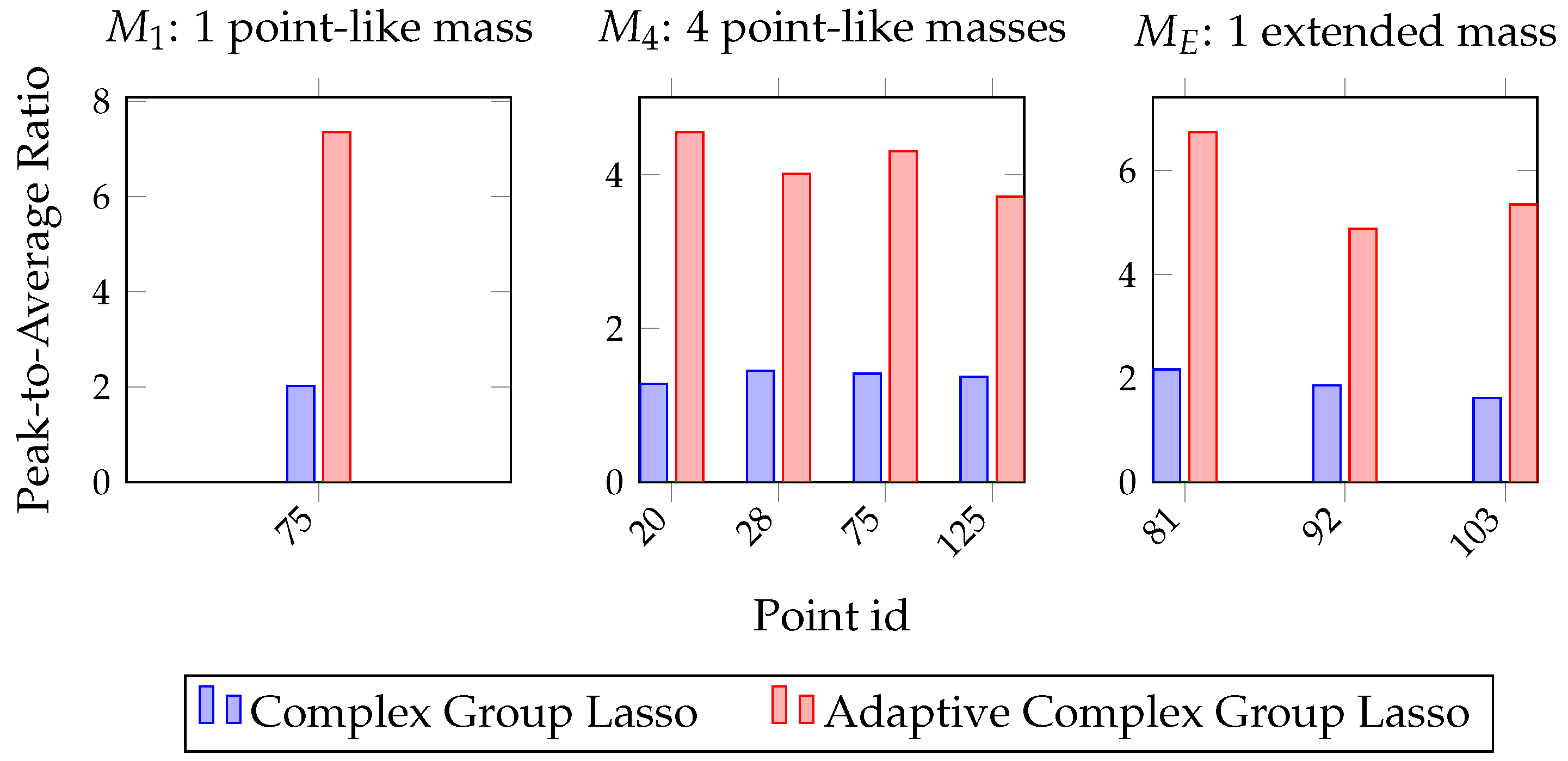
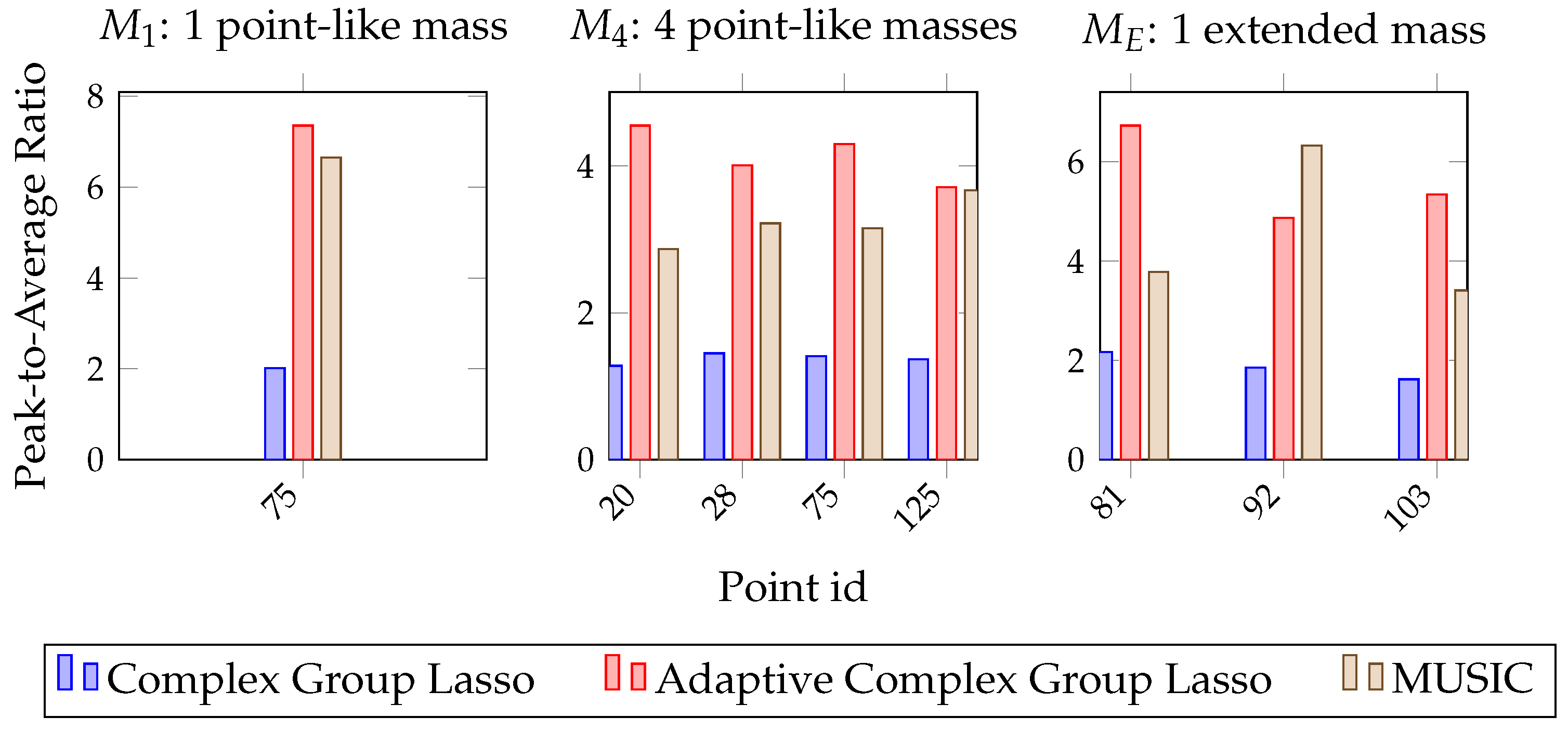
4.5. Quantification and Performance Comparison
5. Performance Comparison against Full-Array Super-Resolution MUSIC
5.1. MUSIC and Super-Resolution Algorithms
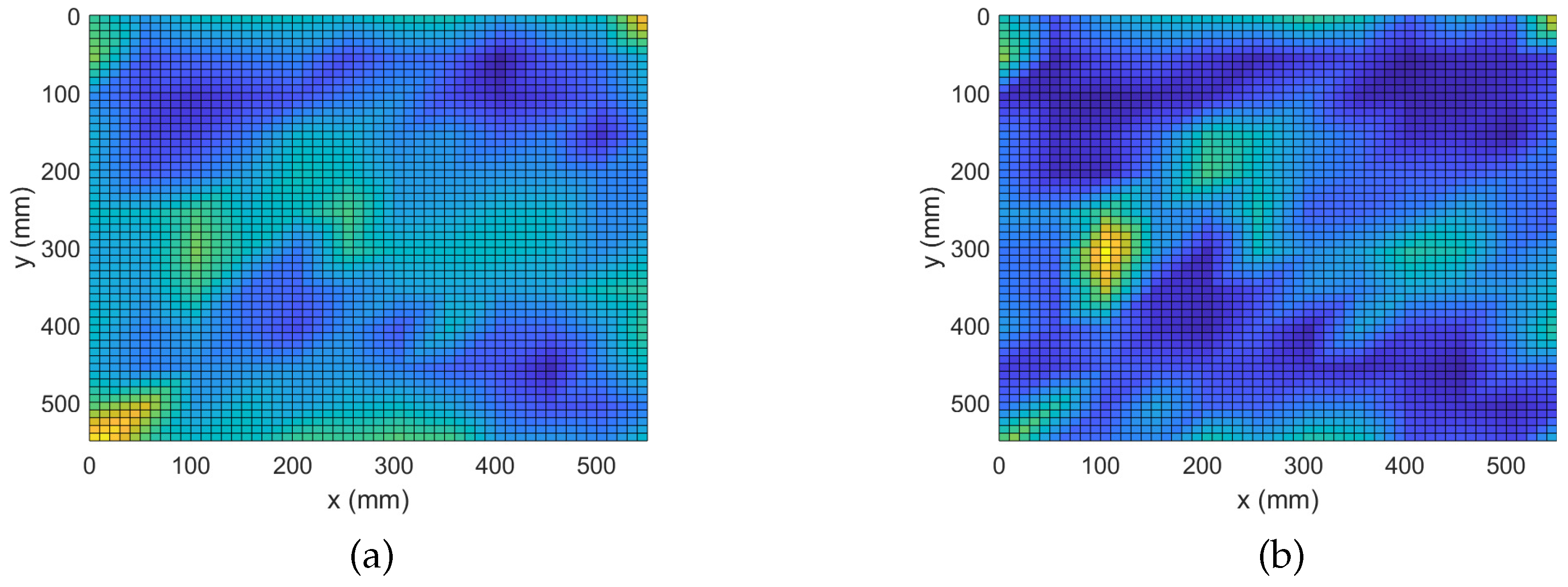
5.2. Single Sensor MUSIC Damage Detection and Performance Comparison
5.3. Full Array MUSIC Damage Detection and Performance Comparison
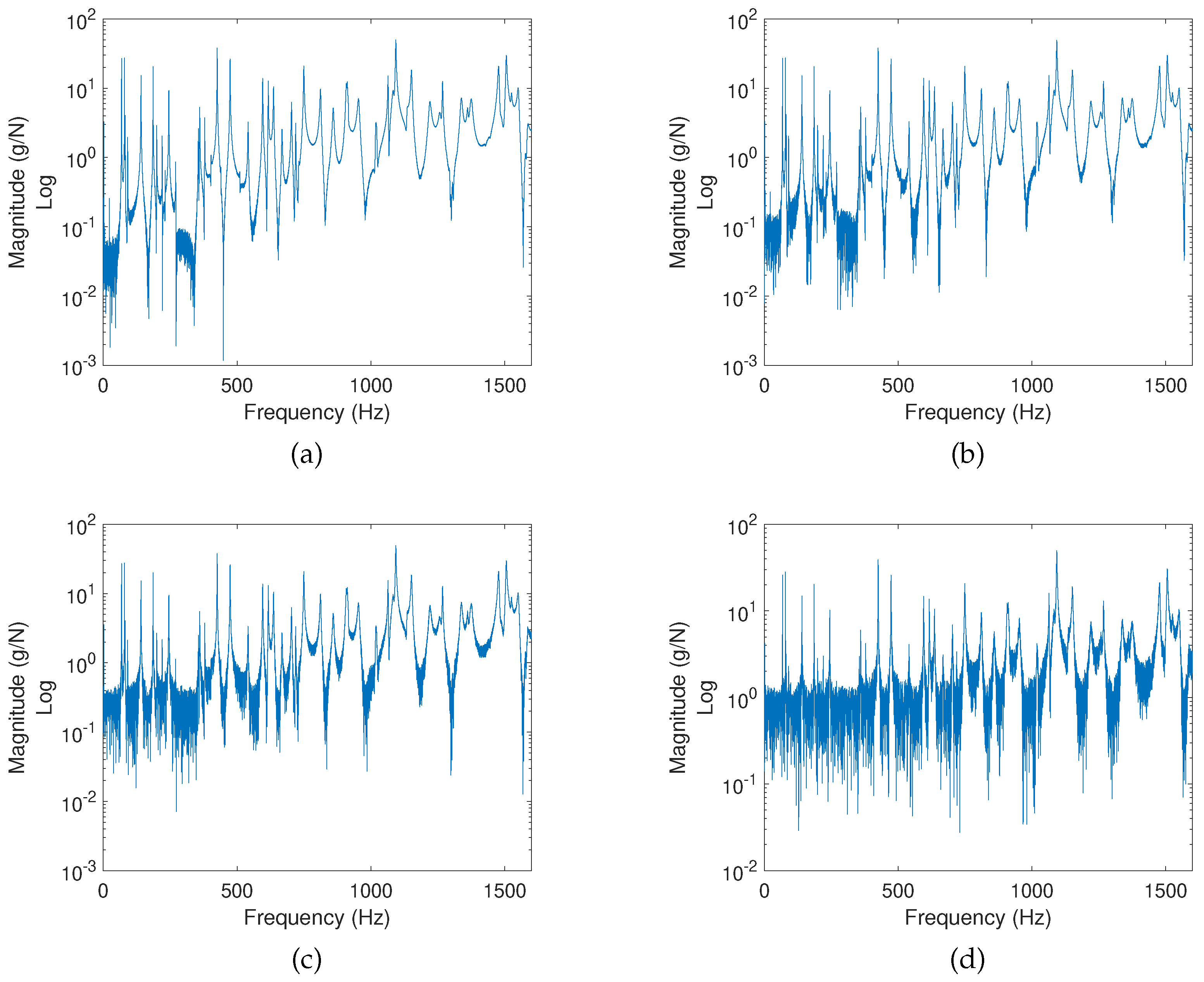
6. Influence of Noise
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| FRF | Frequency Response Function |
| Lasso | Least absolute shrinkage and selection operator |
| MUSIC | Multiple Signal Classification |
| BDI | Broadband Damage Indicator |
| PAR | Peak-to-Average Ratio |
| SNR | Signal to Noise Ratio |
References
- Rytter, A. Vibrational Based Inspection of Civil Engineering Structures. Ph.D. Thesis, University of Aalborg, Aalborg, Denmark, 1993. [Google Scholar]
- Park, J.; Park, Y. Experimental Verification of Fault Identification for Overactuated System With a Scaled-Down Electric Vehicle. Int. J. Automot. Technol. 2020, 21, 1037–1045. [Google Scholar] [CrossRef]
- Balasubramaniam, K.; Sikdar, S.; Fiborek, P.; Malinowski, P.H. Ultrasonic Guided Wave Signal Based Nondestructive Testing of a Bonded Composite Structure Using Piezoelectric Transducers. Signals 2021, 2, 2. [Google Scholar] [CrossRef]
- Khatir, S.; Tiachacht, S.; Le Thanh, C.; Ghandourah, E.; Mirjalili, S.; Abdel Wahab, M. An improved Artificial Neural Network using Arithmetic Optimization Algorithm for damage assessment in FGM composite plates. Compos. Struct. 2021, 273, 114287. [Google Scholar] [CrossRef]
- Xiao, C.; Yu, M.; Wang, H.; Zhang, B.; Wang, D. Prognosis of Electric Scooter With Intermittent Faults: Dual Degradation Processes Approach. IEEE Trans. Veh. Technol. 2022, 71, 1411–1425. [Google Scholar] [CrossRef]
- Harter, H.L. The method of least squares and some alternatives. Part IV. Int. Stat. Rev. 1975, 43, 125–190. [Google Scholar] [CrossRef]
- Hoerl, A.E.; Kennard, R.W. Ridge Regression: Biased Estimation for Nonorthogonal Problems. Technometrics 2000, 42, 80–86. [Google Scholar] [CrossRef]
- Tibshirani, R. Regression Shrinkage and Selection Via the Lasso. J. R. Stat. Soc. Ser. B Methodol. 1996, 58, 267–288. [Google Scholar] [CrossRef]
- Plumbley, M.D.; Blumensath, T.; Daudet, L.; Gribonval, R.; Davies, M.E. Sparse Representations in Audio and Music: From Coding to Source Separation. Proc. IEEE 2010, 98, 995–1005. [Google Scholar] [CrossRef]
- Yang, A.; Kretzler, M.; Janssen, S.; Gulani, V.; Seiberlich, N. Sparse Reconstruction Techniques in Magnetic Resonance Imaging. Investig. Radiol. 2016, 51, 349–364. [Google Scholar] [CrossRef]
- Ogutu, J.O.; Schulz-Streeck, T.; Piepho, H.P. Genomic selection using regularized linear regression models: Ridge regression, lasso, elastic net and their extensions. BMC Proc. 2012, 6, S10. [Google Scholar] [CrossRef] [Green Version]
- Smith, C.B.; Hernandez, E.M. Detection of spatially sparse damage using impulse response sensitivity and LASSO regularization. Inverse Probl. Sci. Eng. 2019, 27, 1–16. [Google Scholar] [CrossRef]
- Chen, Z.; Sun, H. Sparse representation for damage identification of structural systems. Struct. Health Monit. 2021, 20, 1644–1656. [Google Scholar] [CrossRef]
- Hou, R.; Wang, X.; Xia, Y. Sparse damage detection via the elastic net method using modal data. Struct. Health Monit. 2021, 1–17. [Google Scholar] [CrossRef]
- Zou, H.; Hastie, T. Regularization and variable selection via the elastic net. J. R. Stat. Soc. Ser. B (Stat. Methodol.) 2005, 67, 301–320. [Google Scholar] [CrossRef] [Green Version]
- Fan, X.; Li, J. Damage Identification in Plate Structures Using Sparse Regularization Based Electromechanical Impedance Technique. Sensors 2020, 20, 7069. [Google Scholar] [CrossRef]
- Hou, R.; Xia, Y.; Xia, Q.; Zhou, X. Genetic algorithm based optimal sensor placement for L1-regularized damage detection. Struct. Control Health Monit. 2019, 26, e2274. [Google Scholar] [CrossRef] [Green Version]
- Chen, C.; Pan, C.; Chen, Z.; Yu, L. Structural damage detection via combining weighted strategy with trace Lasso. Adv. Struct. Eng. 2018, 22, 597–612. [Google Scholar] [CrossRef]
- Ding, Z.; Li, J.; Hao, H. Structural damage identification using improved Jaya algorithm based on sparse regularization and Bayesian inference. Mech. Syst. Signal Process. 2019, 132, 211–231. [Google Scholar] [CrossRef]
- Yang, Y.; Nagarajaiah, S. Structural damage identification via a combination of blind feature extraction and sparse representation classification. Mech. Syst. Signal Process. 2014, 45, 1–23. [Google Scholar] [CrossRef]
- Wang, W.; Bao, Y.; Zhou, W.; Li, H. Sparse representation for Lamb-wave-based damage detection using a dictionary algorithm. Ultrasonics 2018, 87, 48–58. [Google Scholar] [CrossRef]
- Chen, Z.; Pan, C.; Yu, L. Structural damage detection via adaptive dictionary learning and sparse representation of measured acceleration responses. Measurement 2018, 128, 377–387. [Google Scholar] [CrossRef]
- Kong, Y.; Qin, Z.; Wang, T.; Rao, M.; Feng, Z.; Chu, F. Data-driven dictionary design–based sparse classification method for intelligent fault diagnosis of planet bearings. Struct. Health Monit. 2021, 1–16. [Google Scholar] [CrossRef]
- Mitra, M.; Gopalakrishnan, S. Guided wave based structural health monitoring: A review. Smart Mater. Struct. 2016, 25, 053001. [Google Scholar] [CrossRef]
- Levine, R.M.; Michaels, J.E. Model-based imaging of damage with Lamb waves via sparse reconstruction. J. Acoust. Soc. Am. 2013, 133, 1525–1534. [Google Scholar] [CrossRef]
- Sen, D.; Aghazadeh, A.; Mousavi, A.; Nagarajaiah, S.; Baraniuk, R. Sparsity-based approaches for damage detection in plates. Mech. Syst. Signal Process. 2019, 117, 333–346. [Google Scholar] [CrossRef]
- Alguri, K.S.; Melville, J.; Harley, J.B. Baseline-free guided wave damage detection with surrogate data and dictionary learning. J. Acoust. Soc. Am. 2018, 143, 3807–3818. [Google Scholar] [CrossRef] [Green Version]
- Carlin, M.; Rocca, P.; Oliveri, G.; Viani, F.; Massa, A. Directions-of-arrival estimation through bayesian compressive sensing strategies. IEEE Trans. Antennas Propag. 2013, 61, 3828–3838. [Google Scholar] [CrossRef]
- Wu, Q.; Zhang, Y.D.; Amin, M.G.; Himed, B. Complex multitask Bayesian compressive sensing. In Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing, ICASSP, Florence, Italy, 4–9 May 2014; pp. 3375–3379. [Google Scholar] [CrossRef]
- Yuan, M.; Lin, Y. Model selection and estimation in regression with grouped variables. J. R. Stat. Soc. Ser. B Stat. Methodol. 2006, 68, 49–67. [Google Scholar] [CrossRef]
- Schmidt, R. Multiple emitter location and signal parameter estimation. IEEE Trans. Antennas Propag. 1986, 34, 276–280. [Google Scholar] [CrossRef] [Green Version]
- Marengo, E.A.; Gruber, F.K.; Simonetti, F. Time-reversal MUSIC imaging of extended targets. IEEE Trans. Image Process. 2007, 16, 1967–1984. [Google Scholar] [CrossRef]
- Lev-Ari, H.; Devancy, A. The time-reversal technique re-interpreted: Subspace-based signal processing for multi-static target location. In Proceedings of the 2000 IEEE Sensor Array and Multichannel Signal Processing Workshop, SAM 2000 (Cat. No. 00EX410), Cambridge, MA, USA, 16–17 March 2000; pp. 509–513. [Google Scholar] [CrossRef]
- Mairal, J.; Jenatton, R.; Obozinski, G.; Bach, F. Network Flow Algorithms for Structured Sparsity. Adv. Neural Inf. Processing Syst. 2010, 23, 1558–1566. [Google Scholar] [CrossRef]
- Leng, C.; Lin, Y.; Wahba, G. A note on the LASSO and related procedures in model selection. Stat. Sin. 2004, 16, 4. [Google Scholar]
- Fan, J.; Li, R. Variable Selection via Nonconcave Penalized Likelihood and its Oracle Properties. J. Am. Stat. Assoc. 2001, 96, 1348–1360. [Google Scholar] [CrossRef]
- Zou, H. The adaptive lasso and its oracle properties. J. Am. Stat. Assoc. 2006, 101, 1418–1429. [Google Scholar] [CrossRef] [Green Version]
- Wang, H.; Leng, C. A note on adaptive group lasso. Comput. Stat. Data Anal. 2008, 52, 5277–5286. [Google Scholar] [CrossRef]
- Wang, M.; Tian, G.L. Adaptive group Lasso for high-dimensional generalized linear models. Stat. Pap. 2019, 60, 1469–1486. [Google Scholar] [CrossRef]
- Yue, N.; Aliabadi, M. Hierarchical approach for uncertainty quantification and reliability assessment of guided wave based structural health monitoring. Struct. Health Monit. 2020, 1–26. [Google Scholar] [CrossRef]
- Ihn, J.B.; Chang, F.K. Pitch-catch Active Sensing Methods in Structural Health Monitoring for Aircraft Structures. Struct. Health Monit. 2008, 7, 5–19. [Google Scholar] [CrossRef]
- He, J.; Yuan, F.G. Lamb waves based fast subwavelength imaging using a DORT-MUSIC algorithm. AIP Conf. Proc. 2016, 1706, 030022. [Google Scholar] [CrossRef] [Green Version]
- Lehman, S.K.; Devaney, A.J. Transmission mode time-reversal super-resolution imaging. J. Acoust. Soc. Am. 2003, 113, 2742–2753. [Google Scholar] [CrossRef]
- Labyed, Y.; Huang, L. Ultrasound Time-Reversal MUSIC Imaging of Extended Targets. Ultrasound Med. Biol. 2012, 38, 2018–2030. [Google Scholar] [CrossRef] [PubMed]
- Zhong, Y.; Yuan, S.; Qiu, L. Multiple damage detection on aircraft composite structures using near-field MUSIC algorithm. Sens. Actuators A Phys. 2014, 214, 234–244. [Google Scholar] [CrossRef]
- Becht, P.; Deckers, E.; Claeys, C.; Pluymers, B.; Desmet, W. Loose bolt detection in a complex assembly using a vibro-acoustic sensor array. Mech. Syst. Signal Process. 2019, 130, 433–451. [Google Scholar] [CrossRef]
- Wang, Y.; Egner, F.S.; Willems, T.; Kirchner, M.; Desmet, W. Camera-based experimental modal analysis with impact excitation: Reaching high frequencies thanks to one accelerometer and random sampling in time. Mech. Syst. Signal Process. 2022, 170, 108879. [Google Scholar] [CrossRef]
- Staszewski, W.; Jenal, R.; Klepka, A.; Szwedo, M.; Uhl, T. A Review of Laser Doppler Vibrometry for Structural Health Monitoring Applications. Key Eng. Mater. 2012, 518, 1–15. [Google Scholar]
- Klis, R.; Chatzi, E.N. Vibration monitoring via spectro-temporal compressive sensing for wireless sensor networks. Struct. Infrastruct. Eng. 2017, 13, 195–209. [Google Scholar] [CrossRef]





| S | ||||||||
|---|---|---|---|---|---|---|---|---|
| Point | 17 | 46 | 51 | 67 | 95 | 116 | 122 | 67 |
| x (mm) | 200 | 450 | 100 | 300 | 500 | 350 | 50 | 300 |
| y (mm) | 50 | 150 | 200 | 250 | 350 | 450 | 500 | 250 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dimopoulos, V.; Desmet, W.; Deckers, E. Sparse Damage Detection with Complex Group Lasso and Adaptive Complex Group Lasso. Sensors 2022, 22, 2978. https://doi.org/10.3390/s22082978
Dimopoulos V, Desmet W, Deckers E. Sparse Damage Detection with Complex Group Lasso and Adaptive Complex Group Lasso. Sensors. 2022; 22(8):2978. https://doi.org/10.3390/s22082978
Chicago/Turabian StyleDimopoulos, Vasileios, Wim Desmet, and Elke Deckers. 2022. "Sparse Damage Detection with Complex Group Lasso and Adaptive Complex Group Lasso" Sensors 22, no. 8: 2978. https://doi.org/10.3390/s22082978






