Super-Resolution Ultrasound Imaging Scheme Based on a Symmetric Series Convolutional Neural Network
Abstract
:1. Introduction
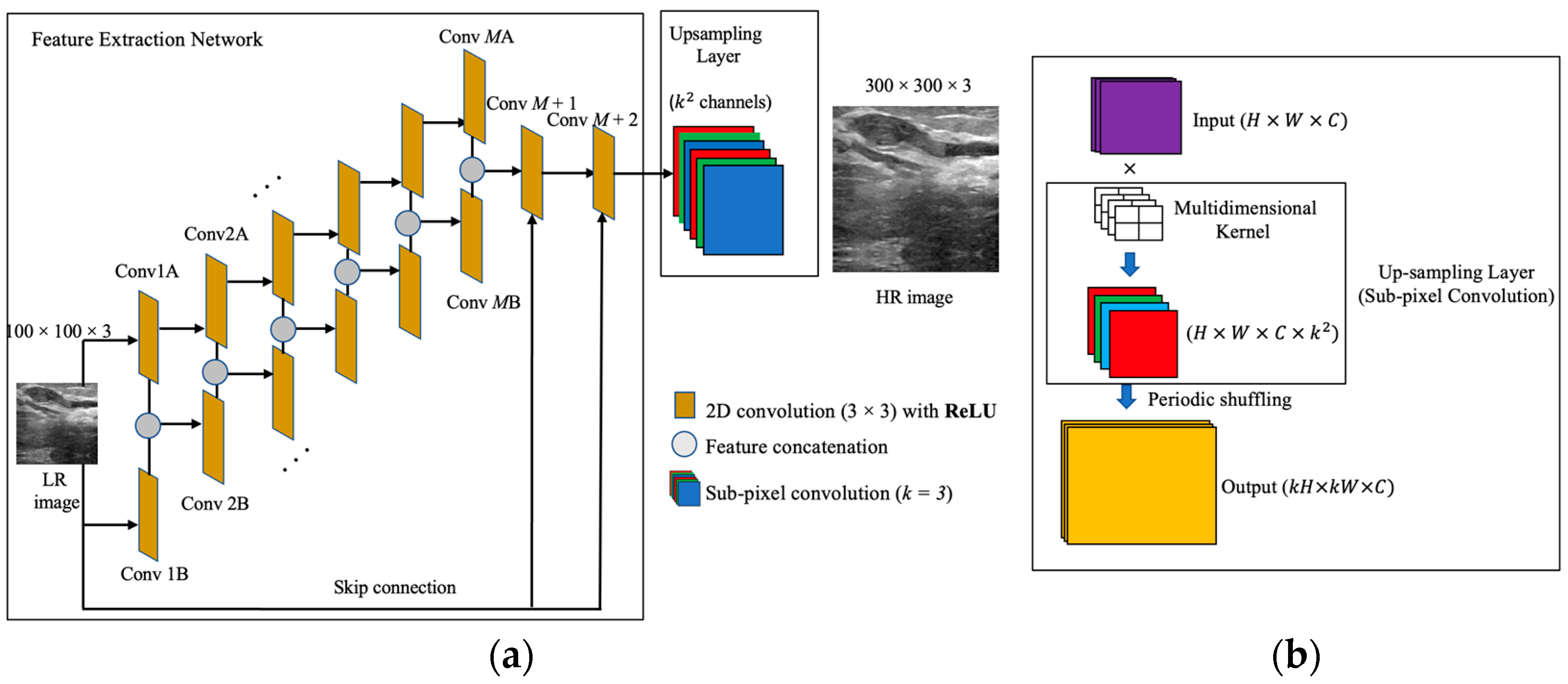
2. The Proposed System
2.1. The Feature Extraction Network
2.2. Up-Sampling Layer
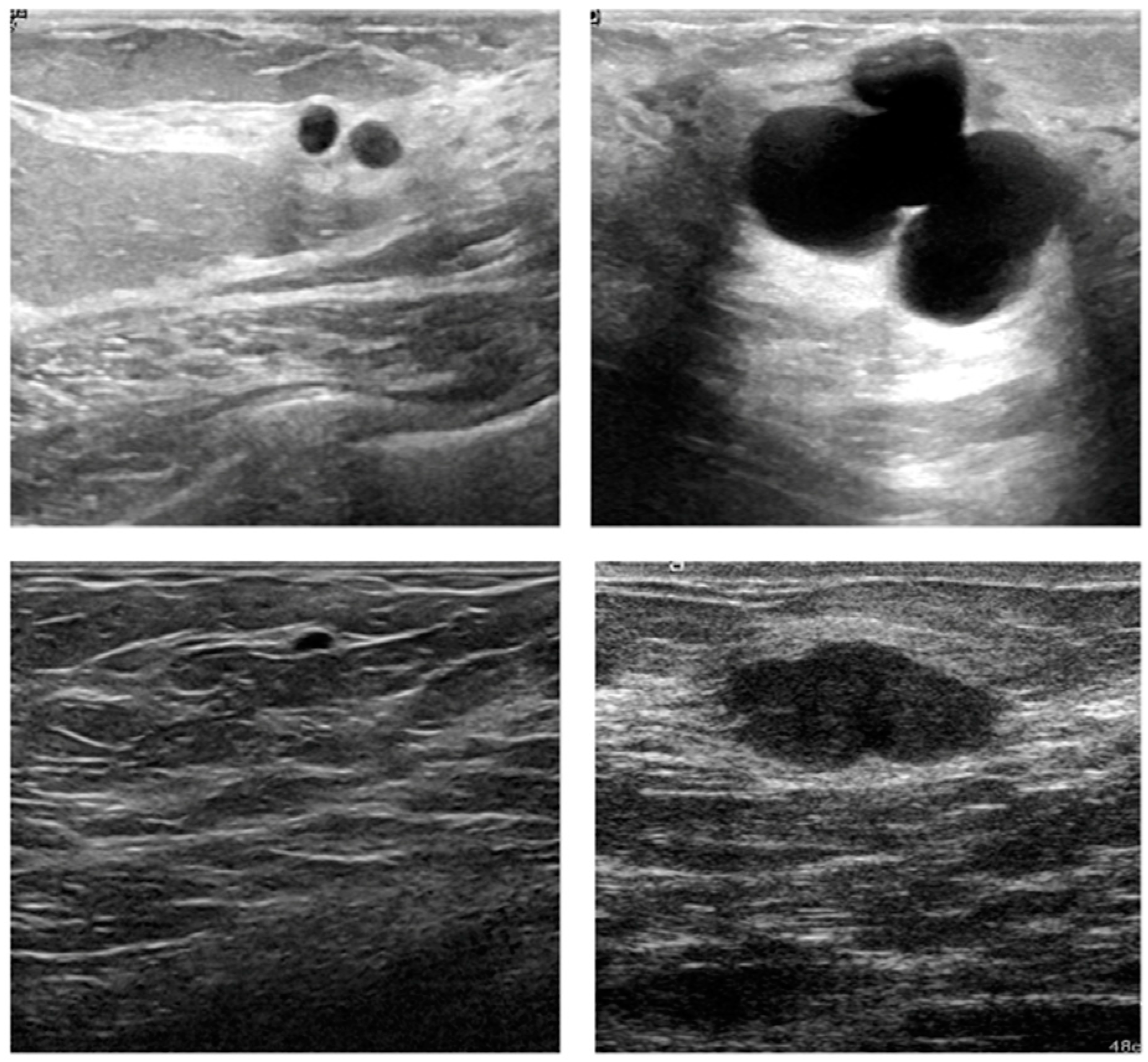
2.3. Datasets
2.4. Data Augmentation
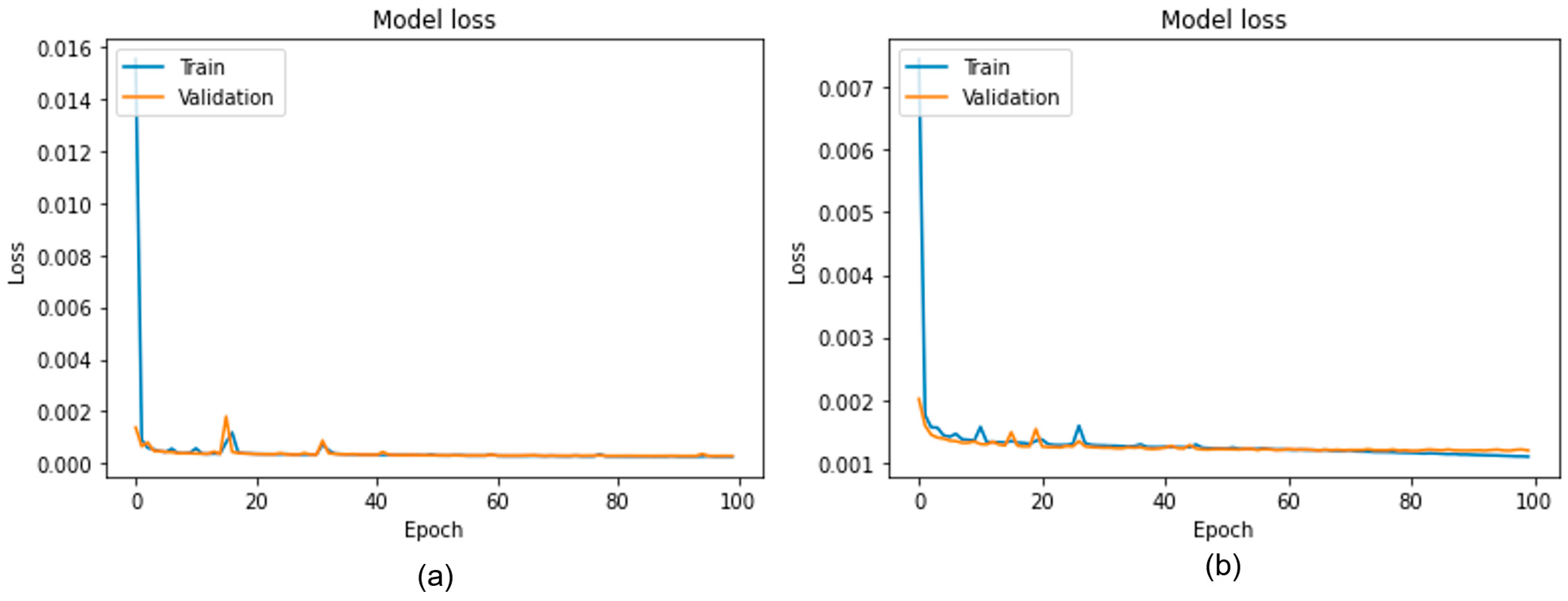
2.5. Training
3. Experiments and Results
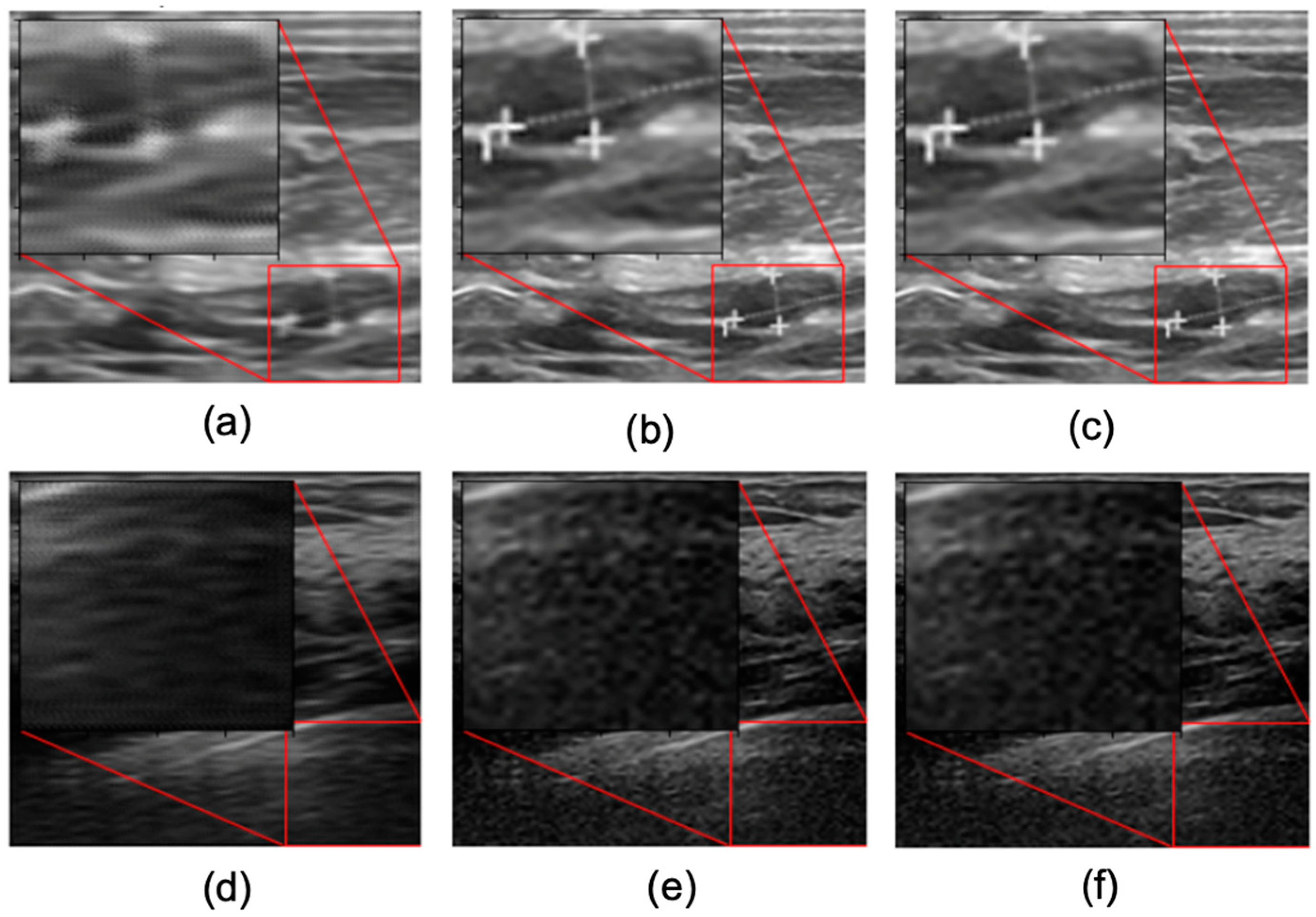
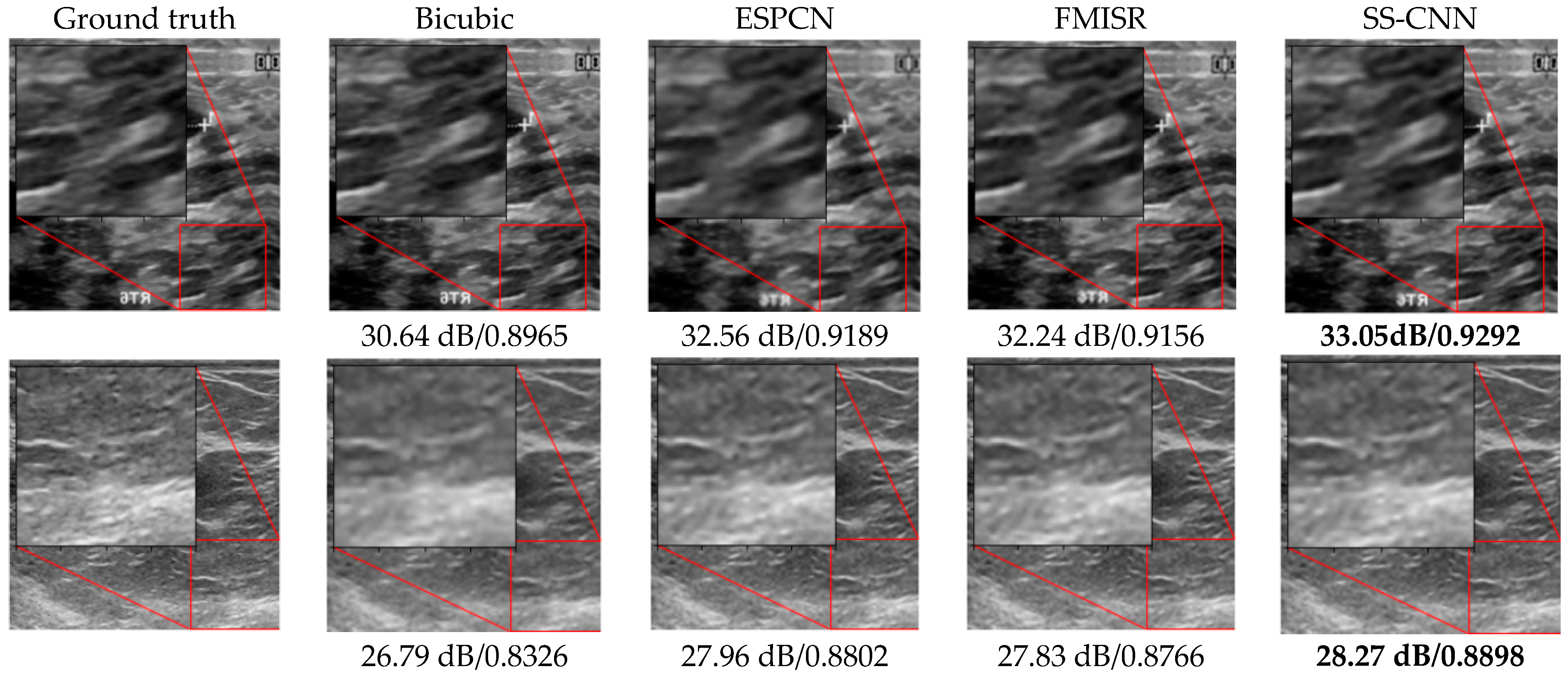
3.1. Visual Assessment
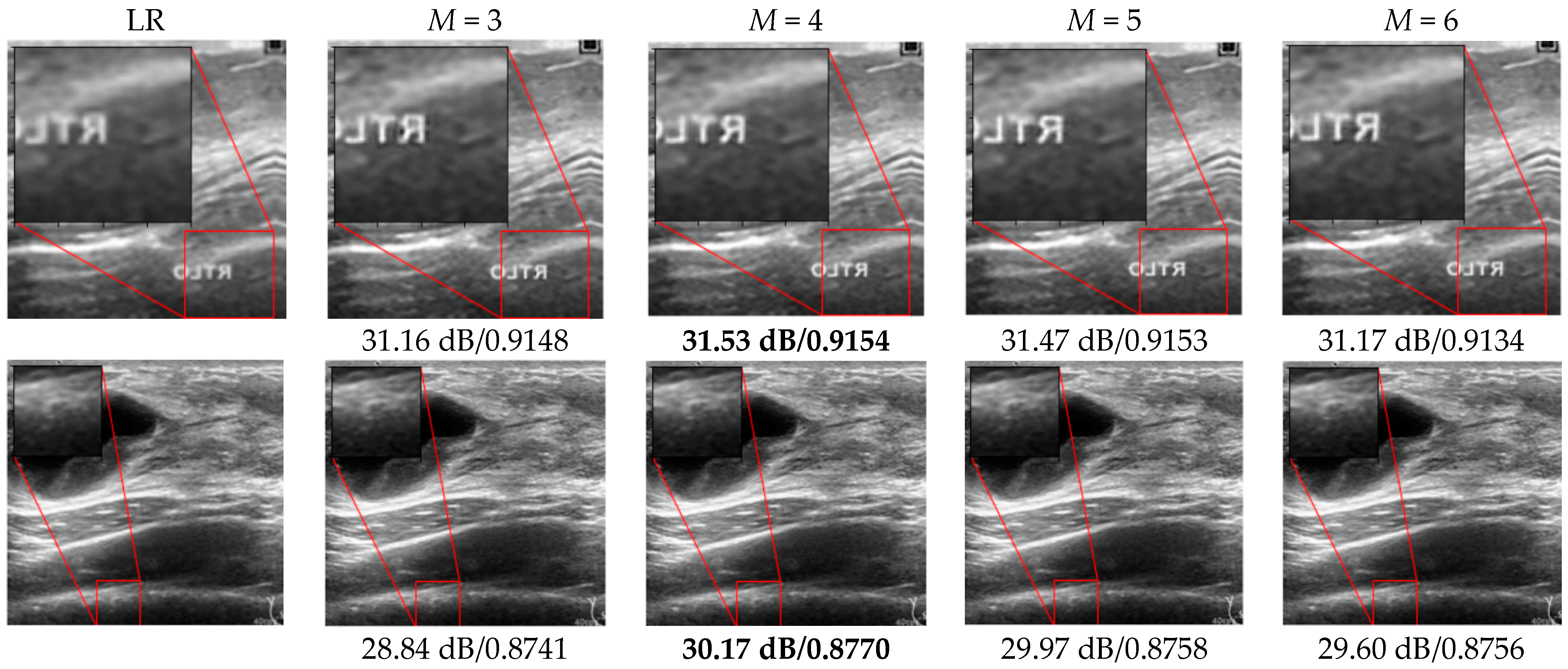
3.2. SR Performance by Varying the FEN Structure
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Akgun, T.; Altunbasak, Y.; Mersereau, R.M. Super-resolution reconstruction of hyperspectral images. IEEE Trans. Image Process. 2005, 14, 1860–1875. [Google Scholar] [CrossRef] [PubMed]
- Shen, H.; Zhang, L.; Huang, B.; Li, P. A MAP approach for joint motion estimation, segmentation, and super resolution. IEEE Trans. Image Process. 2007, 16, 479–490. [Google Scholar] [CrossRef] [PubMed]
- Goto, T.; Fukuoka, T.; Nagashima, F.; Hirano, S.; Sakurai, M. Super-resolution system for 4K-HDTV. In Proceedings of the 22nd International Conference on Pattern Recognition, Stockholm, Sweden, 24–28 August 2014; pp. 4453–4458. [Google Scholar]
- Gunturk, B.K.; Batur, A.U.; Altunbasak, Y.; Hayes, M.H.; Mersereau, R.M. Eigenface-domain super-resolution for face recognition. IEEE Trans. Image Process. 2003, 12, 597–606. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Fang, L.; Monroe, F.; Novak, S.W.; Kirk, L.; Schiavon, C.R.; Yu, S.B.; Zhang, T.; Wu, M.; Kastner, K.; Latif, A.A.; et al. Deep learning-based point scanning super resolution imaging. Nat. Methods 2021, 18, 406–416. [Google Scholar] [CrossRef]
- Cootney, R.W. Ultrasound imaging: Principles and applications in rodent research. ILAR J. 2001, 42, 233–247. [Google Scholar] [CrossRef] [Green Version]
- Christensen-Jeffries, K.; Couture, O.; Dyton, P.A.; Eldar, Y.C.; Hynynen, K.; Kiessling, F.; O’Reilly, M.; Pinton, G.F.; Schmitz, G.; Tang, M.; et al. Super-resolution ultrasound imaging. Ultrasound Med. Biol. 2020, 46, 865–891. [Google Scholar] [CrossRef] [Green Version]
- Zhao, N.; Wei, Q.; Basarab, A.; Kouamé, D.; Tourneret, J. Single image super-resolution of medical ultrasound images using a fast algorithm. In Proceedings of the IEEE 13th International Symposium on Biomedical Imaging (ISBI), Prague, Czech Republic, 13–16 April 2016; pp. 473–476. [Google Scholar]
- Diamantis, K.; Greenaway, A.H.; Anderson, T.; Jensen, J.A.; Dalgarno, P.A.; Sboros, V. Super-resolution axial localization of ultrasound scatter using multi-focal imaging. IEEE Trans. Biomed. Eng. 2017, 65, 1840–1851. [Google Scholar] [CrossRef] [Green Version]
- Zhou, F.; Yang, W.; Liao, Q. Interpolation-based image super-resolution using multisurface fitting. IEEE Trans. Image Process. 2012, 21, 3312–3318. [Google Scholar] [CrossRef]
- Zhang, Y.; Fan, Q.; Bao, F.; Liu, Y.; Zhang, C. Single-image super-resolution based on rational fractal interpolation. IEEE Trans. Image Process. 2018, 27, 3782–3797. [Google Scholar] [CrossRef]
- Zhang, Y.; Liu, J.; Yang, W.; Guo, Z. Image super-resolution based on structure-modulated sparse representation. IEEE Trans. Image Process. 2015, 24, 2797–2810. [Google Scholar] [CrossRef]
- Kulkarni, N.; Nagesh, P.; Gowda, R.; Li, B. Understanding compressive sensing and sparse representation-based super-resolution. IEEE Trans. Circuits Syst. Video Technol. 2011, 22, 778–789. [Google Scholar] [CrossRef]
- Yu, J.; Lavery, L.; Kim, K. Super-resolution ultrasound imaging for microvasculature in vivo with a high temporal accuracy. Sci. Repub. 2018, 8, 13918:1–13918:11. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Mao, X.; Shen, C.; Yang, Y.B. Image restoration using very deep convolutional encoder-decoder networks with symmetric skip connections. arXiv 2016, arXiv:1603.09056. [Google Scholar]
- Haris, M.; Shakhnarovich, G.; Ukita, N. Deep back-projection networks for super-resolution. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 1664–1673. [Google Scholar]
- Shi, W.; Caballero, J.; Huszar, F.; Totz, J.; Aitken, A.P.; Bishop, R.; Rueckert, D.; Wang, Z. Real-time single image and video super-resolution using efficient sub-pixel convolutional neural network. In Proceedings of the IEEE Conference on Computer Vision and pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 1874–1883. [Google Scholar]
- Ahn, N.; Kang, B.; Sohn, K.A. Fast, accurate, and lightweight super-resolution with cascading residual network. arXiv 2018, arXiv:1803.08664. [Google Scholar]
- Gonzalez, R.C. Deep convolutional neural networks [Lecture Notes]. IEEE Signal Process. Mag. 2018, 35, 79–87. [Google Scholar] [CrossRef]
- Lemley, J.; Bazrafkan, S.; Corcoran, P. Deep learning for consumer devices and services: Pushing the limits for machine learning, artificial intelligence, and computer vision. IEEE Consum. Electron. Mag. 2017, 6, 48–56. [Google Scholar] [CrossRef] [Green Version]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Huang, G.; Liu, Z.; Van Der Maaten, L.; Weinberger, K.Q. Densely connected convolutional networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 2261–2269. [Google Scholar]
- Han, W.; Chang, S.; Liu, D.; Yu, M.; Witbrock, M.; Huang, T.S. Image super-resolution via dual-state recurrent networks. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 1654–1663. [Google Scholar]
- Isaac, J.S.; Kulkarni, R. Super resolution techniques for medical image processing. In Proceedings of the International Conference on Technologies for Sustainable Development (ICTSD), Mumbai, India, 4–5 February 2015; pp. 1–6. [Google Scholar]
- Eun, D.; Jang, R.; Ha, W.S.; Lee, H.; Jung, S.C.; Kim, N. Deep-learning-based image quality enhancement of compressed sensing magnetic resonance imaging of vessel wall: Comparison of self-supervised and unsupervised approaches. Sci. Rep. 2020, 10, 13950. [Google Scholar] [CrossRef]
- Zhang, Y.; An, M.Q. Deep learning and transfer learning based super resolution reconstruction from single medical image. J. Healthc. Eng. 2017, 2017, 5859727. [Google Scholar] [CrossRef] [Green Version]
- Liu, H.; Liu, J.; Tao, T.; Hou, S.; Han, J. Perception consistency ultrasound image super-resolution via self-supervised CycleGAN. arXiv 2020, arXiv:2012.14142. [Google Scholar] [CrossRef]
- Abdel-Nasser, M.; Omer, O.A. Ultrasound image enhancement using a deep learning architecture. In Proceedings of the International Conference on Advanced Intelligent Systems and Informatics, Cairo, Egypt, 9–11 September 2017; pp. 639–649. [Google Scholar] [CrossRef]
- Zhang, S.; Liang, G.; Pan, S.; Zheng, L. A fast medical image super resolution method based on deep learning network. IEEE Access 2019, 7, 12319–12327. [Google Scholar] [CrossRef]
- Tong, T.; Li, G.; Liu, X.; Gao, Q. Image super-resolution using dense skip connections. In Proceedings of the IEEE International Conference on Computer Vision (ICCV), Venice, Italy, 22–27 October 2017; pp. 4809–4817. [Google Scholar]
- Mao, X.J.; Shen, C.; Yang, Y.B. Image restoration using convolutional autoencoders with symmetric skip connections. arXiv 2016, arXiv:1606.08921. [Google Scholar]
- Al-Dhabyani, W.; Fahmy, A.; Gomaa, M.; Khaled, H. Deep learning approaches for data augmentation and classification of breast masses using ultraound images. Int. J. Adv. Comput. Sci. Appl. 2019, 10, 618–627. [Google Scholar]
- Yap, M.H.; Pons, G.; Marti, J.; Ganau, S.; Sentis, M.; Zwiggelaar, R.; Davison, A.K.; Martí, R. Automated breast ultrasound lesions detection using convolutional neural networks. IEEE J. Biomed. Health Inform. 2018, 22, 1218–1226. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sun, Y.; Zhang, W.; Gu, H.; Liu, C.; Hong, S.; Xu, W.; Yang, J.; Gui, G. Convolutional neural network based models for improving super-resolution imaging. IEEE Access 2019, 7, 43042–43051. [Google Scholar] [CrossRef]



| Layers | Input | Filters | k | Kernel Size | Output |
|---|---|---|---|---|---|
| Conv1A | (100, 100, 3) | 64 | - | 3 × 3 | (100, 100, 32) |
| Conv1B | (100, 100, 3) | 64 | - | 3 × 3 | (100, 100, 32) |
| Conv2A | Conv1A | 64 | - | 3 × 3 | (100, 100, 32) |
| Conv2B | Concat (Conv 1A, Conv1B) | 64 | - | 3 × 3 | (100, 100, 32) |
| Conv3A | Conv2A | 64 | - | 3 × 3 | (100, 100, 32) |
| Conv3B | Concat (Conv 2A, Conv2B) | 64 | - | 3 × 3 | (100, 100, 32) |
| Conv4A | Conv3A | 64 | - | 3 × 3 | (100, 100, 32) |
| Conv4B | Concat (Conv 3A, Conv3B) | 64 | - | 3 × 3 | (100, 100, 32) |
| Conv5A | Conv4A | 64 | - | 3 × 3 | (100, 100, 32) |
| Conv5B | Concat (Conv 4A, Conv4B) | 64 | - | 3 × 3 | (100, 100, 32) |
| Conv6A | Conv5A | 64 | - | 3 × 3 | (100, 100, 32) |
| Conv6B | Concat (Conv 5A, Conv5B) | 64 | - | 3 × 3 | (100, 100, 32) |
| Conv7 | Concat (Conv 6A, Conv6B) | 32 | - | 1 × 1 | (100, 100, 16) |
| Conv8 | Conv 7 | 3 | - | 1 × 1 | (100, 100, 3) |
| Up-sampling layer | Conv 8 | - | 3 | - | (100, 100, 3 × 32) |
| Periodic shuffling | (100, 100, 3×32) | - | - | - | (300, 300, 3) |
| Parameter | Value |
|---|---|
| Loss function | Mean squared error (MSE) |
| Optimizer | Adam |
| Learning rate | 0.001 |
| Training epochs | 100 |
| Input image | Methods | Mean PSNR [dB] | Mean SSIM | SR Testing Time |
|---|---|---|---|---|
| Dataset A [32] | Bicubic | 31.14 | 0.8861 | - |
| ESPCN [17] | 32.83 | 0.9024 | 0.326 s | |
| FMISR [29] | 32.56 | 0.9011 | 0.255 s | |
| SS-CNN | 33.44 | 0.9178 | 0.310 s | |
| Dataset B [33] | Bicubic | 30.31 | 0.8328 | - |
| ESPCN [17] | 31.62 | 0.8643 | 0.332 s | |
| FMISR [29] | 31.17 | 0.8622 | 0.229 s | |
| SS-CNN | 31.79 | 0.8653 | 0.296 s |
| Dataset | M | Mean PSNR [dB] | Mean SSIM | SR Testing Time |
|---|---|---|---|---|
| Dataset A [32] | 3 | 33.28 | 0.9171 | 0.275 s |
| 4 | 33.54 | 0.9190 | 0.290 s | |
| 5 | 33.50 | 0.9128 | 0.293 s | |
| 6 | 33.44 | 0.9178 | 0.310 s | |
| Dataset B [33] | 3 | 31.72 | 0.8653 | 0.266 s |
| 4 | 31.90 | 0.8677 | 0.284 s | |
| 5 | 31.67 | 0.8669 | 0.291 s | |
| 6 | 31.62 | 0.8668 | 0.296 s |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tamang, L.D.; Kim, B.-W. Super-Resolution Ultrasound Imaging Scheme Based on a Symmetric Series Convolutional Neural Network. Sensors 2022, 22, 3076. https://doi.org/10.3390/s22083076
Tamang LD, Kim B-W. Super-Resolution Ultrasound Imaging Scheme Based on a Symmetric Series Convolutional Neural Network. Sensors. 2022; 22(8):3076. https://doi.org/10.3390/s22083076
Chicago/Turabian StyleTamang, Lakpa Dorje, and Byung-Wook Kim. 2022. "Super-Resolution Ultrasound Imaging Scheme Based on a Symmetric Series Convolutional Neural Network" Sensors 22, no. 8: 3076. https://doi.org/10.3390/s22083076
APA StyleTamang, L. D., & Kim, B.-W. (2022). Super-Resolution Ultrasound Imaging Scheme Based on a Symmetric Series Convolutional Neural Network. Sensors, 22(8), 3076. https://doi.org/10.3390/s22083076







