Investigation of Impact of Walking Speed on Forces Acting on a Foot–Ground Unit
Abstract
:1. Introduction
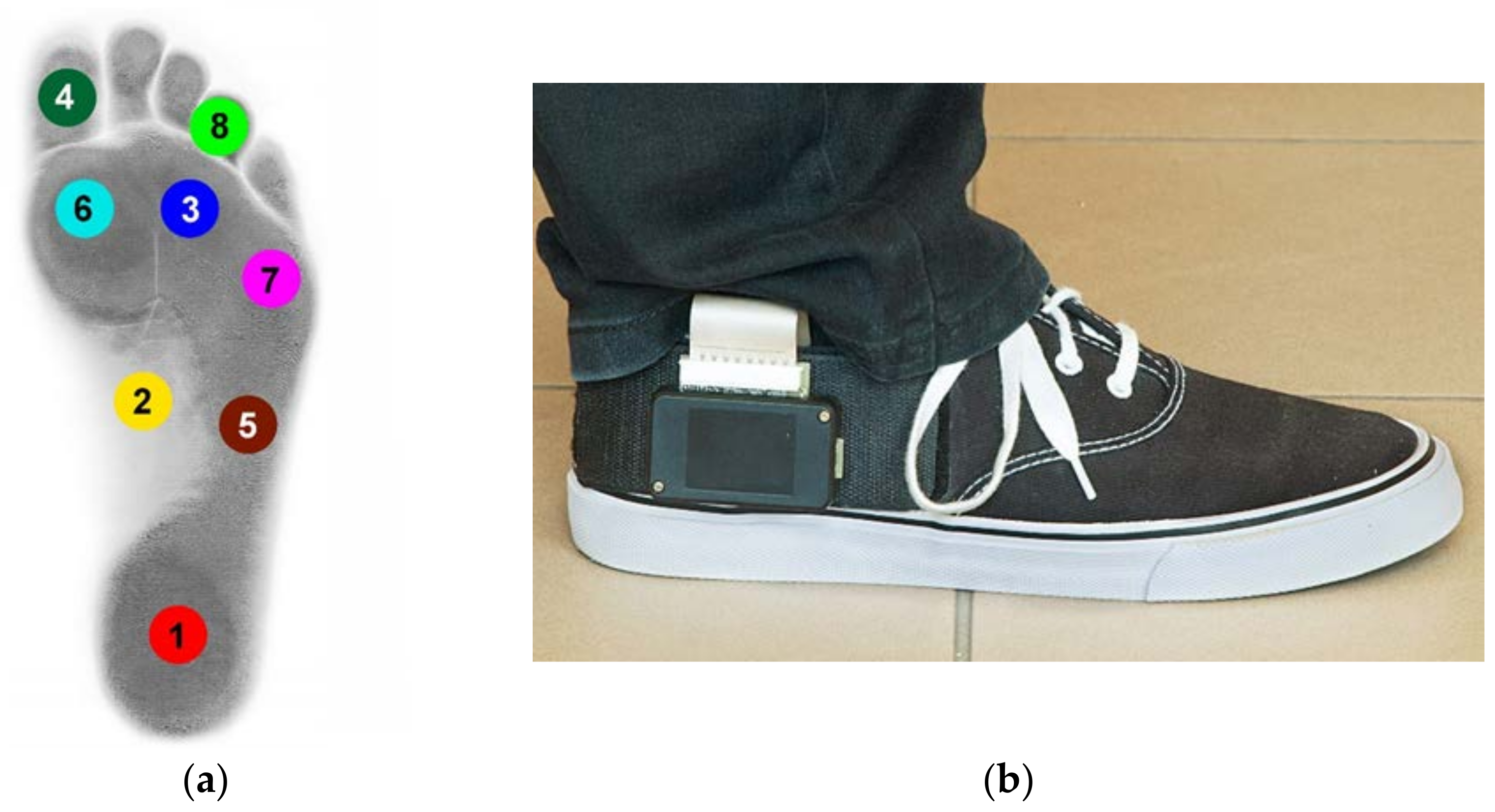
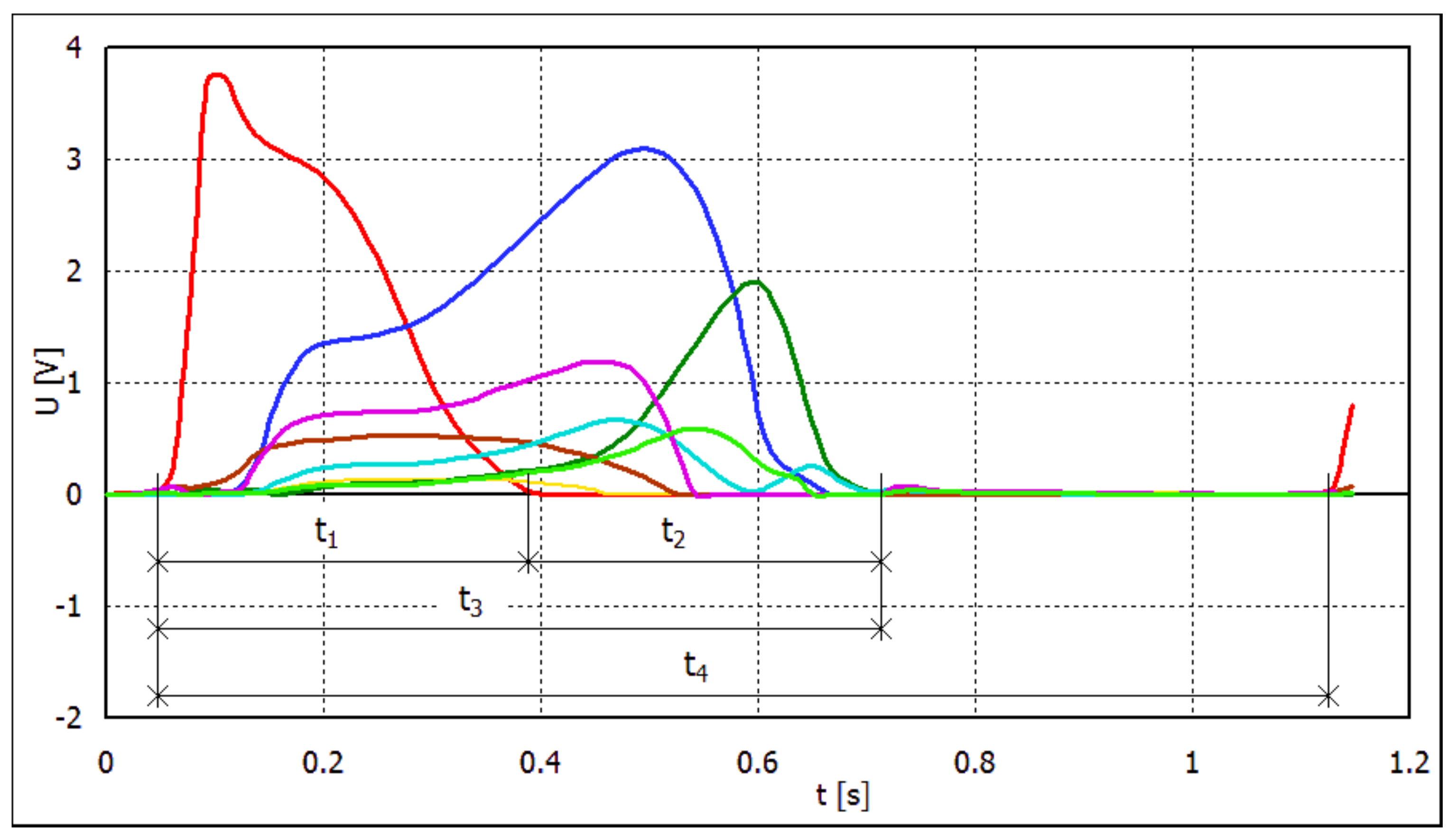
2. Materials and Methods
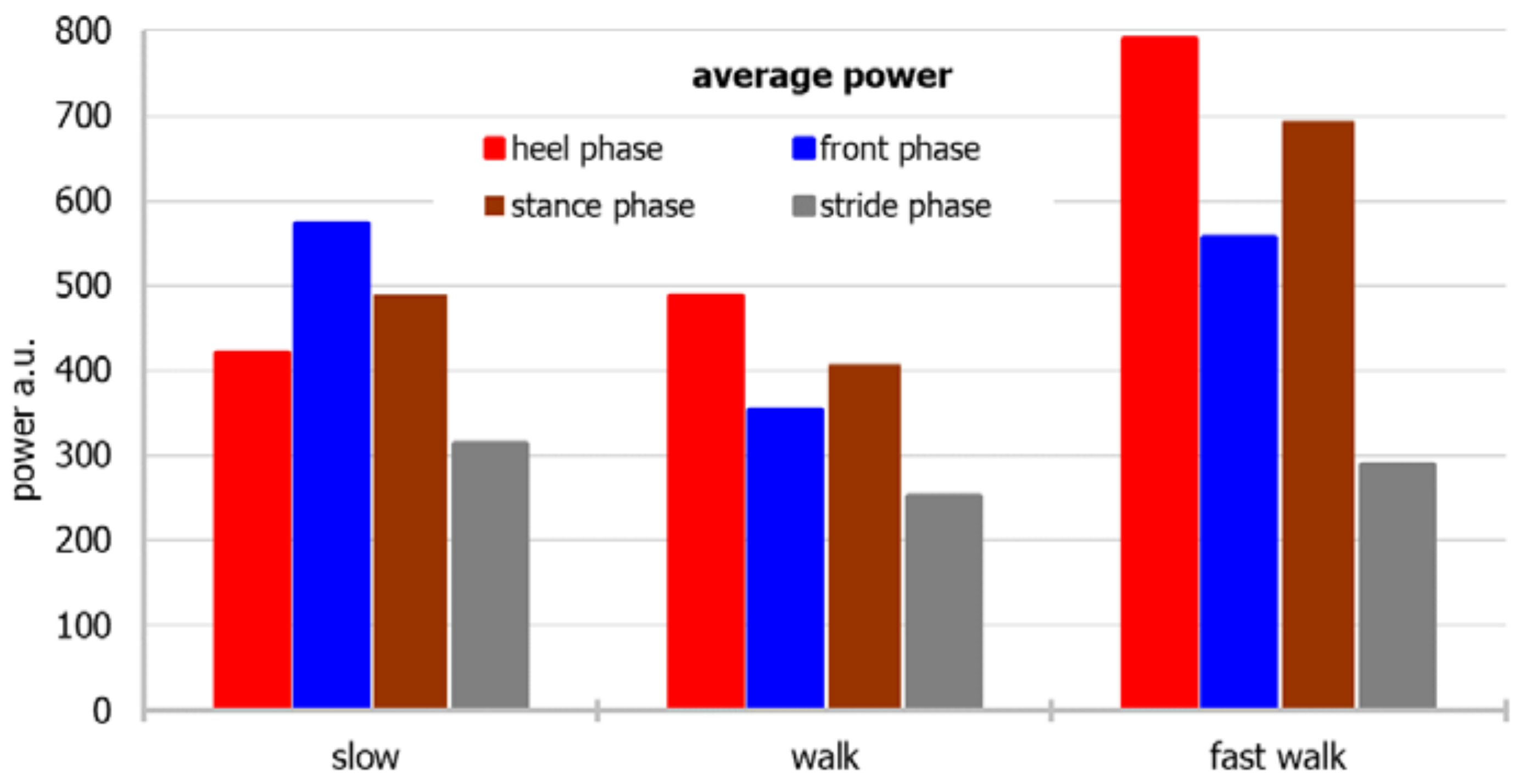
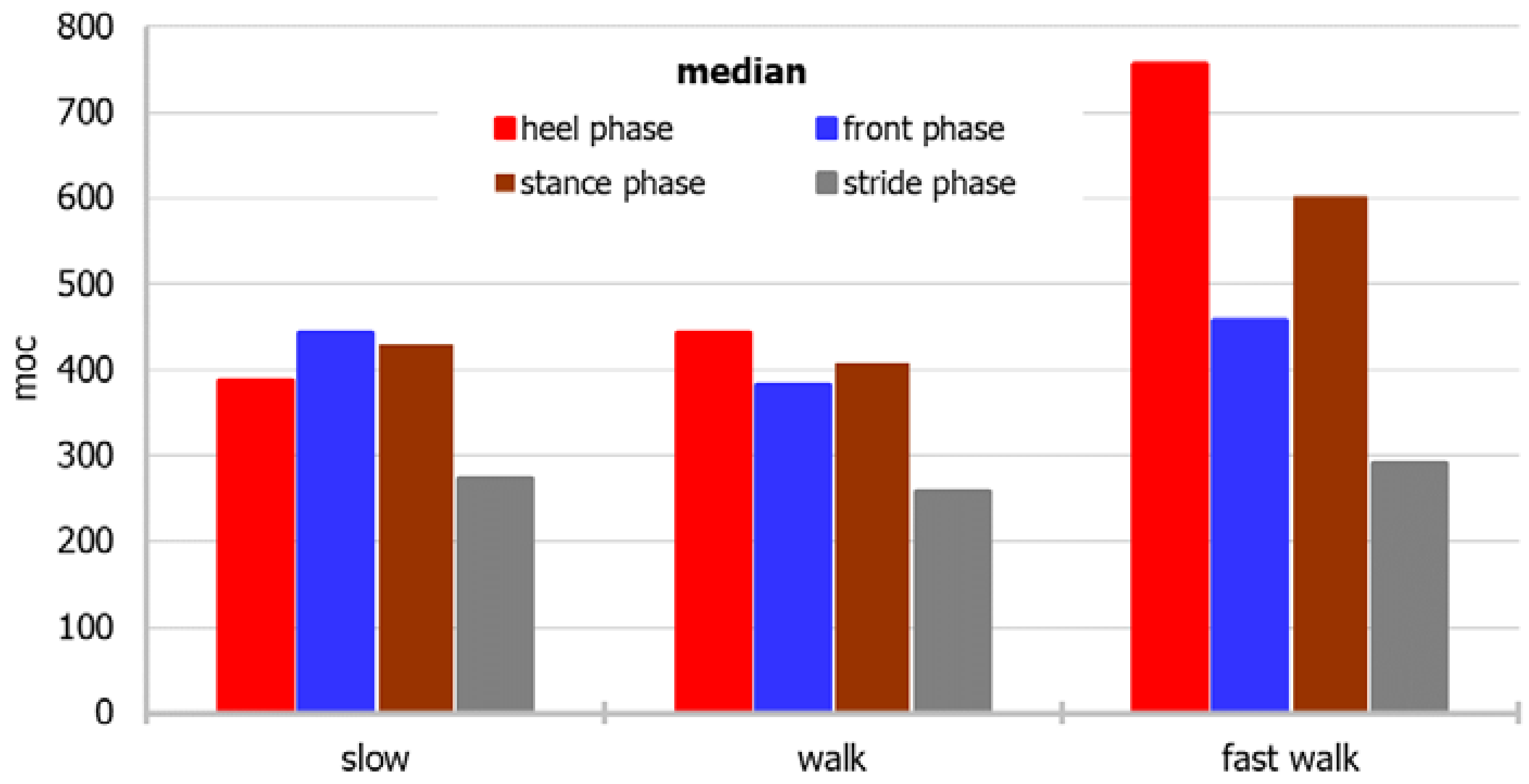
3. Results
3.1. Basic Descriptive Statistics of Measured Quantitative Variables
3.2. Foot-to-Ground Pressure Applied with Respect to Pace of Walk
4. Discussion
5. Conclusions
- Ortopiezometr is a feasible tool for dynamic measurement of foot pressure
- For investigations on walking motions, the plantar pressure analysis system, which uses the power generated on sensors installed in the insoles of shoes, is an alternative to force or energy measurements;
- Regardless of the pace of the walk, the amounts of pressure applied to the foot during step are similar among healthy volunteers;
- Further research is needed to investigate feet with abnormal anatomies.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| M | Me | SD | Sk. | Kurt. | Min. | Max. | W | p | |
|---|---|---|---|---|---|---|---|---|---|
| Normal walk | |||||||||
| Power: heel phase | 486.74 | 442.40 | 285.30 | 1.64 | 3.87 | 134.50 | 1231.00 | 0.87 | 0.066 |
| Power: front phase | 354.06 | 381.95 | 134.13 | −0.28 | −1.36 | 142.30 | 539.00 | 0.94 | 0.451 |
| Power: stance phase | 406.05 | 407.05 | 161.74 | 0.15 | −0.49 | 170.80 | 690.80 | 0.97 | 0.856 |
| Power: stride phase | 252.27 | 257.78 | 104.33 | 0.27 | −0.08 | 100.78 | 456.84 | 0.97 | 0.923 |
| Fast walk | |||||||||
| Power: heel phase | 789.37 | 755.70 | 311.53 | 0.01 | −0.84 | 312.30 | 1319.10 | 0.97 | 0.862 |
| Power: front phase | 556.83 | 457.60 | 317.73 | 0.77 | −0.48 | 192.40 | 1185.60 | 0.91 | 0.230 |
| Power: stance phase | 692.87 | 601.95 | 286.73 | 0.18 | −1.24 | 309.70 | 1160.20 | 0.93 | 0.362 |
| Power: stride phase | 289.45 | 290.88 | 112.49 | 0.16 | −0.79 | 141.69 | 493.71 | 0.93 | 0.412 |
| Slow walk | |||||||||
| Power: heel phase | 420.54 | 386.55 | 206.07 | 0.38 | −0.40 | 103.40 | 762.10 | 0.94 | 0.529 |
| Power: front phase | 572.89 | 443.30 | 404.96 | 1.01 | 0.16 | 151.70 | 1430.60 | 0.89 | 0.101 |
| Power: stance phase | 488.58 | 428.80 | 297.72 | 1.09 | 0.94 | 130.30 | 1147.80 | 0.91 | 0.182 |
| Power: stride phase | 313.52 | 272.91 | 192.43 | 1.15 | 1.33 | 82.10 | 755.49 | 0.90 | 0.181 |
| Normal Walk | Fast Walk | Slow Walk | |
|---|---|---|---|
| Heel phase vs. front phase | 1.00 | 1.00 | 1.00 |
| Heel phase vs. stance phase | 1.00 | 1.00 | 1.00 |
| Heel phase vs. stride phase | 0.005 | <0.001 | 0.841 |
| Front phase vs. stance phase | 1.00 | 1.00 | 1.00 |
| Front phase vs. stride phase | 1.00 | 0.024 | 0.037 |
| Stance phase vs. stride phase | 0.214 | <0.001 | 0.147 |
| Mean Ranks | Me | |
|---|---|---|
| Normal walk | ||
| Power: heel phase | 7.75 | 442.40 |
| Power: front phase | 4.42 | 381.95 |
| Power: stance phase | 6.25 | 407.05 |
| Power: stride phase | 1.92 | 257.78 |
| Fast walk | ||
| Power: heel phase | 11.25 | 755.70 |
| Power: front phase | 8.33 | 457.60 |
| Power: stance phase | 10.42 | 601.95 |
| Power: stride phase | 3.08 | 290.88 |
| Slow walk | ||
| Power: heel phase | 6.50 | 386.55 |
| Power: front phase | 7.92 | 443.30 |
| Power: stance phase | 7.33 | 428.80 |
| Power: stride phase | 2.83 | 272.91 |
| Heel Phase | Front Phase | Stance Phase | Stride Phase | |
|---|---|---|---|---|
| Normal walk vs. fast walk | 1.00 | 0.514 | 0.307 | 1.00 |
| Normal walk vs. slow walk | 1.00 | 1.00 | 1.00 | 1.00 |
| Fast walk vs. slow walk | 0.083 | 1.00 | 1.00 | 1.00 |
| Normal Walk | |||||
|---|---|---|---|---|---|
| Heel Phase | Front Phase | Stance Phase | Stride Phase | ||
| Fast walk | Heel phase | 1.00 | <0.001 | 0.045 | <0.001 |
| Front phase | 1.00 | 0.514 | 1.00 | 0.001 | |
| Stance phase | 1.00 | 0.003 | 0.307 | <0.001 | |
| Stride phase | 0.122 | 1.00 | 1.00 | 1.00 | |
| Slow walk | Heel phase | 1.00 | 1.00 | 1.00 | 0.122 |
| Front phase | 1.00 | 1.00 | 1.00 | 0.003 | |
| Stance phase | 1.00 | 1.00 | 1.00 | 0.015 | |
| Stride phase | 0.055 | 1.00 | 1.00 | 1.00 | |
| Fast Walk | |||||
|---|---|---|---|---|---|
| Heel Phase | Front Phase | Stance Phase | Stride Phase | ||
| Slow walk | Heel phase | 0 | 1.00 | 0.514 | 1.00 |
| Front phase | 1.00 | 1.00 | 1.00 | 0.068 | |
| Stance phase | 0.514 | 1.00 | 1.00 | 0.256 | |
| Stride phase | <0.001 | 0.012 | <0.001 | 1.00 | |
References
- Buldt, A.K.; Allan, J.J.; Landorf, K.B.; Menz, H.B. The relationship between foot posture and plantar pressure during walking in adults: A systematic review. Gait Posture 2018, 62, 56–67. [Google Scholar] [CrossRef] [PubMed]
- Clark, K.P.; Ryan, L.J.; Weyand, P.G. Foot speed, foot-strike and footwear:linking gait mechanics and running ground reaction forces. J. Exp. Biol. 2014, 217 Pt 12, 2037–2040. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Gawronska, K.; Lorkowski, J. Evaluating the Symmetry in Plantar Pressure Distribution under the Toes during Standing in a Postural Pedobarographic Examination. Symmetry 2021, 13, 1476. [Google Scholar] [CrossRef]
- Klöpfer-Krämer, I.; Brand, A.; Wackerle, H.; Müßig, J.; Kröger, I.; Augat, P. Gait analysis—Available platforms for outcome assessment. Injury 2020, 51 (Suppl. S2), S90–S96. [Google Scholar] [CrossRef] [PubMed]
- Lorkowski, J.; Gawronska, K.; Pokorski, M. Pedobarography: A Review on Methods and Practical Use in Foot Disorders. Appl. Sci. 2021, 11, 11020. [Google Scholar] [CrossRef]
- Urry, S. Plantar pressure-measurement sensors. Meas. Sci. Technol. 1999, 10, R16. [Google Scholar] [CrossRef]
- Andriacchi, T.; Ogle, J.; Galante, J. Walking speed as a basis for normal and abnormal gait measurements. J. Biomech. 1977, 10, 261–268. [Google Scholar] [CrossRef]
- Munro, C.F.; Miller, D.I.; Fuglevand, A.J. Ground reaction forces in running: A reexamination. J. Biomech. 1987, 20, 147–155. [Google Scholar] [CrossRef]
- Orlin, M.N.; McPoil, T.G. Plantar Pressure Assessment. Phys. Ther. 2000, 80, 399–409. [Google Scholar] [CrossRef] [Green Version]
- Jasiewicz, B.; Klimiec, E.; Młotek, M.; Guzdek, P.; Duda, S.; Adamczyk, J.; Potaczek, T.; Piekarski, J.; Kołaszczyński, G. Quantitative Analysis of Foot Plantar Pressure During Walking. Med Sci. Monit. 2019, 25, 4916–4922. [Google Scholar] [CrossRef]
- Watanabe, A.; Noguchi, H.; Oe, M.; Sanada, H.; Mori, T. Development of a Plantar Load Estimation Algorithm for Evaluation of Forefoot Load of Diabetic Patients during Daily Walks Using a Foot Motion Sensor. J. Diabetes Res. 2017, 2017, 15350616. [Google Scholar] [CrossRef] [Green Version]
- Zhang, G.; Wong, D.; Wong, I.; Chen, T.; Hong, T.; Peng, Y.; Wang, Y.; Tan, Q.; Zhang, M. Plantar Pressure Variability and Asymmetry in Elderly Performing 60-Minute Treadmill Brisk-Walking: Paving the Way towards Fatigue-Induced Instability Assessment Using Wearable In-Shoe Pressure Sensors. Sensors 2021, 21, 3217. [Google Scholar] [CrossRef]
- Salvati, L.; D’Amore, M.; Fiorentino, A.; Pellegrino, A.; Sena, P.; Villecco, F. On-Road Detection of Driver Fatigue and Drowsiness during Medium-Distance Journeys. Entropy 2021, 23, 135. [Google Scholar] [CrossRef]
- Blomgren, M.; Turan, I.; Agadir, M. Gait analysis in hallux valgus. J. Foot Surg. 1991, 30, 70–71. [Google Scholar]
- Lorkowski, J. Methodology of pedobarographic examination--own experiences and review of literature. Przeglad Lekarski 2006, 63 (Suppl. S5), 23–27. [Google Scholar]
- Arnadottir, S.A.; Mercer, V.S. Effects of footwear on measurements of balance and gait in women between the ages of 65 and 93 years. Phys. Ther. 2000, 80, 17–27. [Google Scholar] [CrossRef] [Green Version]
- Klimiec, E.; Zaraska, W.; Piekarski, J.; Jasiewicz, B. PVDF Sensors—Research on Foot Pressure Distribution in Dynamic Conditions. Adv. Sci. Technol. 2013, 79, 94–99. [Google Scholar] [CrossRef]
- Klimiec, E.; Piekarski, J.; Zaraska, W.; Jasiewicz, B. Electronic measurement system of foot plantar pressure. Microelectron. Int. 2014, 31, 229–234. [Google Scholar] [CrossRef]
- Mlotek, M. Creation of Foot Mobility Model Based on Pressure Distribution on the Ground Using Measurement System Footpressure ITE System in Natural Conditions. Master’s Thesis, Cracow University of Technology, Faculty of Mechanical Engineering, Institute of Applied Mechanics, Kraków, Poland, 2017. (In Polish). [Google Scholar]
- Perry, J.; Burnfield, J.M. Basic functions. In Gait Analysis: Normal and Pathological Function, 2nd ed.; SLACK Incorpo-Rated: West Deptford, NJ, USA, 2010; pp. 19–48. [Google Scholar]
- Clark, K.P.; Ryan, L.J.; Weyand, P.G. A general relationship links gait mechanics and running ground reaction forces. J. Exp. Biol. 2016, 220 Pt 2, 138057–1380258. [Google Scholar] [CrossRef] [Green Version]
- Ly, Q.H.; Alaoui, A.; Erlicher, S.; Baly, L. Towards a footwear design tool: Influence of shoe midsole properties and ground stiffness on the impact force during running. J. Biomech. 2010, 43, 310–317. [Google Scholar] [CrossRef] [Green Version]
- Zadpoor, A.A.; Nikooyan, A.A. Modeling muscle activity to study the effects of footwear on the impact forces and vibrations of the human body during running. J. Biomech. 2010, 43, 186–193. [Google Scholar] [CrossRef]
- Skopljak, A.; Muftic, M.; Sukalo, A.; Masic, I. Pedobarography in Diagnosis and Clinical Application. Acta Inform. Med. 2014, 22, 374–378. [Google Scholar] [CrossRef] [Green Version]
- Mueller, M.J. Use of an In-Shoe Pressure Measurement System in the Management of Patients with Neuropathic Ulcers or Metatarsalgia. J. Orthop. Sports Phys. Ther. 1995, 21, 328–336. [Google Scholar] [CrossRef] [Green Version]
- Buldt, A.K.; Levinger, P.; Murley, G.S.; Menz, H.B.; Nester, C.J.; Landorf, K.B. Foot posture is associated with kinematics of the foot during gait: A comparison of normal, planus and cavus feet. Gait Posture 2015, 42, 42–48. [Google Scholar] [CrossRef]
- Tam, N.; Prins, D.; Divekar, N.V.; Lamberts, R.P. Biomechanical analysis of gait waveform data: Exploring differences between shod and barefoot running in habitually shod runners. Gait Posture 2017, 58, 274–279. [Google Scholar] [CrossRef]
- Chuckpaiwong, B.; Nunley, J.A.; Mall, N.A.; Queen, R.M. The effect of foot type on in-shoe plantar pressure during walking and running. Gait Posture 2008, 28, 405–411. [Google Scholar] [CrossRef]
- Morag, E.; Cavanagh, P. Structural and functional predictors of regional peak pressures under the foot during walking. J. Biomech. 1999, 32, 359–370. [Google Scholar] [CrossRef]
- Fernández-Seguín, L.M.; Mancha, J.D.; Rodríguez, R.S.; Escamilla-Martínez, E.; Martín, B.G.; Ramos-Ortega, J. Comparison of plantar pressures and contact area between normal and cavus foot. Gait Posture 2014, 39, 789–792. [Google Scholar] [CrossRef]
- Kim, H.Y.; Shin, H.S.; Ko, J.H.; Cha, Y.H.; Ahn, J.H.; Hwang, J.Y. Gait Analysis of Symptomatic Flatfoot in Children: An Observational Study. Clin. Orthop. Surg. 2017, 9, 363–373. [Google Scholar] [CrossRef]
- Carson, D.W.; Myer, G.D.; Hewett, T.E.; Heidt, R.S.; Ford, K.R. Increased plantar force and impulse in American football players with high arch compared to normal arch. Foot 2012, 22, 310–314. [Google Scholar] [CrossRef] [Green Version]
- Dixon, S.J. Use of pressure insoles to compare in-shoe loading for modern running shoes. Ergonomics 2008, 51, 1503–1514. [Google Scholar] [CrossRef]
- Han, J.T.; Koo, H.M.; Jung, J.M.; Kim, Y.J.; Lee, J.H. Differences in Plantar Foot Pressure and COP between Flat and Normal Feet During Walking. J. Phys. Ther. Sci. 2011, 23, 683–685. [Google Scholar] [CrossRef] [Green Version]
- Segal, A.; Rohr, E.; Orendurff, M.; Shofer, J.; O’Brien, M.; Sangeorzan, B. The Effect of Walking Speed on Peak Plantar Pressure. Foot Ankle Int. 2004, 25, 926–933. [Google Scholar] [CrossRef]
- Fernandes, W.C.; Machado, A.; Borella, C.; Carpes, F.P. Influência da velocidade da marcha sobre a pressão plantar em sujeitos com osteoartrite unilateral de joelho. Rev. Bras. Reum. 2014, 54, 441–445. [Google Scholar] [CrossRef] [Green Version]
- Takahashi, K.Z.; Worster, K.; Bruening, D.A. Energy neutral: The human foot and ankle subsections combine to produce near zero net mechanical work during walking. Sci. Rep. 2017, 7, 15404. [Google Scholar] [CrossRef]
- Leardini, A.; Benedetti, M.G.; Berti, L.; Bettinelli, D.; Nativo, R.; Giannini, S. Rear-foot, mid-foot and fore-foot motion during the stance phase of gait. Gait Posture 2007, 25, 453–462. [Google Scholar] [CrossRef]
- Leardini, A.; Benedetti, M.G.; Catani, F.; Simoncini, L.; Giannini, S. An anatomically based protocol for the description of foot segment kinematics during gait. Clin. Biomech. 1999, 14, 528–536. [Google Scholar] [CrossRef]
- Okita, N.; Meyers, S.A.; Challis, J.H.; Sharkey, N.A. An objective evaluation of a segmented foot model. Gait Posture 2009, 30, 27–34. [Google Scholar] [CrossRef]
- Leardini, A.; Caravaggi, P.; Theologis, T.; Stebbins, J. Multi-segment foot models and their use in clinical populations. Gait Posture 2019, 69, 50–59. [Google Scholar] [CrossRef]
- Berki, V.; Boswell, M.A.; Ciltea, D.; Guseila, L.M.; Goss, L.; Barnes, S.; Berme, N.; McMillan, G.R.; Davis, B.L. Expanded butterfly plots: A new method to analyze simultaneous pressure and shear on the plantar skin surface during gait. J. Biomech. 2015, 48, 2214–2216. [Google Scholar] [CrossRef]
- Bruening, D.A.; Cooney, K.M.; Buczek, F.L.; Richards, J.G. Measured and estimated ground reaction forces for multi-segment foot models. J. Biomech. 2010, 43, 3222–3226. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Novak, A.C.; Mayich, D.J.; Perry, S.; Daniels, T.R.; Brodsky, J.W. Gait Analysis for Foot and Ankle Surgeons—Topical Review, Part 2: Approaches to multisegment modeling of the foot. Foot Ankle Int. 2014, 35, 178–191. [Google Scholar] [CrossRef] [PubMed]
- Winter, D.A. Energy Generation and Absorption at the Ankle and Knee during Fast, Natural, and Slow Cadences. Clin. Orthop. Relat. Res. 1983, 175, 147–154. [Google Scholar] [CrossRef]
- Hillstrom, H.J.; Song, J.; Kraszewski, A.P.; Hafer, J.; Mootanah, R.; Dufour, A.; Chow, B.S.; Deland, J.T. Foot type biomechanics part 1: Structure and function of the asymptomatic foot. Gait Posture 2013, 37, 445–451. [Google Scholar] [CrossRef] [Green Version]
- Caderby, T.; Yiou, E.; Peyrot, N.; Begon, M.; Dalleau, G. Influence of gait speed on the control of mediolateral dynamic stability during gait initiation. J. Biomech. 2014, 47, 417–423. [Google Scholar] [CrossRef] [Green Version]
- England, S.A.; Granata, K.P. The influence of gait speed on local dynamic stability of walking. Gait Posture 2007, 25, 172–178. [Google Scholar] [CrossRef] [Green Version]
- Fan, Y.; Li, Z.; Han, S.; Lv, C.; Zhang, B. The influence of gait speed on the stability of walking among the elderly. Gait Posture 2016, 47, 31–36. [Google Scholar] [CrossRef]
- Rogan, S.; Taeymans, J.; Bangerter, C.; Simon, S.; Terrier, P.; Hilfiker, R. Influence of single and dual tasks on gait stability and gait speed in the elderly: An explorative study. Gerontol. Geriatr. 2017, 52, 23–27. [Google Scholar] [CrossRef]
- Breine, B.; Malcolm, P.; Frederick, E.C.; De Clercq, D. Relationship between Running Speed and Initial Foot Contact Patterns. Med. Sci. Sports Exerc. 2014, 46, 1595–1603. [Google Scholar] [CrossRef]
- Hellstrom, P.A.R.; Åkerberg, A.; Ekström, M.; Folke, M. Walking Intensity Estimation with a Portable Pedobarography System. Stud. Health Technol. Inform. 2016, 224, 27–32. [Google Scholar] [CrossRef]
- Espy, D.; Yang, F.; Bhatt, T.; Pai, Y.-C. Independent influence of gait speed and step length on stability and fall risk. Gait Posture 2010, 32, 378–382. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Breine, B.; Malcolm, P.; Galle, S.; Fiers, P.; Frederick, E.C.; De Clercq, D. Running speed-induced changes in foot contact pattern influence impact loading rate. Eur. J. Sport Sci. 2019, 19, 774–783. [Google Scholar] [CrossRef] [PubMed]
- Zulkifli, S.S.; Loh, W.P. A state-of-the-art review of foot pressure. Foot Ankle Surg. 2020, 26, 25–32. [Google Scholar] [CrossRef] [PubMed]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jasiewicz, B.; Klimiec, E.; Guzdek, P.; Kołaszczyński, G.; Piekarski, J.; Zaraska, K.; Potaczek, T. Investigation of Impact of Walking Speed on Forces Acting on a Foot–Ground Unit. Sensors 2022, 22, 3098. https://doi.org/10.3390/s22083098
Jasiewicz B, Klimiec E, Guzdek P, Kołaszczyński G, Piekarski J, Zaraska K, Potaczek T. Investigation of Impact of Walking Speed on Forces Acting on a Foot–Ground Unit. Sensors. 2022; 22(8):3098. https://doi.org/10.3390/s22083098
Chicago/Turabian StyleJasiewicz, Barbara, Ewa Klimiec, Piotr Guzdek, Grzegorz Kołaszczyński, Jacek Piekarski, Krzysztof Zaraska, and Tomasz Potaczek. 2022. "Investigation of Impact of Walking Speed on Forces Acting on a Foot–Ground Unit" Sensors 22, no. 8: 3098. https://doi.org/10.3390/s22083098
APA StyleJasiewicz, B., Klimiec, E., Guzdek, P., Kołaszczyński, G., Piekarski, J., Zaraska, K., & Potaczek, T. (2022). Investigation of Impact of Walking Speed on Forces Acting on a Foot–Ground Unit. Sensors, 22(8), 3098. https://doi.org/10.3390/s22083098






