A Transformer-Based Bridge Structural Response Prediction Framework
Abstract
:1. Introduction
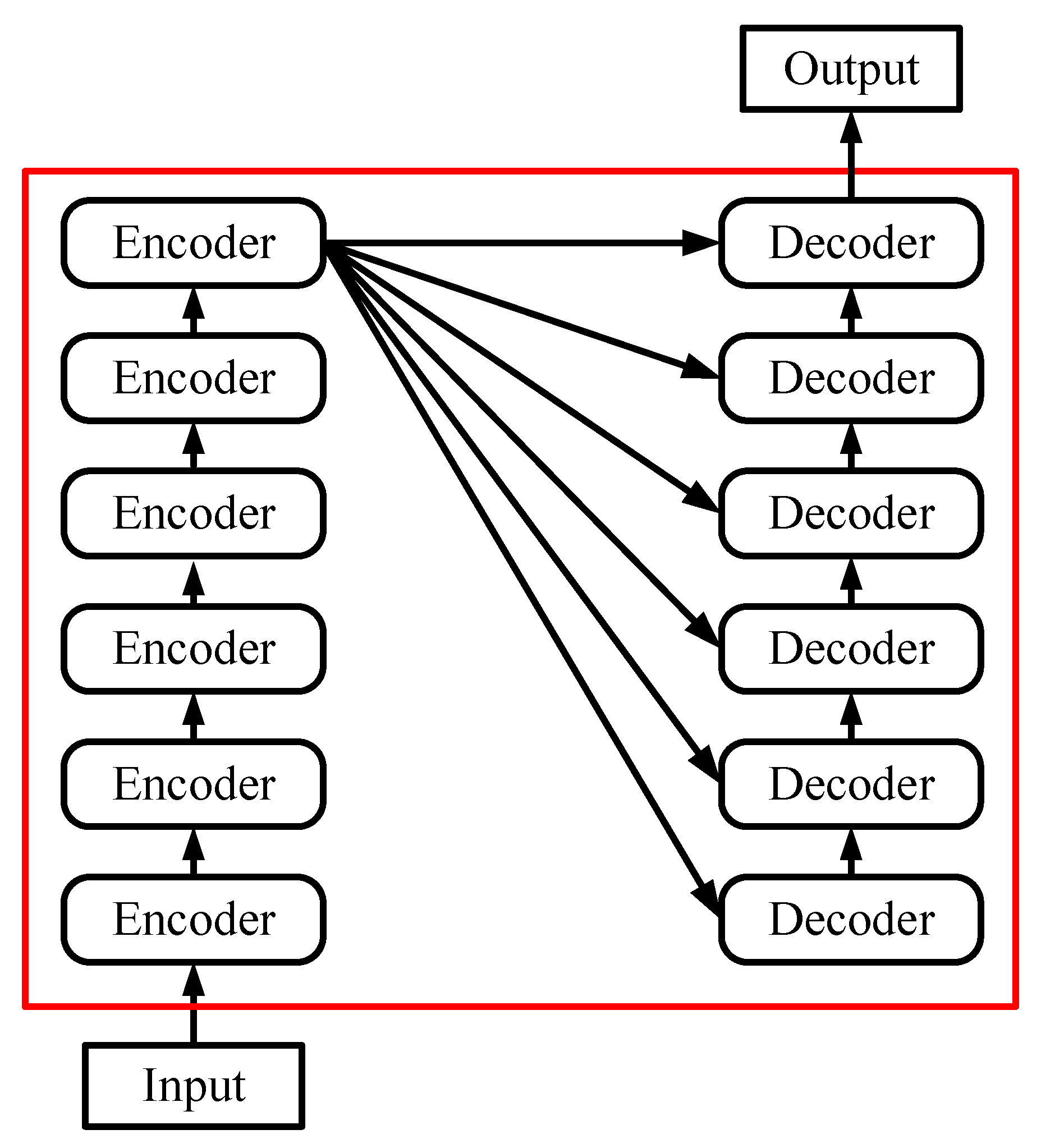
2. Framework for Structural Response Prediction
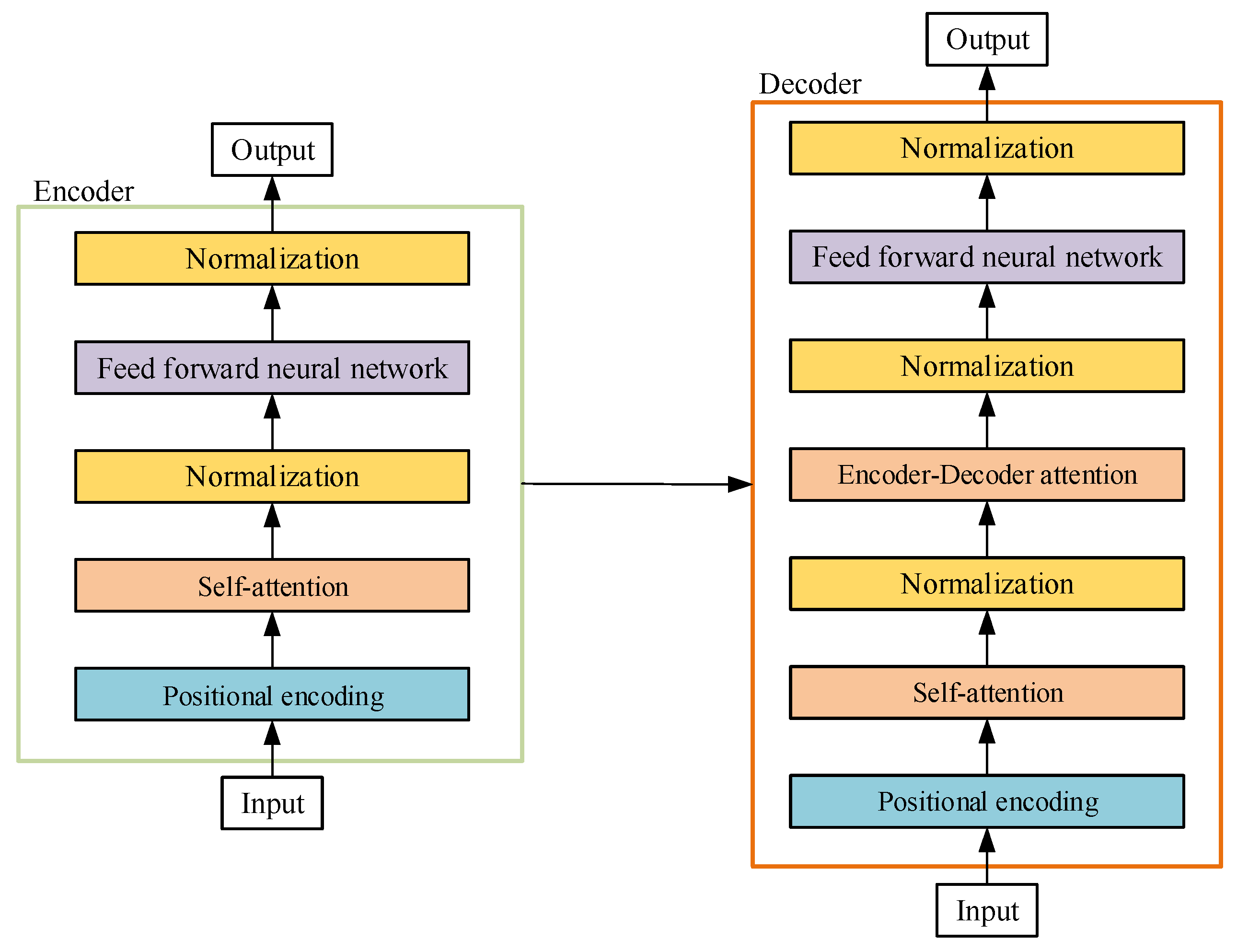
2.1. Attention Mechanism
2.2. Positional Encoding
2.3. Multi-Head Attention
3. Experiment
3.1. Songhua River Bridge Structural Response Dataset
3.2. Training Platform
3.3. Loss Function and Evaluation Metrics
3.4. Experimental Design
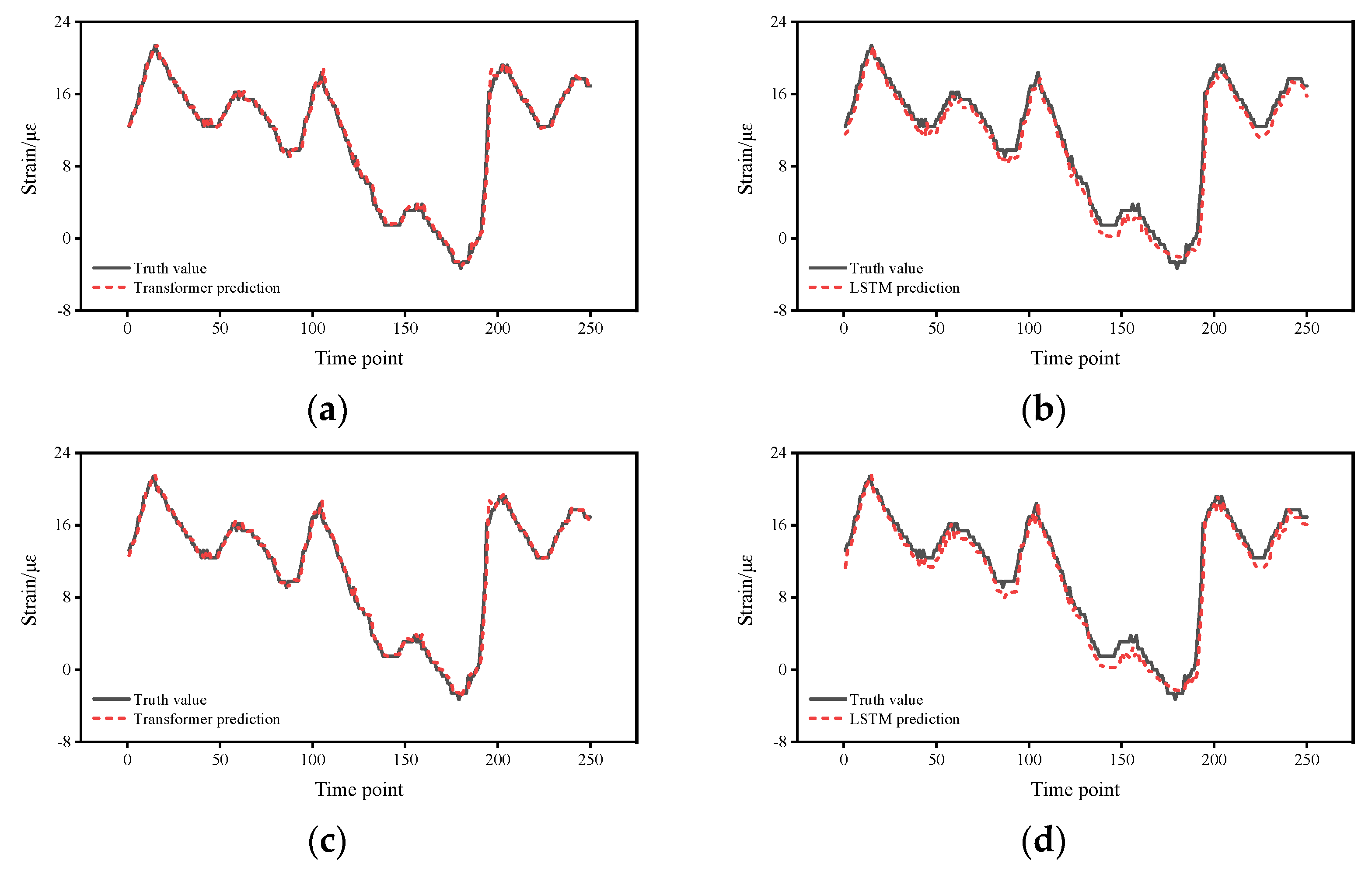
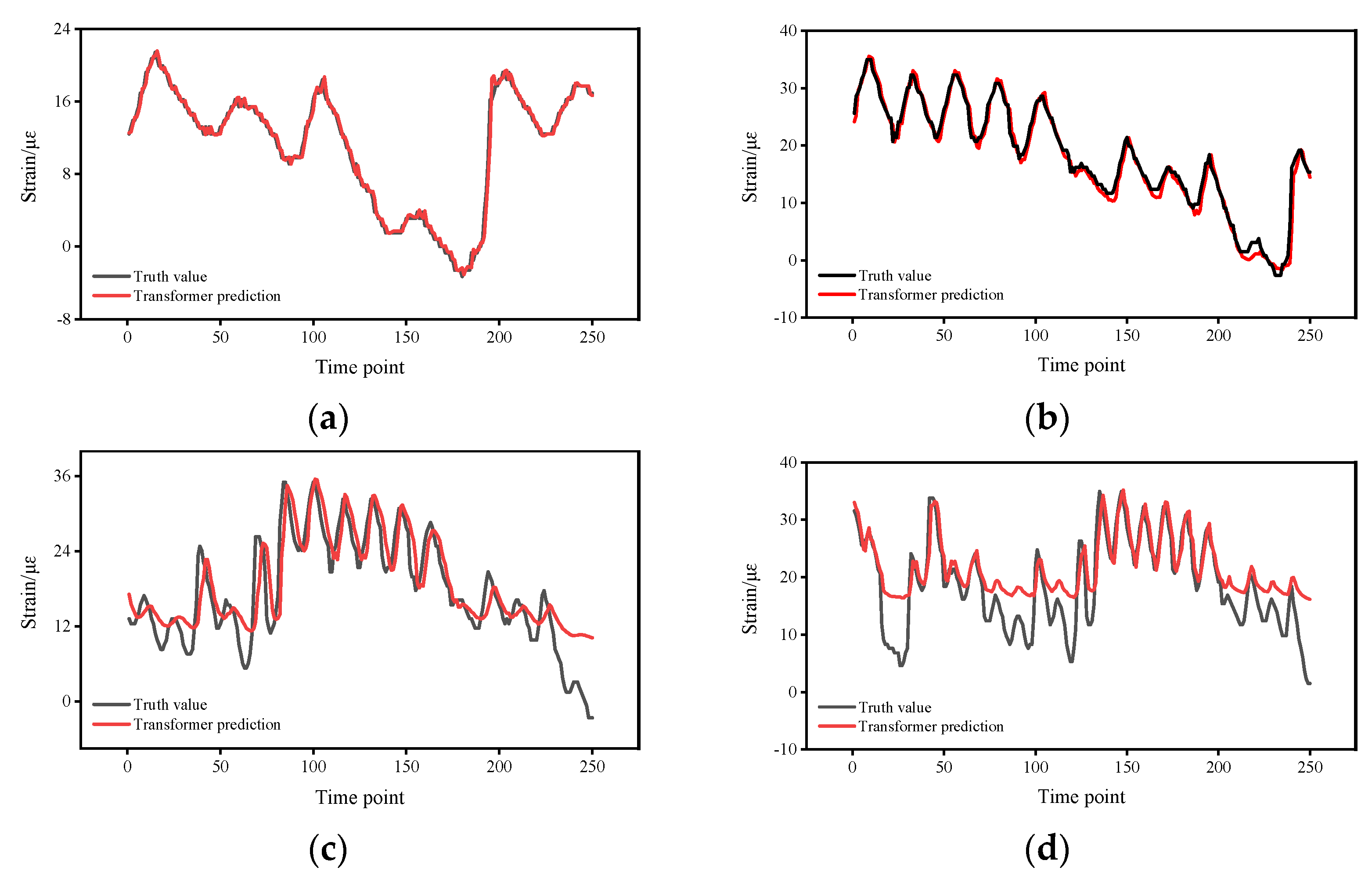
4. Experimental Results
5. Discussion
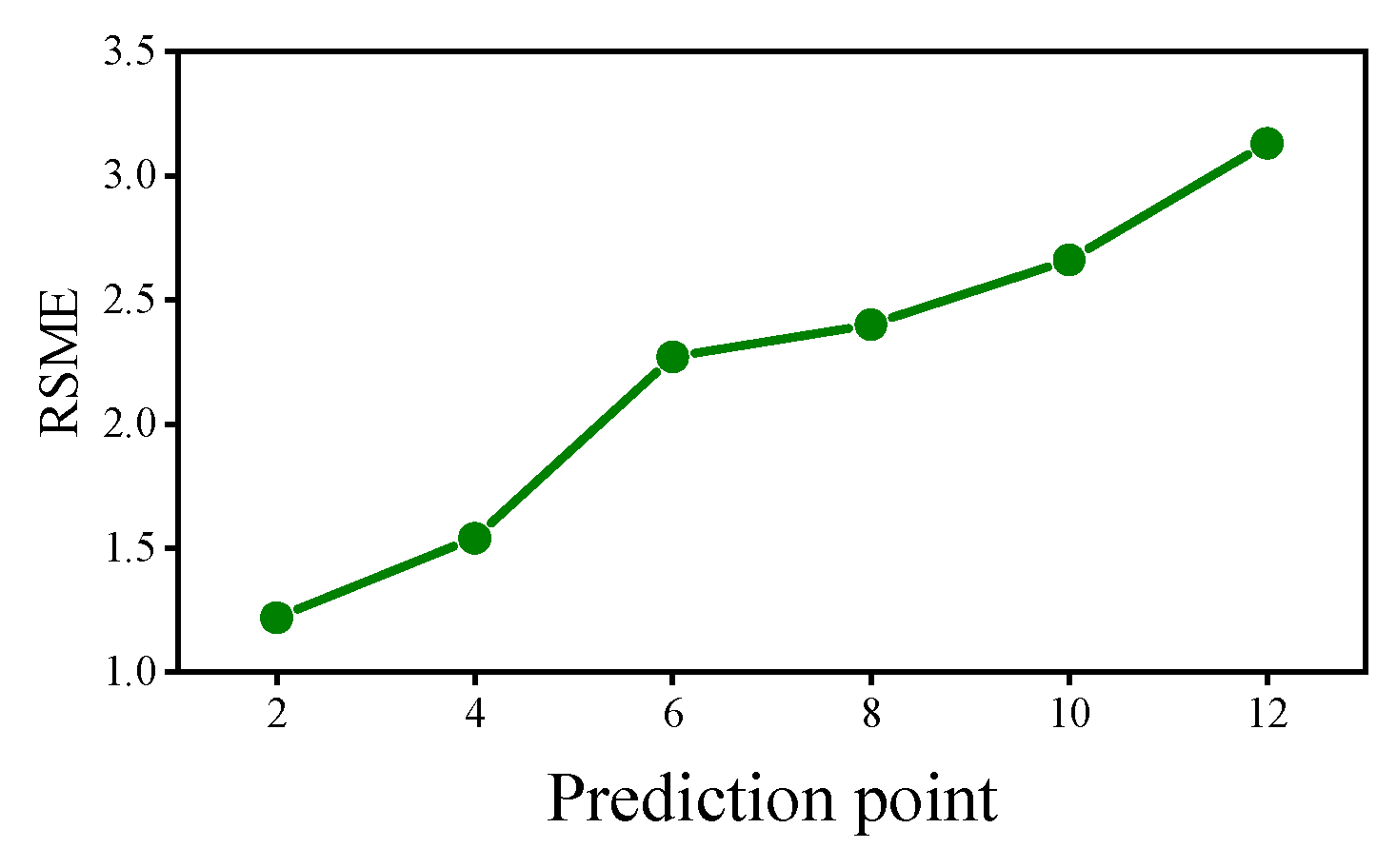
5.1. Impact of Different Number of Prediction Points
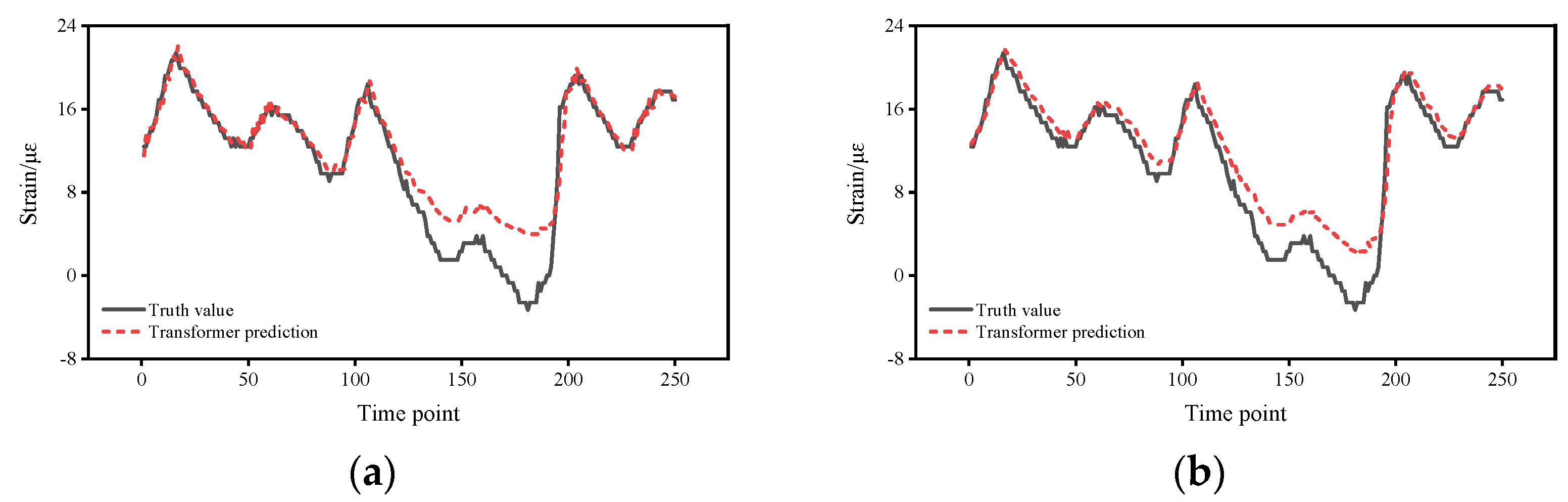
5.2. Impact of Different Time Intervals
6. Limitations
7. Conclusions
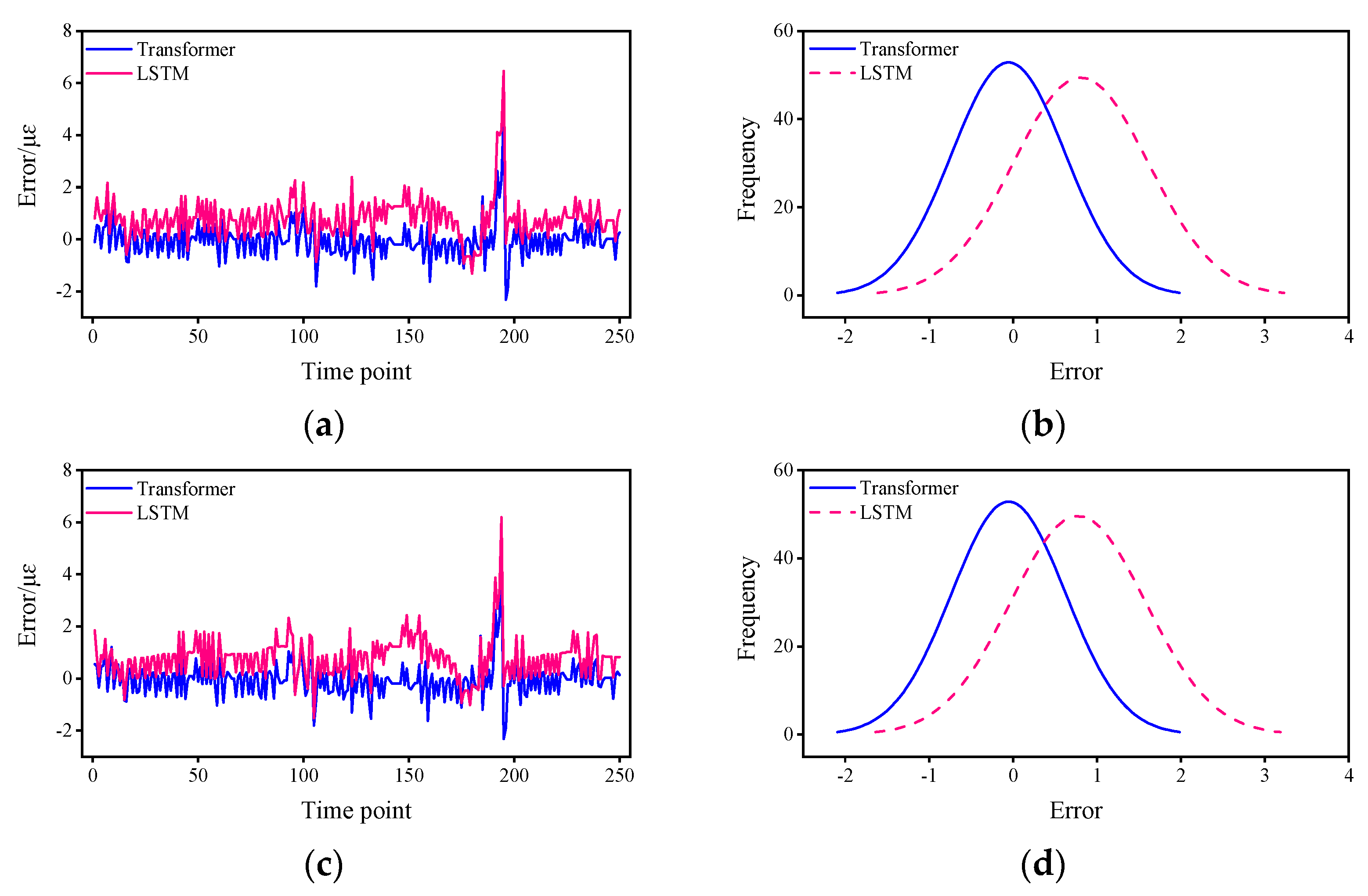
- From the mean value of the error, the mean error of the Transformer is about 19.2%–55.5% of that of the LSTM.
- From the 95% CI, with a much narrower CI for the Transformer of approximately 59.0%–87.7% for the LSTM.
Author Contributions
Funding
Conflicts of Interest
References
- Yi, T.; Li, H.; Gu, M. Recent research and applications of GPS based technology for bridge health monitoring. Sci. China Technol. Sci. 2010, 53, 2597–2610. [Google Scholar] [CrossRef]
- Zhang, X.-J.; Zhang, C. Study of seismic performance and favorable structural system of suspension bridges. Struct. Eng. Mech. 2016, 60, 595–614. [Google Scholar] [CrossRef]
- Zheng, X.; Yang, D.-H.; Yi, T.-H.; Li, H.-N. Bridge influence line identification from structural dynamic responses induced by a high-speed vehicle. Struct. Control. Health Monit. 2020, 27, e2554. [Google Scholar] [CrossRef]
- Zhu, X.Q.; Law, S.S. Structural Health Monitoring Based on Vehicle-Bridge Interaction: Accomplishments and Challenges. Adv. Struct. Eng. 2015, 18, 1999–2015. [Google Scholar] [CrossRef]
- Fujino, Y.; Iwamoto, M.; Ito, M.; Hikami, Y. Wind-Tunnel Experiments Using 3D Models and Response Prediction for a Long-Span Suspension Bridge. J. Wind. Eng. Ind. Aerodyn. 1992, 42, 1333–1344. [Google Scholar] [CrossRef]
- Jakobsen, J.B.; Tanaka, H. Modelling uncertainties in prediction of aeroelastic bridge behavior. J. Wind. Eng. Ind. Aerodyn. 2003, 91, 1485–1498. [Google Scholar] [CrossRef]
- Lee, J.S.; Lee, S.S.; Comp, S.O.C.I. Computational method for the prediction of dynamic response of long-span bridges due to unsteady wind load. In Proceedings of the Conference on High Performance Computing on the Information Superhighway (HPC Asia 97), Seoul, Korea, 28 April–2 May 1997; pp. 419–424. [Google Scholar]
- Yan, G.-Y.; Zhang, Z. Predictive Control of a Cable-Stayed Bridge under Multiple-support Excitations. In Proceedings of the International Conference on Mechanical Materials and Manufacturing Engineering (ICMMME 2011), Nanchang, China, 20–22 June 2011; Volume 66–68, pp. 268–272. [Google Scholar]
- Ding, Y.; Ren, P.; Zhao, H.; Miao, C. Structural health monitoring of a high-speed railway bridge: Five years review and lessons learned. Smart Struct. Syst. 2018, 21, 695–703. [Google Scholar]
- MacKay, D.J. A practical Bayesian framework for backpropagation networks. Neural Comput. 1992, 4, 448–472. [Google Scholar] [CrossRef]
- Ma, X.; Lv, S. Financial credit risk prediction in internet finance driven by machine learning. Neural Comput. Appl. 2019, 31, 8359–8367. [Google Scholar] [CrossRef]
- Wang, W.; Zheng, H.; Wu, Y.J. Prediction of fundraising outcomes for crowdfunding projects based on deep learning: A multimodel comparative study. Soft Comput. 2020, 24, 8323–8341. [Google Scholar] [CrossRef]
- Hartono, A.M.; Ahmad, M. Sadikin, Comparison methods of short term electrical load forecasting. In Proceedings of the 1st International Conference on Industrial, Electrical and Electronics (ICIEE), Anyer, Indonesia, 4–5 September 2018; Volume 218. [Google Scholar]
- Khanesar, M.A.; Lu, J.; Smith, T.; Branson, D. Electrical Load Prediction Using Interval Type-2 Atanassov Intuitionist Fuzzy System: Gravitational Search Algorithm Tuning Approach. Energies 2021, 14, 3591. [Google Scholar] [CrossRef]
- Peng, W.; Xu, L.; Li, C.; Xie, X.; Zhang, G. Stacked autoencoders and extreme learning machine based hybrid model for electrical load prediction. J. Intell. Fuzzy Syst. 2019, 37, 5403–5416. [Google Scholar] [CrossRef]
- Li, W.; Zhao, X.; Liu, S. Traffic Accident Prediction Based on Multivariable Grey Model. Information 2020, 11, 184. [Google Scholar] [CrossRef] [Green Version]
- Zheng, M.; Li, T.; Zhu, R.; Chen, J.; Ma, Z.; Tang, M.; Cui, Z.; Wang, Z. Traffic Accident’s Severity Prediction: A Deep-Learning Approach-Based CNN Network. IEEE Access 2019, 7, 39897–39910. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, T.; Ka-Veng, Y. Construction site information decentralized management using blockchain and smart contracts. Comput. Aided Civ. Infrastruct. Eng. 2021. [Google Scholar] [CrossRef]
- Zhang, Y.; Yuen, K.V. Crack detection using fusion features-based broad learning system and image processing. Comput. Aided Civ. Infrastruct. Eng. 2021, 36, 1568–1584. [Google Scholar] [CrossRef]
- Li, Z.; Li, D. Action recognition of construction workers under occlusion. J. Build. Eng. 2022, 45, 103352. [Google Scholar] [CrossRef]
- Chen, S.; Ge, L. Exploring the attention mechanism in LSTM-based Hong Kong stock price movement prediction. Quant. Financ. 2019, 19, 1507–1515. [Google Scholar] [CrossRef]
- Li, G.; Zhao, X.; Fan, C.; Fang, X.; Li, F.; Wu, Y. Assessment of long short-term memory and its modifications for enhanced short-term building energy predictions. J. Build. Eng. 2021, 43, 103182. [Google Scholar] [CrossRef]
- Zhang, R.; Meng, L.; Mao, Z.; Sun, H. Spatiotemporal Deep Learning for Bridge Response Forecasting. J. Struct. Eng. 2021, 147, 04021070. [Google Scholar] [CrossRef]
- Li, S.; Li, S.; Laima, S.; Li, H. Data-driven modeling of bridge buffeting in the time domain using long short-term memory network based on structural health monitoring. Struct. Control. Health Monit. 2021, 28, e2772. [Google Scholar] [CrossRef]
- Ahmed, B.; Mangalathu, S.; Jeon, J.-S. Seismic damage state predictions of reinforced concrete structures using stacked long short-term memory neural networks. J. Build. Eng. 2022, 46, 103737. [Google Scholar] [CrossRef]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, Ł.; Polosukhin, I. Attention is all you need. In Proceedings of the 31st Conference on Neural Information Processing Systems (NIPS 2017), Long Beach, CA, USA, 4–9 December 2017; Volume 30. [Google Scholar]
- Mnih, V.; Heess, N.; Graves, A. Recurrent models of visual attention. In Proceedings of the 27th International Conference on Neural Information Processing Systems, Montreal, Canada, 8–13 December 2014; Volume 27. [Google Scholar]
- Sutskever, I.; Vinyals, O.; Le, Q.V. Sequence to sequence learning with neural networks. In Proceedings of the 27th International Conference on Neural Information Processing Systems, Montreal, Canada, 8–13 December 2014; Volume 27. [Google Scholar]
- Xu, K.; Ba, J.; Kiros, R.; Cho, K.; Courville, A.; Salakhudinov, R.; Zemel, R.; Bengio, Y. Show, attend and tell: Neural image caption generation with visual attention. In Proceedings of the 32nd International Conference on Machine Learning, PMLR, Lille, France, 6–11 July 2015; pp. 2048–2057. [Google Scholar]
- Takase, S.; Okazaki, N. Positional encoding to control output sequence length. arXiv 2019, arXiv:1904.07418. [Google Scholar]
- Li, J.; Tu, Z.; Yang, B.; Lyu, M.R.; Zhang, T. Multi-head attention with disagreement regularization. arXiv 2018, arXiv:1810.10183. [Google Scholar]






| Sensor No. | Mean Error | 95%CI | ||
|---|---|---|---|---|
| Transformer | LSTM | Transformer | LSTM | |
| 1 | 0.48 | 0.90 | (−1.29, 1.28) | (−0.79, 2.14) |
| 2 | 0.48 | 0.85 | (−1.29, 1.28) | (−0.75, 2.26) |
| 3 | 0.37 | 1.12 | (−1.03, 0.89) | (−0.35, 2.64) |
| 9 | 0.31 | 1.61 | (−1.04, 0.70) | (0.35, 3.30) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Z.; Li, D.; Sun, T. A Transformer-Based Bridge Structural Response Prediction Framework. Sensors 2022, 22, 3100. https://doi.org/10.3390/s22083100
Li Z, Li D, Sun T. A Transformer-Based Bridge Structural Response Prediction Framework. Sensors. 2022; 22(8):3100. https://doi.org/10.3390/s22083100
Chicago/Turabian StyleLi, Ziqi, Dongsheng Li, and Tianshu Sun. 2022. "A Transformer-Based Bridge Structural Response Prediction Framework" Sensors 22, no. 8: 3100. https://doi.org/10.3390/s22083100
APA StyleLi, Z., Li, D., & Sun, T. (2022). A Transformer-Based Bridge Structural Response Prediction Framework. Sensors, 22(8), 3100. https://doi.org/10.3390/s22083100





