A Novel Clock Parameterization and Its Implications for Precise Point Positioning and Ionosphere Estimation
Abstract
:1. Introduction
2. Novel Clock Parameterization
3. Implications of the Proposed Clock Parametrization
3.1. Implication for Ionosphere Estimation
3.2. Implication for User Positioning
4. Referring Higher Frequency Measurements to Re-Parameterized Clocks
5. Results
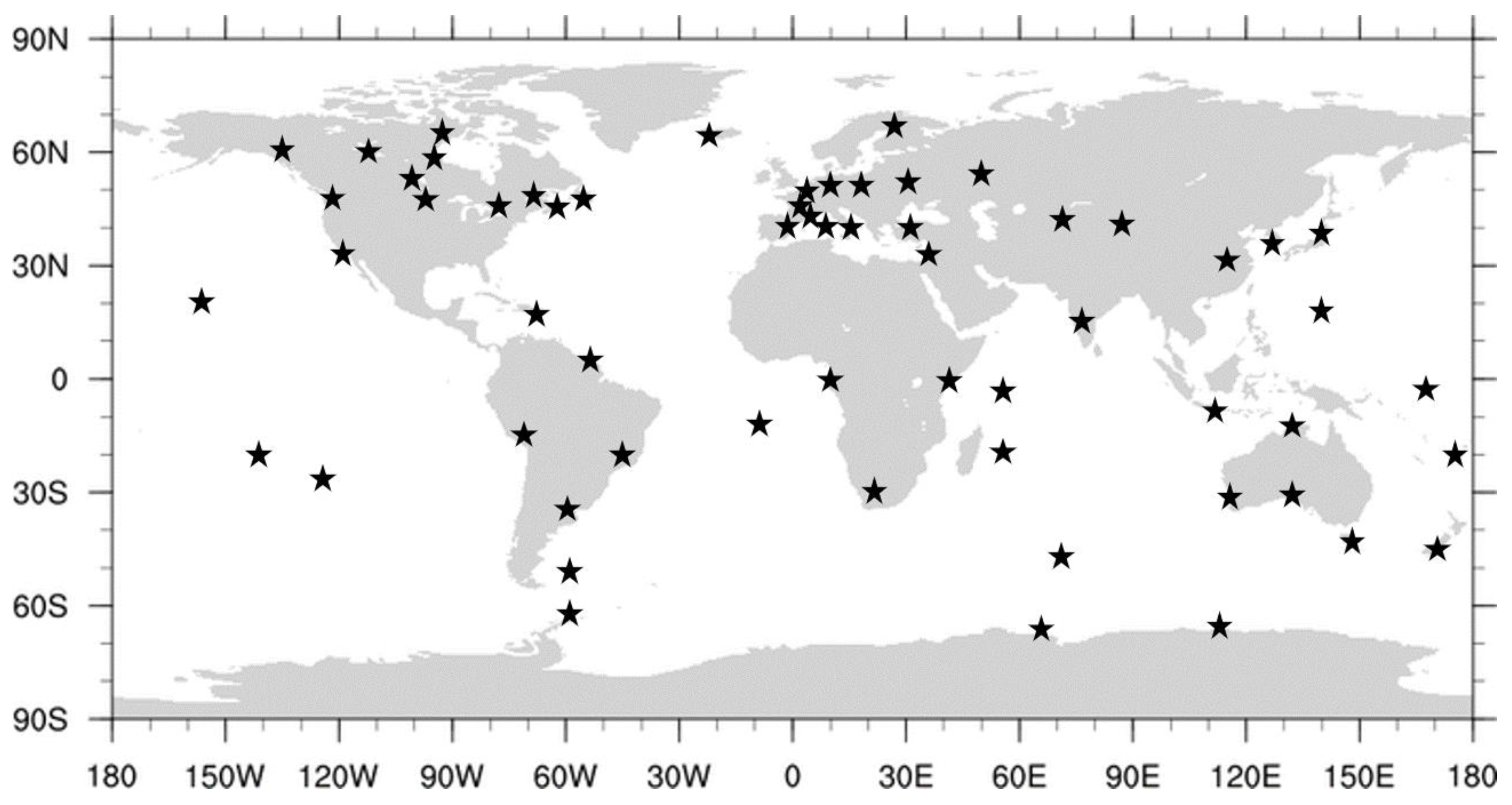
5.1. Data Processing and Corrections Generation
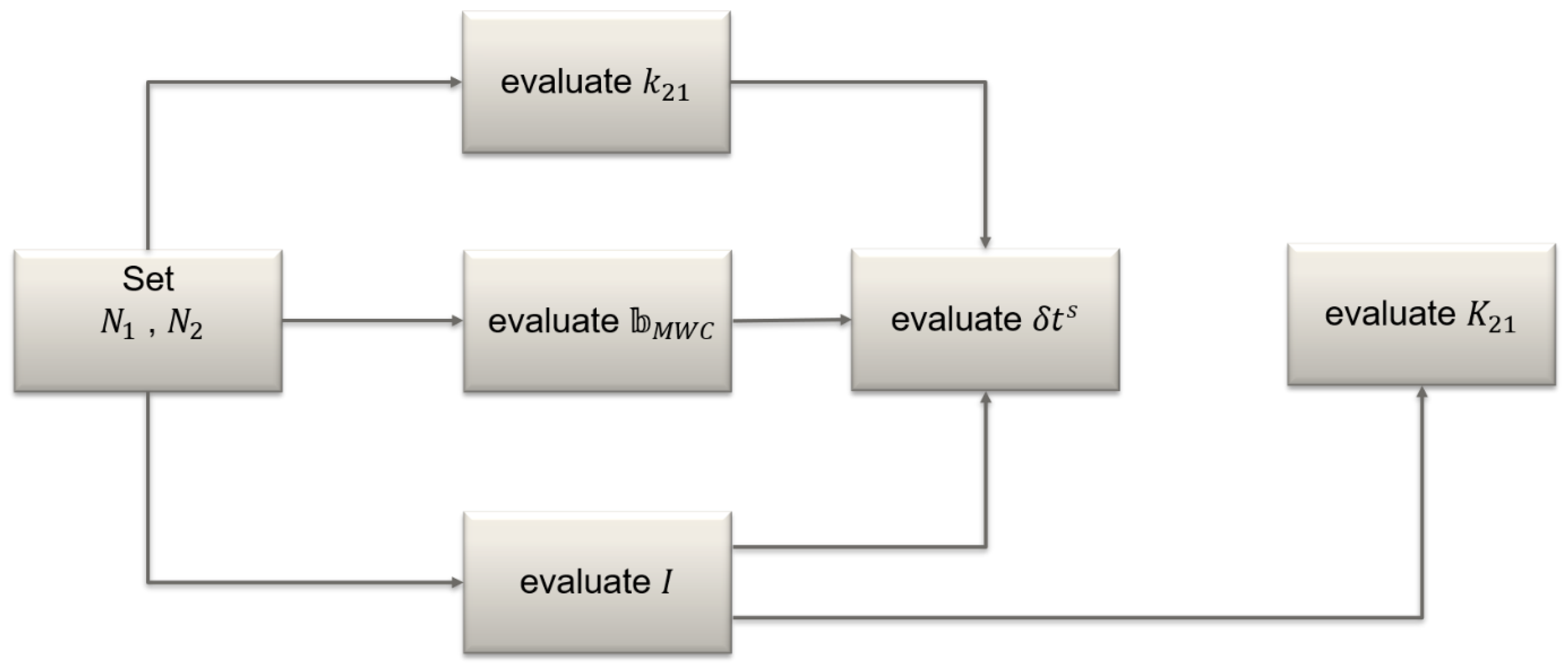
- The differential phase bias and the ionospheric slant delay were evaluated using the geometry-free combination of carrier phases. At the first epoch, pairs of ambiguities and were sought such that their geometry-free combination matched as close as possible the geometry-free measurements. These ambiguities were held fixed at the subsequent epochs, so far as no cycle slips occur. If a cycle slip was detected by using the M-W and Geometry-Free combinations, its size was determined and the ambiguities and were corrected accordingly. The remaining non-zero part was split into the constant () and the time-varying () parts. The latter was assumed to be zero at the first epoch, so STEC at the first epoch equaled the corresponding IGS GIM ionosphere estimate and at the subsequent epochs was reconstructed as GIM ionosphere estimates at the initial epoch plus evaluated from the carrier phases.
- Once and were fixed, we could find and evaluate the bias from the M-W combination.
- Having , , , available, the evaluation was adjusted to the new parameterization clock error from carrier phases on L1.
- With , we evaluated code DCB from the geometry-free code measurements.
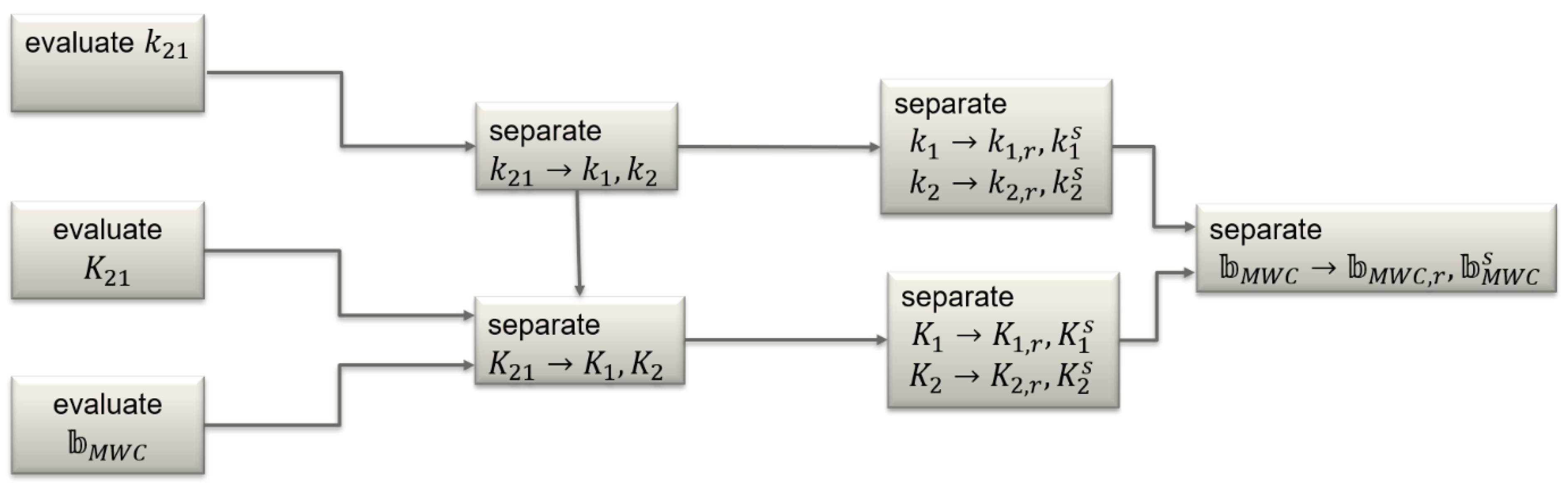
- Obtain , , , from and ;
- Separate the receiver- and satellite-specific parts of the code and carrier phase hardware biases and ;
- Use and to compute and .
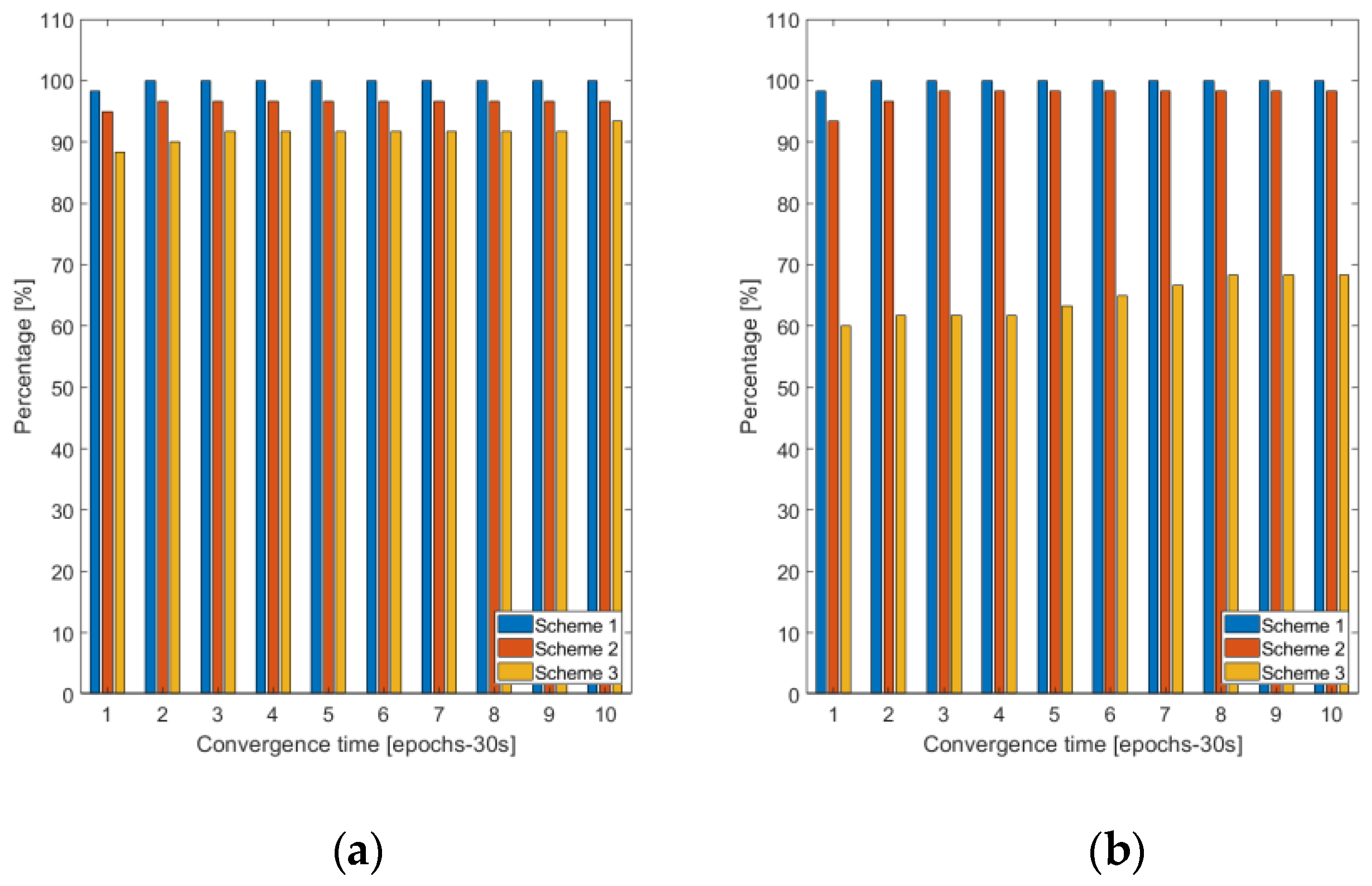
5.2. Static User Positioning
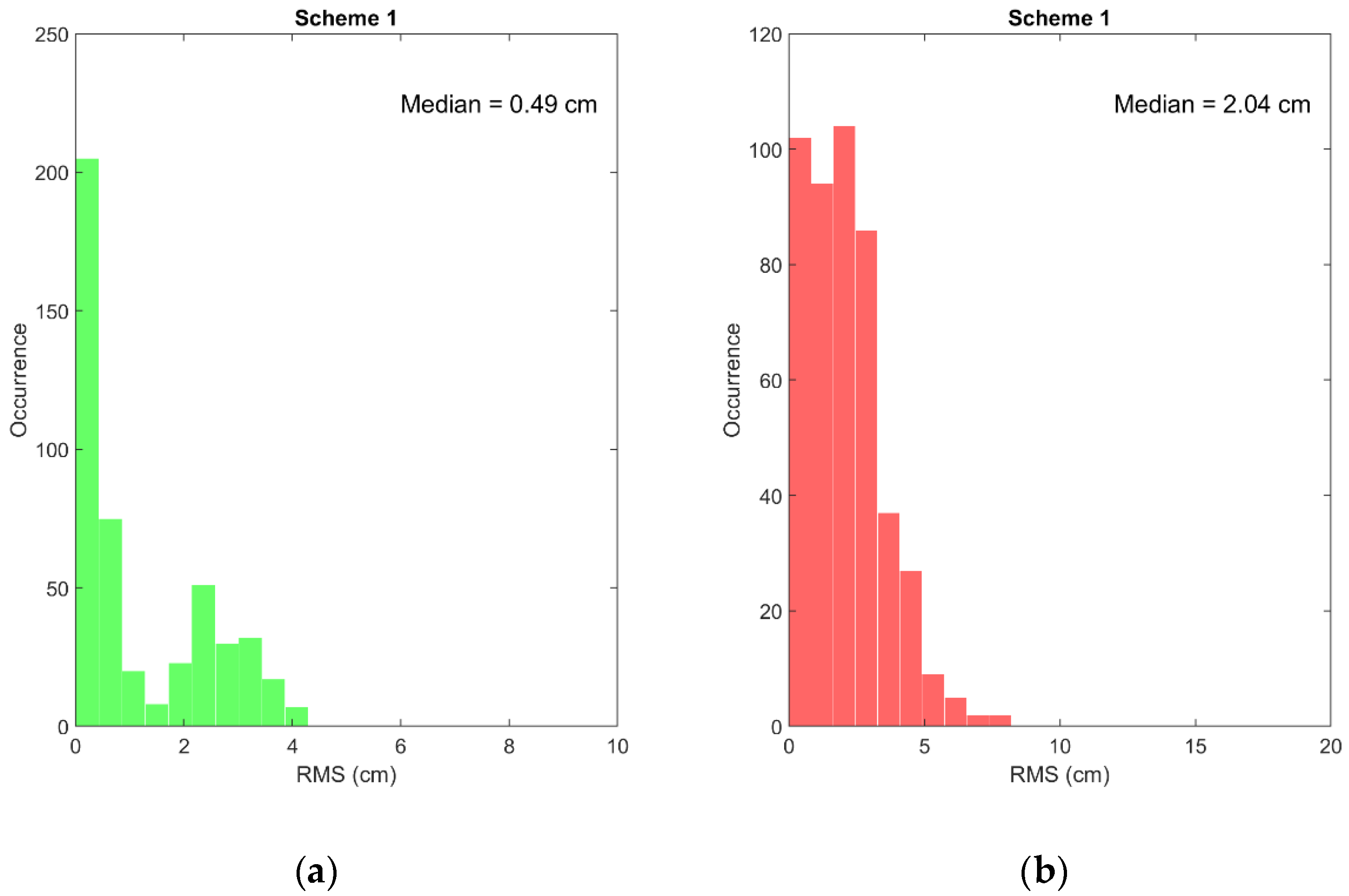
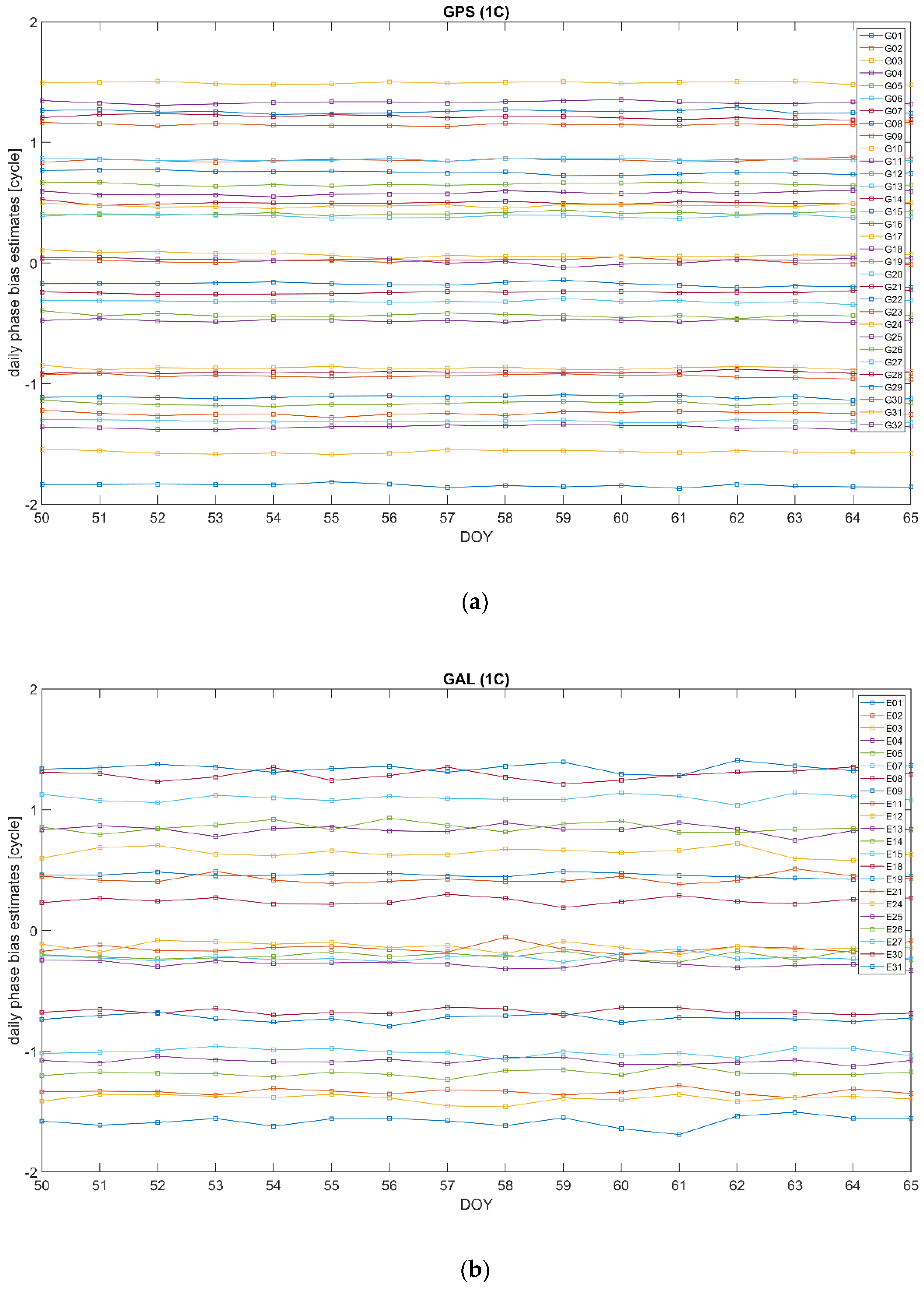
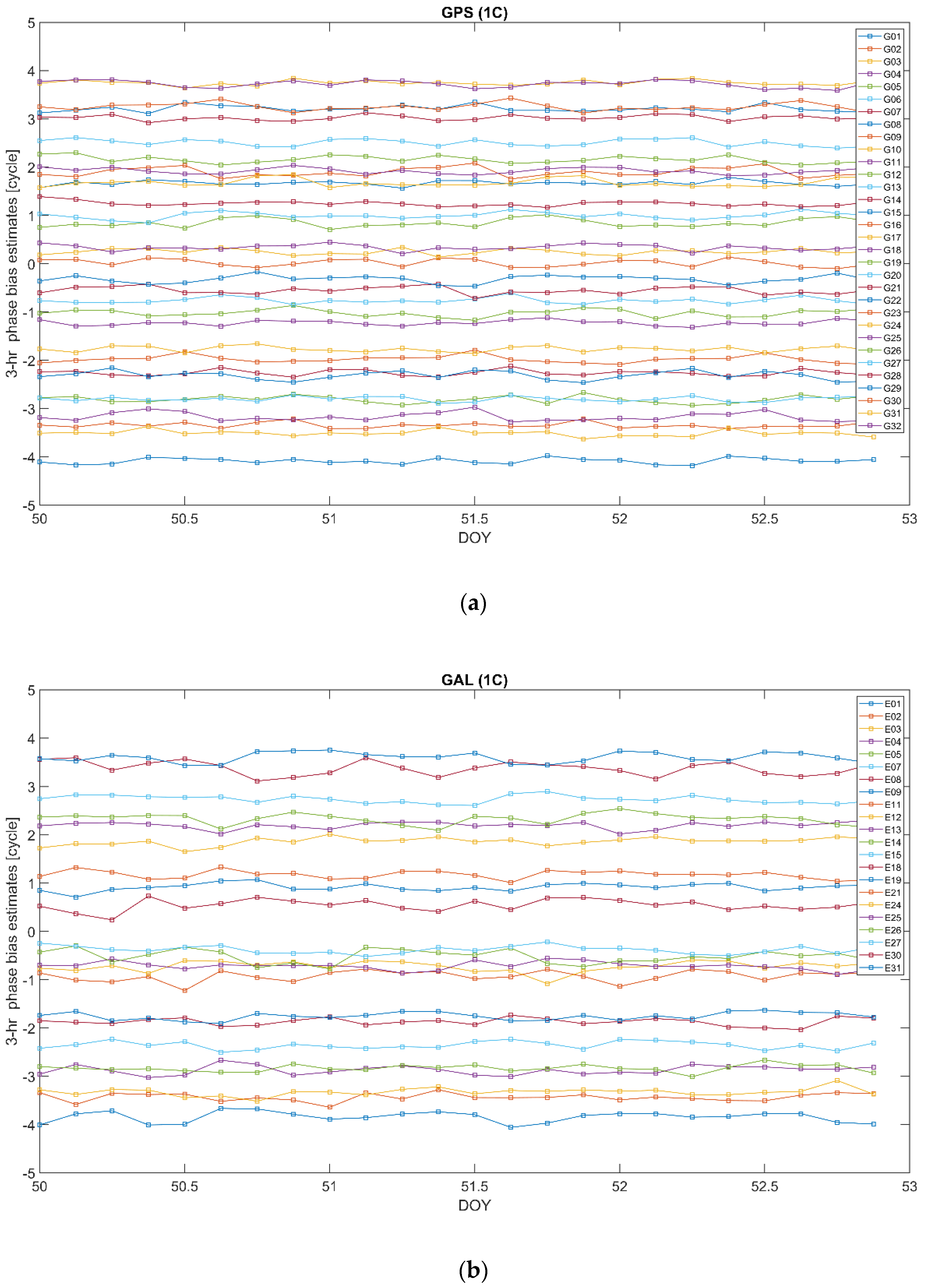
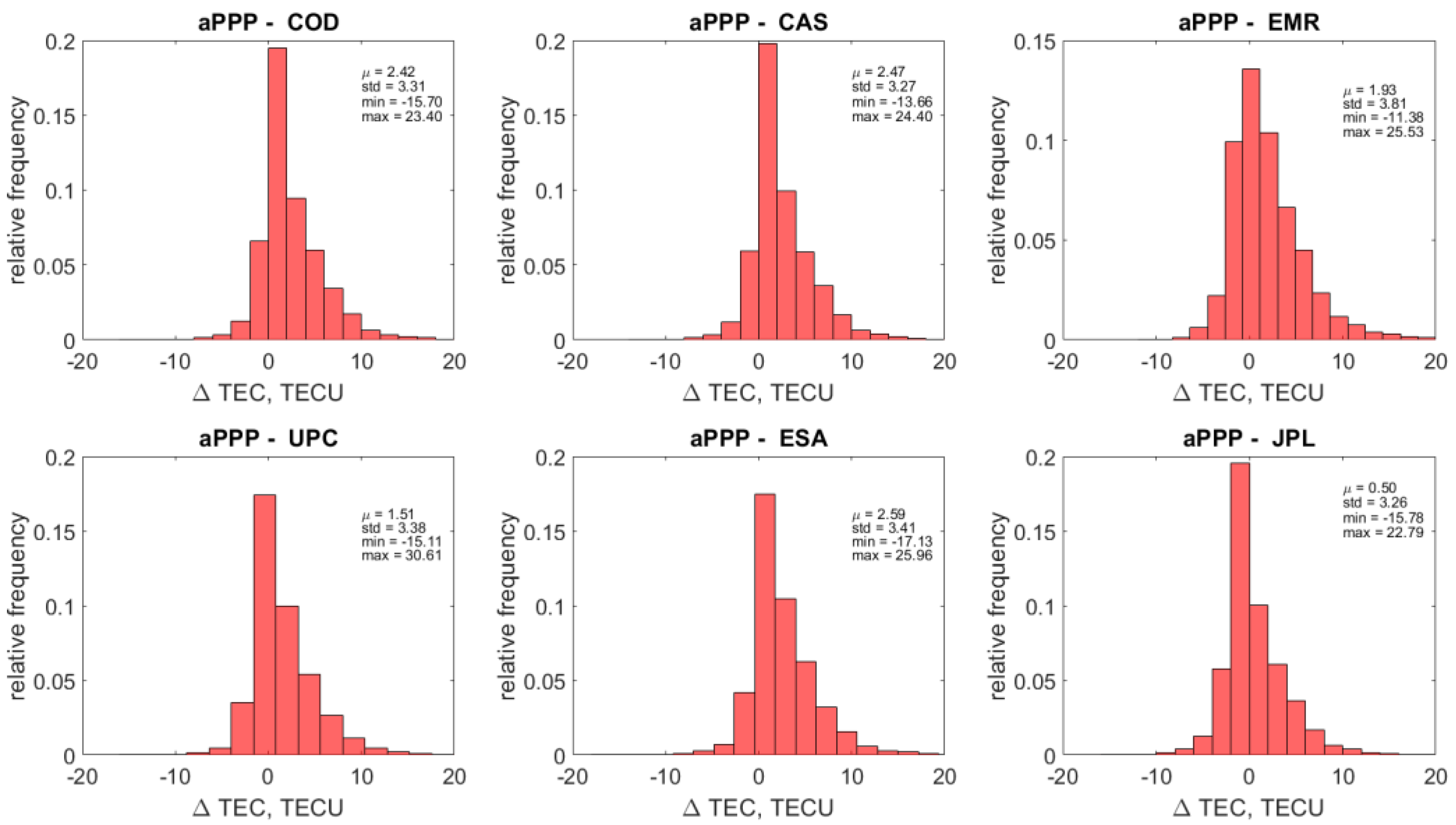
5.3. Stability Analysis of Bias
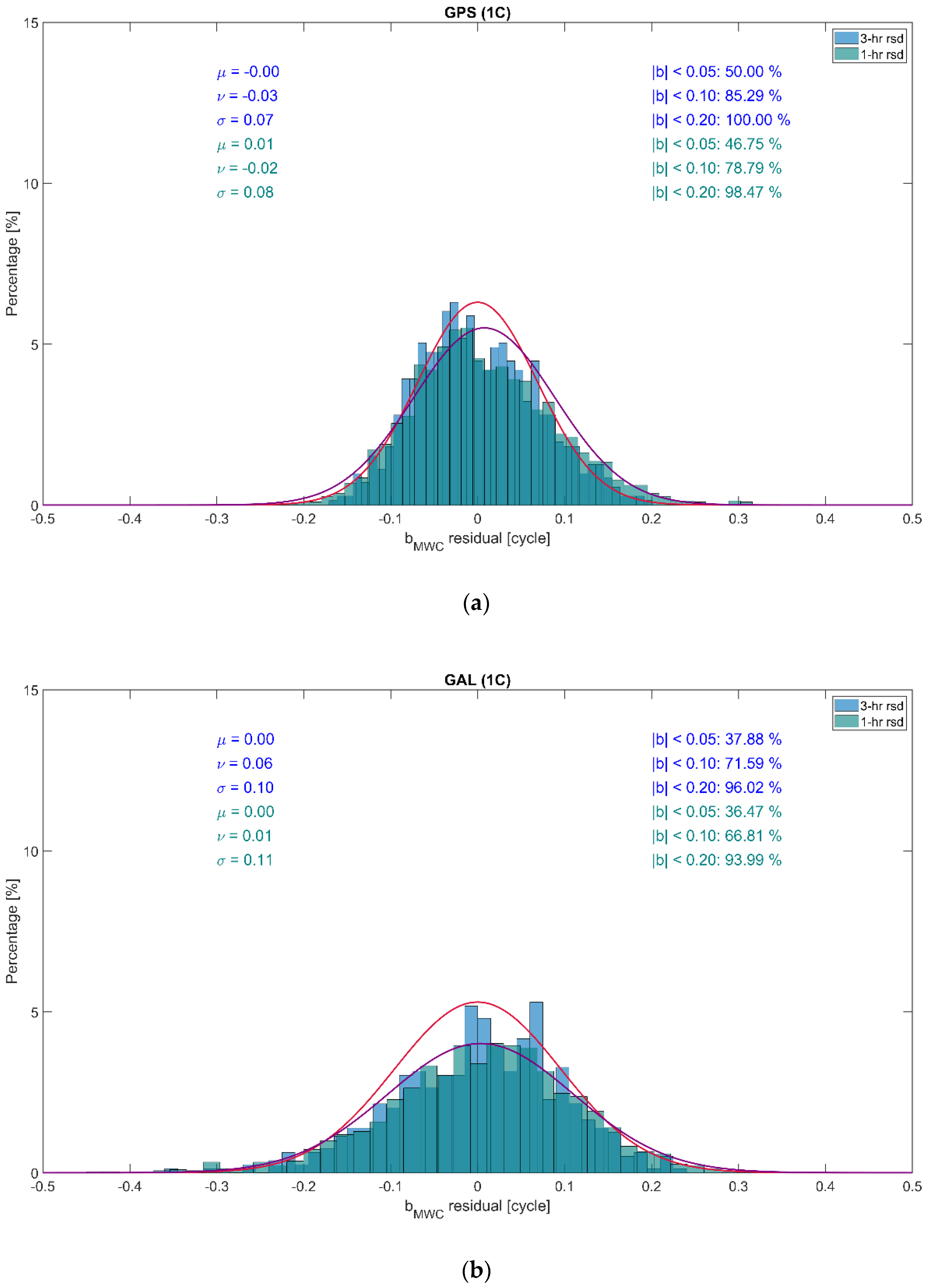
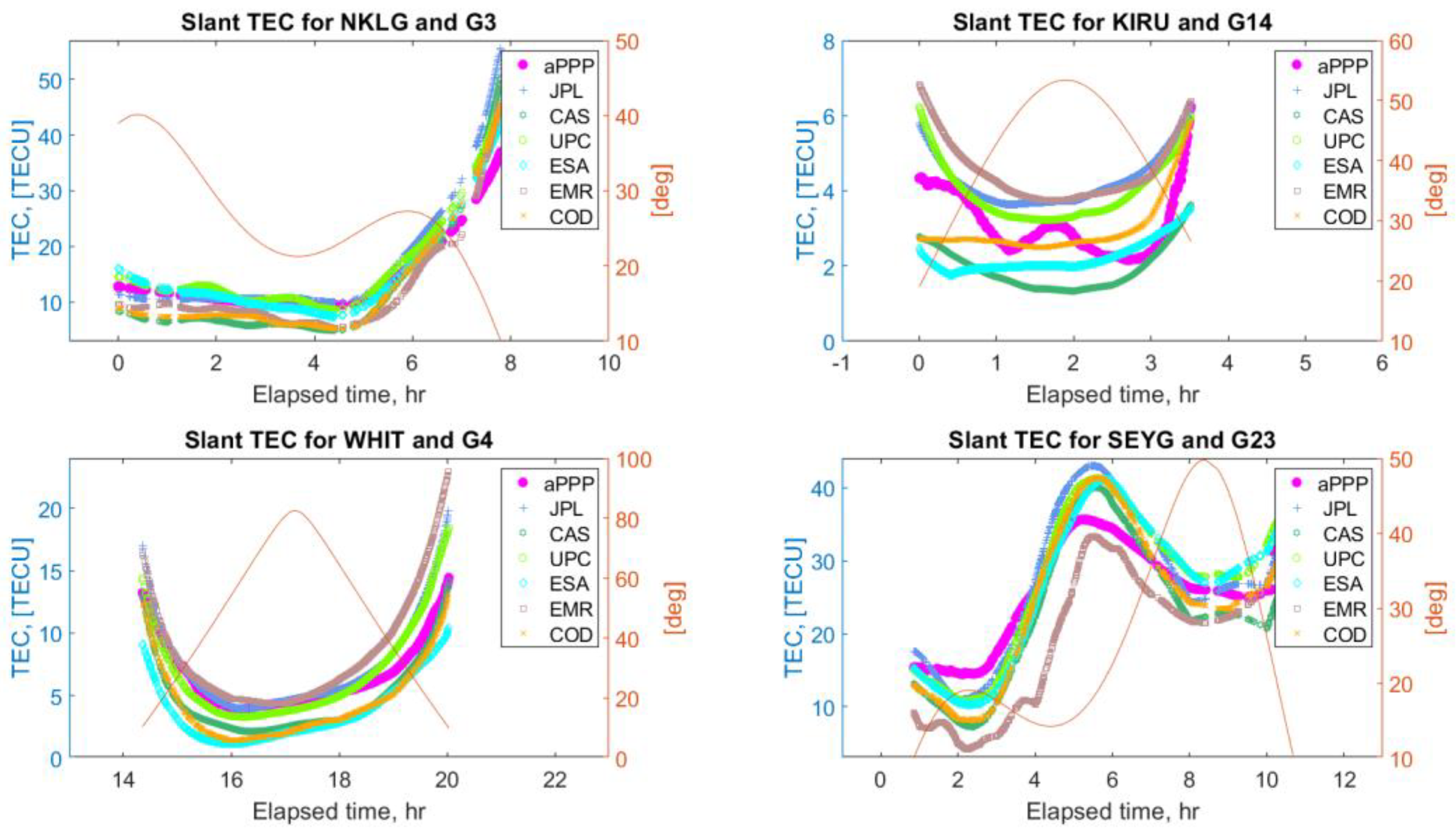
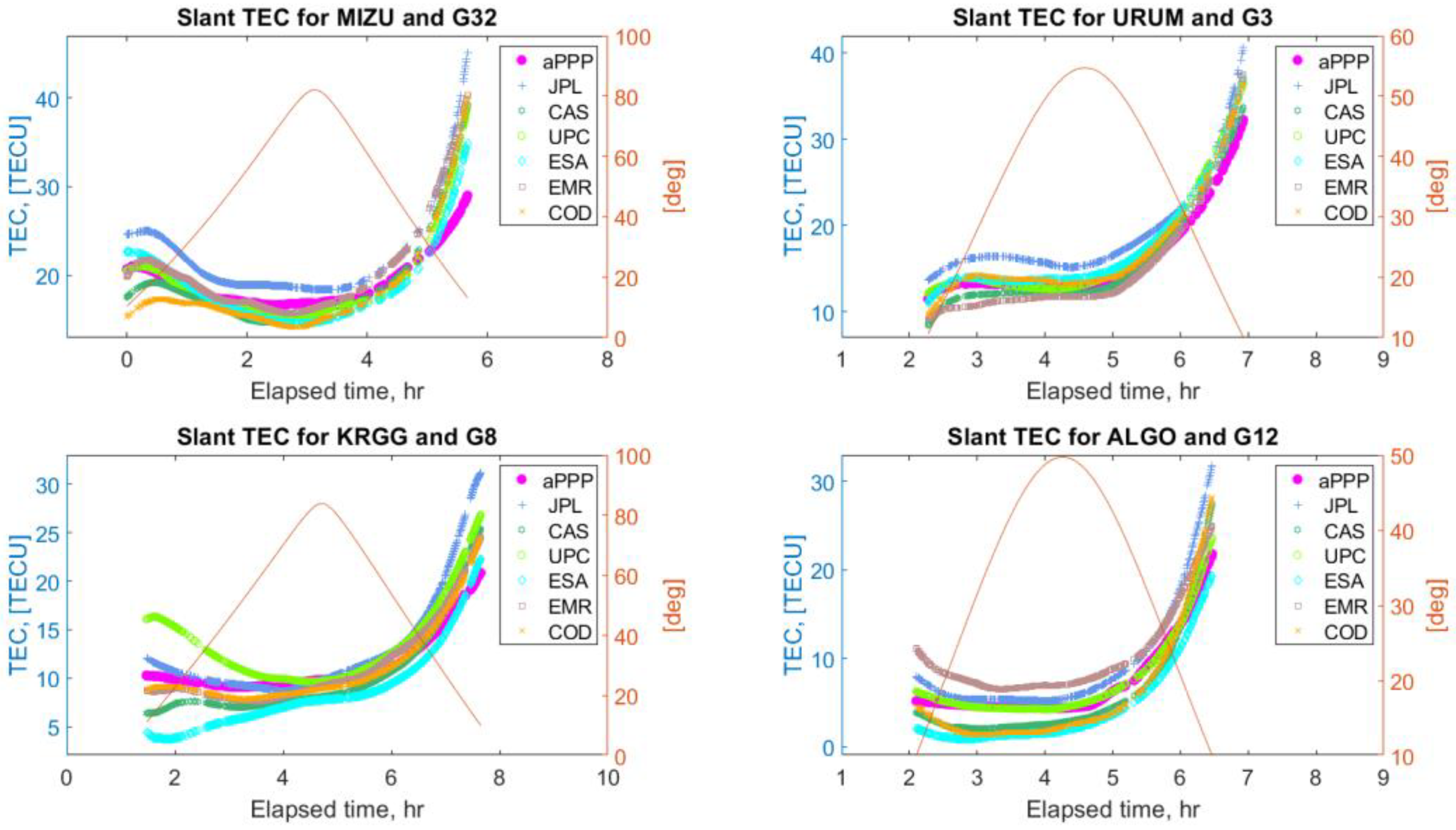
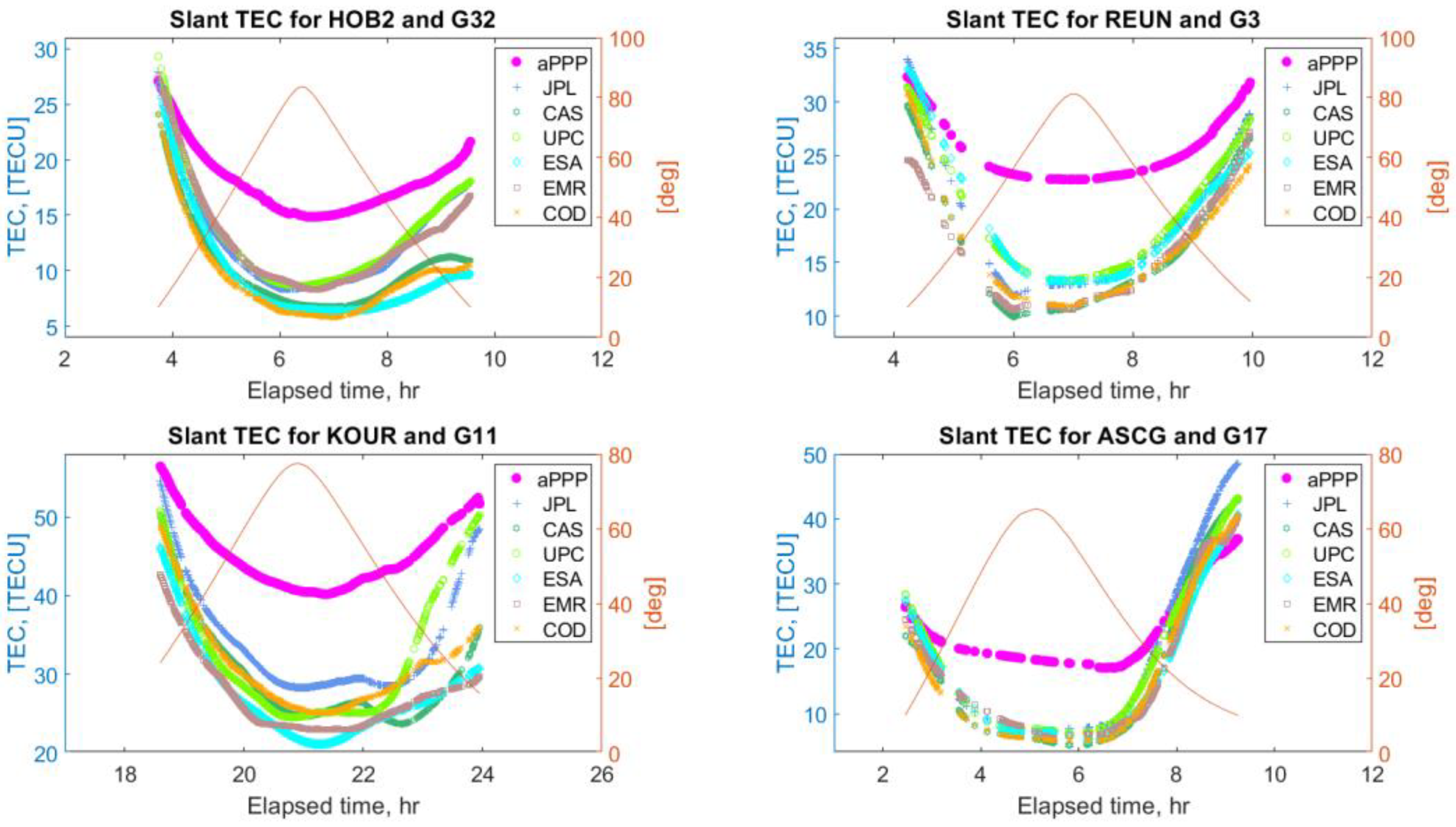
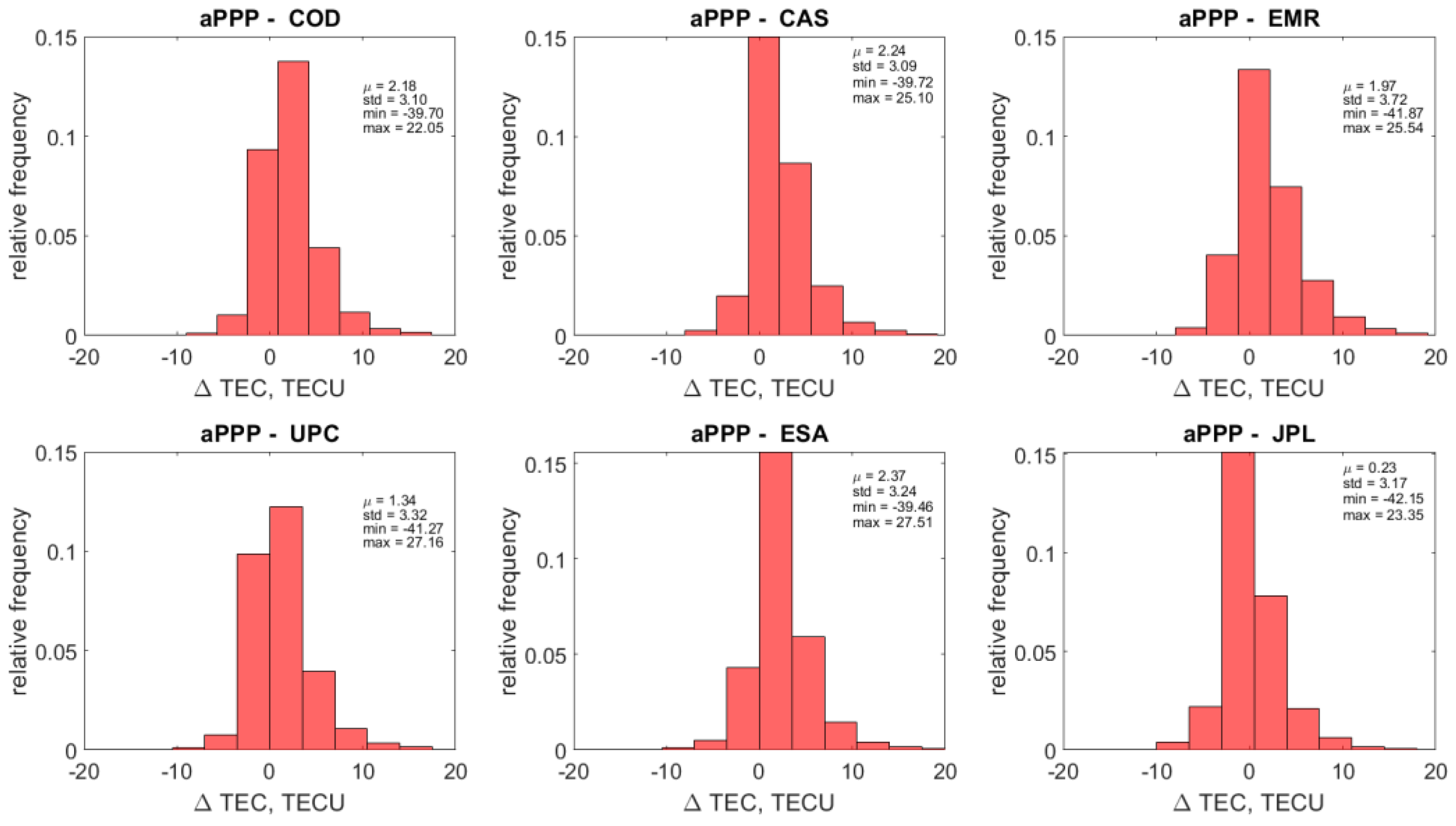
5.4. Retrieval of Ionosphere Slant Delays
6. Summary and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Weinbach, U. Feasibility and Impact of Receiver Clock Modeling in Precise GPS Data Analysis. Ph.D. Thesis, Wissenschaftliche Arbeiten der Fachrichtung Geodaesie und Geoinformatik der Leibniz Universitaet Hannover, Hannover, Germany, 2013. [Google Scholar]
- El-Mowafy, A.; Deo, M.; Rizos, C. On biases in precise point positioning with multi-constellation and multi-frequency GNSS data. Meas. Sci. Technol. 2016, 27, 03510227. [Google Scholar] [CrossRef]
- Subirana, J.S.; Zornoza, J.M.J.; Hernández-Pajares, M. GNSS Data Processing—Volume I: Fundamentals and Algorithms; ESA TM-23/1; ESA Communications: Noordwijk, The Netherlands, May 2013; ISBN 9789292218867. [Google Scholar]
- Kouba, J. A Guide to Using International GNSS Service (IGS) Products. 2009. Available online: https://files.igs.org/pub/resource/pubs/UsingIGSProductsVer21_cor.pdf (accessed on 10 March 2022).
- Lou, Y.; Zheng, F.; Gu, S.; Wang, C.; Guo, H.; Feng, Y. Multi-GNSS precise point positioning with raw single-frequency and dual-frequency measurement models. GPS Solut. 2015, 20, 849–862. [Google Scholar] [CrossRef]
- Liu, F.; Gao, Y. Triple-Frequency GPS Precise Point Positioning Ambiguity Resolution Using Dual-Frequency Based IGS Precise Clock Products. Int. J. Aerosp. Eng. 2017, 2017, 7854323. [Google Scholar] [CrossRef]
- Liu, T.; Yuan, Y.; Zhang, B.; Wang, N.; Tan, B.; Chen, Y. Multi-GNSS precise point positioning (MGPPP) using raw observations. J. Geod. 2016, 91, 253–268. [Google Scholar] [CrossRef]
- Deo, M.; El-Mowafy, A. Triple-frequency GNSS models for PPP with float ambiguity estimation: Performance comparison using GPS. Surv. Rev. 2018, 50, 249–261. [Google Scholar] [CrossRef] [Green Version]
- Liu, T.; Zhang, B.; Yuan, Y.; Li, M. Real-Time Precise Point Positioning (RTPPP) with raw observations and its application in real-time regional ionospheric VTEC modeling. J. Geod. 2018, 92, 1267–1283. [Google Scholar] [CrossRef]
- Xiao, G.; Li, P.; Gao, Y.; Heck, B. Unified Model for Multi-Frequency PPP Ambiguity Resolution and Test Results with Galileo and BeiDou Triple-Frequency Observations. Remote Sens. 2019, 11, 116. [Google Scholar] [CrossRef] [Green Version]
- Li, M.; Zhang, B.; Yuan, Y.; Zhao, C. Single-frequency precise point positioning (PPP) for retrieving ionospheric TEC from BDS B1 data. GPS Solut. 2018, 23, 11. [Google Scholar] [CrossRef]
- Rovira-Garcia, A.; Juan, J.M.; Sanz, J.; González-Casado, G.; Ibáñez, D. Accuracy of ionospheric models used in GNSS and SBAS: Methodology and analysis. J. Geod. 2016, 90, 229–240. [Google Scholar] [CrossRef]
- Loyer, S.; Perosanz, F.; Mercier, F.; Capdeville, H.; Marty, J. Zero-difference GPS ambiguity resolution at CNES–CLS IGS Analysis Center. J. Geod. 2012, 86, 991–1003. [Google Scholar] [CrossRef]
- Håkansson, M.; Jensen, A.B.; Horemuz, M.; Hedling, G. Review of code and phase biases in multi-GNSS positioning. GPS Solut. 2016, 21, 849–860. [Google Scholar] [CrossRef] [Green Version]
- Motooka, N.; Hirokawa, R.; Nakakuki, K.; Fujita, S.; Miya, M.; Sato, Y. CLASLIB: An Open-source Toolkit for Low-cost high-precision PPP-RTK Positioning. In Proceedings of the 32nd International Technical Meeting of the Satellite Division of The Institute of Navigation (ION) GNSS+ Meeting, Miami, FL, USA, 16–20 September 2019; pp. 3695–3707. [Google Scholar] [CrossRef]
- CODE Analysis Center. Available online: https://www.aiub.unibe.ch/research/code___analysis_center/index_eng.html (accessed on 10 March 2022).
- Wu, J.; Wu, S.; Hajj, G.; Bertiger, W.; Lichten, S. Effects of Antenna Orientation on GPS Carrier Phase. Manuscr. Geod. 1992, 18, 1647–1660. [Google Scholar]
- Leandro, R.; Santos, M.; Langley, R. UNB neutral atmosphere models, development and performance. In Proceedings of the Institute of Navigation (ION) National Technical Meeting, Monterey, CA, USA, 18–20 January 2006; pp. 564–573. [Google Scholar]
- Boehm, J.; Niell, A.; Tregoning, P.; Schuh, H. Global Mapping Function (GMF): A new empirical mapping function based on numerical weather model data. Geophys. Res. Lett. 2006, 33. [Google Scholar] [CrossRef] [Green Version]
- IERS. International Earth Rotation and Reference System Services Conventions. Technical Note 21. 1996. Available online: https://www.iers.org/IERS/EN/Publications/TechnicalNotes/tn21.html (accessed on 10 March 2022).
- Altamimi, Z.; Rebischung, P.; Métivier, L.; Collilieux, X. ITRF2014: A new release of the International Terrestrial Reference Frame modeling non-linear station motions: ITRF2014. J. Geophys. Res. Solid Earth. 2016, 121, 6109–6131. [Google Scholar] [CrossRef] [Green Version]
- Khodabandeh, A.; Teunissen, P.J. An analytical study of PPP-RTK corrections: Precision, correlation and user-impact. J. Geod. 2015, 89, 1109–1132. [Google Scholar] [CrossRef]
- Deng, Y.; Guo, F.; Ren, X.; Ma, F.; Zhang, X. Estimation and analysis of multi-GNSS observable-specific code biases. GPS Solut. 2021, 25, 100. [Google Scholar] [CrossRef]
- Collins, P. Isolating and Estimating Undifferenced GPS Integer Ambiguities. In Proceedings of the Institute of Navigation (ION) National Technical Meeting, San Diego, CA, USA, 28–30 January 2008; pp. 720–732. [Google Scholar]
- Ge, M.; Gendt, G.; Rothacher, M.; Shi, C.; Liu, J. Resolution of GPS carrier-phase ambiguities in Precise Point Positioning (PPP) with daily observations. J. Geod. 2008, 82, 401. [Google Scholar] [CrossRef] [Green Version]
- Laurichesse, D.; Mercier, F.; Berthias, J.; Broca, P.; Cerri, L. Integer Ambiguity Resolution on Undifferenced GPS Phase Measurements and Its Application to PPP and Satellite Precise Orbit Determination. Navigation 2007, 56, 135–149. [Google Scholar] [CrossRef]
- Geng, J.; Teferle, F.; Meng, X.; Dodson, A. Towards PPP-RTK: Ambiguity resolution in real-time precise point positioning. Adv. Space Res. 2011, 47, 1664–1673. [Google Scholar] [CrossRef] [Green Version]
- Banville, S.; Geng, J.; Loyer, S.; Schaer, S.; Springer, T.; Strasser, S. On the interoperability of IGS products for precise point positioning with ambiguity resolution. J. Geod. 2020, 94, 10. [Google Scholar] [CrossRef]
- Villiger, A.; Schaer, S.; Dach, R.; Prange, L.; Susnik, A.; Jäggi, A. Determination of GNSS pseudo-absolute code biases and their long-term combination. J. Geod. 2019, 93, 1487–1500. [Google Scholar] [CrossRef]
- Teunissen, P.; Khodabandeh, A. Review and principles of PPP-RTK methods. J. Geod. 2014, 89, 217–240. [Google Scholar] [CrossRef]
- Verhagen, S.; Li, B. LAMBDA Software Package: Matlab Implementation, Version 3.0; Delft University of Technology and Curtin University: Perth, Australia, 2012.
- Li, Y.; Li, B.; Gao, Y. Improved PPP Ambiguity Resolution Considering the Stochastic Characteristics of Atmospheric Corrections from Regional Networks. Sensors 2015, 15, 29893–29909. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Teunissen, P. An optimality property of the integer least-squares estimator. J. Geod. 1999, 73, 587–593. [Google Scholar] [CrossRef]
- Verhagen, S.; Li, B.; Teunissen, P. Ps-LAMBDA: Ambiguity success rate evaluation software for interferometric applications. Comput. Geosci. 2013, 54, 361–376. [Google Scholar] [CrossRef] [Green Version]
- Li, W.; Li, Z.; Wang, N.; Liu, A.; Zhou, K.; Yuan, H.; Krankowski, A. A satellite-based method for modeling ionospheric slant TEC from GNSS observations: Algorithm and validation. GPS Solut. 2022, 26, 14. [Google Scholar] [CrossRef]
- Feltens, J.; Bellei, G.; Springer, T.; Kints, M.; Zandbergen, R.; Budnik, F.; Schönemann, E. Tropospheric and ionospheric media calibrations based on global navigation satellite system observation data. J. Space Weather Space Clim. 2018, 8, A30. [Google Scholar] [CrossRef]
- Coster, A.; Gaposchkin, E.; Thornton, L. Real-Time Ionospheric Monitoring System Using GPS. Navigation 1992, 39, 191–204. [Google Scholar] [CrossRef]




| Bias | Conventional Parameterization |
|---|---|
| L1 carrier phase bias | |
| L2 carrier phase bias | |
| Wide-lane bias | |
| Ionosphere-free bias | |
| Geometry-free bias |
| Bias | Conventional Parameterization | Proposed Parameterization |
|---|---|---|
| L1 bias | ||
| L2 bias | ||
| Wide-lane bias | ||
| Ionosphere-free bias | ||
| Melbourne-Wübenna bias | ||
| Geometry-free bias |
| Item | Models |
|---|---|
| Constellations | GPS+GALILEO |
| Procedure | Corrections generation: network processing/user positioning: PPP-RTK |
| Estimator | User positioning: KF |
| Observations | Undifferenced carrier phases, narrow-lane code |
| Signal selection | GPS: L1/L2; GAL: E1/E5a |
| Sampling interval | |
| cutoff angle | |
| Phase wind-up | Applied [17] |
| Tropospheric delay | UNB3 m [18] with GMF [19] |
| Ionospheric delay | Evaluated using GIM as a-priori information, provided as corrections |
| Receiver clock | Estimated on the user side, random walk |
| Station displacement | Solid Earth tide, polar tide, ocean loading tide: IERS Conventions 1996 [20] |
| Terrestrial frame | ITRF 2014 [21] |
| Satellite orbit | CODE final orbits |
| Satellite clock | CODE 30-sec clocks, adjusted to the new parameterization and provided as corrections |
| Phase ambiguities | Network processing: set to integers/user positioning: LAMBDA PAR |
| Station coordinates | Network processing: precise in ITRF14/user positioning: estimated |
| Satellite PCO | Corrected using IGS values |
| GIM ID | Ionosphere Maps from |
|---|---|
| CAS | Chinese Academy of Science |
| CODE | Center for Orbit Determination in Europe, Bern, Switzerland |
| EMR | National Resources Canada |
| ESA | European Space Agency |
| JPL | Jet Propulsion Laboratory, Pasadena, USA |
| UPC | Polytechnic University of Catalonia, Barcelona |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Keshin, M.; Sato, Y.; Nakakuki, K.; Hirokawa, R. A Novel Clock Parameterization and Its Implications for Precise Point Positioning and Ionosphere Estimation. Sensors 2022, 22, 3117. https://doi.org/10.3390/s22093117
Keshin M, Sato Y, Nakakuki K, Hirokawa R. A Novel Clock Parameterization and Its Implications for Precise Point Positioning and Ionosphere Estimation. Sensors. 2022; 22(9):3117. https://doi.org/10.3390/s22093117
Chicago/Turabian StyleKeshin, Maxim, Yuki Sato, Kenji Nakakuki, and Rui Hirokawa. 2022. "A Novel Clock Parameterization and Its Implications for Precise Point Positioning and Ionosphere Estimation" Sensors 22, no. 9: 3117. https://doi.org/10.3390/s22093117
APA StyleKeshin, M., Sato, Y., Nakakuki, K., & Hirokawa, R. (2022). A Novel Clock Parameterization and Its Implications for Precise Point Positioning and Ionosphere Estimation. Sensors, 22(9), 3117. https://doi.org/10.3390/s22093117






