Analytical Model of Eccentric Induction Machines Using the Conformal Winding Tensor Approach
Abstract
:1. Introduction
- Numerical models, mostly based on the finite elements method (FEM). They can accurately reproduce the behaviour of the eccentric IM [20], but they require detailed information about construction aspects of the IM and are computationally intensive. This problem can be alleviated using order-reduction models [21], solving the machine at some positions and performing a field reconstruction based on them or with hybrid FEM-analytical models [22,23,24].
- Analytical models, based on a network of magnetically coupled circuits [25]. Their accuracy may not be as high as FEM models, but they are much faster to build and solve, need only the most basic motor parameters [26], and can correctly reproduce the position and amplitude of the fault-related harmonic components [27].
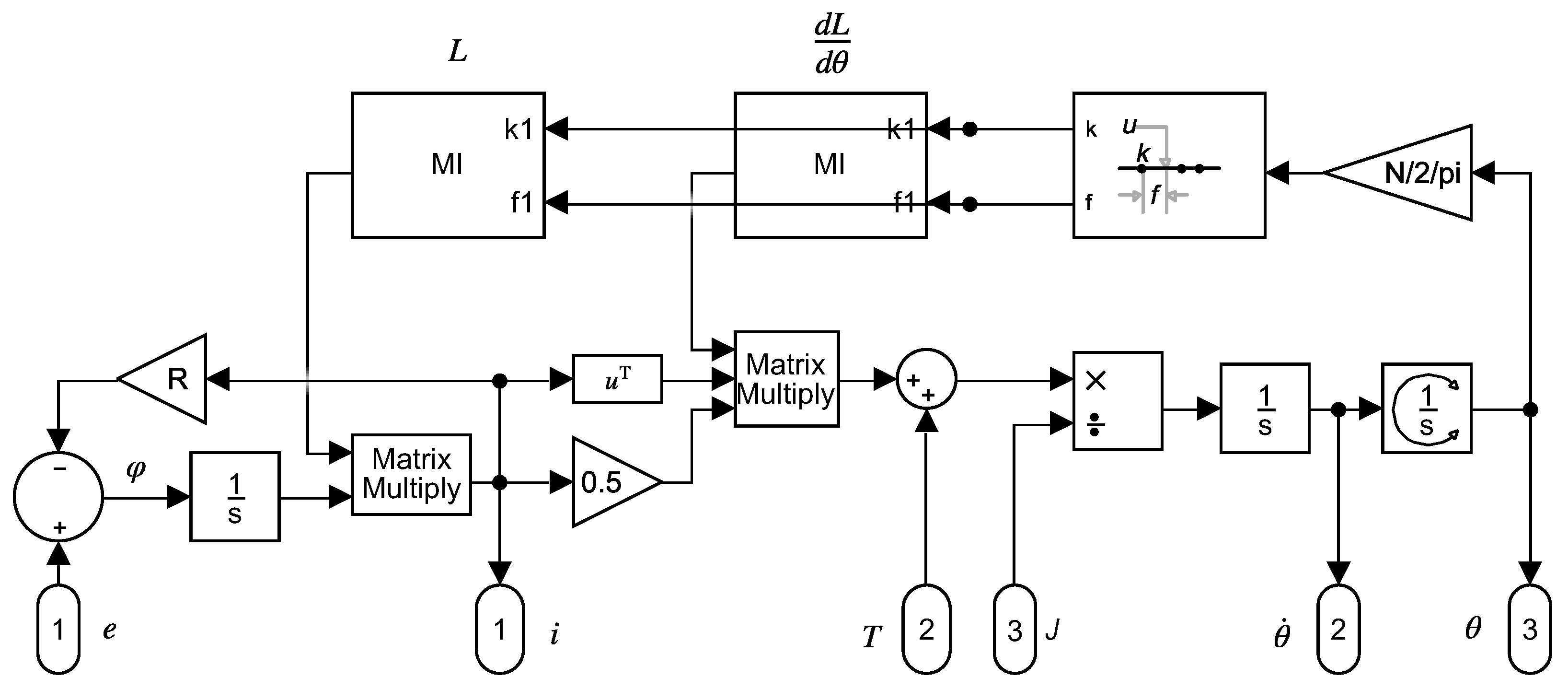
2. Simple Analytical Model of the IM
- is the voltage vector, which represents the terminal voltages applied to the n windings;
- is the flux linkage vector, which represents the flux linkages of the n windings;
- is the current vector, which represents the n winding currents;
- is the resistance tensor. It is a square matrix, with components, for which its elements are winding resistances.
3. Determination of the Parameters of the IM Model
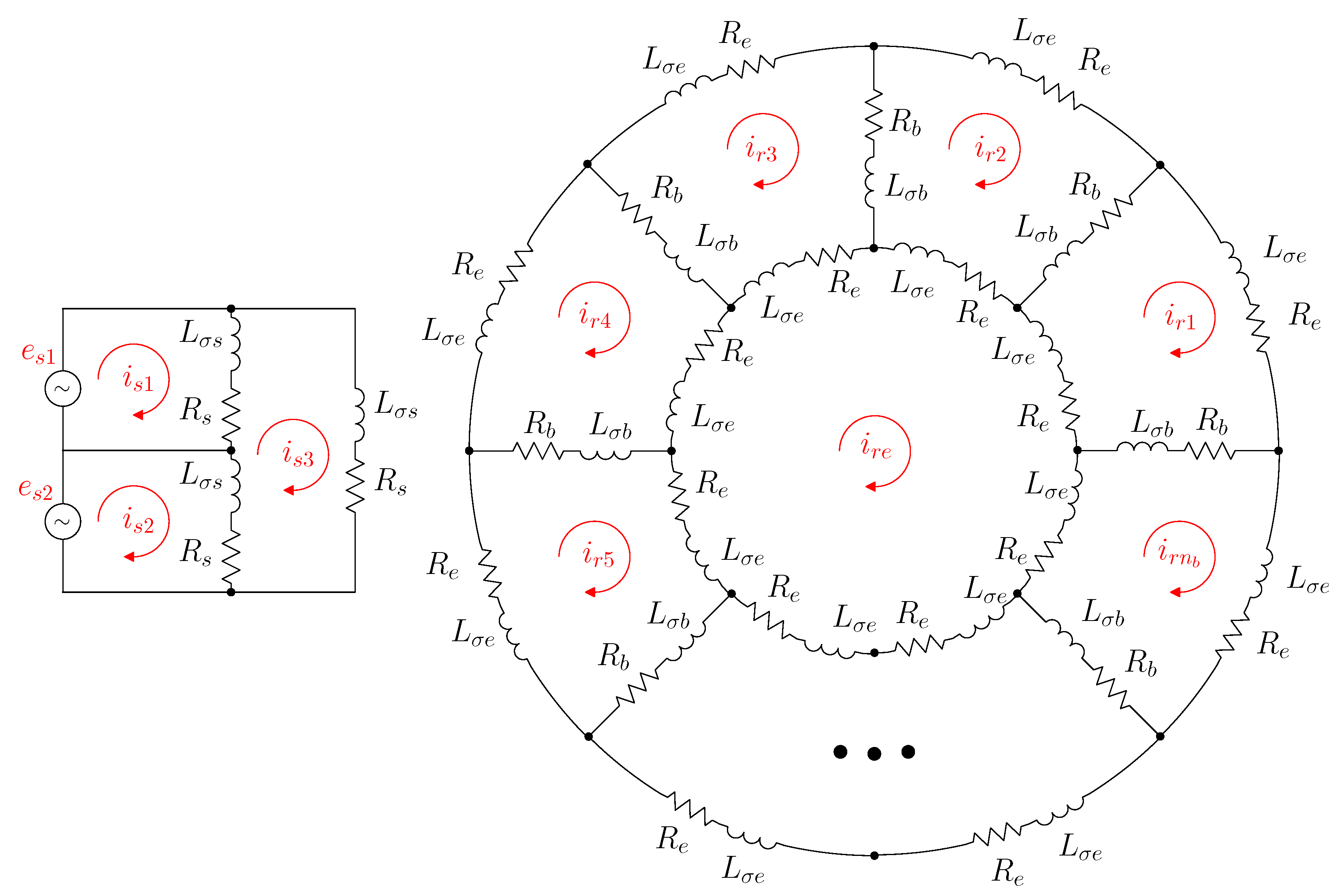
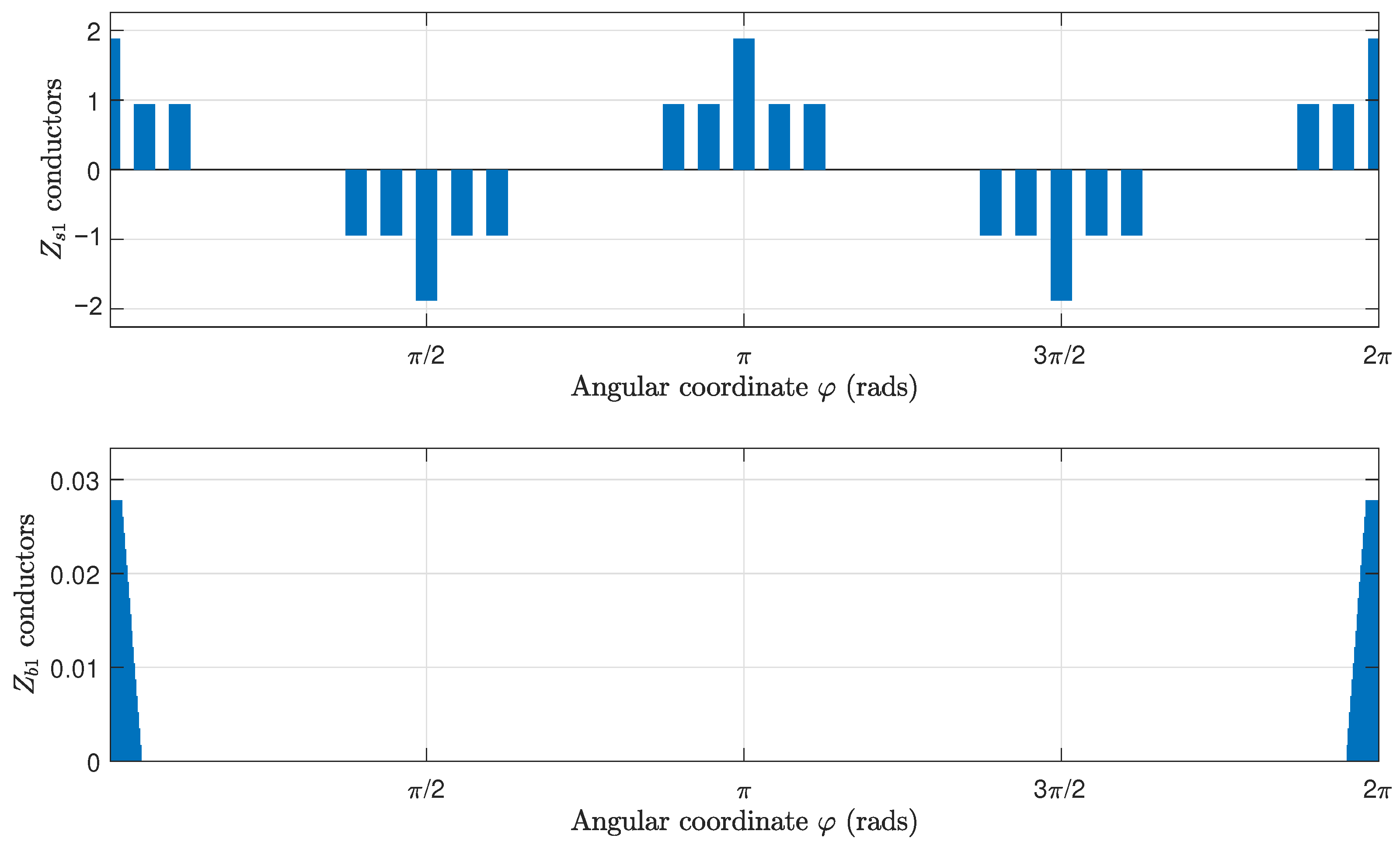
3.1. Resistance Matrix of the Primitive IM Network
3.2. Inductance Matrix of the Primitive Network
3.3. From the Primitive IM Network to the Actual One Using the Connection Matrix

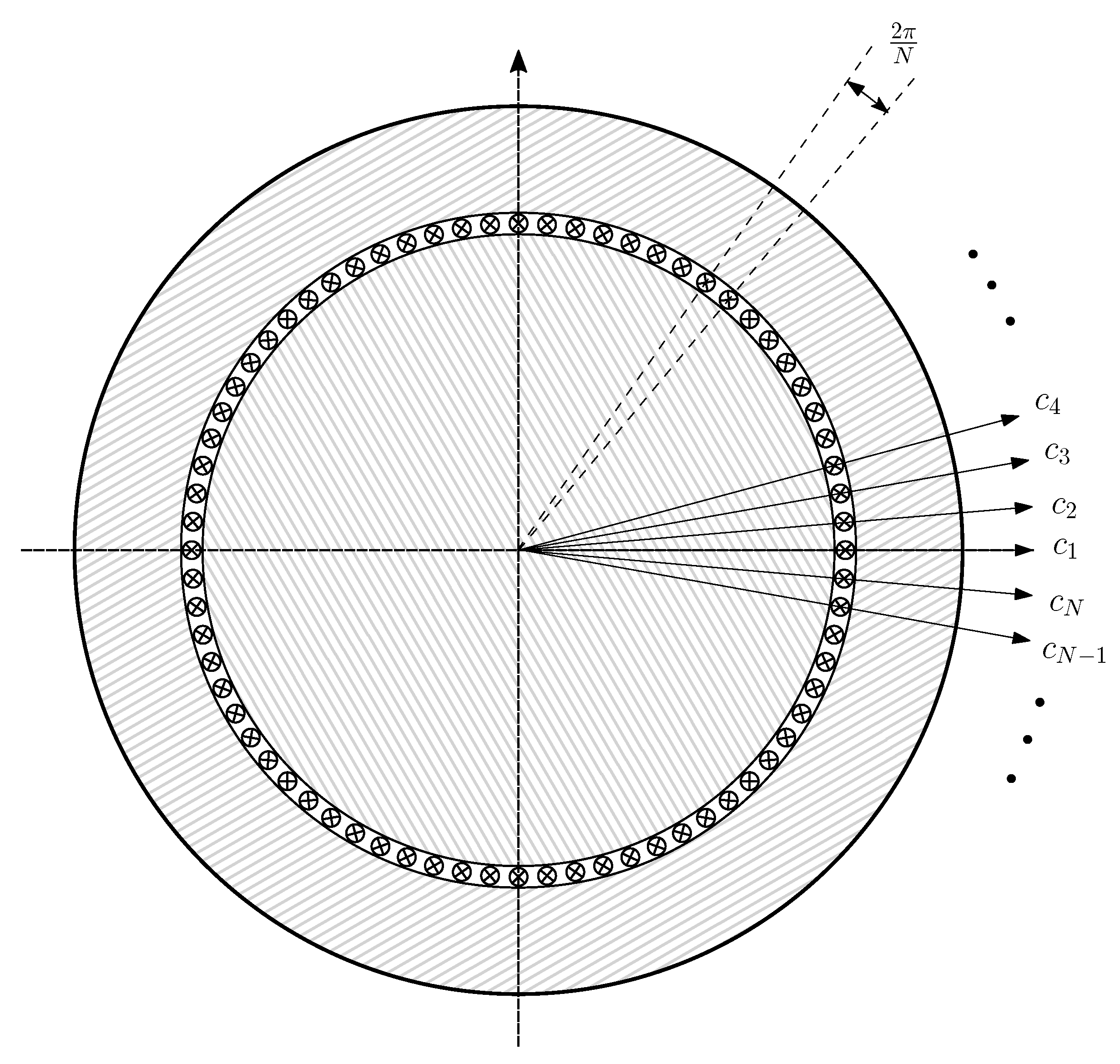
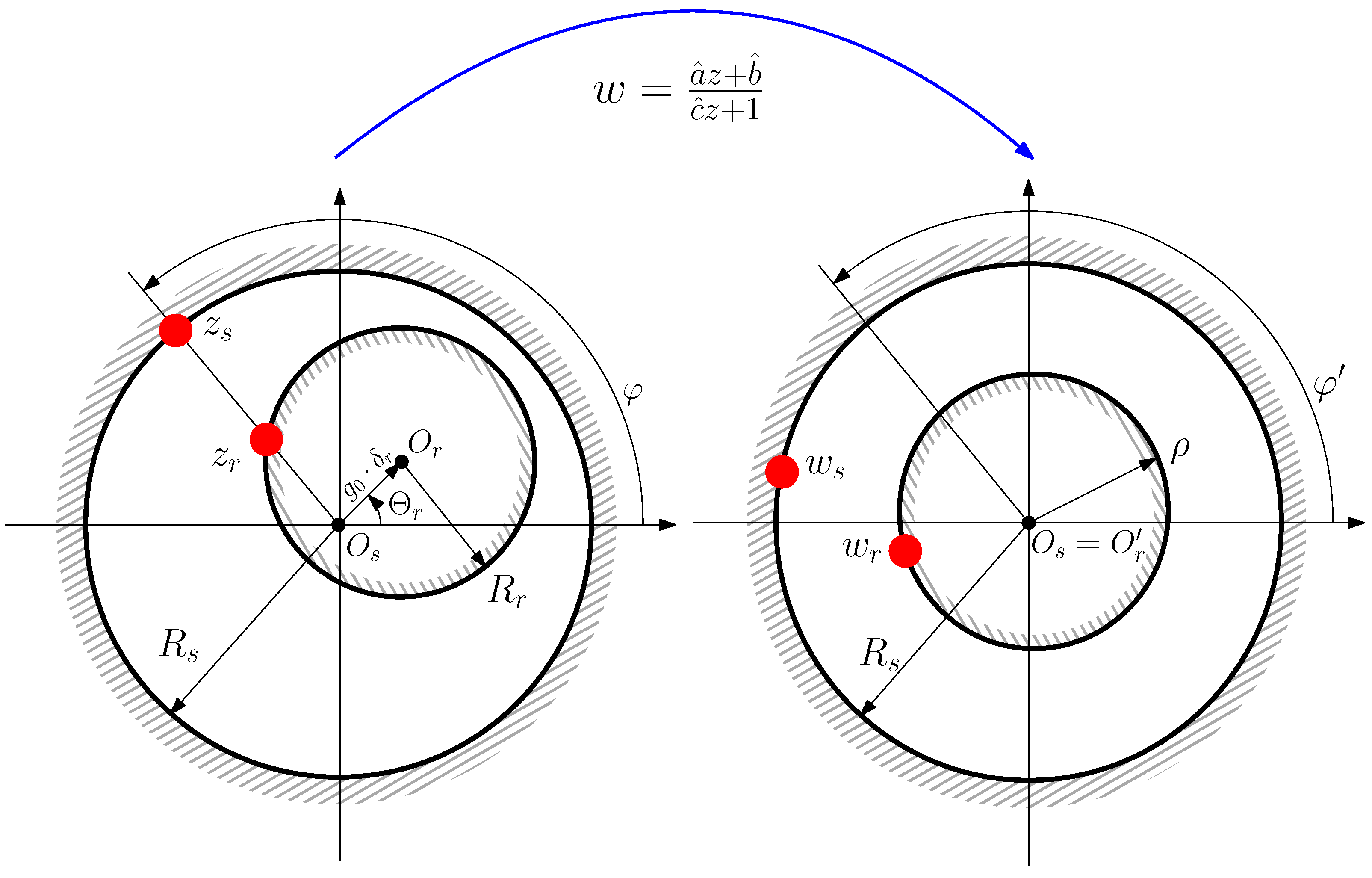
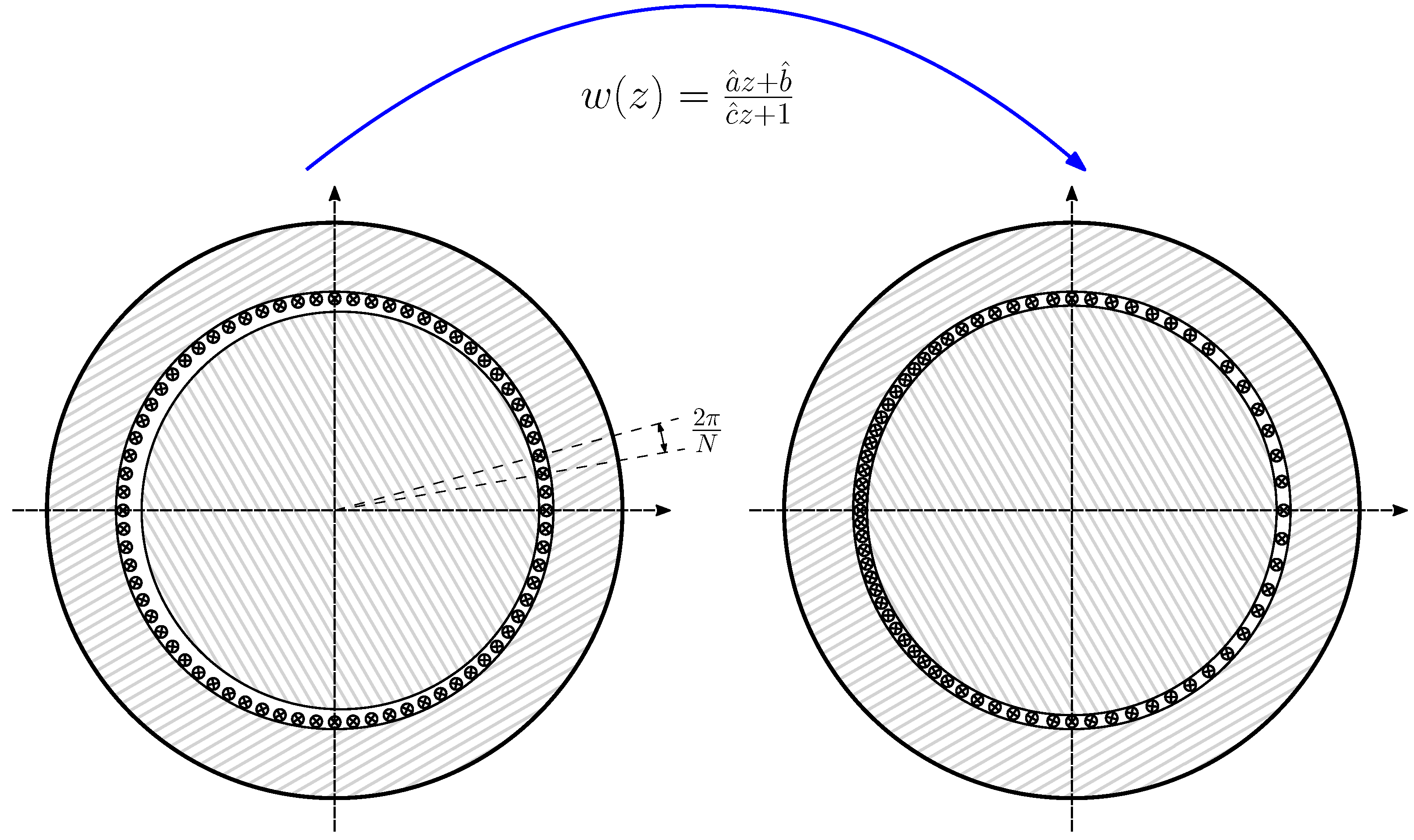
4. Computation of the Main Inductance Matrix of the Healthy and the Eccentric IM Using the Conformal Winding Tensor Approach
- A primitive spatial network, similarly to Figure 4, is constructed by removing all interconnections between winding conductors and short circuiting each one without changing their spatial positions. For this simple network, the matrix with the partial inductances between conductors is obtained, which makes it easier to take into account the effect of IM eccentricity.
- A transformation matrix, similarly to (12), is constructed. It represents the interconnections of the conductors of each winding for each angular position of the rotor, i.e., the winding tensor.

4.1. Partial Inductance Matrix of the Conductors in an Eccentric IM
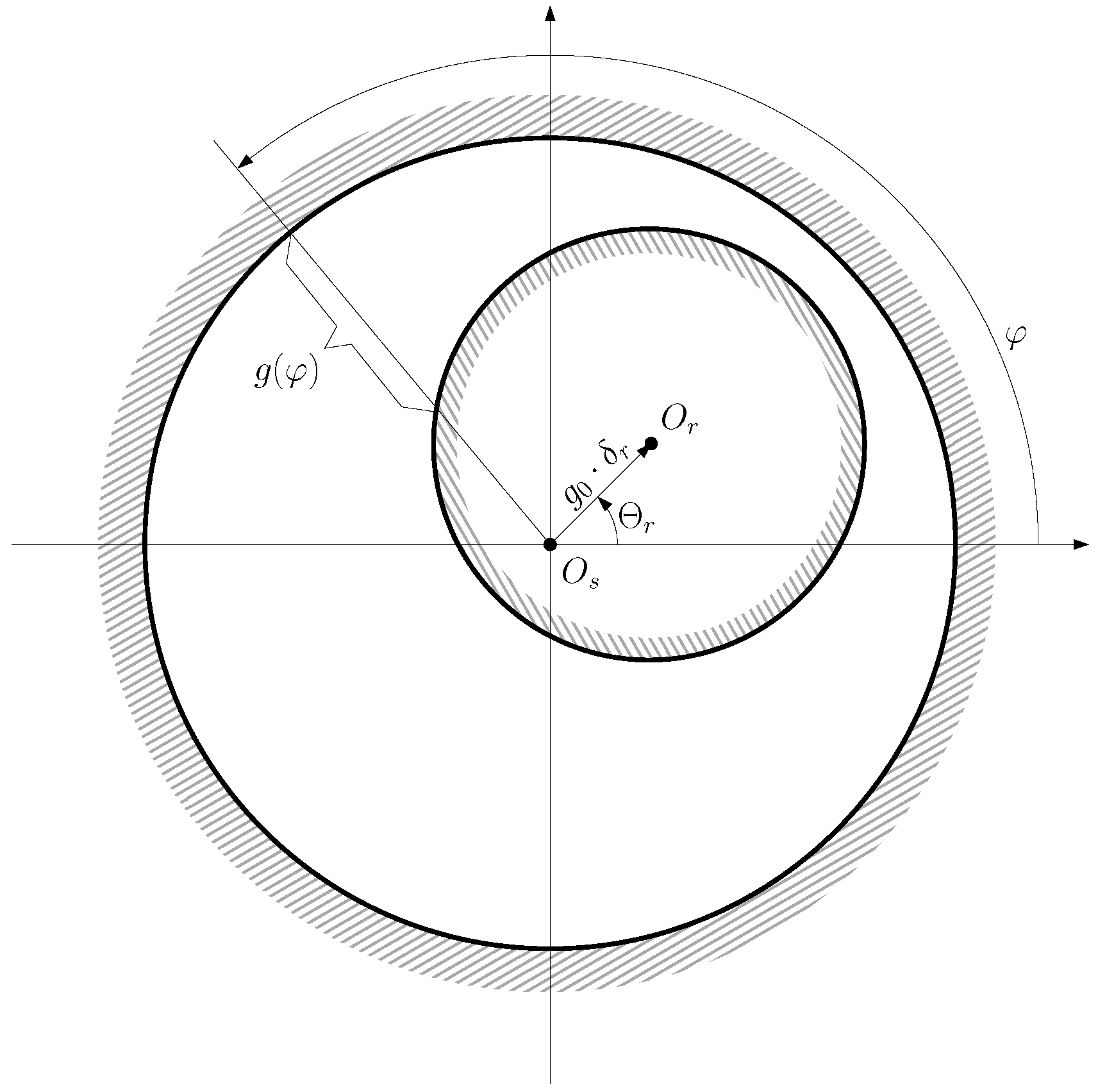
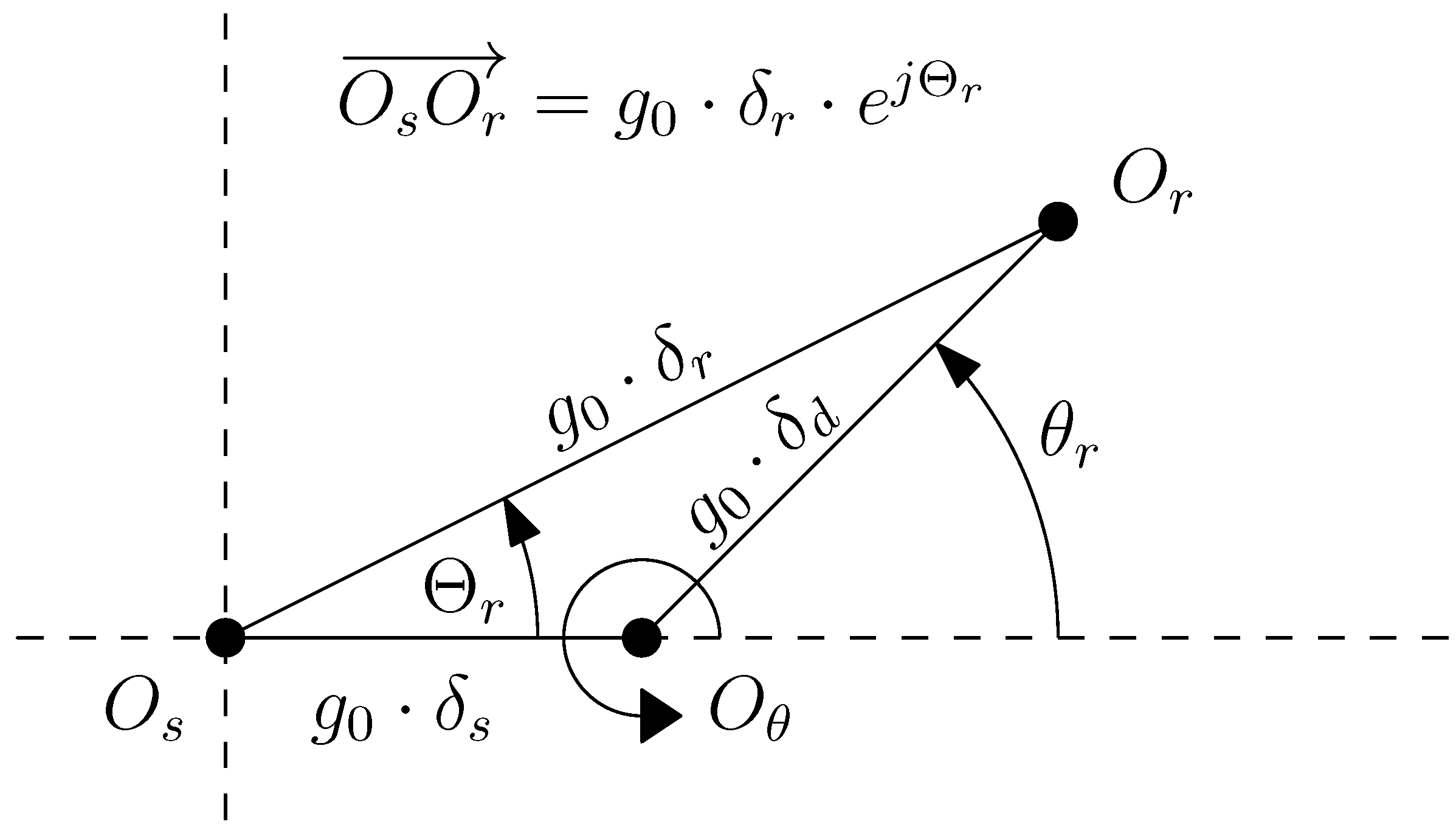
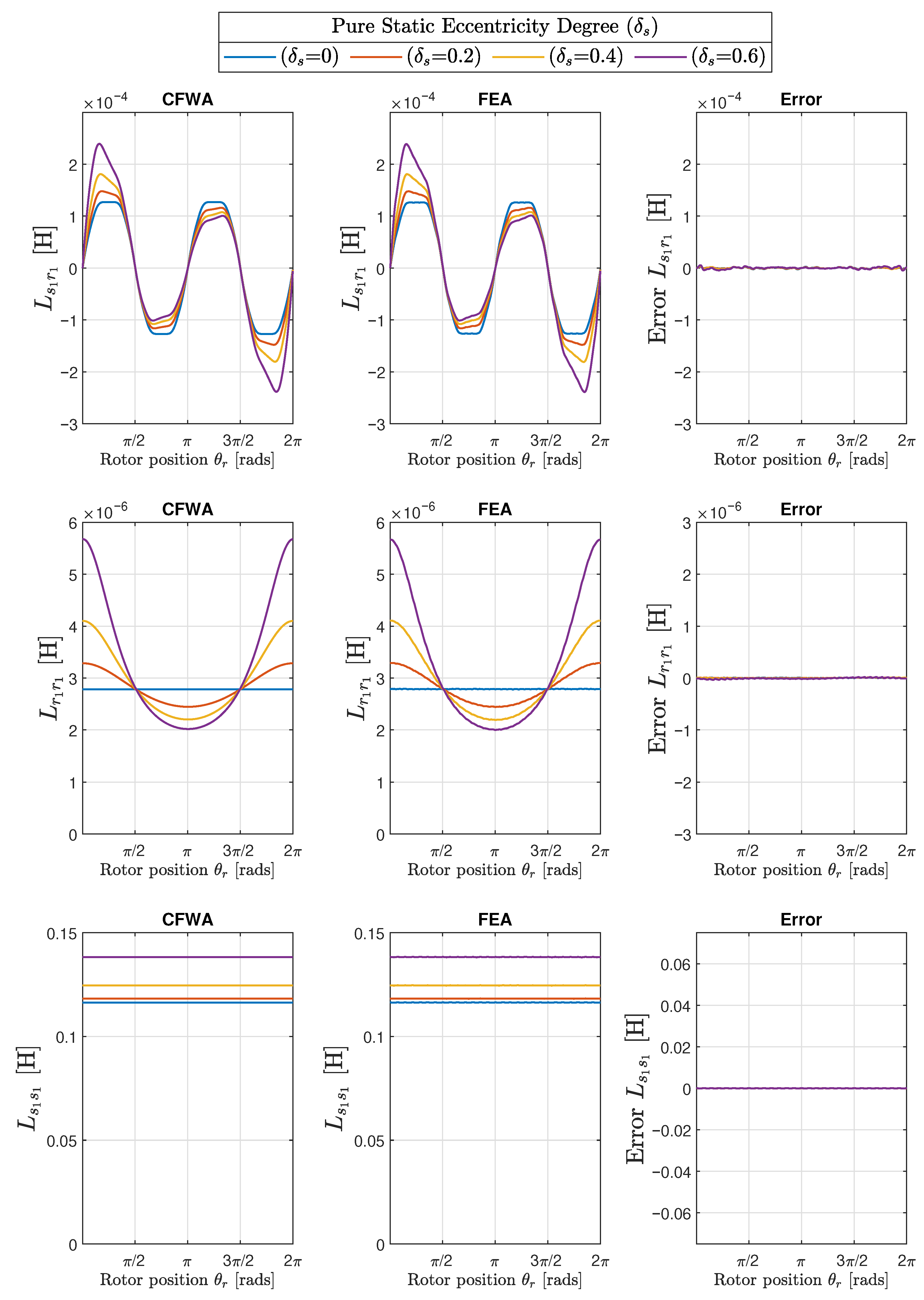
- A pure static eccentricity (SE) is characterized (Figure 8) by a displacement of the axis of rotation of the rotor () with respect to the geometric center of the stator (). The axis of rotation of rotor coincides with the geometric center of the rotor. It can be caused by misalignments of the mounted bearings or of the bearing plates. The rotor is not centered with the stator bore, but it rotates around its own geometric centre: that is, = constant in Figure 7. The air gap length is non uniform, but its shape does not change when the rotor turns (Figure 8).
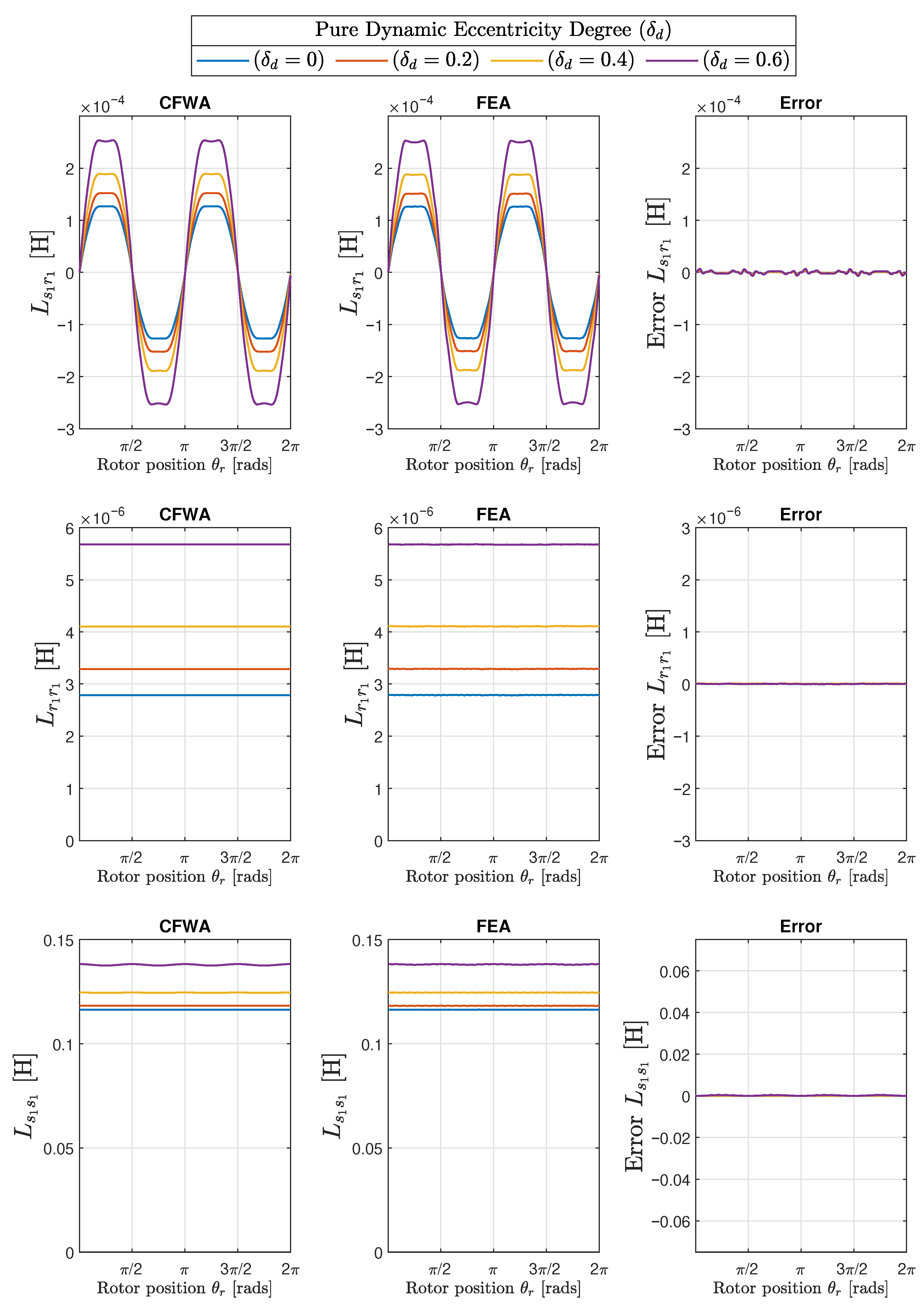
- A pure dynamic eccentricity (DE) is characterized (Figure 9) by a displacement of the geometric centre of the rotor () from its axis of rotation (), which coincides with the axis of the stator bore (). It can be caused by a manufacturing defect, a bent shaft, bearings defects, etc. Under DE, the center of the rotor rotates along a circular path in Figure 7, with the same speed as the rotor. In this case, the position of the minimum air gap rotates with the rotor (Figure 9)
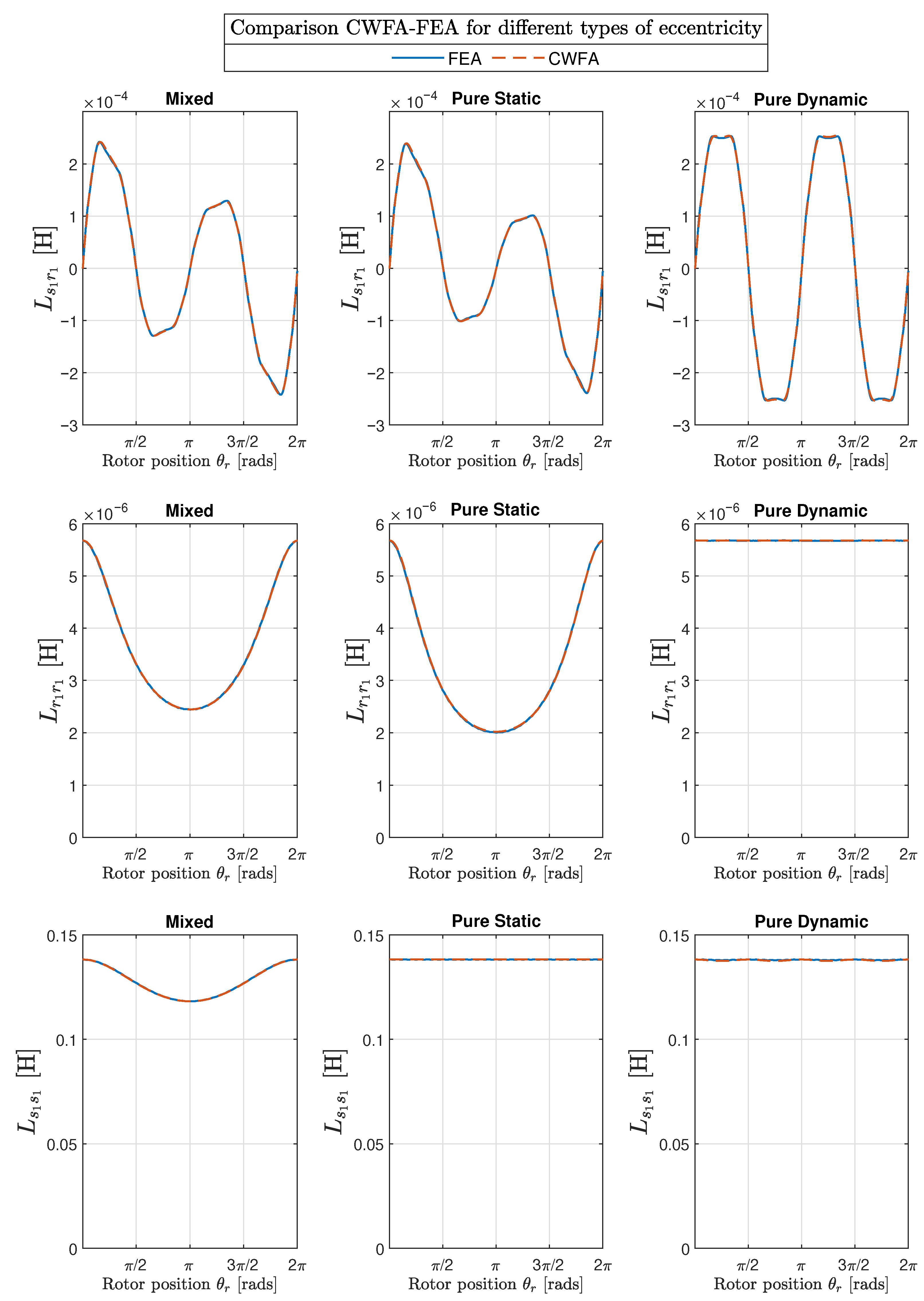
- A mixed eccentricity fault (ME) consists of the simultaneous presence of SE and DE (Figure 10). In this case, the axis of rotation ( in Figure 10) is displaced both from the geometric center of the stator (), as in the case of pure static eccentricity, and from the centre of the rotor (), as in the case of pure dynamic eccentricity.
4.2. Simplified Formulation of the Partial Inductance between Conductors in Case of Rotor Eccentricity with the Conformal Winding Tensor Approach
5. Numerical Validation
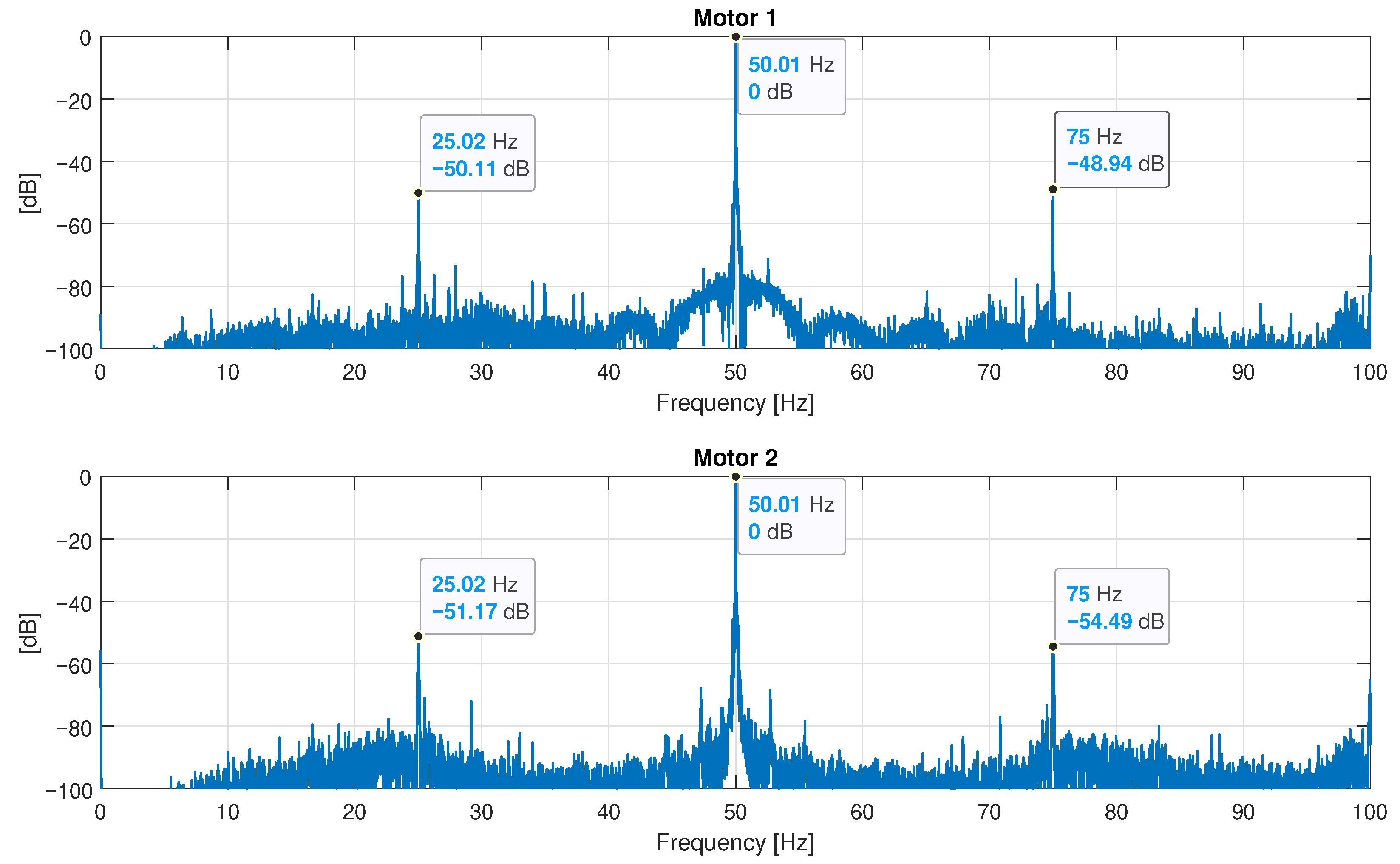
6. Experimental Validation
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A. Commercial IM
Appendix B. Computer Features
Appendix C. Current Clamp
References
- Jiang, S.B.; Wong, P.K.; Guan, R.; Liang, Y.; Li, J. An Efficient Fault Diagnostic Method for Three-Phase Induction Motors Based on Incremental Broad Learning and Non-Negative Matrix Factorization. IEEE Access 2019, 7, 17780–17790. [Google Scholar] [CrossRef]
- Xiao, D.; Huang, Y.; Zhao, L.; Qin, C.; Shi, H.; Liu, C. Domain Adaptive Motor Fault Diagnosis Using Deep Transfer Learning. IEEE Access 2019, 7, 80937–80949. [Google Scholar] [CrossRef]
- Drakaki, M.; Karnavas, Y.L.; Tzionas, P.; Chasiotis, I.D. Recent Developments Towards Industry 4.0 Oriented Predictive Maintenance in Induction Motors. Procedia Comput. Sci. 2021, 180, 943–949. [Google Scholar] [CrossRef]
- Tchakoua, P.; Wamkeue, R.; Ouhrouche, M.; Slaoui-Hasnaoui, F.; Tameghe, T.A.; Ekemb, G. Wind Turbine Condition Monitoring: State-of-the-Art Review, New Trends, and Future Challenges. Energies 2014, 7, 2595–2630. [Google Scholar] [CrossRef] [Green Version]
- Garcia-Calva, T.A.; Morinigo-Sotelo, D.; Fernandez-Cavero, V.; Garcia-Perez, A.; Romero-Troncoso, R.d.J. Early Detection of Broken Rotor Bars in Inverter-Fed Induction Motors Using Speed Analysis of Startup Transients. Energies 2021, 14, 1469. [Google Scholar] [CrossRef]
- Mejia-Barron, A.; Tapia-Tinoco, G.; Razo-Hernandez, J.R.; Valtierra-Rodriguez, M.; Granados-Lieberman, D. A neural network-based model for MCSA of inter-turn short-circuit faults in induction motors and its power hardware in the loop simulation. Comput. Electr. Eng. 2021, 93, 107234. [Google Scholar] [CrossRef]
- Mahmud, M.; Wang, W. A Smart Sensor-based cEMD Technique for Rotor Bar Fault Detection in Induction Motors. IEEE Trans. Instrum. Meas. 2021, 70, 1–11. [Google Scholar] [CrossRef]
- Deekshit, K.K.C.; Rao, M.V.G.; Rao, R.S. Fault Indexing Parameter Based Fault Detection in Induction Motor via MCSA with Wiener Filtering. Electr. Power Compon. Syst. 2020, 48, 2048–2062. [Google Scholar] [CrossRef]
- Rezaee-Alam, F.; Rezaeealam, B.; Naeini, V. An Improved Winding Function Theory for Accurate Modeling of Small and Large Air-Gap Electric Machines. IEEE Trans. Magn. 2021, 57, 1–13. [Google Scholar] [CrossRef]
- Pal, R.S.C.; Mohanty, A.R. A Simplified Dynamical Model of Mixed Eccentricity Fault in a Three-Phase Induction Motor. IEEE Trans. Ind. Electron. 2021, 68, 4341–4350. [Google Scholar] [CrossRef]
- Bagheri, A.; Ojaghi, M.; Bagheri, A. Air-gap eccentricity fault diagnosis and estimation in induction motors using unscented Kalman filter. Int. Trans. Electr. Energy Syst. 2020, 30, e12450. [Google Scholar] [CrossRef]
- Salah, A.A.; Dorrell, D.G.; Guo, Y. A Review of the Monitoring and Damping Unbalanced Magnetic Pull in Induction Machines Due to Rotor Eccentricity. IEEE Trans. Ind. Appl. 2019, 55, 2569–2580. [Google Scholar] [CrossRef]
- DeBortoli, M.; Salon, S.; Burow, D.; Slavik, C. Effects of rotor eccentricity and parallel windings on induction machine behavior: A study using finite element analysis. IEEE Trans. Magn. 1993, 29, 1676–1682. [Google Scholar] [CrossRef]
- Xu, X.; Han, Q.; Chu, F. Review of Electromagnetic Vibration in Electrical Machines. Energies 2018, 11, 1779. [Google Scholar] [CrossRef] [Green Version]
- Culbert, I.; Letal, J. Signature Analysis for Online Motor Diagnostics: Early Detection of Rotating Machine Problems Prior to Failure. IEEE Ind. Appl. Mag. 2017, 23, 76–81. [Google Scholar] [CrossRef]
- Puche-Panadero, R.; Martinez-Roman, J.; Sapena-Bano, A.; Burriel-Valencia, J.; Riera-Guasp, M. Fault Diagnosis in the Slip–Frequency Plane of Induction Machines Working in Time-Varying Conditions. Sensors 2020, 20, 3398. [Google Scholar] [CrossRef]
- Terron-Santiago, C.; Martinez-Roman, J.; Puche-Panadero, R.; Sapena-Bano, A. A Review of Techniques Used for Induction Machine Fault Modelling. Sensors 2021, 21, 4855. [Google Scholar] [CrossRef]
- Tran, M.Q.; Elsisi, M.; Mahmoud, K.; Liu, M.K.; Lehtonen, M.; Darwish, M.M.F. Experimental Setup for Online Fault Diagnosis of Induction Machines via Promising IoT and Machine Learning: Towards Industry 4.0 Empowerment. IEEE Access 2021, 9, 115429–115441. [Google Scholar] [CrossRef]
- Singh, A.; Grant, B.; DeFour, R.; Sharma, C.; Bahadoorsingh, S. A review of induction motor fault modeling. Electr. Power Syst. Res. 2016, 133, 191–197. [Google Scholar] [CrossRef]
- Bouzid, S.; Viarouge, P.; Cros, J. Real-Time Digital Twin of a Wound Rotor Induction Machine Based on Finite Element Method. Energies 2020, 13, 5413. [Google Scholar] [CrossRef]
- Mekahlia, A.; Semail, E.; Scuiller, F.; Zahr, H. Reduced-Order Model of Rotor Cage in Multiphase Induction Machines: Application on the Prediction of Torque Pulsations. Math. Comput. Appl. 2020, 25, 11. [Google Scholar] [CrossRef] [Green Version]
- Sapena-Bano, A.; Chinesta, F.; Puche-Panadero, R.; Martinez-Roman, J.; Pineda-Sanchez, M. Model reduction based on sparse identification techniques for induction machines: Towards the real time and accuracy-guaranteed simulation of faulty induction machines. Int. J. Electr. Power Energy Syst. 2021, 125, 106417. [Google Scholar] [CrossRef]
- Sapena-Bano, A.; Chinesta, F.; Pineda-Sanchez, M.; Aguado, J.; Borzacchiello, D.; Puche-Panadero, R. Induction machine model with finite element accuracy for condition monitoring running in real time using hardware in the loop system. Int. J. Electr. Power Energy Syst. 2019, 111, 315–324. [Google Scholar] [CrossRef]
- Asad, B.; Vaimann, T.; Belahcen, A.; Kallaste, A.; Rassõlkin, A.; Iqbal, M.N. The Cluster Computation-Based Hybrid FEM–Analytical Model of Induction Motor for Fault Diagnostics. Appl. Sci. 2020, 10, 7572. [Google Scholar] [CrossRef]
- Del Pizzo, A.; Di Noia, L.P.; Fedele, E. A Simple Analytical Model of Static Eccentricity for PM Brushless Motors and Validation through FEM Analysis. Energies 2020, 13, 3420. [Google Scholar] [CrossRef]
- Gomez, A.F.; Sobczyk, T. Distortion of currents fault signature in induction motors with faulty cage under influence of mechanical torque oscillations. Prz. Elektrotech. 2017, 93, 48–52. [Google Scholar] [CrossRef]
- Sobczyk, T.J. Extreme possibilities of circuital models of electrical machines. Electr. Power Qual. Util. J. 2006, 12, 103–112. [Google Scholar]
- Rallabandi, V.; Taran, N.; Ionel, D.M.; Zhou, P. Inductance Testing for IPM Synchronous Machines According to the New IEEE Std 1812 and Typical Laboratory Practices. IEEE Trans. Ind. Appl. 2019, 55, 2649–2659. [Google Scholar] [CrossRef]
- Filipović-Grčić, D.; Filipović-Grčić, B.; Capuder, K. Modeling of three-phase autotransformer for short-circuit studies. Int. J. Electr. Power Energy Syst. 2014, 56, 228–234. [Google Scholar] [CrossRef]
- Kron, G.; Hoffmann, B. Tensor for Circuits; Dover Books on Science; Dover: Mineola, NY, USA, 1959. [Google Scholar]
- Dorrell, D.; Thomson, W.; Roach, S. Analysis of airgap flux, current, and vibration signals as a function of the combination of static and dynamic airgap eccentricity in 3-phase induction motors. IEEE Trans. Ind. Appl. 1997, 33, 24–34. [Google Scholar] [CrossRef]
- Faiz, J.; Ardekanei, I.; Toliyat, H. An evaluation of inductances of a squirrel-cage induction motor under mixed eccentric conditions. IEEE Trans. Energy Convers. 2003, 18, 252–258. [Google Scholar] [CrossRef]
- Concordia, C. Synchronous Machines: Theory and Performance; Wiley: Hoboken, NJ, USA, 1951. [Google Scholar]
- Fu, Q.; Yue, S.; He, B.; Fu, N. Multiple coupled circuit modelling approach for squirrel cage induction machine under single-broken-bar fault with stator winding functions decomposed in d–q rotor reference frame. IET Electr. Power Appl. 2019, 13, 889–900. [Google Scholar] [CrossRef]
- Faiz, J.; Rezaee-Alam, F. A new hybrid analytical model based on winding function theory for analysis of surface mounted permanent magnet motors. COMPEL-Int. J. Comput. Math. Electr. Electron. Eng. 2019, 38, 745–758. [Google Scholar] [CrossRef]
- Martinez-Roman, J.; Puche-Panadero, R.; Sapena-Bano, A.; Pineda-Sanchez, M.; Perez-Cruz, J.; Riera-Guasp, M. Winding Tensor Approach for the Analytical Computation of the Inductance Matrix in Eccentric Induction Machines. Sensors 2020, 20, 3058. [Google Scholar] [CrossRef]
- Pineda-Sanchez, M.; Puche-Panadero, R.; Martinez-Roman, J.; Sapena-Bano, A.; Riera-Guasp, M.; Perez-Cruz, J. Partial Inductance Model of Induction Machines for Fault Diagnosis. Sensors 2018, 18, 2340. [Google Scholar] [CrossRef] [Green Version]
- Martinez-Roman, J.; Puche-Panadero, R.; Sapena-Bano, A.; Terron-Santiago, C.; Burriel-Valencia, J.; Pineda-Sanchez, M. Analytical Model of Induction Machines with Multiple Cage Faults Using the Winding Tensor Approach. Sensors 2021, 21, 5076. [Google Scholar] [CrossRef]
- Sapena-Bano, A.; Martinez-Roman, J.; Puche-Panadero, R.; Pineda-Sanchez, M.; Perez-Cruz, J.; Riera-Guasp, M. Induction Machine Model with Space Harmonics for the Diagnosis of Rotor Eccentricity, based on the Convolution Theorem. Int. J. Electr. Power Energy Syst. 2020, 117, 105625. [Google Scholar] [CrossRef]
- Rezaee-Alam, F.; Rezaeealam, B. An enhanced analytical technique based on winding function theory for analysis of induction motors. Int. Trans. Electr. Energy Syst. 2021, 31, e12863. [Google Scholar] [CrossRef]
- Puche-Panadero, R.; Pineda-Sanchez, M.; Riera-Guasp, M.; Martinez-Roman, J.; Perez-Cruz, J.; Sapena-Bano, A. Inductances of an Eccentric Induction Machine via Conformal Mapping and the Convolution Theorem. In Proceedings of the 2019 19th International Symposium on Electromagnetic Fields in Mechatronics, Electrical and Electronic Engineering (ISEF), Nancy, France, 29–31 August 2019; pp. 1–2. [Google Scholar] [CrossRef]
- Tessarolo, A.; Bruzzese, C. Study of eccentric round-rotor synchronous machines through conformal mapping. Part I: Inductances and air-gap field. In Proceedings of the 2016 Eleventh International Conference on Ecological Vehicles and Renewable Energies (EVER), Monte Carlo, Monaco, 6–8 April 2016. [Google Scholar] [CrossRef]
- Tessarolo, A.; Bruzzese, C. Study of eccentric round-rotor synchronous machines through conformal mapping. Part II: Unbalanced magnetic pull. In Proceedings of the 2016 Eleventh International Conference on Ecological Vehicles and Renewable Energies (EVER), Monte Carlo, Monaco, 6–8 April 2016. [Google Scholar] [CrossRef]
- Maurice, O.; Reineix, A.; Durand, P.; Dubois, F. Kron’s method and cell complexes for magnetomotive and electromotive forces. IAENG Int. J. Appl. Math. 2014, 44, 191–193. [Google Scholar]
- Gabriel, K. Equivalent Circuits of Electric Machinery; Dover Publications: Mineola, NY, USA, 1929. [Google Scholar]
- Park, R.H. Two-reaction theory of synchronous machines generalized method of analysis-part I. Trans. Am. Inst. Electr. Eng. 1929, 48, 716–727. [Google Scholar] [CrossRef]
- Kron, G. The application of tensors to the analsis of rotating electrical machinery. GE Rev. 1938, 36, 103 et seq. [Google Scholar]
- Kron, G. Non-Riemannian Dynamics of Rotating Electrical Machinery. J. Math. Phys. 1934, 13, 103–194. [Google Scholar] [CrossRef]
- Peretti, L.; Zigliotto, M. Automatic procedure for induction motor parameter estimation at standstill. IET Electr. Power Appl. 2012, 6, 214–224. [Google Scholar] [CrossRef]
- Duan, F.; Živanović, R.; Al-Sarawi, S.; Mba, D. Induction Motor Parameter Estimation Using Sparse Grid Optimization Algorithm. IEEE Trans. Ind. Inform. 2016, 12, 1453–1461. [Google Scholar] [CrossRef]
- Lee, S.H.; Yoo, A.; Lee, H.J.; Yoon, Y.D.; Han, B.M. Identification of Induction Motor Parameters at Standstill Based on Integral Calculation. IEEE Trans. Ind. Appl. 2017, 53, 2130–2139. [Google Scholar] [CrossRef]
- Yang, S.; Ding, D.; Li, X.; Xie, Z.; Zhang, X.; Chang, L. A Novel Online Parameter Estimation Method for Indirect Field Oriented Induction Motor Drives. IEEE Trans. Energy Convers. 2017, 32, 1562–1573. [Google Scholar] [CrossRef]
- Toliyat, H.; Levi, E.; Raina, M. A review of RFO induction motor parameter estimation techniques. IEEE Trans. Energy Convers. 2003, 18, 271–283. [Google Scholar] [CrossRef]
- Qi, X. Rotor resistance and excitation inductance estimation of an induction motor using deep-Q-learning algorithm. Eng. Appl. Artif. Intell. 2018, 72, 67–79. [Google Scholar] [CrossRef]
- Guedes, J.J.; Castoldi, M.F.; Goedtel, A.; Agulhari, C.M.; Sanches, D.S. Parameters estimation of three-phase induction motors using differential evolution. Electr. Power Syst. Res. 2018, 154, 204–212. [Google Scholar] [CrossRef]
- Ikeda, M.; Hiyama, T. Simulation Studies of the Transients of Squirrel-Ccage Induction Motors. IEEE Trans. Energy Convers. 2007, 22, 233–239. [Google Scholar] [CrossRef]
- Alberti, L.; Bianchi, N.; Bolognani, S. A Very Rapid Prediction of IM Performance Combining Analytical and Finite-Element Analysis. IEEE Trans. Ind. Appl. 2008, 44, 1505–1512. [Google Scholar] [CrossRef]
- Jan, S. Determination of slot leakage inductance for three-phase induction motor winding using an analytical method. Arch. Electr. Eng. 2013, 62, 569–591. [Google Scholar]
- Grover, F.W. Inductance Calculations; Van Nostrand: New York, NY, USA, 1946. [Google Scholar]
- Hoeijmakers, M.J. An induction machine model based on analytic two-dimensional field computations. In Proceedings of the Symposium on Power Electronics, Electrical Drives, Automation and Motion (SPEEDAM), Capri, Italy, 16–18 June 2004; pp. 43–48. [Google Scholar]
- Sapena-Bano, A.; Martinez-Roman, J.; Puche-Panadero, R.; Pineda-Sanchez, M.; Perez-Cruz, J.; Riera-Guasp, M. Induction machine model with space harmonics for fault diagnosis based on the convolution theorem. Int. J. Electr. Power Energy Syst. 2018, 100, 463–481. [Google Scholar] [CrossRef]
- Joksimovic, G.; Durovic, M.; Penman, J.; Arthur, N. Dynamic simulation of dynamic eccentricity in induction machines-winding function approach. IEEE Trans. Energy Convers. 2000, 15, 143–148. [Google Scholar] [CrossRef]
- Nandi, S.; Bharadwaj, R.M.; Toliyat, H.A. Performance Analysis of a Three-Phase Induction Motor Under Mixed Eccentricity Condition. IEEE Trans. Energy Convers. 2002, 17, 392–399. [Google Scholar] [CrossRef]
- Faiz, J.; Tabatabaei, I. Extension of winding function theory for nonuniform air gap in electric machinery. IEEE Trans. Magn. 2002, 38, 3654–3657. [Google Scholar] [CrossRef] [Green Version]
- Bossio, G.; DeAngelo, C.; Solsona, J.; Garcia, G.; Valla, M. A 2-D Model of the Induction Machine: An Extension of the Modified Winding Function Approach. IEEE Trans. Energy Convers. 2004, 19, 144–150. [Google Scholar] [CrossRef]
- Ai, D.; Zhu, H.; Luo, H. Sensitivity of embedded active PZT sensor for concrete structural impact damage detection. Constr. Build. Mater. 2016, 111, 348–357. [Google Scholar] [CrossRef]
- Giurgiutiu, V.; Reynolds, A.; Rogers, C.A. Experimental Investigation of E/M Impedance Health Monitoring for Spot-Welded Structural Joints. J. Intell. Mater. Syst. Struct. 1999, 10, 802–812. [Google Scholar] [CrossRef] [Green Version]
- Kaur, N.; Li, L.; Bhalla, S.; Xia, Y.; Ni, P.; Adhikari, S. Integration and evaluation of multiple piezo configurations for optimal health monitoring of reinforced concrete structures. J. Intell. Mater. Syst. Struct. 2017, 28, 2717–2736. [Google Scholar] [CrossRef]
- Elloumi, N.; Bortolozzi, M.; Tessarolo, A. On the Analytical Determination of the Complex Relative Permeance Function for Slotted Electrical Machines. In Proceedings of the 2020 International Conference on Electrical Machines (ICEM), Gothenburg, Sweden, 23–26 August 2020; Volume 1, pp. 253–258. [Google Scholar] [CrossRef]
- Faiz, J.; Ebrahimi, B.; Akin, B.; Toliyat, H. Dynamic analysis of mixed eccentricity signatures at various operating points and scrutiny of related indices for induction motors. IET Electr. Power Appl. 2010, 4, 1. [Google Scholar] [CrossRef]
- Faiz, J.; Ebrahimi, B.M.; Toliyat, H.; Abu-Elhaija, W. Mixed-fault diagnosis in induction motors considering varying load and broken bars location. Energy Convers. Manag. 2010, 51, 1432–1441. [Google Scholar] [CrossRef]
- Benbouzid, M.E.H. A review of induction motors signature analysis as a medium for faults detection. IEEE Trans. Ind. Electron. 2000, 47, 984–993. [Google Scholar] [CrossRef] [Green Version]
- Concari, C.; Franceschini, G.; Tassoni, C. Toward Practical Quantification of Induction Drive Mixed Eccentricity. IEEE Trans. Ind. Appl. 2011, 47, 1232–1239. [Google Scholar] [CrossRef]





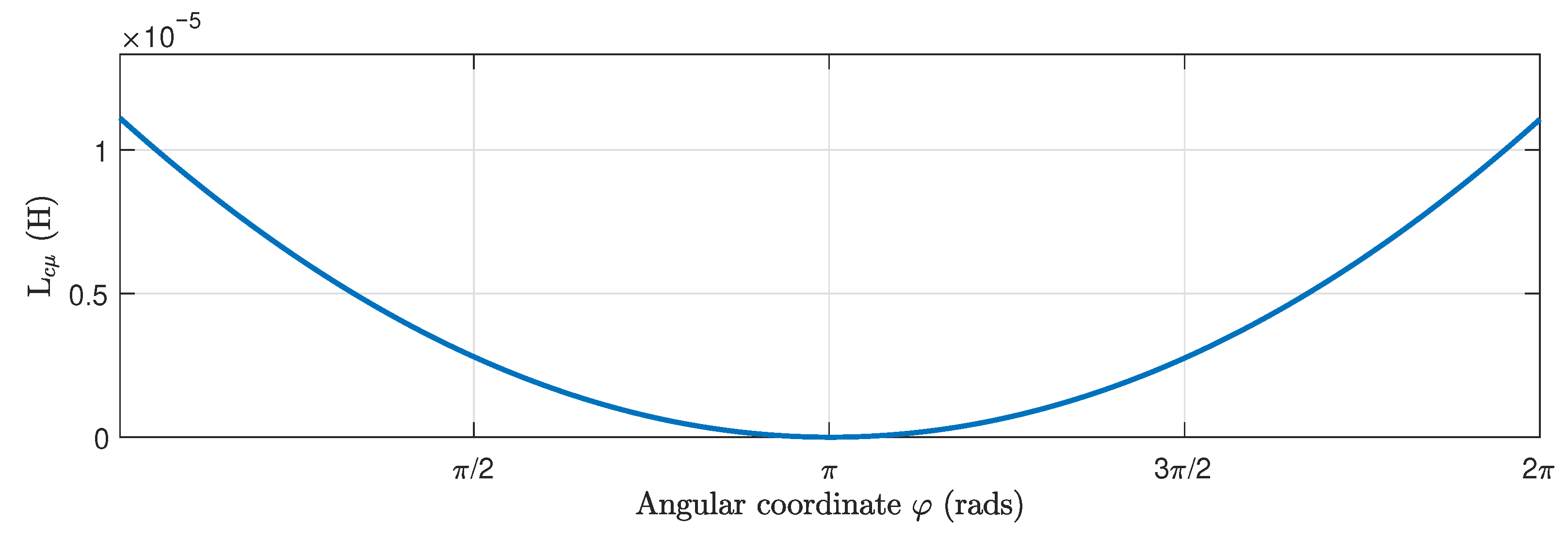
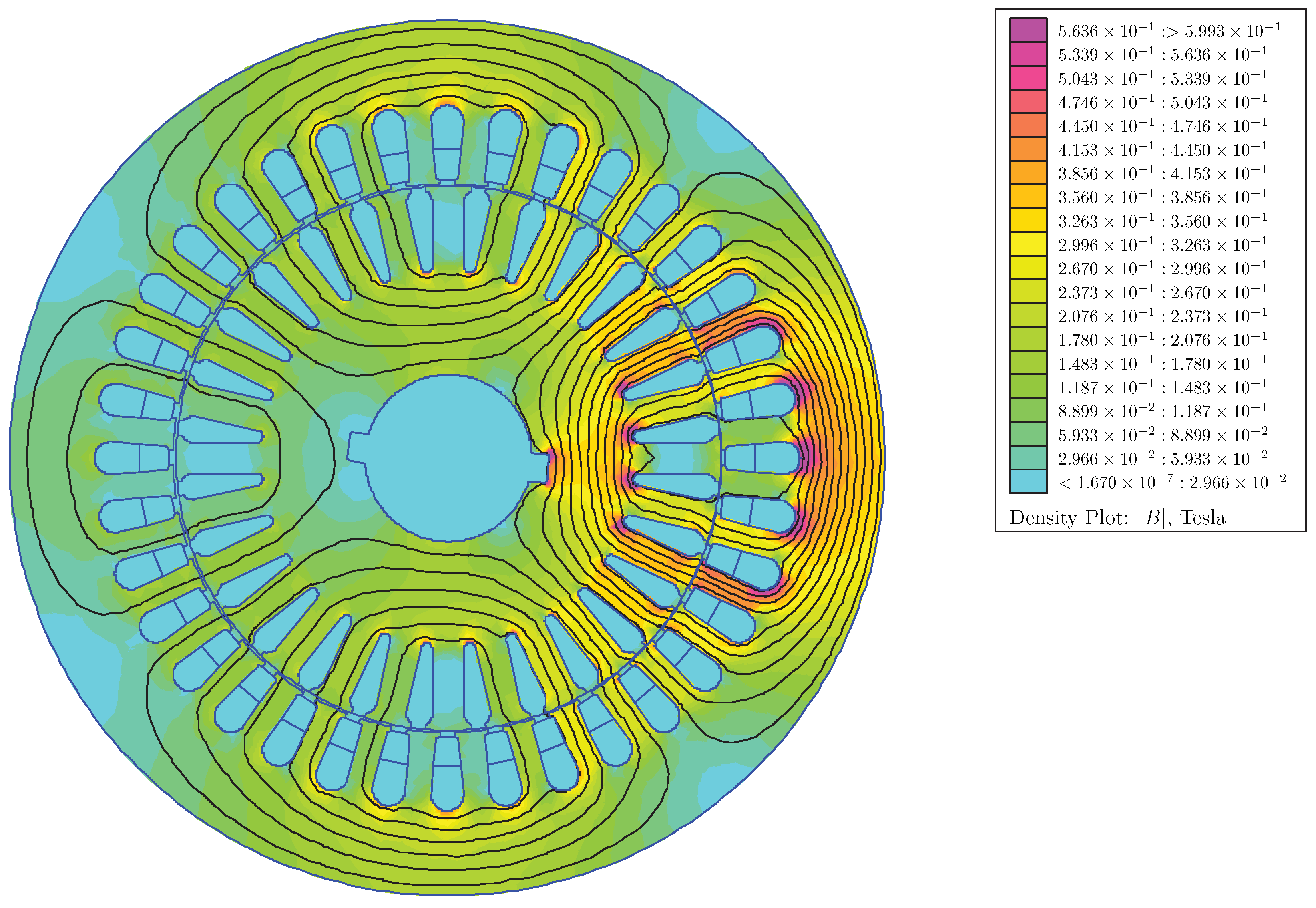
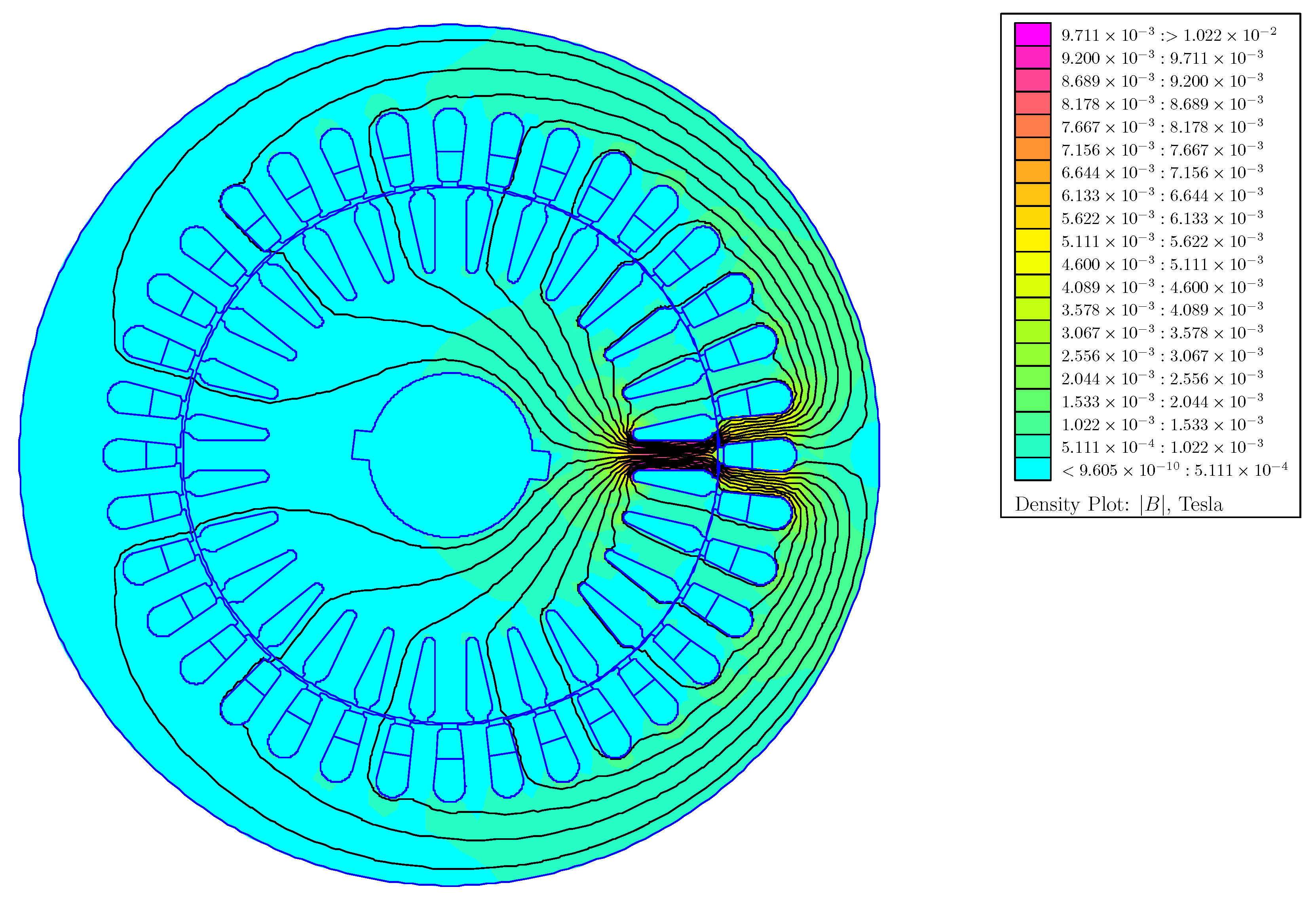
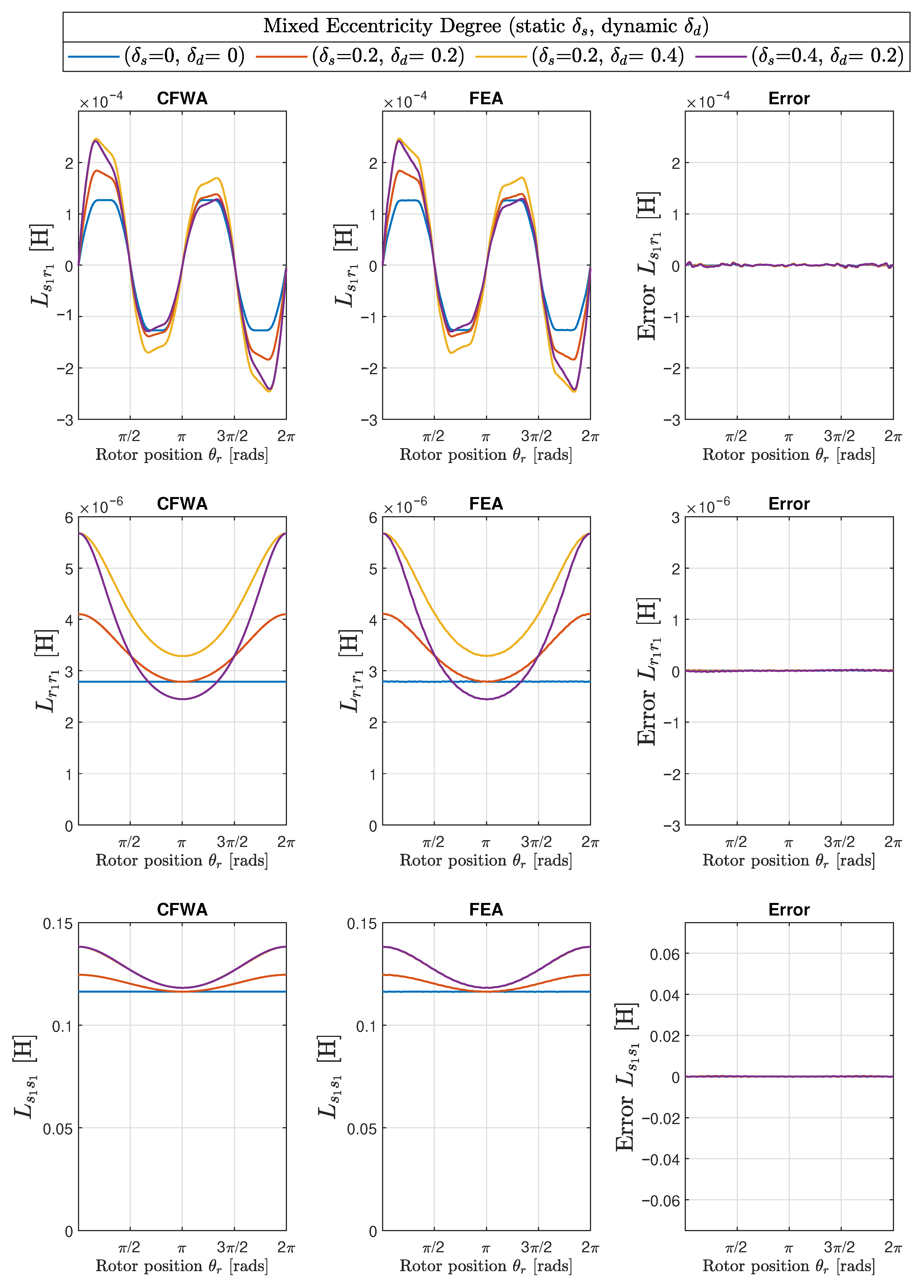


| Degree of Eccentricity | ||||
|---|---|---|---|---|
| Static | Dynamic | Error | Error | Error |
| 0.0 | 0.0 | 1.10 × 10−6 | 2.84 × 10−9 | 3.69 × 10−5 |
| 0.0 | 0.2 | 1.39 × 10−6 | 3.45 × 10−9 | 3.86 × 10−5 |
| 0.0 | 0.4 | 1.84 × 10−6 | 5.20 × 10−9 | 6.80 × 10−5 |
| 0.0 | 0.6 | 2.65 × 10−6 | 2.60 × 10−9 | 2.46 × 10−4 |
| 0.2 | 0.0 | 1.13 × 10−6 | 4.54 × 10−9 | 3.85 × 10−5 |
| 0.2 | 0.2 | 1.48 × 10−6 | 5.20 × 10−9 | 4.24 × 10−5 |
| 0.2 | 0.4 | 2.06 × 10−6 | 6.83 × 10−9 | 1.20 × 10−4 |
| 0.4 | 0.0 | 1.29 × 10−6 | 7.94 × 10−9 | 4.38 × 10−5 |
| 0.4 | 0.2 | 1.85 × 10−6 | 9.27 × 10−9 | 8.27 × 10−5 |
| 0.6 | 0.0 | 1.82 × 10−6 | 1.48 × 10−8 | 5.29 × 10−5 |
| Motor | Eccentricity Degree | Amplitude of the Fault Harmonics | ||
|---|---|---|---|---|
| Static | Dynamic | Hz | Hz | |
| Motor 1 | Unknown | Unknown | −50.11 dB | −48.94 dB |
| Motor 2 | Unknown | Unknown | −51.17 dB | −54.49 dB |
| Simulated | 0 | 0 | <−100 dB | <−100 dB |
| 0.05 | 0.05 | −62.31 dB | −62.86 dB | |
| 0.1 | 0.05 | −56.32 dB | −56.68 dB | |
| 0.05 | 0.1 | −56.32 dB | −56.68 dB | |
| 0.1 | 0.1 | −50.29 dB | −50.55 dB | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Terron-Santiago, C.; Martinez-Roman, J.; Puche-Panadero, R.; Sapena-Bano, A.; Burriel-Valencia, J.; Pineda-Sanchez, M. Analytical Model of Eccentric Induction Machines Using the Conformal Winding Tensor Approach. Sensors 2022, 22, 3150. https://doi.org/10.3390/s22093150
Terron-Santiago C, Martinez-Roman J, Puche-Panadero R, Sapena-Bano A, Burriel-Valencia J, Pineda-Sanchez M. Analytical Model of Eccentric Induction Machines Using the Conformal Winding Tensor Approach. Sensors. 2022; 22(9):3150. https://doi.org/10.3390/s22093150
Chicago/Turabian StyleTerron-Santiago, Carla, Javier Martinez-Roman, Ruben Puche-Panadero, Angel Sapena-Bano, Jordi Burriel-Valencia, and Manuel Pineda-Sanchez. 2022. "Analytical Model of Eccentric Induction Machines Using the Conformal Winding Tensor Approach" Sensors 22, no. 9: 3150. https://doi.org/10.3390/s22093150






