Representation of In-Service Performance for Cable-Stayed Railway–Highway Combined Bridges Based on Train-Induced Response’s Sensing Data and Knowledge
Abstract
:1. Introduction
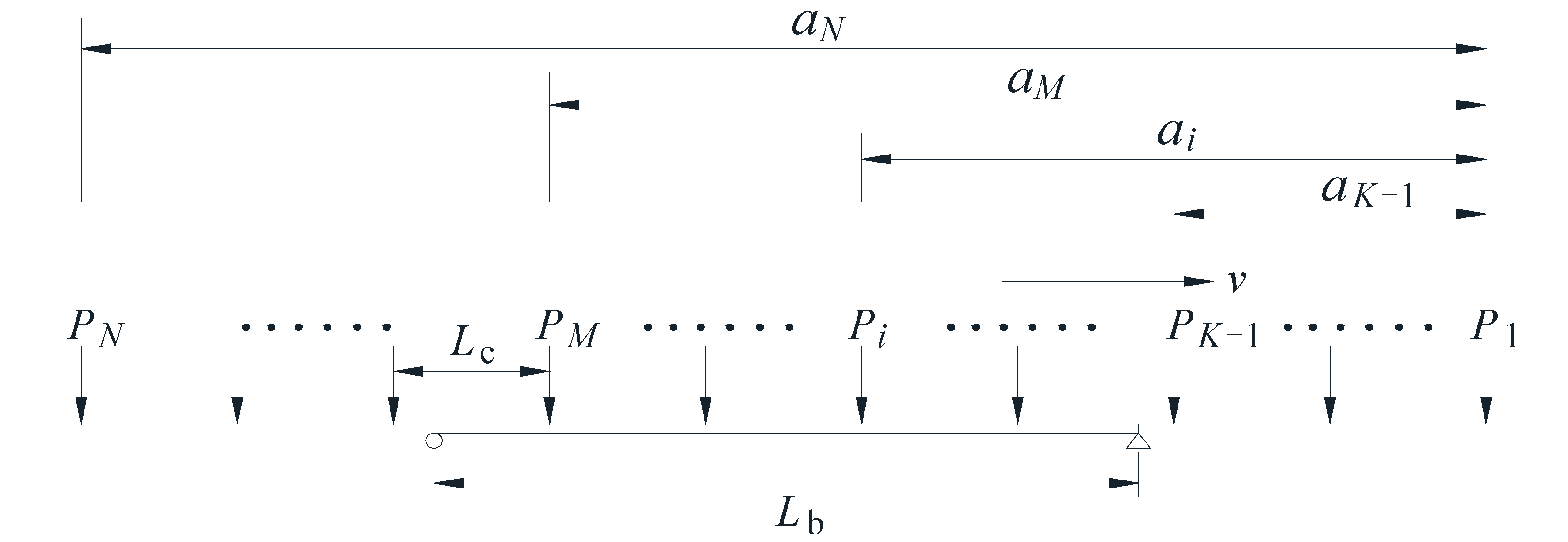
2. Case Study Bridge and Sensor Deployment
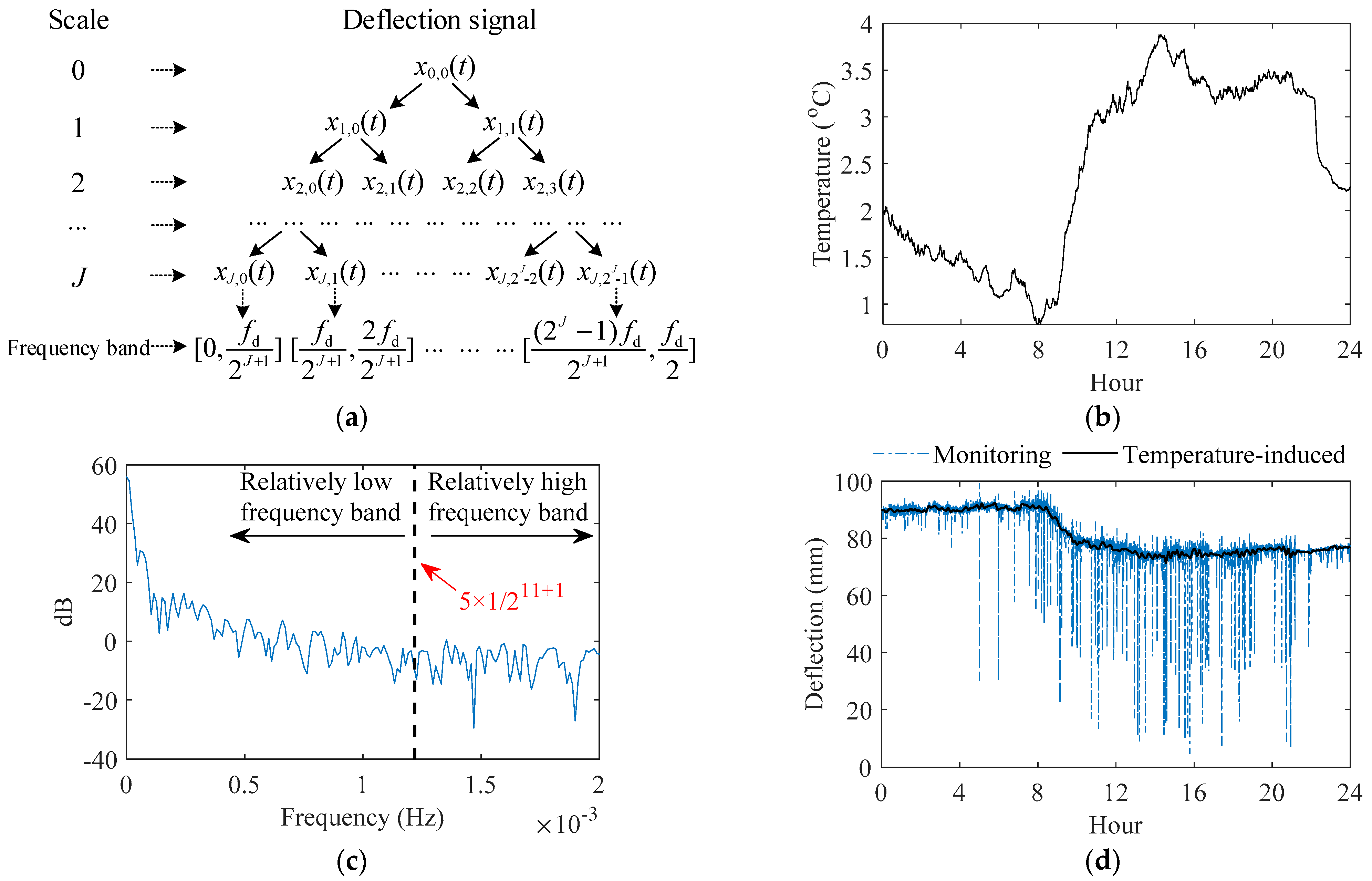
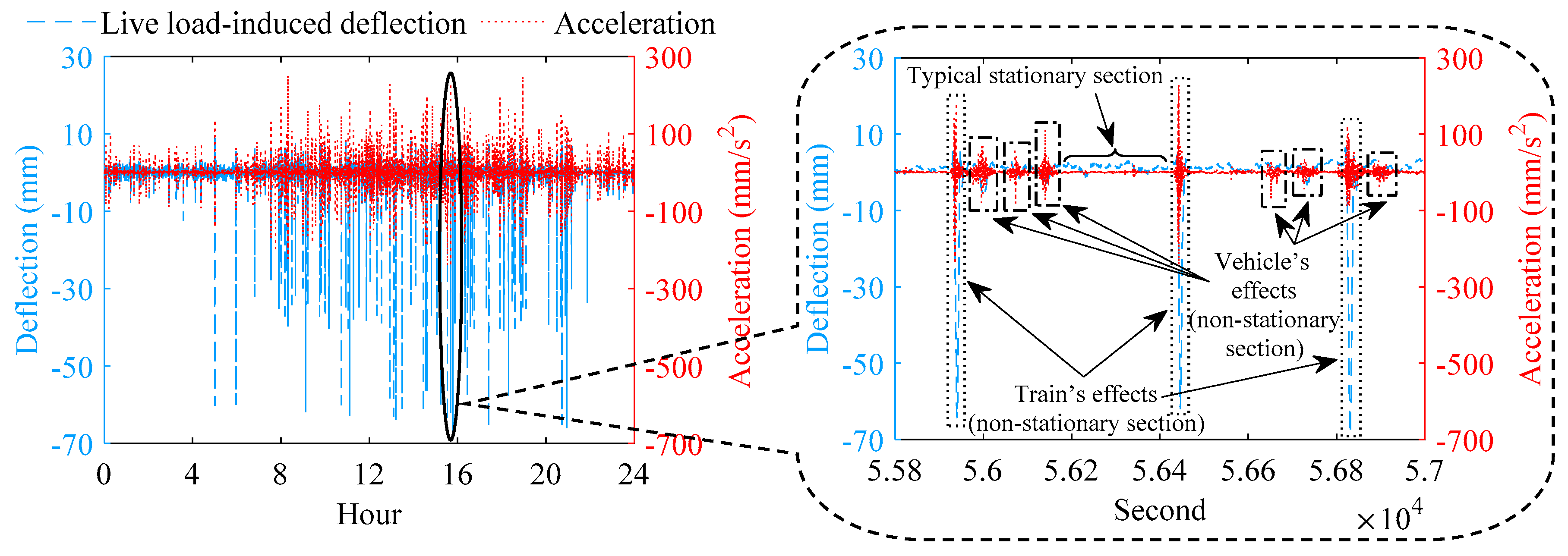
3. Feature Extraction of Train′s Effects from Multiple Types of Sensing Data
4. Knowledge of Train-Induced Response from Theoretical Calculation
5. Representation of Bridge Deformation and Dynamic Performance
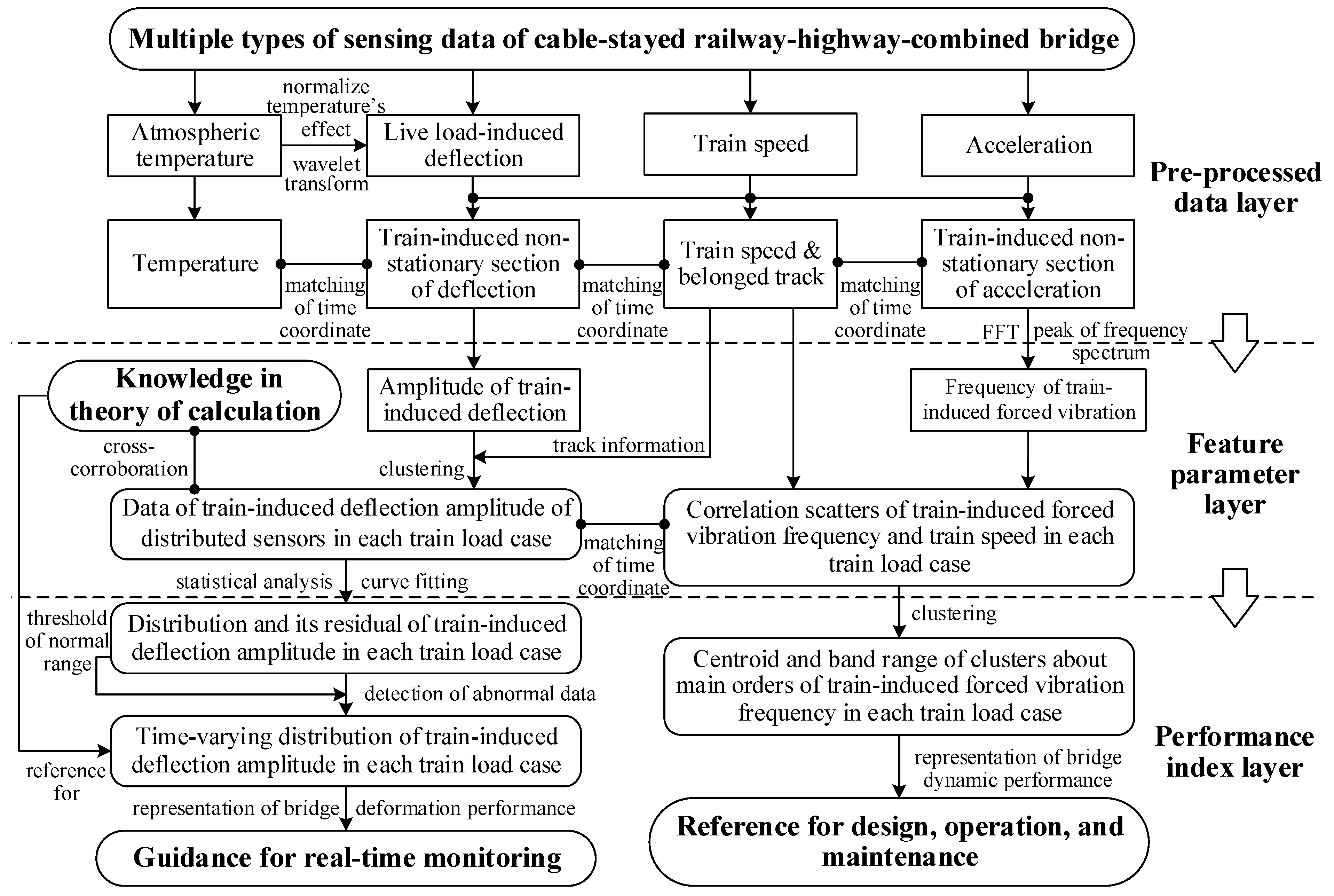
5.1. Framework for Representation of Bridge In-Service Performance
5.2. Classification of Feature Parameter about Different Cases of Train Load
5.3. Obtainment and Application of Performance Index for Representation
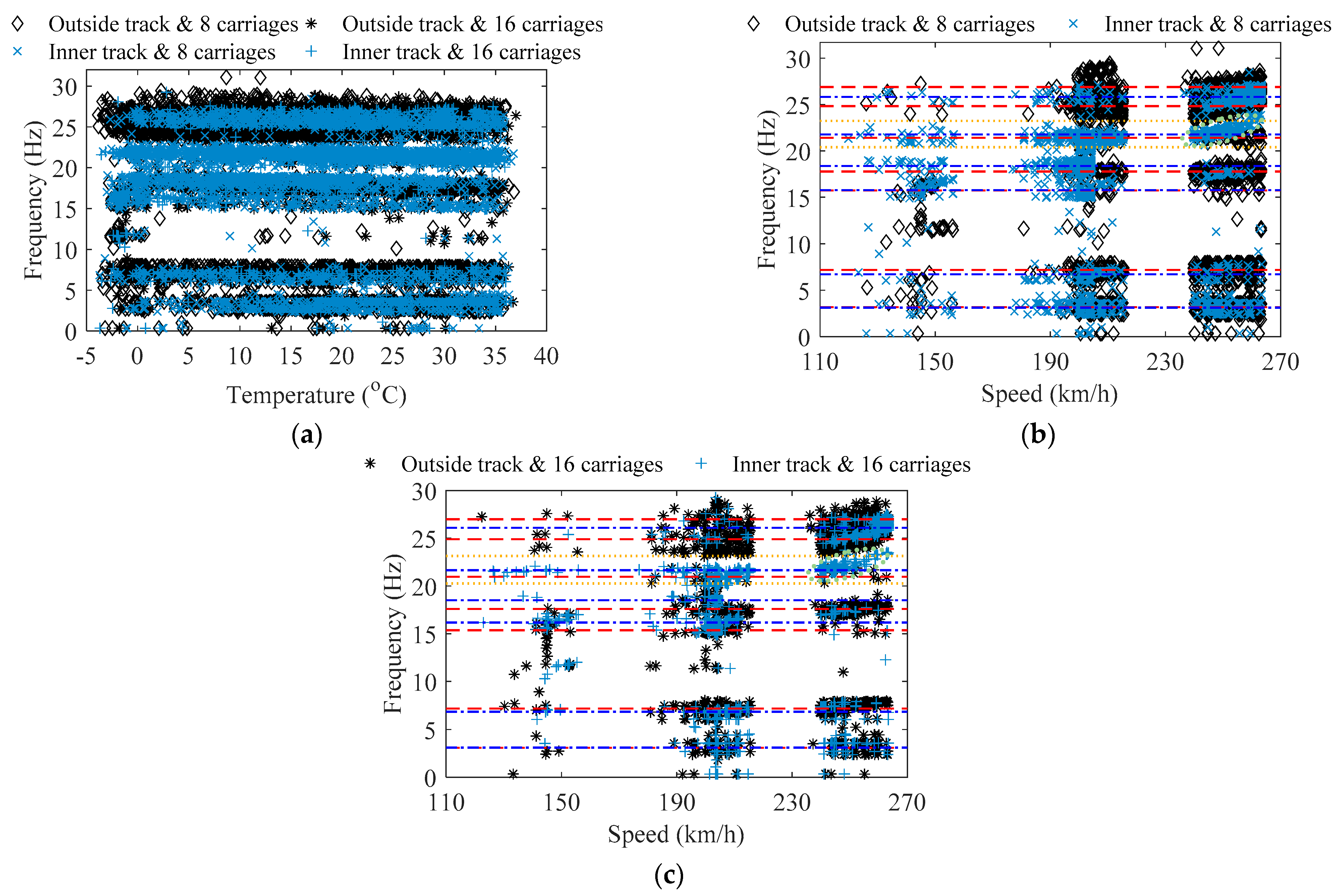
5.3.1. Dynamic Performance of In-Service Bridges
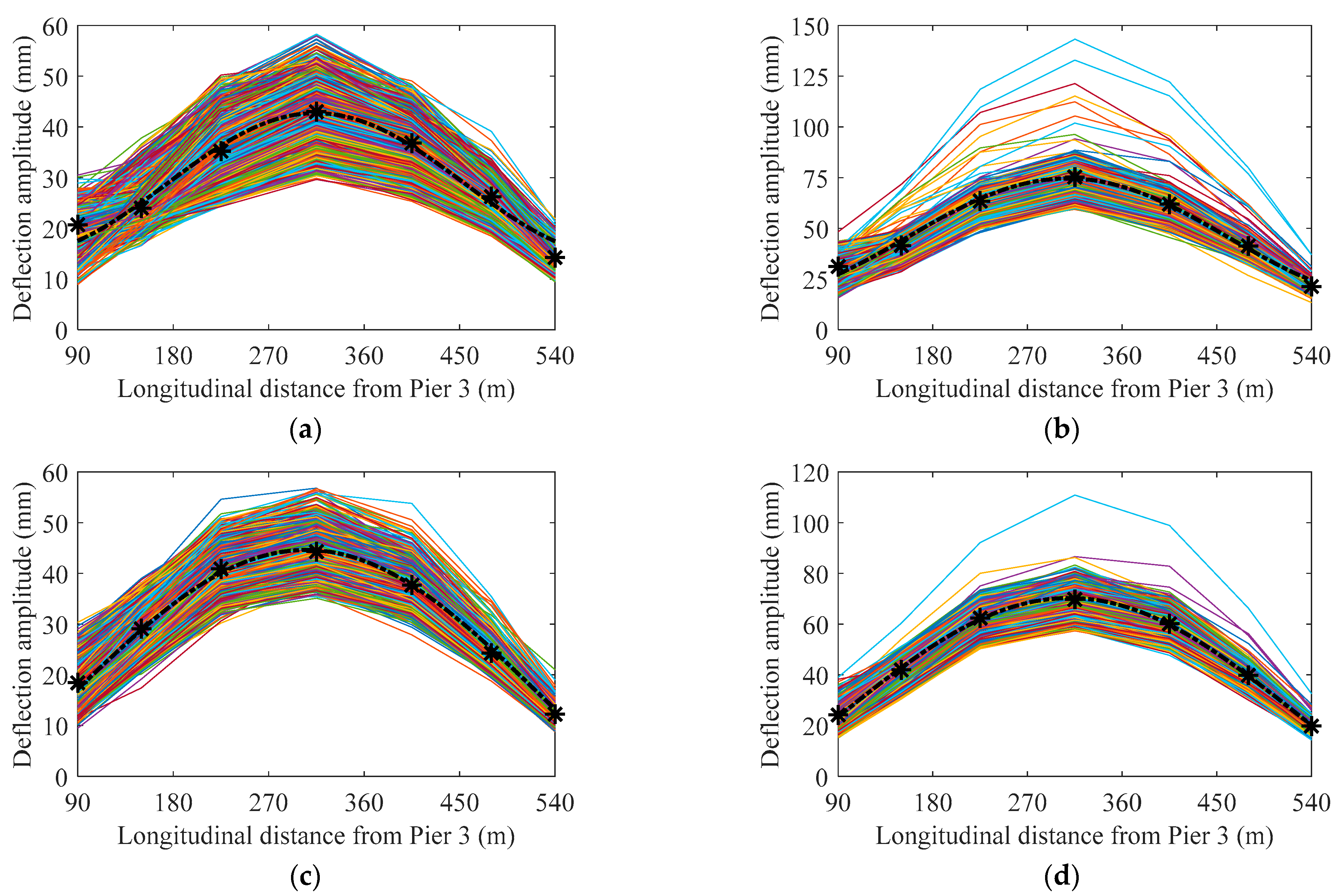
5.3.2. Deformation Performance of In-Service Bridges
6. Conclusions
- After the normalization of temperature′s effect on the deflection data, train-induced non-stationary sections of deflection and acceleration are automatically distinguished and extracted based on the characteristics of the time series signal of live load-induced deflection, train speed, and acceleration.
- Derived calculational theory proves that the train-induced deflection amplitude under 16 carriages train is larger than that under 8 carriages. This provides knowledge for the clustering of feature parameters of train-induced response for different cases of train load.
- Clusters of the main orders of the frequency of train-induced forced vibration are obtained via hierarchical clustering. Their stability for temperature and train speed are discussed and validated. The centroid and band range of each cluster are calculated as the index to represent the current dynamic performance of the bridge.
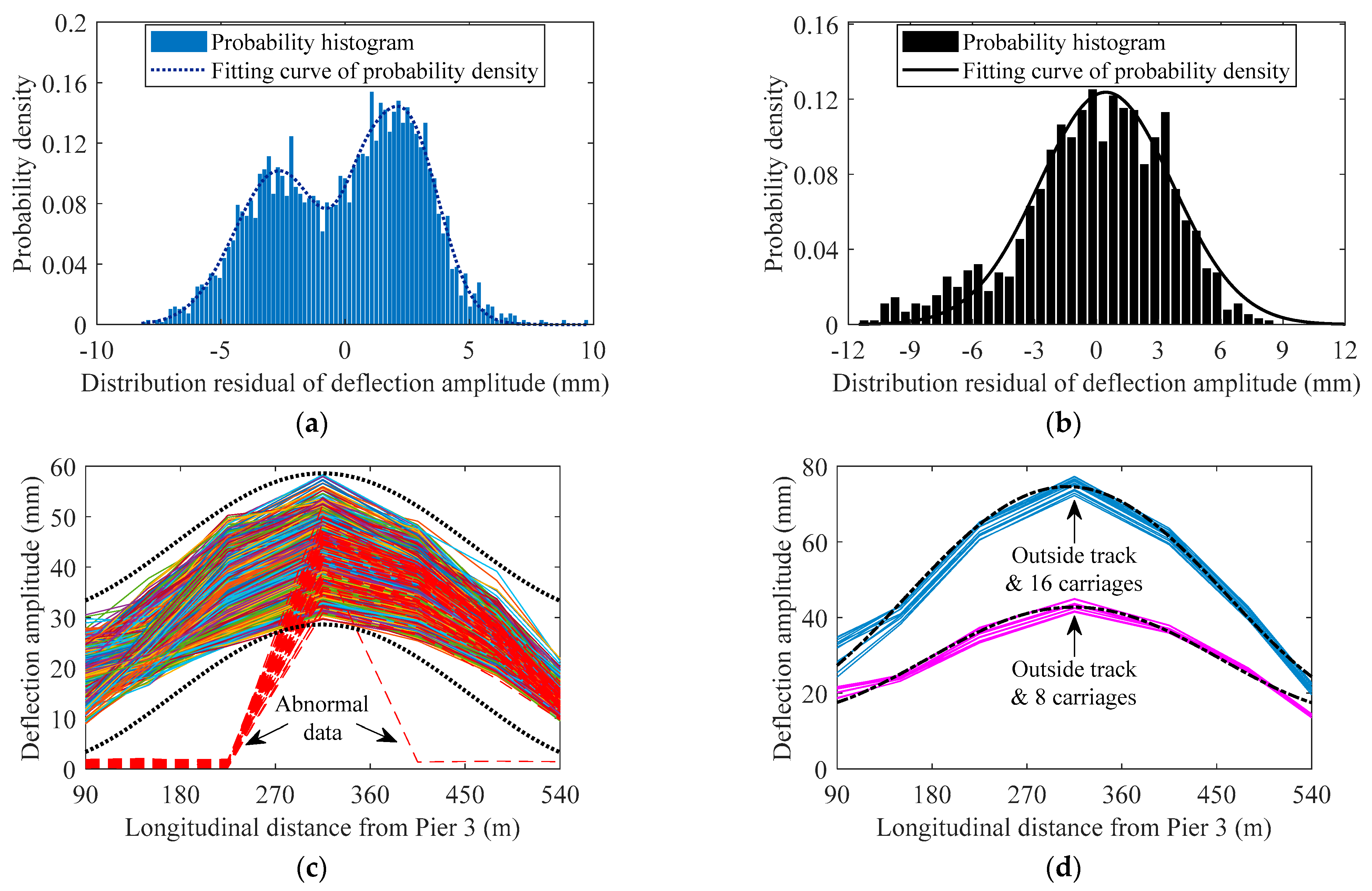
- Distribution of the centroid of the train-induced deflection amplitude of the bridge main span driven by the data of multiple sensors is fitted as the index, which is used to represent the long-term deterioration of the deformation performance of the bridge. The statistical threshold of the normal range of the distribution of train-induced deflection amplitude is determined to detect and clean the data with abnormal signals.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Li, A.Q.; Ding, Y.L.; Wang, H.; Guo, T. Analysis and assessment of bridge health monitoring mass data—Progress in research/development of “Structural Health Monitoring”. Sci. China Technol. Sci. 2012, 55, 2212–2224. [Google Scholar] [CrossRef]
- Li, H.; Ou, J.P. The state of the art in structural health monitoring of cable-stayed bridges. J. Civ. Struct. Health Monit. 2015, 6, 43–67. [Google Scholar] [CrossRef]
- Nagarajaiah, S.; Erazo, K. Structural monitoring and identification of civil infrastructure in the United States. Struct. Monit. Maint. 2016, 3, 51–69. [Google Scholar] [CrossRef]
- Zhang, J.; Tian, Y.D.; Yang, C.Q.; Wu, B.T.; Wu, Z.S.; Wu, G.; Zhang, X.; Zhou, L.M. Vibration and Deformation Monitoring of a Long-Span Rigid-Frame Bridge with Distributed Long-Gauge Sensors. J. Aerosp. Eng. 2017, 30, B4016014. [Google Scholar] [CrossRef]
- Zheng, X.; Yang, D.H.; Yi, T.H.; Li, H.N. Development of bridge influence line identification methods based on direct measurement data: A comprehensive review and comparison. Eng. Struct. 2019, 198, 109539. [Google Scholar] [CrossRef]
- Bao, Y.Q.; Chen, Z.C.; Wei, S.Y.; Xu, Y.; Tang, Z.Y.; Li, H. The State of the Art of Data Science and Engineering in Structural Health Monitoring. Engineering 2019, 5, 234–242. [Google Scholar] [CrossRef]
- Li, J.Z.; Su, M.B. The resonant vibration for a simply supported girder bridge under high-speed trains. J. Sound Vib. 1999, 224, 897–915. [Google Scholar] [CrossRef]
- Yang, Y.B.; Lin, C.W. Vehicle-bridge interaction dynamics and potential applications. J. Sound Vib. 2005, 284, 205–226. [Google Scholar] [CrossRef]
- Mao, L.; Lu, Y. Critical Speed and Resonance Criteria of Railway Bridge Response to Moving Trains. J. Bridge Eng. 2013, 18, 131–141. [Google Scholar] [CrossRef]
- Tu, B.; Dong, Y.; Fang, Z. Time-Dependent Reliability and Redundancy of Corroded Prestressed Concrete Bridges at Material, Component, and System Levels. J. Bridge Eng. 2019, 24, 04019085. [Google Scholar] [CrossRef]
- Bhuyan, M.D.H.; Gautier, G.; Le Touz, N.; Döhler, M.; Hille, F.; Dumoulin, J.; Mevel, L. Vibration-based damage localization with load vectors under temperature changes. Struct. Control Health Monit. 2019, 26, e2439. [Google Scholar] [CrossRef] [Green Version]
- Jang, J.; Smyth, A.W. Data-driven models for temperature distribution effects on natural frequencies and thermal prestress modeling. Struct. Control Health Monit. 2020, 27, e2489. [Google Scholar] [CrossRef]
- Feng, S.Z.; Han, X.; Ma, Z.J.; Królczyk, G.; Li, Z.X. Data-driven algorithm for real-time fatigue life prediction of structures with stochastic parameters. Comput. Methods Appl. Mech. Eng. 2020, 372, 113373. [Google Scholar] [CrossRef]
- Tarozzi, M.; Pignagnoli, G.; Benedetti, A. Identification of damage-induced frequency decay on a large-scale model bridge. Eng. Struct. 2020, 221, 111039. [Google Scholar] [CrossRef]
- Chen, Y.Y.; Dong, J.C.; Tong, Z.J.; Jiang, R.J.; Yue, Y. Flexural behavior of composite box girders with corrugated steel webs and trusses. Eng. Struct. 2020, 209, 110275. [Google Scholar] [CrossRef]
- Moravej, H.; Chan, T.H.T.; Jesus, A.; Nguyen, K. Computation-Effective Structural Performance Assessment Using Gaussian Process-Based Finite Element Model Updating and Reliability Analysis. Int. J. Struct. Stab. Dyn. 2020, 20, 2042003. [Google Scholar] [CrossRef]
- Zaborac, J.; Perez, B.; Hrynyk, T.; Bayrak, O. Structural performance assessment of a 60-year-old reinforced concrete bent cap. Struct. Concr. 2020, 21, 2549–2564. [Google Scholar] [CrossRef]
- Liu, Q.M.; Thompson, D.J.; Xu, P.P.; Feng, Q.S.; Li, X.Z. Investigation of train-induced vibration and noise from a steel-concrete composite railway bridge using a hybrid finite element-statistical energy analysis method. J. Sound Vib. 2020, 471, 115197. [Google Scholar] [CrossRef]
- Lin, K.Q.; Xu, Y.L.; Lu, X.Z.; Guan, Z.G.; Li, J.Z. Cluster computing-aided model updating for a high-fidelity finite element model of a long-span cable-stayed bridge. Earthq. Eng. Struct. Dyn. 2020, 49, 904–923. [Google Scholar] [CrossRef]
- Guo, W.; Zeng, C.; Gou, H.Y.; Gu, Q.; Wang, T.; Zhou, H.M.; Zhang, B.; Wu, J.L. Real-time hybrid simulation of high-speed train-track-bridge interactions using the moving load convolution integral method. Eng. Struct. 2021, 228, 111537. [Google Scholar] [CrossRef]
- Kernicky, T.; Whelan, M.; Rauf, U.; Al-Shaer, E. Structural identification using a nonlinear constraint satisfaction processor with interval arithmetic and contractor programming. Comput. Struct. 2017, 188, 1–16. [Google Scholar] [CrossRef] [Green Version]
- Li, Z.J.; Feng, M.Q.; Luo, L.X.; Feng, D.M.; Xu, X.L. Statistical analysis of modal parameters of a suspension bridge based on Bayesian spectral density approach and SHM data. Mech. Syst. Signal Process. 2018, 98, 352–367. [Google Scholar] [CrossRef]
- Erazo, K.; Sen, D.; Nagarajaiah, S.; Sun, L.M. Vibration-based structural health monitoring under changing environmental conditions using Kalman filtering. Mech. Syst. Signal Process. 2019, 117, 1–15. [Google Scholar] [CrossRef]
- Yang, X.M.; Yi, T.H.; Qu, C.X.; Li, H.N.; Liu, H. Modal Identification of High-Speed Railway Bridges through Free-Vibration Detection. J. Eng. Mech. 2020, 146, 04020107. [Google Scholar] [CrossRef]
- Sen, D.; Erazo, K.; Zhang, W.; Nagarajaiah, S.; Sun, L.M. On the effectiveness of principal component analysis for decoupling structural damage and environmental effects in bridge structures. J. Sound Vib. 2019, 457, 280–298. [Google Scholar] [CrossRef]
- Surace, C.; Bovsunovsky, A. The use of frequency ratios to diagnose structural damage in varying environmental conditions. Mech. Syst. Signal Process. 2020, 136, 106523. [Google Scholar] [CrossRef]
- Narazaki, Y.; Gomez, F.; Hoskere, V.; Smith, M.D.; Spencer, B.F. Efficient development of vision-based dense three-dimensional displacement measurement algorithms using physics-based graphics models. Struct. Health Monit. 2021, 20, 1841–1863. [Google Scholar] [CrossRef]
- Weng, Y.F.; Shan, J.Z.; Lu, Z.; Lu, X.L.; Spencer, B.F. Homography-based structural displacement measurement for large structures using unmanned aerial vehicles. Comput.-Aided Civ. Infrastruct. Eng. 2021, 36, 1114–1128. [Google Scholar] [CrossRef]
- Arabi, S.; Shafei, B. Multi-stressor fatigue assessment of steel sign-support structures: A case study in Iowa. Eng. Struct. 2019, 200, 109721. [Google Scholar] [CrossRef]
- Anastasopoulos, D.; De Roeck, G.; Reynders, E.P.B. One-year operational modal analysis of a steel bridge from high-resolution macrostrain monitoring: Influence of temperature vs. retrofitting. Mech. Syst. Signal Process. 2021, 161, 107951. [Google Scholar] [CrossRef]
- Deng, Y.; Li, A.Q.; Chen, S.R.; Feng, D.M. Serviceability assessment for long-span suspension bridge based on deflection measurements. Struct. Control Health Monit. 2018, 25, e2254. [Google Scholar] [CrossRef]
- Zhou, Y.; Sun, L.M. A comprehensive study of the thermal response of a long-span cable-stayed bridge: From monitoring phenomena to underlying mechanisms. Mech. Syst. Signal Process. 2019, 124, 330–348. [Google Scholar] [CrossRef]
- Zheng, X.; Yang, D.H.; Yi, T.H.; Li, H.N. Bridge influence line identification from structural dynamic responses induced by a high-speed vehicle. Struct. Control Health Monit. 2020, 27, e2544. [Google Scholar] [CrossRef]
- Zhao, H.W.; Ding, Y.L.; Li, A.Q.; Ren, Z.Z.; Yang, K. Live-load strain evaluation of the prestressed concrete box-girder bridge using deep learning and clustering. Struct. Health Monit. 2020, 19, 1051–1063. [Google Scholar] [CrossRef]
- Wang, Y.W.; Ni, Y.Q.; Zhang, Q.H.; Zhang, C. Bayesian approaches for evaluating wind-resistant performance of long-span bridges using structural health monitoring data. Struct. Control Health Monit. 2021, 28, e2699. [Google Scholar] [CrossRef]
- Ding, Y.L.; Zhao, H.W.; Deng, L.; Li, A.Q.; Wang, M.Y. Early warning of abnormal train-induced vibrations for a steel-truss arch railway bridge. J. Bridge Eng. 2017, 22, 05017011. [Google Scholar] [CrossRef] [Green Version]
- Zhao, H.W.; Ding, Y.L.; Nagarajaiah, S.; Li, A.Q. Behavior Analysis and Early Warning of Girder Deflections of a Steel-Truss Arch Railway Bridge under the Effects of Temperature and Trains: Case Study. J. Bridge Eng. 2019, 24, 05018013. [Google Scholar] [CrossRef]
- Huang, H.B.; Yi, T.H.; Li, H.N.; Liu, H. Strain-Based Performance Warning Method for Bridge Main Girders under Variable Operating Conditions. J. Bridge Eng. 2020, 25, 04020013. [Google Scholar] [CrossRef]
- Zhao, H.W.; Ding, Y.L.; Li, A.Q.; Liu, X.W.; Chen, B.; Lu, J. Evaluation and Early Warning of Vortex-Induced Vibration of Existed Long-Span Suspension Bridge Using Multisource Monitoring Data. J. Perform. Constr. Facil. 2021, 35, 04021007. [Google Scholar] [CrossRef]
- Sarmadi, H.; Yuen, K.V. Early damage detection by an innovative unsupervised learning method based on kernel null space and peak-over-threshold. Comput.-Aided Civ. Infrastruct. Eng. 2021, 36, 1150–1167. [Google Scholar] [CrossRef]
- Gandomi, A.; Haider, M. Beyond the hype: Big data concepts, methods, and analytics. Int. J. Inf. Manag. 2015, 35, 137–144. [Google Scholar] [CrossRef] [Green Version]
- Gou, H.Y.; Zhao, T.Q.; Qin, S.Q.; Zheng, X.G.; Pipinato, A.; Bao, Y. In-situ testing and model updating of a long-span cable-stayed railway bridge with hybrid girders subjected to a running train. Eng. Struct. 2022, 253, 113823. [Google Scholar] [CrossRef]
- Civera, M.; Surace, C. Instantaneous Spectral Entropy: An Application for the Online Monitoring of Multi-Storey Frame Structures. Buildings 2022, 12, 310. [Google Scholar] [CrossRef]
- Mahjoubi, S.; Barhemat, R.; Bao, Y. Optimal placement of triaxial accelerometers using hypotrochoid spiral optimization algorithm for automated monitoring of high-rise buildings. Autom. Constr. 2020, 118, 103273. [Google Scholar] [CrossRef]
- Bao, Y.Q.; Tang, Z.Y.; Li, H.; Zhang, Y.F. Computer vision and deep learning-based data anomaly detection method for structural health monitoring. Struct. Health Monit. 2019, 18, 401–421. [Google Scholar] [CrossRef]
- Gou, H.Y.; Chen, X.Y.; Bao, Y. A wind hazard warning system for safe and efficient operation of high-speed trains. Autom. Constr. 2021, 132, 103952. [Google Scholar] [CrossRef]
- Zhao, H.W.; Ding, Y.L.; Li, A.Q.; Sheng, W.; Geng, F.F. Digital modeling on the nonlinear mapping between multi-source monitoring data of in-service bridges. Struct. Control Health Monit. 2020, 27, e2618. [Google Scholar] [CrossRef]
- Ruan, H.S.; Qu, A.P.; He, Y.D.; Miao, R.C.; Li, L.A. Study of structural seismic response characteristics of long span rail-cum-road steel truss girder cable-stayed bridges. Bridge Constr. 2015, 45, 32–38. (In Chinese) [Google Scholar]
- Chopra, A.K. Dynamics of Structures: Theory and Applications Earthquake Engineering, 5th ed.; Pearson Education, Inc.: Upper Saddle River, NJ, USA, 2017. [Google Scholar]
- National Railway Administration of the People’s Republic of China. TB 10621-2014: Code for Design of High Speed Railway; China Railway Publishing House: Beijing, China, 2014. (In Chinese)
- Zhang, T.; Ramakrishnan, R.; Livny, M. BIRCH: A new data clustering algorithm and its applications. Data Min. Knowl. Discov. 1997, 1, 141–182. [Google Scholar] [CrossRef]
- Górski, P.; Napieraj, M.; Konopka, E. Variability evaluation of dynamic characteristics of highway steel bridge based on daily traffic-induced vibrations. Measurement 2020, 164, 108074. [Google Scholar] [CrossRef]
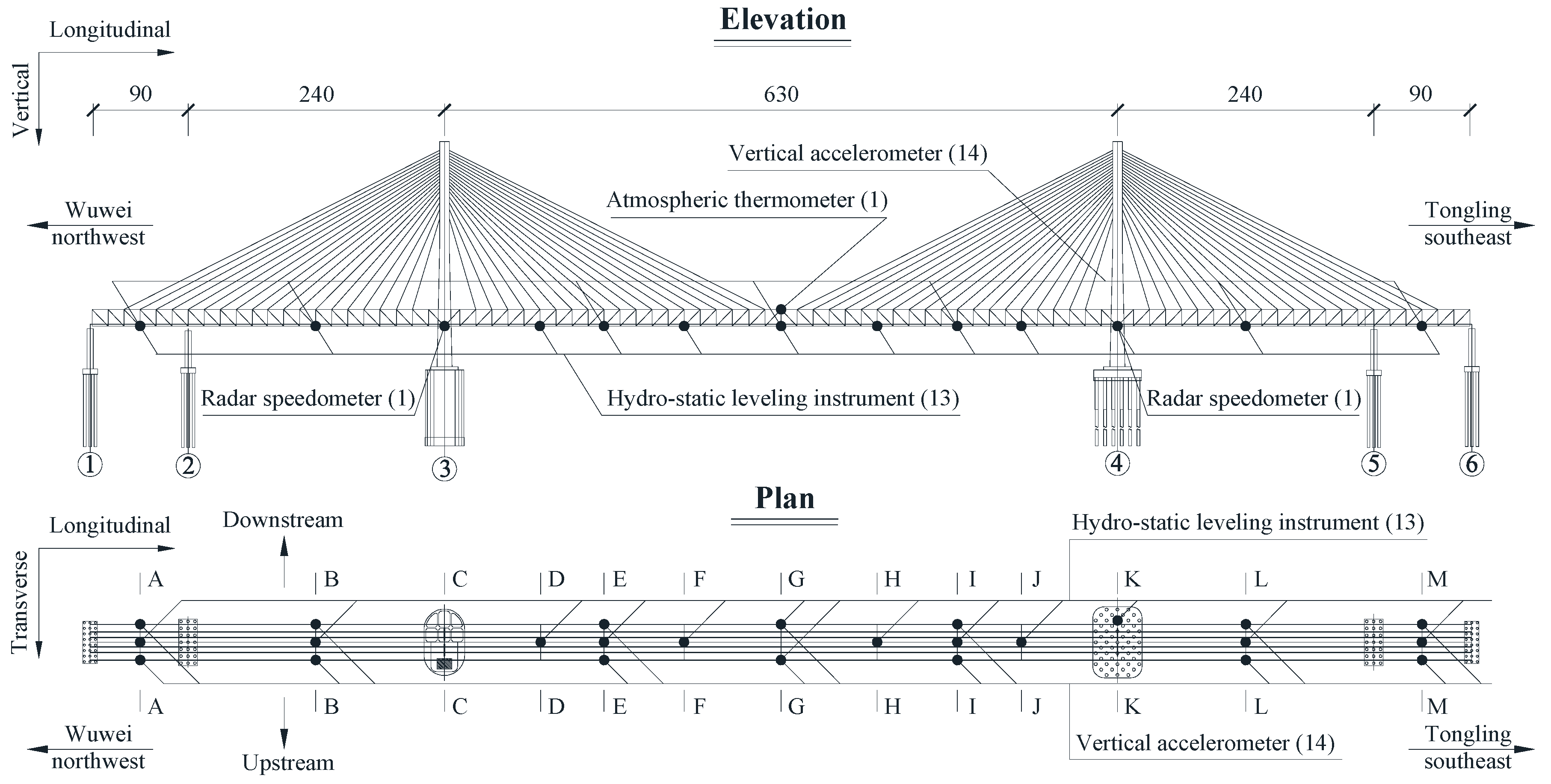
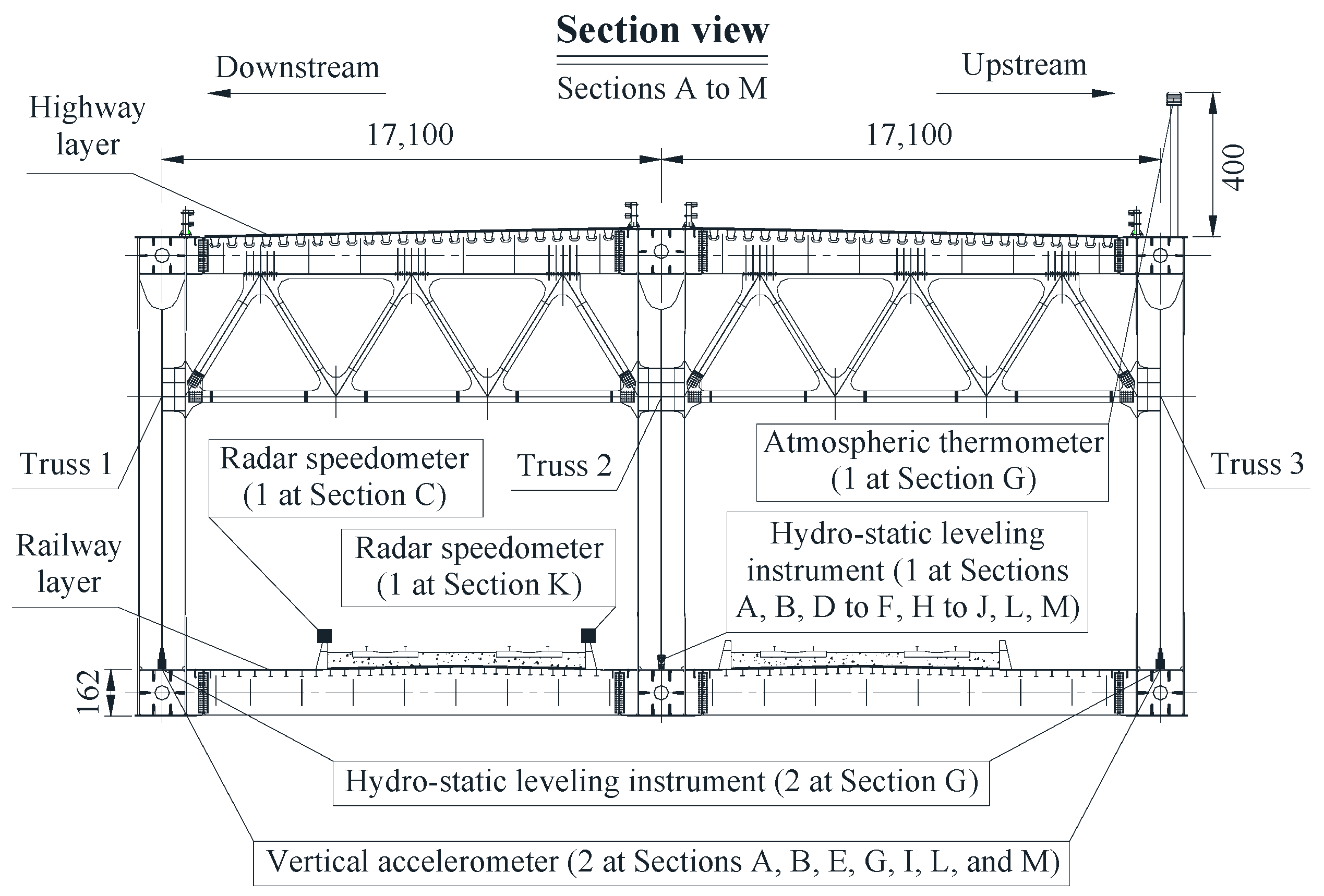




| Sensor Type | Sampling Frequency | Sensing Content | Data Unit |
|---|---|---|---|
| Hydrostatic leveling instrument | 5 Hz | Deflection (Displacement) | mm |
| Accelerometer | 100 Hz | Acceleration | mm/s2 |
| Atmospheric thermometer | 1 Hz | Temperature | °C |
| Radar speedometer | 10 Hz | Speed | km/h |
| Case 1 | Case 2 | Case 3 | Case 4 |
|---|---|---|---|
| Outside track and 8 carriages | Outside track and 16 carriages | Inner track and 8 carriages | Inner track and 16 carriages |
| Case | Centroid (Unit: Hz) | ||||||
|---|---|---|---|---|---|---|---|
| 1st Order | 2nd Order | 3rd Order | 4th Order | 5th Order | 6th Order | 7th Order | |
| Outside track and 8 carriages | 3.18 | 7.19 | 15.74 | 17.78 | 21.41 | 24.82 | 26.89 |
| Outside track and 16 carriages | 3.09 | 7.20 | 15.37 | 17.59 | 20.96 | 24.90 | 26.99 |
| Inner track and 8 carriages | 3.12 | 6.71 | 15.77 | 18.37 | 21.77 | 25.81 | / |
| Inner track and 16 carriages | 3.11 | 6.86 | 16.17 | 18.51 | 21.66 | 26.09 | / |
| Case | Item | Lower and Upper Limits of the Band Range (Unit: Hz) | ||||||
|---|---|---|---|---|---|---|---|---|
| 1st Order | 2nd Order | 3rd Order | 4th Order | 5th Order | 6th Order | 7th Order | ||
| Outside track and 8 carriages | lower | 1.75 | 6.28 | 14.69 | 17.21 | 20.56 | 23.92 | 25.92 |
| upper | 4.61 | 8.10 | 16.79 | 18.37 | 22.27 | 25.73 | 27.87 | |
| Outside track and 16 carriages | lower | 1.56 | 6.32 | 14.60 | 16.79 | 19.98 | 23.72 | 26.10 |
| upper | 4.63 | 8.09 | 16.14 | 18.40 | 21.91 | 26.07 | 27.89 | |
| Inner track and 8 carriages | lower | 1.82 | 5.69 | 14.69 | 17.60 | 20.60 | 24.84 | / |
| upper | 4.42 | 7.73 | 16.86 | 19.11 | 22.94 | 26.79 | / | |
| Inner track and 16 carriages | lower | 1.32 | 6.05 | 15.10 | 17.87 | 20.46 | 24.80 | / |
| upper | 4.91 | 7.68 | 17.25 | 19.16 | 22.85 | 27.39 | / | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, H.-W.; Ding, Y.-L.; Li, A.-Q. Representation of In-Service Performance for Cable-Stayed Railway–Highway Combined Bridges Based on Train-Induced Response’s Sensing Data and Knowledge. Sensors 2022, 22, 3247. https://doi.org/10.3390/s22093247
Zhao H-W, Ding Y-L, Li A-Q. Representation of In-Service Performance for Cable-Stayed Railway–Highway Combined Bridges Based on Train-Induced Response’s Sensing Data and Knowledge. Sensors. 2022; 22(9):3247. https://doi.org/10.3390/s22093247
Chicago/Turabian StyleZhao, Han-Wei, You-Liang Ding, and Ai-Qun Li. 2022. "Representation of In-Service Performance for Cable-Stayed Railway–Highway Combined Bridges Based on Train-Induced Response’s Sensing Data and Knowledge" Sensors 22, no. 9: 3247. https://doi.org/10.3390/s22093247
APA StyleZhao, H.-W., Ding, Y.-L., & Li, A.-Q. (2022). Representation of In-Service Performance for Cable-Stayed Railway–Highway Combined Bridges Based on Train-Induced Response’s Sensing Data and Knowledge. Sensors, 22(9), 3247. https://doi.org/10.3390/s22093247








