Analysis of Small Sea-Surface Targets Detection Performance According to Airborne Radar Parameters in Abnormal Weather Environments
Abstract
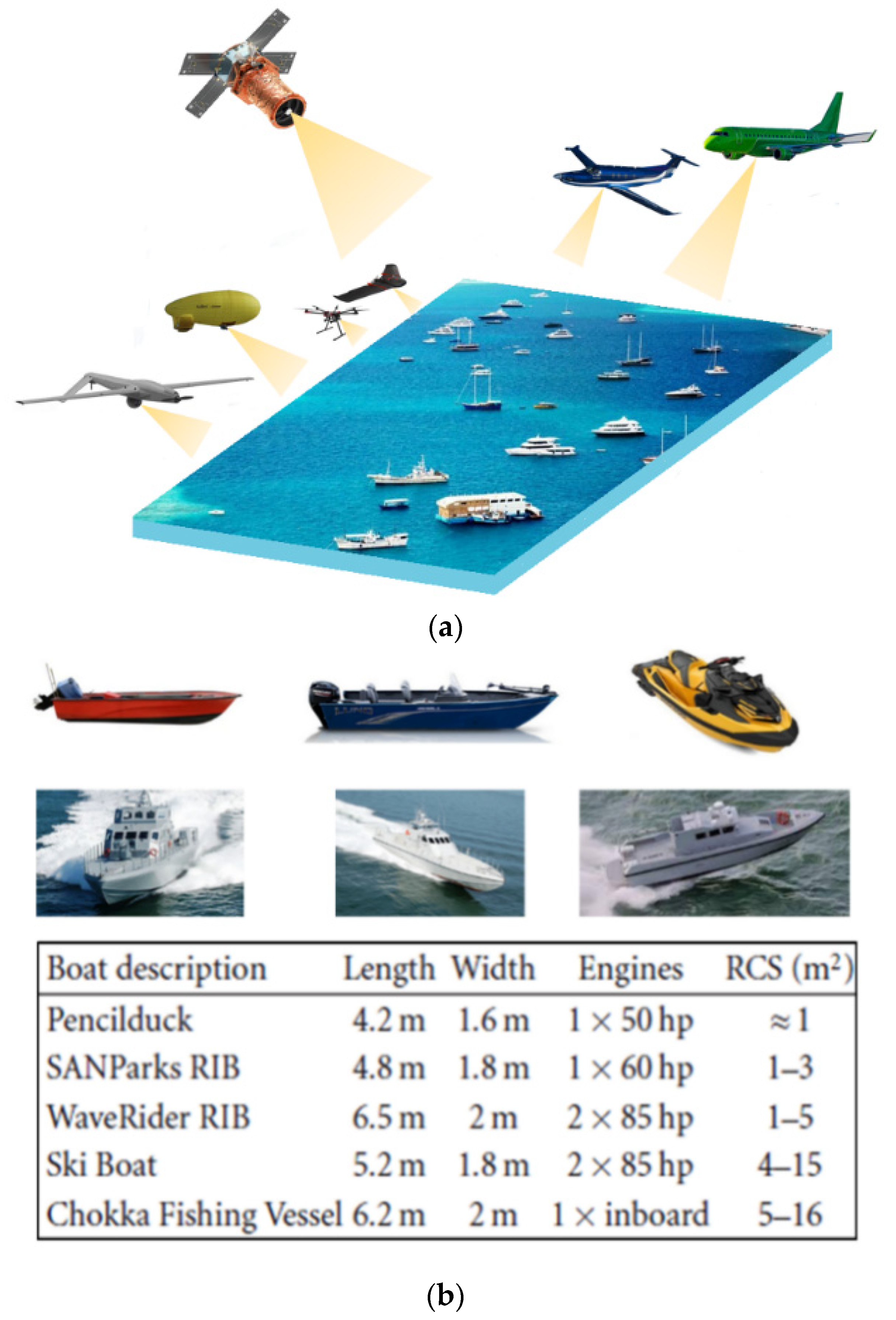
:1. Introduction
2. Amplitude Factors of Target Echo and Sea Clutter
2.1. Echo Signal Model of Target
- : peak transmitted power (W), : radar cross section of target ()
- : single pass antenna power gain, λ: radar wavelength (m)
- : instantaneous range to target (m), : radar loss
- : atmospheric and propagation loss.
2.2. Echo Signal Model of Sea Clutter
3. Propagation Environment—Effect of Atmospheric Medium and Sea Surface on Radar Signal Characteristics
3.1. Atmospheric Precipitation Losses and Weather Environment Models
3.2. Sea Scatter and Its Impact on Targets Detection
3.2.1. Empirical Sea Clutter Model for Airborne Radar
3.2.2. Sea Clutter Amplitude with Compound K-Distribution Model
3.2.3. Signal-to-Clutter Ratio
- SCR increases with the distance separating the radar and the resolution cell containing the target. Detection of a target of the same RCS is more difficult in the case where this target is close to the radar, because as we have seen, the clutter RCS decreases with distance.
- The smaller the reflectivity of the target to be detected, the weaker the SCR. Weaker target responses, as from small vessels, will be undetectable when their echoes are not stronger than that of the sea clutter. Therefore, when clutter is severe, a high RCS is necessary.
- SCR decreases with sea state. Thus, in a calm sea state, the influence of clutter is weak, the echo only has to compete with received sea clutter, and quite low RCS may give adequate detection range. However, in a rough sea state, surface backscattering covers the object echo that is submerged by the clutter and influences its detection.



4. Doppler Frequency of Target Based on Scenario of UAV Dynamic Model
4.1. Geometry of the Problem: UAV Radar Measurement Model
4.2. Doppler Frequency of Target
5. Conclusions and Future Work
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Rahmes, M.; Chester, D.; Hunt, J.; Chiasson, B. Optimizing cooperative cognitive search and rescue UAVs. Proc. SPIE 2018, 10643, 106430T. [Google Scholar]
- Varlamis, I.; Tserpes, K.; Sardianos, C. Detecting Search and Rescue missions from AIS data. In Proceedings of the 2018 IEEE 34th International Conference on Data Engineering Workshops (ICDEW), Paris, France, 16–20 April 2018; pp. 60–65. [Google Scholar]
- Perry, J.H.; Ryan, R.J. Small-scale unmanned aerial vehicles in environmental remote sensing: Challenges and opportunities. GISci. Remote Sens. 2011, 48, 99–111. [Google Scholar]
- Zhang, C.; John, M.K. The application of small unmanned aerial systems for precision agriculture: A review. Precision Agric. 2012, 13, 693–712. [Google Scholar] [CrossRef]
- Chen, A.Y.; Huang, Y.N.; Han, J.Y.; Kang, S.C. A review of rotorcraft unmanned aerial vehicle (UAV) developments and applications in civil engineering. Smart Struct. Syst. 2014, 13, 1065–1094. [Google Scholar]
- Beard, R.; Kingston, D.; Quigley, M.; Snyder, D.; Christiansen, R.; Johnson, W.; McLain, T.; Goodrich, M. Autonomous vehicle technologies for small fixed-wing UAVs. J. Aerosp. Comput. Inf. Commun. 2005, 2, 92–108. [Google Scholar] [CrossRef] [Green Version]
- Everaerts, J. The use of unmanned aerial vehicles (UAVs) for remote sensing and mapping. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2008, 37, 1187–1192. [Google Scholar]
- Ehsani, R.; Sankaran, S.; Maja, J.; Neto, J.C. Affordable multirotor Remote sensing platform for applications in precision horticulture. In Proceedings of the International Conference on Precision Agriculture, Sacramento, CA, USA, 20–23 July 2014. [Google Scholar]
- Koo, V.C.; Chan, Y.K.; Gobi, V.; Chua, M.Y.; Lim, C.H.; Lim, C.S.; Thum, C.C.; Lim, T.S.; Ahmad, Z.; Mahmood, K.A.; et al. A New Unmanned Aerial Vehicle Synthetic Aperture Radar for Environmental Monitoring. Prog. Electromagn. Res. 2012, 122, 245–268. [Google Scholar] [CrossRef] [Green Version]
- Dill, S.; Schreiber, E.; Engel, M.; Heinzel, A.; Peichl, M. A drone carried multichannel Synthetic Aperture Radar for advanced buried object detection. In Proceedings of the 2019 IEEE Radar Conference (RadarConf), Boston, MA, USA, 22–26 April 2019. [Google Scholar]
- Deguchi, T.; Sugiyama, T.; Kishimoto, M. R&D of Drone-Borne SAR System. Int. Arch. Photogrammetry Remote Sens. Spat. Inf. Sci. 2019, 42, 263–267. [Google Scholar]
- Tarchi, D.; Guglieri, G.; Vespe, M.; Gioia, C.; Sermi, F.; Kyovtorov, V. Mini-Radar System for Flying Platforms. Demography. In Proceedings of the 2017 IEEE International Workshop on Metrology for AeroSpace (MetroAeroSpace), Padua, Italy, 21–23 June 2017; Migration & Governance Unit: Ispra, Italy, 2017. [Google Scholar]
- U.S. Army Roadmap for UAS 2010–2035; U.S. Army UAS Center of Excellence: Fort Rucker, AL, USA.
- Herselman, P.L.; Baker, C.J.; de Wind, H.J. An analysis of X-band calibrated sea clutter and small boat reflectivity at medium-to-low grazing angles. Int. J. Navig. Obs. 2008, 2008, 347518. [Google Scholar] [CrossRef] [Green Version]
- Kerr, E. Propagation of Short Radio Waves, 2nd ed.; Peter Peregrinus: London, UK, 1987; ISBN 0863410995. [Google Scholar]
- Blake, L.V. Prediction of radar range. In Radar Handbook, 1st ed.; Skolnik, M., Ed.; McGraw Hill: New York, NY, USA, 1970. [Google Scholar]
- Skolnik, M. Radar Handbook, 2nd ed.; McGraw-Hill Companies: New York, NY, USA, Chapter 13.
- Watts, S. Modeling and simulation of coherent sea clutter. IEEE Trans. Aerosp. Electron. Syst. 2012, 48, 3303–3317. [Google Scholar] [CrossRef]
- Maurici, W. Long: Radar Reflectivity of Land and Sea; Artech Hause: Boston, MA, USA, 2001. [Google Scholar]
- Kuttikkad, S.; Chellappa, R. Non-Gaussian CFAR Techniques for Target Detection in High Resolution SAR Images. In Proceedings of the 1st International Conference on Image Processing, Austin, TX, USA, 13–16 November 1994; pp. 910–914. [Google Scholar]
- Aalo, V.A.; Peppas, K.P.; Efthymoglou, G. Performance of CA-CFAR detectors in nonhomogeneous positive alpha-stable clutter. IEEE Trans. Aerosp. Electron. Syst. 2015, 51, 2027–2038. [Google Scholar] [CrossRef]
- El-Darymli, K.; McGuire, P.; Power, D.; Moloney, C.R. Target detection in synthetic aperture radar imagery: A state-of-the-art survey. J. Appl. Remote Sens. 2013, 7, 071598. [Google Scholar] [CrossRef] [Green Version]
- Antipov, I. Simulation of Sea Clutter Returns; Defense Science and Technology Organization Canberra: Canberra, Australia, 1998. [Google Scholar]
- Ward, K.D.; Tough, R.J.A.; Watts, S. Sea Clutter: Scattering, the K Distribution and Radar Performance; The Institution of Engineering and Technology: London, UK, 2006. [Google Scholar]
- Trunk, G.V.; George, S.F. Detection of Targets in Non-Gaussian Sea Clutter. IEEE Trans. Aerosp. Electron.Syst. 1970, AES-6, 620–628. [Google Scholar] [CrossRef]
- Sekine, M.; Mao, Y. Weibull RADAR Clutter, (IEE RADAR Sonar and Navigation and Avionics); IET: Stevenage, UK, 1990. [Google Scholar]
- Walker, D. Experimentally motivated model for low grazing angle radar Doppler spectra of the sea surface. IEEE Proc. Radar Sonar Navig. 2000, 147, 114–120. [Google Scholar] [CrossRef]
- Radiocommunication Sector of International Telecommunication Union. Recommendation ITU-R P.676-10: Attenuation by Atmospheric Gases; Radiocommunication Sector of International Telecommunication Union: Geneva, Switzerland, 2013. [Google Scholar]
- Radiocommunication Sector of International Telecommunication Union. Recommendation ITU-R P.840-6: Attenuation Due to Clouds and Fog; Radiocommunication Sector of International Telecommunication Union: Geneva, Switzerland, 2013. [Google Scholar]
- Arage Hassen, A. Indicators for the Signal Degradation and Optimization of Automotive Radar Sensors Under Adverse Weather Conditions. Ph.D. Thesis, TU Darmstadt, Darmstadt, Germnay, 2007. [Google Scholar]
- Huang, J.; Jiang, S.; Lu, X. Rain backscattering properties and effects on the radar performance at mm wave band. Int. J. Infrared Millim. Waves 2001, 22, 917–922. [Google Scholar] [CrossRef]
- Kulemin, G.P. Millimeter-Wave Radar Targets and Clutter; Artech House: Boston, MA, USA, 2003. [Google Scholar]
- Briggs, J.N. Target Detection by Marine Radar; The Institution of Electrical Engineers: London, UK, 2004. [Google Scholar]
- Marshall, J.S.; Palmer, W.M.K. The distribution of raindrops with size. J. Meteorol. 1948, 5, 165–166. [Google Scholar] [CrossRef]
- Rain, A Water Resource (Pamphlet); U.S. Geological Survey: Reston, VA, USA, 1988.
- Radiocommunication Sector of International Telecommunication Union. Recommendation ITU-R P.838-3: Specific Attenuation Model for Rain for Use in Prediction Methods; Radiocommunication Sector of International Telecommunication Union: Geneva, Switzerland, 2005. [Google Scholar]
- Lim, T.-H.; Choo, H. Prediction of Target Detection Probability Based on Air-to-Air Long-Range Scenarios in Anomalous Atmospheric Environments; The Department of Electronic and Electrical Engineering, Hongik University: Seoul, Korea, 2021. [Google Scholar]
- Conte, E.; Longo, M.M. LOPS—Modelling and Simulation of Non-Rayleigh Radar Clutter. In IEEE Proceedings on Radar and Signal Processing, Part F; IET Digital Library, 1991; Volume 138, pp. 121–130. Available online: https://digital-library.theiet.org/content/journals/10.1049/ip-f-2.1991.0018 (accessed on 27 February 2022).
- Technology Service Corporation. 1990, Section 5.6.1: Backscatter from Sea, RADAR Workstation; Technology Service Corporation: Santa Monica, CA, USA, 1990; Volume 2, pp. 177–186. [Google Scholar]
- Reilly, J.P. Clutter Models for Shipboard RADAR Applications: 0.5 to 70 GHz; Technical Report, Task 3-1-18; Multisensor Propagation Data and Clutter Modelling, NATO AAW System Program Office, NAAW-88-062R; NATO: Brussels, Belgium, 10 June 1988. [Google Scholar]
- Gregers-Hansen, V.; Mital, R. An Empirical Sea Clutter Model for Low Grazing Angles. In Proceedings of the IEEE RADAR Conference 2009, Pasadena, CA, USA, 4–8 May 2009; pp. 1–5. [Google Scholar]
- Brekke, E.; Hallingstad, O.; Glattetre, J. Tracking small targets in heavy-tailed clutter using amplitude information. IEEE J. Ocean. Eng. 2010, 35, 314–329. [Google Scholar] [CrossRef]
- Ward, K.D.; Tough, R.J.A.; Watts, S. Sea Clutter: Scattering, the K Distribution and Radar Performance, 2nd ed.; Institute Engineering and Technology: Raiwind, Pakistan, 2013. [Google Scholar]
- Crisp, D.J.; Rosenberg, L.; Stacy, N.J. Modelling X-band Sea-Clutter with the K distribution: Shape Parameter Variation. In Proceedings of the IEEE International Radar Conference, Bordeaux, France, 12–16 October 2009. [Google Scholar]
- Dong, Y. Distribution of X-Band High Resolution and High Grazing Angle Sea-Clutter; Research Report DSTO-RR-0316; DSTO: Canberra, Australia, 2006. [Google Scholar]
- Currie, N. Radar Reflectivity Measurement: Techniques and Applications; Artech House: Boston, MA, USA, 1989. [Google Scholar]
- Currie, N. Techniques of Radar Reflectivity Measurement; Artech House: Boston, MA, USA, 1984. [Google Scholar]
- Moon, T.T.; Bawden, P.J. High resolution RCS measurements of boats. IEEE Proc. F-Radar Signal Processing 1991, 138, 218–222. [Google Scholar] [CrossRef]
- Skolnik, M. Introduction to Radar Systems, 2nd ed.; McGraw-Hill Kogakusha: New York, NY, USA, 1980. [Google Scholar]
- Brooker, G.; Lobsey, C.; Hennessy, R. Radar Cross Sections of Small Boats at 94 GHz; Acfr/Amme, University of Sydney: Sydney, NSW, Australia, 2006. [Google Scholar]
- Blackman, S.; Popoli, R. Design and Analysis of Modern Tracking Systems (Artech House Radar Library); Artech House: Boston, MA, USA, 1999. [Google Scholar]
- Ramachandra, K. Kalman Filtering Techniques for Radar Tracking; Marcel Dekker: New York, NY, USA, 2000. [Google Scholar]
- Watts, S. A new method for the simulation of coherent sea clutter. In Proceedings of the 2011 IEEE RadarCon (RADAR), Kansas City, MO, USA, 23–27 May 2011; IEEE: Piscataway, NJ, USA, 2011; pp. 52–57. [Google Scholar]















| Category | Size | Maximum Gross Takeoff Weight (MGTW) (lbs) | Normal Operating Altitude (ft) | Airspeed (Knots) |
|---|---|---|---|---|
| Group 1 | Small | 0–20 | <1.200 AGL * | <100 |
| Group 2 | Medium | 21–55 | <3.500 | <250 |
| Group 3 | Large | <1320 | <18.000 MSL ** | <250 |
| Group 4 | Larger | >1320 | <18.000 MSL | Any airspeed |
| Group 5 | Largest | >1320 | >18.000 | Any airspeed |
| Frequency, GHz | Radar Range, km | Attenuation Due to Gas, dB | Attenuation Due to Cloud, dB | Attenuation Due to Rain, dB | ||||
|---|---|---|---|---|---|---|---|---|
|
Water Vapor Density g/m3 | Liquide Water Density g/m3 | Rainfall Rate mm/h | ||||||
| 5 | 30 | 0.05 | 0.5 | 1 | 4 | 16 | ||
| 10 | 8 | 0.17 | 0.93 | 0.04 | 0.43 | 0.16 | 0.89 | 4.92 |
| 30 | 0.65 | 3.5 | 0.16 | 1.6 | 0.39 | 2.18 | 11.40 | |
| 14 | 8 | 0.28 | 1.97 | 0.08 | 0.83 | 0.48 | 2.33 | 10.91 |
| 30 | 1.07 | 7.38 | 0.31 | 3.13 | 1.2 | 5.7 | 25.28 | |
| 18 | 8 | 0.65 | 4.62 | 0.14 | 1.37 | 0.92 | 4.08 | 17.61 |
| 30 | 2.43 | 17.34 | 0.51 | 5.15 | 2.27 | 9.96 | 40.80 | |
| Azimuth 3 dB beamwidth | 0.37° | 0.43° | 0.33° |
| Elevation 3 dB beamwidth | 11.0° | 4.0° | 1.8° |
| Reduction of rain clutter power level | 0 dB | 3.7 dB | 8.4 dB |
| Douglas Sea Scale Degree | Wave Height (Meters) | Characteristics |
|---|---|---|
| 0 | 0 | Calm (glassy) |
| 1 | 0 to 0.1 | Calm (rippled) |
| 2 | 0.1 to 0.5 | Smooth (wavelets) |
| 3 | 0.5 to 1.25 | Slight |
| 4 | 1.25 to 2.5 | Moderate |
| 5 | 2.5 to 4 | Rough |
| 6 | 4 to 6 | Very rough |
| 7 | 6 to 9 | High |
| 8 | 9 to 14 | Very high |
| 9 | Over 14 | Phenomenal |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bounaceur, H.; Khenchaf, A.; Le Caillec, J.-M. Analysis of Small Sea-Surface Targets Detection Performance According to Airborne Radar Parameters in Abnormal Weather Environments. Sensors 2022, 22, 3263. https://doi.org/10.3390/s22093263
Bounaceur H, Khenchaf A, Le Caillec J-M. Analysis of Small Sea-Surface Targets Detection Performance According to Airborne Radar Parameters in Abnormal Weather Environments. Sensors. 2022; 22(9):3263. https://doi.org/10.3390/s22093263
Chicago/Turabian StyleBounaceur, Hamza, Ali Khenchaf, and Jean-Marc Le Caillec. 2022. "Analysis of Small Sea-Surface Targets Detection Performance According to Airborne Radar Parameters in Abnormal Weather Environments" Sensors 22, no. 9: 3263. https://doi.org/10.3390/s22093263
APA StyleBounaceur, H., Khenchaf, A., & Le Caillec, J.-M. (2022). Analysis of Small Sea-Surface Targets Detection Performance According to Airborne Radar Parameters in Abnormal Weather Environments. Sensors, 22(9), 3263. https://doi.org/10.3390/s22093263







