A Multi-Mode Switching Variational Bayesian Adaptive Kalman Filter Algorithm for the SINS/PNS/GMNS Navigation System of Pelagic Ships
Abstract
:1. Introduction
- As an autonomous integrated system for ocean-going ships, the SINS/PNS/GMNS integrated navigation system is subject to complex environmental interference. Hence, the statistics of the measurement noises should be estimated in real time instead of being prescribed as constant. In this paper, the variational Bayesian method is adopted to estimate the noise statistics along with the system state based on real-time observations from PNS and GMNS.
- The reliability of the SINS/PNS/GMNS integrated navigation system is affected by the uncertainties in pelagic environment. For example, severe degradation of the accuracy in the integrated navigation system might be caused when the ship encounters harsh weather conditions or travels through an iron–nickel mining sea area. In order to enhance the reliability of the SINS/PNS/GMNS integrated navigation system, an interference evaluation algorithm and mode switching mechanism are developed in this paper. With the proposed scheme, the abrupt change resulting from harsh environmental conditions can be detected timely and the filtering mode can be switched smoothly, thereby ensuring the reliability of the integrated navigation system.
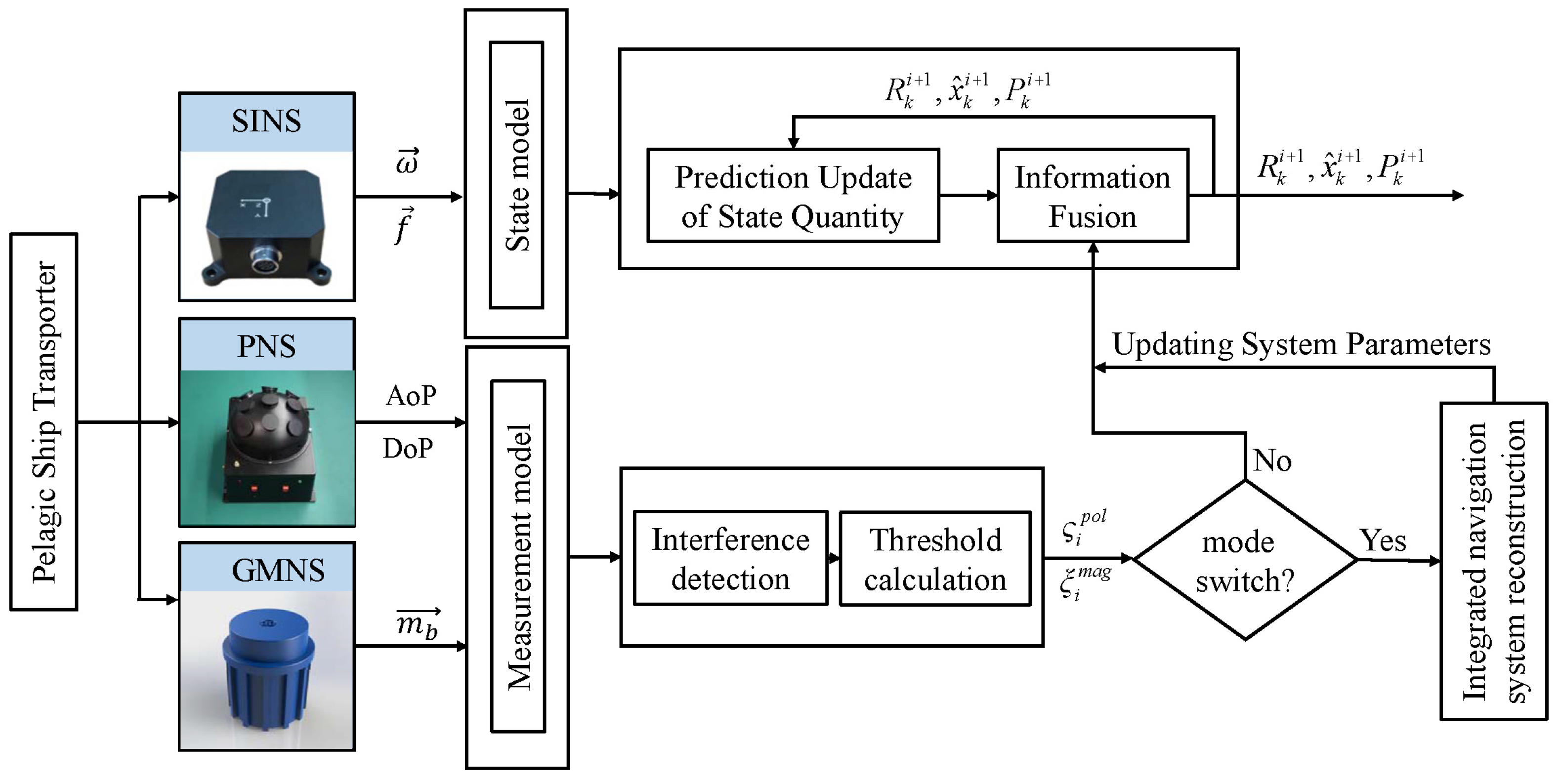
2. Methods
2.1. SINS/PNS/GMNS Integrated Navigation Model and the Conjugate Prior Distribution of Noise
2.1.1. SINS/PNS/GMNS Integrated Navigation Model
2.1.2. Conjugate Prior Distribution of Measurement Noise
2.2. Adaptive Posterior Estimation Based on Variational Bayesian Algorithm
2.3. Interference Evaluation Algorithm and Mode Switching Mechanism of the SINS/PNS/GMNS Integrated System
2.3.1. Interference Evaluation Algorithm and Multi-Mode Switching Mechanism of the Polarization System
- Case I: When , the interference evaluation parameter satisfies . The physical meaning is that when the polarization sensor works under the condition that DoP value is above the upper bound threshold , there are slight interference noises in the acquired measurement data. The weight of polarization navigation is equal to 1. The states of the navigation system can be estimated by the VBAKF algorithm smoothly in time. Accordingly, this case is defined as the case of slight interference, i.e., Case SI.
- Case II: When , the interference evaluation parameter satisfies . It is indicated that the polarization sensor is working with a certain extent interference. In this case, the estimation of noise statistical properties needs to weigh the measurement information and the prior noise information at the same time, and then estimate the measurement noise comprehensively. Accordingly, this case is defined as the case of interference-tolerance, i.e., Case TI. The measurement noise covariance can be estimated as:
- Case III: When , the interference evaluation parameter turns out to be . In this case, it indicates that the degree of interference exceeds the handling ability of the polarization system, and the polarization system is judged to be invalid. Accordingly, this case is defined as the case of excessive interference, i.e., Case EI. Further, with , the polarization system will be isolated and the filter should be reconstructed. The system measurement model will switch to be:
2.3.2. Interference Evaluation Algorithm and Mode Switching Mechanism of the Geomagnetic System
- Case I: When , the interference evaluation parameter . In this case, the interferences in GMNS data are slight and can be effectively estimated and compensated by the VBAKF algorithm. Accordingly, this case is defined as the case of slight interference, i.e., Case SI.
- Case II: When , the interference evaluation parameter is calculated to be a normalized weight coefficient. In this case, the GMNS should work with a certain extent interference. Thus, the estimation of noise statistics needs to weigh the measurement information and the prior noise information at the same time. Accordingly, this case is defined as the case of interference-tolerance, i.e., Case TI. The measurement noise covariance can be estimated comprehensively as:In Equation (26), indicates the prior measurement error covariance; indicates the measurement error covariance calculated by the VBAKF algorithm.
- Case III: When , the interference evaluation parameter . In this case, it indicates that the Earth’s magnetic field is disturbed severely by abnormal magnetic fields, and the GMNS system cannot work effectively. Accordingly, this case is defined as the case of excessive interference, i.e., Case EI. Further, with , the geomagnetic system will be isolated and the filter will be reconstructed. The system measurement model will switch to be:
2.4. Multi-Mode Switching VBAKF Algorithm Summary
| Algorithm 1: The MMS-VBAKF Algorithm |
| Input: When , initialize: Navigation parameter estimation: For , do (1) Obtain the polarization measurement values DoP and AoP, calculate , and select the mode; (2) Case SI: : for , do The fixed-point iteration mechanism and the VBAKF algorithm are used to update in real-time; End for; (3) Case TI: : Update of the covariance matrix of polarization measurement noise: ; ; (4) Case EI: : The polarization system was evaluated to be failed. Isolate the polarization system, and switch the system measurement model to: ; Restructure the integrated navigation system, and use fixed-point iteration mechanism and VBAKF algorithm to update in real-time; (5) Obtain the geomagnetic measurement value, calculate the geomagnetic mode switching factor, and select the mode; (6) Case SI: : for , do The fixed-point iteration mechanism and the VBAKF algorithm are used to update in real-time; End for; (7) Case TI: : The geomagnetic noise covariance matrix is updated to: ; Further update ; (8) Case EI: : It was evaluated that the geomagnetic system was out of work. Isolate the geomagnetic system, and switch the system measurement model to: ; Restructure the integrated navigation system, and use fixed-point iteration mechanism and VBAKF algorithm to update ; End for Output: |
3. Results Analysis and Discussion
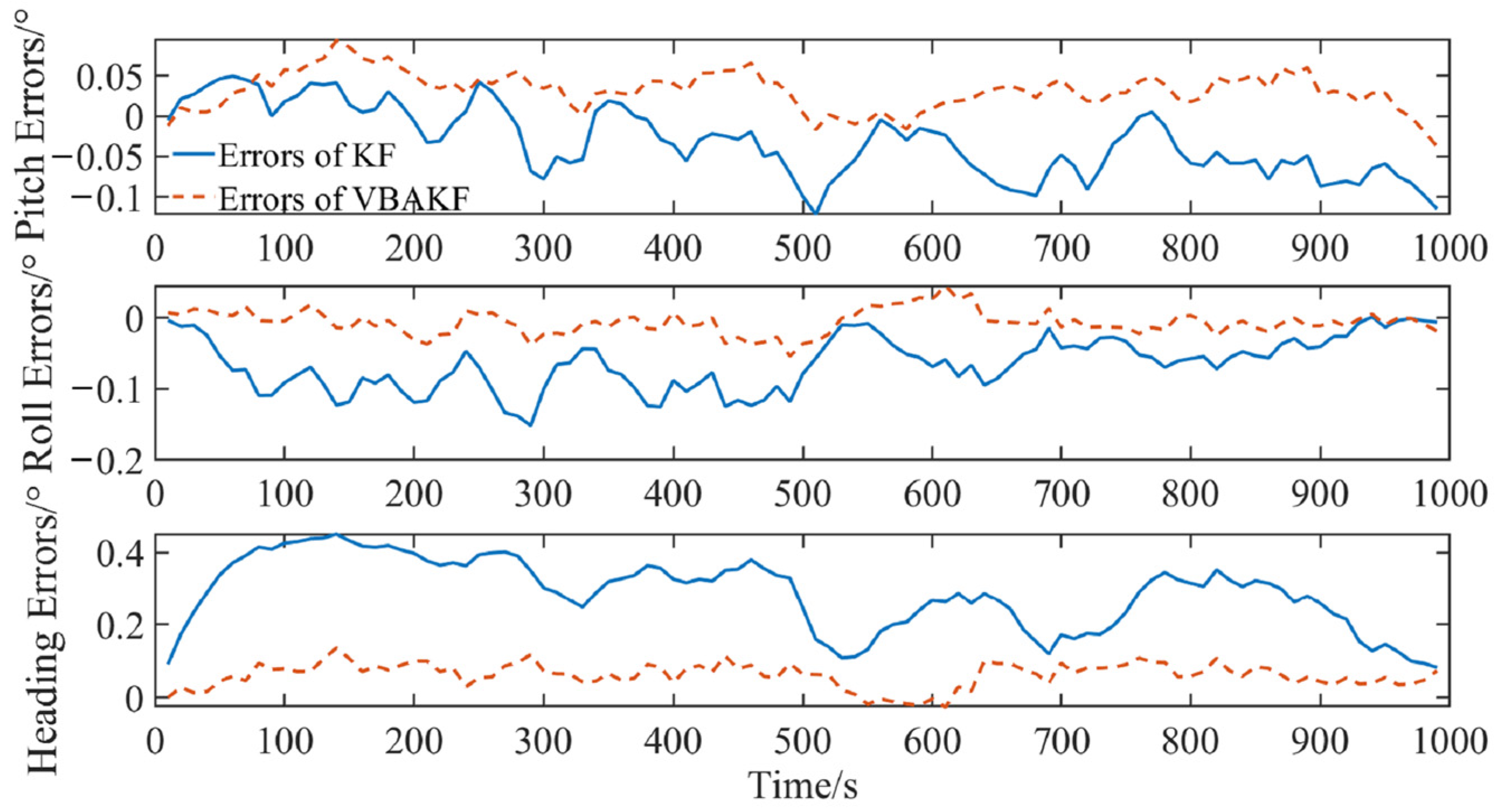
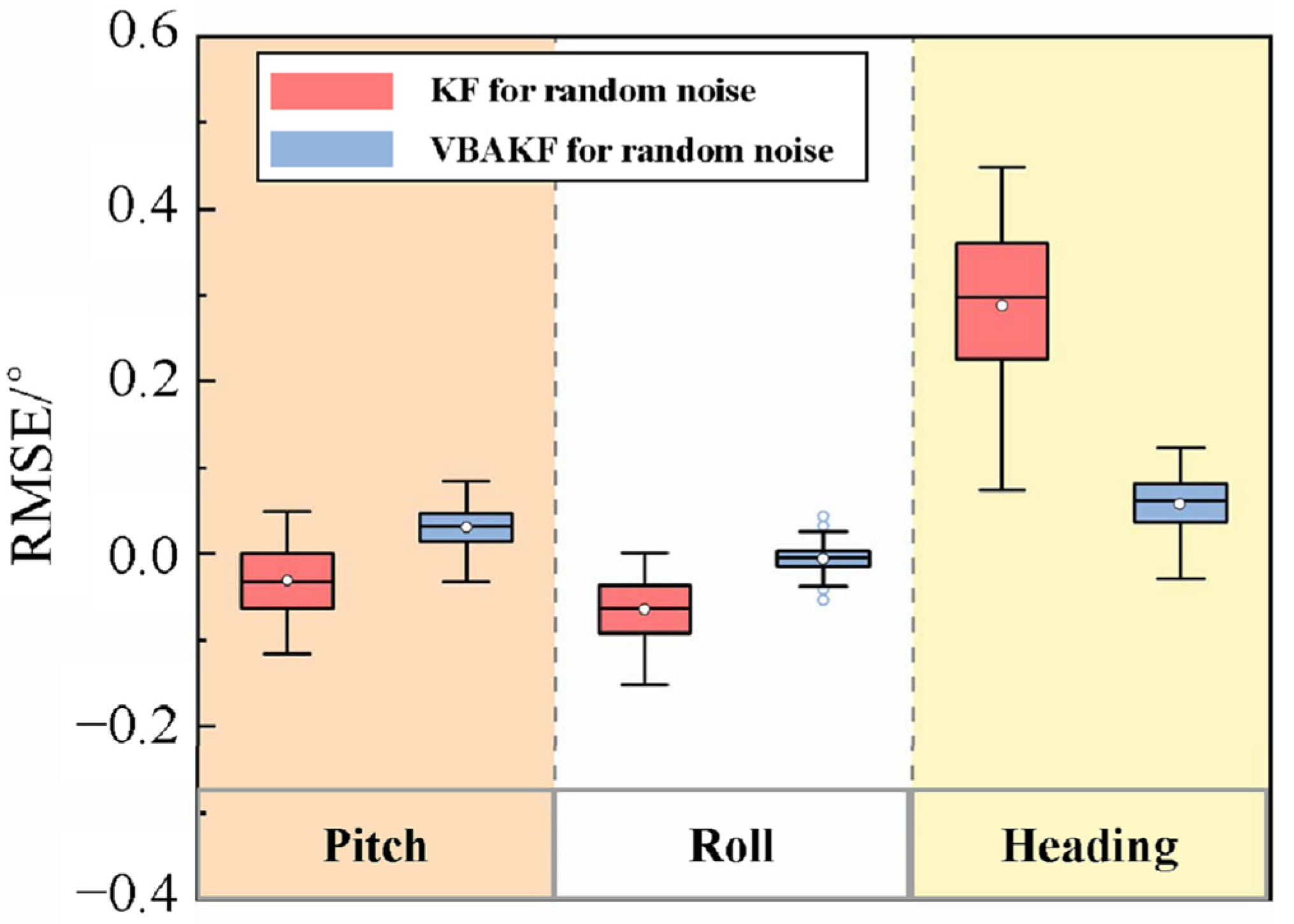
3.1. Random Unknown Noise Situation
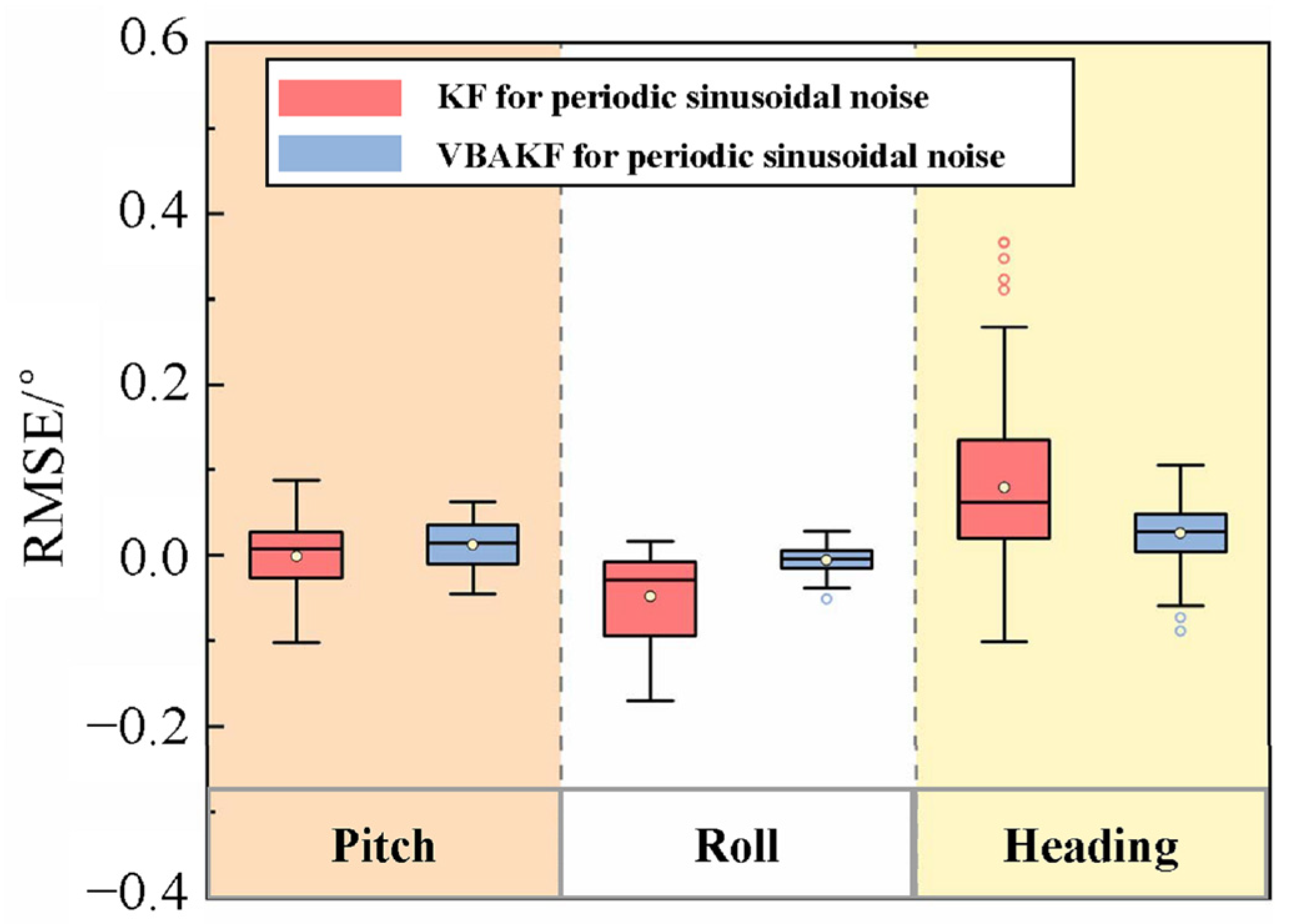
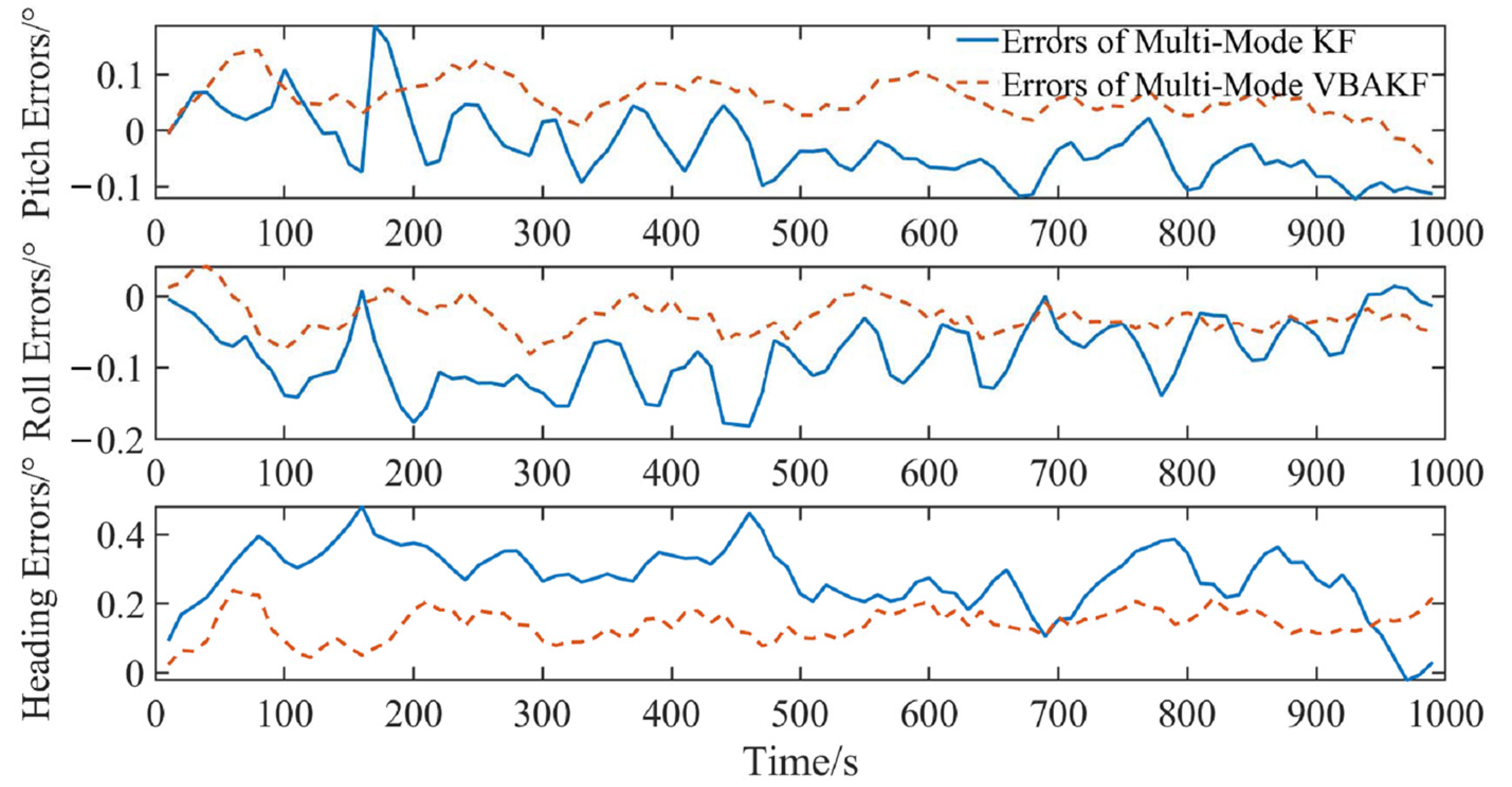
3.2. Periodic Sinusoidal Characteristic Noise Situation
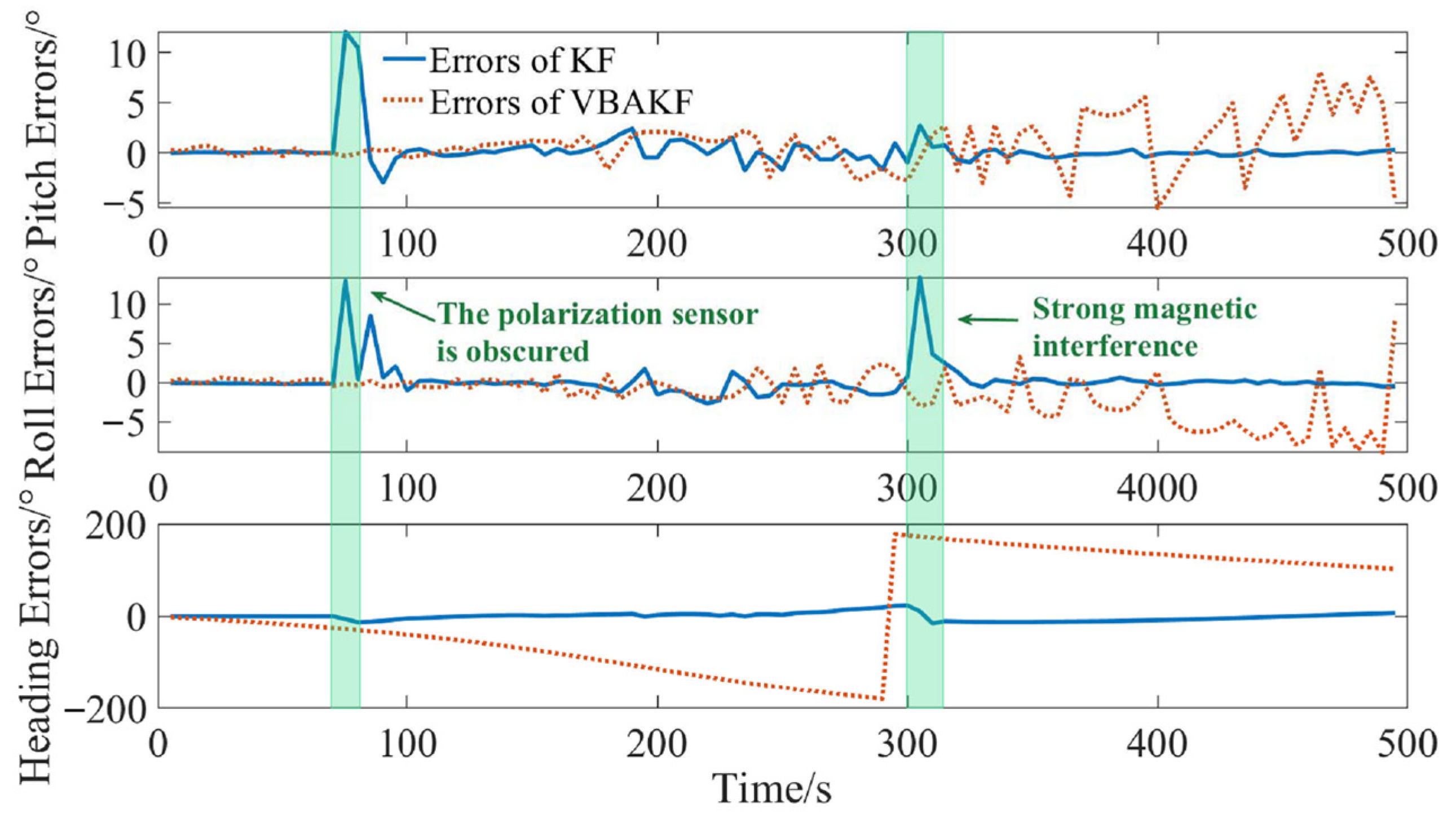
3.3. Situation Where Part of the Integrated Navigation System Become Invalid
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Li, Q.; Ben, Y.; Yu, F. System reset of transversal strapdown INS for ship in polar region. Measurement 2015, 60, 247–257. [Google Scholar] [CrossRef]
- Zhang, J.; Han, Y.; Zheng, C. Underwater target localization using long baseline positioning system. Appl. Acoust. 2016, 111, 129–134. [Google Scholar] [CrossRef]
- Guan, T.; Zhang, G.; Chen, P. A terrain matching navigation algorithm for UAV. In Proceedings of the 33rd Chinese Control and Decision Conference (CCDC), Kunming, China, 22–24 May 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 5203–5207. [Google Scholar]
- Zhang, C.; Guo, C.; Zhang, D. Ship navigation via GPS/IMU/LOG integration using adaptive fission particle filter. Ocean. Eng. 2018, 156, 435–445. [Google Scholar] [CrossRef]
- Wei, Y.; Ding, Z.; Huang, H. A non-contact measurement method of ship block using image-based 3D reconstruction technology. Ocean. Eng. 2019, 178, 463–475. [Google Scholar] [CrossRef]
- Han, J.; Cho, Y.; Kim, J. Coastal SLAM with marine radar for USV operation in GPS-restricted situations. IEEE J. Ocean. Eng. 2019, 44, 300–309. [Google Scholar] [CrossRef]
- Zhang, J.; Yang, J.; Wang, S.; Liu, X.; Wang, Y.; Yu, X. A self-contained interactive iteration positioning and orientation coupled navigation method based on skylight polarization. Control Eng. Pract. 2021, 111, 104810. [Google Scholar] [CrossRef]
- Yang, J.; Du, T.; Liu, X. Method and implementation of a bioinspired polarization-based attitude and heading reference system by integration of polarization compass and inertial sensors. IEEE Trans. Ind. Electron. 2019, 67, 9802–9812. [Google Scholar] [CrossRef]
- Yang, J.; Liu, X.; Zhang, Q. Global autonomous positioning in GNSS-challenged environments: A bioinspired strategy by polarization pattern. IEEE Trans. Ind. Electron. 2020, 68, 6308–6317. [Google Scholar] [CrossRef]
- Zhi, W.; Chu, J.; Li, J. A novel attitude determination system aided by polarization sensor. Sensors 2018, 18, 158. [Google Scholar] [CrossRef] [Green Version]
- Collett, M.; Collett, T.; Bisch, S.; Wehner, R. Local and global vectors in desert ant navigation. Nature 1998, 394, 269–272. [Google Scholar] [CrossRef]
- Pahl, M.; Zhu, H.; Tautz, J. Large scale homing in honeybees. PLoS ONE 2011, 6, e19669. [Google Scholar] [CrossRef] [Green Version]
- Reppert, S.M.; Zhu, H.; White, R.H. Polarized light helps monarch butterflies navigate. Curr. Biol. 2004, 14, 155–158. [Google Scholar] [CrossRef]
- Lambrinos, D.; Kobayashi, H.; Pfeifer, R. An autonomous agent navigating with a polarized light compass. Adapt. Behav. 1997, 6, 131–161. [Google Scholar] [CrossRef]
- NCEI Geomagnetic Modeling Team and British Geological Survey. World Magnetic Model 2020; NOAA National Centers for Environmental Information: Asheville, NC, USA, 2019. [Google Scholar]
- Wahdan, A.; Georgy, J.; Abdelfatah, W.F. Magnetometer calibration for portable navigation devices in vehicles using a fast and autonomous technique. IEEE Trans. Intell. Transp. Syst. 2014, 15, 2347–2352. [Google Scholar] [CrossRef]
- Wu, Y.; Zou, D.; Liu, P. Dynamic magnetometer calibration and alignment to inertial sensors by Kalman filtering. IEEE Trans. Control. Syst. Technol. 2017, 26, 716–723. [Google Scholar] [CrossRef] [Green Version]
- Springmann, J.C.; Cutler, J.W. Attitude-independent magnetometer calibration with time-varying bias. J. Guid. Control. Dyn. 2012, 35, 1080–1088. [Google Scholar] [CrossRef]
- Kok, M.; Schön, T.B. Magnetometer calibration using inertial sensors. IEEE Sens. J. 2016, 16, 5679–5689. [Google Scholar] [CrossRef] [Green Version]
- Horvath, G.; Barta, A.; Gal, J.; Suhai, B.; Haiman, O. Ground-based full-sky imaging polarimetry of rapidly changing skies and its use for polarimetric cloud detection. Appl. Opt. 2002, 41, 543–559. [Google Scholar] [CrossRef] [PubMed]
- Miyazaki, D.; Ammar, M.; Kawakami, R.; Ikeuchi, K. Estimating sunlight polarization using a fish-eye lens. IPSJ Trans. Comput. Vis. Appl. 2009, 1, 288–300. [Google Scholar] [CrossRef] [Green Version]
- Suhai, B.; Horvath, G. How well does the Rayleigh model describe the e-vector distribution of skylight in clear and cloudy conditions? A full-sky polarimetric study. J. Opt. Soc. Am. A 2004, 21, 1669–1676. [Google Scholar] [CrossRef]
- Raymond, L.; Lee, J.; Samudio, O.R. Spectral polarization of clear and hazy coastal skies. Appl. Opt. 2012, 51, 7499–7508. [Google Scholar]
- Ma, T.; Hu, X.; Zhang, L.; Lian, J.; He, X.; Wang, Y.; Xian, Z. An evaluation of skylight polarization patterns for navigation. Sensors 2015, 15, 5895–5913. [Google Scholar] [CrossRef] [Green Version]
- Ren, H.; Yang, J.; Liu, X. Sensor modeling and calibration method based on extinction ratio error for camera-based polarization navigation sensor. Sensors 2020, 20, 3779. [Google Scholar] [CrossRef]
- Fan, C.; Hu, X.; Lian, J. Design and calibration of a novel camera-based bio-inspired polarization navigation sensor. IEEE Sens. J. 2016, 16, 3640–3648. [Google Scholar] [CrossRef]
- Yang, J.; Niu, B.; Du, T. Disturbance analysis and performance test of the polarization sensor based on polarizing beam splitter. Sens. Rev. 2019, 39, 341–351. [Google Scholar] [CrossRef]
- Liu, X.; Yang, J.; Guo, L. Design and calibration model of a bioinspired attitude and heading reference system based on compound eye polarization compass. Bioinspiration Biomim. 2020, 16, 016001. [Google Scholar] [CrossRef]
- Chu, J.; Guan, C.; Liu, Z. Self-adaptive robust algorithm applied on compact real-time polarization sensor for navigation. Opt. Eng. 2020, 59, 027107. [Google Scholar] [CrossRef]
- Zhao, D.; Liu, X.; Zhao, H.J. Seamless integration of polarization compass and inertial navigation data with a self-learning multi-rate residual correction algorithm. Measurement 2021, 170, 108694. [Google Scholar] [CrossRef]
- Shen, C.; Xiong, Y.; Zhao, D. Multi-rate strong tracking square-root cubature Kalman filter for MEMS-INS/GPS/polarization compass integrated navigation system. Mech. Syst. Signal Process. 2022, 163, 108146. [Google Scholar] [CrossRef]
- Yuan, M.; He, X.; Hu, X. Polarized skylight/MIMU/geomagnetic orientation algorithm based on adaptive Kalman filter. In Proceedings of the 2020 Chinese Automation Congress (CAC), Shanghai, China, 6–8 November 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 1645–1650. [Google Scholar]
- Zhang, H.; Zhang, H.; Xu, G.; Liu, H.; Liu, X. Attitude anti-interference federal filtering algorithm for MEMS-SINS/GPS/magnetometer/SV integrated navigation system. Meas. Control 2020, 53, 46–60. [Google Scholar] [CrossRef] [Green Version]
- Jiang, C.; Zhang, S.; Zhang, Q. Adaptive estimation of multiple fading factors for GPS/INS integrated navigation systems. Sensors 2017, 17, 1254. [Google Scholar] [CrossRef] [Green Version]
- Shan, G.; Park, B.; Nam, S. A 3-dimensional triangulation scheme to improve the accuracy of indoor localization for IoT services. In Proceedings of the 2015 IEEE Pacific Rim Conference on Communications, Computers and Signal Processing (PACRIM), Victoria, BC, Canada, 24–26 August 2015; IEEE: Piscataway, NJ, USA, 2015; pp. 359–363. [Google Scholar]
- Qin, Y.Y.; Zhang, H.Y.; Wang, S.H. Kalman Filtering and Integrated Navigation Principle, 3rd ed.; Northwestern Polytechnical University Press: Xi’an, China, 2015. [Google Scholar]
- Beal, M.J. Variational Algorithms for Approximate Bayesian Inference; University of London: London, UK; University College London: London, UK, 2003. [Google Scholar]
- Zhu, H.; Zhang, G.; Li, Y. A novel robust Kalman filter with unknown non-stationary heavy-tailed noise. Automatica 2021, 127, 109511. [Google Scholar] [CrossRef]
- Blei, D.; Kucukelbir, A.; McAuliffe, J. Variational inference: A review for statisticians. J. Am. Stat. Assoc. 2017, 112, 859–877. [Google Scholar] [CrossRef] [Green Version]



| Sensors | Performance Parameters | Frequency |
|---|---|---|
| Gyro | constant drift: 2.0 °/h random drift: 0.5 °/h | 10 Hz |
| Accelerometer | constant bias: 500 μg random bias: 50 μg | 10 Hz |
| Polarization sensor | 1 Hz | |
| Geomagnetic sensor | 1 Hz |
| Method | RMSE (/°) | ||
|---|---|---|---|
| Pitch | Roll | Heading | |
| KF | 0.052 | 0.074 | 0.303 |
| VBAKF | 0.038 | 0.017 | 0.066 |
| Method | RMSE (/°) | ||
|---|---|---|---|
| Pitch | Roll | Heading | |
| KF | 0.041 | 0.071 | 0.128 |
| VBAKF | 0.029 | 0.015 | 0.046 |
| Time Interval | Whether to Interfere | Cause of Interference | |
|---|---|---|---|
| Case 1 | (0 s, 140 s] | no | / |
| Case 2 | (140 s, 160 s] | Polarization interference | Sensor occlusion, etc. |
| Case 3 | (160 s, 600 s] | no | / |
| Case 4 | (600 s, 630 s] | Magnetic interference | Submarine iron–nickel ore, etc. |
| Case 5 | (630 s, 1000 s] | no | / |
| Method | RMSE (/°) | ||
|---|---|---|---|
| Pitch | Roll | Heading | |
| KF | 0.066 | 0.093 | 0.293 |
| VBAKF | 0.067 | 0.035 | 0.147 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, J.; Wang, S.; Li, W.; Qiu, Z. A Multi-Mode Switching Variational Bayesian Adaptive Kalman Filter Algorithm for the SINS/PNS/GMNS Navigation System of Pelagic Ships. Sensors 2022, 22, 3372. https://doi.org/10.3390/s22093372
Zhang J, Wang S, Li W, Qiu Z. A Multi-Mode Switching Variational Bayesian Adaptive Kalman Filter Algorithm for the SINS/PNS/GMNS Navigation System of Pelagic Ships. Sensors. 2022; 22(9):3372. https://doi.org/10.3390/s22093372
Chicago/Turabian StyleZhang, Jie, Shanpeng Wang, Wenshuo Li, and Zhenbing Qiu. 2022. "A Multi-Mode Switching Variational Bayesian Adaptive Kalman Filter Algorithm for the SINS/PNS/GMNS Navigation System of Pelagic Ships" Sensors 22, no. 9: 3372. https://doi.org/10.3390/s22093372
APA StyleZhang, J., Wang, S., Li, W., & Qiu, Z. (2022). A Multi-Mode Switching Variational Bayesian Adaptive Kalman Filter Algorithm for the SINS/PNS/GMNS Navigation System of Pelagic Ships. Sensors, 22(9), 3372. https://doi.org/10.3390/s22093372






