Free Space Ground to Satellite Optical Communications Using Kramers–Kronig Transceiver in the Presence of Atmospheric Turbulence
Abstract
:1. Introduction
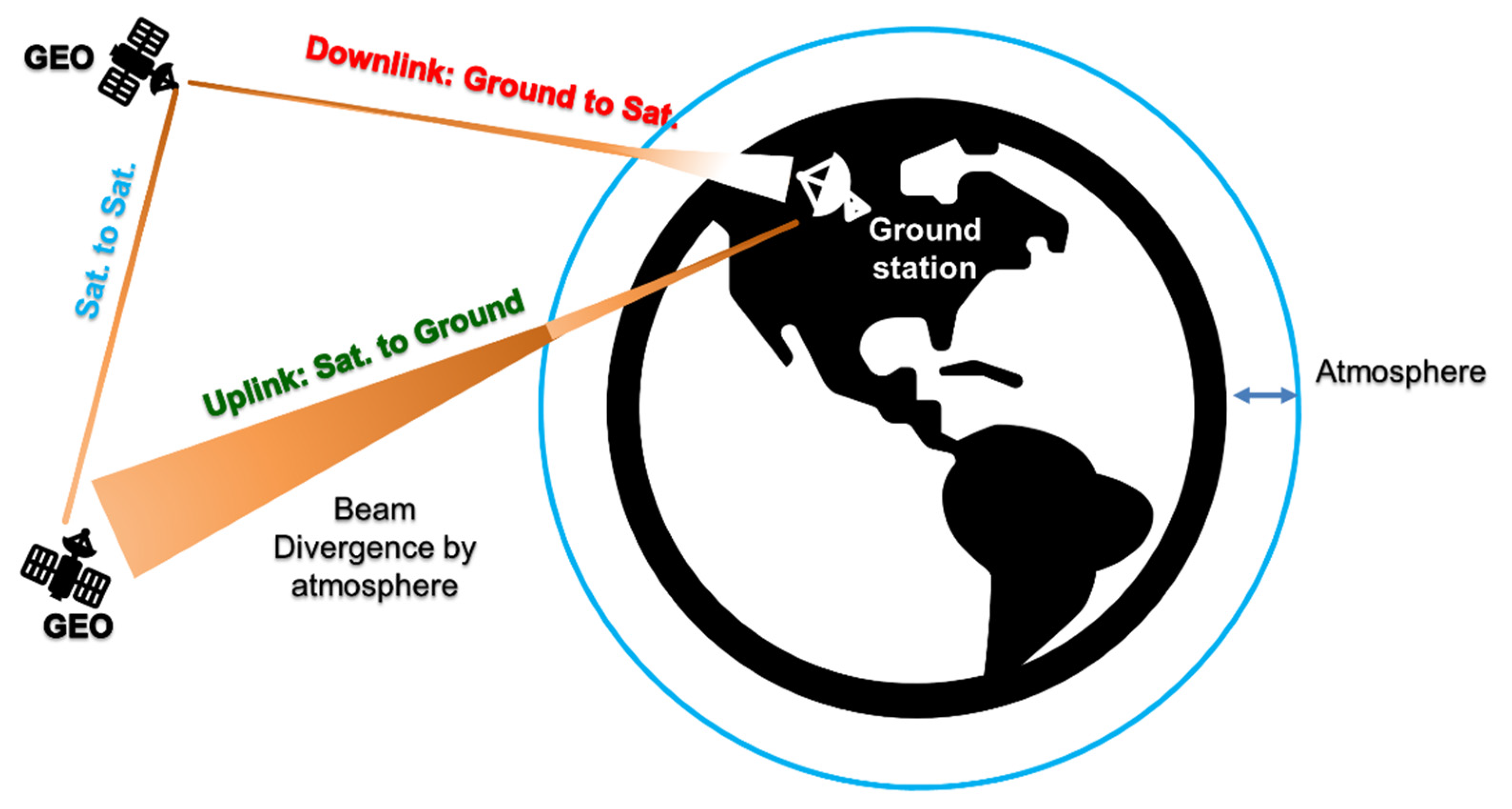
2. Background on Atmospheric Turbulence for FSO System
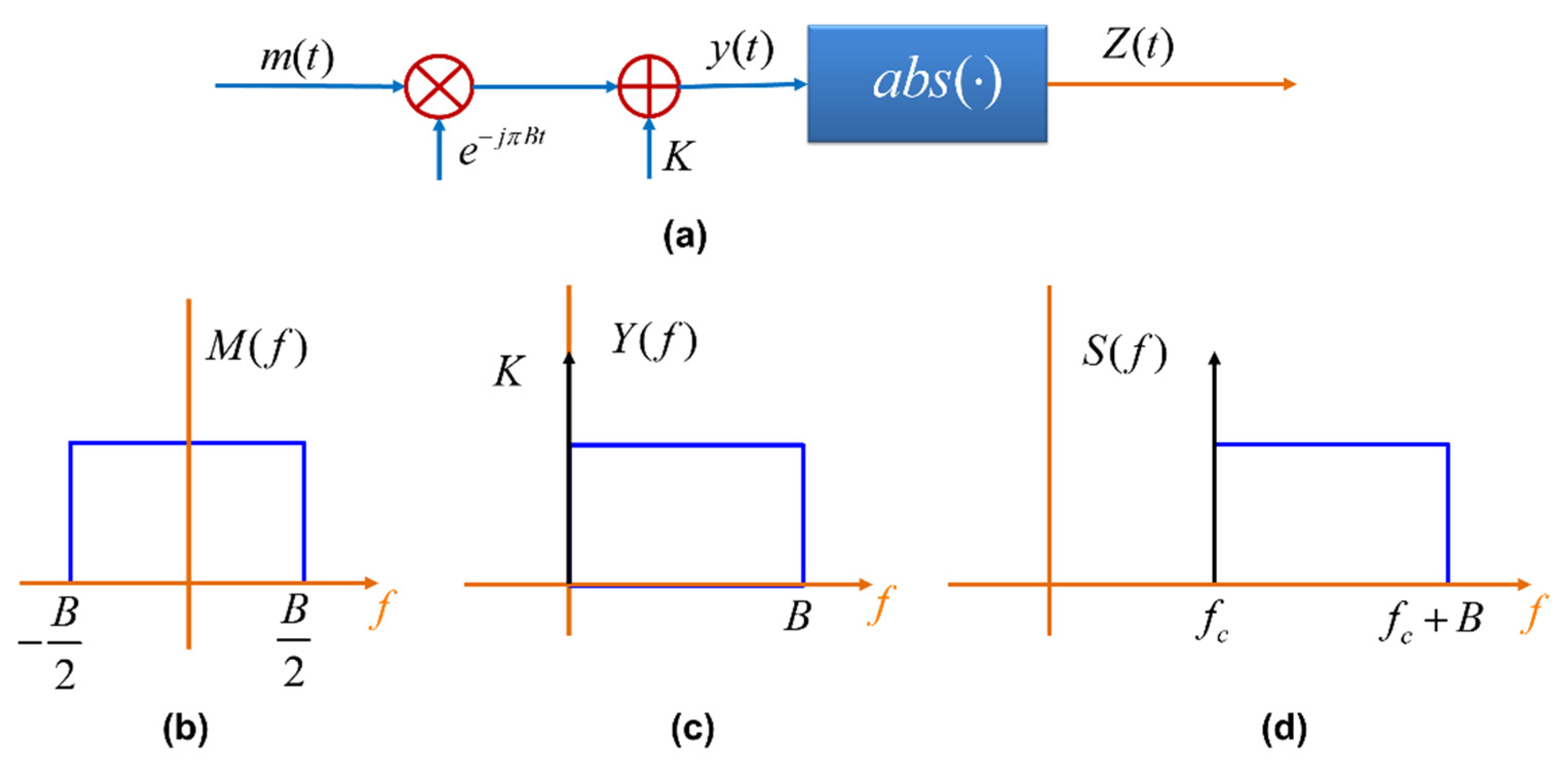
3. KK-Based FSO Communications
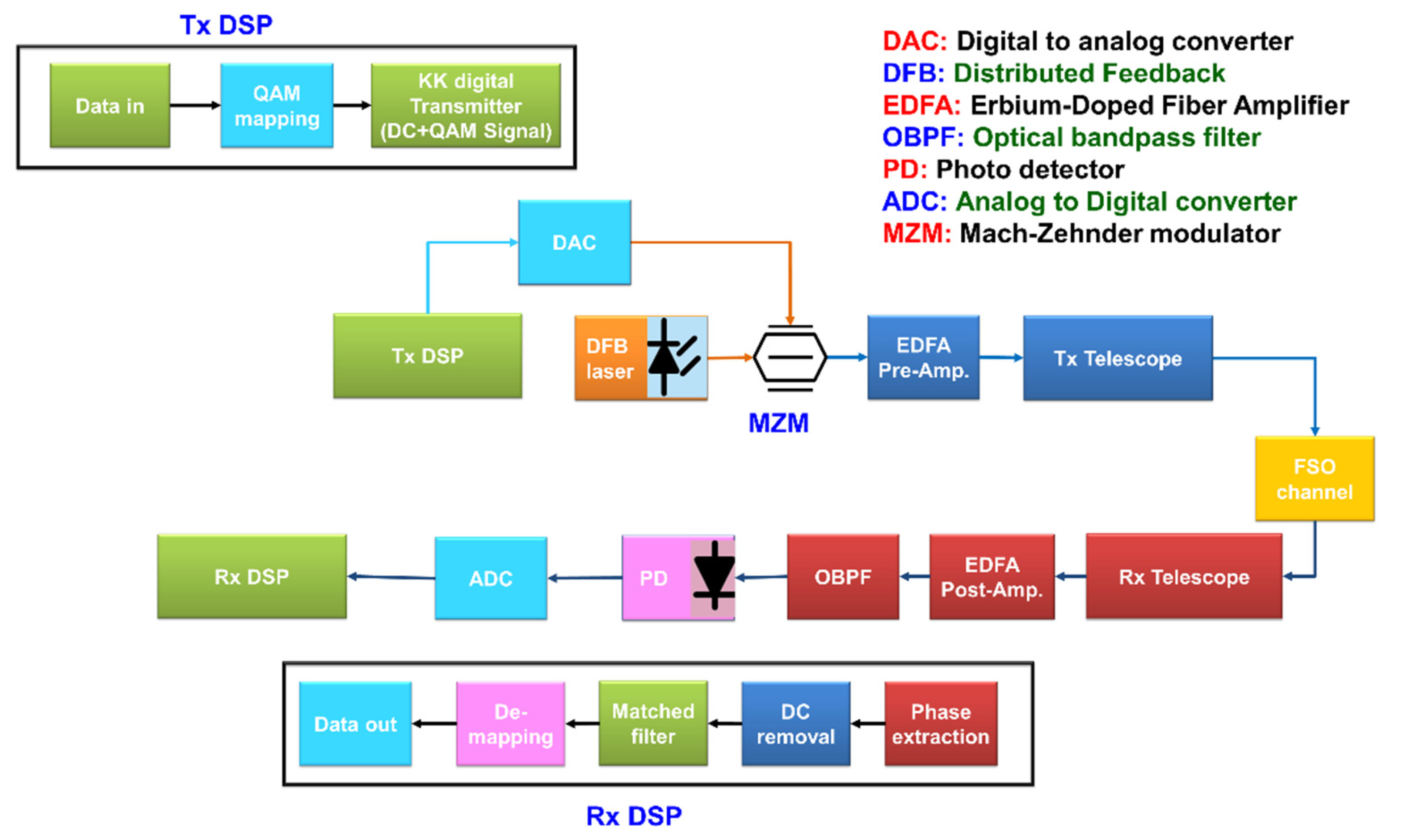
4. FSO System Design
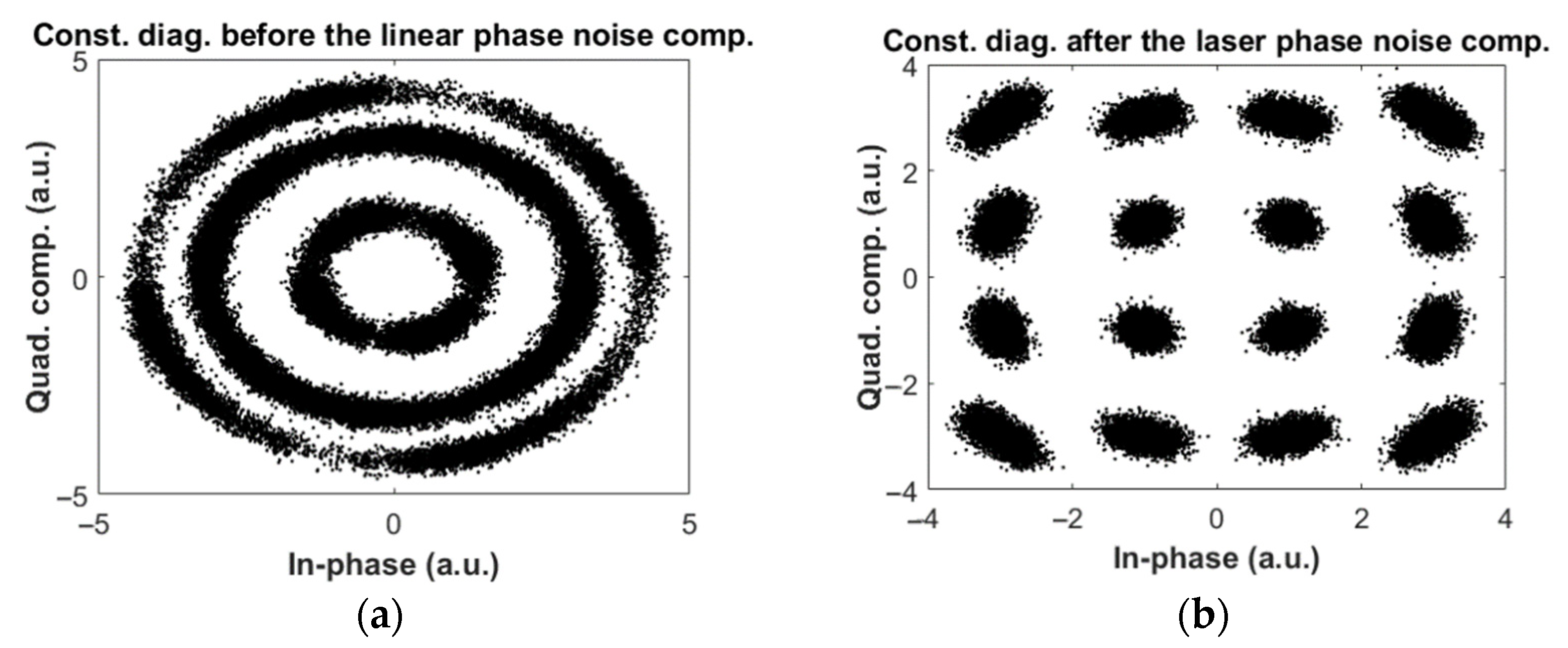
5. Simulation Results and Discussion
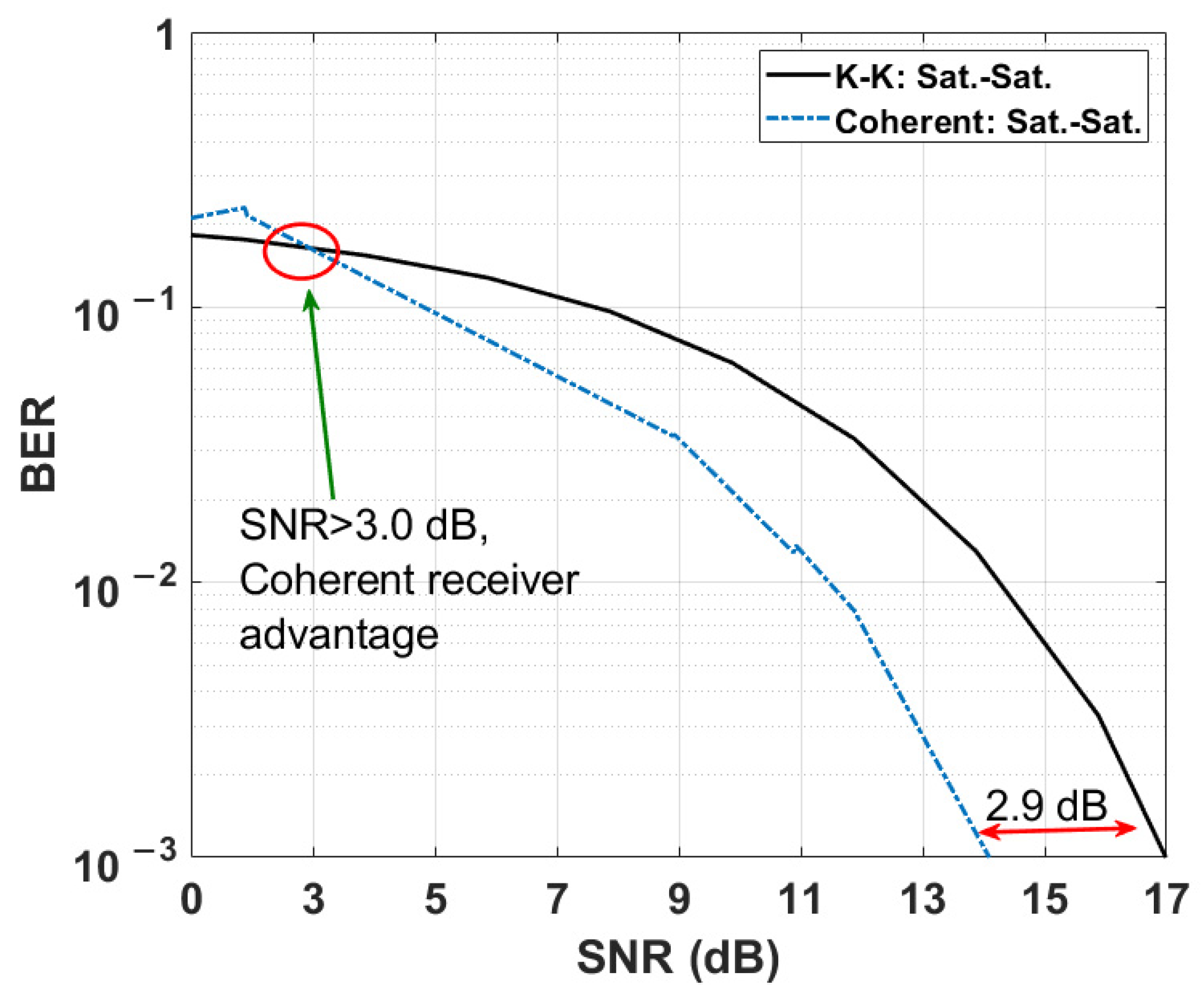
5.1. Comparison of KK and Coherent Systems without Scintillation
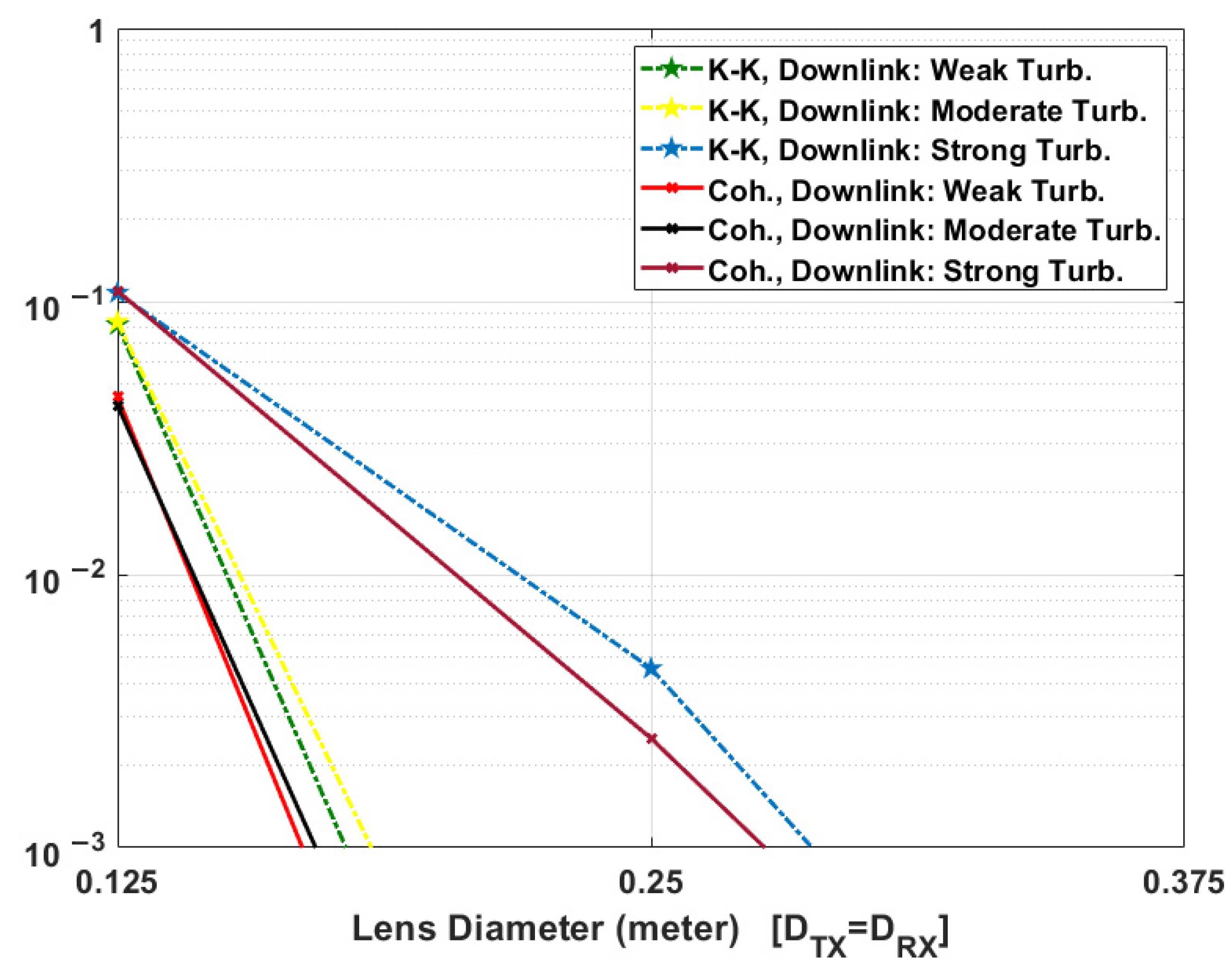
5.2. Comparison between KK and Coherent Systems in the Presence of Scintillation
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Whitmer, R.; Ohlmann, R.; Hance, H.; Cuff, K. Ultra-Wide Bandwidth Laser Communications: Part I-System Considerations for a Satellite Link. Proc. IEEE 1970, 58, 1710–1714. [Google Scholar] [CrossRef]
- Koepf, G.A.; Marshalek, R.G.; Begley, D.L. Space Laser Communications: A Review of Major Programs in the United States. Intl. J. Electon. Commun. 2002, 56, 232–242. [Google Scholar] [CrossRef]
- Fidler, F.; Knapek, M.; Horwath, J.; Leeb, W.R. Optical Communications for High-Altitude Platforms. IEEE J. Sel. Top. Quantum Electron. 2010, 16, 1058–1070. [Google Scholar] [CrossRef]
- Fidler, F. Optical Communications from High Altitude Platforms. Ph.D. Thesis, Institute of Communications and Radio Frequency Engineering, Vienna University of Technology, Vienna, Austria, 2007. Available online: http://publik.tuwien.ac.at/files/PubDat_112010.pdf (accessed on 17 November 2021).
- Ip, E.; Lau, A.P.T.; Barros, D.J.F.; Khan, J.M. Coherent detection in optical fiber systems. Opt. Exp. 2008, 16, 753–791. [Google Scholar] [CrossRef]
- Kumar, S.; Deen, M.J. Fiber Optic Communications: Fundamentals and Applications; John Wiley & Sons: Hoboken, NJ, USA, 2014. [Google Scholar]
- Kronig, R.L. On the theory of the dispersion of X-rays. J. Opt. Soc. Am. 1926, 12, 547–557. [Google Scholar] [CrossRef]
- Kramers, H.A. La diffusion de la lumiere par les atomes. Atti Congr. Intern. Fis. 1927, 2, 545–557. [Google Scholar]
- Cini, M. The response characteristics of linear systems. J. Appl. Phys. 1950, 21, 8–10. [Google Scholar] [CrossRef]
- Gell-Mann, M.; Goldberger, M.L. The formal theory of scattering. Phys. Rev. 1953, 91, 398–408. [Google Scholar] [CrossRef] [Green Version]
- Heisenberg, W. Quantum theory of fields and elementary particles. Rev. Mod. Phys. 1957, 29, 269–278. [Google Scholar] [CrossRef]
- Mecozzi, A. Retrieving the full optical response from amplitude data by Hilbert transform. Opt. Commun. 2009, 282, 4183–4187. [Google Scholar] [CrossRef]
- Mecozzi, A. A necessary and sufficient condition for minimum phase and implications for phase retrieval. arXiv 2016, arXiv:1606.04861. [Google Scholar]
- Antonelli, C.; Mecozzi, A.; Shtaif, M.; Chen, X.; Chandrasekhar, S.; Winzer, P.J. Kramers–Kronig coherent receiver. Optica 2016, 3, 1220–1227. [Google Scholar]
- Lorences-Riesgo, A.; Guiomar, F.P.; Sousa, A.N.; Teixeira, A.L.; Muga, N.J.; Medeiros, M.D.C.; Monteiro, P. 200G Outdoor Free-Space-Optics Link Using a Single-Photodiode Receiver. IEEE/OSA J. Lightwave Technol. 2020, 32, 394–400. [Google Scholar] [CrossRef]
- Wei, Y.; Zhou, Y.; Liu, C.; Wang, K.; Zhang, J.; Wang, F.; Ding, J.; Yu, J. SSB Single Carrier and Multicarrier in C-Band FSO Transmission with KK Receiver. IEEE/OSA J. Lightwave Technol. 2020, 38, 5000–5007. [Google Scholar] [CrossRef]
- Farid, A.; Hranilovic, S. Outage capacity optimization for free-space optical links with pointing errors. J. Lightwave Technol. 2007, 25, 1702–1710. [Google Scholar] [CrossRef] [Green Version]
- Arnon, S. Effects of atmospheric turbulence and building sway on optical wireless communication systems. Opt. Lett. 2003, 28, 129–131. [Google Scholar] [CrossRef]
- Kedar, D.; Arnon, S. Optical wireless communication through fog in the presence of pointing errors. Appl. Opt. 2003, 42, 4946–4954. [Google Scholar] [CrossRef]
- Zhang, R.; Hu, N.; Zhou, H.; Zou, K.; Su, X.; Zhou, Y.; Song, H.; Pang, K.; Song, H.; Minoofar, A.; et al. Turbulence-resilient pilot-assisted self-coherent free-space optical communications using automatic optoelectronic mixing of many modes. Nat. Photon. 2021, 15, 743–750. [Google Scholar] [CrossRef]
- Noll, R.J. Zernike polynomials and atmospheric turbulence. J. Opt. Soc. Am. 1976, 66, 207–211. [Google Scholar] [CrossRef]
- Dikmelik, Y.; Davidson, F.M. Fiber-coupling efciency for free-space optical communication through atmospheric turbulence. Appl. Opt. 2005, 44, 4946–4952. [Google Scholar] [CrossRef]
- Fried, D.L. Optical Resolution Through a Randomly Inhomogeneous Medium for Very Long and Very Short Exposures. J. Opt. Soc. Am. 1966, 56, 1372–1379. [Google Scholar] [CrossRef]
- Pfennigbauer, M. Design of Optical Space-to-Ground Links for the International Space Station. Ph.D. Thesis, Institut fur Nachrichtentechnik und Hochfrequenztechnik, TU Wien, Vienna, Austria, 2004. [Google Scholar]
- Andrews, L.C.; Phillips, R.L. Laser Beam Propagation through Random Media, 2nd ed.; SPIE: Bellingham, WA, USA, 2005. [Google Scholar]
- Pratt, W.K. Laser Communication Systems, 1st ed.; Wiley: New York, NY, USA, 1969. [Google Scholar]
- Shin, W.-H.; Choi, J.-Y.; Han, S.-K. Fixed threshold on-off keying differential detection for satellite optical communications. Opt. Express 2019, 27, 1590–1596. [Google Scholar] [CrossRef] [PubMed]
- Hulea, M.; Ghassemlooy, Z.; Rajbhandari, S.; Tang, X. Compensating for Optical Beam Scattering and Wandering in FSO Communications. J. Lightwave Technol. 2014, 32, 1323–1328. [Google Scholar] [CrossRef]
- Raj, A.A.B.; Selvi, A.J.V.; Durai, K.D.; Singaravelu, R.S. Intensity feedback-based beam wandering mitigation in free-space optical communication using neural control technique. EURASIP J. Wirel. Commun. Netw. 2014, 2014, 160. [Google Scholar] [CrossRef] [Green Version]
- Yan, X.; Guo, L.; Cheng, M.; Li, J. Controlling abruptly autofocusing vortex beams to mitigate crosstalk and vortex splitting in free-space optical communication. Opt. Express 2018, 26, 12605–12619. [Google Scholar] [CrossRef]
- Proakis, J.G.; Salehi, M. Digital Communications, 5th ed.; McGraw Hill: Boston, MA, USA, 2007; Chapter 4. [Google Scholar]
- Jin, C.; Shevchenko, N.A.; Li, Z.; Popov, S.; Chen, Y.; Xu, T. Nonlinear Coherent Optical Systems in the Presence of Equalization Enhanced Phase Noise. J. Lightwave Technol. 2021, 39, 4646–4653. [Google Scholar] [CrossRef]
- Pfau, T.; Hoffmann, S.; Noé, R. Hardware-efficient coherent digital receiver concept with feedforward carrier recovery for M-QAM constellations. J. Lightwave Technol. 2009, 27, 989–999. [Google Scholar] [CrossRef]
- Zhang, L.M.; Kschischang, F.R. Staircase codes with 6% to 33% overhead. J. Lightwave Technol. 2014, 32, 1999–2002. [Google Scholar] [CrossRef] [Green Version]
- Shao, S.; Hailes, P.; Wang, T.Y.; Wu, J.Y.; Maunder, R.G.; Al-Hashimi, B.M.; Hanzo, L. Survey of turbo, LDPC, and polar decoder ASIC implementations. IEEE Commun. Surv. Tutor. 2019, 21, 2309–2333. [Google Scholar] [CrossRef] [Green Version]
- Fang, Y.; Bu, Y.; Chen, P.; Lau, F.C.M.; Al Otaibi, S. Irregular-mapped protograph LDPC-coded modulation: A bandwidth-efficient solution for 6G-enabled mobile networks. IEEE Trans. Intell. Transp. Syst. 2021, 1–14. [Google Scholar] [CrossRef]
- Bioglio, V.; Condo, C.; Land, I. Design of polar codes in 5G new radio. IEEE Commun. Surv. Tutor. 2020, 23, 29–40. [Google Scholar] [CrossRef] [Green Version]
- Deen, M.J.; Basu, P.K. Silicon Photonics: Fundamentals and Devices; John Wiley & Sons: Hoboken, NJ, USA, 2012. [Google Scholar]




| Simulation Parameters | Value/Variable |
|---|---|
| Pre-amp. gain (Tx) | 30 (dB) |
| Post-amp. gain (Rx) | 30 (dB) |
| Noise figure (NF) pre-amp (Tx) | 5 |
| Noise figure (NF) post-amp (Rx) | 3.3 |
| Average transmit signal power (PT) | 30 (dBm) |
| Number transmitted symbols | 6,553,600 |
| Modulation format | 16 QAM |
| Telescope diameter (Tx) | 0.25 (m) |
| Telescope diameter (Rx) | 0.25 (m) |
| Data rate | 40 (Gb/s) |
| Over-sampling factor | 4 |
| Symbol rate | 10 (GS/s) |
| Pulse shape | Root-raised cosine |
| Roll-off factor | 0.1 |
| Link distance | 35,000 (km) |
| Zenith angle | 0 (deg) |
| PD responsivity | 0.8 (A/W) |
| Laser wavelength | 1550 (nm) |
| RMS of wind speed | 21 (m/s) |
| Wind speed close to ground | 5 (m/s) |
| Tropopause height | 9.4 (km) |
| Tropopause thickness | 4.8 (km) |
| Turbulence model [4] | Hufnagel-Valley model (H-V model) |
| Structure parameter at height h using H-V model [4] | |
| Turbulence close to ground (weak) | 1.7 × 10−14 (m−2/3) [4] |
| Turbulence close to ground (moderate) | 1.0 × 10−13 (m−2/3) [4] |
| Turbulence close to ground (strong) | 2.0 × 10−11 (m−2/3) [27] |
| Divergence factor (Tx) | 0.942 |
| 0.2 | |
| 0.8 | |
| 0.8 | |
| 0.8 | |
| 0.8 | |
| Responsivity R, | 1.1 (A/W) |
| Atmospheric loss (downlink/uplink), Aatm | 1.0 (dB) |
| Fried parameter, r0 (weak turbulence) | 200 (mm) |
| Fried parameter, r0 (moderate turbulence) | 80 (mm) |
| Fried parameter, r0 (strong turbulence) | 20 (mm) |
| Background noise (BN) (daytime, max sunlight, clear sky) | 1.544 × 10−25 (W/Hz) |
| Optical filter bandwidth | 12.5 (GHz) |
| Absolute temperature | 290 (°K) |
| Laser linewidth (Tx) | 22 (KHz) |
| Performance Factor | KK | Coherent | IMDD |
|---|---|---|---|
| Transmitter power efficiency | Low | High | Low |
| Hardware cost [38] | Low | High | Low |
| Mode mixing efficiency | Good | Low | Good |
| DSP computational cost | Moderate | High | Low |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Naghshvarianjahromi, M.; Kumar, S.; Deen, M.J. Free Space Ground to Satellite Optical Communications Using Kramers–Kronig Transceiver in the Presence of Atmospheric Turbulence. Sensors 2022, 22, 3435. https://doi.org/10.3390/s22093435
Naghshvarianjahromi M, Kumar S, Deen MJ. Free Space Ground to Satellite Optical Communications Using Kramers–Kronig Transceiver in the Presence of Atmospheric Turbulence. Sensors. 2022; 22(9):3435. https://doi.org/10.3390/s22093435
Chicago/Turabian StyleNaghshvarianjahromi, Mahdi, Shiva Kumar, and M. Jamal Deen. 2022. "Free Space Ground to Satellite Optical Communications Using Kramers–Kronig Transceiver in the Presence of Atmospheric Turbulence" Sensors 22, no. 9: 3435. https://doi.org/10.3390/s22093435





