A Novel Method for Detecting the Two-Degrees-of-Freedom Angular Displacement of a Spherical Pair, Based on a Capacitive Sensor
Abstract
:1. Introduction
2. Measurement Principle
2.1. The Structure Model of the Spherical Capacitive Sensor
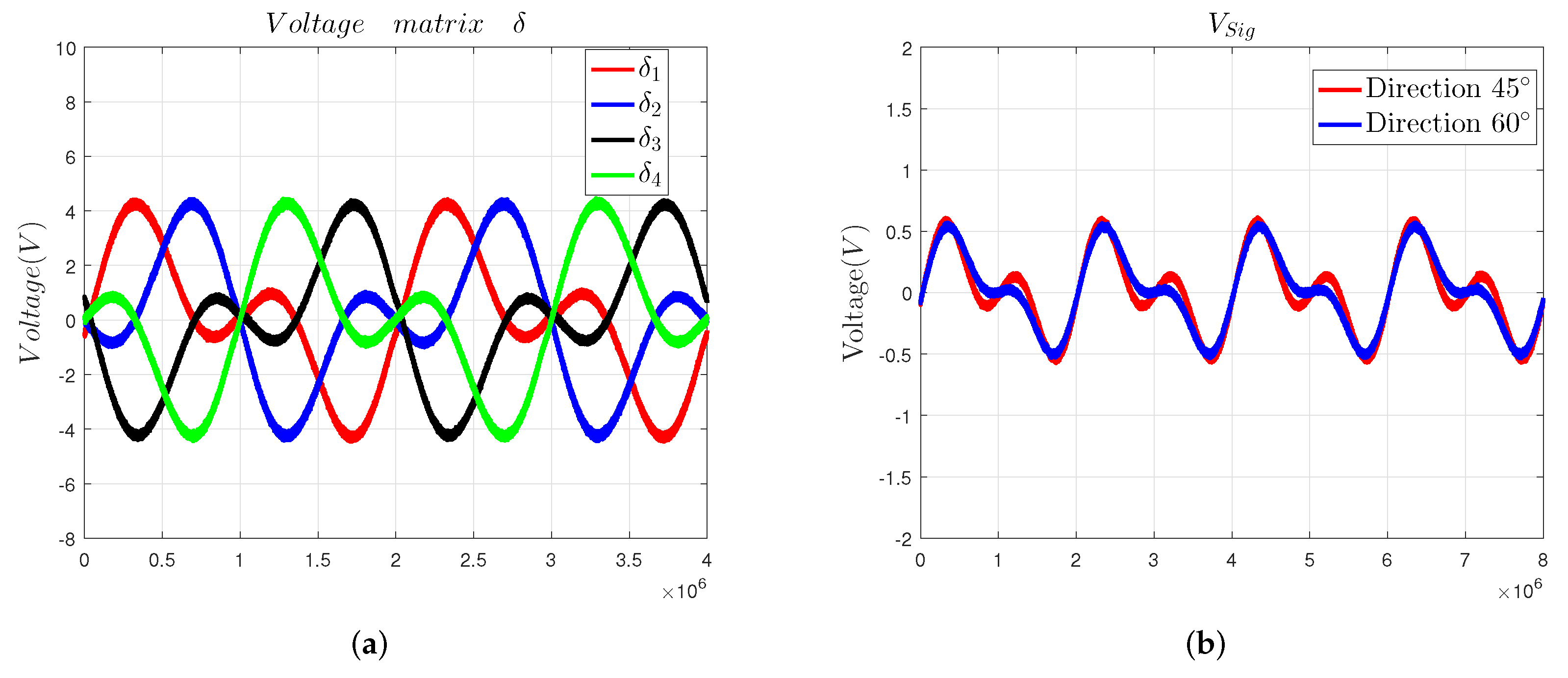
2.2. 2-DOF Angular Displacement Signal Measurement
2.3. 2-DOF Angular Displacement Signal Decoupling Method
3. Simulation Setup
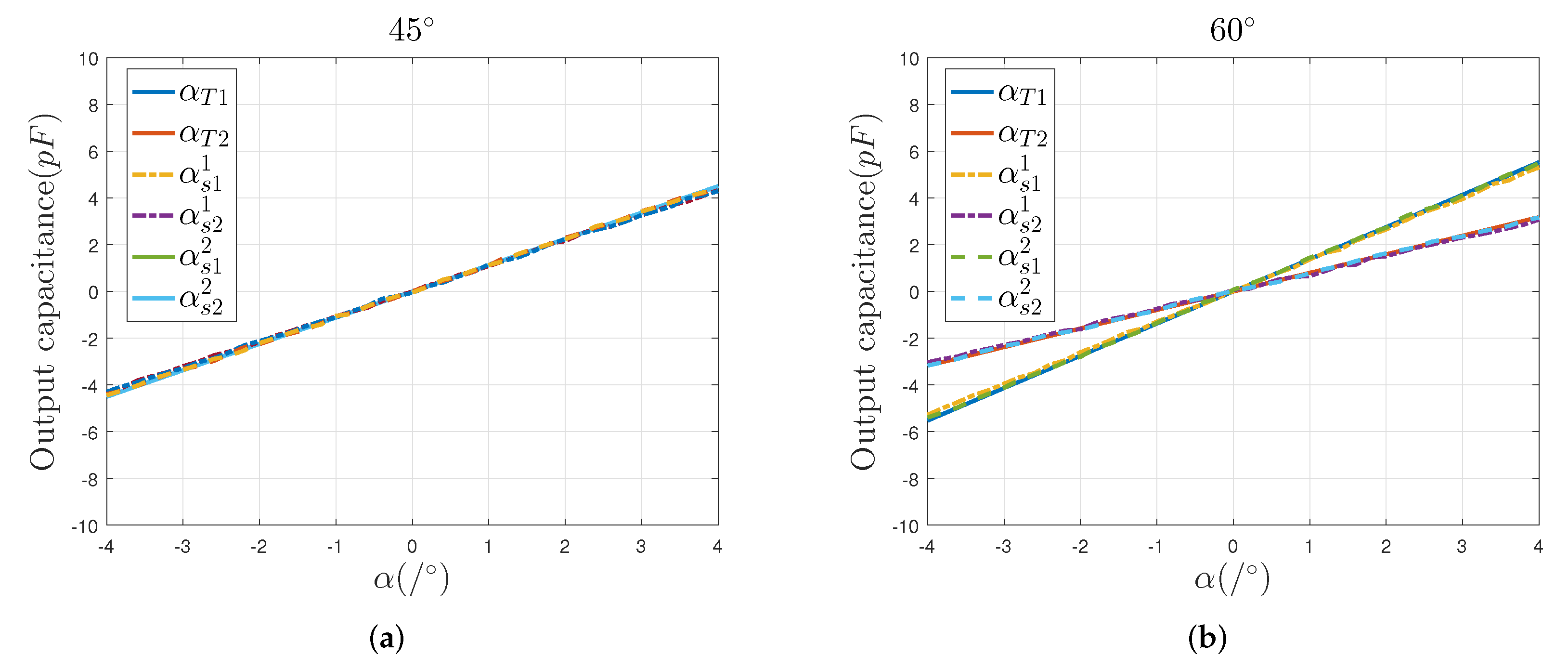
3.1. Finite Element Simulation and Analysis
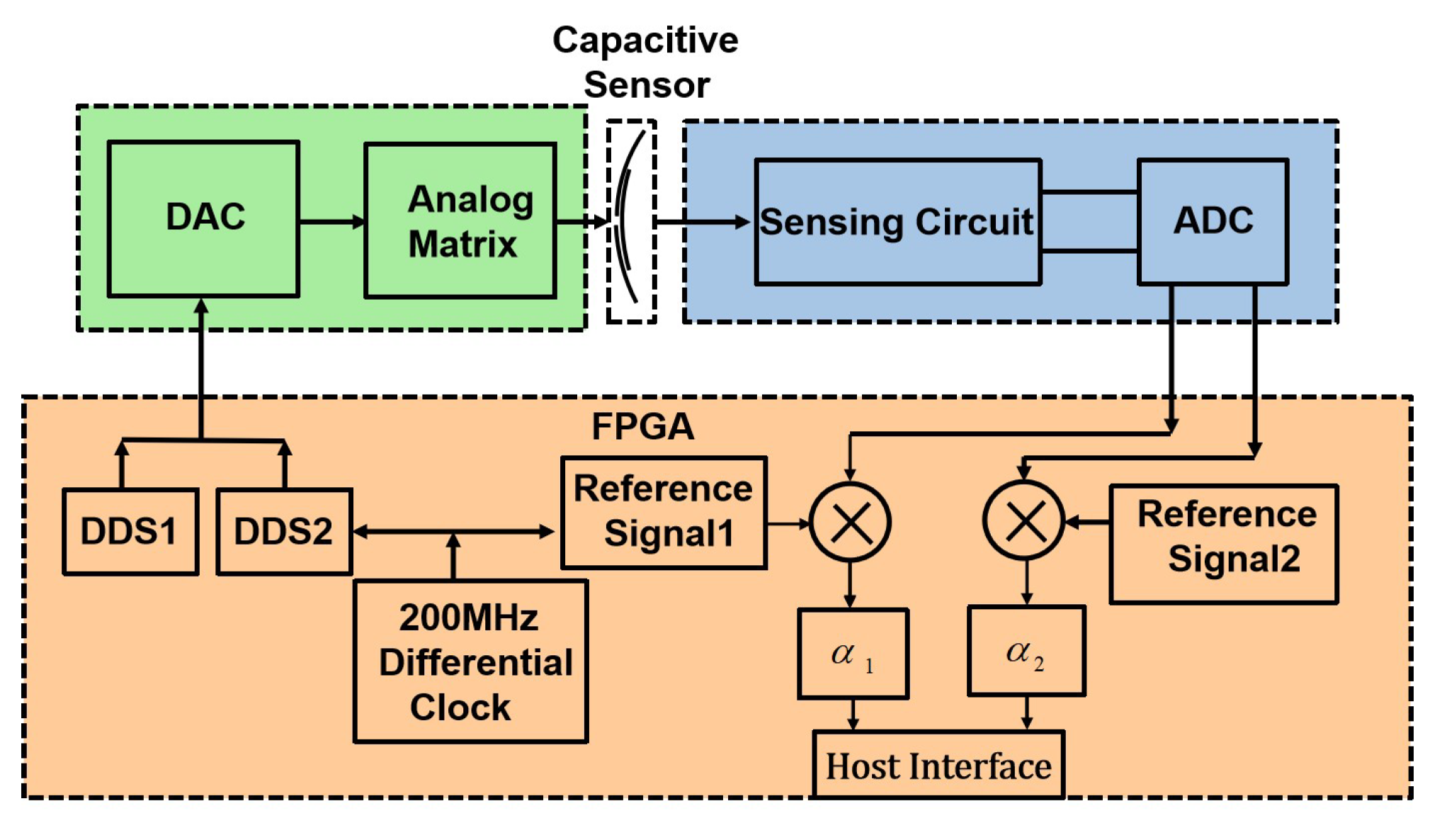
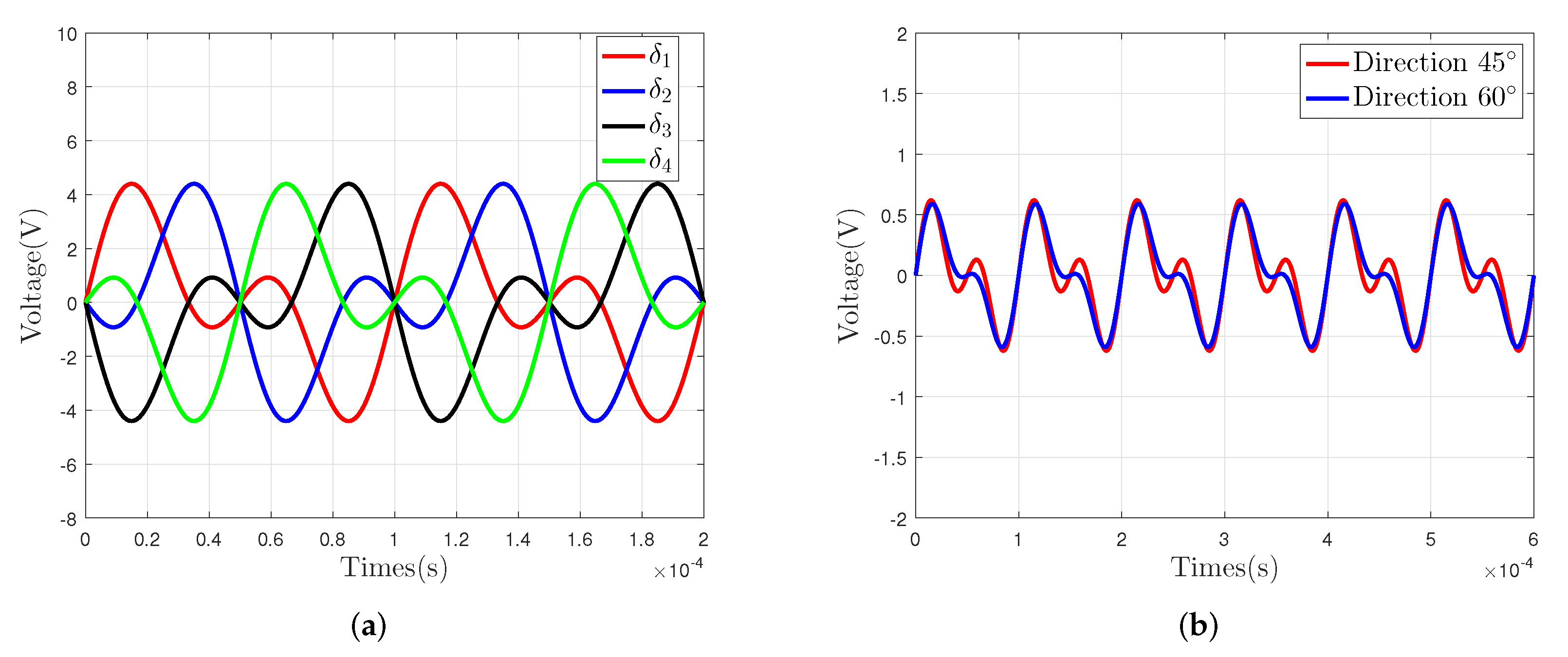
3.2. Signal Processing Circuit Simulation
4. Experimental Setup
5. Measurement Experiments
5.1. Signal Processing Circuit
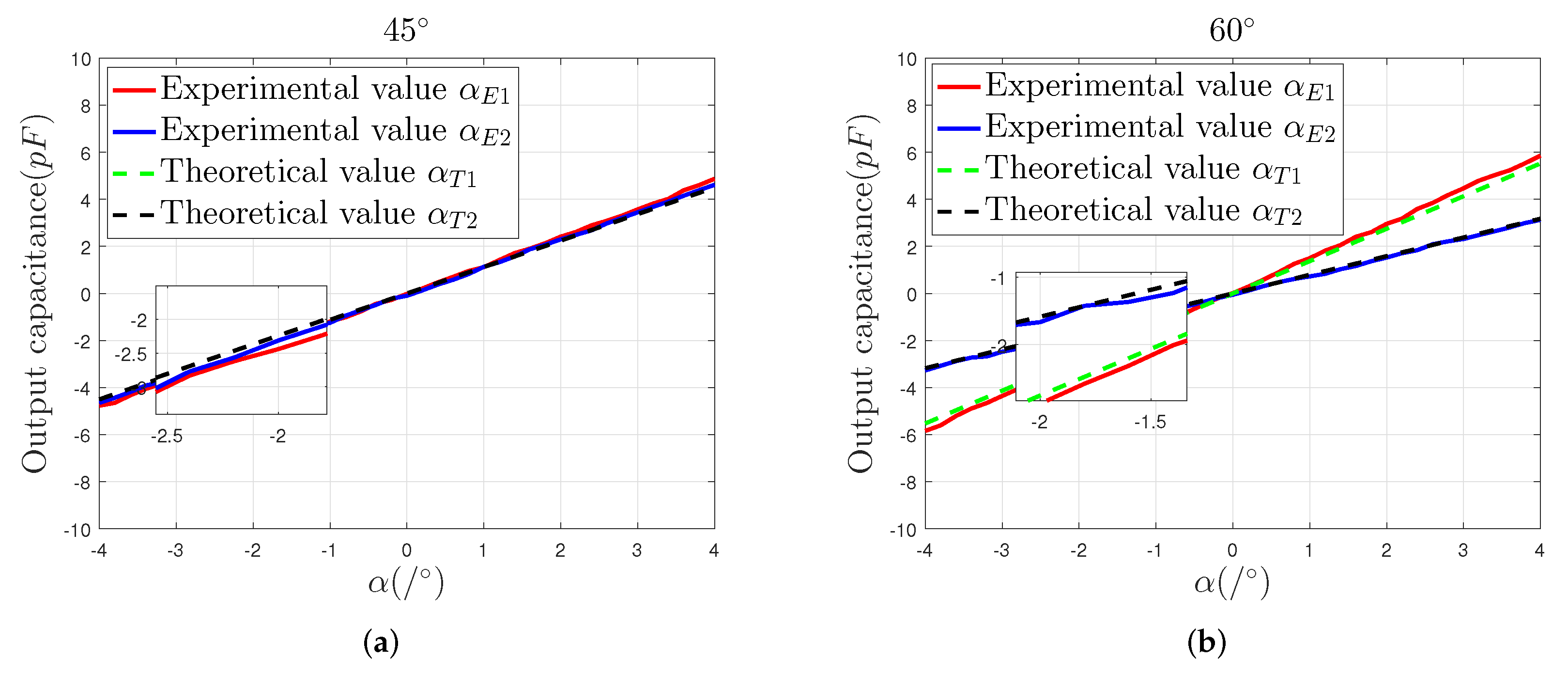
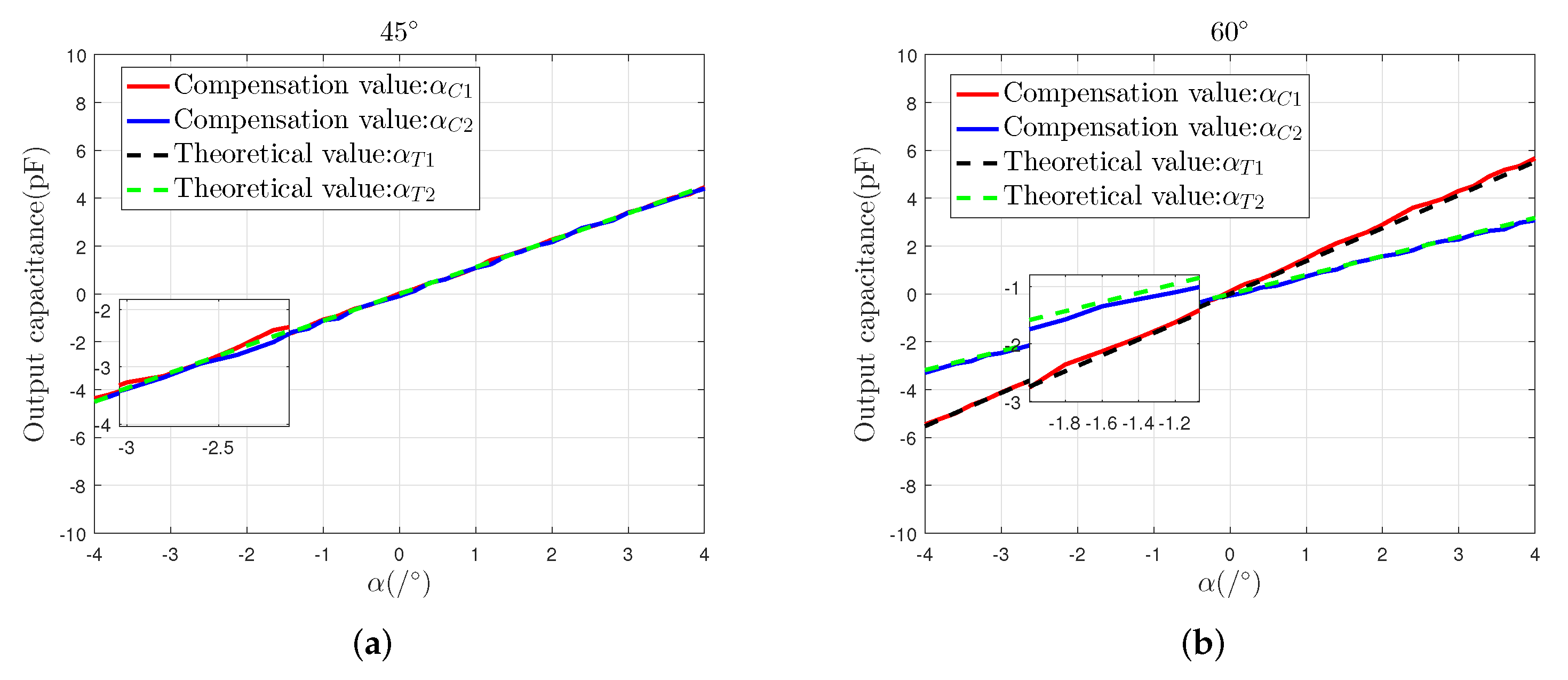
5.2. Angular Displacement Measurement
6. Conclusions
- Simulation and experimental results show that the mathematical model established, based on the differential four-quadrant electrode structure, can accurately predict the variation relationship between the 2-DOF angular displacement signal of the sensing electrode and the differential output capacitance;
- The signal processing circuit can decouple the components and of the 2-DOF angular displacement signal coupled in the differential capacitance signal into two voltage signals with different frequencies;
- Experimental results show that within the 2-DOF angular displacement range of , the results measured by the designed sensor system are up to of the theoretical results. In addition, the influence of common-mode noise can be effectively reduced through numerical compensation;
- The spherical capacitive sensor proposed in this study has an integrated structure. It can be integrated into the spherical pair, effectively avoiding the influence of accumulated installation errors on measurement accuracy. That is important for promoting the application of the spherical pair in aviation optoelectronic pods.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Leninger, B. Autonomous real-time ground ubiquitous surveillance-imaging system (ARGUS-IS). Proc. Spie Int. Soc. Opt. Eng. 2008, 6981, 69810H–69811H. [Google Scholar]
- Garner, H. Design and analysis of an absolute non-contact orientation sensor for wrist motion control. In Proceedings of the 2001 IEEE/ASME International Conference on Advanced Intelligent Mechatronics, Como, Italy, 8–12 July 2001; Volume 1, pp. 69–74. [Google Scholar]
- Lee, K.M.; Zhou, D. A real-time optical sensor for simultaneous measurement of three-DOF motions. IEEE/ASME Trans. Mech. 2004, 9, 499–507. [Google Scholar] [CrossRef]
- Lim, C.K. A novel approach for positional sensing of a spherical geometry. Sens. Actuators A Phys. 2011, 168, 328–334. [Google Scholar] [CrossRef]
- Wang, W. Design and Control of a Novel Spherical Permanent Magnet Actuator with Three Degrees of Freedom. IEEE/ASME Trans. Mechatron. 2003, 8, 457–468. [Google Scholar] [CrossRef]
- Foong, S. Harnessing Embedded Magnetic Fields for Angular Sensing With Nanodegree Accuracy. IEEE/ASME Trans. Mechatron. 2012, 17, 687–696. [Google Scholar] [CrossRef]
- Yang, W. Simulation and analysis of influence of magnetic field distribution in intelligent ball hinge. China Meas. Test 2017, 43, 130–133. [Google Scholar]
- Hu, P. Optimized design and accuracy improvement of intelligent ball hinge. Chin. J. Sci. Instrum. 2018, 39, 132–140. [Google Scholar]
- Hu, P. A New Modeling Method of Angle Measurement for Intelligent Ball Joint Based on BP-RBF Algorithm. Appl. Sci. 2019, 9, 2850. [Google Scholar] [CrossRef] [Green Version]
- Liao, P. Measurement of the Precision Spatial Rotation Angle of Ball Joint Based on Artificial Neural Network. Master’s Thesis, Hefei University of Technology, Hefei, China, 2018. [Google Scholar]
- Hu, P. Measurement method of rotation angle and clearance in intelligent spherical hinge. Meas. Sci. Technol. 2018, 29, 064012. [Google Scholar] [CrossRef]
- Hu, P. A New Method for Measuring the Rotational Angles of a Precision Spherical Joint Using Eddy Current Sensors. Sensors 2020, 20, 4020. [Google Scholar] [CrossRef] [PubMed]
- Wang, W. A Novel Approach for Detecting Rotational Angles of a Precision Spherical Joint Based on a Capacitive Sensor. Micromachines 2019, 10, 280. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zou, M. Fiber-Tip Polymer Clamped-Beam Probe for High-Sensitivity Nanoforce Measurements; LAM: Fremont, CA, USA, 2021; p. 10. [Google Scholar]
- Geng, Z. Review of Geometric Error Measurement and Compensation Techniques of Ultra-Precision Machine Tools; LAM: Fremont, CA, USA, 2021; p. 2. [Google Scholar]
- Ahn, H.-J. Nonlinear analysis of cylindrical capacitive sensor. Meas. Sci. Technol. 2005, 3, 699. [Google Scholar] [CrossRef]
- LI, X. The influence of electric-field bending on the nonlinearity of capacitive sensors. IEEE Trans. Instrum. Meas. 2000, 49, 256–259. [Google Scholar] [CrossRef] [Green Version]
- Kui, X. A T-Type Capacitive Sensor Capable of Measuring5-DOF Error Motions of Precision Spindles. Sensors 2017, 17, 1975. [Google Scholar]


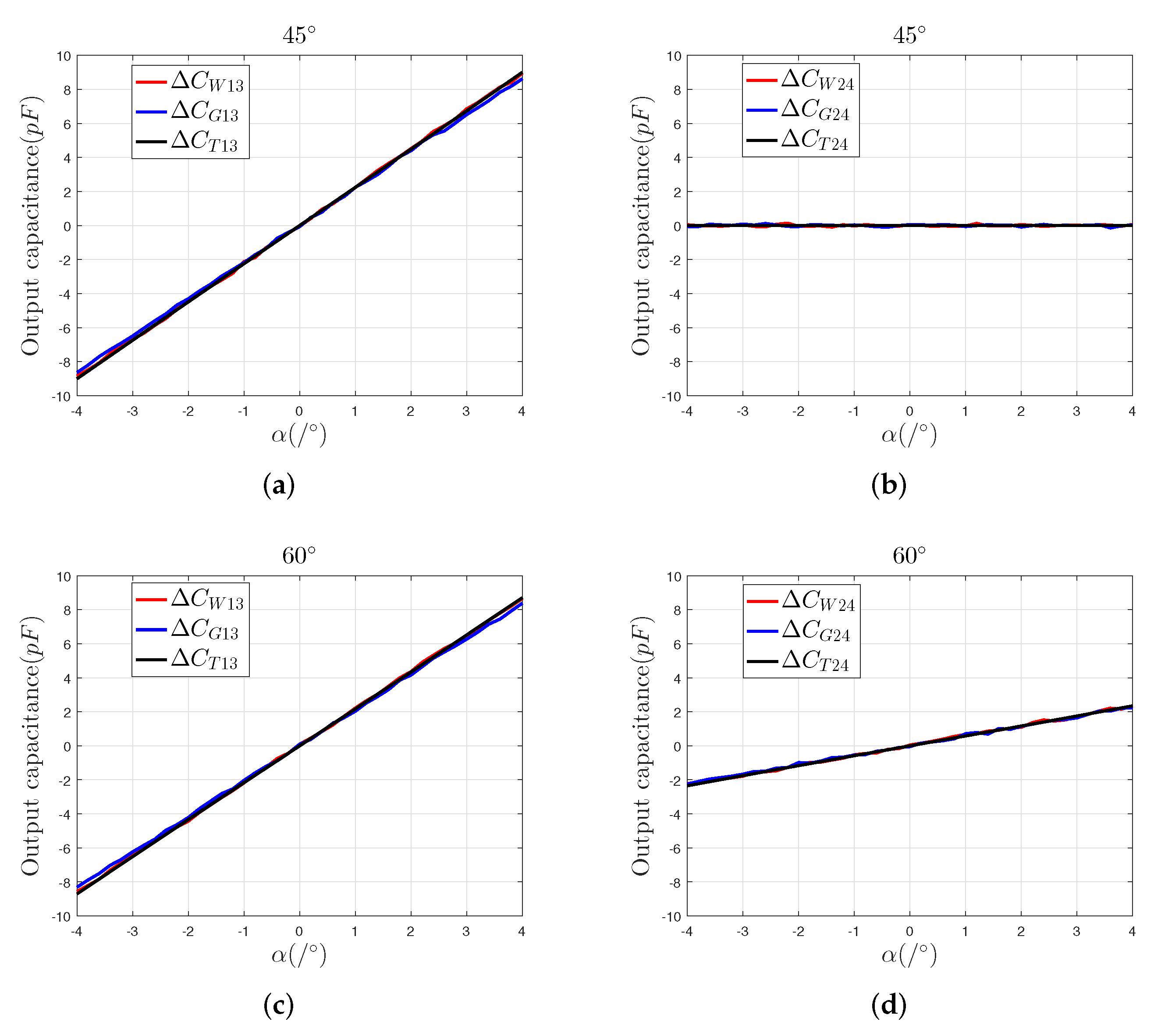



| Driving Electrode | Symbol | Value | Unit |
| The curvature radius | 127 | mm | |
| The projection circle radius | 50 | mm | |
| Thickness | 1 | um | |
| Sensing Electrode | Symbol | Value | Unit |
| Start angle | |||
| Stop angle | 4 | ||
| The curvature radius | R | 126 | mm |
| The projection circle radius | r | 40 | mm |
| Thickness | T | 1 | um |
| Spherical Electrode Dimensional Parameters | Dimension |
|---|---|
| The curvature radius of the driving electrode () | 127 mm |
| The curvature radius of the sensing electrode (R) | 126 mm |
| The projection circle radius of the driving electrode () | 50 mm |
| The projection circle radius of the sensing electrode (r) | 40 mm |
| The gap between the driving electrode and sensing electrode (d) | 1 mm |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, S.; Xu, Y.; Xu, Y.; Ma, T.; Wang, H.; Hou, J.; Liu, D.; Shen, H. A Novel Method for Detecting the Two-Degrees-of-Freedom Angular Displacement of a Spherical Pair, Based on a Capacitive Sensor. Sensors 2022, 22, 3437. https://doi.org/10.3390/s22093437
Yang S, Xu Y, Xu Y, Ma T, Wang H, Hou J, Liu D, Shen H. A Novel Method for Detecting the Two-Degrees-of-Freedom Angular Displacement of a Spherical Pair, Based on a Capacitive Sensor. Sensors. 2022; 22(9):3437. https://doi.org/10.3390/s22093437
Chicago/Turabian StyleYang, Shengqi, Yulei Xu, Yongsen Xu, Tianxiang Ma, Hao Wang, Jinghua Hou, Dachuan Liu, and Honghai Shen. 2022. "A Novel Method for Detecting the Two-Degrees-of-Freedom Angular Displacement of a Spherical Pair, Based on a Capacitive Sensor" Sensors 22, no. 9: 3437. https://doi.org/10.3390/s22093437
APA StyleYang, S., Xu, Y., Xu, Y., Ma, T., Wang, H., Hou, J., Liu, D., & Shen, H. (2022). A Novel Method for Detecting the Two-Degrees-of-Freedom Angular Displacement of a Spherical Pair, Based on a Capacitive Sensor. Sensors, 22(9), 3437. https://doi.org/10.3390/s22093437






