Machine Learning-Based View Synthesis in Fourier Lightfield Microscopy
Abstract
:1. Introduction
2. Materials and Methods
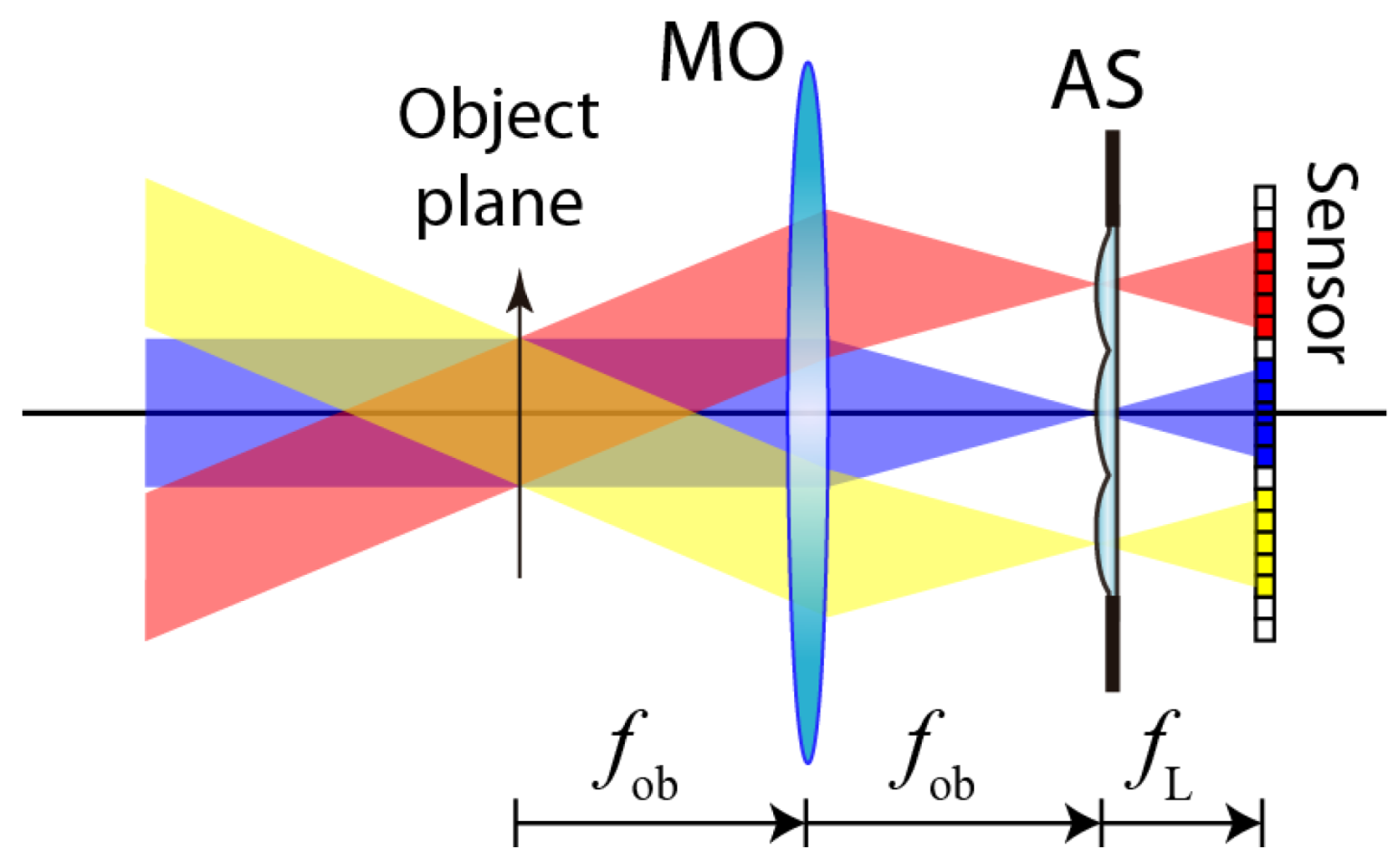
2.1. Fourier Lightfield Microscopy
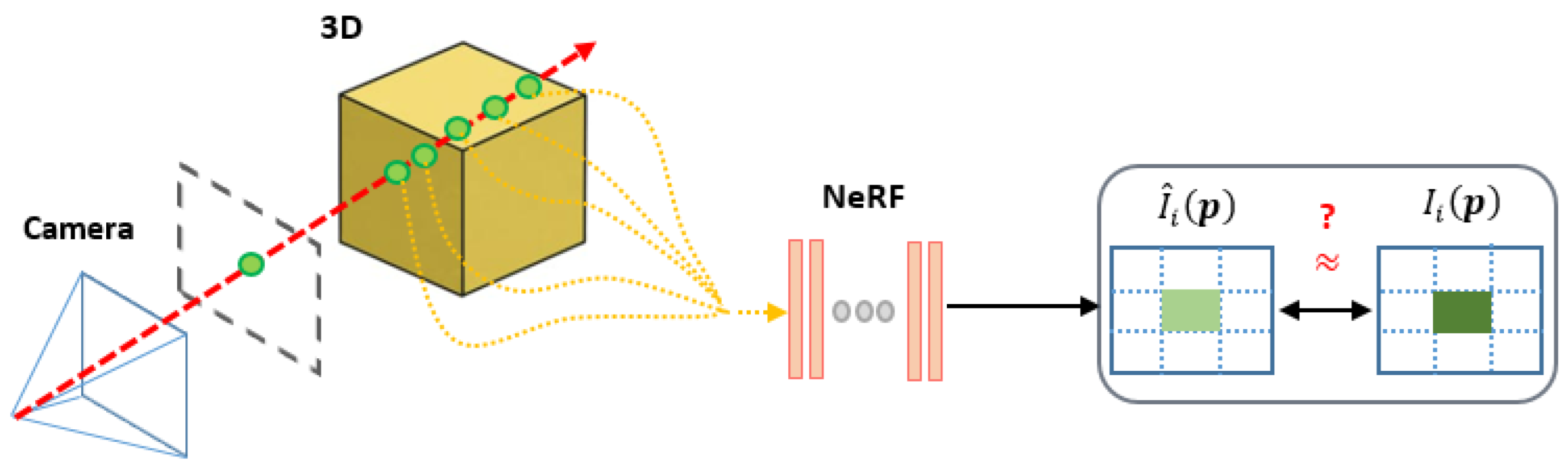
2.2. Neural Radiance Field, with Simultaneous Inference of Calibration Parameters
3. Results and Discussion
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| 3D | Three-dimensional |
| AS | Aperture stop |
| EI | Elemental image |
| FLMic | Fourier lightfield microscopy |
| IEP | Inferred extrinsic parameters |
| MLA | Microlens array |
| MLP | Multilayer perceptron |
| NeRF | Neural radiance field |
| NA | Numerical aperture |
| NVS | Novel view synthesis |
| PCB | Printed circuit board |
| R | Relay |
| SfM | Structure-from-motion |
| VR | Virtual reality |
References
- Landy, M.; Movshon, J.A. The Plenoptic Function and the Elements of Early Vision. Comput. Model. Vis. Process. 1991, 1, 3–20. [Google Scholar]
- Levoy, M.; Hanrahan, P. Light Field Rendering. In Proceedings of the 23rd Annual Conference on Computer Graphics and Interactive Techniques, SIGGRAPH’96, New Orleans, LA, USA, 4–9 August 1996; Association for Computing Machinery: New York, NY, USA, 1996; pp. 31–42. [Google Scholar] [CrossRef]
- Gortler, S.J.; Grzeszczuk, R.; Szeliski, R.; Cohen, M.F. The Lumigraph. In Proceedings of the 23rd Annual Conference on Computer Graphics and Interactive Techniques, SIGGRAPH’96, New Orleans, LA, USA, 4–9 August 1996; Association for Computing Machinery: New York, NY, USA, 1996; pp. 43–54. [Google Scholar] [CrossRef] [Green Version]
- Wang, H.; Yan, B.; Sang, X.; Chen, D.; Wang, P.; Qi, S.; Ye, X.; Guo, X. Dense view synthesis for three-dimensional light-field displays based on position-guiding convolutional neural network. Opt. Lasers Eng. 2022, 153, 106992. [Google Scholar] [CrossRef]
- Moreau, A.; Piasco, N.; Tsishkou, D.; Stanciulescu, B.; Fortelle, A.d.L. LENS: Localization enhanced by NeRF synthesis. In Proceedings of the 5th Conference on Robot Learning, London, UK, 8–11 November 2021; Volume 164, pp. 1347–1356. [Google Scholar]
- Martin-Brualla, R.; Radwan, N.; Sajjadi, M.S.M.; Barron, J.T.; Dosovitskiy, A.; Duckworth, D. NeRF in the Wild: Neural Radiance Fields for Unconstrained Photo Collections. In Proceedings of the 2021 Computer Vision and Pattern Recognition conference (CVPR), Online, 19–25 June 2021. [Google Scholar]
- Mildenhall, B.; Srinivasan, P.P.; Tancik, M.; Barron, J.T.; Ramamoorthi, R.; Ng, R. NeRF: Representing Scenes as Neural Radiance Fields for View Synthesis. Commun. ACM 2021, 65, 99–106. [Google Scholar] [CrossRef]
- Christen, M. Ray Tracing on GPU. Master’s Thesis, University of Applied Sciences Basel (FHBB), Basel, Switzerland, 19 January 2005. [Google Scholar]
- Schönberger, J.; Zheng, E.; Pollefeys, M.; Frahm, J.M. Pixelwise View Selection for Unstructured Multi-View Stereo. In Proceedings of the European Conference on Computer Vision (ECCV), Amsterdam, The Netherlands, 11–14 October 2016; Volume 9907. [Google Scholar] [CrossRef]
- Schönberger, J.L.; Frahm, J.M. Structure-from-Motion Revisited. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 4104–4113. [Google Scholar] [CrossRef]
- Niemeyer, M.; Barron, J.T.; Mildenhall, B.; Sajjadi, M.S.M.; Geiger, A.; Radwan, N. RegNeRF: Regularizing Neural Radiance Fields for View Synthesis from Sparse Inputs. arXiv 2021, arXiv:2112.00724. [Google Scholar]
- Müller, T.; Evans, A.; Schied, C.; Keller, A. Instant Neural Graphics Primitives with a Multiresolution Hash Encoding. arXiv 2022, arXiv:2201.05989. [Google Scholar]
- Yu, A.; Ye, V.; Tancik, M.; Kanazawa, A. pixelNeRF: Neural Radiance Fields from One or Few Images. In Proceedings of the 2021 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Nashville, TN, USA, 20–25 June 2021; pp. 4576–4585. [Google Scholar] [CrossRef]
- Pumarola, A.; Corona, E.; Pons-Moll, G.; Moreno-Noguer, F. D-NeRF: Neural Radiance Fields for Dynamic Scenes. In Proceedings of the 2021 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Nashville, TN, USA, 20–25 June 2021; pp. 10313–10322. [Google Scholar] [CrossRef]
- Wang, Z.; Wu, S.; Xie, W.; Chen, M.; Prisacariu, V. NeRF--: Neural Radiance Fields without Known Camera Parameters. arXiv 2021, arXiv:2102.07064. [Google Scholar]
- Llavador, A.; Sola-Pikabea, J.; Saavedra, G.; Javidi, B.; Martínez-Corral, M. Resolution improvements in integral microscopy with Fourier plane recording. Opt. Express 2016, 24, 20792–20798. [Google Scholar] [CrossRef] [Green Version]
- Scrofani, G.; Sola-Pikabea, J.; Llavador, A.; Sanchez-Ortiga, E.; Barreiro, J.C.; Saavedra, G.; Garcia-Sucerquia, J.; Martínez-Corral, M. FIMic: Design for ultimate 3D-integral microscopy of in-vivo biological samples. Biomed. Opt. Express 2018, 9, 335–346. [Google Scholar] [CrossRef]
- Guo, C.; Liu, W.; Hua, X.; Li, H.; Jia, S. Fourier light-field microscopy. Opt. Express 2019, 27, 25573–25594. [Google Scholar] [CrossRef]
- Scrofani, G.; Saavedra, G.; Martínez-Corral, M.; Sánchez-Ortiga, E. Three-dimensional real-time darkfield imaging through Fourier lightfield microscopy. Opt. Express 2020, 28, 30513–30519. [Google Scholar] [CrossRef]
- Hua, X.; Liu, W.; Jia, S. High-resolution Fourier light-field microscopy for volumetric multi-color live-cell imaging. Optica 2021, 8, 614–620. [Google Scholar] [CrossRef] [PubMed]
- Galdon, L.; Yun, H.; Saavedra, G.; Garcia-Sucerquia, J.; Barreiro, J.C.; Martinez-Corral, M.; Sanchez-Ortiga, E. Handheld and Cost-Effective Fourier Lightfield Microscope. Sensors 2022, 22, 1459. [Google Scholar] [CrossRef] [PubMed]
- Cong, L.; Wang, Z.; Chai, Y.; Hang, W.; Shang, C.; Yang, W.; Bai, L.; Du, J.; Wang, K.; Wen, Q. Rapid whole brain imaging of neural activity in freely behaving larval zebrafish (Danio rerio). Elife 2017, 6, e28158. [Google Scholar] [CrossRef] [PubMed]
- Yoon, Y.G.; Wang, Z.; Pak, N.; Park, D.; Dai, P.; Kang, J.S.; Suk, H.J.; Symvoulidis, P.; Guner-Ataman, B.; Wang, K.; et al. Sparse decomposition light-field microscopy for high speed imaging of neuronal activity. Optica 2020, 7, 1457–1468. [Google Scholar] [CrossRef]
- Sims, R.R.; Rehman, S.A.; Lenz, M.O.; Benaissa, S.I.; Bruggeman, E.; Clark, A.; Sanders, E.W.; Ponjavic, A.; Muresan, L.; Lee, S.F.; et al. Single molecule light field microscopy. Optica 2020, 7, 1065–1072. [Google Scholar] [CrossRef]
- Sánchez-Ortiga, E.; Scrofani, G.; Saavedra, G.; Martinez-Corral, M. Optical Sectioning Microscopy Through Single-Shot Lightfield Protocol. IEEE Access 2020, 8, 14944–14952. [Google Scholar] [CrossRef]
- Sánchez-Ortiga, E.; Llavador, A.; Saavedra, G.; García-Sucerquia, J.; Martínez-Corral, M. Optical sectioning with a Wiener-like filter in Fourier integral imaging microscopy. Appl. Phys. Lett. 2018, 113, 214101. [Google Scholar] [CrossRef]
- Stefanoiu, A.; Scrofani, G.; Saavedra, G.; Martínez-Corral, M.; Lasser, T. What about computational super-resolution in fluorescence Fourier light field microscopy? Opt. Express 2020, 28, 16554–16568. [Google Scholar] [CrossRef] [PubMed]
- Vizcaino, J.P.; Wang, Z.; Symvoulidis, P.; Favaro, P.; Guner-Ataman, B.; Boyden, E.S.; Lasser, T. Real-time light field 3D microscopy via sparsity-driven learned deconvolution. In Proceedings of the 2021 IEEE International Conference on Computational Photography (ICCP), Haifa, Israel, 23–25 May 2021; pp. 1–11. [Google Scholar]
- Levoy, M.; Ng, R.; Adams, A.; Footer, M.; Horowitz, M. Light Field Microscopy. ACM Trans. Graph. 2006, 25, 924–934. [Google Scholar] [CrossRef]
- Representing Scenes as Neural Radiance Fields for View Synthesis. Available online: https://www.matthewtancik.com/nerf (accessed on 16 March 2022).
- Broxton, M.; Grosenick, L.; Yang, S.; Cohen, N.; Andalman, A.; Deisseroth, K.; Levoy, M. Wave optics theory and 3-D deconvolution for the light field microscope. Opt. Express 2013, 21, 25418–25439. [Google Scholar] [CrossRef] [PubMed]



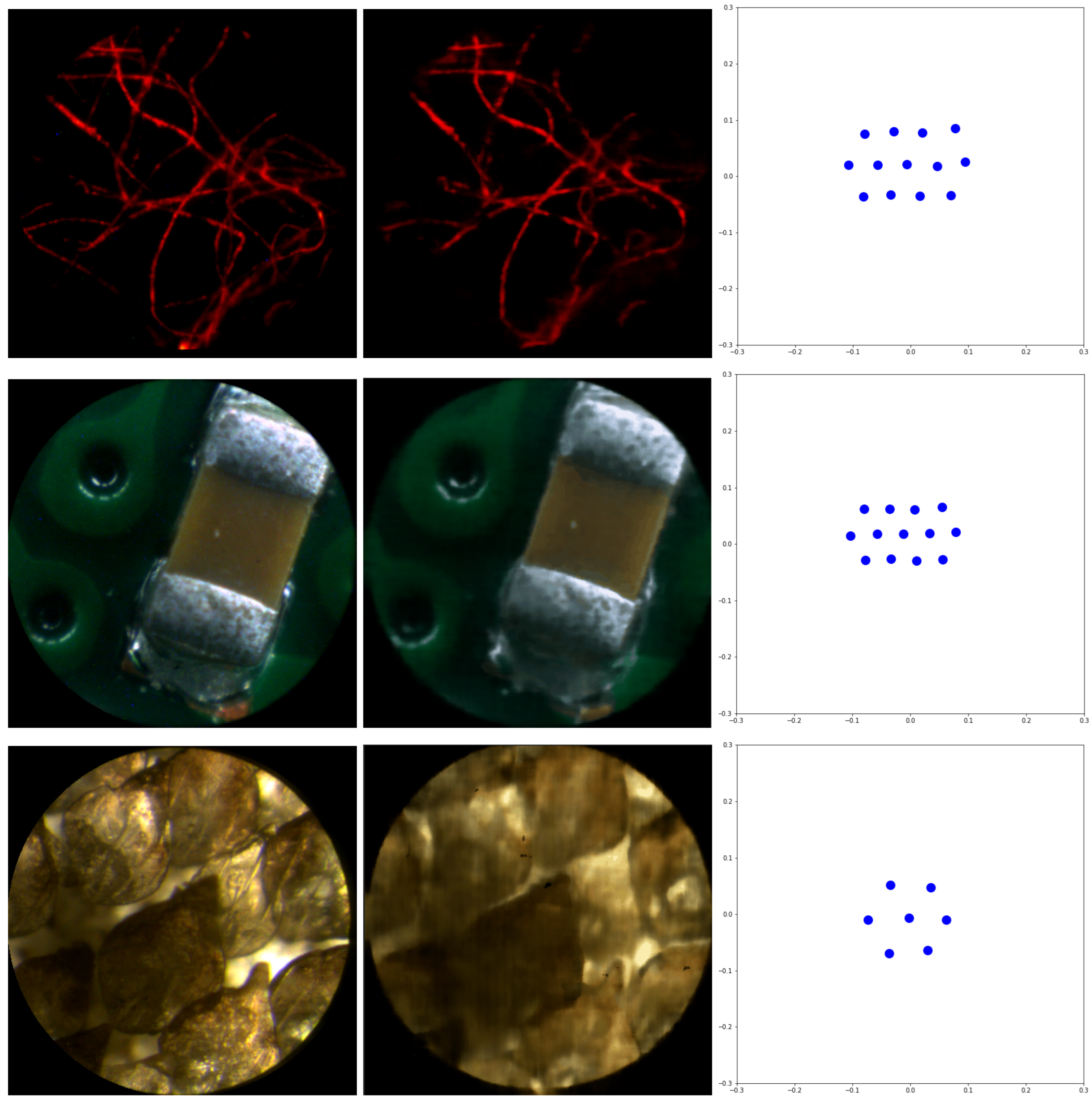

| Sample | MO | fR1 | NEI | Illumination Type |
|---|---|---|---|---|
| fiber | 10×/0.45 | 200 mm | 9 | Epi-Fluorescence |
| chip | 10×/0.45 | 200 mm | 9 | Epi-Reflection |
| shark | 20×/0.40 | 180 mm | 4 | Brightfield |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rostan, J.; Incardona, N.; Sanchez-Ortiga, E.; Martinez-Corral, M.; Latorre-Carmona, P. Machine Learning-Based View Synthesis in Fourier Lightfield Microscopy. Sensors 2022, 22, 3487. https://doi.org/10.3390/s22093487
Rostan J, Incardona N, Sanchez-Ortiga E, Martinez-Corral M, Latorre-Carmona P. Machine Learning-Based View Synthesis in Fourier Lightfield Microscopy. Sensors. 2022; 22(9):3487. https://doi.org/10.3390/s22093487
Chicago/Turabian StyleRostan, Julen, Nicolo Incardona, Emilio Sanchez-Ortiga, Manuel Martinez-Corral, and Pedro Latorre-Carmona. 2022. "Machine Learning-Based View Synthesis in Fourier Lightfield Microscopy" Sensors 22, no. 9: 3487. https://doi.org/10.3390/s22093487
APA StyleRostan, J., Incardona, N., Sanchez-Ortiga, E., Martinez-Corral, M., & Latorre-Carmona, P. (2022). Machine Learning-Based View Synthesis in Fourier Lightfield Microscopy. Sensors, 22(9), 3487. https://doi.org/10.3390/s22093487








