Design, Fabrication and Characterisation of Multi-Parameter Optical Sensors Dedicated to E-Skin Applications
Abstract
:1. Introduction
2. Waveguide Operation
3. Materials and Methods
4. Results
4.1. Waveguide Characterisation
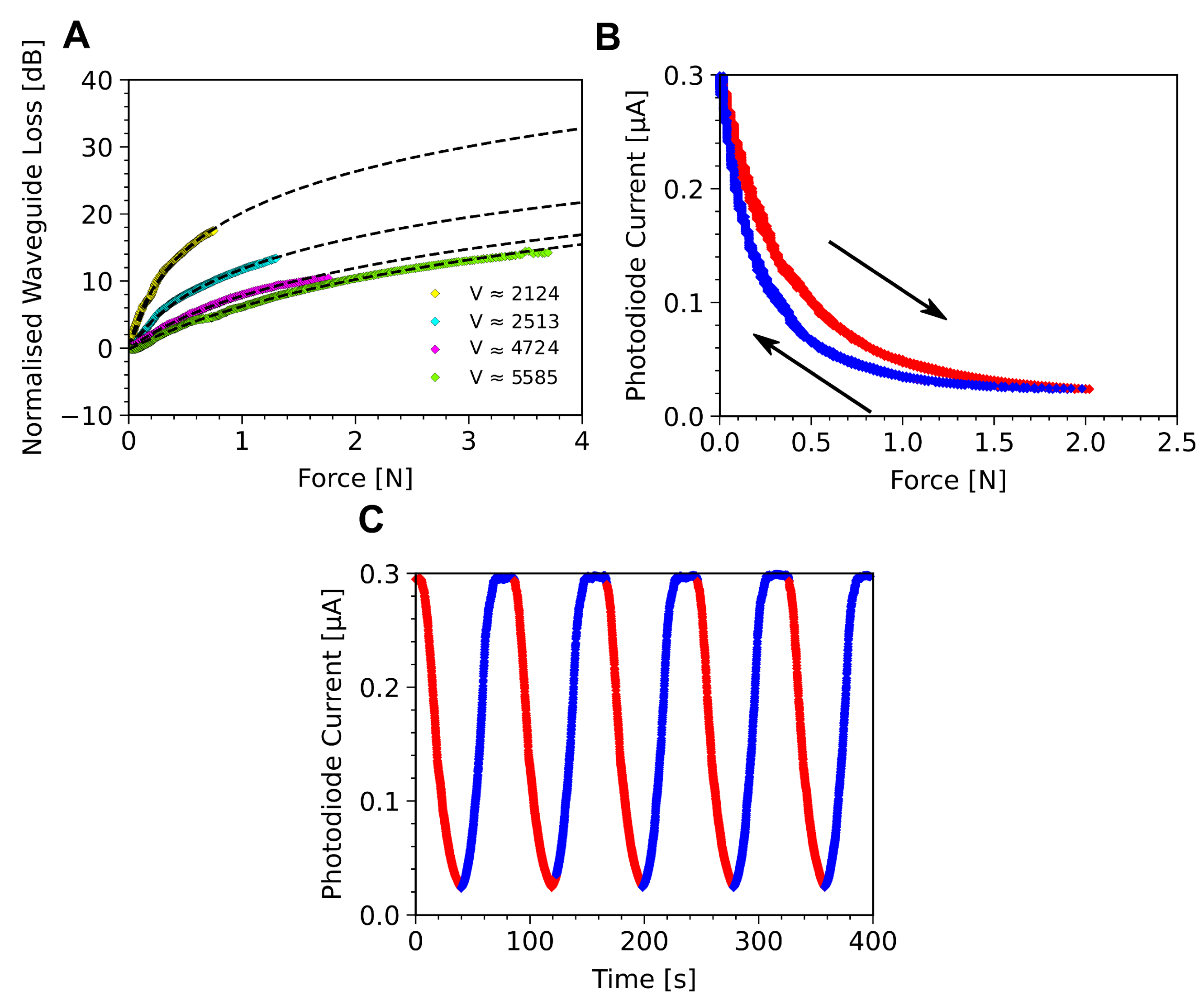
4.2. Compression Force Sensor Characterisation
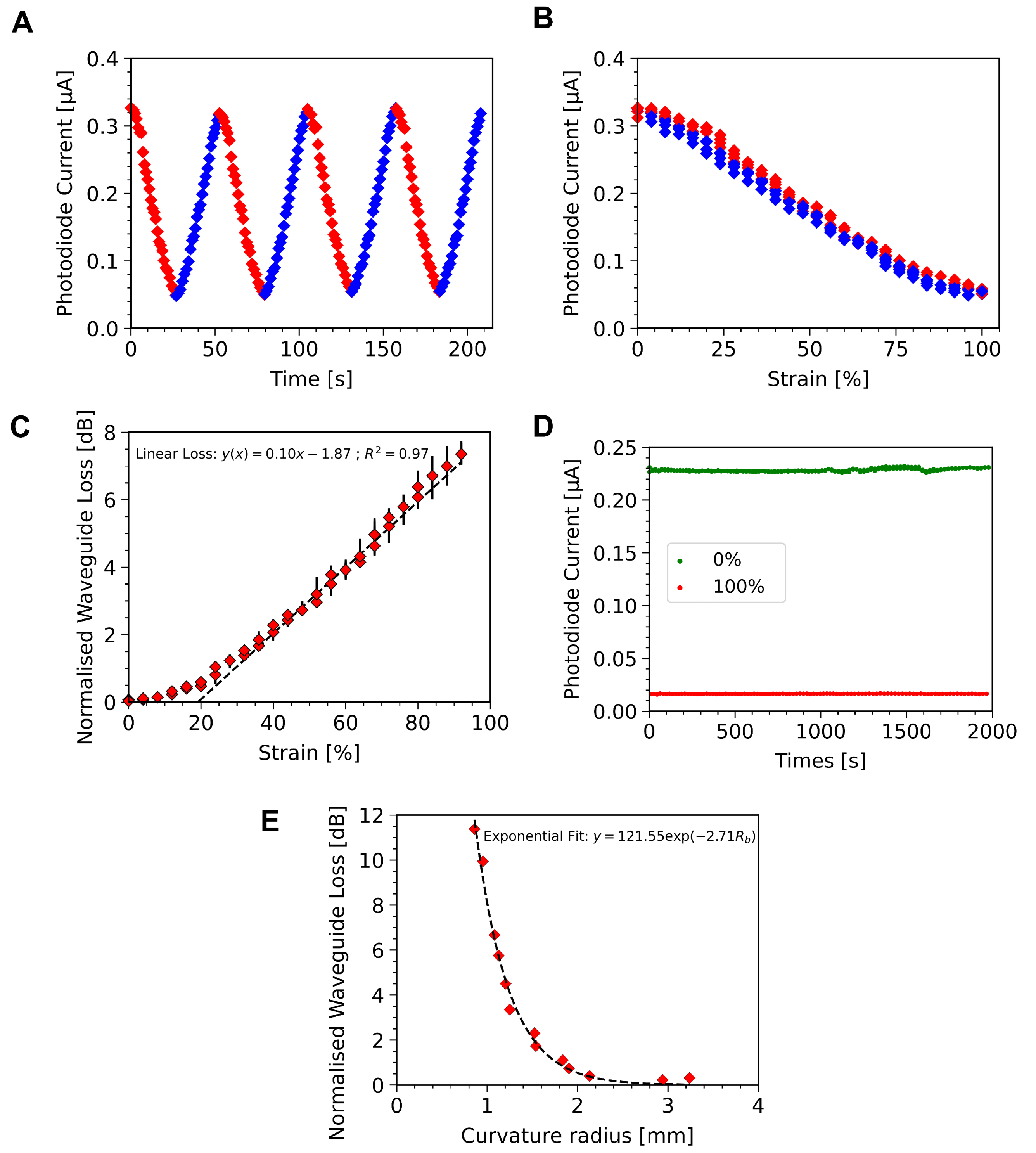
4.3. Strain Sensor Characterisation
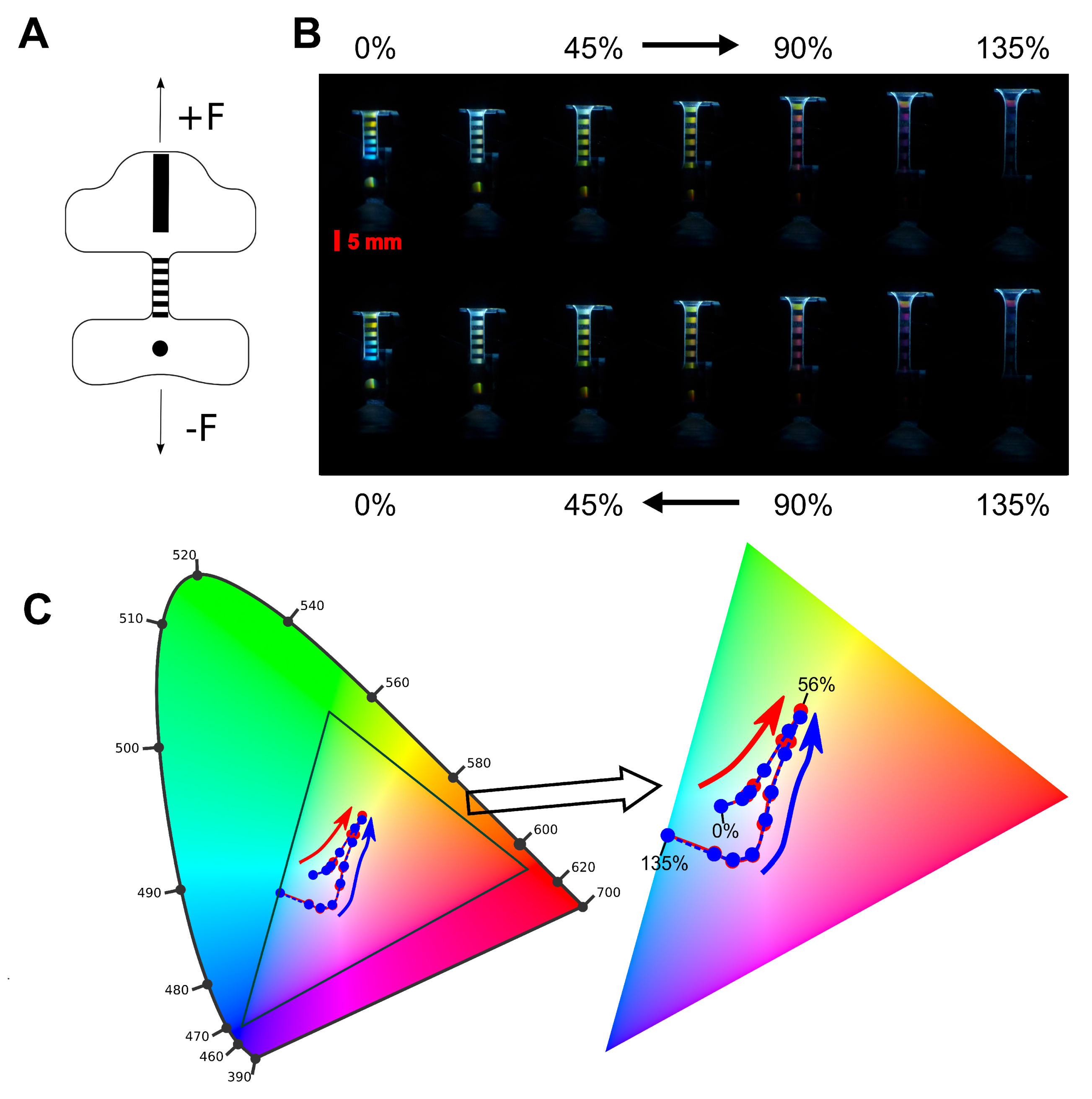
4.4. Colourimetry Strain Sensor Characterisation
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Waveguide Fabrication
Appendix B. Waveguide Characterisation
References
- García Núñez, C.; Manjakkal, L.; Dahiya, R. Energy autonomous electronic skin. Npj Flex. Electron. 2019, 3, 1. [Google Scholar] [CrossRef]
- Kim, C.Y.; Ku, M.J.; Qazi, R.; Nam, H.J.; Park, J.W.; Nam, K.S.; Oh, S.; Kang, I.; Jang, J.H.; Kim, W.Y.; et al. Soft subdermal implant capable of wireless battery charging and programmable controls for applications in optogenetics. Nat. Commun. 2021, 12, 535. [Google Scholar] [CrossRef] [PubMed]
- Zhao, P.; Li, B.; Tang, Z.; Gao, Y.; Tian, H.; Chen, H. Stretchable photonic crystals with periodic cylinder shaped air holes for improving mechanochromic performance. Smart Mater. Struct. 2019, 28, 075037. [Google Scholar] [CrossRef]
- Sontheimer, R.D. Skin Is Not the Largest Organ. J. Investig. Dermatol. 2014, 134, 581–582. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Peng, Y.; Yang, N.; Xu, Q.; Dai, Y.; Wang, Z. Recent Advances in Flexible Tactile Sensors for Intelligent Systems. Sensors 2021, 21, 5392. [Google Scholar] [CrossRef]
- Fastier-Wooller, J.W.; Dau, V.T.; Dinh, T.; Tran, C.D.; Dao, D.V. Pressure and temperature sensitive e-skin for in situ robotic applications. Mater. Des. 2021, 208, 109886. [Google Scholar] [CrossRef]
- Li, M.; Liang, J.; Wang, X.; Zhang, M. Ultra-Sensitive Flexible Pressure Sensor Based on Microstructured Electrode. Sensors 2020, 20, 371. [Google Scholar] [CrossRef] [Green Version]
- Poeggel, S.; Tosi, D.; Duraibabu, D.; Leen, G.; McGrath, D.; Lewis, E. Optical Fibre Pressure Sensors in Medical Applications. Sensors 2015, 15, 17115–17148. [Google Scholar] [CrossRef] [Green Version]
- Roriz, P.; Frazão, O.; Lobo-Ribeiro, A.B.; Santos, J.L.; Simões, J.A. Review of fiber-optic pressure sensors for biomedical and biomechanical applications. J. Biomed. Opt. 2013, 18, 050903. [Google Scholar] [CrossRef] [Green Version]
- Torrijos-Morán, L.; Lisboa, B.D.; Soler, M.; Lechuga, L.M.; García-Rupérez, J. Integrated optical bimodal waveguide biosensors: Principles and applications. Results Opt. 2022, 9, 100285. [Google Scholar] [CrossRef]
- Quan, Y.J.; Kim, Y.G.; Kim, M.S.; Min, S.H.; Ahn, S.H. Stretchable Biaxial and Shear Strain Sensors Using Diffractive Structural Colors. ACS Nano 2020, 14, 5392–5399. [Google Scholar] [CrossRef]
- Ranade, S.; Syeda, R.; Patapoutian, A. Mechanically Activated Ion Channels. Neuron 2015, 87, 1162–1179. [Google Scholar] [CrossRef] [Green Version]
- Yang, W.; Sherman, V.R.; Gludovatz, B.; Schaible, E.; Stewart, P.; Ritchie, R.O.; Meyers, M.A. On the tear resistance of skin. Nat. Commun. 2015, 6, 6649. [Google Scholar] [CrossRef] [Green Version]
- Trung, T.Q.; Lee, N.E. Flexible and Stretchable Physical Sensor Integrated Platforms for Wearable Human-Activity Monitoringand Personal Healthcare. Adv. Mater. 2016, 28, 4338–4372. [Google Scholar] [CrossRef]
- Kwok, S.J.J.; Forward, S.; Wertheimer, C.M.; Liapis, A.C.; Kim, M.; Seiler, T.G.; Birngruber, R.; Kochevar, I.E.; Yun, S.H. Selective Equatorial Sclera Crosslinking in the Orbit Using a Metal-Coated Polymer Waveguide. Investig. Ophthalmol. Vis. Sci. 2019, 60, 2563–2570. [Google Scholar] [CrossRef] [Green Version]
- Heiden, A.; Preninger, D.; Lehner, L.; Baumgartner, M.; Drack, M.; Woritzka, E.; Schiller, D.; Gerstmayr, R.; Hartmann, F.; Kaltenbrunner, M. 3D printing of resilient biogels for omnidirectional and exteroceptive soft actuators. Sci. Robot. 2022, 7, eabk2119. [Google Scholar] [CrossRef]
- Guo, J.; Liu, X.; Jiang, N.; Yetisen, A.K.; Yuk, H.; Yang, C.; Khademhosseini, A.; Zhao, X.; Yun, S.H. Highly Stretchable, Strain Sensing Hydrogel Optical Fibers. Adv. Mater. 2016, 28, 10244–10249. [Google Scholar] [CrossRef]
- Huang, Z.; Hao, Y.; Li, Y.; Hu, H.; Wang, C.; Nomoto, A.; Pan, T.; Gu, Y.; Chen, Y.; Zhang, T.; et al. Three-dimensional integrated stretchable electronics. Nat. Electron. 2018, 1, 473–480. [Google Scholar] [CrossRef]
- Sekitani, T.; Noguchi, Y.; Hata, K.; Fukushima, T.; Aida, T.; Someya, T. A Rubberlike Stretchable Active Matrix Using Elastic Conductors. Science 2008, 321, 1468–1472. [Google Scholar] [CrossRef] [Green Version]
- Li, L.; Lin, H.; Qiao, S.; Huang, Y.Z.; Li, J.Y.; Michon, J.; Gu, T.; Alosno-Ramos, C.; Vivien, L.; Yadav, A.; et al. Monolithically integrated stretchable photonics. Light Sci. Appl. 2018, 7, 17138. [Google Scholar] [CrossRef]
- Yu, X. Skin-integrated wireless haptic interfaces for virtual and augmented reality. Nature 2019, 575, 473–479. [Google Scholar] [CrossRef] [PubMed]
- Kim, R.H.; Kim, D.H.; Xiao, J.; Kim, B.H.; Park, S.I.; Panilaitis, B.; Ghaffari, R.; Yao, J.; Li, M.; Liu, Z.; et al. Waterproof AlInGaP optoelectronics on stretchable substrates with applications in biomedicine and robotics. Nat. Mater. 2010, 9, 929–937. [Google Scholar] [CrossRef] [PubMed]
- Kim, H.J.; Sim, K.; Thukral, A.; Yu, C. Rubbery electronics and sensors from intrinsically stretchable elastomeric composites of semiconductors and conductors. Sci. Adv. 2017, 3, e1701114. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Boutry, C.M.; Negre, M.; Jorda, M.; Vardoulis, O.; Chortos, A.; Khatib, O.; Bao, Z. A hierarchically patterned, bioinspired e-skin able to detect the direction of applied pressure for robotics. Sci. Robot. 2018, 3, eaau6914. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Z.; Zhao, L.; Shi, J. Mechanics and Strategies for Wrinkling Suppression: A Review. Front. Mech. Eng. 2022, 8, 910415. [Google Scholar] [CrossRef]
- Byun, S.H.; Sim, J.; Agno, K.C.; Jeong, J.W. Materials and manufacturing strategies for mechanically transformative electronics. Mater. Today Adv. 2020, 7, 100089. [Google Scholar] [CrossRef]
- Shibata, Y.; Nishimura, A.; Niwa, S.; Osawa, Y.; Uemiya, T. Optical Sensors. U.S. Patent 4,750,796, 14 June 1988. [Google Scholar]
- Cai, D.; Neyer, A.; Kuckuk, R.; Heise, H. Optical absorption in transparent PDMS materials applied for multimode waveguides fabrication. Opt. Mater. 2008, 30, 1157–1161. [Google Scholar] [CrossRef]
- Huang, C.S.; Pun, E.Y.B.; Wang, W.C. Fabrication of an elastomeric rib waveguide Bragg grating filter. J. Opt. Soc. Am. B 2009, 26, 1256. [Google Scholar] [CrossRef]
- Kruse, K.; Middlebrook, C.T. Polymer taper bridge for silicon waveguide to single mode waveguide coupling. Opt. Commun. 2016, 362, 87–95. [Google Scholar] [CrossRef]
- Gan, X.; Pervez, N.; Kymissis, I.; Hatami, F.; Englund, D. A high-resolution spectrometer based on a compact planar two dimensional photonic crystal cavity array. Appl. Phys. Lett. 2012, 100, 231104. [Google Scholar] [CrossRef]
- Peng, W.; Liao, Q.; Song, H. A nanograting-based flexible and stretchable waveguide for tactile sensing. Nanoscale Res. Lett. 2021, 16, 23. [Google Scholar] [CrossRef]
- Li, H.W.; Kang, D.J.; Blamire, M.G.; Huck, W.T.S. Focused ion beam fabrication of silicon print masters. Nanotechnology 2003, 14, 220–223. [Google Scholar] [CrossRef]
- Quan, Y.J.; Kim, M.S.; Kim, Y.; Ahn, S.H. Colour-tunable 50% strain sensor using surface-nanopatterning of soft materials via nanoimprinting with focused ion beam milling process. CIRP Ann. 2019, 68, 595–598. [Google Scholar] [CrossRef]
- De Sio, L.; Cuennet, J.G.; Vasdekis, A.E.; Psaltis, D. All-optical switching in an optofluidic polydimethylsiloxane: Liquid crystal grating defined by cast-molding. Appl. Phys. Lett. 2010, 96, 131112. [Google Scholar] [CrossRef] [Green Version]
- Guo, H.; Tang, J.; Qian, K.; Tsoukalas, D.; Zhao, M.; Yang, J.; Zhang, B.; Chou, X.; Liu, J.; Xue, C.; et al. Vectorial strain gauge method using single flexible orthogonal polydimethylsiloxane gratings. Sci. Rep. 2016, 6, 23606. [Google Scholar] [CrossRef] [Green Version]
- Mohapatra, S.; Moirangthem, R.S. Fabrication of flexible and economical plasmonic biosensor using gold nanograting imprinted on hot-melt adhesive film for label-free sensing of immunoglobulin proteins. Sens. Actuators B Chem. 2019, 301, 127070. [Google Scholar] [CrossRef]
- Wu, C.; Chin, C.S.M.; Huang, Q.; Chan, H.Y.; Yu, X.; Roy, V.A.L.; Li, W.J. Rapid nanomolding of nanotopography on flexible substrates to control muscle cell growth with enhanced maturation. Microsyst. Nanoeng. 2021, 7, 89. [Google Scholar] [CrossRef]
- Park, S.; Heo, S.W.; Lee, W.; Inoue, D.; Jiang, Z.; Yu, K.; Jinno, H.; Hashizume, D.; Sekino, M.; Yokota, T.; et al. Self-powered ultra-flexible electronics via nano-grating-patterned organic photovoltaics. Nature 2018, 561, 516–521. [Google Scholar] [CrossRef]
- Okamoto, K. Fundamentals of Optical Waveguides, 2nd ed.; Elsevier: Amsterdam, The Netherlands; Boston, MA, USA, 2006. [Google Scholar]
- Santiago-Alvarado, A.; Cruz-Félix, A.S.; González-García, J.; Sánchez-López, O.; Mendoza-Jasso, A.J.; Hernández-Castillo, I. Polynomial fitting techniques applied to opto-mechanical properties of PDMS Sylgard 184 for given curing parameters. Mater. Res. Express 2020, 7, 045301. [Google Scholar] [CrossRef]
- Johnston, I.D.; McCluskey, D.K.; Tan, C.K.L.; Tracey, M.C. Mechanical characterization of bulk Sylgard 184 for microfluidics and microengineering. J. Micromech. Microeng. 2014, 24, 035017. [Google Scholar] [CrossRef]
- Peng, W.; Wu, H. Flexible and Stretchable Photonic Sensors Based on Modulation of Light Transmission. Adv. Opt. Mater. 2019, 7, 1900329. [Google Scholar] [CrossRef]
- Ramuz, M.; Tee, B.C.K.; Tok, J.B.H.; Bao, Z. Transparent, Optical, Pressure-Sensitive Artificial Skin for Large-Area Stretchable Electronics. Adv. Mater. 2012, 24, 3223–3227. [Google Scholar] [CrossRef] [PubMed]
- Chapter 1—Physical Characteristics of CD and DVD Media. In CD and DVD Forensics; Crowley, P.; Kleiman, D. (Eds.) Syngress: Burlington, VT, USA, 2006; pp. 1–28. [Google Scholar] [CrossRef]
- Azmayesh-Fard, S.M.; Flaim, E.; McMullin, J.N. PDMS biochips with integrated waveguides. J. Micromech. Microeng. 2010, 20, 087002. [Google Scholar] [CrossRef]
- Vaicekauskaite, J.; Mazurek, P.; Vudayagiri, S.; Skov, A.L. Mapping the mechanical and electrical properties of commercial silicone elastomer formulations for stretchable transducers. J. Mater. Chem. C 2020, 8, 1273–1279. [Google Scholar] [CrossRef]
- Levi, A.; Piovanelli, M.; Furlan, S.; Mazzolai, B.; Beccai, L. Soft, Transparent, Electronic Skin for Distributed and Multiple Pressure Sensing. Sensors 2013, 13, 6578–6604. [Google Scholar] [CrossRef] [Green Version]
- Kodl, G. A new optical waveguide pressure sensor using evanescent field. In Proceedings of the 2004 Proceedings. 54th Electronic Components and Technology Conference (IEEE Cat. No.04CH37546), Las Vegas, NV, USA, 4 June 2004; Volume 2, pp. 1943–1946. [Google Scholar] [CrossRef]
- Petermann, K. Fundamental mode microbending loss in graded-index and W fibres. Opt. Quant. Electron. 1977, 9, 167–175. [Google Scholar] [CrossRef]
- Zhao, H.; O’Brien, K.; Li, S.; Shepherd, R.F. Optoelectronically innervated soft prosthetic hand via stretchable optical waveguides. Sci. Robot. 2016, 1, eaai7529. [Google Scholar] [CrossRef] [Green Version]
- Bai, H.; Li, S.; Barreiros, J.; Tu, Y.; Pollock, C.R.; Shepherd, R.F. Stretchable distributed fiber-optic sensors. Science 2020, 370, 848–852. [Google Scholar] [CrossRef]
- Marcatili, E.A.J. Bends in Optical Dielectric Guides. Bell Syst. Tech. J. 1969, 48, 2103–2132. [Google Scholar] [CrossRef]
- Mutlu, R.; Alici, G.; in het Panhuis, M.; Spinks, G.M. 3D Printed Flexure Hinges for Soft Monolithic Prosthetic Fingers. Soft Robot. 2016, 3, 120–133. [Google Scholar] [CrossRef]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fliegans, L.; Troughton, J.; Divay, V.; Blayac, S.; Ramuz, M. Design, Fabrication and Characterisation of Multi-Parameter Optical Sensors Dedicated to E-Skin Applications. Sensors 2023, 23, 114. https://doi.org/10.3390/s23010114
Fliegans L, Troughton J, Divay V, Blayac S, Ramuz M. Design, Fabrication and Characterisation of Multi-Parameter Optical Sensors Dedicated to E-Skin Applications. Sensors. 2023; 23(1):114. https://doi.org/10.3390/s23010114
Chicago/Turabian StyleFliegans, Lionel, Joseph Troughton, Valentin Divay, Sylvain Blayac, and Marc Ramuz. 2023. "Design, Fabrication and Characterisation of Multi-Parameter Optical Sensors Dedicated to E-Skin Applications" Sensors 23, no. 1: 114. https://doi.org/10.3390/s23010114
APA StyleFliegans, L., Troughton, J., Divay, V., Blayac, S., & Ramuz, M. (2023). Design, Fabrication and Characterisation of Multi-Parameter Optical Sensors Dedicated to E-Skin Applications. Sensors, 23(1), 114. https://doi.org/10.3390/s23010114





