Discovering Key Sub-Trajectories to Explain Traffic Prediction
Abstract
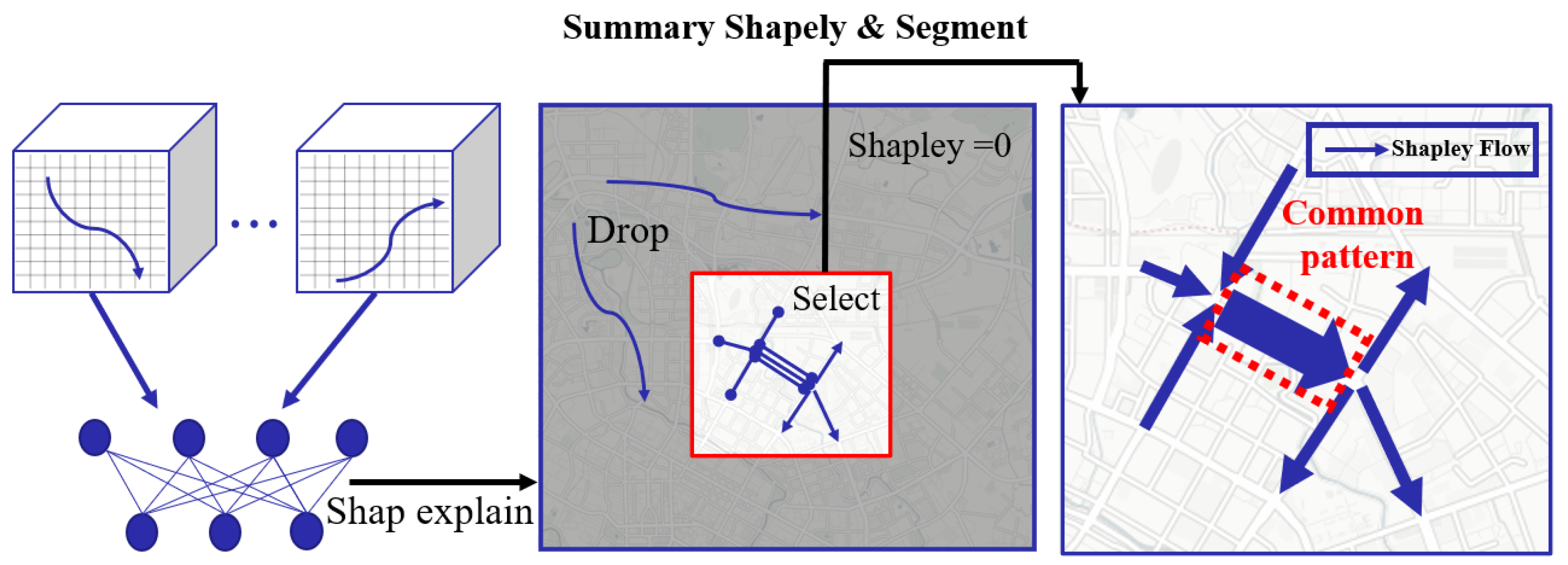
:1. Introduction
- (1)
- We propose Trajectory Shapley, a method that can effectively extract features from in–out flow and interpret neural networks. As far as we know, we are the first to introduce the Shapley value into crowd prediction;
- (2)
- In order to understand the pattern of trajectories from randomly distributed trajectories, we use submodules to discover key sub-trajectories that are representative of a certain distribution;
- (3)
- We validate the effectiveness of our approach on two real-world public datasets. Experimental results show that our approach achieves notably better performance in the aspects of coverage and summarization.
2. Architecture
3. Preliminaries
4. Trajectory Shapley
4.1. Trajectory Shapley
| Algorithm 1 Trajectory Shapley |
| Input: Randomly selected background sample , Explain region coordinate (x, y) in terms of grid, Set trajectories in t time slot, Flow tensor , pretrain model f. Output: |
4.2. Maximum Explainability Coverage
4.3. Trajectory Segment
4.4. Trajectory Shapley Maximum Coverage
| Algorithm 2 Trajectory Shapley maximum coverage |
| Input: The Trajectory Shapley set M calculated by Algorithm 1, Trajectories set in t time slot, Submodular distance threshold . Output: sub-trajectories}
|
5. Experiments
5.1. Classic Prediction Methods for Comparison
- •
- CNN: We used a basic deep learning predictor constructed with four CNN layers. The tensor is represented by . The CNN predictor utilizes four Conv layers to take the current observed t-step frames as input and predicts the next frame as output;
- •
- ST-GCN [17]: For ST-GCN, we set the adjacency matrix to have the same receptive field as the CNN. The receptive field was set on the basis of a grid. It is regulated by the distance parameter . The three layer channels in the ST-Conv block were 64, 64, and 64, respectively. Both the graph convolution kernel size K and temporal convolution kernel size were set to 3 in the model.
- •
- DNN: We straightened in–out flow grids into vectors and used them as the output of DNNs. We also erased the time information in DNNs and used five layers of a fully connected network. The feature size of each layer was .
5.2. Case Study
5.2.1. Case Study of Trajectory Shapley Visualization
5.2.2. Case Study of Explainable Summarization
Subset Trajectories
Subsets Segment
Trajectory Shapley Cover
Common Shapley Flow
Result Analysis
5.3. Parameter Analysis
6. Related Work
6.1. Urban Computing and Crowd Prediction
6.2. Explainable Model
6.3. Trajectory Cluster
7. Conclusions and Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zheng, Y.; Zhang, L.; Xie, X.; Ma, W.Y. Mining interesting locations and travel sequences from GPS trajectories. In Proceedings of the 18th International Conference on World Wide Web, Madrid, Spain, 20–24 April 2009; pp. 791–800. [Google Scholar]
- Zhang, J.; Zheng, Y.; Qi, D. Deep spatio-temporal residual networks for citywide crowd flows prediction. In Proceedings of the Thirty-First AAAI Conference on Artificial Intelligence, San Francisco, CA, USA, 4–9 February 2018. [Google Scholar]
- Zhang, J.; Zheng, Y.; Qi, D.; Li, R.; Yi, X. DNN-based prediction model for spatio-temporal data. In Proceedings of the 24th ACM SIGSPATIAL International Conference on Advances in Geographic Information Systems, Burlingame, CA, USA, 31 October–3 November 2016; pp. 1–4. [Google Scholar]
- Yao, H.; Wu, F.; Ke, J.; Tang, X.; Jia, Y.; Lu, S.; Gong, P.; Ye, J.; Li, Z. Deep multi-view spatial-temporal network for taxi demand prediction. In Proceedings of the Thirty-Second AAAI Conference on Artificial Intelligence, New Orleans, AK, USA, 2–7 February 2018. [Google Scholar]
- Yao, H.; Tang, X.; Wei, H.; Zheng, G.; Li, Z. Revisiting spatial-temporal similarity: A deep learning framework for traffic prediction. In Proceedings of the AAAI Conference on Artificial Intelligence, Honolulu, HI, USA, 27 January–1 February 2019; Volume 33, pp. 5668–5675. [Google Scholar]
- Simonyan, K.; Vedaldi, A.; Zisserman, A. Deep inside convolutional networks: Visualising image classification models and saliency maps. arXiv 2013, arXiv:1312.6034. [Google Scholar]
- Sundararajan, M.; Taly, A.; Yan, Q. Gradients of counterfactuals. arXiv 2016, arXiv:1611.02639. [Google Scholar]
- Smilkov, D.; Thorat, N.; Kim, B.; Viégas, F.; Wattenberg, M. Smoothgrad: Removing noise by adding noise. arXiv 2017, arXiv:1706.03825. [Google Scholar]
- Ribeiro, M.T.; Singh, S.; Guestrin, C. “Why should I trust you?” Explaining the predictions of any classifier. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; pp. 1135–1144. [Google Scholar]
- Lundberg, S.; Lee, S.I. A unified approach to interpreting model predictions. arXiv 2017, arXiv:1705.07874. [Google Scholar]
- Cheng, Z.; Yang, Y.; Wang, W.; Hu, W.; Zhuang, Y.; Song, G. Time2graph: Revisiting time series modeling with dynamic shapelets. In Proceedings of the AAAI Conference on Artificial Intelligence, New York, NY, USA, 7–12 February 2020; Volume 34, pp. 3617–3624. [Google Scholar]
- Ye, L.; Keogh, E. Time series shapelets: A new primitive for data mining. In Proceedings of the 15th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Paris, France, 28 June–1 July 2009; pp. 947–956. [Google Scholar]
- Shapley, L.S. A value for n-person games. Contrib. Theory Games 1953, 2, 307–317. [Google Scholar]
- Weber, R.J. Probabilistic values for games. In The Shapley Value. Essays in Honor of Lloyd S. Shapley; Cambridge University Press: Cambridge, UK, 1988; pp. 101–119. [Google Scholar]
- Lee, J.G.; Han, J.; Whang, K.Y. Trajectory clustering: A partition-and-group framework. In Proceedings of the 2007 ACM SIGMOD International Conference on Management of Data, Beijing, China, 11–14 June 2007; pp. 593–604. [Google Scholar]
- Hinton, G.; Vinyals, O.; Dean, J. Distilling the knowledge in a neural network. arXiv 2015, arXiv:1503.02531. [Google Scholar]
- Yu, B.; Yin, H.; Zhu, Z. Spatio-temporal graph convolutional networks: A deep learning framework for traffic forecasting. arXiv 2017, arXiv:1709.04875. [Google Scholar]
- Fan, Z.; Song, X.; Shibasaki, R.; Adachi, R. CityMomentum: An online approach for crowd behavior prediction at a citywide level. In Proceedings of the 2015 ACM International Joint Conference on Pervasive and Ubiquitous Computing, Osaka, Japan, 7–11 September 2015; pp. 559–569. [Google Scholar]
- Song, X.; Zhang, Q.; Sekimoto, Y.; Shibasaki, R.; Yuan, N.J.; Xie, X. Prediction and simulation of human mobility following natural disasters. ACM Trans. Intell. Syst. Technol. (TIST) 2016, 8, 1–23. [Google Scholar] [CrossRef]
- Wang, L.; Yu, Z.; Guo, B.; Ku, T.; Yi, F. Moving destination prediction using sparse dataset: A mobility gradient descent approach. ACM Trans. Knowl. Discov. Data (TKDD) 2017, 11, 1–33. [Google Scholar] [CrossRef]
- Yang, Z.; Lian, D.; Yuan, N.J.; Xie, X.; Rui, Y.; Zhou, T. Indigenization of urban mobility. Phys. A Stat. Mech. Its Appl. 2017, 469, 232–243. [Google Scholar] [CrossRef] [Green Version]
- Zhang, J.; Guo, B.; Han, Q.; Ouyang, Y.; Yu, Z. CrowdStory: Multi-layered event storyline generation with mobile crowdsourced data. In Proceedings of the 2016 ACM International Joint Conference on Pervasive and Ubiquitous Computing: Adjunct, Heidelberg, Germany, 12–16 September 2016; pp. 237–240. [Google Scholar]
- Konishi, T.; Maruyama, M.; Tsubouchi, K.; Shimosaka, M. CityProphet: City-scale irregularity prediction using transit app logs. In Proceedings of the 2016 ACM International Joint Conference on Pervasive and Ubiquitous Computing, Heidelberg, Germany, 12–16 September 2016; pp. 752–757. [Google Scholar]
- Chawla, S.; Zheng, Y.; Hu, J. Inferring the root cause in road traffic anomalies. In Proceedings of the 2012 IEEE 12th International Conference on Data Mining, Brussels, Belgium, 10–13 December 2012; IEEE: Piscataway, NJ, USA, 2012; pp. 141–150. [Google Scholar]
- Jian, S.; Rey, D.; Dixit, V. An integrated supply-demand approach to solving optimal relocations in station-based carsharing systems. Netw. Spat. Econ. 2019, 19, 611–632. [Google Scholar] [CrossRef]
- Kim, T.Y.; Cho, S.B. Predicting residential energy consumption using CNN-LSTM neural networks. Energy 2019, 182, 72–81. [Google Scholar] [CrossRef]
- Zheng, Y.; Capra, L.; Wolfson, O.; Yang, H. Urban computing: Concepts, methodologies, and applications. ACM Trans. Intell. Syst. Technol. (TIST) 2014, 5, 1–55. [Google Scholar] [CrossRef]
- Li, Y.; Yu, R.; Shahabi, C.; Liu, Y. Diffusion convolutional recurrent neural network: Data-driven traffic forecasting. arXiv 2017, arXiv:1707.01926. [Google Scholar]
- Yu, H.; Wu, Z.; Wang, S.; Wang, Y.; Ma, X. Spatiotemporal recurrent convolutional networks for traffic prediction in transportation networks. Sensors 2017, 17, 1501. [Google Scholar] [CrossRef] [Green Version]
- Zhang, K.; Zheng, L.; Liu, Z.; Jia, N. A deep learning based multitask model for network-wide traffic speed prediction. Neurocomputing 2020, 396, 438–450. [Google Scholar] [CrossRef]
- Jiang, R.; Cai, Z.; Wang, Z.; Yang, C.; Fan, Z.; Song, X.; Tsubouchi, K.; Shibasaki, R. VLUC: An Empirical Benchmark for Video-Like Urban Computing on Citywide Crowd and Traffic Prediction. arXiv 2019, arXiv:1911.06982. [Google Scholar]
- Zonoozi, A.; Kim, J.j.; Li, X.L.; Cong, G. Periodic-CRN: A Convolutional Recurrent Model for Crowd Density Prediction with Recurring Periodic Patterns. In Proceedings of the IJCAI, Stockholm, Sweden, 13–19 July 2018; pp. 3732–3738. [Google Scholar]
- Song, H.; Wang, W.; Zhao, S.; Shen, J.; Lam, K.M. Pyramid dilated deeper convlstm for video salient object detection. In Proceedings of the European conference on computer vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 715–731. [Google Scholar]
- Geng, X.; Li, Y.; Wang, L.; Zhang, L.; Yang, Q.; Ye, J.; Liu, Y. Spatiotemporal multi-graph convolution network for ride-hailing demand forecasting. In Proceedings of the AAAI Conference on Artificial Intelligence, Honolulu, HI, USA, 27–28 January 2019; Volume 33, pp. 3656–3663. [Google Scholar]
- Bach, S.; Binder, A.; Montavon, G.; Klauschen, F.; Müller, K.R.; Samek, W. On pixel-wise explanations for non-linear classifier decisions by layer-wise relevance propagation. PLoS ONE 2015, 10, e0130140. [Google Scholar] [CrossRef] [Green Version]
- Zeiler, M.D.; Fergus, R. Visualizing and understanding convolutional networks. In Proceedings of the European conference on computer vision, Zurich, Switzerland, 6–12 September 2014; pp. 818–833. [Google Scholar]
- Springenberg, J.T.; Dosovitskiy, A.; Brox, T.; Riedmiller, M. Striving for simplicity: The all convolutional net. arXiv 2014, arXiv:1412.6806. [Google Scholar]
- Nair, V.; Hinton, G.E. Rectified linear units improve restricted boltzmann machines. In Proceedings of the ICML, Madison, WI, USA, 21–24 June 2010. [Google Scholar]
- Agarwal, P.K.; Fox, K.; Munagala, K.; Nath, A.; Pan, J.; Taylor, E. Subtrajectory clustering: Models and algorithms. In Proceedings of the 37th ACM SIGMOD-SIGACT-SIGAI Symposium on Principles of Database Systems, Houston, TX, USA, 10–15 June 2018; pp. 75–87. [Google Scholar]
- Hung, C.C.; Peng, W.C.; Lee, W.C. Clustering and aggregating clues of trajectories for mining trajectory patterns and routes. VLDB J. 2015, 24, 169–192. [Google Scholar] [CrossRef]
- Pelekis, N.; Kopanakis, I.; Kotsifakos, E.; Frentzos, E.; Theodoridis, Y. Clustering trajectories of moving objects in an uncertain world. In Proceedings of the 2009 Ninth IEEE International Conference on Data Mining, Miami, FL, USA, 6–9 December 2009; IEEE: Piscataway, NJ, USA, 2009; pp. 417–427. [Google Scholar]
- Wu, Y.; Shen, H.; Sheng, Q.Z. A cloud-friendly RFID trajectory clustering algorithm in uncertain environments. IEEE Trans. Parallel Distrib. Syst. 2014, 26, 2075–2088. [Google Scholar] [CrossRef]
- Shen, J.; Peng, J.; Shao, L. Submodular trajectories for better motion segmentation in videos. IEEE Trans. Image Process. 2018, 27, 2688–2700. [Google Scholar] [CrossRef] [PubMed]
- Ferreira, N.; Klosowski, J.T.; Scheidegger, C.E.; Silva, C.T. Vector field k-means: Clustering trajectories by fitting multiple vector fields. In Proceedings of the Computer Graphics Forum; Wiley Online Library: New York, NY, USA, 2013; Volume 32, pp. 201–210. [Google Scholar]
- Chan, T.H.; Guerqin, A.; Sozio, M. Fully dynamic k-center clustering. In Proceedings of the 2018 World Wide Web Conference, Lyon, France, 23–27 April 2018; pp. 579–587. [Google Scholar]
- Gudmundsson, J.; Valladares, N. A GPU approach to subtrajectory clustering using the Fréchet distance. IEEE Trans. Parallel Distrib. Syst. 2014, 26, 924–937. [Google Scholar] [CrossRef]
- Andrienko, G.; Andrienko, N.; Rinzivillo, S.; Nanni, M.; Pedreschi, D.; Giannotti, F. Interactive visual clustering of large collections of trajectories. In Proceedings of the 2009 IEEE Symposium on Visual Analytics Science and Technology, Atlantic City, NJ, USA, 12–13 October 2009; IEEE: Piscataway, NJ, USA, 2009; pp. 3–10. [Google Scholar]
- Han, B.; Liu, L.; Omiecinski, E. Road-network aware trajectory clustering: Integrating locality, flow, and density. IEEE Trans. Mob. Comput. 2013, 14, 416–429. [Google Scholar]
- Zheng, K.; Zheng, Y.; Yuan, N.J.; Shang, S.; Zhou, X. Online discovery of gathering patterns over trajectories. IEEE Trans. Knowl. Data Eng. 2013, 26, 1974–1988. [Google Scholar] [CrossRef]









Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, H.; Fan, Z.; Chen, J.; Zhang, L.; Song, X. Discovering Key Sub-Trajectories to Explain Traffic Prediction. Sensors 2023, 23, 130. https://doi.org/10.3390/s23010130
Wang H, Fan Z, Chen J, Zhang L, Song X. Discovering Key Sub-Trajectories to Explain Traffic Prediction. Sensors. 2023; 23(1):130. https://doi.org/10.3390/s23010130
Chicago/Turabian StyleWang, Hongjun, Zipei Fan, Jiyuan Chen, Lingyu Zhang, and Xuan Song. 2023. "Discovering Key Sub-Trajectories to Explain Traffic Prediction" Sensors 23, no. 1: 130. https://doi.org/10.3390/s23010130
APA StyleWang, H., Fan, Z., Chen, J., Zhang, L., & Song, X. (2023). Discovering Key Sub-Trajectories to Explain Traffic Prediction. Sensors, 23(1), 130. https://doi.org/10.3390/s23010130






