Properties and Applications of Random Lasers as Emerging Light Sources and Optical Sensors: A Review
Abstract
:1. Introduction
2. RL Emission Properties
2.1. Lasing Threshold Characterization and Reduction
2.2. Peak Wavelength Shift (Tunability)
2.2.1. Relative Redshift Realization
2.2.2. Relative Blueshift Realization
2.3. Coherence
2.3.1. Characteristics of Spectral Modes
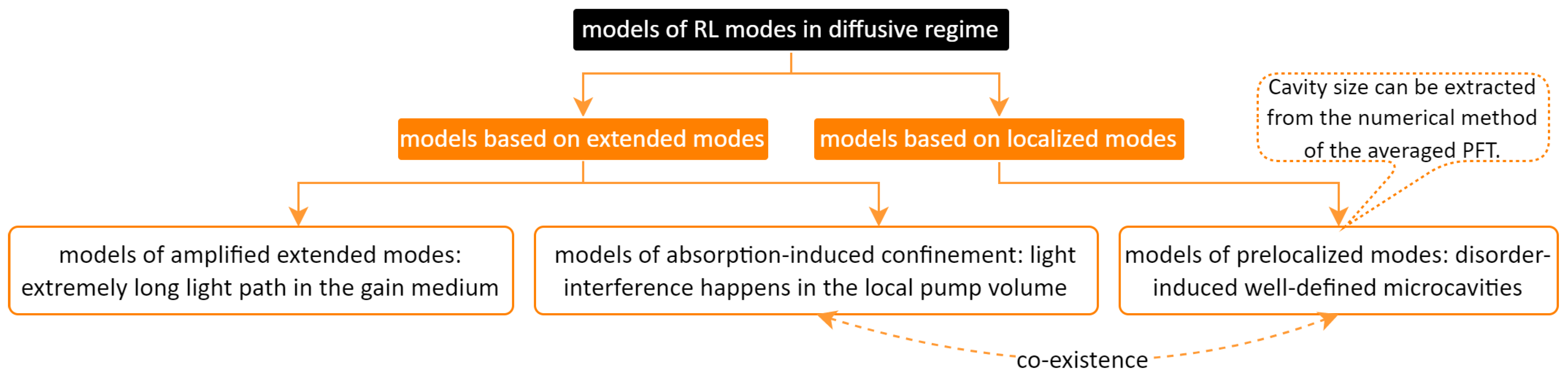
2.3.2. Characteristics of Spatial Modes
Amplified Extended Modes
Absorption-Induced Confined Modes
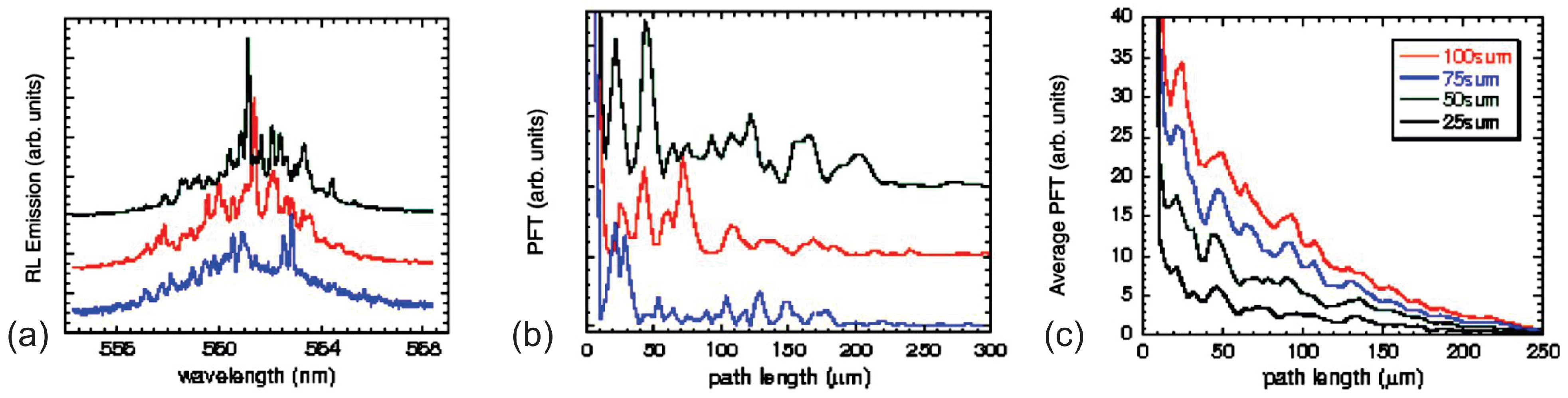
Prelocalized Modes and Size Calculation of the Prelocalized Cavity
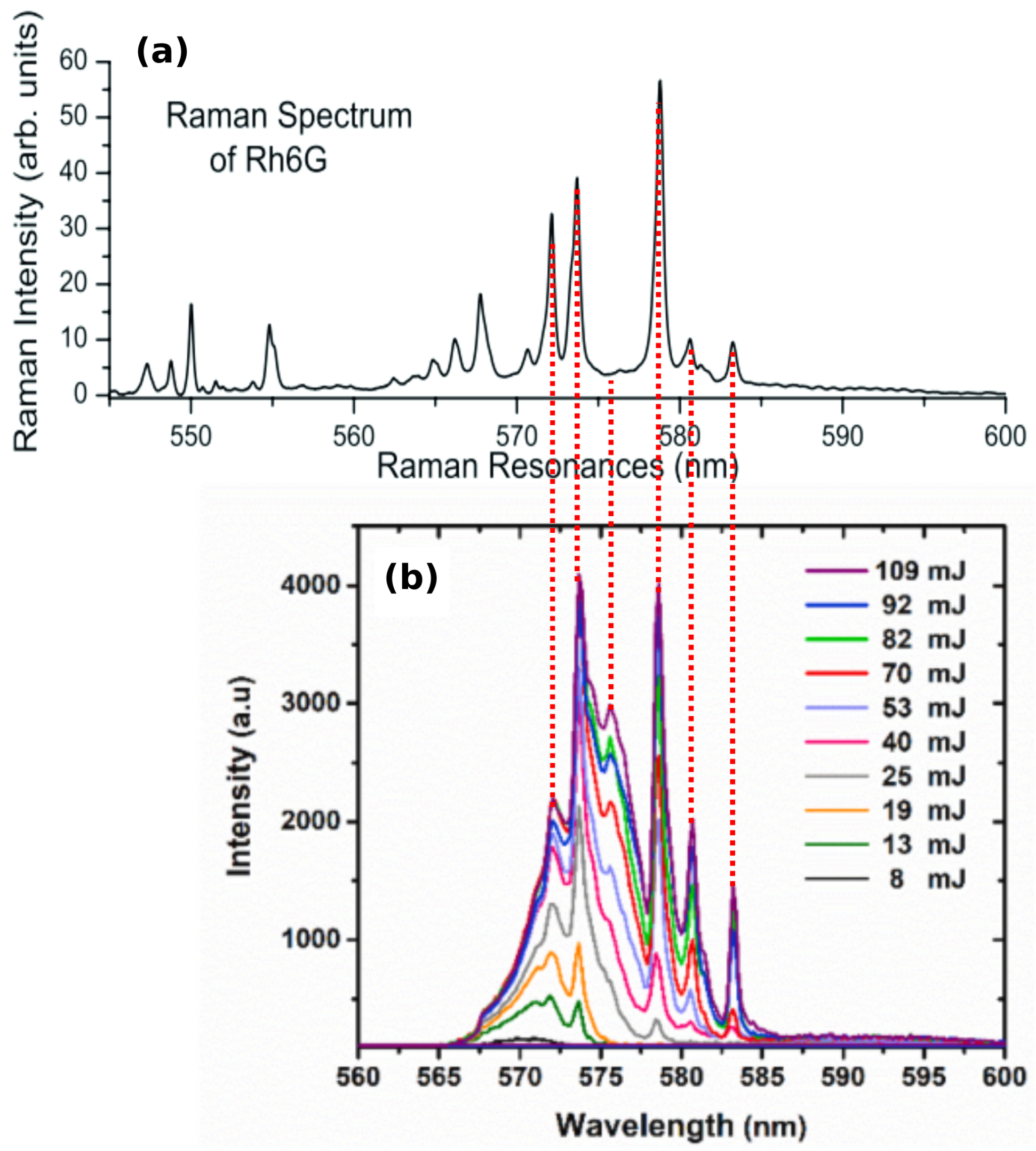
3. Emerging RL Physics: Stimulated Raman Scattering
4. Applications of RLs
4.1. RL as a Light Source
4.1.1. Bio-Compatible RLs
4.1.2. Stretchable or Bendable RLs
4.1.3. Wavelength-Tunable or Multicolor RLs
4.2. RL as an Optical Sensor
4.2.1. RLs for Optomechanical and bio-Chemical Sensing
4.2.2. RLs for Tissue or Cell Differentiation
4.2.3. RLs for Cancer Diagnosis or Therapy
5. Summary and Outlook
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| RL | random laser |
| FP | Fabry–Pérot |
| Rh640 | Rhodamine 640 |
| WGM | whispering gallery mode |
| SF | superfluorescence |
| SL | superluminescence |
| ASE | amplified spontaneous emission |
| SR | superradiance |
| SRS | stimulated Raman scattering |
| RSB | replica symmetry breaking |
| NP | nanoparticle |
| RhB | Rhodamine B |
| R6G | Rhodamine 6G |
| PFT | power Fourier transform |
| RRL | random Raman laser |
| AF | Air Force |
| RGB | red–green–blue |
| Pe-NC | perovskite nanocrystal |
| NW | nanowire |
| DCJTB | 4-(dicyanomethylene)-2-tert-butyl-6-(1,1,7,7-tetra-methyljulolidin-4-yl-vinyl)-4H-pyran |
| PM567 | Pyrromethene567 |
| F8BT | poly[(9,9-dioctylfluorenyl-2,7-diyl)-alt-co-(1,4-benzo-(2,1,3)-thiadiazole)] |
| MDMO-PPV | poly[2-methoxy-5-(3,7-dimethyloctyloxy)-1,4-phenylenevinylene] |
| PFO | poly[9,9-dioctylfluorenyl-2,7-diyl] |
| C440 | coumarin 440 |
| C153 | coumarin 153 |
| C6 | coumarin 6 |
| IgG | immunoglobulin |
| HTT | huntigtin |
| Tx | tamoxifen |
Appendix A
| RL Medium | Pump Condition | Spectra | RL or Raman |
|---|---|---|---|
| ZnO nanospheres and R6G methanol colloid in flask | 532 nm, 7 ns, 3 mm pump spot | 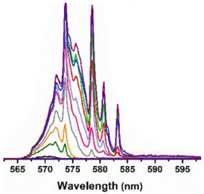 Adapted from Ref. [140] with permission from the Elsevier. Adapted from Ref. [140] with permission from the Elsevier. | R6G Raman lines |
| TiO and R6G ethanol colloid in cuvette | 532 nm, 5 ns, mm pump spot | 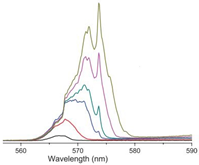 Adapted from Ref. [141] with permission from the IOP Publishing. Adapted from Ref. [141] with permission from the IOP Publishing. | R6G Raman lines |
| Ag nanowires and R6G methanol colloid in cuvette | 532 nm, 10 ns, 3 mm pump spot |  Adapted from Ref. [85] with permission from the American Chemical Society. Adapted from Ref. [85] with permission from the American Chemical Society. | R6G Raman lines |
| R6G and Ag nanowires ethanol colloid dispersed in a beaker | 532 nm, 10 ns, 8 mm pump spot | 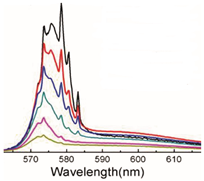 Adapted from Ref. [164] with permission from the Optica Publishing. Adapted from Ref. [164] with permission from the Optica Publishing. | R6G Raman lines |
| R6G doped PMMA acetone solution spin-coated onto hydrothermal oxidation treated Zn sheets | 532 nm, 9 ns, 1 mm × 10 mm pump stripe | 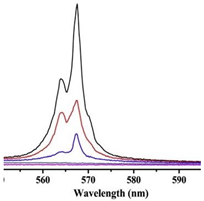 Adapted from Ref. [165] with permission from the Elsevier. Adapted from Ref. [165] with permission from the Elsevier. | R6G Raman lines |
| R6G and TiO urchins ethylene glycol colloid dispersed in a glass cuvette | 532 nm, 120 ps, 2 mm pump spot | 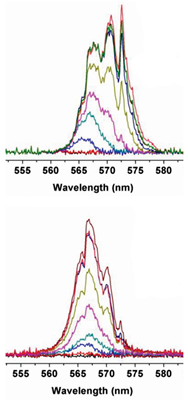 Adapted from Ref. [12] with permission from SPIE and the authors. Adapted from Ref. [12] with permission from SPIE and the authors. | R6G Raman lines |
| Au-Ag nanowires and R6G ethanol colloid in cuvette | 532 nm, 8 ns |  Adapted from Ref. [142] with permission from the American Chemical Society. Adapted from Ref. [142] with permission from the American Chemical Society. | R6G Raman lines |
| R6G methanol solution spin-coated onto a 1 µm thick ZnO nanowires integrated polyethylene terephthalate (PET) film | 532 nm, 5 ns, 50 µm × 6 mm pump stripe | 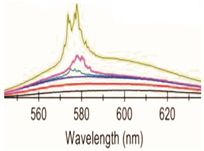 Adapted from Ref. [45] with permission from the Royal Society of Chemistry. Adapted from Ref. [45] with permission from the Royal Society of Chemistry. | RL spikes and R6G Raman lines |
| R6G and Au nanorods ethylene glycol colloid deposited between a reflecting plate and MgF plate | 532 nm, 7 ns, 70 µm × 8 mm pump stripe | 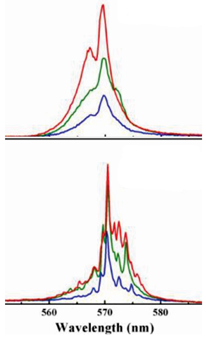 Adapted from Ref. [166] with permission from SPIE and the authors. Adapted from Ref. [166] with permission from SPIE and the authors. | RL spikes and R6G Raman lines |
| R6G and Ag nanowires ethanol polydimethylsiloxane (PDMS) mixture press-coated onto a silicone rubber slab | 532 nm, 8 ns, mm × 8 mm pump stripe | 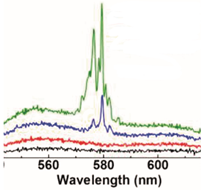 Adapted from Ref. [48] with permission from the Elsevier. Adapted from Ref. [48] with permission from the Elsevier. | RL spikes and possible R6G Raman lines |
References
- Ambartsumyan, R.V.; Basov, N.G.; Kryukov, P.G. A Laser with a Nonresonant Feedback. IEEE J. Quantum Electron. 1966, QE-2, 442. [Google Scholar] [CrossRef]
- Letokhov, V. Generation of Light by a Scattering Medium with Negative Resonance Absorption. Sov. J. Exp. Theor. Phys. 1968, 26, 835. [Google Scholar]
- Markushev, V.M.; Zolin, V.F.; Briskina, C.M. Luminescence and stimulated emission of neodymium in sodium lanthanum molybdate powders. Sov. J. Quantum Electron. 1986, 16, 281. [Google Scholar] [CrossRef]
- Lawandy, N.M.; Balachandran, R.M.; Gomes, A.S.L.; Sauvaln, E. Laser action in strongly scattering media. Nature 1994, 368, 436. [Google Scholar] [CrossRef]
- Wiersma, D.S.; Lagendijk, A. Light diffusion with gain and random lasers. Phys. Rev. E 1996, 54, 4256–4265. [Google Scholar] [CrossRef] [Green Version]
- Polson, R.C.; Raikh, M.E.; Valy Vardeny, Z. Universality in unintentional laser resonators in π-conjugated polymer films. C. R. Phys. 2002, 3, 509–521. [Google Scholar] [CrossRef]
- Li, Y.; Xie, K.; Zhang, X.; Hu, Z.; Ma, J.; Chen, X.; Zhang, J.; Liu, Z.; Chen, D. Coherent Random Lasing Realized in Polymer Vesicles. Photonic Sens. 2020, 10, 254–264. [Google Scholar] [CrossRef] [Green Version]
- Wiersma, D.S.; Cavalieri, S. Temperature-controlled random laser action in liquid crystal infiltrated systems. Phys. Rev. E 2002, 66, 56612. [Google Scholar] [CrossRef] [Green Version]
- Ferjani, S.; Barna, V.; De Luca, A.; Versace, C.; Strangi, G. Random lasing in freely suspended dye-doped nematic liquid crystals. Opt. Lett. 2008, 33, 557. [Google Scholar] [CrossRef]
- Cao, H.; Zhao, Y.G. Random Laser Action in Semiconductor Powder. Phys. Rev. Lett. 1999, 82, 2278. [Google Scholar] [CrossRef] [Green Version]
- El-Dardiry, R.G.; Mosk, A.P.; Muskens, O.L.; Lagendijk, A. Experimental studies on the mode structure of random lasers. Phys. Rev. A 2010, 81, 43830. [Google Scholar] [CrossRef]
- Gummaluri, V.S.; Nair, R.V.; Vijayan, C. Random lasing from a colloidal gain medium with urchin-like TiO2 structures. In Proceedings of the SPIE 9920, the Active Photonic Materials VIII, San Diego, CA, USA, 16 September 2016. [Google Scholar] [CrossRef]
- Fan, S.; Zhang, X.; Wang, Q.; Zhang, C.; Wang, Z.; Lan, R. Inflection point of the spectral shifts of the random lasing in dye solution with TiO2 nanoscatterers. J. Phys. Appl. Phys. 2009, 42, 15105. [Google Scholar] [CrossRef]
- Ling, Y.; Cao, H.; Burin, A.L.; Ratner, M.A.; Liu, X.; Chang, R.P. Investigation of random lasers with resonant feedback. Phys. Rev. A 2001, 64, 63808. [Google Scholar] [CrossRef] [Green Version]
- Ismail, W.Z.W.; Kamil, W.M.W.A.; Dawes, J.M. Enhancement of Random Laser Properties on Solid Polymer Films by Increasing Scattering Effect. J. Russ. Laser Res. 2019, 40, 364–369. [Google Scholar] [CrossRef]
- Dai, G.; Wang, L.; Deng, L. Flexible random laser from dye doped stretchable polymer film containing nematic liquid crystal. Opt. Mater. Express 2020, 10, 68. [Google Scholar] [CrossRef]
- Li, J.; Li, X.; Zheng, T.; Chu, J.; Shen, C.; Sang, Y.; Hu, S.; Guo, J. Random lasing based on abalone shell. Opt. Commun. 2021, 493, 126979. [Google Scholar] [CrossRef]
- Caixeiro, S.; Gaio, M.; Marelli, B.; Omenetto, F.G.; Sapienza, R. Silk-Based Biocompatible Random Lasing. Adv. Opt. Mater. 2016, 4, 998–1003. [Google Scholar] [CrossRef] [Green Version]
- Liu, X.; Li, T.; Yi, T.; Wang, C.; Li, J.; Xu, M.; Huang, D.; Liu, S.; Jiang, S.; Ding, Y. Random laser action from a natural flexible biomembrane-based device. J. Mod. Opt. 2016, 63, 1248–1253. [Google Scholar] [CrossRef]
- Li, X.; Gong, F.; Liu, D.; He, S.; Yuan, H.; Dai, L.; Cai, X.; Liu, J.; Guo, J.; Jin, Y.; et al. A lotus leaf based random laser. Org. Electron. 2019, 69, 216–219. [Google Scholar] [CrossRef]
- Dey, A.; Pramanik, A.; Kumbhakar, P.; Biswas, S.; Pal, S.K.; Ghosh, S.K.; Kumbhakar, P. Manoeuvring a natural scatterer system in random lasing action and a demonstration of speckle free imaging. OSA Contin. 2021, 4, 1712. [Google Scholar] [CrossRef]
- Wang, C.S.; Chang, T.Y.; Lin, T.Y.; Chen, Y.F. Biologically inspired flexible quasi-single-mode random laser: An integration of Pieris canidia butterfly wing and semiconductors. Sci. Rep. 2014, 4, 6736. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhang, D.; Kostovski, G.; Karnutsch, C.; Mitchell, A. Random lasing from dye doped polymer within biological source scatters: The pomponia imperatorial cicada wing random nanostructures. Org. Electron. 2012, 13, 2342–2345. [Google Scholar] [CrossRef]
- Chen, S.W.; Lu, J.Y.; Hung, B.Y.; Chiesa, M.; Tung, P.H.; Lin, J.H.; Yang, T.C.K. Random lasers from photonic crystal wings of butterfly and moth for speckle-free imaging. Opt. Express 2021, 29, 2065. [Google Scholar] [CrossRef] [PubMed]
- Polson, R.C.; Vardeny, Z.V. Organic random lasers in the weak-scattering regime. Phys. Rev. B 2005, 71, 45205. [Google Scholar] [CrossRef]
- Song, Q.; Xu, Z.; Choi, S.H.; Sun, X.; Xiao, S.; Akkus, O.; Kim, Y.L. Detection of nanoscale structural changes in bone using random lasers. Biomed. Opt. Express 2010, 1, 1401. [Google Scholar] [CrossRef] [Green Version]
- Hohmann, M.; Dörner, D.; Mehari, F.; Chen, C.; Späth, M.; Müller, S.; Albrecht, H.; Klämpfl, F.; Schmidt, M. Investigation of random lasing as a feedback mechanism for tissue differentiation during laser surgery. Biomed. Opt. Express 2019, 10, 807. [Google Scholar] [CrossRef]
- Lahoz, F.; Acebes, A.; González-Hernández, T.; de Armas-Rillo, S.; Soler-Carracedo, K.; Cuesto, G.; Mesa-Infante, V. Random lasing in brain tissues. Org. Electron. 2019, 75, 105389. [Google Scholar] [CrossRef]
- Lahoz, F.; Martín, I.R.; Urgellés, M.; Marín, R.; Saavedra, C.J.; Boto, A.; Díaz, M. Random laser in biological tissues impregnated with a fluorescent anticancer drug. Laser Phys. Lett. 2015, 12, 45805. [Google Scholar] [CrossRef]
- Polson, R.C.; Vardeny, Z.V. Random lasing in human tissues. Appl. Phys. Lett. 2004, 85, 1289–1291. [Google Scholar] [CrossRef]
- Mogharari, N.; Sajad, B. Random Laser Emission Spectra of the Normal and Cancerous Thyroid Tissues. Iran. J. Sci. Technol. Trans. A Sci. 2019, 43, 2055–2060. [Google Scholar] [CrossRef]
- Wang, Y.; Duan, Z.; Qiu, Z.; Zhang, P.; Wu, J.; Dingke, A.; Xiang, T. Random lasing in human tissues embedded with organic dyes for cancer diagnosis. Sci. Rep. 2017, 7, 8385. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhang, D.; Wang, Y.; Tang, J.; Mu, H. Random laser marked PLCD1 gene therapy effect on human breast cancer. J. Appl. Phys. 2019, 125, 203102. [Google Scholar] [CrossRef]
- He, J.; Hu, S.; Ren, J.; Cheng, X.; Hu, Z.; Wang, N.; Zhang, H.; Lam, R.H.; Tam, H.Y. Biofluidic Random Laser Cytometer for Biophysical Phenotyping of Cell Suspensions. ACS Sens. 2019, 4, 832–840. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Niyuki, R.; Fujiwara, H.; Ishikawa, Y.; Koshizaki, N.; Tsuji, T.; Sasaki, K. Toward single-mode random lasing within a submicrometre-sized spherical ZnO particle film. J. Opt. 2016, 18, 35202. [Google Scholar] [CrossRef] [Green Version]
- Ta, V.D.; Caixeiro, S.; Fernandes, F.M.; Sapienza, R. Microsphere Solid-State Biolasers. Adv. Opt. Mater. 2017, 5, 1601022. [Google Scholar] [CrossRef] [Green Version]
- Chen, Q.; Chen, Y.C.; Zhang, Z.; Wu, B.; Coleman, R.; Fan, X. An integrated microwell array platform for cell lasing analysis. Lab Chip 2017, 17, 2814–2820. [Google Scholar] [CrossRef]
- Xu, Z.; Tong, J.; Shi, X.; Deng, J.; Zhai, T. Tailoring whispering gallery lasing and random lasing in a compound cavity. Polymers 2020, 12, 656. [Google Scholar] [CrossRef] [Green Version]
- Chen, Y.C.; Tan, X.; Sun, Q.; Chen, Q.; Wang, W.; Fan, X. Laser-emission imaging of nuclear biomarkers for high-contrast cancer screening and immunodiagnosis. Nat. Biomed. Eng. 2017, 1, 724–735. [Google Scholar] [CrossRef] [Green Version]
- Dai, D.C. Brief comment: Dicke Superradiance and Superfluorescence Find Application for Remote Sensing in Air. arXiv 2011, arXiv:1108.5360. [Google Scholar]
- Wiersma, D.S. The physics and applications of random lasers. Nat. Phys. 2008, 4, 359. [Google Scholar] [CrossRef]
- Nastishin, Y.; Dudok, T.H. Optically pumped mirror less lasing. A review. part I. random lasing. Ukr. J. Phys. Opt. 2013, 14, 146–170. [Google Scholar] [CrossRef]
- Hou, Y.; Zhou, Z.; Zhang, C.; Tang, J.; Fan, Y.; Xu, F.F. Full-color flexible laser displays based on random laser arrays. Sci. China Mater. 2021, 64, 2805–2812. [Google Scholar] [CrossRef]
- Germano, G.C.M.; Machado, Y.D.R.; Martinho, L.; Fernandes, S.N.; Costa, A.M.L.M.; Pecoraro, E.; Gomes, A.S.L.; Carvalho, I.C.S. Flexible random lasers in dye-doped bio-degradable cellulose nanocrystalline needles. J. Opt. Soc. Am. B 2020, 37, 24–29. [Google Scholar] [CrossRef]
- Lee, Y.J.; Yeh, T.W.; Yang, Z.P.; Yao, Y.C.; Chang, C.Y.; Tsai, M.T.; Sheu, J.K. A curvature-tunable random laser. Nanoscale 2019, 11, 3534–3545. [Google Scholar] [CrossRef] [PubMed]
- Lee, Y.J.; Chou, C.Y.; Yang, Z.P.; Nguyen, T.B.H.; Yao, Y.C.; Yeh, T.W.; Tsai, M.T.; Kuo, H.C. Flexible random lasers with tunable lasing emissions. Nanoscale 2018, 10, 10299–10742. [Google Scholar] [CrossRef]
- Bian, Y.; Shi, X.; Hu, M.; Wang, Z. A ring-shaped random laser in momentum space. Nanoscale 2020, 12, 3166–3173. [Google Scholar] [CrossRef] [PubMed]
- Tong, J.; Shi, X.; Li, S.; Chen, C.; Zhai, T.; Zhang, X. Tunable plasmonic random laser based on a wedge shaped resonator. Org. Electron. 2019, 75, 105337. [Google Scholar] [CrossRef]
- Redding, B.; Choma, M.A.; Cao, H. Speckle-free laser imaging using random laser illumination. Nat. Photonics 2012, 6, 355–359. [Google Scholar] [CrossRef] [Green Version]
- Späth, M.; Klämpfl, F.; Stelzle, F.; Hohmann, M.; Lengenfelder, B.; Schmidt, M. A quantitative evaluation of the use of medical lasers in German hospitals. J. Biophotonics 2020, 13, e201900238. [Google Scholar] [CrossRef]
- Septiadi, D.; Barna, V.; Saxena, D.; Sapienza, R.; Genovese, D.; De Cola, L. Biolasing from Individual Cells in a Low-Q Resonator Enables Spectral Fingerprinting. Adv. Opt. Mater. 2020, 8, 1901573. [Google Scholar] [CrossRef] [Green Version]
- Hohmann, M.; Späth, M.; Ni, D.; Dörner, D.; Lengenfelder, B.; Klämpfl, F.; Schmidt, M. Random laser as a potential tool for the determination of the scattering coefficient. Biomed. Opt. Express 2021, 12, 5439. [Google Scholar] [CrossRef] [PubMed]
- Kitur, J.; Zhu, G.; Bahoura, M.; Noginov, M.A. Dependence of the random laser behavior on the concentrations of dye and scatterers. J. Opt. 2010, 12, 24009. [Google Scholar] [CrossRef] [Green Version]
- de Oliveira, M.C.A.; de Sousa, F.W.S., Jr.; Santos, F.A.; Abeg, L.M.G.; Alencar, M.A.R.C.; Rodrigues, J.J., Jr.; de Oliveiraa, H.P. Dye-doped electrospun fibers for use as random laser generator: The influence of spot size and scatter concentration. Opt. Mater. 2020, 101, 109722. [Google Scholar] [CrossRef]
- Yi, J.; Feng, G.; Yang, L.; Yao, K.; Yang, C.; Song, Y.; Zhou, S. Behaviors of the Rh6G random laser comprising solvents and scatterers with different refractive indices. Opt. Commun. 2012, 285, 5276–5282. [Google Scholar] [CrossRef]
- Meng, X.; Fujita, K.; Murai, S.; Konishi, J.; Mano, M.; Tanaka, K. Random lasing in ballistic and diffusive regimes for macroporous silica-based systems with tunable scattering strength. Opt. Express 2010, 18, 12153. [Google Scholar] [CrossRef] [PubMed]
- Briones-Herrera, J.C.; Cuando-Espitia, N.; Sánchez-Arévalo, F.M.; Hernández-Cordero, J. Evaluation of mechanical behavior of soft tissue by means of random laser emission. Rev. Sci. Instrum. 2013, 84, 104301. [Google Scholar] [CrossRef] [PubMed]
- Wan Ismail, W.Z.; Liu, G.; Zhang, K.; Goldys, E.M.; Dawes, J.M. Dopamine sensing and measurement using threshold and spectral measurements in random lasers. Opt. Express 2016, 24, A85–A91. [Google Scholar] [CrossRef]
- Gaio, M.; Caixeiro, S.; Marelli, B.; Omenetto, F.G.; Sapienza, R. Gain-Based Mechanism for pH Sensing Based on Random Lasing. Phys. Rev. Appl. 2017, 7, 34005. [Google Scholar] [CrossRef] [Green Version]
- Shi, X.; Ge, K.; Tong, J.H.; Zhai, T. Low-cost biosensors based on a plasmonic random laser on fiber facet. Opt. Express 2020, 28, 12233. [Google Scholar] [CrossRef]
- Xu, Z.; Hong, Q.; Ge, K.; Shi, X.; Wang, X.; Deng, J.; Zhou, Z.X.; Zhai, T. Random Lasing from Label-Free Living Cells for Rapid Cytometry of Apoptosis. Nano Lett. 2022, 22, 172–178. [Google Scholar] [CrossRef]
- Armas-Rillo, S.D.; Fumagallo-Reading, F.; Luis-Ravelo, D.; Abdul-Jalbar, B.; González-Hernández, T.; Lahoz, F. Random Lasing Detection of Mutant Huntingtin Expression in Cells. Sensors 2021, 21, 3825. [Google Scholar] [CrossRef] [PubMed]
- Cao, H.; Xu, J.Y.; Ling, Y.; Burin, A.L.; Seeling, E.W.; Liu, X.; Chang, R.P. Random lasers with coherent feedback. IEEE J. Sel. Top. Quantum Electron. 2003, 9, 111–119. [Google Scholar] [CrossRef] [Green Version]
- Cao, H. Review on latest developments in random lasers with coherent feedback. J. Phys. Math. Gen. 2005, 38, 10497–10535. [Google Scholar] [CrossRef]
- Zaitsev, O.; Deych, L. Recent developments in the theory of multimode random lasers. J. Opt. Pure Appl. Opt. 2010, 12, 24001. [Google Scholar] [CrossRef] [Green Version]
- Sapienza, R. Determining random lasing action. Nat. Rev. Phys. 2019, 1, 690–695. [Google Scholar] [CrossRef] [Green Version]
- Gomes, A.S. Nanocomposite-Based Random Lasers: A Review on Basics and Applications; Elsevier Inc.: Amsterdam, The Netherlands, 2020; pp. 45–79. [Google Scholar] [CrossRef]
- Gomes, A.S.; Moura, A.L.; de Araújo, C.B.; Raposo, E.P. Recent advances and applications of random lasers and random fiber lasers. Prog. Quantum Electron. 2021, 78, 100343. [Google Scholar] [CrossRef]
- Choi, S.H.; Kim, Y.L. The potential of naturally occurring lasing for biological and chemical sensors. Biomed. Eng. Lett. 2014, 4, 201–212. [Google Scholar] [CrossRef]
- Sznitko, L.; Mysliwiec, J.; Miniewicz, A. The role of polymers in random lasing. J. Polym. Sci. Part B Polym. Phys. 2015, 53, 951–974. [Google Scholar] [CrossRef]
- Luan, F.; Gu, B.; Gomes, A.S.; Yong, K.T.; Wen, S.; Prasad, P.N. Lasing in nanocomposite random media. Nano Today 2015, 10, 168–192. [Google Scholar] [CrossRef]
- Kamil, N.A.I.M.; Ismail, W.Z.W.; Ismail, I.; Balakrishnan, S.R.; Sahrim, M.; Jamaludin, J.; Othman, M.; Suhaimi, S. Principles and characteristics of random lasers and their applications in medical, bioimaging and biosensing. AIP Conf. Proc. 2020, 2203, 20017. [Google Scholar] [CrossRef]
- Azmi, A.N.; Wan Ismail, W.Z.; Abu Hassan, H.; Halim, M.M.; Zainal, N.; Muskens, O.L.; Wan Ahmad Kamil, W.M. Review of Open Cavity Random Lasers as Laser-Based Sensors. ACS Sens. 2022, 7, 914–928. [Google Scholar] [CrossRef] [PubMed]
- Stylianakis, M.M.; Maksudov, T.; Panagiotopoulos, A.; Kakavelakis, G.; Petridis, K. Inorganic and hybrid perovskite based laser devices: A Review. Materials 2019, 12, 859. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Chen, Y.C.; Fan, X. Biological Lasers for Biomedical Applications. Adv. Opt. Mater. 2019, 7, 1900377. [Google Scholar] [CrossRef]
- Pan, T.; Lu, D.; Xin, H.; Li, B. Biophotonic probes for bio-detection and imaging. Light Sci. Appl. Appl. 2021, 10, 124. [Google Scholar] [CrossRef]
- van der Molen, K.L.; Mosk, A.P.; Lagendijk, A. Quantitative analysis of several random lasers. Opt. Commun. 2007, 278, 110–113. [Google Scholar] [CrossRef] [Green Version]
- Van Der Molen, K.L.; Mosk, A.P.; Lagendijk, A. Intrinsic intensity fluctuations in random lasers. Phys. Rev. A At. Mol. Opt. Phys. 2006, 74, 53808. [Google Scholar] [CrossRef] [Green Version]
- Zhai, T.; Zhou, Y.; Chen, S.; Wang, Z.; Shi, J.; Liu, D.; Zhang, X. Pulse-duration-dependent and temperature-tunable random lasing in a weakly scattering structure formed by speckles. Phys. Rev. A At. Mol. Opt. Phys. 2010, 82, 23824. [Google Scholar] [CrossRef]
- Leonetti, M.; López, C. Active subnanometer spectral control of a random laser. Appl. Phys. Lett. 2013, 102, 71105. [Google Scholar] [CrossRef] [Green Version]
- Ignesti, E.; Tommasi, F.; Fini, L.; Lepri, S.; Radhalakshmi, V.; Wiersma, D.; Cavalieri, S. Experimental and theoretical investigation of statistical regimes in random laser emission. Phys. Rev. A 2013, 88, 33820. [Google Scholar] [CrossRef] [Green Version]
- Consoli, A.; Lopez, C. Emission regimes of random lasers with spatially localized feedback. Opt. Express 2016, 24, 10912–10920. [Google Scholar] [CrossRef]
- Redding, B.; Choma, M.A.; Cao, H. Spatial coherence of random laser emission. Opt. Lett. 2011, 36, 3404. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Oliveira, N.T.C.; Vieira, A.M.; Araújo, C.B.D.; Martins, W.S.; Oliveira, R.A.D.; Reyna, A.S. Light Disorder as a Degree of Randomness to Improve the Performance of Random Lasers. Phys. Rev. Appl. 2021, 15, 064062. [Google Scholar] [CrossRef]
- Vieira, A.M.; Oliveira, N.T.C.; De Araújo, C.B.; Martins, W.S.; De Oliveira, R.A.; Reyna, A.S. Influence of the Excitation Light Disorder on the Spatial Coherence in the Stimulated Raman Scattering and Random Lasing Coupled Regime. J. Phys. Chem. C 2021, 125, 5919. [Google Scholar] [CrossRef]
- Leonetti, M.; Conti, C.; Lopez, C. The mode-locking transition of random lasers. Nat. Photonics 2011, 5, 615–617. [Google Scholar] [CrossRef] [Green Version]
- Leonetti, M.; Conti, C.; López, C. Random laser tailored by directional stimulated emission. Phys. Rev. A At. Mol. Opt. Phys. 2012, 85, 43841. [Google Scholar] [CrossRef] [Green Version]
- Kumar, B.; Homri, R.; Priyanka.; Maurya, S.K.; Lebental, M.; Sebbah, P. Localized modes revealed in random lasers. Optica 2021, 8, 1033. [Google Scholar] [CrossRef]
- Tommasi, F.; Ignesti, E.; Fini, L.; Martelli, F.; Cavalieri, S. Random laser based method for direct measurement of scattering properties. Opt. Express 2018, 26, 27615–27627. [Google Scholar] [CrossRef]
- Noginov, M.A.; Zhu, G.; Frantz, A.A.; Novak, J.; Williams, S.N.; Fowlkes, I. Dependence of NdSc3(BO3)4 random laser parameters on particle size. J. Opt. Soc. Am. B 2004, 21, 191. [Google Scholar] [CrossRef]
- Okamoto, T.; Adachi, S. Effect of particle size and shape on nonresonant random laser action of dye-doped polymer random media. Opt. Rev. 2010, 17, 300–304. [Google Scholar] [CrossRef]
- Ning, S.; Dai, K.; Zhang, N.; Zhang, Y.; Wu, Y.; Huang, J.; Xue, T.; Zhang, F. Improving the random lasing performance using Au@SiO2 nanocubes-silver film hybrid structure. J. Lumin. 2021, 231, 117788. [Google Scholar] [CrossRef]
- Fan, S.; Zhang, X.; Wang, Q.; Zhang, C.; Wang, Z. Inflection point of the spectral shifts of the random lasing in dye solution showing transformation to weak localization. In Proceedings of the SPIE 7201, Laser Applications in Microelectronic and Optoelectronic Manufacturing VII, San Jose, CA, USA, 24 February 2009. [Google Scholar] [CrossRef]
- Ye, L.; Feng, Y.; Lu, C.; Hu, G.; Cui, Y. Coherent random lasing from liquid waveguide gain layer containing silica nanoparticles. Laser Phys. Lett. 2016, 13, 105002. [Google Scholar] [CrossRef]
- Shi, X.; Chang, Q.; Tong, J.; Feng, Y.; Wang, Z.; Liu, D. Temporal profiles for measuring threshold of random lasers pumped by ns pulses. Sci. Rep. 2017, 7, 5325. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Uppu, R.; Mujumdar, S. Lévy exponents as universal identifiers of threshold and criticality in random lasers. Phys. Rev. A At. Mol. Opt. Phys. 2014, 90, 25801. [Google Scholar] [CrossRef] [Green Version]
- Lepri, S.; Cavalieri, S.; Oppo, G.L.; Wiersma, D.S. Statistical regimes of random laser fluctuations. Phys. Rev. A At. Mol. Opt. Phys. 2007, 75, 63820. [Google Scholar] [CrossRef] [Green Version]
- Lippi, G.L.; Wang, T.; Puccioni, G.P. Phase Transitions in small systems: Why standard threshold definitions fail for nanolasers. Chaos Solitons Fractals 2022, 157, 111850. [Google Scholar] [CrossRef]
- Ghofraniha, N.; Viola, I.; Di Maria, F.; Barbarella, G.; Gigli, G.; Leuzzi, L.; Conti, C. Experimental evidence of replica symmetry breaking in random lasers. Nat. Commun. 2015, 6, 6058. [Google Scholar] [CrossRef] [Green Version]
- Conti, C.; DelRe, E. Photonics and the Nobel Prize in Physics. Nat. Photonics 2022, 16, 6–7. [Google Scholar] [CrossRef]
- Haddawi, S.F.; Humud, H.R.; Hamidi, S.M. Signature of plasmonic nanoparticles in multi-wavelength low power random lasing. Opt. Laser Technol. 2020, 121, 105770. [Google Scholar] [CrossRef]
- Ismail, W.Z.W.; Dawes, J.M. Synthesis and Characterization of Silver-Gold Bimetallic Nanoparticles for Random Lasing. Nanomaterials 2022, 12, 607. [Google Scholar] [CrossRef]
- Wan, Y.; Wang, H.; Li, H.; Ye, R.; Zhang, X.; Lyu, J.; Cai, Y. Low-threshold random lasers enhanced by titanium nitride nanoparticles suspended randomly in gain solutions. Opt. Express 2022, 30, 8222. [Google Scholar] [CrossRef]
- He, J.; Chan, W.k.E.; Cheng, X.; Tse, M.l.V.; Lu, C.; Wai, P.K.A.; Savovic, S.; Tam, H.Y. Experimental and Theoretical Investigation of the Polymer Optical Fiber Random Laser with Resonant Feedback. Adv. Opt. Mater. 2018, 6, 1701187. [Google Scholar] [CrossRef]
- Pramanik, A.; Biswas, S.; Kumbhakar, P.; Kumbhakar, P. External feedback assisted reduction of the lasing threshold of a continuous wave random laser in a dye doped polymer film and demonstration of speckle free imaging. J. Lumin. 2021, 230, 117720. [Google Scholar] [CrossRef]
- Chen, Y.C.; Chen, Q.; Tan, X.; Chen, G.; Bergin, I.; Aslam, M.N.; Fan, X. Chromatin laser imaging reveals abnormal nuclear changes for early cancer detection. Biomed. Opt. Express 2019, 10, 838. [Google Scholar] [CrossRef] [PubMed]
- Chen, Y.C.; Chen, Q.; Wu, X.; Tan, X.; Wang, J.; Fan, X. A robust tissue laser platform for analysis of formalin-fixed paraffin-embedded biopsies. Lab Chip 2018, 18, 1057–1065. [Google Scholar] [CrossRef]
- Chen, Y.C.; Chen, Q.; Zhang, T.; Wang, W.; Fan, X. Versatile tissue lasers based on high-Q Fabry-Pérot microcavities. Lab Chip 2017, 17, 538–548. [Google Scholar] [CrossRef] [Green Version]
- Wang, W.; Zhou, C.; Zhang, T.; Chen, J.; Liu, S.; Fan, X. Optofluidic laser array based on stable high-Q Fabry-Pérot microcavities. Lab Chip 2015, 15, 3862. [Google Scholar] [CrossRef] [Green Version]
- Karl, M.; Dietrich, C.P.; Schubert, M.; Samuel, I.D.; Turnbull, G.A.; Gather, M.C. Single cell induced optical confinement in biological lasers. J. Phys. D Appl. Phys. 2017, 50, 84005. [Google Scholar] [CrossRef]
- Ignesti, E.; Tommasi, F.; Fini, L.; Martelli, F.; Azzali, N.; Cavalieri, S. A new class of optical sensors: A random laser based device. Sci. Rep. 2016, 6, 35225. [Google Scholar] [CrossRef] [Green Version]
- Zehentbauer, F.M.; Moretto, C.; Stephen, R.; Thevar, T.; Gilchrist, J.R.; Pokrajac, D.; Richard, K.L.; Kiefer, J. Fluorescence spectroscopy of Rhodamine 6G: Concentration and solvent effects. Spectrochim. Acta Part A Mol. Biomol. 2014, 121, 147–151. [Google Scholar] [CrossRef]
- Bavali, A.; Parvin, P.; Mortazavi, S.Z.; Mohammadian, M.; Mousavi Pour, M.R.; Pour, M.R.M. Red / blue spectral shifts of laser-induced fluorescence emission due to different nanoparticle suspensions in various dye solutions. Appl. Opt. 2014, 53, 5398–5409. [Google Scholar] [CrossRef]
- Dominguez, C.T.; Maltez, R.L.; dos Reis, R.M.S.; de Melo, L.S.A.; de Araújo, C.B.; Gomes, A.S.L. Dependence of random laser emission on silver nanoparticle density in PMMA films containing rhodamine 6G. J. Opt. Soc. Am. B 2011, 28, 1118. [Google Scholar] [CrossRef]
- Beckering, G.; Zilker, S.J.; Haarer, D. Spectral measurements of the emission from highly scattering gain media. Opt. Lett. 1997, 22, 1427. [Google Scholar] [CrossRef] [PubMed]
- Ta, V.D.; Caixeiro, S.; Saxena, D.; Sapienza, R. Biocompatible Polymer and Protein Microspheres with Inverse Photonic Glass Structure for Random Micro-Biolasers. Adv. Photonics Res. 2021, 2, 2100036. [Google Scholar] [CrossRef]
- Zhou, H.; Feng, G.; Yao, K.; Yang, C.; Yi, J.; Zhou, S. Fiber-based tunable microcavity fluidic dye laser. Opt. Lett. 2013, 38, 3604. [Google Scholar] [CrossRef]
- El-Dardiry, R.G.; Lagendijk, A. Tuning random lasers by engineered absorption. Appl. Phys. Lett. 2011, 98, 161106. [Google Scholar] [CrossRef]
- Zhang, W.; Cue, N.; Yoo, K.M. Emission linewidth of laser action in random gain media. Opt. Lett. 1995, 20, 961. [Google Scholar] [CrossRef]
- Papadakis, V.M.; Stassinopoulos, A.; Anglos, D.; Anastasiadis, S.H.; Giannelis, E.P.; Papazoglou, D.G. Single-shot temporal coherence measurements of random lasing media. J. Opt. Soc. Am. B 2007, 24, 31. [Google Scholar] [CrossRef]
- Ismail, W.Z.W.; Liu, D.; Clement, S.; Coutts, D.W.; Goldys, E.M.; Dawes, J.M. Spectral and coherence signatures of threshold in random lasers. J. Opt. 2014, 16, 105008. [Google Scholar] [CrossRef]
- Noginov, M.A.; Egarievwe, S.U.; Noginova, N.; Caulfield, H.J.; Wang, J.C. Interferometric studies of coherence in a powder laser. Opt. Mater. 1999, 12, 127–134. [Google Scholar] [CrossRef]
- Yin, L.; Liang, Y.; Yu, B.; Wu, Y.; Ma, J.; Xie, K.; Zhang, W.; Zou, G.; Hu, Z.; Zhang, Q. Quantitative analysis of “Δl = ls - lg” to coherent random lasing in solution systems with a series of solvents ordered by refractive index. RSC Adv. 2016, 6, 98066–98070. [Google Scholar] [CrossRef]
- Cao, M.; Zhang, Y.; Song, X.; Che, Y.; Zhang, H.; Dai, H.; Zhang, G.; Yao, J. Random lasing in a colloidal quantum dot-doped disordered polymer. Opt. Express 2016, 24, 9325. [Google Scholar] [CrossRef] [PubMed]
- Jiang, X.; Feng, S.; Soukoulis, C.M.; Zi, J.; Joannopoulos, J.D.; Cao, H. Coupling, competition, and stability of modes in random lasers. Phys. Rev. B Condens. Matter Mater. Phys. 2004, 69, 104202. [Google Scholar] [CrossRef] [Green Version]
- Jiang, X.; Cao, H.; Ling, Y.; Xu, J.Y.; Soukoulis, C.M. Mode repulsion and mode coupling in random lasers. Phys. Rev. B Condens. Matter Mater. Phys. 2003, 67, 161101(R). [Google Scholar] [CrossRef] [Green Version]
- Lin, S.; Wang, Z.; Li, J.; Chen, S.; Rao, Y.; Peng, G.; Gomes, A.S. Nonlinear dynamics of four-wave mixing, cascaded stimulated Raman scattering and self Q-switching in a common-cavity ytterbium/raman random fiber laser. Opt. Laser Technol. 2021, 134, 106613. [Google Scholar] [CrossRef]
- Vanneste, C.; Sebbah, P. Selective Excitation of Localized Modes in Active Random Media. Phys. Rev. Lett. 2001, 87, 183903. [Google Scholar] [CrossRef]
- Wiersma, D.S.; Bartolini, P.; Lagendijk, A.; Righini, R. Localization of light in a disordered medium. Nature 1997, 390, 671–673. [Google Scholar] [CrossRef]
- Mujumdar, S.; Ricci, M.; Torre, R.; Wiersma, D.S. Amplified extended modes in random lasers. Phys. Rev. Lett. 2004, 93, 53903. [Google Scholar] [CrossRef] [Green Version]
- Yamilov, A.; Wu, X.H.; Cao, H.; Burin, A.L. Absorption induced confinement of lasing modes in diffusive random medium. Opt. Lett. 2005, 30, 2430. [Google Scholar] [CrossRef] [Green Version]
- Apalkov, V.M.; Raikh, M.E.; Shapiro, B. Random resonators and prelocalized modes in disordered dielectric films. Phys. Rev. Lett. 2002, 89, 16802. [Google Scholar] [CrossRef]
- Raikh, M.E.; Apalkov, V.M.; Shapiro, B.; Polson, R.C.; Vardeny, Z.V. Coherent random lasing: Trapping of light by the disorder. Proceedings of SPIE 5472, Noise and Information in Nanoelectronics, Sensors, and Standards II, Maspalomas, Gran Canaria Island, Spain, 25 May 2004. [Google Scholar] [CrossRef]
- Wu, X.; Fang, W.; Yamilov, A.; Chabanov, A.A.; Asatryan, A.A.; Botten, L.C.; Cao, H. Random lasing in weakly scattering systems. Phys. Rev. A 2006, 74, 53812. [Google Scholar] [CrossRef] [Green Version]
- Wu, X.; Cao, H. Statistics of random lasing modes in weakly scattering systems. Opt. Lett. 2007, 32, 3089. [Google Scholar] [CrossRef] [PubMed]
- Vanneste, C.; Sebbah, P.; Cao, H. Lasing with resonant feedback in weakly scattering random systems. Phys. Rev. Lett. 2007, 98, 143902. [Google Scholar] [CrossRef] [PubMed]
- Polson, R.C.; Raikh, M.E.; Vardeny, Z.V. Universal properties of random lasers. IEEE J. Sel. Top. Quantum Electron. 2003, 9, 120–123. [Google Scholar] [CrossRef]
- Cao, H.; Ling, Y.; Xu, J.Y.; Burin, A.L. Probing localized states with spectrally resolved speckle techniques. Phys. Rev. E Stat. Phys. Plasmas Fluids Related Interdiscip. Top. 2002, 66, 25601. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hosseini, M.S.; Yazdani, E.; Sajad, B. Narrow-band random Raman lasing from Rhodamine 6G assisted by cascaded stimulated Raman scattering effect. Sci. Rep. 2021, 11, 21747. [Google Scholar] [CrossRef]
- Hosseini, M.S.; Yazdani, E.; Sajad, B.; Mehradnia, F. Random Raman laser of Rhodamine 6G dye containing ZnO nanospheres. J. Lumin. 2021, 232, 117863. [Google Scholar] [CrossRef]
- De Oliveira, P.C.; Santos, W.Q.; Oliveira, I.N.; Jacinto, C. Random laser and stimulated Raman scattering in liquid solutions of rhodamine dyes. Laser Phys. Lett. 2019, 16, 55002. [Google Scholar] [CrossRef]
- Shi, X.; Chang, Q.; Bian, Y.; Cui, H.; Wang, Z. Line Width-Tunable Random Laser Based on Manipulating Plasmonic Scattering. ACS Photonics 2019, 6, 2245–2251. [Google Scholar] [CrossRef]
- Yashchuk, V.P. Coupled effect of stimulated Raman scattering and random lasing of dyes in multiple scattering medium. Laser Phys. 2015, 25, 75702. [Google Scholar] [CrossRef]
- Réhault, J.; Crisafi, F.; Kumar, V.; Ciardi, G.; Marangoni, M.; Cerullo, G.; Polli, D. Broadband stimulated Raman scattering with Fourier-transform detection. Opt. Express 2015, 23, 25235. [Google Scholar] [CrossRef] [Green Version]
- Hokr, B.H.; Bixler, J.N.; Cone, M.T.; Mason, J.D.; Beier, H.T.; Noojin, G.D.; Petrov, G.I.; Golovan, L.A.; Thomas, R.J.; Rockwell, B.A.; et al. Bright emission from a random Raman laser. Nat. Commun. 2014, 5, 4356. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Gatin, E.; Nagy, P.; Paun, I.; Dubok, O.; Bucur, V.; Windisch, P. Raman Spectroscopy: Application in Periodontal and Oral Regenerative Surgery for Bone Evaluation. Irbm 2019, 40, 279–285. [Google Scholar] [CrossRef]
- Abdallah, A.; Mahmoud, A.; Mokhtar, M.; Mousa, A.; Ayoub, H.S.; Elbashar, Y.H. Raman spectroscopic and advanced signal processing analyses for real time standoff detection and identification of explosives. Opt. Quantum Electron. 2022, 54, 1–21. [Google Scholar] [CrossRef]
- Siddique, M.; Yang, L.; Wang, Q.Z.; Alfano, R.R. Mirrorless laser action from optically pumped dye-treated animal tissues. Opt. Commun. 1995, 117, 475–479. [Google Scholar] [CrossRef]
- Zhai, T.; Wang, Y.; Chen, L.; Wu, X.; Li, S.; Zhang, X. Red-green-blue laser emission from cascaded polymer membranes. Nanoscale 2015, 7, 19935–19939. [Google Scholar] [CrossRef] [PubMed]
- Zhai, T.; Niu, L.; Cao, F.; Tong, F.; Li, S.; Wang, M.; Zhang, X. A RGB random laser on an optical fiber facet. RSC Adv. 2017, 7, 45852–45855. [Google Scholar] [CrossRef] [Green Version]
- Wang, Y.; Shi, X.; Sun, Y.; Zheng, R.; Wei, S.; Shi, J.; Wang, Z.; Liu, D. Cascade-pumped random lasers with coherent emission formed by Ag–Au porous nanowires. Opt. Lett. 2014, 39, 5. [Google Scholar] [CrossRef]
- Chen, S.; Zhao, X.; Wang, Y.; Shi, J.; Liu, D. White light emission with red-green-blue lasing action in a disordered system of nanoparticles. Appl. Phys. Lett. 2012, 101, 123508. [Google Scholar] [CrossRef]
- Hu, M.; Bian, Y.; Shen, H.; Wang, Z. A humidity-tailored film random laser. Org. Electron. 2020, 86, 105923. [Google Scholar] [CrossRef]
- Chen, Z.; Zhang, Y.; Chu, S.; Sun, R.; Wang, J.; Chen, J.; Wei, B.; Zhang, X.; Zhou, W.; Shi, Y.; et al. Grain Boundary Induced Ultralow Threshold Random Laser in a Single GaTe Flake. ACS Appl. Mater. Interfaces 2020, 12, 23323–23329. [Google Scholar] [CrossRef]
- Mujumdar, S.; Cavalieri, S.; Wiersma, D.S. Temperature-tunable random lasing: Numerical calculations and experiments. J. Opt. Soc. Am. B 2004, 21, 201. [Google Scholar] [CrossRef]
- Hisch, T.; Liertzer, M.; Pogany, D.; Mintert, F.; Rotter, S. Pump-controlled directional light emission from random lasers. Phys. Rev. Lett. 2013, 111, 23902. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Leong, E.S.; Yu, S.F.; Abiyasa, A.P.; Lau, S.P. Polarization characteristics of ZnO rib waveguide random lasers. Appl. Phys. Lett. 2006, 88, 2004–2007. [Google Scholar] [CrossRef]
- Shi, X.; Song, W.; Guo, D.; Tong, J.; Zhai, T. Selectively Visualizing the Hidden Modes in Random Lasers for Secure Communication. Laser Photonics Rev. 2021, 15, 2100295. [Google Scholar] [CrossRef]
- Song, Q.; Xiao, S.; Zhou, X.; Liu, L.; Xu, L.; Wu, Y.; Wang, Z. Liquid crystals based tunable high-Q directional random laser from a planar random microcavity. Opt. Infobase Conf. Pap. 2007, 32, 373–375. [Google Scholar] [CrossRef]
- Yao, F.; Zhou, W.; Bian, H.; Zhang, Y.; Pei, Y.; Sun, X.; Lv, Z. Polarization and polarization control of random lasers from dye-doped nematic liquid crystals. Opt. Lett. 2013, 38, 1557. [Google Scholar] [CrossRef]
- Bian, Y.; Yuan, H.; Zhao, J.; Liu, D.; Gong, W.; Wang, Z. External Electric Field Tailored Spatial Coherence of Random Lasing. Crystals 2022, 12, 1160. [Google Scholar] [CrossRef]
- Trivedi, M.; Saxena, D.; Ng, W.K.; Sapienza, R.; Volpe, G. Self-organized lasers from reconfigurable colloidal assemblies. Nat. Phys. 2022, 18, 939–944. [Google Scholar] [CrossRef]
- The Nobel Committee for Physics. Scientific Background on the Nobel Prize in Physics 2021: “For Groundbreaking Contributions to Our Understanding of Complex Physical Systems”; Technical Report; The Nobel Committee for Physics: Stockholm, Sweden, 2022. [Google Scholar]
- Sun, Y.; Wang, Z.; Shi, X.; Wang, Y.; Zhao, X.; Chen, S.; Shi, J.; Zhou, J.; Liu, D. Coherent plasmonic random laser pumped by nanosecond pulses far from the resonance peak of silver nanowires. J. Opt. Soc. Am. B 2013, 30, 2523. [Google Scholar] [CrossRef]
- Zhang, H.; Feng, G.; Zhang, H.; Yang, C.; Yin, J.; Zhou, S. Random laser based on Rhodamine 6G (Rh6G) doped poly (methyl methacrylate) (PMMA) films coating on ZnO nanorods synthesized by hydrothermal oxidation. Results Phys. 2017, 7, 2968–2972. [Google Scholar] [CrossRef]
- Yin, J.; Feng, G.; Zhou, S.; Zhang, H.H.; Wang, S.; Zhang, H.H. The effect of the size of Au nanorods on random laser action in a disordered media of ethylene glycol doped with Rh6G dye. Nanophotonics VI 2016, 9884, 988426. [Google Scholar] [CrossRef]
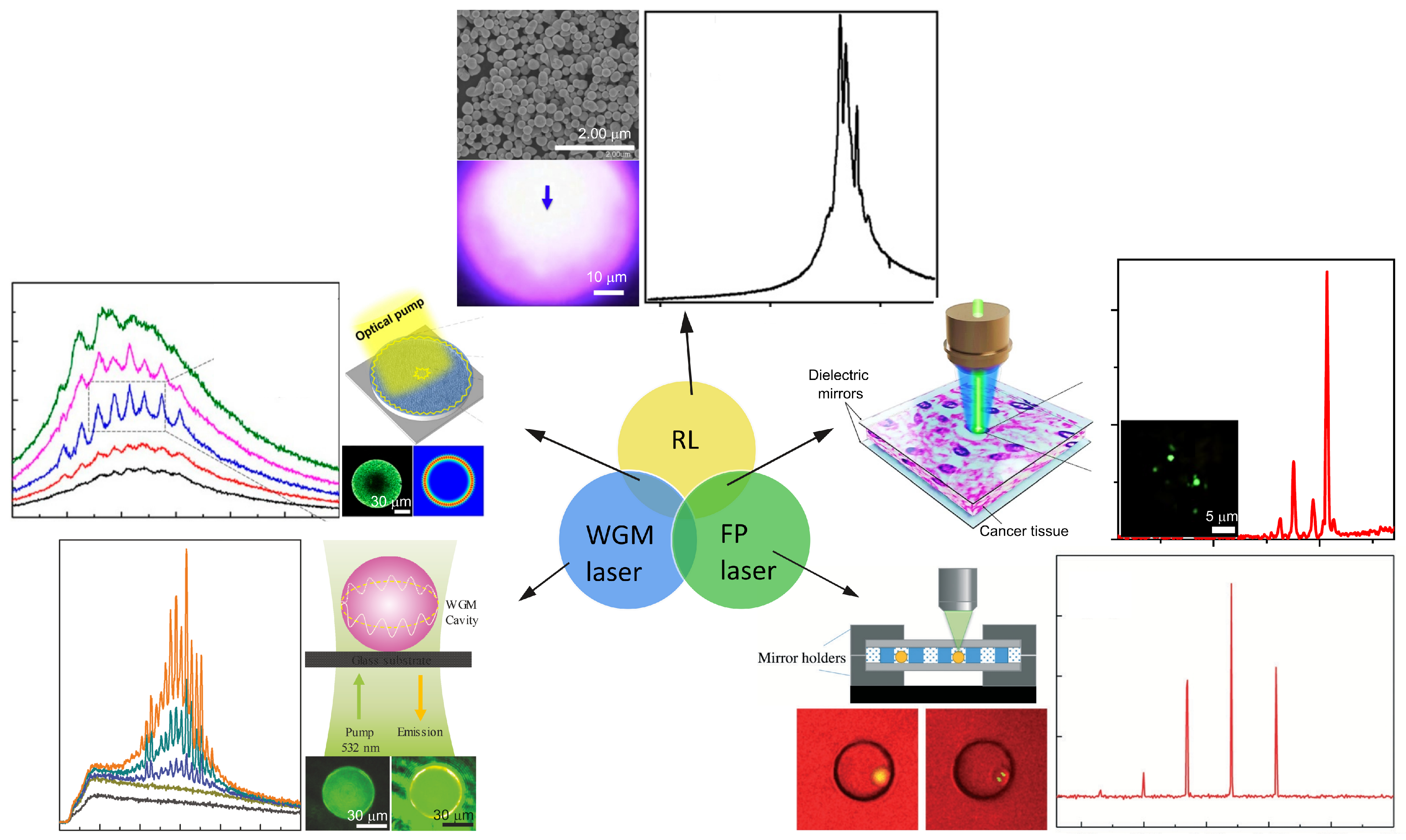

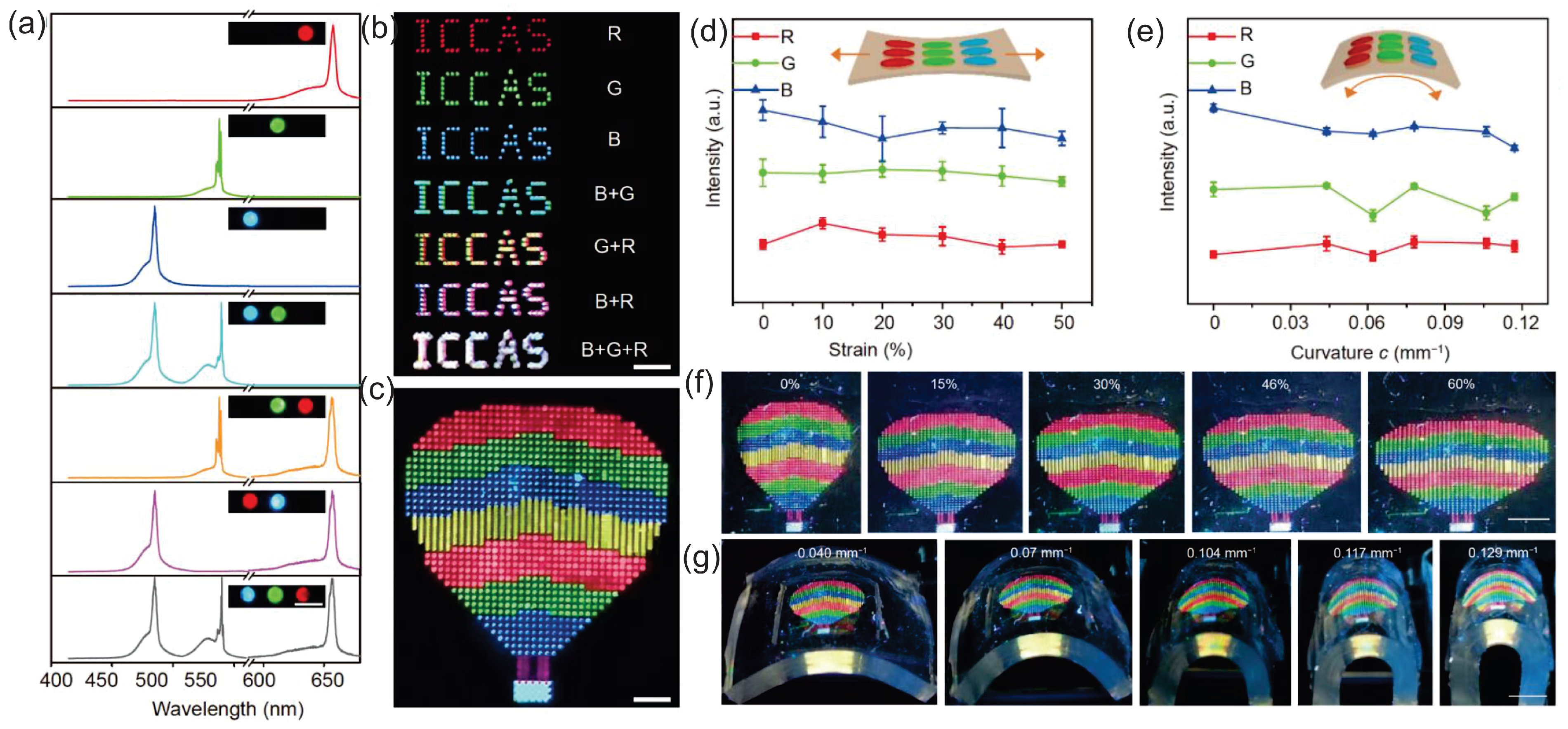
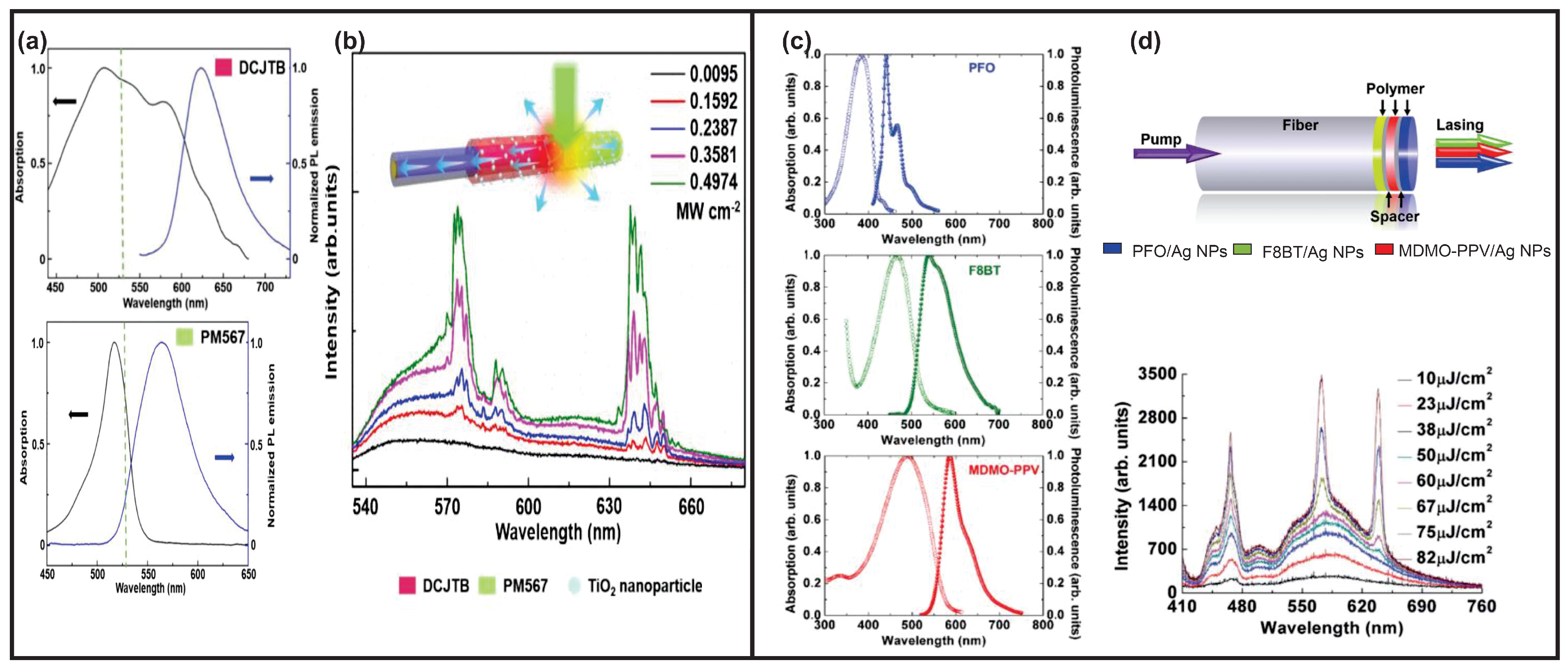

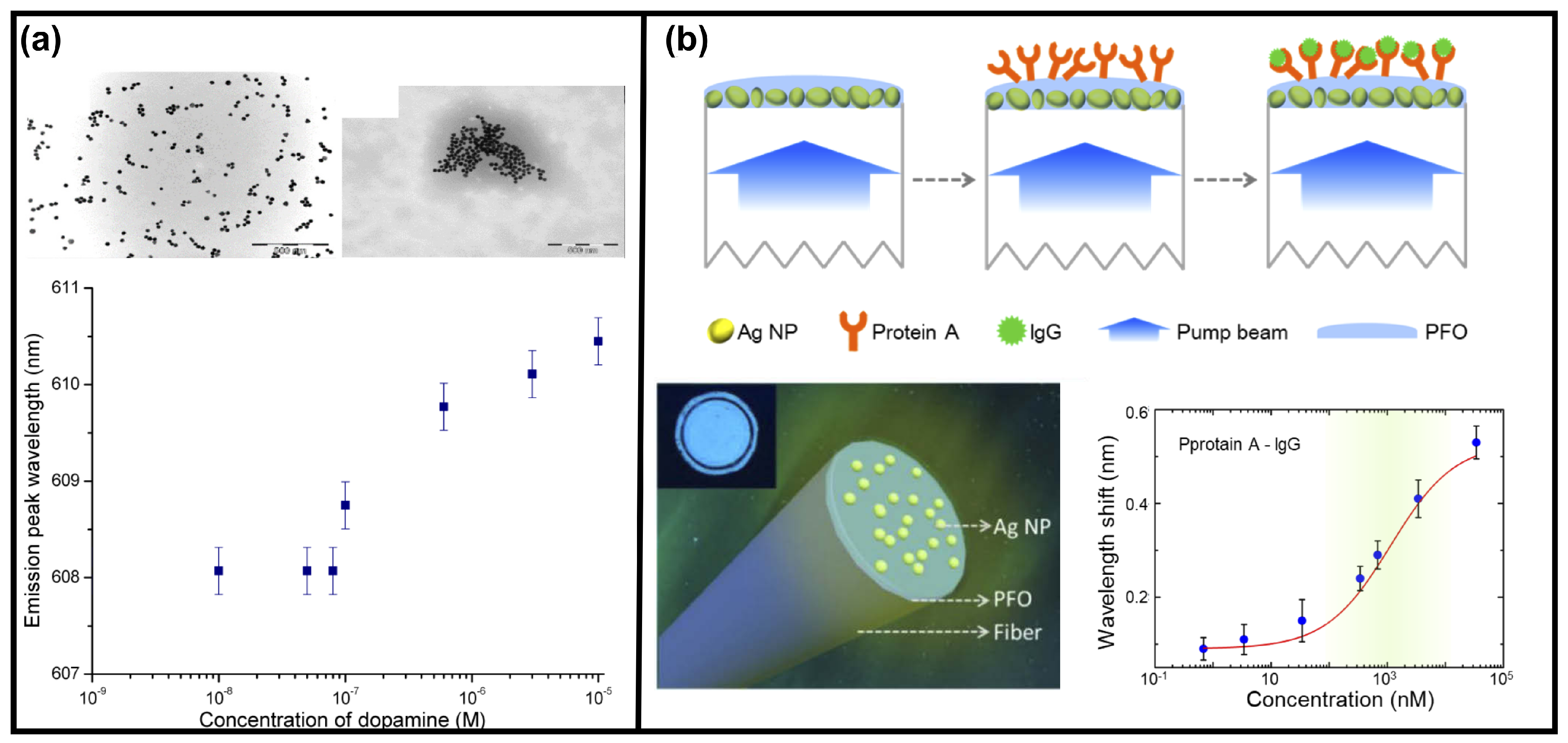
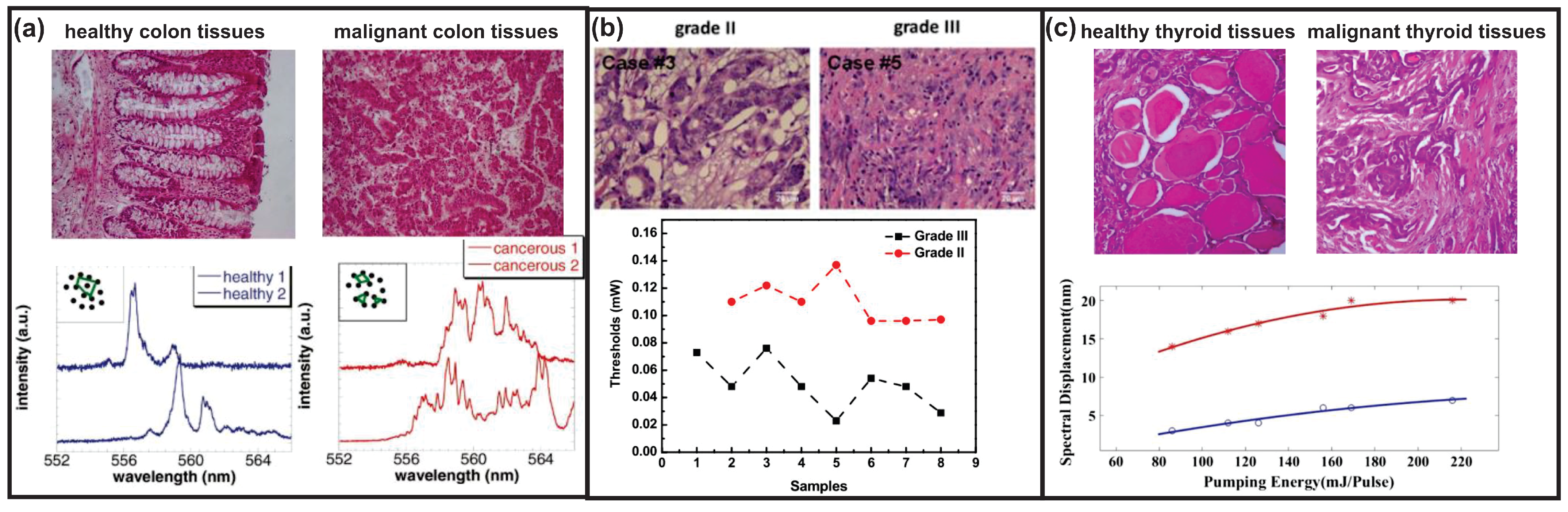
| RL Emission Properties | Influence Factors | Experimental Parameters |
|---|---|---|
| Lasing threshold Tunability Coherence | Illumination | pump temporal profile (pulse duration) [78,79,80,81] |
| pump spatial profile (size and shape) [14,54,80,82,83,84,85,86,87,88] | ||
| Scatterers | concentration [7,15,53,54] | |
| size [89,90,91] | ||
| shape [12,91,92] | ||
| Dye | concentration [7,13,14,53,93] | |
| Solvent | refractive index difference [55,56] | |
| Collection | angles [21,47,60,94] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ni, D.; Späth, M.; Klämpfl, F.; Hohmann, M. Properties and Applications of Random Lasers as Emerging Light Sources and Optical Sensors: A Review. Sensors 2023, 23, 247. https://doi.org/10.3390/s23010247
Ni D, Späth M, Klämpfl F, Hohmann M. Properties and Applications of Random Lasers as Emerging Light Sources and Optical Sensors: A Review. Sensors. 2023; 23(1):247. https://doi.org/10.3390/s23010247
Chicago/Turabian StyleNi, Dongqin, Moritz Späth, Florian Klämpfl, and Martin Hohmann. 2023. "Properties and Applications of Random Lasers as Emerging Light Sources and Optical Sensors: A Review" Sensors 23, no. 1: 247. https://doi.org/10.3390/s23010247
APA StyleNi, D., Späth, M., Klämpfl, F., & Hohmann, M. (2023). Properties and Applications of Random Lasers as Emerging Light Sources and Optical Sensors: A Review. Sensors, 23(1), 247. https://doi.org/10.3390/s23010247








