Weigh-in-Motion System Based on an Improved Kalman and LSTM-Attention Algorithm
Abstract
1. Introduction
2. Establishment of the WIM Filter
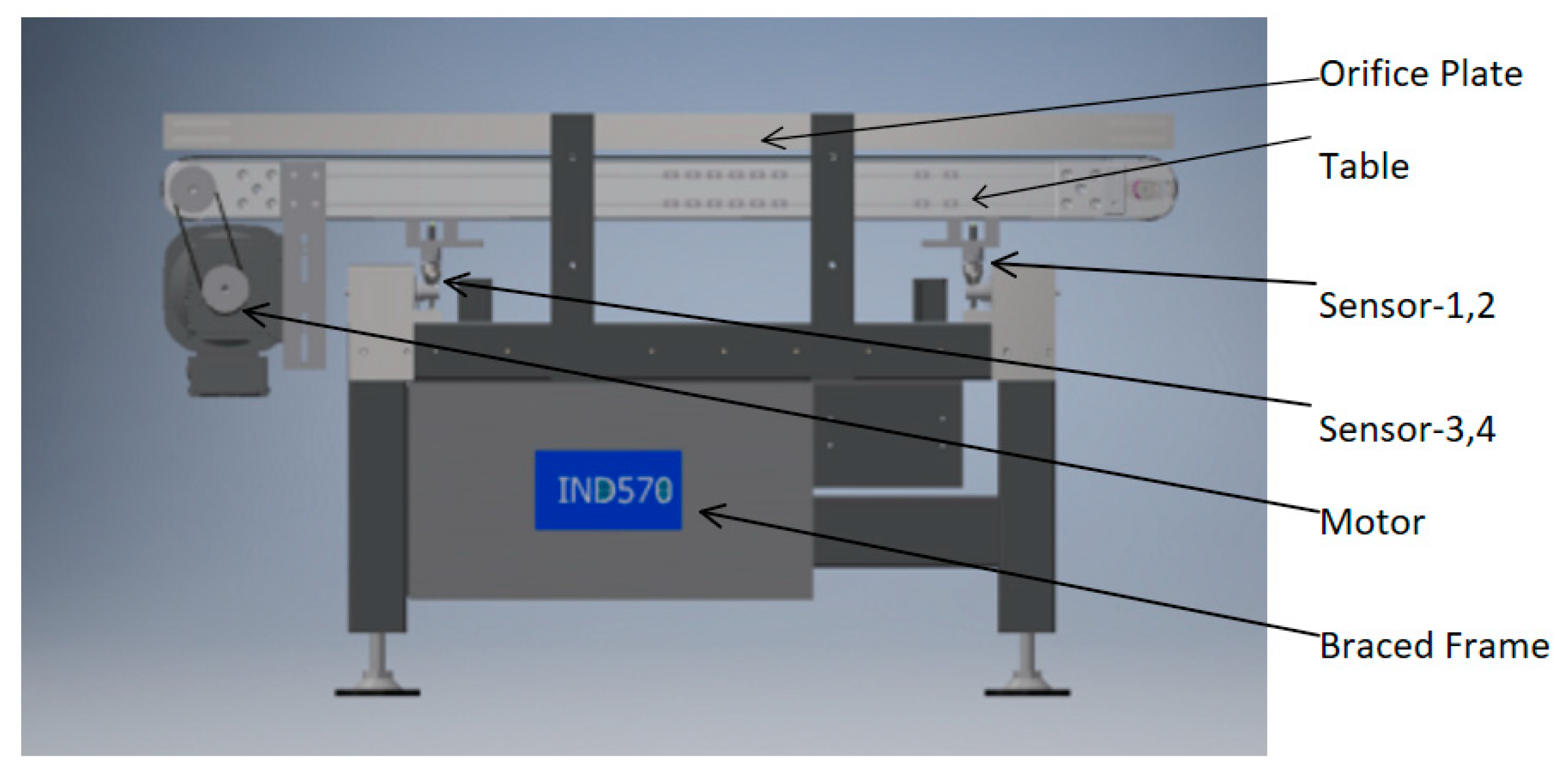
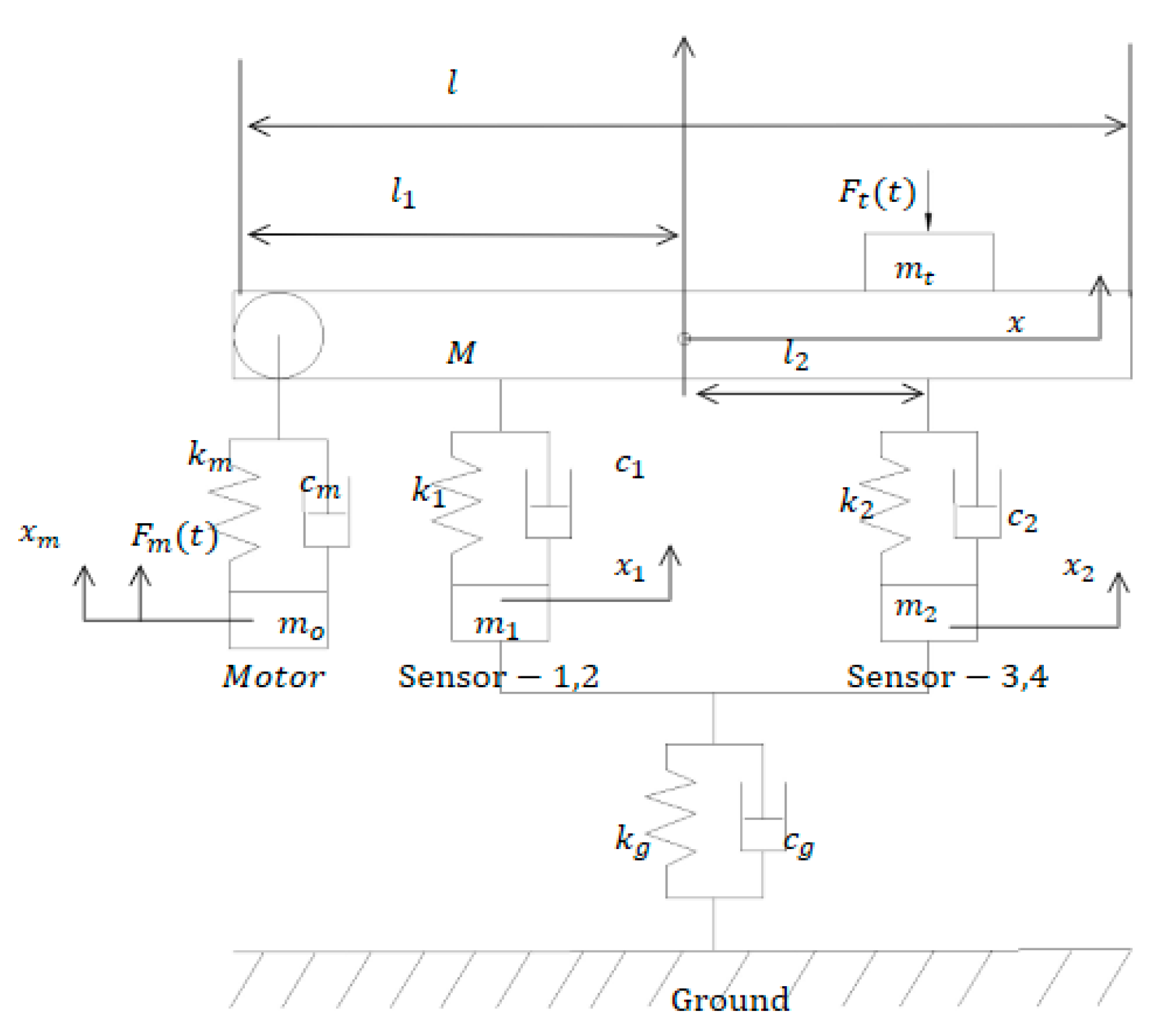
2.1. Establishment and Analysis of the Dynamic Model
- (1)
- The valid sampling point is reduced with increasing belt speed. Compared with Figure 3a,b, the signal is mainly influenced by low-frequency noise in low speed. Vibration noise shows more obvious effects, especially under high load due to sensor-1 and sensor-2 being closed to the cargo input side.
- (2)
- The signal indicates a nonlinearity and nonstationary process with increasing belt speed. More seriously, the measuring process is less than the system steady-state time with the decreasing sampling point, as shown in Figure 3c–f.
- (3)
- The pressure sensor is typically oscillatory underdamped; it is crucial to reduce the various internal and external noise from various working conditions. Self-excited vibration is mainly influenced by the genetic frequency, as a high frequency noise, it differs from other signals and can be filtered by a low-pass filter.
2.2. Algorithm of KFTS
- (1)
- Prediction: Calculate least-square (LS) state based on the state transition matrix and process noise matrix Wk−1. The station of k + 1 can be calculated as follows:where is the WIM system’s state estimation matrix at time tk−1; the state prediction covariance matrix can be described as:where is the WIM’s state-prediction covariance matrix at time tk; is the WIM’s state estimation covariance matrix at time tk−1 and is the adaptive factor at k − 1.
- (2)
- Measurement: Calculate the error vector i(tk) based on the pressure sensor’s actual signal Z (tk), and i (tk) can be described as:where J is the Jacobian matrix of the measurement signal and can be calculated using a numerical differential.
- (3)
- Calculate Parameter: The theoretical innovation matrix Ck, actual innovation matrix , adaptive factor and Kalman gain Kk can be calculated from the following equations:where N is the length of time scale, determined by the sampled frequency, belt speed and length of the tableboard, i.e., the number of sampling points; is the trace of the innovation matrix. The updated value usually deviates from the actual value due to the noises that are from model and measurement error. It is necessary to apply the actual innovation matrix to codetermine adaptive factor . When updating Kk, the self-adapting equation is given as Equation (21):Qk and Rk are reversely adjusted matrices to enhance the estimation accuracy. When is a constant value, the KFTS degrades into the traditional extended Kalman filter.
- (4)
- Output: Calculate the filtered signal at time k:
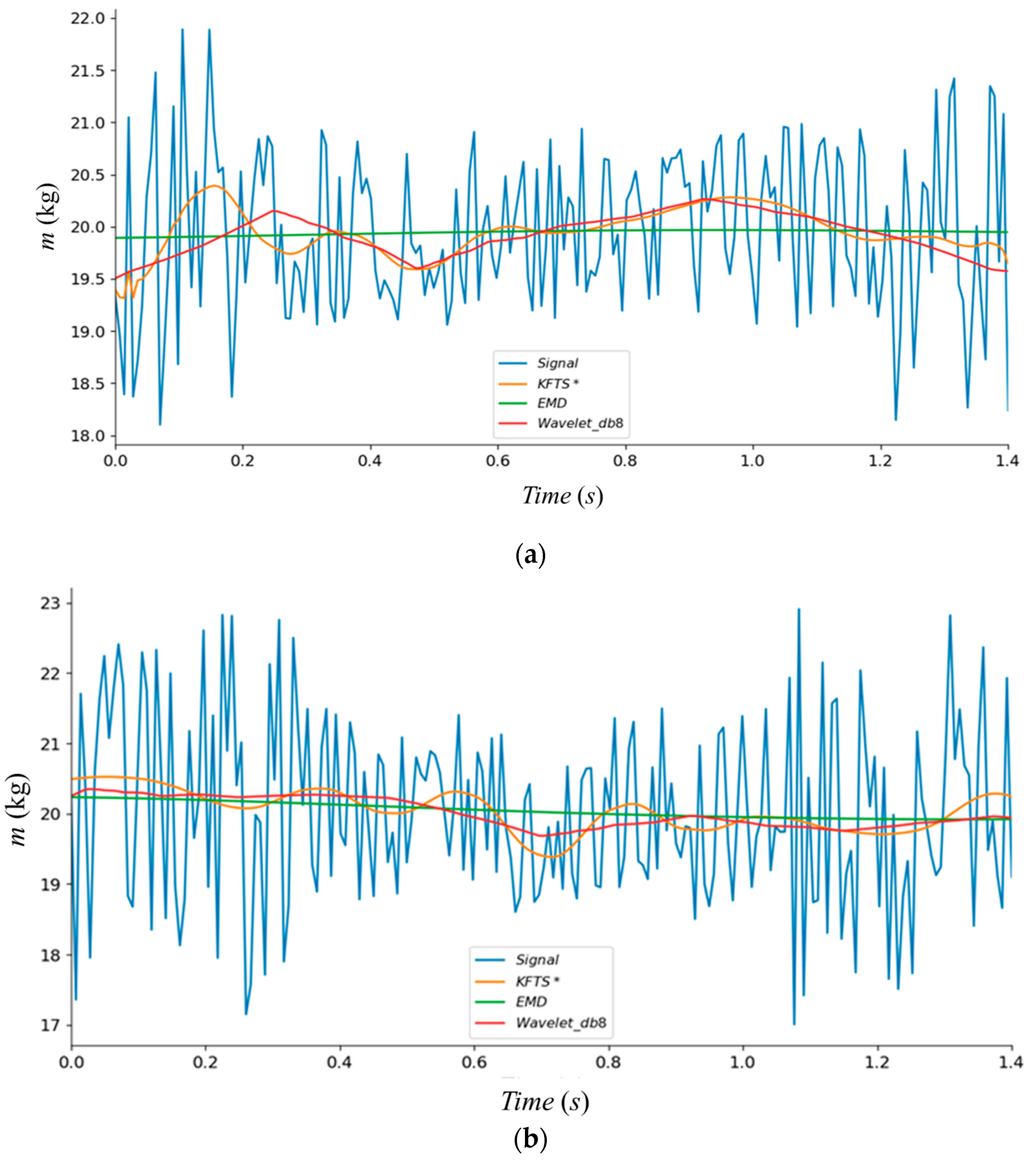
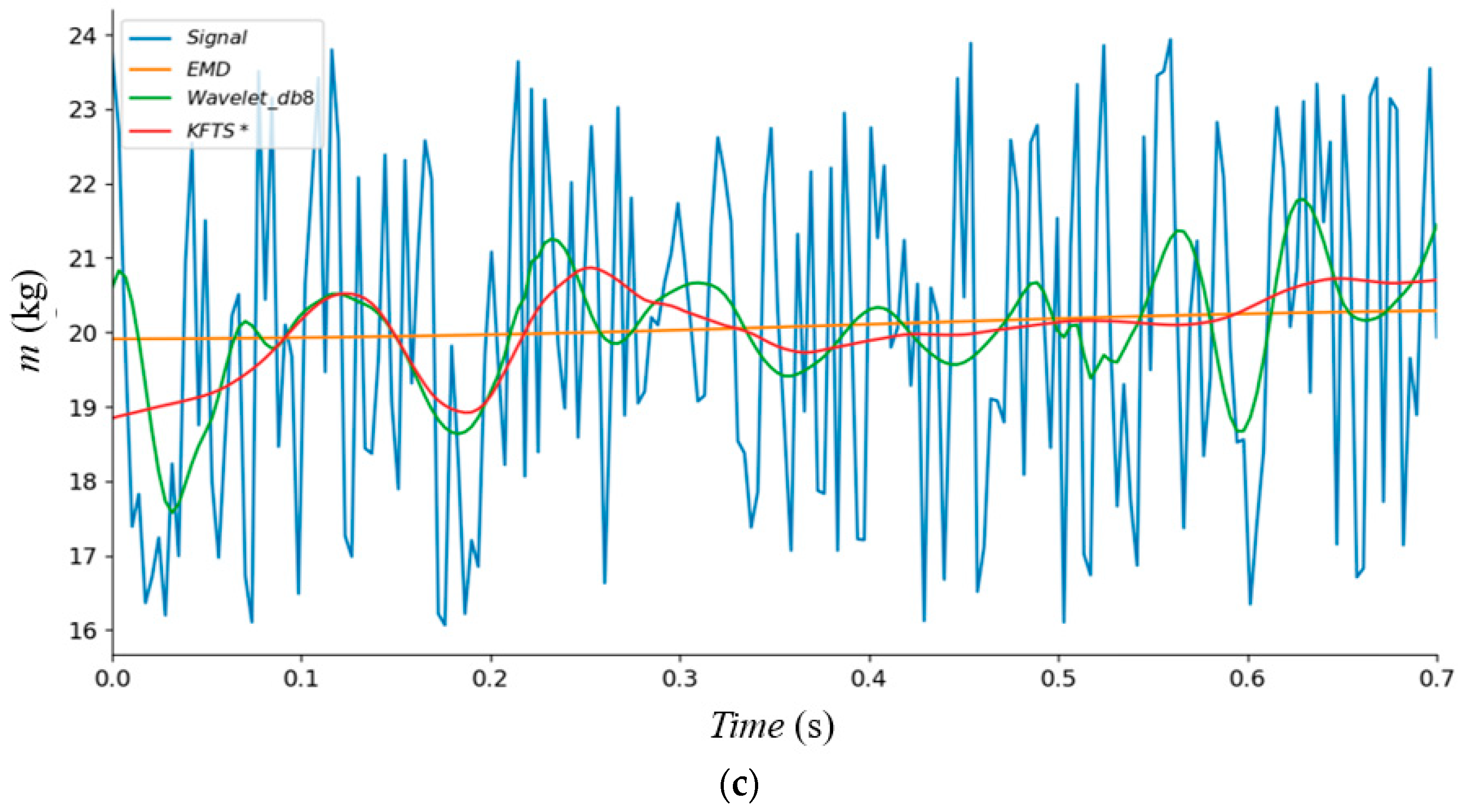
2.3. Performance Comparison
3. Building the Deep Learning Model
3.1. Training Dataset
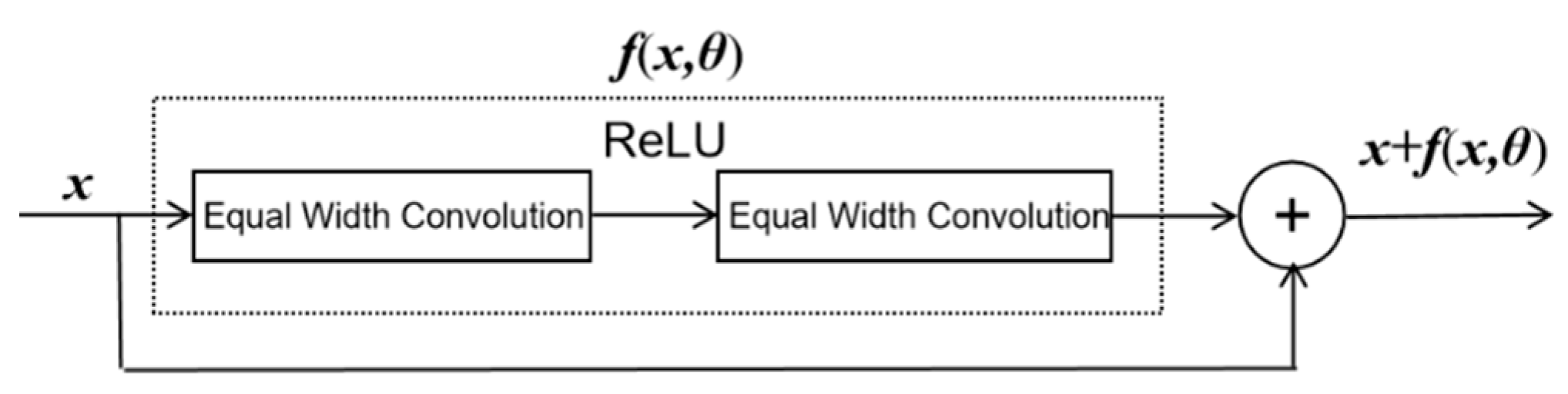
3.2. Residual Connection Module
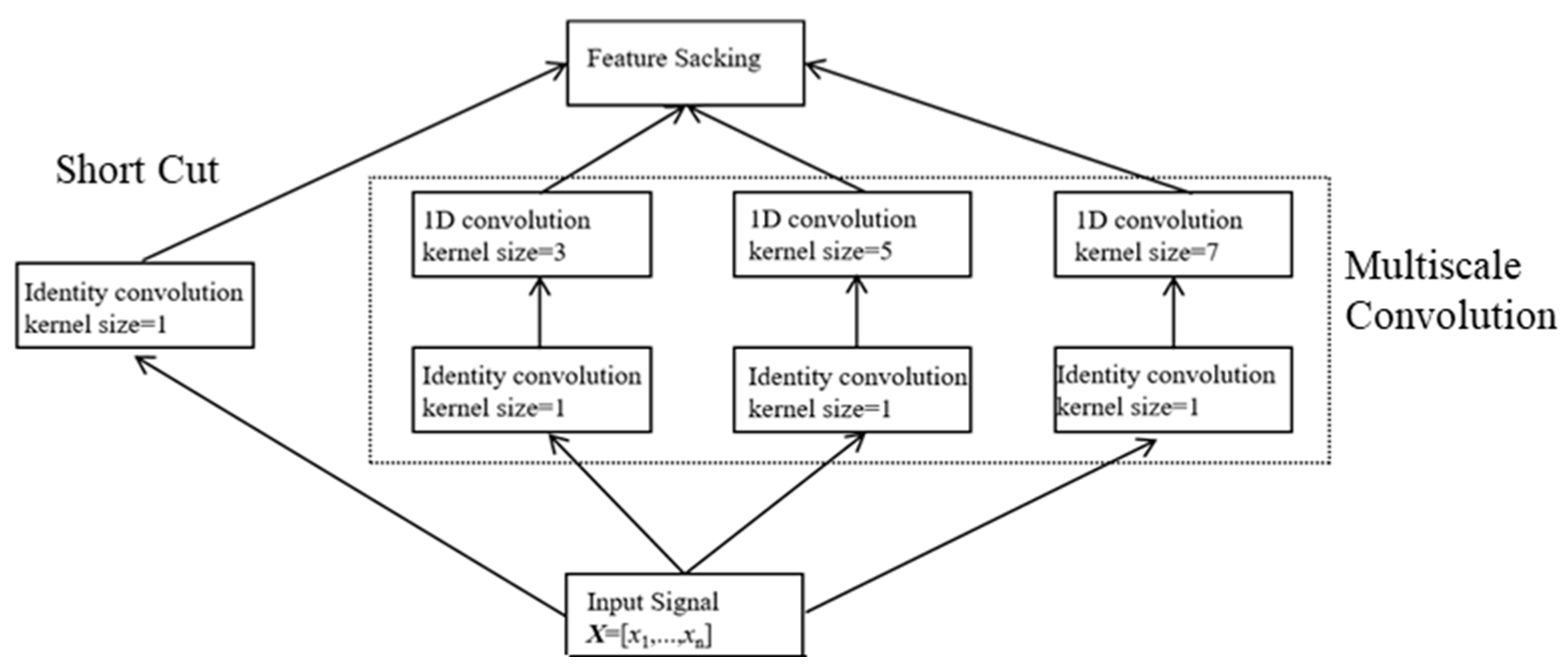
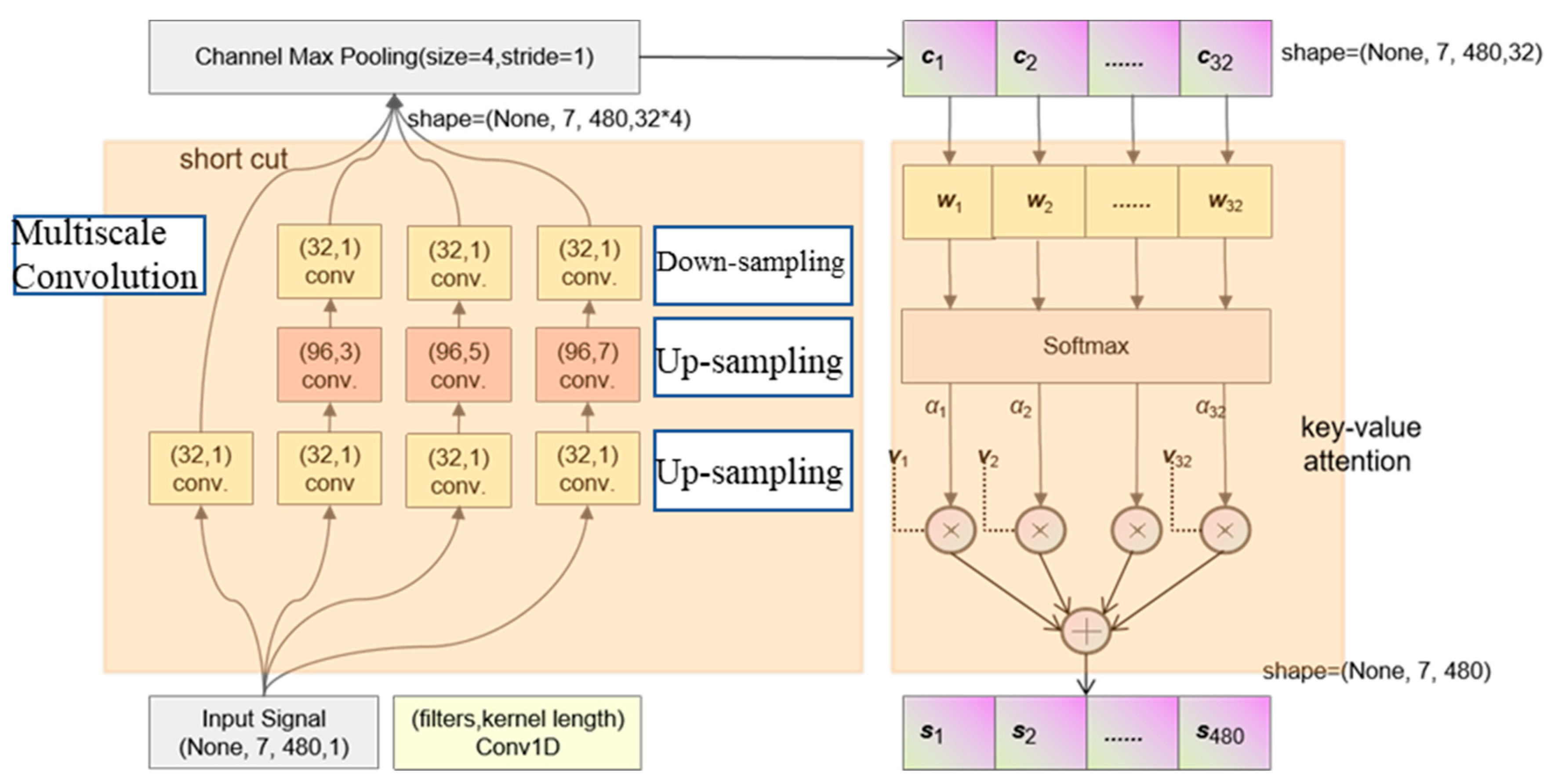
3.3. Multiscale Feature Extraction
3.4. Attention Mechanism Layer
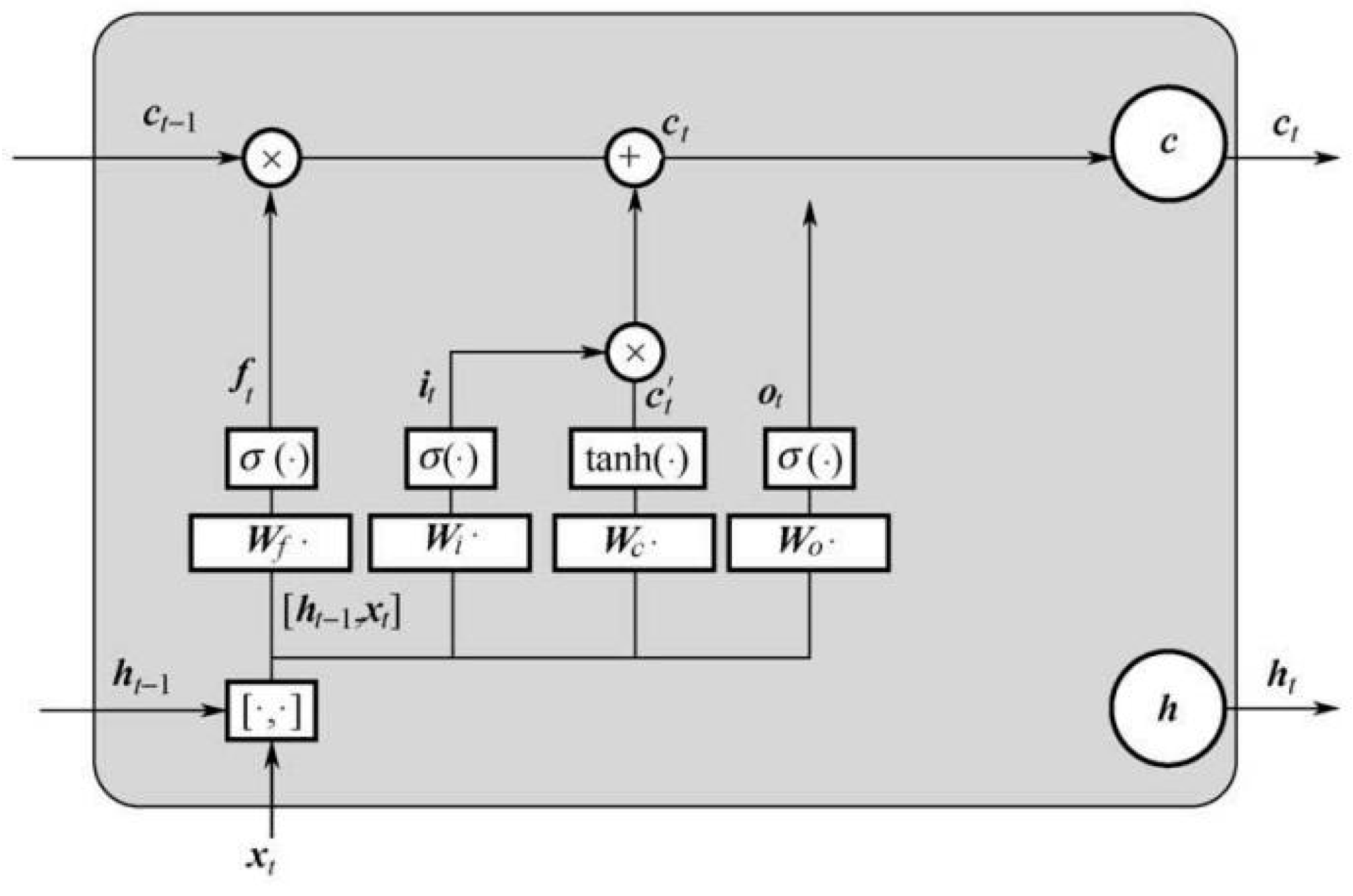
3.5. Long Short-Term Memory (LSTM) Layers
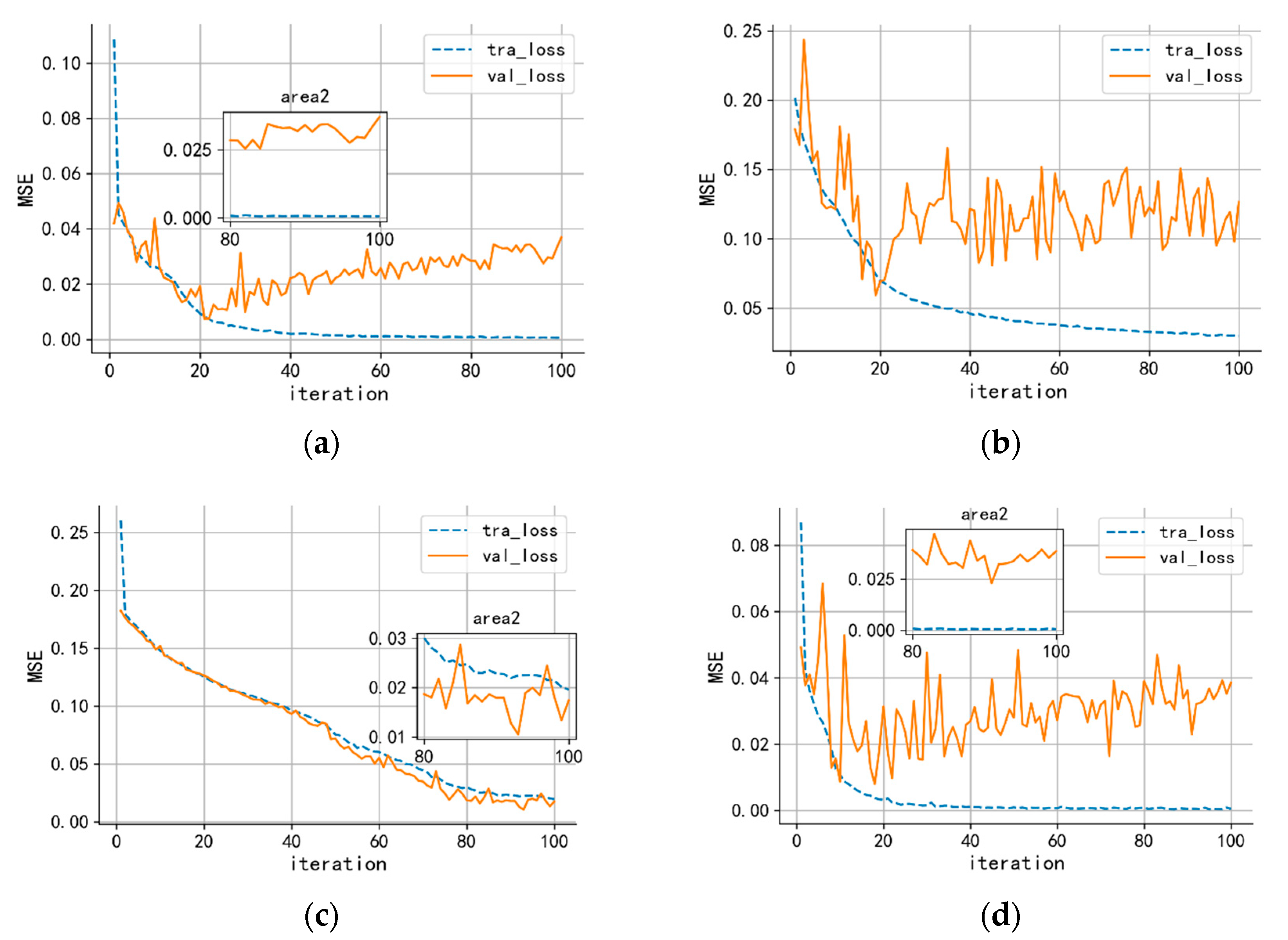
3.6. Model Training
4. Performance under a Practical Engineering Situation
Building the Testing Environment
5. Conclusions
- (1)
- The pressure signal’s noise indicates increasing nonlinearity, greatly affecting the accuracy and stability of the weight check in motion as the speed increases.
- (2)
- The improved Kalman filter can efficiently use the WIM system’s state matrix to estimate the system’s actual situation and filters the noise under different speeds.
- (3)
- Compared with the traditional models, a deep learning-based model decreases error and can greatly improve the system’s measurement accuracy.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Khalili, M.; Vishwakarma, G.; Ahmed, S.; Papagiannakis, A.T. Development of a low-power weigh-in-motion system using cylindrical piezoelectric elements. Int. J. Transp. Sci. Technol. 2022, 11, 496–508. [Google Scholar] [CrossRef]
- Wu, J. Sustainable development of green reverse logistics based on blockchain. Energy Rep. 2022, 8, 11547–11553. [Google Scholar] [CrossRef]
- Liang, Z.; Chiu, Y.-H.; Guo, Q.; Liang, Z. Low-carbon logistics efficiency: Analysis on the statistical data of the logistics industry of 13 cities in Jiangsu Province, China. Res. Transp. Bus. Manag. 2022, 43, 100740. [Google Scholar] [CrossRef]
- Burnos, P.; Gajda, J.; Sroka, R.; Wasilewska, M.; Dolega, C. High Accuracy Weigh-In-Motion Systems for Direct Enforcement. Sensors 2021, 21, 8046. [Google Scholar] [CrossRef] [PubMed]
- Xu, S.; Chen, X.; Fu, Y.; Xu, H.; Hong, K. Research on Weigh-in-Motion Algorithm of Vehicles Based on BSO-BP. Sensors 2022, 22, 2109. [Google Scholar] [CrossRef]
- Yang, H.; Yang, Y.; Hou, Y.; Liu, Y.; Liu, P.; Wang, L.; Ma, Y. Investigation of the Temperature Compensation of Piezoelectric Weigh-In-Motion Sensors Using a Machine Learning Approach. Sensors 2022, 22, 2396. [Google Scholar] [CrossRef]
- Pintão, B.; Mosleh, A.; Vale, C.; Montenegro, P.; Costa, P. Development and Validation of a Weigh-in-Motion Methodology for Railway Tracks. Sensors 2022, 22, 1976. [Google Scholar] [CrossRef]
- Shokravi, H.; Shokravi, H.; Bakhary, N.; Heidarrezaei, M.; Koloor, S.S.R.; Petrů, M. Vehicle-Assisted Techniques for Health Monitoring of Bridges. Sensors 2020, 20, 3460. [Google Scholar] [CrossRef]
- Niedźwiecki, M.; Meller, M.; Pietrzak, P. System identification based approach to dynamic weighing revisited. Mech. Syst. Signal Process. 2016, 80, 582–599. [Google Scholar] [CrossRef]
- Gajda, J.; Sroka, R.; Burnos, P. Sensor Data Fusion in Multi-Sensor Weigh-In-Motion Systems. Sensors 2020, 20, 3357. [Google Scholar] [CrossRef]
- Yee, E.; Stewart, J.P.; Schoenberg, F.P. Characterization and utilization of noisy displacement signals from simple shear device using linear and kernel regression methods. Soil Dyn. Earthq. Eng. 2011, 31, 25–32. [Google Scholar] [CrossRef]
- Manarikkal, I.; Elasha, F.; Mba, D. Diagnostics and prognostics of planetary gearbox using CWT, auto regression (AR) and K-means algorithm. Appl. Acoust. 2021, 184, 108314. [Google Scholar] [CrossRef]
- Botros, J.; Mourad-Chehade, F.; Laplanche, D. CNN and SVM-Based Models for the Detection of Heart Failure Using Electrocardiogram Signals. Sensors 2022, 22, 9190. [Google Scholar] [CrossRef]
- Zhang, Z.; Yin, G.; Wu, Z. Joint Estimation of Mass and Center of Gravity Position for Distributed Drive Electric Vehicles Using Dual Robust Embedded Cubature Kalman Filter. Sensors 2022, 22, 10018. [Google Scholar] [CrossRef]
- Lu, H.; Ge, Z.; Song, Y.; Jiang, D.; Zhou, T.; Qin, J. A temporal-aware LSTM enhanced by loss-switch mechanism for traffic flow forecasting. Neurocomputing 2020, 427, 169–178. [Google Scholar] [CrossRef]
- Masud, M.M.; Haider, S.W. Effect of static weight errors on Weigh-in-Motion (WIM) system accuracy. Measurement 2023, 206, 112301. [Google Scholar] [CrossRef]
- Elbeltagi, R. High Speed Weighing System Analysis via Mathematical Modelling; Massey University: Auckland, New Zealand, 2012. [Google Scholar]
- Halimic, M.; Balachandran, W.; Enab, Y. Fuzzy logic estimator for dynamic weighing system. In Proceedings of the 1996 5th IEEE International Conference on Fuzzy Systems, Part 3 (of 3), New Orleans, LA, USA, 8–11 September 1996; pp. 2123–2129. [Google Scholar]
- Luyao, W. Study on the Linkage Development of Logistics Industry and Agriculture: A Case Study of Kaifeng. In Proceedings of the 2022 8th International Conference on Information Management (ICIM), Cambridge, UK, 25–27 March 2022; pp. 218–222. [Google Scholar] [CrossRef]
- Alonge, F.; Cusumano, P.; D’Ippolito, F.; Garraffa, G.; Livreri, P.; Sferlazza, A. Localization in Structured Environments with UWB Devices without Acceleration Measurements, and Velocity Estimation Using a Kalman–Bucy Filter. Sensors 2022, 22, 6308. [Google Scholar] [CrossRef]
- Huo, Z.; Wang, F.; Shen, H.; Sun, X.; Zhang, J.; Li, Y.; Chu, H. Optimal Compensation of MEMS Gyroscope Noise Kalman Filter Based on Conv-DAE and MultiTCN-Attention Model in Static Base Environment. Sensors 2022, 22, 7249. [Google Scholar] [CrossRef]
- Xiong, K.; Zhou, P.; Wei, C. Autonomous Navigation of Unmanned Aircraft Using Space Target LOS Measurements and QLEKF. Sensors 2022, 22, 6992. [Google Scholar] [CrossRef]
- Okoniewski, P.; Piskorowski, J. A concept of IIR filters with time-varying coefficients and equalised group delay response. Meas. J. Int. Meas. Confed. 2015, 60, 13–24. [Google Scholar] [CrossRef]
- Zhang, J.Y.; Ying, Y.B.; Jiang, H.Y. Application of optimized digital filters and asymmetrically trimmed mean to improve the accuracy of dynamic egg weighing. Trans. ASABE 2017, 60, 1099–1111. [Google Scholar] [CrossRef]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef] [PubMed]
- Burnos, P.; Rys, D. The Effect of Flexible Pavement Mechanics on the Accuracy of Axle Load Sensors in Vehicle Weigh-In-Motion Systems. Sensors 2017, 17, 2053. [Google Scholar] [CrossRef] [PubMed]
- Feng, N.; Kang, X.; Han, H.; Liu, G.; Zhang, Y.; Mei, S. Research on a Dynamic Algorithm for Cow Weighing Based on an SVM and Empirical Wavelet Transform. Sensors 2020, 20, 5363. [Google Scholar] [CrossRef] [PubMed]
- Cai, S.; Chen, D.; Fan, B.; Du, M.; Bao, G.; Li, G. Gait phases recognition based on lower limb sEMG signals using LDA-PSO-LSTM algorithm. Biomed. Signal Process. Control 2023, 80, 104272. [Google Scholar] [CrossRef]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Delving deep into rectifiers: Surpassing human-level performance on imagenet classification. In Proceedings of the International Conference on Computer Vision, Las Condes, Chile, 11–18 December 2015; pp. 1026–1034. [Google Scholar]
- Dai, Y.; Zhou, Q.; Leng, M.; Yang, X.; Wang, Y. Improving the Bi-LSTM model with XGBoost and attention mechanism: A combined approach for short-term power load prediction. Appl. Soft Comput. 2022, 130, 109632. [Google Scholar] [CrossRef]
- Fu, R.; Huang, T.; Li, M.; Sun, Q.; Chen, Y. A multimodal deep neural network for prediction of the driver’s focus of attention based on anthropomorphic attention mechanism and prior knowledge. Expert Syst. Appl. 2023, 214, 119157. [Google Scholar] [CrossRef]
- Lv, H.; Chen, J.; Pan, T.; Zhang, T.; Feng, Y.; Liu, S. Attention mechanism in intelligent fault diagnosis of machinery: A review of technique and application. Measurement 2022, 199, 111594. [Google Scholar] [CrossRef]
- Wang, W.; Li, Q.; Xie, J.; Hu, N.; Wang, Z.; Zhang, N. Research on emotional semantic retrieval of attention mechanism oriented to audio-visual synesthesia. Neurocomputing 2023, 519, 194–204. [Google Scholar] [CrossRef]
- Li, W.; Chakraborty, M.; Sha, Y.; Zhou, K.; Faber, J.; Rümpker, G.; Stöcker, H.; Srivastava, N. A study on small magnitude seismic phase identification using 1D deep residual neural network. Artif. Intell. Geosci. 2022, 3, 115–122. [Google Scholar] [CrossRef]
- Meade, B.J. Reply to: One neuron versus deep learning in aftershock prediction. Nature 2019, 574, E1–E4. [Google Scholar] [CrossRef]



| A—Belt Speed (m/min) | B—Load Weight (kg) | C—Temperature (°C) | |
|---|---|---|---|
| A1B1C1 | 45 | 1 | −10 |
| A1B2C2 | 45 | 5 | 0 |
| A1B3C3 | 45 | 10 | 10 |
| A1B4C4 | 45 | 20 | 20 |
| A1B5C5 | 45 | 30 | 40 |
| A2B1C2 | 60 | 1 | 0 |
| A2B2C3 | 60 | 5 | 10 |
| A2B3C4 | 60 | 10 | 20 |
| A2B4C5 | 60 | 20 | 40 |
| A2B5C1 | 60 | 30 | −10 |
| A3B1C3 | 90 | 1 | 10 |
| A3B2C4 | 90 | 5 | 20 |
| A3B3C5 | 90 | 10 | 40 |
| A3B4C1 | 90 | 20 | −10 |
| A3B5C2 | 90 | 30 | 0 |
| A4B1C4 | 120 | 1 | 20 |
| A4B2C5 | 120 | 5 | 40 |
| A4B3C1 | 120 | 10 | −10 |
| A4B4C2 | 120 | 20 | 0 |
| A4B5C3 | 120 | 30 | 10 |
| SVM | |||
|---|---|---|---|
| v = 30 (m/min) | 0.054 | 0.071 | 0.0700 |
| v = 60 (m/min) | 0.077 | 0.115 | 0.0997 |
| v = 90 (m/min) | 0.121 | 0.157 | 0.1568 |
| v = 120 (m/min) | 0.238 | 0.329 | 0.3084 |
| FCN | |||
|---|---|---|---|
| v = 30 (m/min) | 0.074 | 0.091 | 0.0959 |
| v = 60 (m/min) | 0.107 | 0.183 | 0.1386 |
| v = 90 (m/min) | 0.143 | 0.294 | 0.1853 |
| v = 120 (m/min) | 0.278 | 0.410 | 0.3603 |
| FCN | |||
|---|---|---|---|
| v = 30 (m/min) | 0.046 | 0.0053 | 0.0596 |
| v = 60 (m/min) | 0.097 | 0.0063 | 0.1256 |
| v = 90 (m/min) | 0.115 | 0.0074 | 0.1490 |
| v = 120 (m/min) | 0.218 | 0.0137 | 0.2824 |
| Our Model | |||
|---|---|---|---|
| v = 30 (m/min) | 0.034 | 0.041 | 0.0441 |
| v = 60 (m/min) | 0.057 | 0.091 | 0.0739 |
| v = 90 (m/min) | 0.084 | 0.132 | 0.1089 |
| v = 120 (m/min) | 0.108 | 0.194 | 0.1401 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shi, B.; Jiang, Y.; Bao, Y.; Chen, B.; Yang, K.; Chen, X. Weigh-in-Motion System Based on an Improved Kalman and LSTM-Attention Algorithm. Sensors 2023, 23, 250. https://doi.org/10.3390/s23010250
Shi B, Jiang Y, Bao Y, Chen B, Yang K, Chen X. Weigh-in-Motion System Based on an Improved Kalman and LSTM-Attention Algorithm. Sensors. 2023; 23(1):250. https://doi.org/10.3390/s23010250
Chicago/Turabian StyleShi, Baidi, Yongfeng Jiang, Yefeng Bao, Bingyan Chen, Ke Yang, and Xianming Chen. 2023. "Weigh-in-Motion System Based on an Improved Kalman and LSTM-Attention Algorithm" Sensors 23, no. 1: 250. https://doi.org/10.3390/s23010250
APA StyleShi, B., Jiang, Y., Bao, Y., Chen, B., Yang, K., & Chen, X. (2023). Weigh-in-Motion System Based on an Improved Kalman and LSTM-Attention Algorithm. Sensors, 23(1), 250. https://doi.org/10.3390/s23010250







