Data-Driven Low-Frequency Oscillation Event Detection Strategy for Railway Electrification Networks
Abstract
:1. Introduction
- An automatic fault detection strategy based on ML is designed and implemented. Most of the studies carried out to date have focused only on the LFO event modelling and analysis of the possible causes [5,6,7,8,9,10,11,12]. The authors in [7] also analyse the influence that the characteristics of the traction units have on the occurrence of oscillations. This could lead to hardware and control software design improvements to mitigate these events.
- The dataset used for both training and testing of the algorithms is based on field data. That is, the industrial partner has detected and recorded manually different LFO events during the operation of its train fleet, which facilitates the development of supervised ML methodologies. This differs from the rest of the articles, as most of them are based on simulation or testbench data.
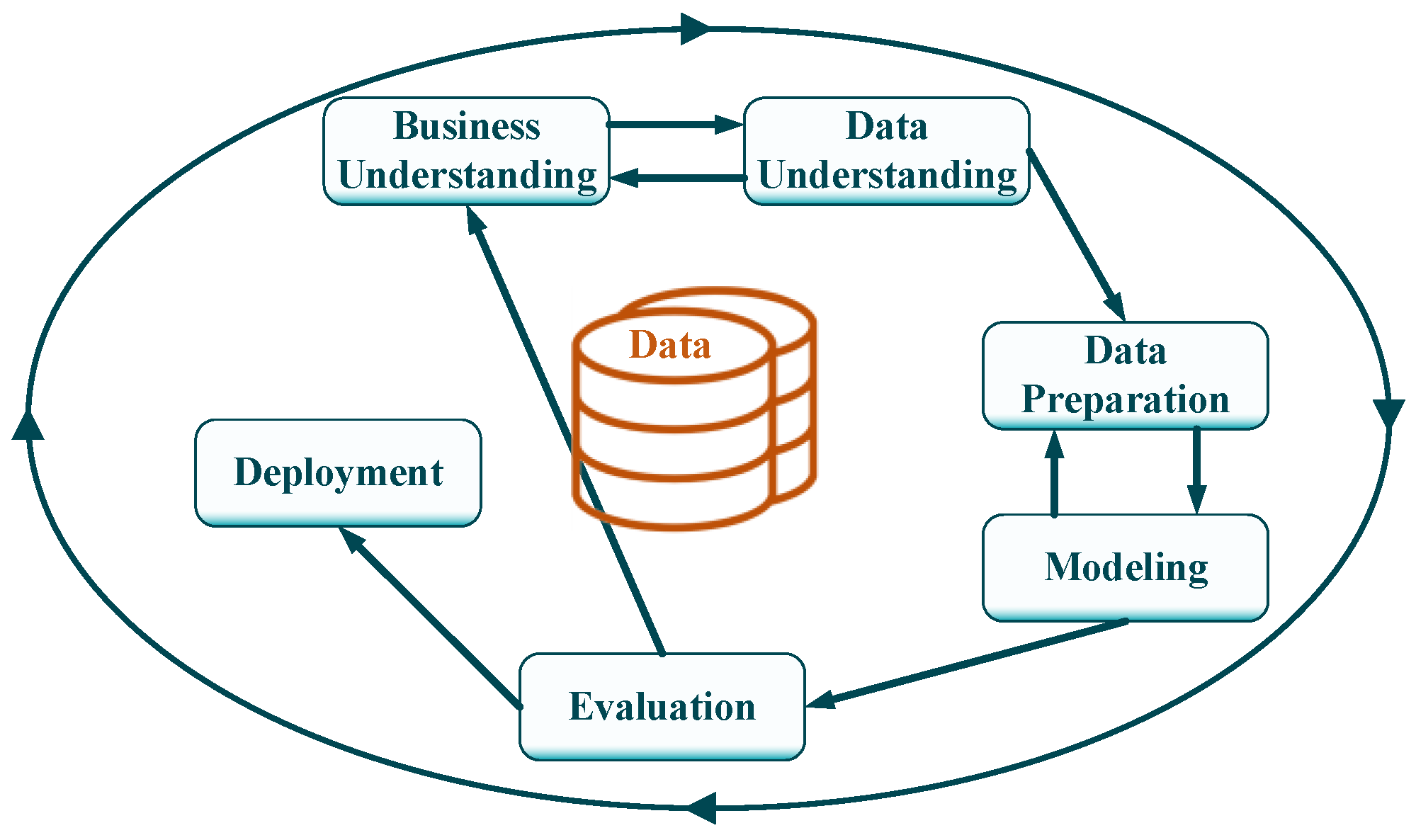
- Most DM scientific works follow the same steps to prepare data, train ML models, and evaluate their results. However, they do not follow any industry standard, which could make it difficult to deploy in an industrial application. Therefore, in this research, the DM project is structured based on the CRISP-DM methodology, established as the de facto approach for industrial DM projects [13,14,15]. Figure 1 shows the CRISP-DM methodology and its main steps.
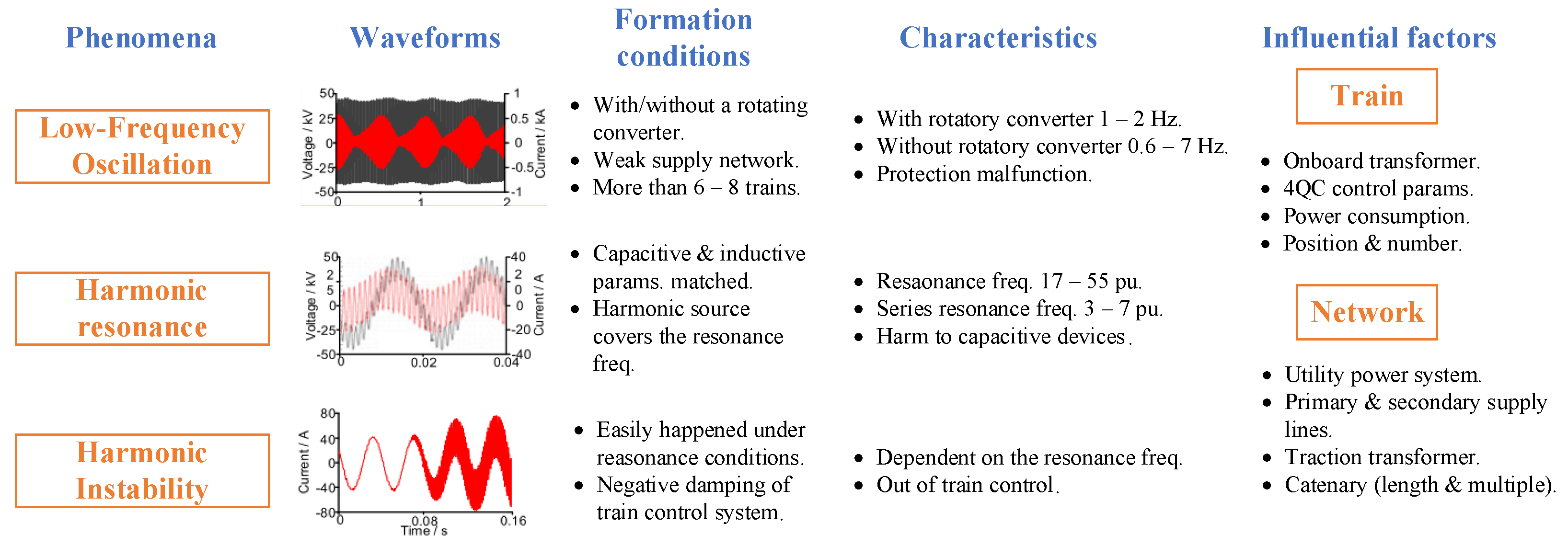
2. Power Quality and Stability Problems in Railway Applications
- 1.
- In a railway system which has adopted the rotary frequency converter (RFC) as the power supply solution. The typical oscillatory frequency () is approximately 10–30% of the respective power system’s fundamental frequency ().
- 2.
- In a railway system equipped with a static frequency converter (SFC) as a power supply solution and where several trains with four quadrant converters are in standby mode (auxiliary loads) located in the same railway depot, away from the traction substation (TSS). This leads to a 0.6–7 Hz LFO of the catenary voltage.
- The number of vehicles and the load current in the same network sector.
- The contact line distance. The longer the contact line is, the larger the source impedance that increases the probability of instabilities will be.
- The line side traction converter control parameter tuning.
3. Data Preparation
3.1. Data Selection
3.2. Data Cleaning
- Standardizing and adapting variable names.
- Filtering null values and replacing them using forward and backward filling techniques.
- Detecting and cleaning outliers.
3.3. Data Construction
4. Model Training
4.1. Training Phase
- Logistic regression (LR).
- Support vector machines (SVM).
- Random forest (RF).
- Naïve Bayes (NB).
- k-Nearest neighbours (kNN).
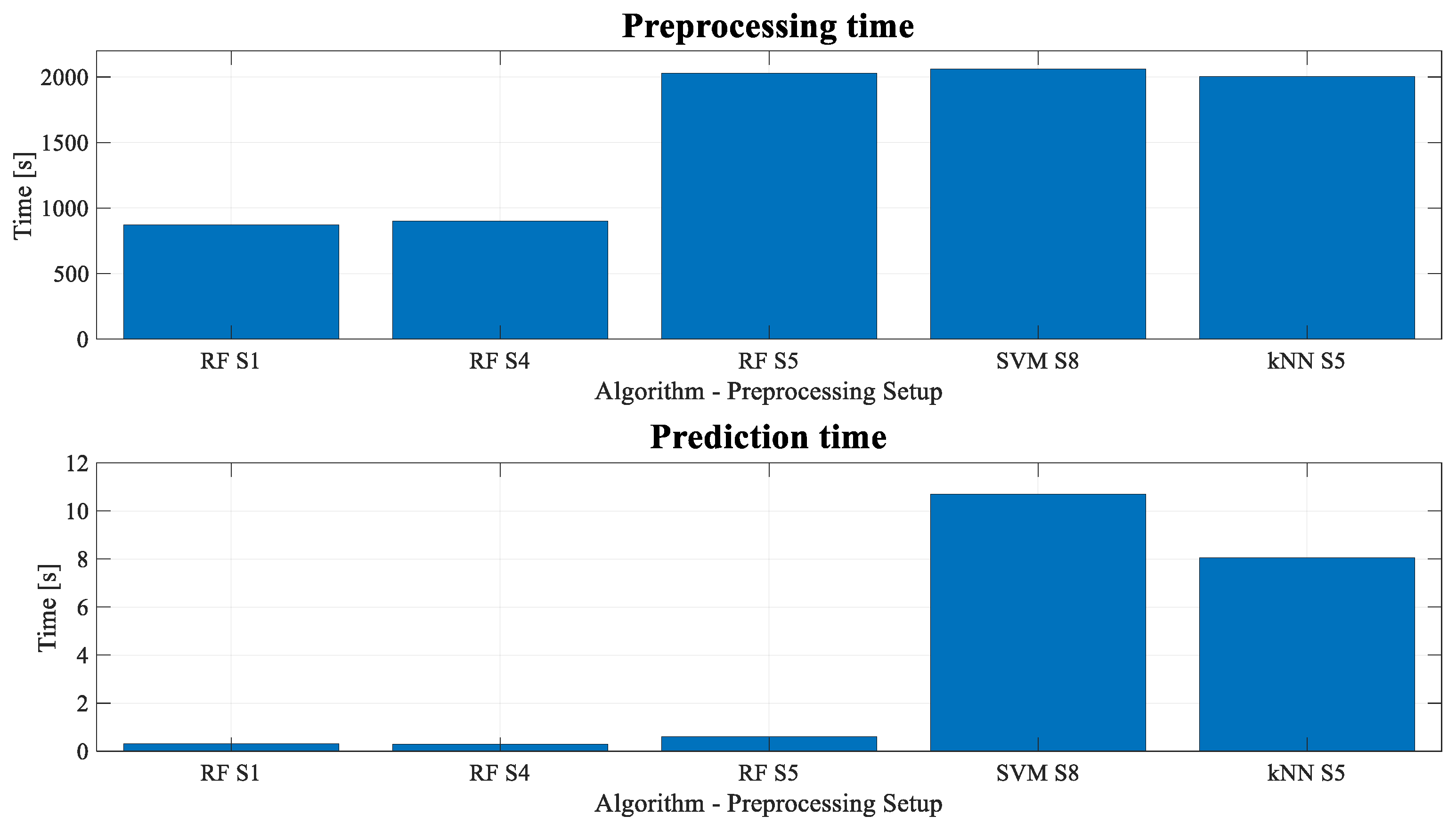
4.2. Model Assessment
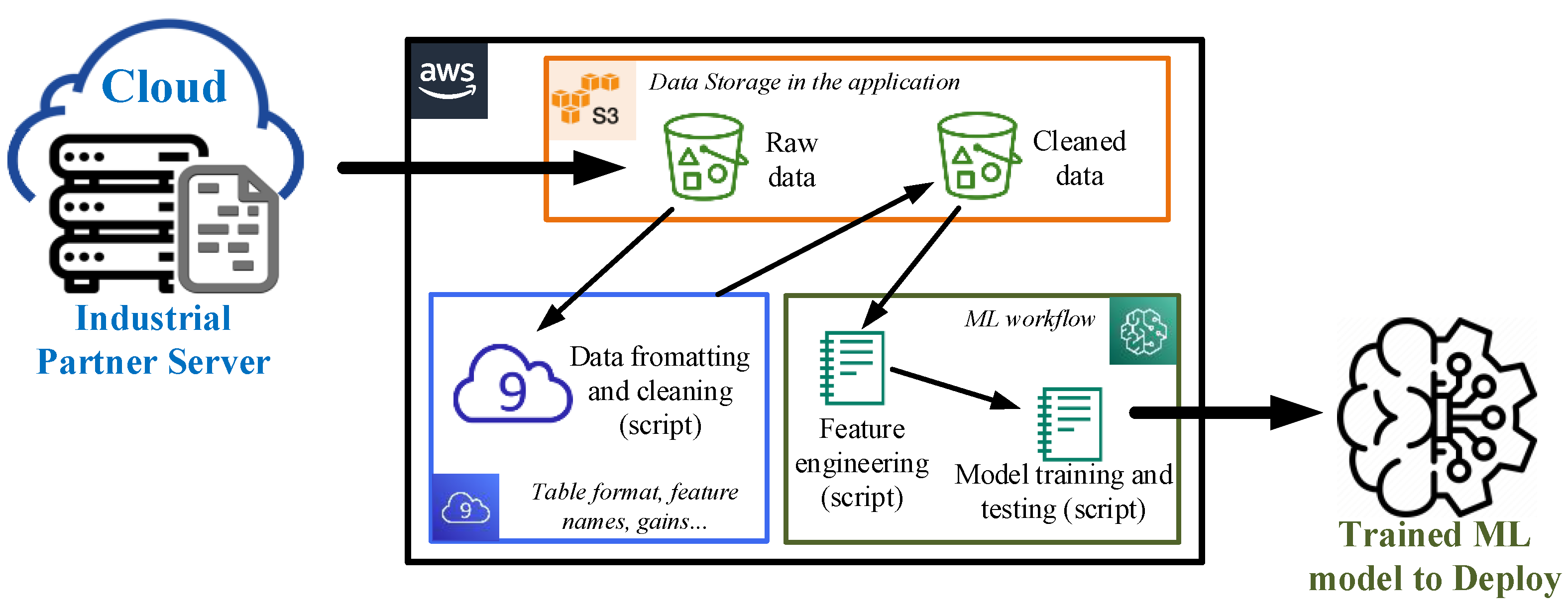
5. Deployment
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| ML | Machine Learning |
| CRISP-DM | Cross-Industry Standard Process for Data Mining |
| LFO | Low-Frequency Oscillation |
| TCU | Traction Control Unit |
| SND | Standard Normal Distribution |
| SVM | Support Vector Machine |
| RF | Random Forest |
| kNN | k Nearest Neighbour |
| NB | Naïve Bayes |
| AWS | Amazon Web Services |
References
- Ebrahimzadeh, E.; Blaabjerg, F.; Wang, X.; Bak, C.L. Modeling and Identification of Harmonic Instability Problems in Wind Farms. In Proceedings of the 2016 IEEE Energy Conversion Congress and Exposition (ECCE), Milwaukee, WI, USA, 18–22 September 2016; IEEE: Piscataway, NJ, USA, 2016; pp. 1–6. [Google Scholar]
- Li, T.; Gole, A.M.; Zhao, C. Harmonic Instability in MMC-HVDC Converters Resulting From Internal Dynamics. IEEE Trans. Power Deliv. 2016, 31, 1738–1747. [Google Scholar] [CrossRef]
- Hu, H.; Zhou, Y.; Li, X.; Lei, K. Low-Frequency Oscillation in Electric Railway Depot: A Comprehensive Review. IEEE Trans. Power Electron. 2021, 36, 295–314. [Google Scholar] [CrossRef]
- EN 50388:2012 (EN); European Standards (EN); Railway Applications—Fixed Installations and Rolling Stock—Technical Criteria for the Coordination between Power Supply and Rolling Stock to Achieve Interoperability—Part 2: Stability and Harmonics. Available online: https://standards.iteh.ai/catalog/standards/clc/fd5d3267-2aed-42f9-add6-d7bfcac78762/en-50388-2012 (accessed on 23 November 2022).
- Hu, H.; Tao, H.; Blaabjerg, F.; Wang, X.; He, Z.; Gao, S. Train–Network Interactions and Stability Evaluation in High-Speed Railways–Part I: Phenomena and Modeling. IEEE Trans. Power Electron. 2018, 33, 4627–4642. [Google Scholar] [CrossRef]
- Hu, H.; Tao, H.; Wang, X.; Blaabjerg, F.; He, Z.; Gao, S. Train–Network Interactions and Stability Evaluation in High-Speed Railways—Part II: Influential Factors and Verifications. IEEE Trans. Power Electron. 2018, 33, 4643–4659. [Google Scholar] [CrossRef]
- Frutos, P.; Ladoux, P.; Roux, N.; Larrazabal, I.; Guerrero, J.M.; Briz, F. Low Frequency Stability of AC Railway Traction Power Systems: Analysis of the Influence of Traction Unit Parameters. Electronics 2022, 11, 1593. [Google Scholar] [CrossRef]
- Wang, Y.; Li, T.; Liu, J.; Liu, F.; Su, Y.; Zhang, Q.; Zhang, W.; Liu, Z. Modeling and Analysis of Low-Frequency Oscillation for Electrified Railway under Mixed Operation of Passenger and Freight Trains. Energies 2022, 15, 7544. [Google Scholar] [CrossRef]
- Zhou, Y.; Hu, H.; Yang, X.; Yang, J.; He, Z.; Gao, S. Low Frequency Oscillation Traceability and Suppression in Railway Electrification Systems. IEEE Trans. Ind. Appl. 2019, 55, 7699–7711. [Google Scholar] [CrossRef]
- Laury, J. Stability of Low-Frequency AC Railways Models and Transient Stability. Ph.D. Thesis, Luleå University of Technology, Luleå, Sweden, 2019. [Google Scholar]
- Cheng, S.; Ma, L.; Ge, X.; Peng, L.; Liu, H. Low-Frequency Oscillation Analysis in Train-Traction Power Supply System Using an SISO Voltage Loop Model. IEEE Trans. Transp. Electrif. 2022, 8, 636–648. [Google Scholar] [CrossRef]
- Paul, F.G.; Guerrero, J.M.; Muniategui-Aspiazu, I.; Vicente-Makazaga, I.; Endemano-Isasi, A.; Ortega-Rodriguez, D.; Briz, F. Power-Hardware-in-the-Loop Emulation of the Low-Frequency Oscillation Phenomenon in AC Railway Networks. IEEE Access 2022, 10, 87374–87386. [Google Scholar] [CrossRef]
- Pete, C.; Julian, C.; Randy, K.; Thomas, K.; Thomas, R.; Colin, S.; Wirth, R. Crisp-Dm 1.0. Step-by-Step Data Mining Guide; SPSS lnc.: Chicago, IL, USA, 2000. [Google Scholar]
- Martinez-Plumed, F.; Contreras-Ochando, L.; Ferri, C.; Hernandez-Orallo, J.; Kull, M.; Lachiche, N.; Ramirez-Quintana, M.J.; Flach, P. CRISP-DM Twenty Years Later: From Data Mining Processes to Data Science Trajectories. IEEE Trans. Knowl. Data Eng. 2021, 33, 3048–3061. [Google Scholar] [CrossRef] [Green Version]
- Saleh, S.J.; Ali, S.Q.; Zeki, A.M. Random Forest vs. SVM vs. KNN in Classifying Smartphone and Smartwatch Sensor Data Using CRISP-DM. In Proceedings of the 2020 International Conference on Data Analytics for Business and Industry: Way Towards a Sustainable Economy (ICDABI). Sakheer, Bahrain, 26 October 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 1–4. [Google Scholar]
- Möllerstedt, E.; Bernhardsson, B. Out of Control Because of Harmonics-an Analysis of the Harmonic Response of an Inverter Locomotive. IEEE Control Syst. 2000, 20, 70–81. [Google Scholar] [CrossRef]
- Danielsen, S. Electric Traction Power System Stability: Low-Frequency Interaction between Advanced Rail Vehicles and a Rotary Frequency Converter. Ph.D. Thesis, Norwegian University of Science and Technology, Trondheim, Norway, 2010. [Google Scholar]
- Hu, H.; Tao, H.; Blaabjerg, F.; Wang, X.; He, Z.; Gao, S. Atlab. IEEE Trans. Power Electron. 2018, 33, 4627–4642. [Google Scholar] [CrossRef]
- Wang, H.; Mingli, W.; Sun, J. Analysis of Low-Frequency Oscillation in Electric Railways Based on Small-Signal Modeling of Vehicle-Grid System in Dq Frame. IEEE Trans. Power Electron. 2015, 30, 5318–5330. [Google Scholar] [CrossRef]
- Pan, P.; Hu, H.; Yang, X.; Blaabjerg, F.; Wang, X.; He, Z. Impedance Measurement of Traction Network and Electric Train for Stability Analysis in High-Speed Railways. IEEE Trans. Power Electron. 2018, 33, 10086–10100. [Google Scholar] [CrossRef]
- Danielsen, S.; Molinas, M.; Toftevaag, T.; Fosso, O.B. Constant Power Load Characteristic’s Influence on the Low-Frequency Interaction between Advanced Electrical Rail Vehicle and Railway Traction Power Supply with Rotary Converters. In Proceedings of the Modern Electric Traction (MET), Gdansk, Poland, 22–23 January 2009. [Google Scholar]
- Lv, X.; Wang, X.; Member, S.; Che, Y.; Li, L. Dynamic Phasor Modelling and Low-Frequency Oscillation Analysis of the Single-Phase Vehicle-Grid System. CSEE J. Power Energy Syst. 2020, 1, 1–13. [Google Scholar] [CrossRef]
- Jiang, X.; Hu, H.; He, Z.; Tao, H.; Qian, Q. Study on Low-Frequency Voltage Fluctuation of Traction Power Supply System Introduced by Multiple Modern Trains. Electr. Power Syst. Res. 2017, 146, 246–257. [Google Scholar] [CrossRef]
- Bian, D.; Yu, Z.; Shi, D.; Diao, R.; Wang, Z. A Robust Real-Time Low-Frequency Oscillation Detection and Analysis (LFODA) System with Innovative Ensemble Filtering. CSEE J. Power Energy Syst. 2020, 6, 174–183. [Google Scholar] [CrossRef]
- Perangin-Angin, D.J.; Bachtiar, F.A. Classification of Stress in Office Work Activities Using Extreme Learning Machine Algorithm and One-Way ANOVA F-Test Feature Selection. In Proceedings of the 2021 4th International Seminar on Research of Information Technology and Intelligent Systems (ISRITI), Yogyakarta, Indonesia, 16 December 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 503–508. [Google Scholar]
- Zhuang, H.; Liu, X.; Wang, H.; Qin, C.; Li, Y.; Li, W.; Shi, Y. Diagnosis of Early Stage Parkinson’s Diseases on Quantitative Susceptibility Mapping Using Complex Network with One-Way ANOVA F-Test Feature Selection. J. Mech. Med. Biol. 2021, 21, 2140026. [Google Scholar] [CrossRef]
- Hossin, M.; Sulaiman, M.N. A Review on Evaluation Metrics for Data Classification Evaluations. Int. J. Data Min. Knowl. Manag. Process 2015, 5, 1–11. [Google Scholar] [CrossRef]

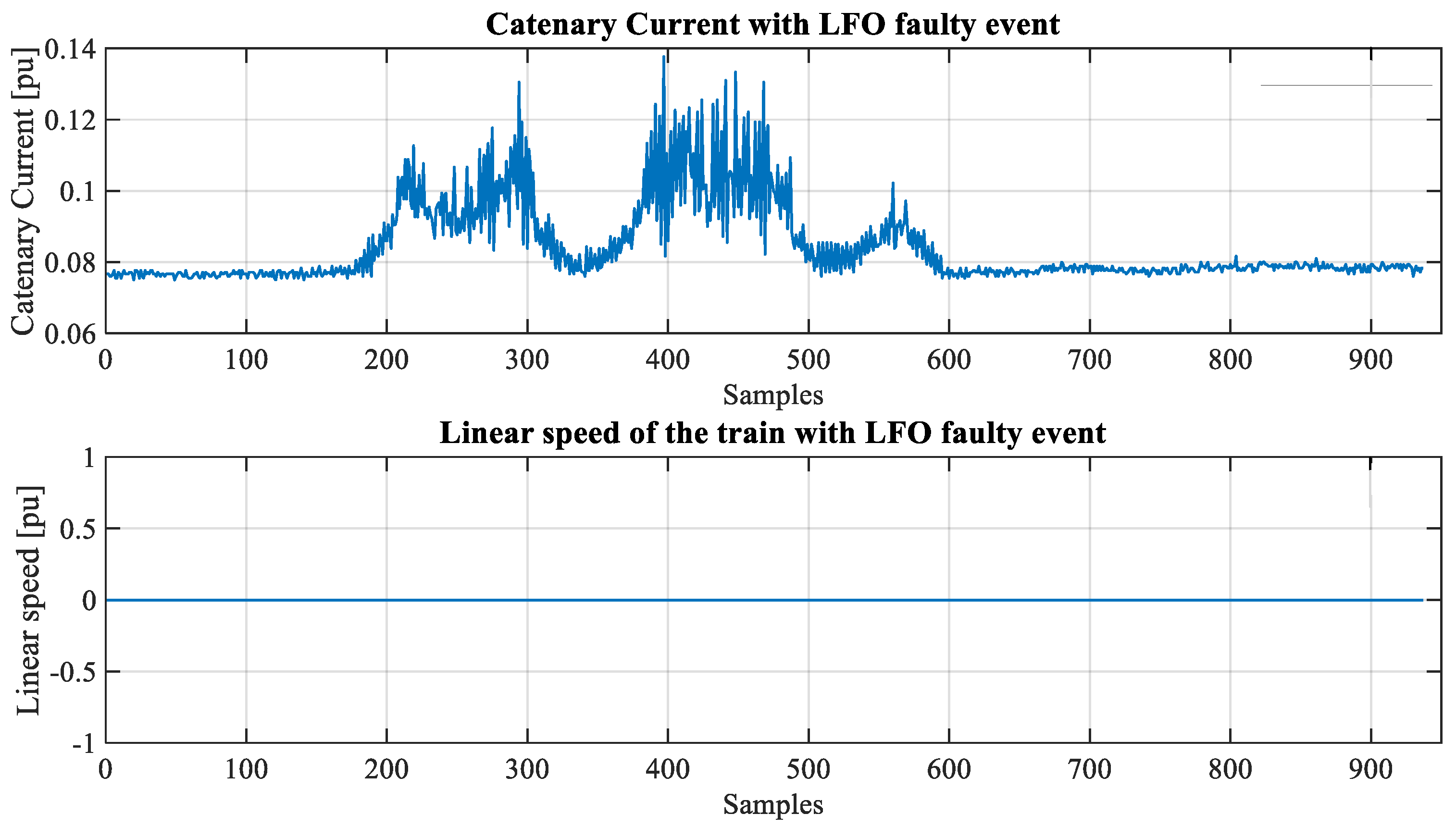
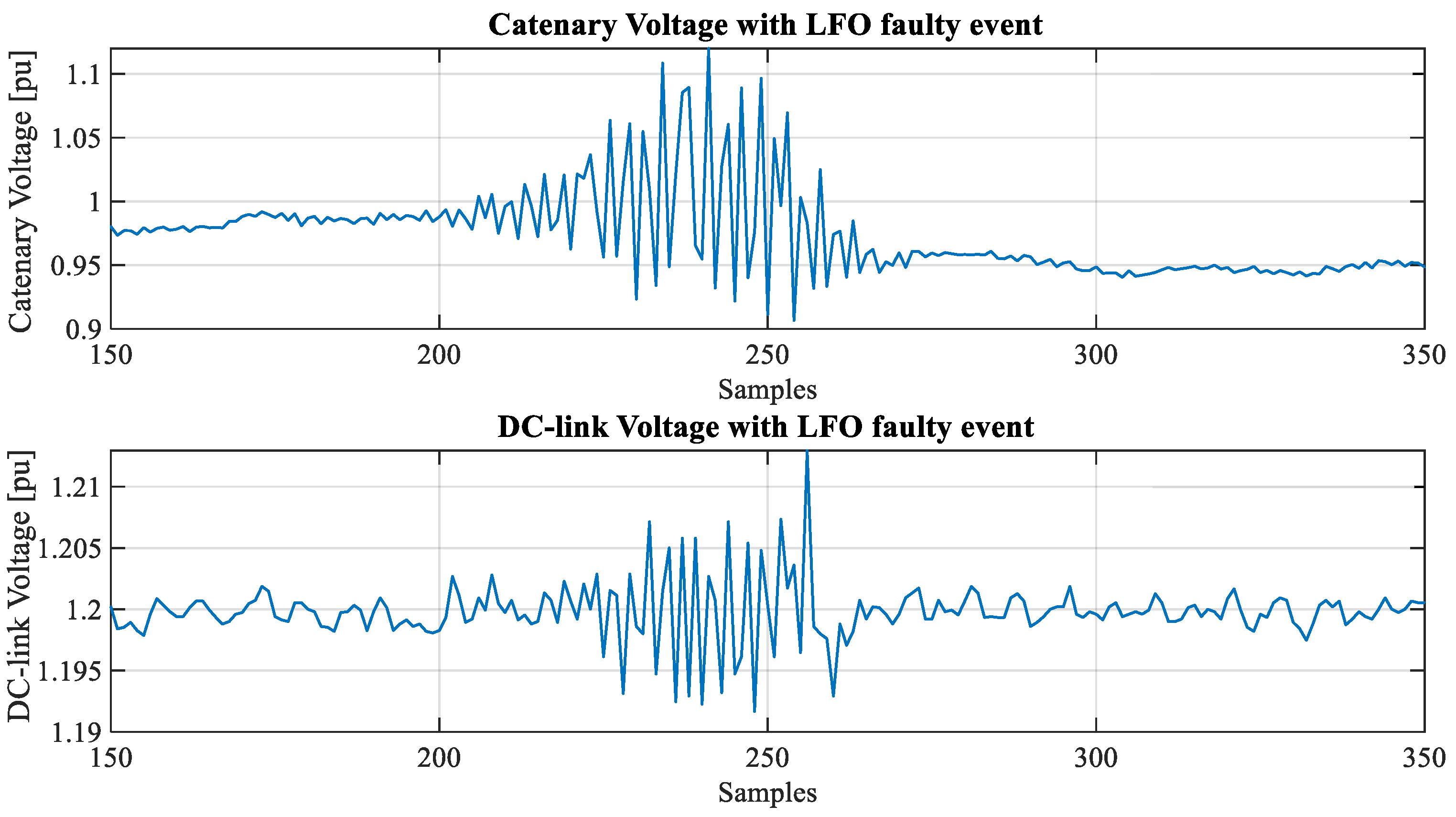
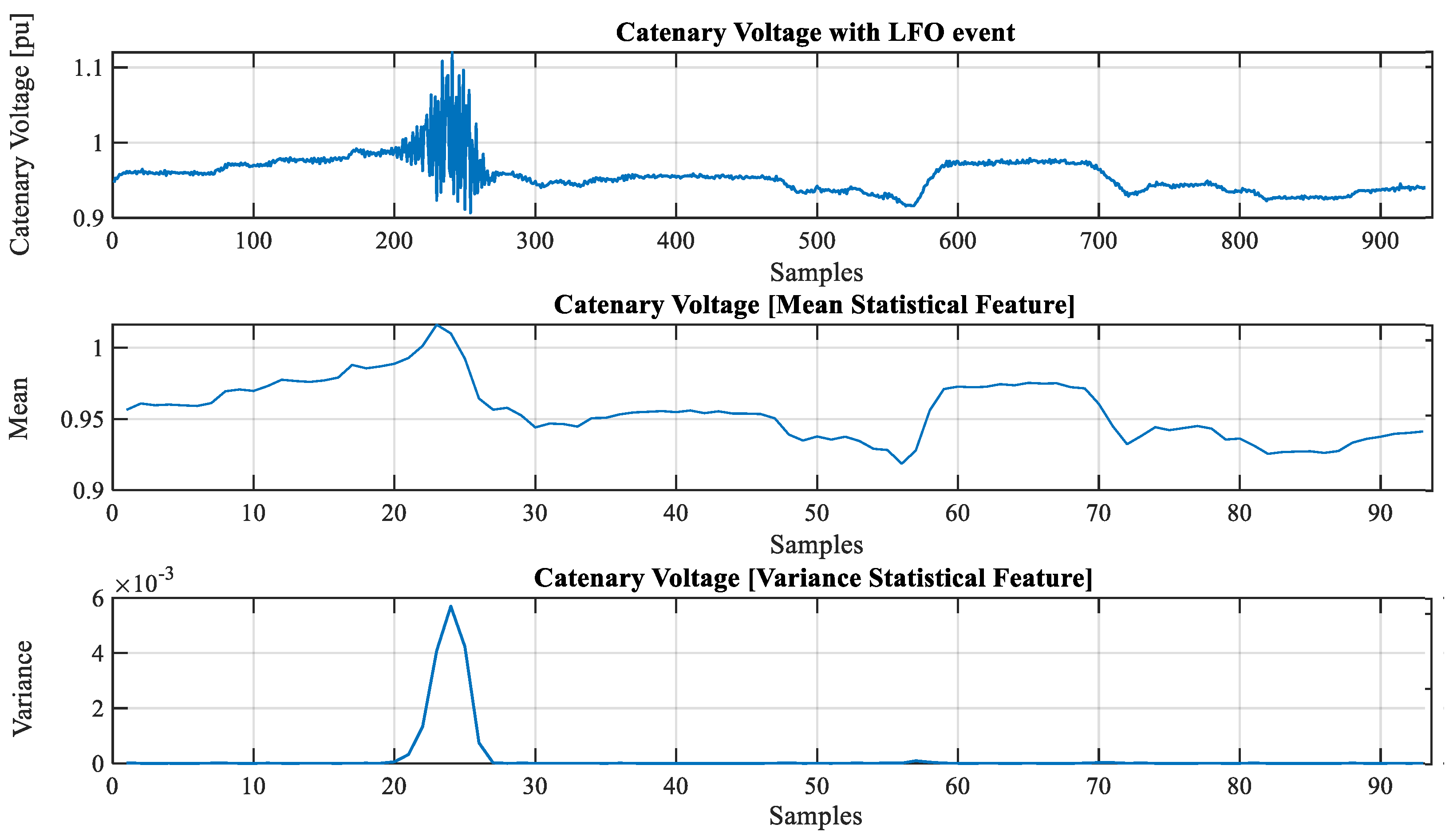
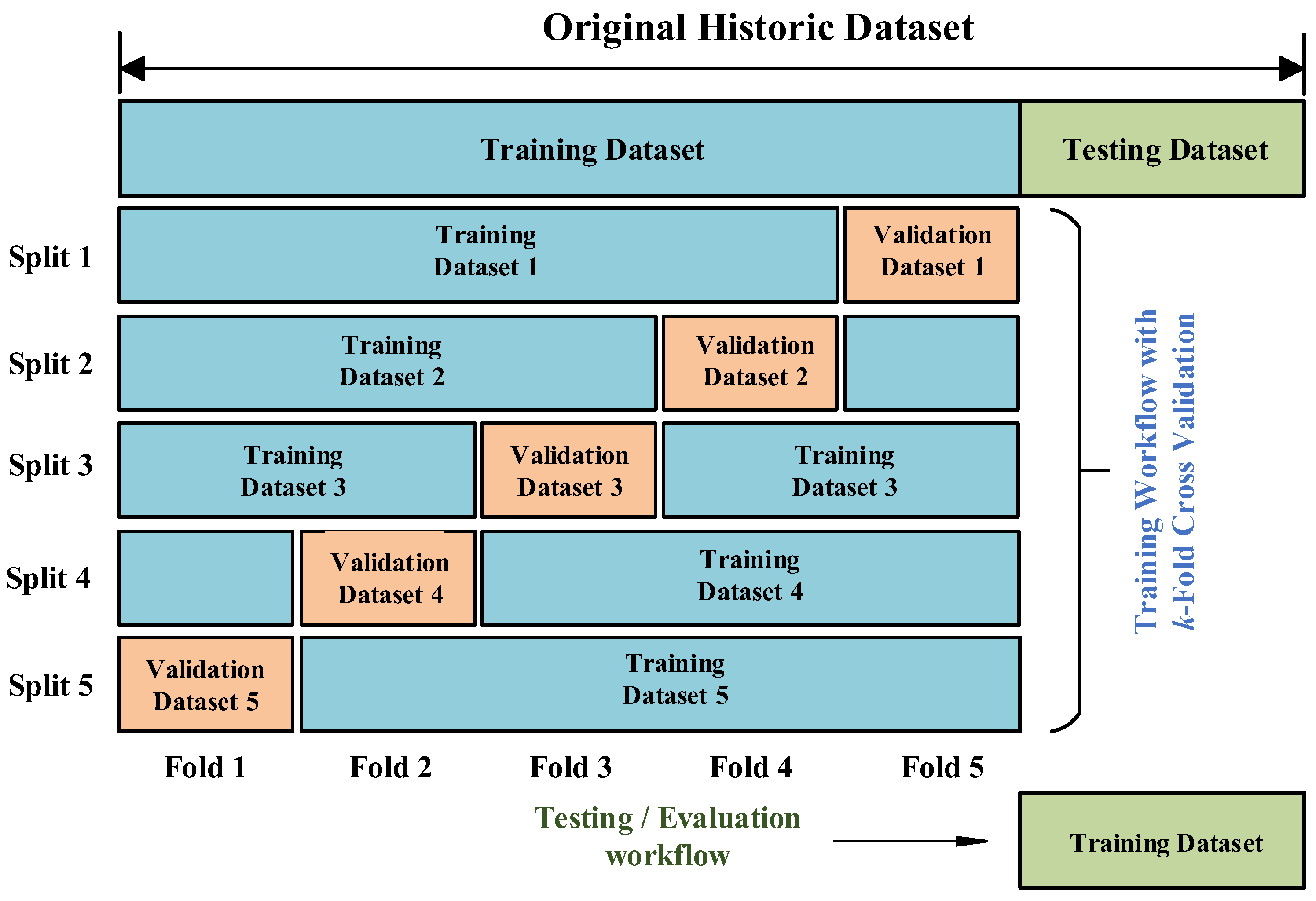
| Statistical Feature | Description |
|---|---|
| Maximum | |
| Minimum | |
| Average | |
| Variance | |
| Standard Deviation | |
| Range | |
| Root Mean Square | |
| Kurtosis | |
| Skewness |
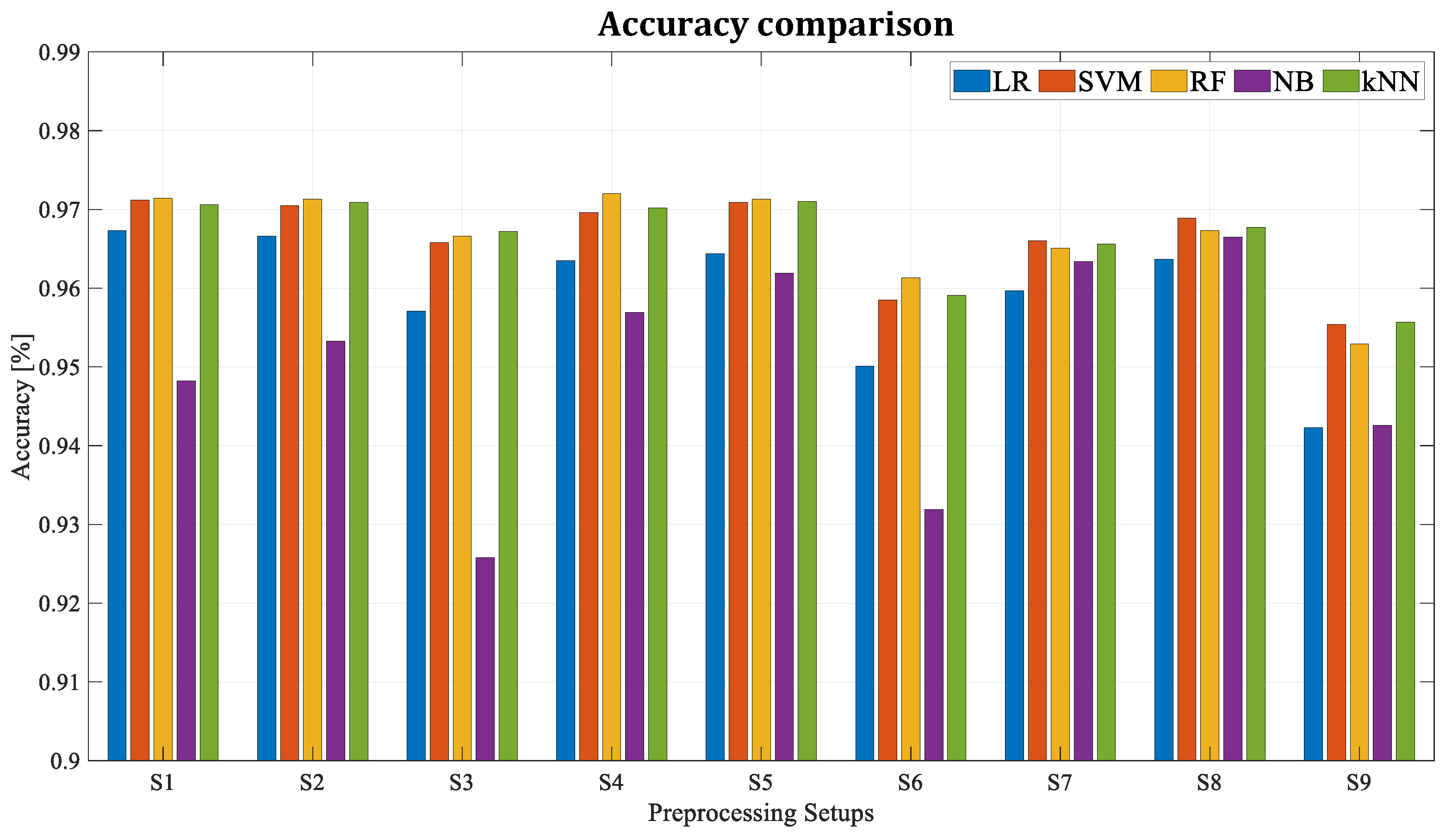
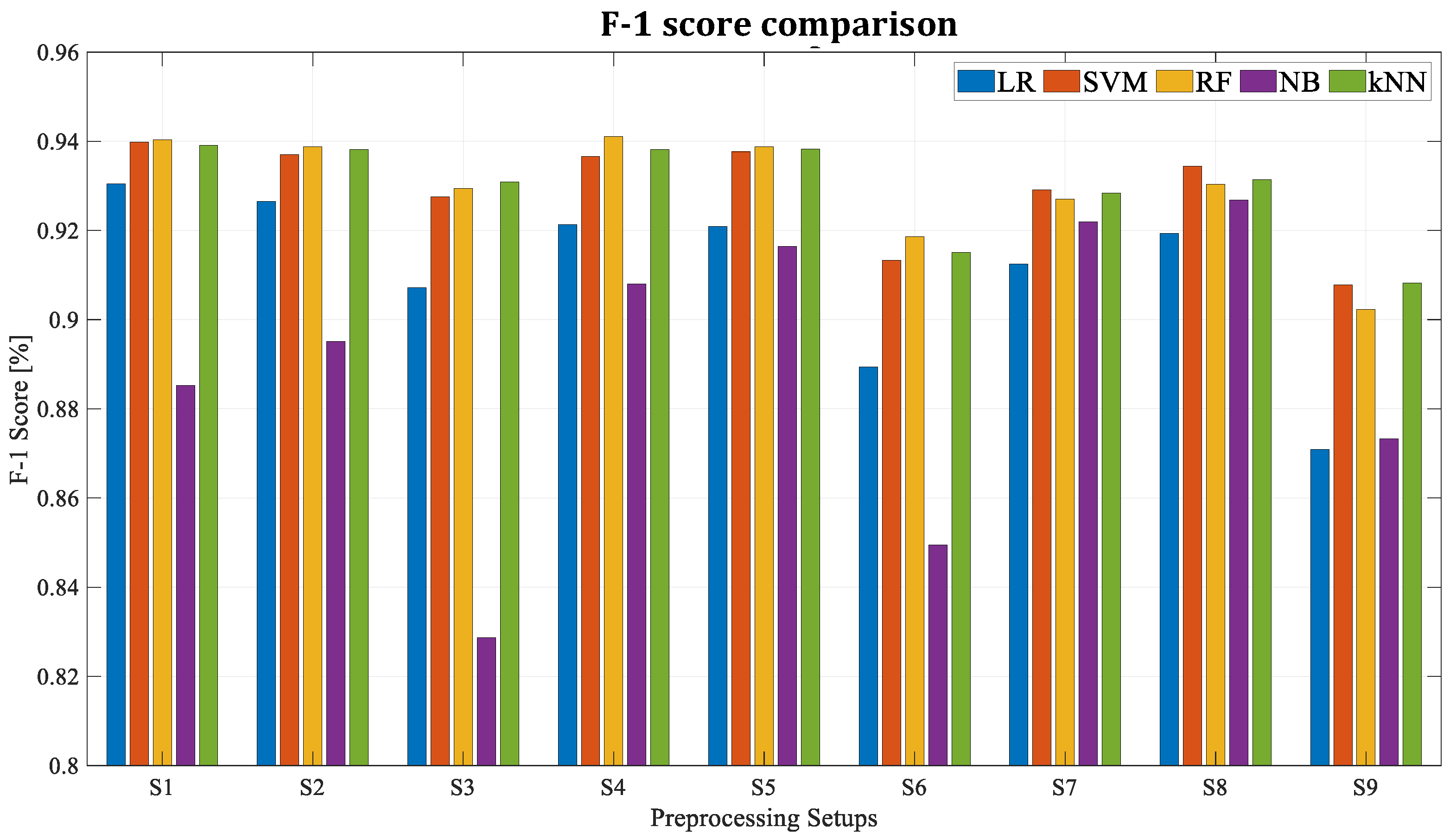
| LR | SVM | RF | NB | kNN | |
|---|---|---|---|---|---|
| Accuracy (%) | 96.7 | 97.1 | 97.1 | 95.3 | 97.1 |
| F-1 Score (%) | 92.7 | 93.7 | 93.9 | 89.5 | 93.8 |
| S1 | S2 | S3 | S4 | S5 | S6 | S7 | S8 | S9 | |
|---|---|---|---|---|---|---|---|---|---|
| Nº of samples/window | 10 | 5 | 20 | 10 | 5 | 20 | 10 | 5 | 20 |
| Nº of selected features | 30 | 30 | 30 | 15 | 15 | 15 | 5 | 5 | 5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gonzalez-Jimenez, D.; Del-Olmo, J.; Poza, J.; Garramiola, F.; Madina, P. Data-Driven Low-Frequency Oscillation Event Detection Strategy for Railway Electrification Networks. Sensors 2023, 23, 254. https://doi.org/10.3390/s23010254
Gonzalez-Jimenez D, Del-Olmo J, Poza J, Garramiola F, Madina P. Data-Driven Low-Frequency Oscillation Event Detection Strategy for Railway Electrification Networks. Sensors. 2023; 23(1):254. https://doi.org/10.3390/s23010254
Chicago/Turabian StyleGonzalez-Jimenez, David, Jon Del-Olmo, Javier Poza, Fernando Garramiola, and Patxi Madina. 2023. "Data-Driven Low-Frequency Oscillation Event Detection Strategy for Railway Electrification Networks" Sensors 23, no. 1: 254. https://doi.org/10.3390/s23010254









