Development and Testing of a Compact Autorefractor Based on Double-Pass Imaging
Abstract
:1. Introduction
2. Materials and Methods
2.1. Physical Concept
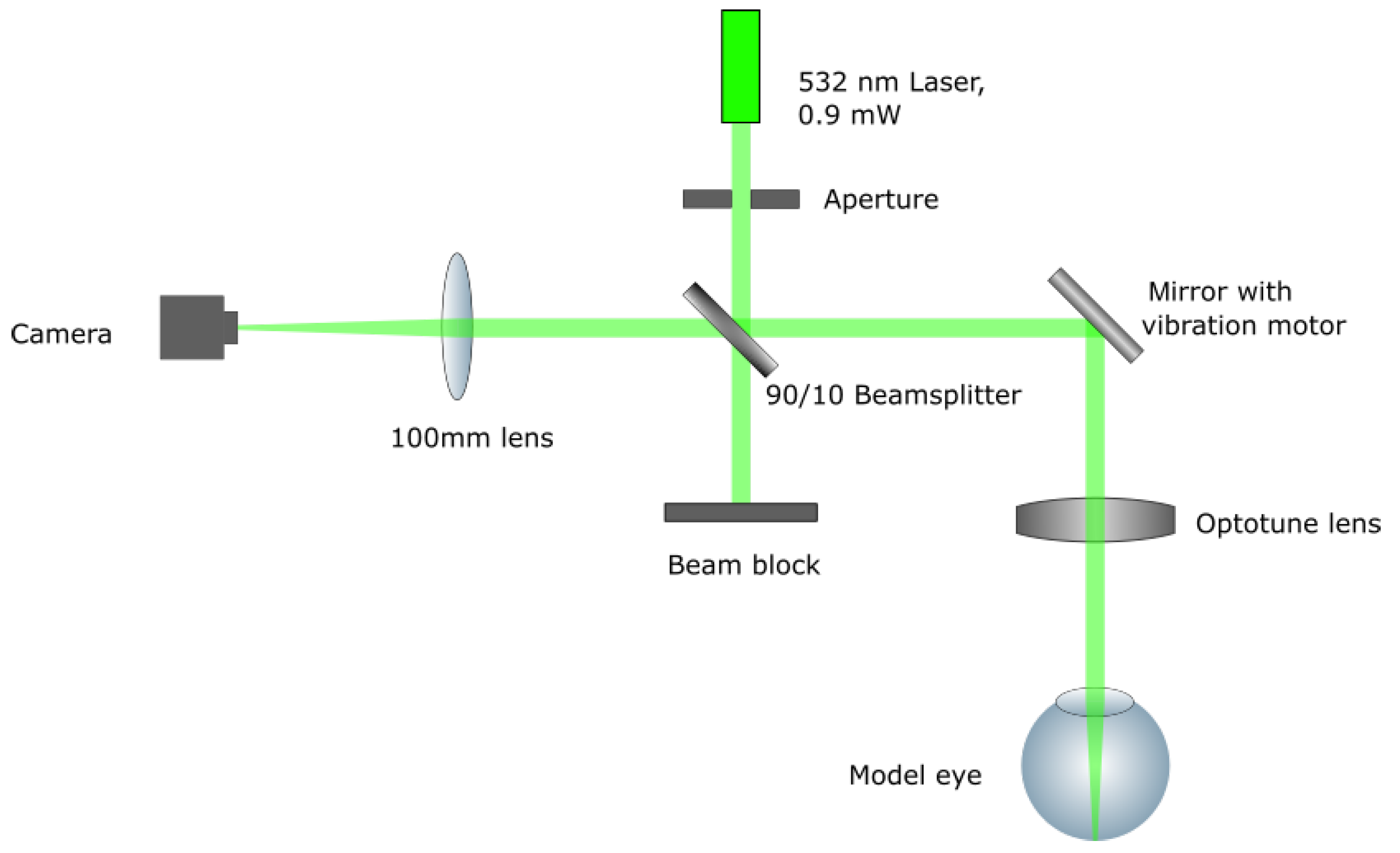
2.2. Setup
2.3. Software
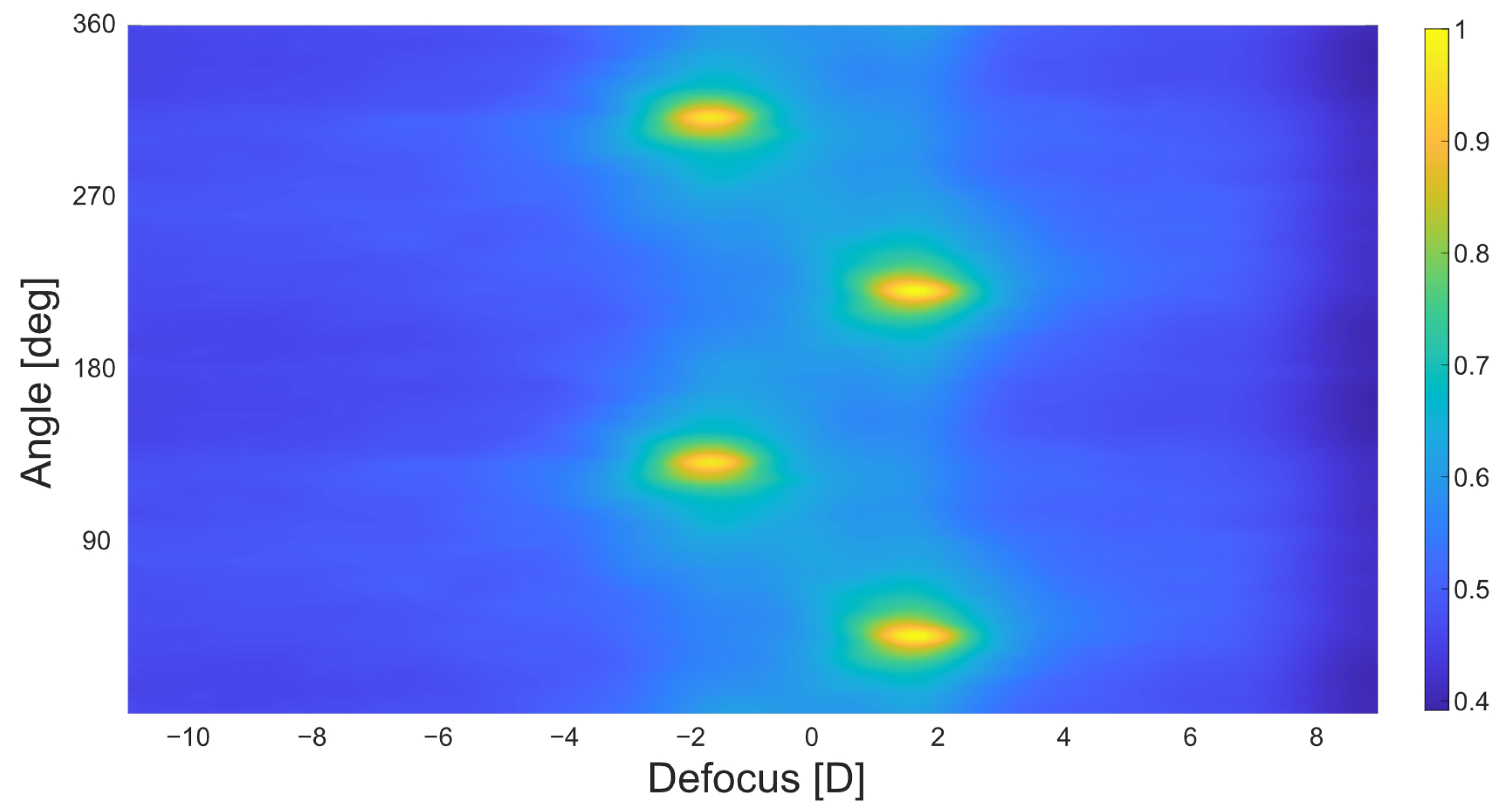
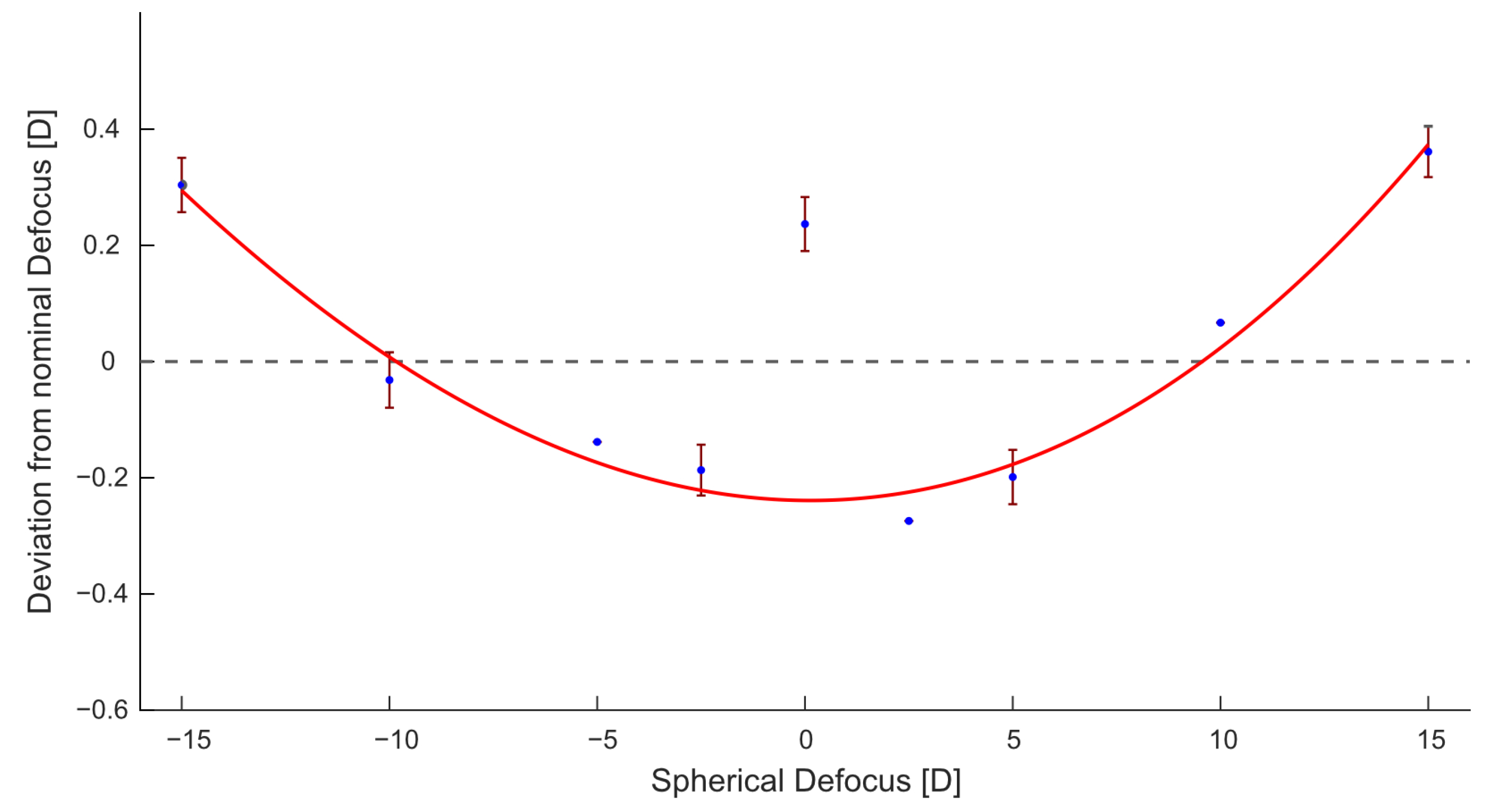
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Bourne, R.R.; Stevens, G.A.; White, R.A.; Smith, J.L.; Flaxman, S.R.; Price, H.; Jonas, J.B.; Keeffe, J.; Leasher, J.; Naidoo, K.; et al. Causes of vision loss worldwide, 1990–2010: A systematic analysis. Lancet Glob. Health 2013, 1, e339–e349. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Resnikoff, S.; Pascolini, D.; Mariotti, S.P.; Pokharel, G.P. Global magnitude of visual impairment caused by uncorrected refractive errors in 2004. Bull. World Health Organ. 2008, 86, 63–70. [Google Scholar] [CrossRef] [PubMed]
- Wong, T.Y.; Ferreira, A.; Hughes, R.; Carter, G.; Mitchell, P. Epidemiology and disease burden of pathologic myopia and myopic choroidal neovascularization: An evidence-based systematic review. Am. J. Ophthalmol. 2014, 157, 9–25. [Google Scholar] [CrossRef] [PubMed]
- Smith, T.; Frick, K.; Holden, B.; Fricke, T.; Naidoo, K. Potential lost productivity resulting from the global burden of uncorrected refractive error. Bull. World Health Organ. 2009, 87, 431–437. [Google Scholar] [CrossRef]
- Fricke, T.; Holden, B.; Wilson, D.; Schlenther, G.; Naidoo, K.; Resnikoff, S.; Frick, K. Global cost of correcting vision impairment from uncorrected refractive error. Bull. World Health Organ. 2012, 90, 728–738. [Google Scholar] [CrossRef]
- Vitale, S.; Ellwein, L.; Cotch, M.F.; Ferris, F.L.; Sperduto, R. Prevalence of refractive error in the United States, 1999–2004. Arch. Ophthalmol. 2008, 126, 1111–1119. [Google Scholar] [CrossRef] [Green Version]
- Holden, B.A.; Fricke, T.R.; Wilson, D.A.; Jong, M.; Naidoo, K.S.; Sankaridurg, P.; Wong, T.Y.; Naduvilath, T.J.; Resnikoff, S. Global prevalence of myopia and high myopia and temporal trends from 2000 through 2050. Ophthalmology 2016, 123, 1036–1042. [Google Scholar] [CrossRef] [Green Version]
- Pan, C.W.; Dirani, M.; Cheng, C.Y.; Wong, T.Y.; Saw, S.M. The age-specific prevalence of myopia in Asia: A meta-analysis. Optom. Vis. Sci. 2015, 92, 258–266. [Google Scholar] [CrossRef]
- Hung, T. Epidemiologic study of the prevalence and severity of myopia among schoolchildren in Taiwan in 2000. J. Formos. Med. Assoc. 2001, 100, 684–691. [Google Scholar]
- Cleary, G.; Spalton, D.; Patel, P.; Lin, P.F.; Marshall, J. Diagnostic accuracy and variability of autorefraction by the Tracey Visual Function Analyzer and the Shin-Nippon NVision-K 5001 in relation to subjective refraction. Ophthalmic Physiol. Opt. 2009, 29, 173–181. [Google Scholar] [CrossRef]
- Ohlendorf, A.; Leube, A.; Wahl, S. Steps towards smarter solutions in optometry and ophthalmology—Inter-device agreement of subjective methods to assess the refractive errors of the eye. Healthcare 2016, 4, 41. [Google Scholar] [CrossRef] [PubMed]
- Rodriguez-Lopez, V.; Dorronsoro, C. Beyond traditional subjective refraction. Curr. Opin. Ophthalmol. 2022, 33, 228–234. [Google Scholar] [CrossRef] [PubMed]
- Artal, P. Handbook of Visual Optics: Instrumentation and Vision Correction; CRC Press: Boca Raton, FL, USA, 2017; Volume II. [Google Scholar]
- Schimitzek, T.; Wesemann, W. Clinical evaluation of refraction using a handheld wavefront autorefractor in young and adult patients. J. Cataract. Refract. Surg. 2002, 28, 1655–1666. [Google Scholar] [CrossRef]
- Durr, N.J.; Dave, S.R.; Vera-Diaz, F.A.; Lim, D.; Dorronsoro, C.; Marcos, S.; Thorn, F.; Lage, E. Design and clinical evaluation of a handheld wavefront autorefractor. Optom. Vis. Sci. 2015, 92, 1140–1147. [Google Scholar] [CrossRef] [Green Version]
- Rubio, M.; Hernández, C.S.; Seco, E.; Perez-Merino, P.; Casares, I.; Dave, S.R.; Lim, D.; Durr, N.J.; Lage, E. Validation of an affordable handheld wavefront autorefractor. Optom. Vis. Sci. 2019, 96, 726–732. [Google Scholar] [CrossRef] [PubMed]
- Ciuffreda, K.J.; Rosenfield, M. Evaluation of the SVOne: A handheld, smartphone-based autorefractor. Optom. Vis. Sci. 2015, 92, 1133. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bastawrous, A.; Leak, C.; Howard, F.; Kumar, V. Validation of near eye tool for refractive assessment (NETRA)–pilot study. J. Mob. Technol. Med. 2012, 1, 6–16. [Google Scholar] [CrossRef] [Green Version]
- McBRIEN, N.A.; Millodot, M. Clinical evaluation of the Canon Autoref R-1. Am. J. Optom. Physiol. Opt. 1985, 62, 786–792. [Google Scholar] [CrossRef] [PubMed]
- Santamaría, J.; Artal, P.; Bescós, J. Determination of the point-spread function of human eyes using a hybrid optical–digital method. JOSA A 1987, 4, 1109–1114. [Google Scholar] [CrossRef]
- Williams, D.R.; Brainard, D.H.; McMahon, M.J.; Navarro, R. Double-pass and interferometric measures of the optical quality of the eye. JOSA A 1994, 11, 3123–3135. [Google Scholar] [CrossRef] [Green Version]
- Wolffsohn, J.; Hunt, O.; Gilmartin, B. Continuous measurement of accommodation in human factor applications. Ophthalmic Physiol. Opt. 2002, 22, 380–384. [Google Scholar] [CrossRef] [PubMed]
- Visiometrics HD Analyzer. Available online: https://www.ophthalmologyweb.com/1315-News/120477-Visiometrics-launches-the-HD-Analyzer-A-next-generation-Optical-Quality-Analysis-System/ (accessed on 4 November 2022).
- Artal, P. Handbook of Visual Optics: Fundamentals and Eye Optics; CRC Press: Boca Raton, FL, USA, 2017. [Google Scholar]
- Halpaap, D.; García-Guerra, C.E.; Vilaseca, M.; Masoller, C. Speckle reduction in double-pass retinal images. Sci. Rep. 2019, 9, 4469. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- García-Guerra, C.E.; Aldaba, M.; Arjona, M.; Pujol, J. Speckle reduction in double-pass retinal images using variable-focus lenses. J. Eur. Opt. Soc.-Rapid Publ. 2015, 10. [Google Scholar] [CrossRef] [Green Version]
- Optotune Switzerland AG Optotune EL-3-10. Available online: https://www.optotune.com/el-3-10-lens (accessed on 29 June 2022).
- ISO 10342:2010; Ophthalmic Instruments—Eye Refractometers. International Organization for Standardization: Geneva, Switzerland, 2010.
- Marín, J.M.; Torres-Sepúlveda, W.; Henao, J.; Mira-Agudelo, A.; Rueda, E. Optical characterization of electro-optics lenses for researching in optics. In Optical System Alignment, Tolerancing, and Verification XIII; SPIE: Bellingham, WA, USA, 2020; Volume 11488, pp. 186–194. [Google Scholar]
- Torres-Sepúlveda, W.A.; Escobar, J.D.H.; Marín, J.A.M.; Mira-Agudelo, A.; Muñoz, E.A.R. Hysteresis characterization of an electrically focus-tunable lens. Opt. Eng. 2020, 59, 044103. [Google Scholar] [CrossRef]
- Jeganathan, S.E.; Valikodath, N.; Niziol, L.M.; Hansen, V.S.; Apostolou, H.; Woodward, M.A. Accuracy of a Smartphone-Based Autorefractor Compared to Gold-Standard Refraction. Optom. Vis. Sci. Off. Publ. Am. Acad. Optom. 2018, 95, 1135. [Google Scholar] [CrossRef] [PubMed]
- Kumar, R.S.; Moe, C.A.; Kumar, D.; Rackenchath, M.V.; AV, S.D.; Nagaraj, S.; Wittberg, D.M.; Stamper, R.L.; Keenan, J.D. Accuracy of autorefraction in an adult Indian population. PLoS ONE 2021, 16, e0251583. [Google Scholar] [CrossRef] [PubMed]
- Gwiazda, J.; Weber, C. Comparison of spherical equivalent refraction and astigmatism measured with three different models of autorefractors. Optom. Vis. Sci. 2004, 81, 56–61. [Google Scholar] [CrossRef]
| Nominal [D] | Measured Average [D] | Deviation [D] | |||||
|---|---|---|---|---|---|---|---|
| Sph | Cyl | Angle [deg] | Sph | Cyl | Angle [deg] | Sph | Cyl |
| −15 | −15.304 | −0.115 | 0.304 | 0.115 | |||
| −10 | −9.968 | −0.048 | −0.032 | 0.048 | |||
| −5 | −4.862 | 0.000 | −0.138 | 0.000 | |||
| −2.5 | −2.313 | −0.067 | −0.187 | 0.067 | |||
| 0 | −0.237 | −0.038 | 0.237 | 0.038 | |||
| 2.5 | 2.774 | 0.000 | −0.274 | 0.000 | |||
| 5 | 5.199 | −0.038 | −0.199 | 0.038 | |||
| 10 | 9.933 | −0.038 | 0.067 | 0.038 | |||
| 15 | 14.639 | −0.067 | 0.361 | 0.067 | |||
| −3 | 0 | −0.070 | −3.217 | 0.100 | 0.070 | 0.217 | |
| −3 | 90 | −0.032 | −3.207 | 91.000 | 0.032 | 0.207 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Emmerich, L.; Ohlendorf, A.; Leube, A.; Suchkov, N.; Wahl, S. Development and Testing of a Compact Autorefractor Based on Double-Pass Imaging. Sensors 2023, 23, 362. https://doi.org/10.3390/s23010362
Emmerich L, Ohlendorf A, Leube A, Suchkov N, Wahl S. Development and Testing of a Compact Autorefractor Based on Double-Pass Imaging. Sensors. 2023; 23(1):362. https://doi.org/10.3390/s23010362
Chicago/Turabian StyleEmmerich, Linus, Arne Ohlendorf, Alexander Leube, Nikolai Suchkov, and Siegfried Wahl. 2023. "Development and Testing of a Compact Autorefractor Based on Double-Pass Imaging" Sensors 23, no. 1: 362. https://doi.org/10.3390/s23010362
APA StyleEmmerich, L., Ohlendorf, A., Leube, A., Suchkov, N., & Wahl, S. (2023). Development and Testing of a Compact Autorefractor Based on Double-Pass Imaging. Sensors, 23(1), 362. https://doi.org/10.3390/s23010362






