Hybrid Refractive-Diffractive Lens with Reduced Chromatic and Geometric Aberrations and Learned Image Reconstruction
Abstract
:1. Introduction
- (1)
- On the optical side, we describe our design process for the hybrid refractive-diffractive lens that minimizes chromatic and geometric aberrations from the concept to the manufactured prototype.
- (2)
- On the software side, we present our deep-learning image reconstruction that combines a lab-captured dataset with real images extended with our image augmentation to obtain artifacts-free image reconstruction, with PSNR reaching 28 dB on test images and delivered a good visual quality for the captured real scenes.
2. Chromatic Aberration Compensation Design of the Diffractive Element of Our Refractive-Diffractive Optical System
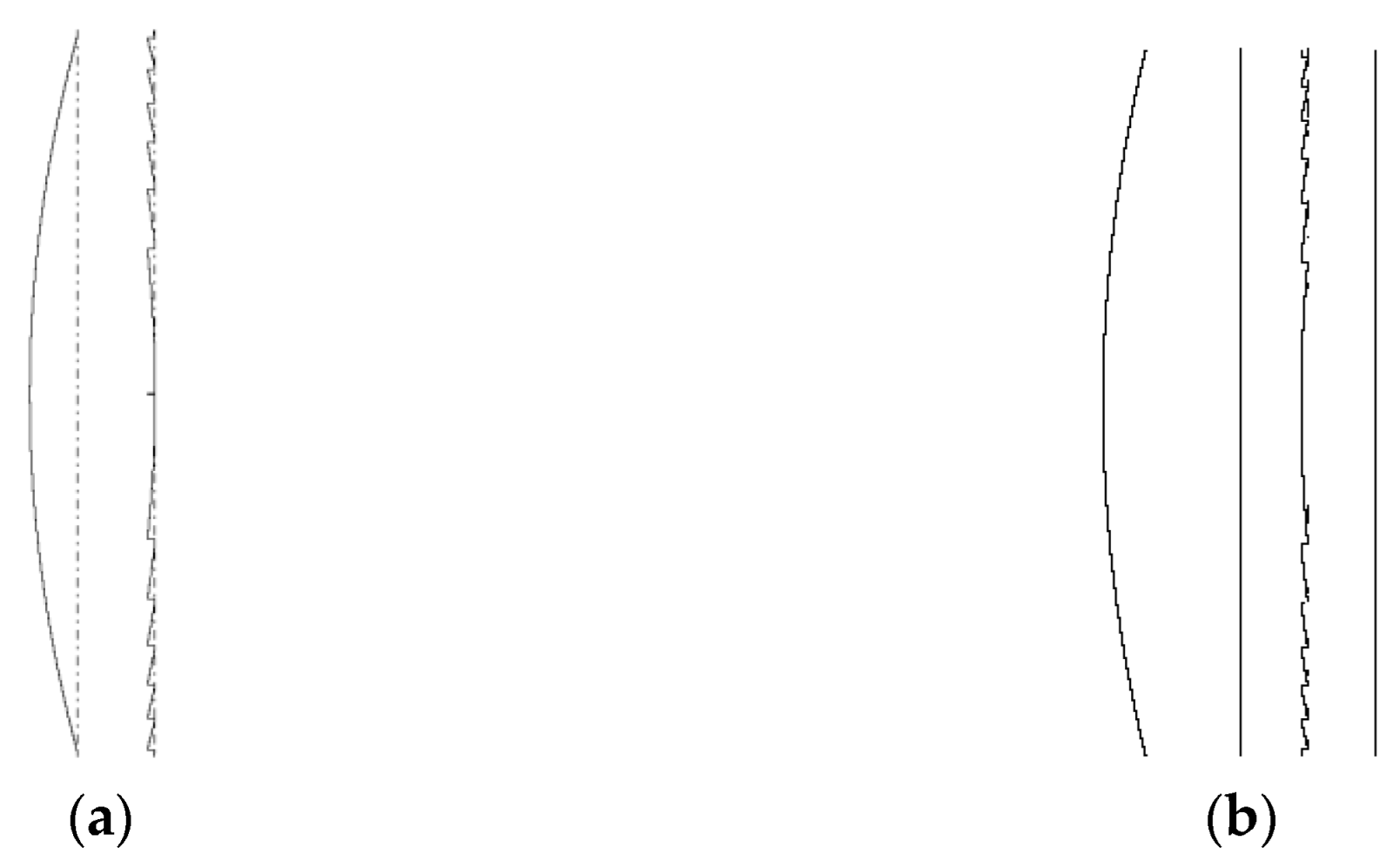
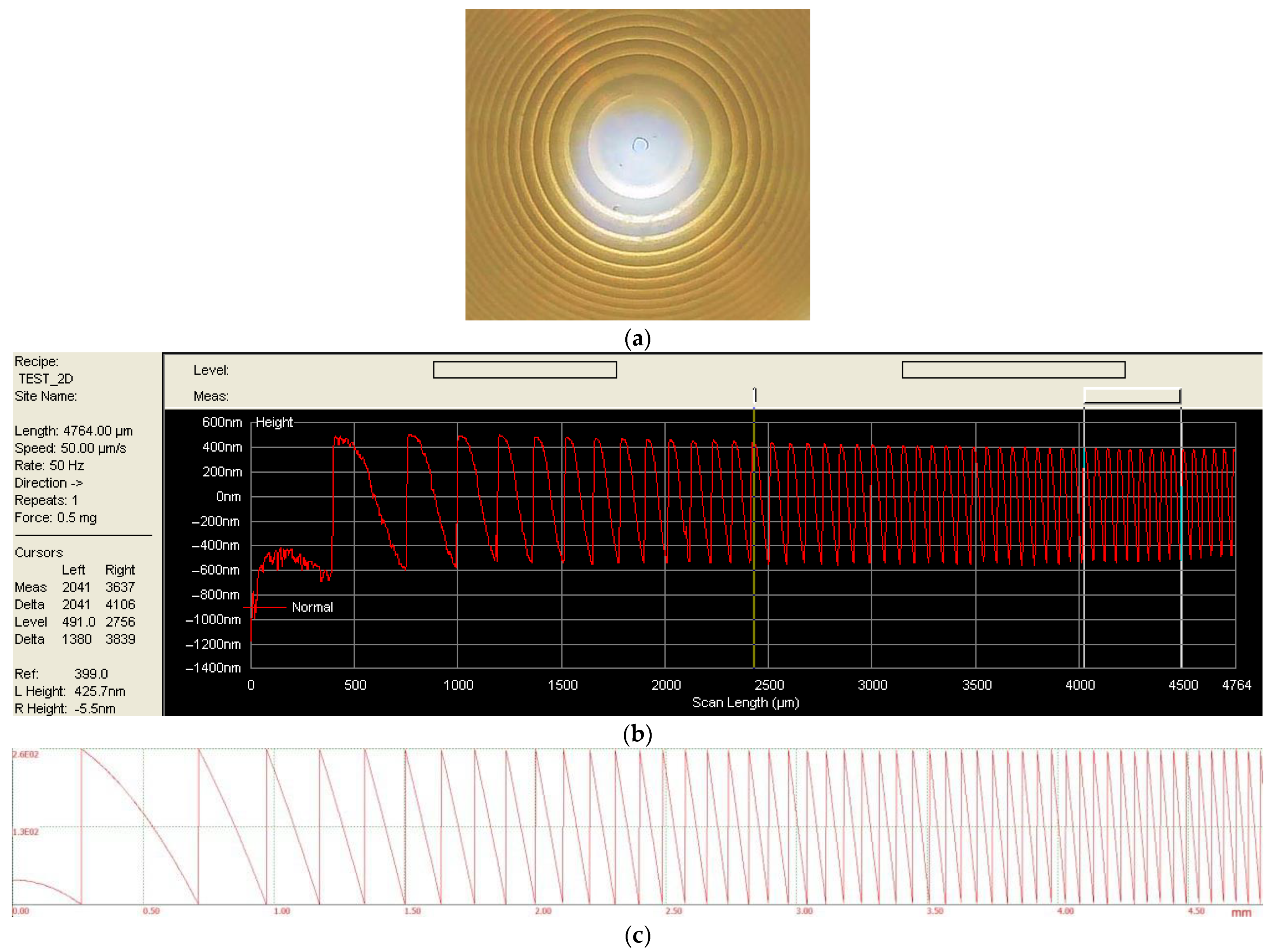
3. Manufacturing of the Diffractive Lens
4. Deep Learning-Based Image Reconstruction
4.1. Deep Learning-Based Image Reconstruction Overview
4.2. False Edge Level (FEL) Criteria
4.3. Dataset Capture and Data Augmentation Strategy
4.4. Network Architecture
4.5. Training with the FEL Criteria for the Artifact-Free Reconstruction
4.6. Data Augmentation Experiments
4.7. Final Training Settings
5. Conclusions
- -
- We designed and optimized our hybrid lens system in the in-house software HARMONY to compensate for the lack of sufficiently powerful capabilities in widely available optical simulation tools. With full modeling flexibility, we designed the diffractive element to compensate for off-axis geometric aberrations of the refractive element and ensured that chromatic aberrations reached zero for two boundary wavelengths, ensuring robust performance on the whole visible spectrum. For the manufacturing, we used widely available laser writing hardware, which ensures the reproducibility of our results and allows for inexpensive mass production later.
- -
- For image post-processing, we deployed an end-to-end deep learning-based image reconstruction with the architecture inspired by the UNet. To generate images used for training, we built a straightforward capture-from-screen automated laboratory setup. Intensive illumination ensured high-quality capture, and we artificially added ISO noise and exposure adjustments to augment the test set to ensure that our apparatus could perform well in a variety of lighting conditions outside of the capture setup.
- -
- Initial experiments using a widely used PSNR metric for quality assessment showed that our neural network training produced inferior results when real-world pictures were processed. With a non-augmented test set of 613 images, we achieved a PSNR of 28.09 dB. When augmented with ISO noise and exposure adjustments, PSNR went down to 27.08 dB on the test set but showed better visual results with real-world images. Seeing the limitations of PSNR for our scenario, we invented a novel quality validation criterion that is aligned with human perception of quality, which we called FEL (false edge level) criteria. This allowed us to confirm that our trained neural network performs exceptionally well when it reconstructs real-world images often made under challenging lighting conditions. To argue our selection of this validation criterion, we present the data and images comparing the performance of the reconstruction with PSNR versus FEL, with FEL being a clear winner despite the fact that the resulting images have somewhat lower PSNR on the test set. The key to this validation advancement was not only the introduction of FEL but our use of a real image patch during the training without the need to produce a corresponding ground truth image.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. Estimation PSF of the Hybrid System
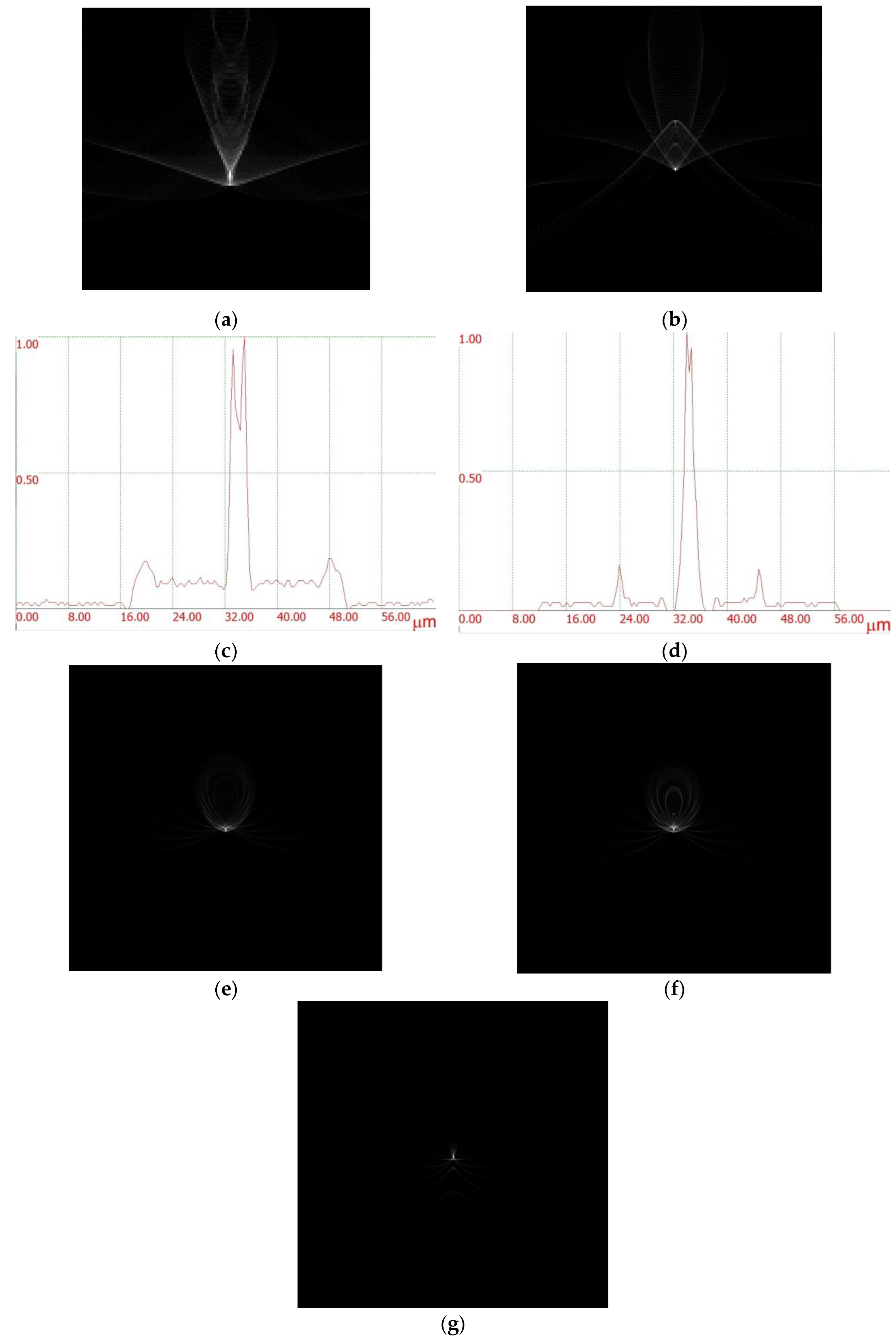
Appendix B. Comparing Training Convergence of the CNN-Based Image Reconstruction Models

References
- Lohmann, A.W. A New Class of Varifocal Lenses. Appl. Opt. 1970, 9, 1669–1671. [Google Scholar] [CrossRef] [PubMed]
- Stone, T.; George, N. Hybrid diffractive-refractive lenses and achromats. Appl. Opt. 1988, 27, 2960–2971. [Google Scholar] [CrossRef] [PubMed]
- Dubik, B.; Koth, S.; Nowak, J.; Zaja̧c, M. Hybrid lens with corrected sphero-chromatic aberration. Opt. Laser Technol. 1995, 27, 315–319. [Google Scholar] [CrossRef]
- Meyers, M.M. Diffractive optics at Eastman Kodak Co. Proc. SPIE Int. Soc. Opt. Eng. 1996, 2689, 228–254. [Google Scholar]
- Hong, Y.G.; Bowron, J.W. Novel optics for high performance digital projection systems and monitors (current & future). Proc. SPIE Int. Soc. Opt. Eng. 2003, 5002, 111–122. [Google Scholar]
- Greisukh, G.I.; Ezhov, E.G.; Levin, I.A.; Stepanov, S.A. Design of the double-telecentric high-aperture diffractive-refractive objectives. Appl. Opt. 2011, 50, 3254–3258. [Google Scholar] [CrossRef]
- Greisukh, G.I.; Ezhov, E.G.; Kazin, S.V.; Sidyakina, Z.A.; Stepanov, S.A. Visual assessment of the influence of adverse diffraction orders on the quality of image formed by the refractive—Diffractive optical system. Comput. Opt. 2014, 38, 418–424. [Google Scholar] [CrossRef]
- Zhang, S.; Zhou, L.; Xue, C.; Wang, L. Design and simulation of a superposition compound eye system based on hybrid diffractive-refractive lenses. Appl. Opt. 2017, 56, 7442–7449. [Google Scholar] [CrossRef] [PubMed]
- Lenkova, G.A. Diffractive-Refractive Intraocular Lenses with Binary Structures. Optoelectron. Instrum. Data Process. 2018, 54, 469–476. [Google Scholar] [CrossRef]
- Flores, A.; Wang, M.R.; Yang, J.J. Achromatic hybrid refractive-diffractive lens with extended depth of focus. Appl. Opt. 2004, 43, 5618–5630. [Google Scholar] [CrossRef]
- Sweeney, D.W.; Sommargren, G.E. Harmonic diffractive lenses. Appl. Opt. 1995, 34, 2469–2475. [Google Scholar] [CrossRef] [PubMed]
- Khonina, S.N.; Volotovsky, S.G.; Ustinov, A.V.; Kharitonov, S.I. Analysis of focusing light by a harmonic diffractive lens with regard for the refractive index dispersion. Comput. Opt. 2017, 41, 338–347. [Google Scholar] [CrossRef]
- Yang, J.; Twardowski, P.; Gérard, P.; Yu, W.; Fontaine, J. Chromatic analysis of harmonic Fresnel lenses by FDTD and angular spectrum methods. Appl. Opt. 2018, 57, 5281–5287. [Google Scholar] [CrossRef] [PubMed]
- Zhang, B.; Piao, M.; Cui, Q. Achromatic annular folded lens with reflective-diffractive optics. Opt. Express 2019, 27, 32337–32348. [Google Scholar] [CrossRef]
- Bregenzer, N.; Bawart, M.; Bernet, S. Zoom system by rotation of toroidal lenses. Opt. Express 2020, 28, 3258–3269. [Google Scholar] [CrossRef]
- Evdokimova, V.V.; Petrov, M.V.; Klyueva, M.A.; Zybin, E.Y.; Kosianchuk, V.V.; Mishchenko, I.B.; Novikov, V.M.; Selvesiuk, N.I.; Ershov, E.I.; Ivliev, N.A.; et al. Deep learning-based video stream reconstruction in mass production diffractive optical. Comput. Opt. 2021, 45, 130–141. [Google Scholar] [CrossRef]
- Ivliev, N.; Evdokimova, V.; Podlipnov, V.; Petrov, M.; Ganchevskaya, S.; Tkachenko, I.; Abrameshin, D.; Yuzifovich, Y.; Nikonorov, A.; Skidanov, R.; et al. First Earth-Imaging CubeSat with Harmonic Diffractive Lens. Remote Sens. 2022, 14, 2230. [Google Scholar] [CrossRef]
- Dun, X.; Ikoma, H.; Wetzstein, G.; Wang, Z.; Cheng, X.; Peng, Y. Learned rotationally symmetric diffractive achromat for full-spectrum computational imaging. Optica 2020, 7, 913–922. [Google Scholar] [CrossRef]
- Peng, Y.; Sun, Q.; Dun, X.; Wetzstein, G.; Heidrich, W.; Heide, F. Learned large field-of-view imaging with thin-plate optics. ACM Trans. Graph. 2019, 38, 219. [Google Scholar] [CrossRef] [Green Version]
- Nikonorov, A.; Petrov, M.; Bibikov, S.; Yakimov, P.; Kutikova, V.; Yuzifovich, Y.; Morozov, A.; Skidanov, R.; Kazanskiy, N. Toward Ultralightweight Remote Sensing With Harmonic Lenses and Convolutional Neural Networks. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 11, 3338–3348. [Google Scholar] [CrossRef]
- Ronneberger, O. U-Net: Convolutional networks for biomedical image segmentation. In Medical Image Computing and Computerassisted Intervention—MICCAI; Navab, N., Hornegger, J., Wells, W.M., Frangi, A.F., Eds.; Springer: New York, NY, USA; Dordrecht, The Netherlands; London, UK, 2015; pp. 234–241. [Google Scholar] [CrossRef] [Green Version]
- Mao, S.; Zhao, J. Design and analysis of a hybrid optical system containing a multilayer diffractive optical element with improved diffraction efficiency. Appl. Opt. 2020, 59, 5888–5895. [Google Scholar] [CrossRef] [PubMed]
- Piao, M.; Zhang, B.; Dong, K. Design of achromatic annular folded lens with multilayer diffractive optics for the visible and near-IR wavebands. Opt. Express 2020, 28, 29076–29085. [Google Scholar] [CrossRef]
- Choi, H.; Yoon, Y.J.; Kim, B.; Lee, S.H.; Kim, W.C.; Park, N.C.h.; Park, Y.P.; Kang, S. Design of Hybrid Lens for Compact Camera Module Considering Diffraction Effect. Jpn. J. Appl. Phys. 2008, 47, 6678. [Google Scholar] [CrossRef]
- Skidanov, R.V.; Ganchevskaya, S.V.; Vasiliev, V.S.; Blank, V.A. Systems of generalized harmonic lenses for image formation. Opt. J. 2022, 89, 13–19. [Google Scholar] [CrossRef]
- Wang, Z.; Chen, J.; Hoi, S.C.H. Deep Learning for Image Super-resolution: A Survey. IEEE Trans. Pattern Anal. Mach. Intell. 2020, 43, 3365–3387. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bhat, G.; Danelljan, M.; Timofte, R.; Cao, Y.; Cao, Y.; Chen, M.; Chen, X.; Cheng, S.; Dudhane, A.; Fan, H.; et al. NTIRE 2022 Burst Super-Resolution Challenge. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR) Workshops, New Orleans, LA, USA, 19–20 June 2022; pp. 1041–1061. [Google Scholar]
- Dong, C.; Loy, C.C.; He, K.; Tang, X. Learning a deep convolutional network for image super-resolution. In Proceedings of the European Conference on Computer Vision (ECCV), Zurich, Switzerland, 6–12 September 2014. [Google Scholar]
- Kim, J.; Lee, J.K.; Lee, K.M. Accurate image super-resolution using very deep convolutional networks. In Proceedings of the CVPR, Las Vegas, NV, USA, 27–30 June 2016. [Google Scholar]
- Zhang, Y.; Tian, Y.; Kong, Y.; Zhong, B.; Fu, Y. Residual dense network for image super-resolution. In Proceedings of the CVPR, Salt Lake City, UT, USA, 18–22 June 2018. [Google Scholar]
- Zhang, Y.; Li, K.; Li, K.; Wang, L.; Zhong, B.; Fu, Y. Image super-resolution using very deep residual channel attention networks. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018. [Google Scholar]
- Zhang, K.; Zuo, W.; Zhang, L. Learning a single convolutional super-resolution network for multiple degradations. In Proceedings of the CVPR, Salt Lake City, UT, USA, 18–22 June 2018. [Google Scholar]
- Wang, X.; Xie, L.; Dong, C.; Shan, Y. Real-ESRGAN: Training Real-World Blind Super-Resolution with Pure Synthetic Data. In Proceedings of the IEEE/CVF International Conference on Computer Vision Workshops (ICCVW), Montreal, BC, Canada, 11–17 October 2021; pp. 1904–1914. [Google Scholar]
- Nikonorov, A.; Evdokimova, V.; Petrov, M.; Yakimov, P.; Bibikov, S.; Yuzifovich, Y.; Skidanov, R.; Kazanskiy, N. Deep learningbased imaging using single-lens and multi-aperture diffractive optical systems. In Proceedings of the 2019 IEEE/CVF International Conference on Computer Vision Workshop (ICCVW), Seoul, Republic of Korea, 27–28 October 2019; pp. 3969–3977. [Google Scholar]
- Soh, J.W.; Cho, S.; Cho, N.I. Metatransfer learning for zero-shot super-resolution. In Proceedings of the CVPR, Seattle, WA, USA, 13–19 June 2020. [Google Scholar] [CrossRef]
- Wang, L.; Wang, Y.; Dong, X.; Xu, Q.; Yang, J.; An, W.; Guo, Y. Unsupervised degradation representation learning for blind superresolution. In Proceedings of the CVPR, Virtual, 19–25 June 2021. [Google Scholar] [CrossRef]
- Kirillova, A.; Lyapustin, E.; Antsiferova, A.; Vatolin, D. ERQA: Edge-Restoration Quality Assessment for Video Super-Resolution. ArXiv 2021, arXiv:2110.09992. [Google Scholar]
- Kingma, D.P.; Adam, J.B. A method for stochastic optimization. In Proceedings of the International Conference on Learning Representations, Banff, AB, Canada, 14–16 April 2014. [Google Scholar]
- Foi, A.; Trimeche, M.; Katkovnik, V.; Egiazarian, K. Practical Poissonian-Gaussian Noise Modeling and Fitting for Single-Image Raw-Data. IEEE Trans. Image Process. 2008, 17, 1737–1754. [Google Scholar] [CrossRef] [Green Version]
- Guo, S.; Yan, Z.; Zhang, K.; Zuo, W.; Zhang, L. Toward Convolutional Blind Denoising of Real Photographs. In Proceedings of the CVPR, Long Beach, CA, USA, 16–20 June 2019. [Google Scholar] [CrossRef] [Green Version]
- Do More with Less Data. Available online: https://albumentations.ai/ (accessed on 6 October 2022).
- Ying, Z.; Li, G.; Ren, Y.; Wang, R.; Wang, W. A New Low-Light Image Enhancement Algorithm Using Camera Response Model. In Proceedings of the IEEE International Conference on Computer Vision Workshops (ICCVW), Venice, Italy, 22–29 October 2017; pp. 3015–3022. [Google Scholar] [CrossRef]












| № | Augmentation | The Best Point Selection Criteria | PSNR of Validation Set (dB) | FEL (%) | PSNR of the Test Set (dB) | Reconstructed Patch, Min-FEL Criterion |
|---|---|---|---|---|---|---|
| 1 | No augmentation | Max-PSNR | 27.71 | 30.69 | 27.68 | Figure 8d Figure 8e |
| Min-FEL | 26.56 | 14.48 | 27.01 | |||
| 2 | ISO noise with a probability of 0.5 and intensity of 0.1 | Max-PSNR | 27.52 | 3.32 | 28.09 | - Figure 10a |
| Min-FEL | 27.13 | 2.83 | 27.65 | |||
| 3 | ISO noise (0.5 probability), random intensity 0.1, 0.2, 0.3 | Max-PSNR | 27.42 | 1.47 | 27.4 | - Figure 10b and Figure 11a |
| Min-FEL | 27.29 | 1.35 | 27.37 | |||
| 4 | ISO noise with a probability of 0.5, random intensity 0.1, 0.2, 0.3; varying exposure | Max-PSNR | 26.46 | 1.69 | 27.08 | - Figure 10c and Figure 11b |
| Min-FEL | 26.2 | 1.29 | 26.91 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Evdokimova, V.V.; Podlipnov, V.V.; Ivliev, N.A.; Petrov, M.V.; Ganchevskaya, S.V.; Fursov, V.A.; Yuzifovich, Y.; Stepanenko, S.O.; Kazanskiy, N.L.; Nikonorov, A.V.; et al. Hybrid Refractive-Diffractive Lens with Reduced Chromatic and Geometric Aberrations and Learned Image Reconstruction. Sensors 2023, 23, 415. https://doi.org/10.3390/s23010415
Evdokimova VV, Podlipnov VV, Ivliev NA, Petrov MV, Ganchevskaya SV, Fursov VA, Yuzifovich Y, Stepanenko SO, Kazanskiy NL, Nikonorov AV, et al. Hybrid Refractive-Diffractive Lens with Reduced Chromatic and Geometric Aberrations and Learned Image Reconstruction. Sensors. 2023; 23(1):415. https://doi.org/10.3390/s23010415
Chicago/Turabian StyleEvdokimova, Viktoria V., Vladimir V. Podlipnov, Nikolay A. Ivliev, Maxim V. Petrov, Sofia V. Ganchevskaya, Vladimir A. Fursov, Yuriy Yuzifovich, Sergey O. Stepanenko, Nikolay L. Kazanskiy, Artem V. Nikonorov, and et al. 2023. "Hybrid Refractive-Diffractive Lens with Reduced Chromatic and Geometric Aberrations and Learned Image Reconstruction" Sensors 23, no. 1: 415. https://doi.org/10.3390/s23010415
APA StyleEvdokimova, V. V., Podlipnov, V. V., Ivliev, N. A., Petrov, M. V., Ganchevskaya, S. V., Fursov, V. A., Yuzifovich, Y., Stepanenko, S. O., Kazanskiy, N. L., Nikonorov, A. V., & Skidanov, R. V. (2023). Hybrid Refractive-Diffractive Lens with Reduced Chromatic and Geometric Aberrations and Learned Image Reconstruction. Sensors, 23(1), 415. https://doi.org/10.3390/s23010415






