An Improved TDOA Method for Land-Based Long-Range HF Skywave Source Geolocation and Experimental Results
Abstract
:1. Introduction
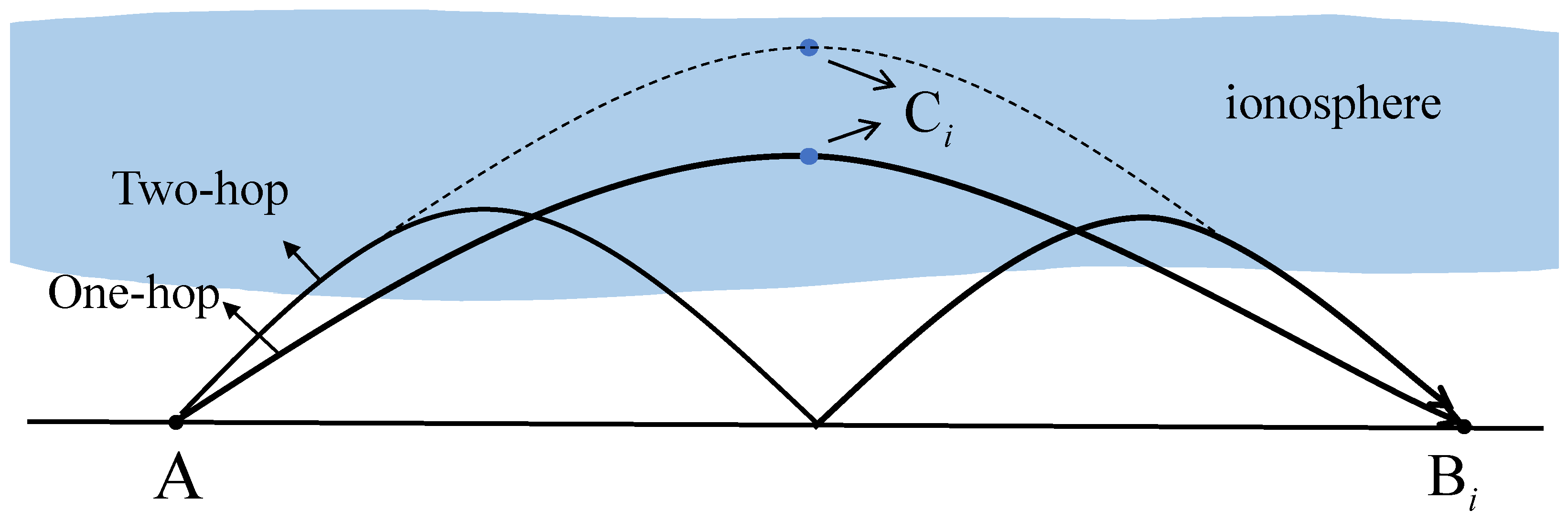
2. System Model
3. Geolocation Method
4. Simulation and Experimental Results
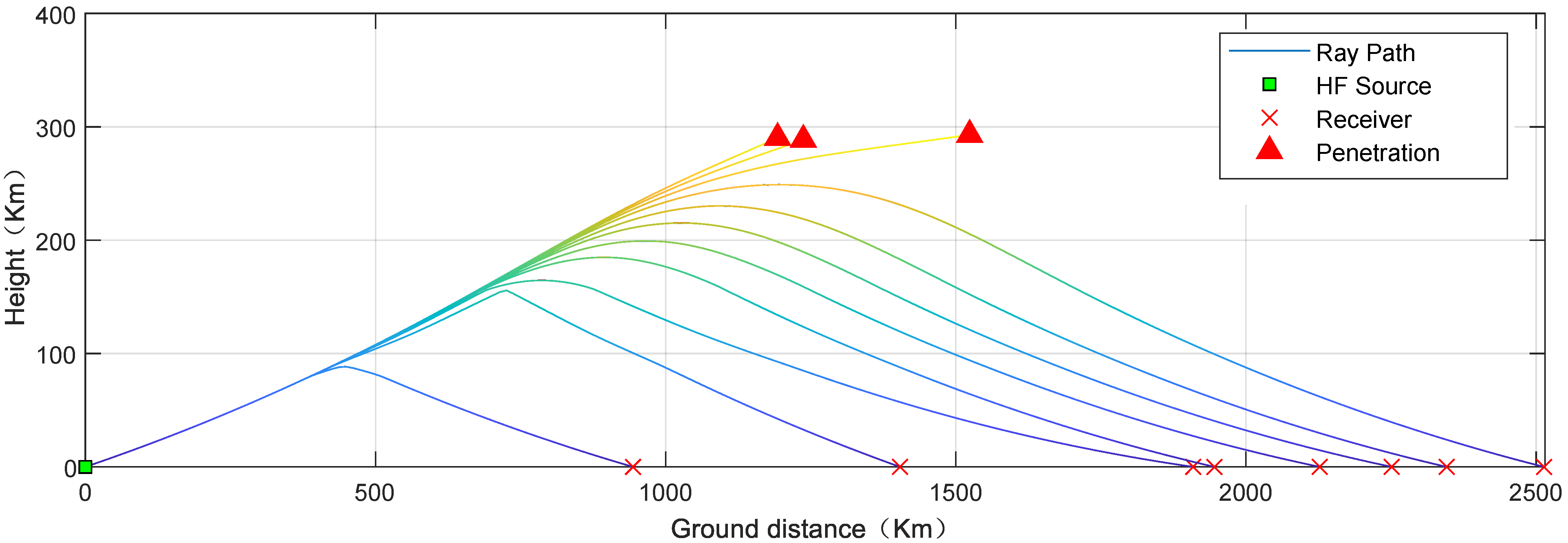
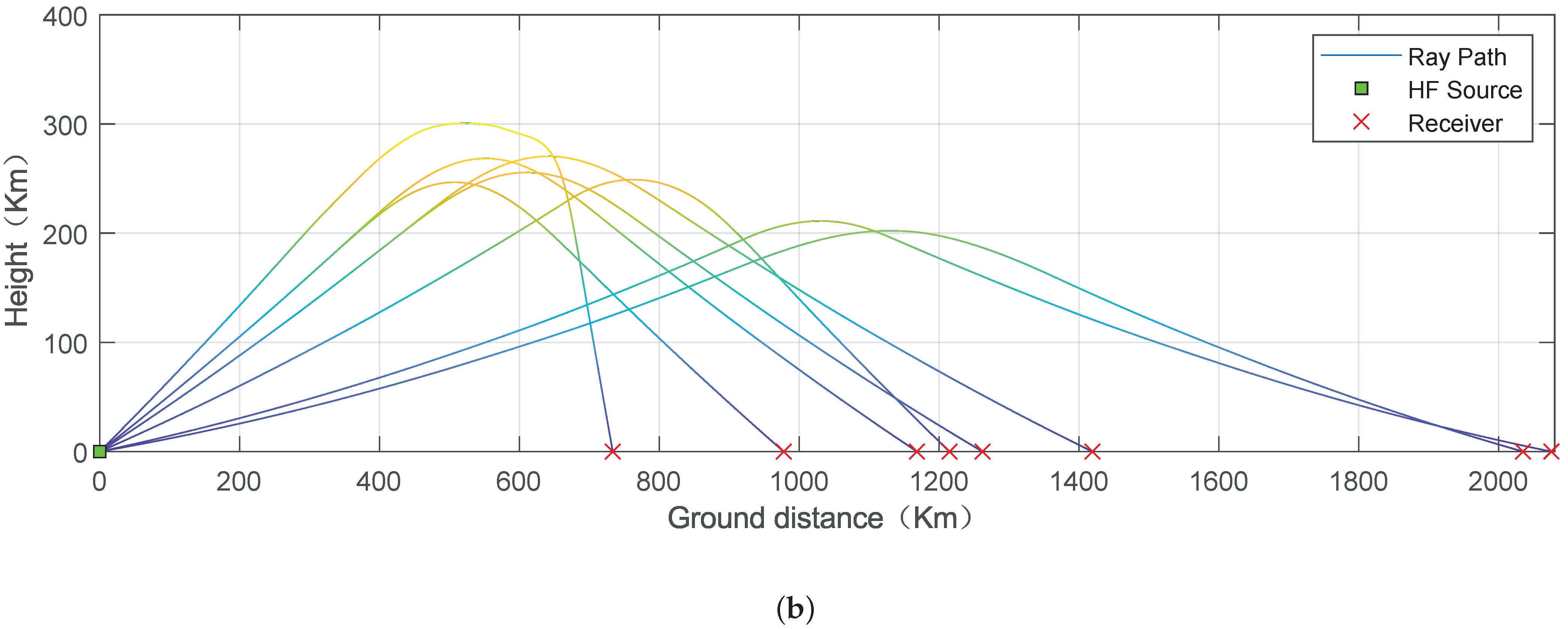
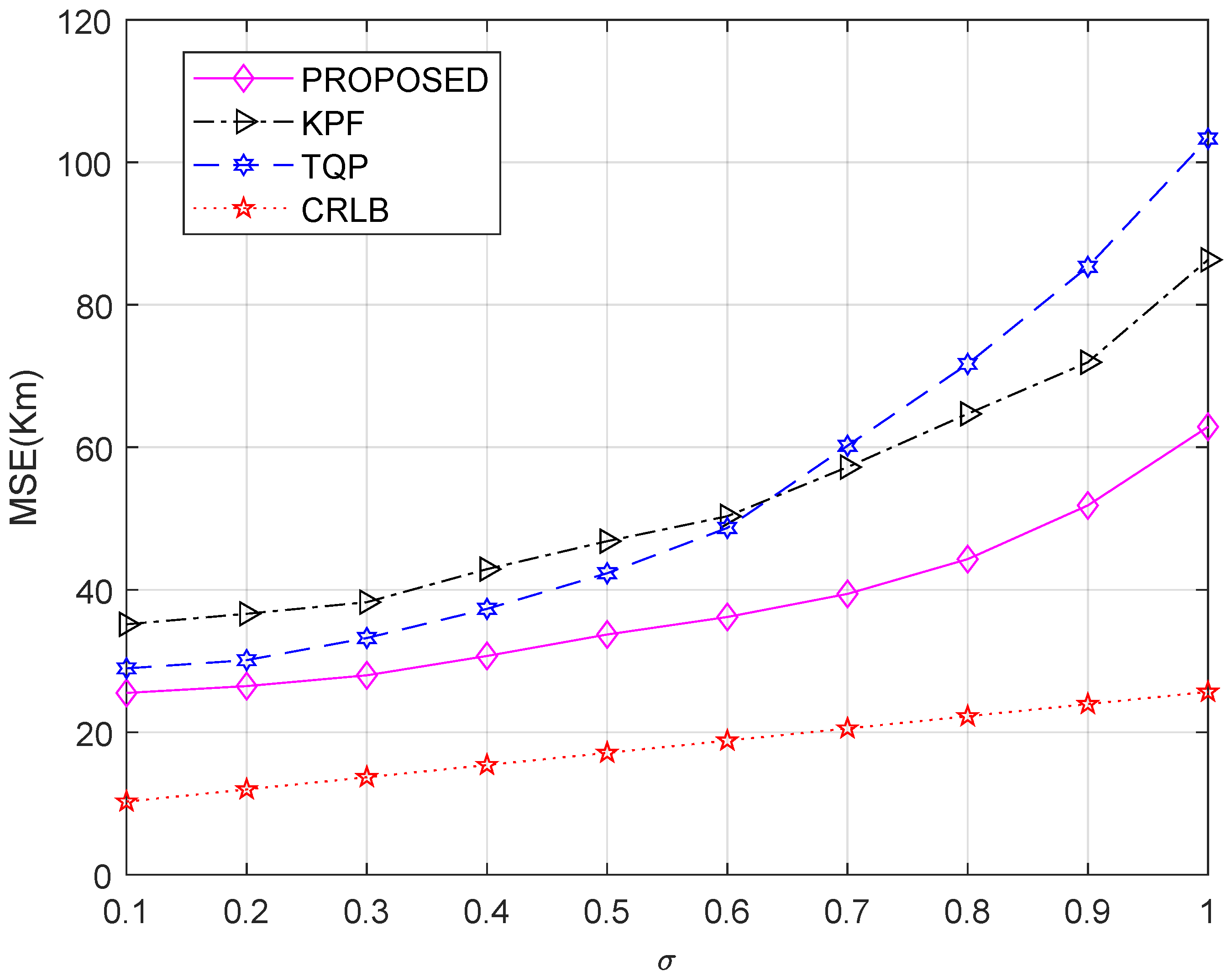
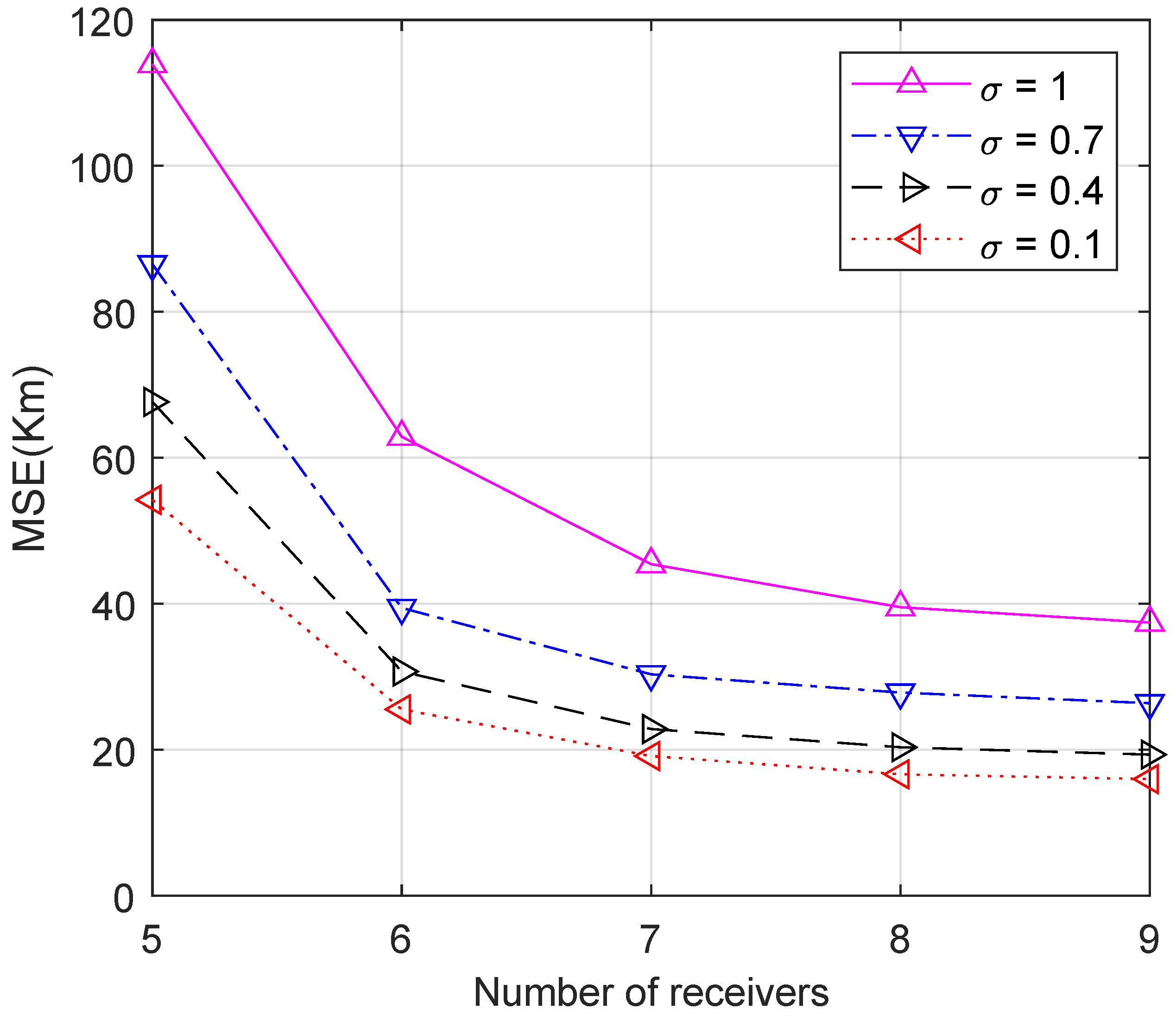
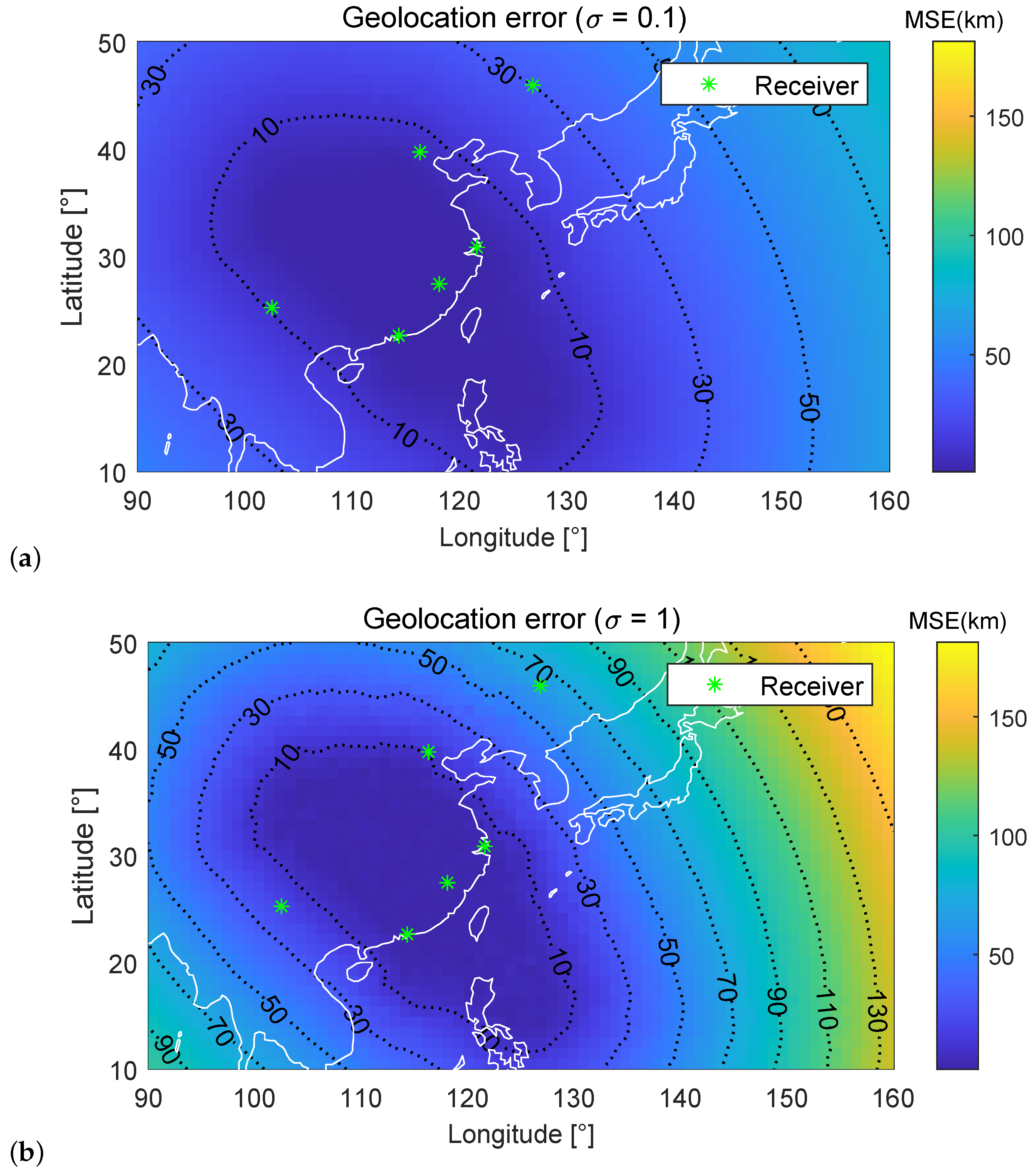
4.1. Simulation Setup and Results
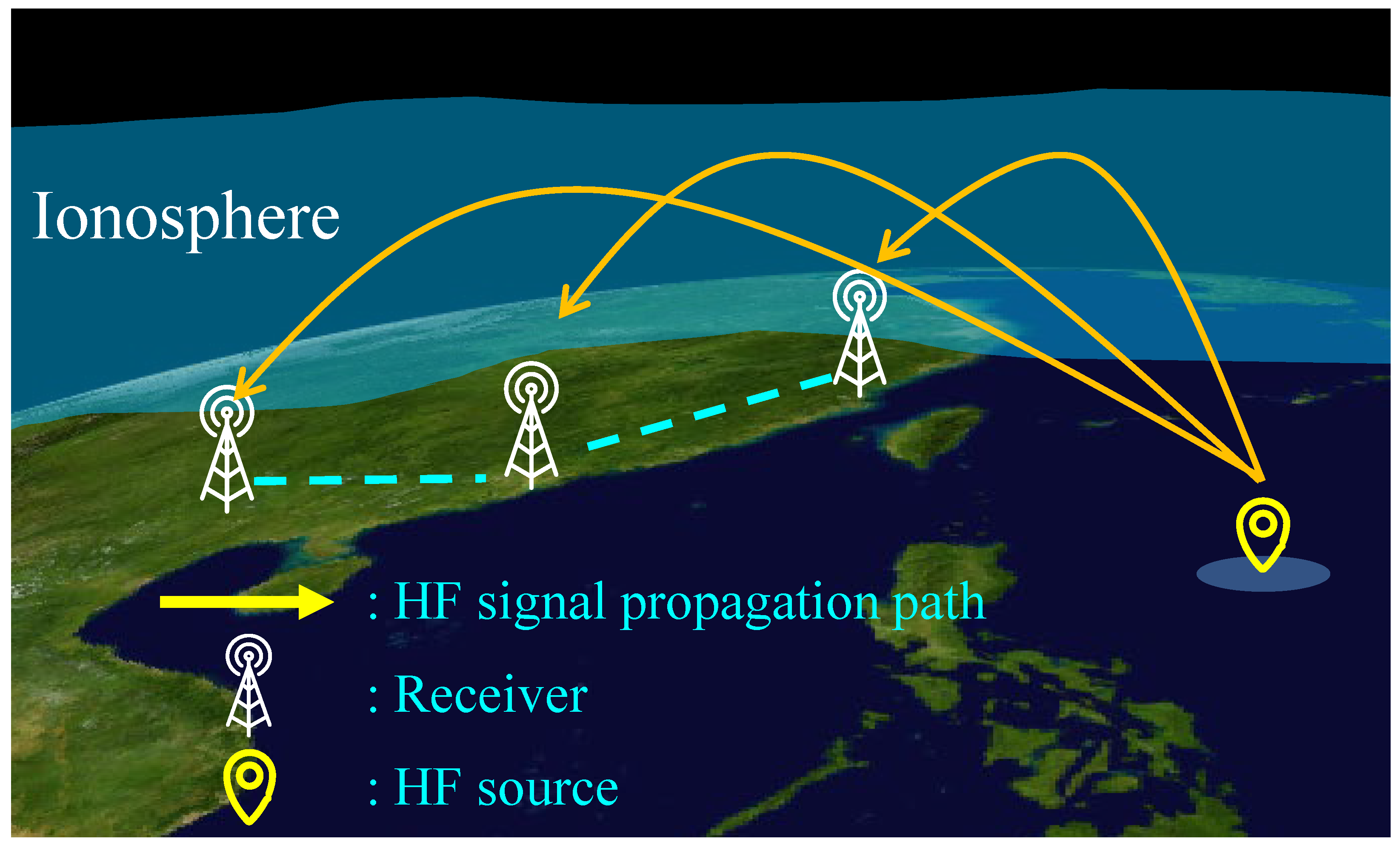
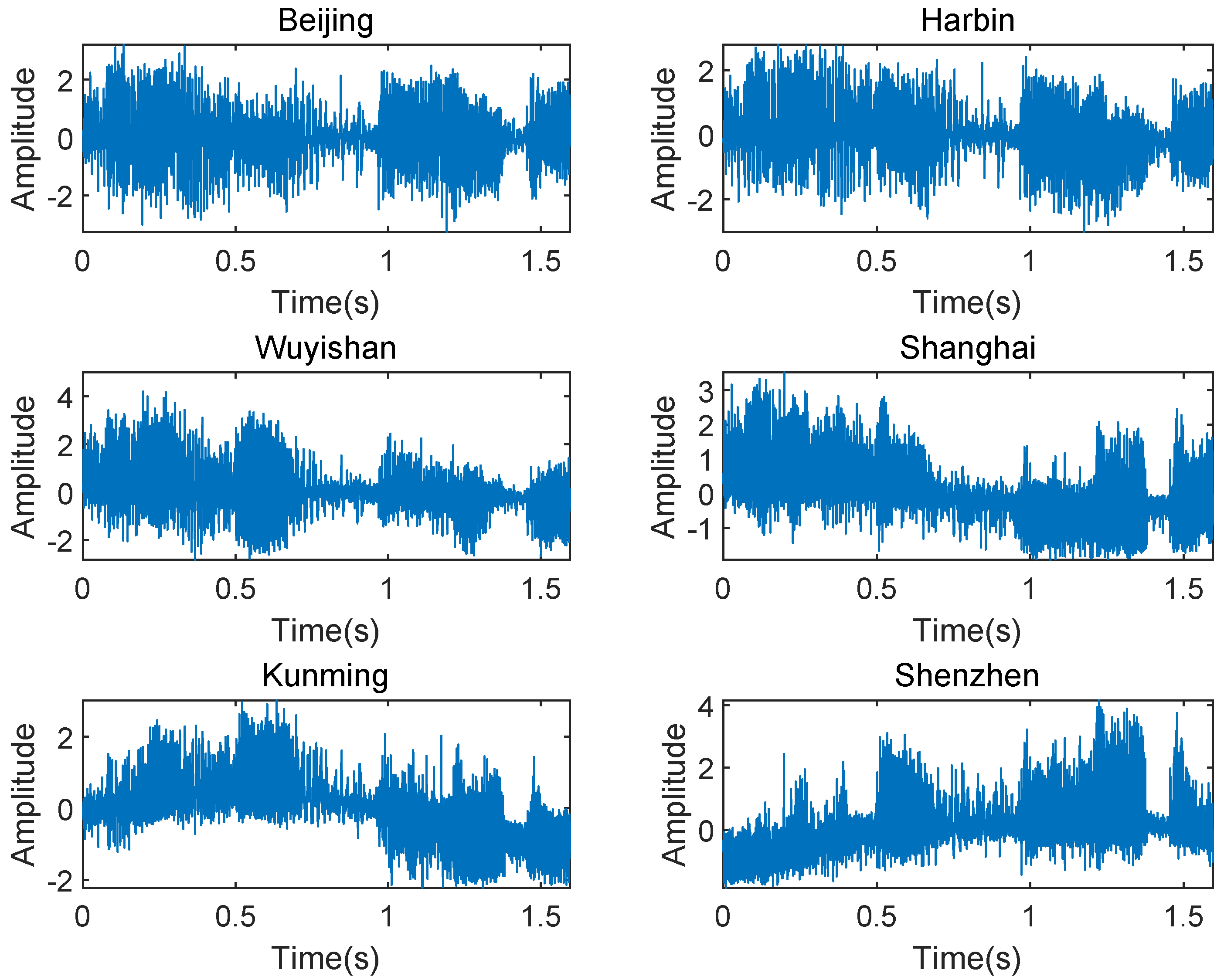
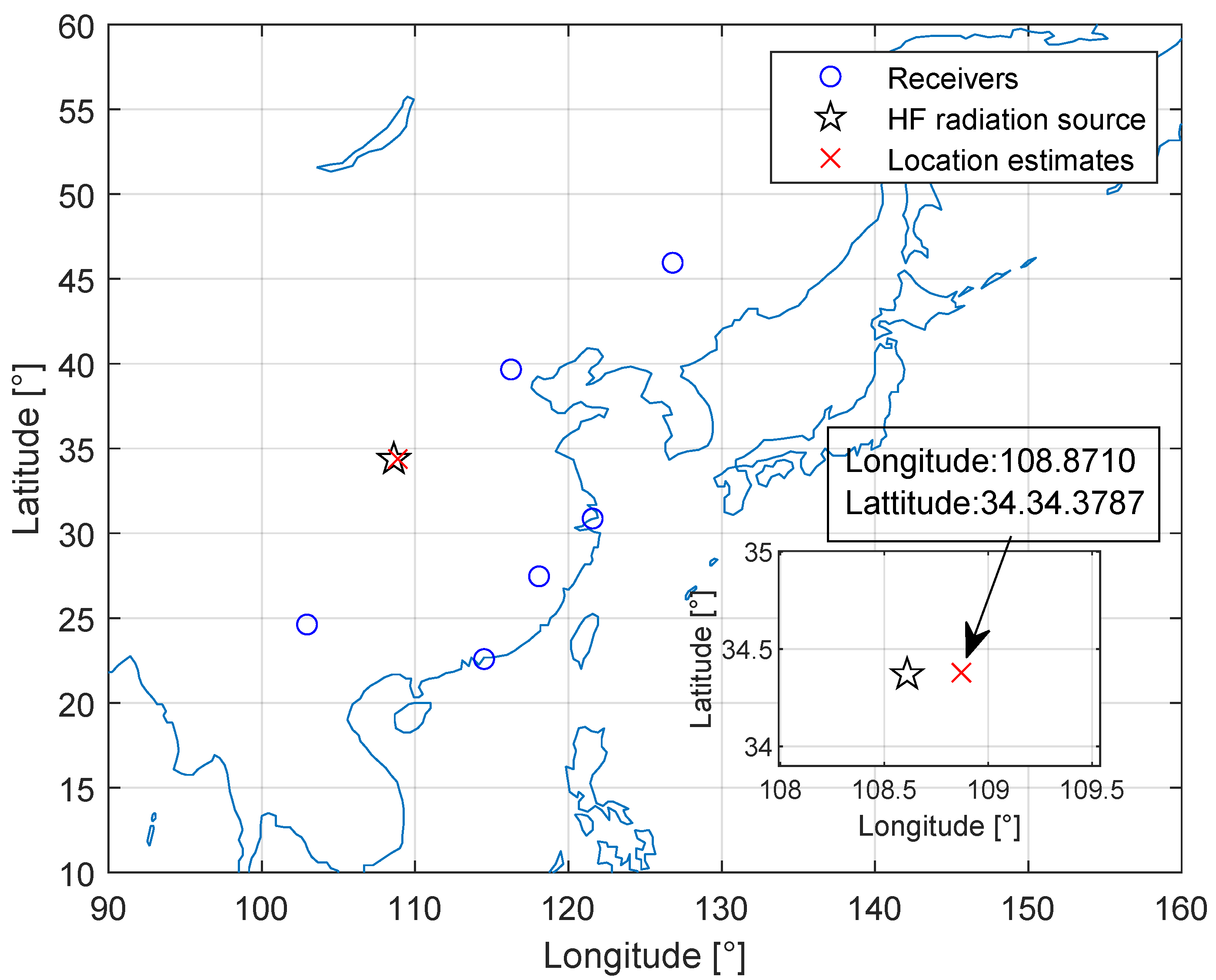
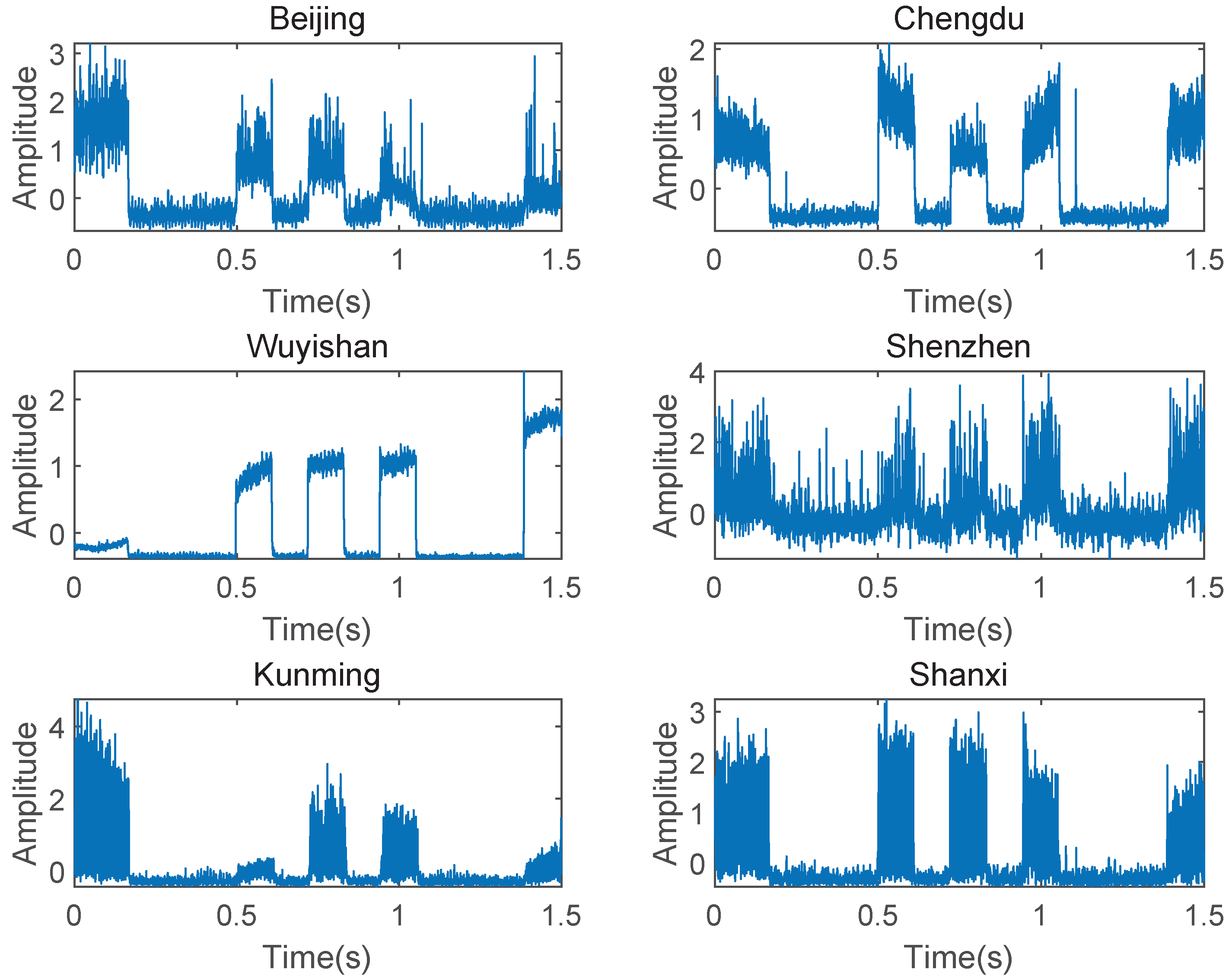
4.2. Experimental Setup and Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
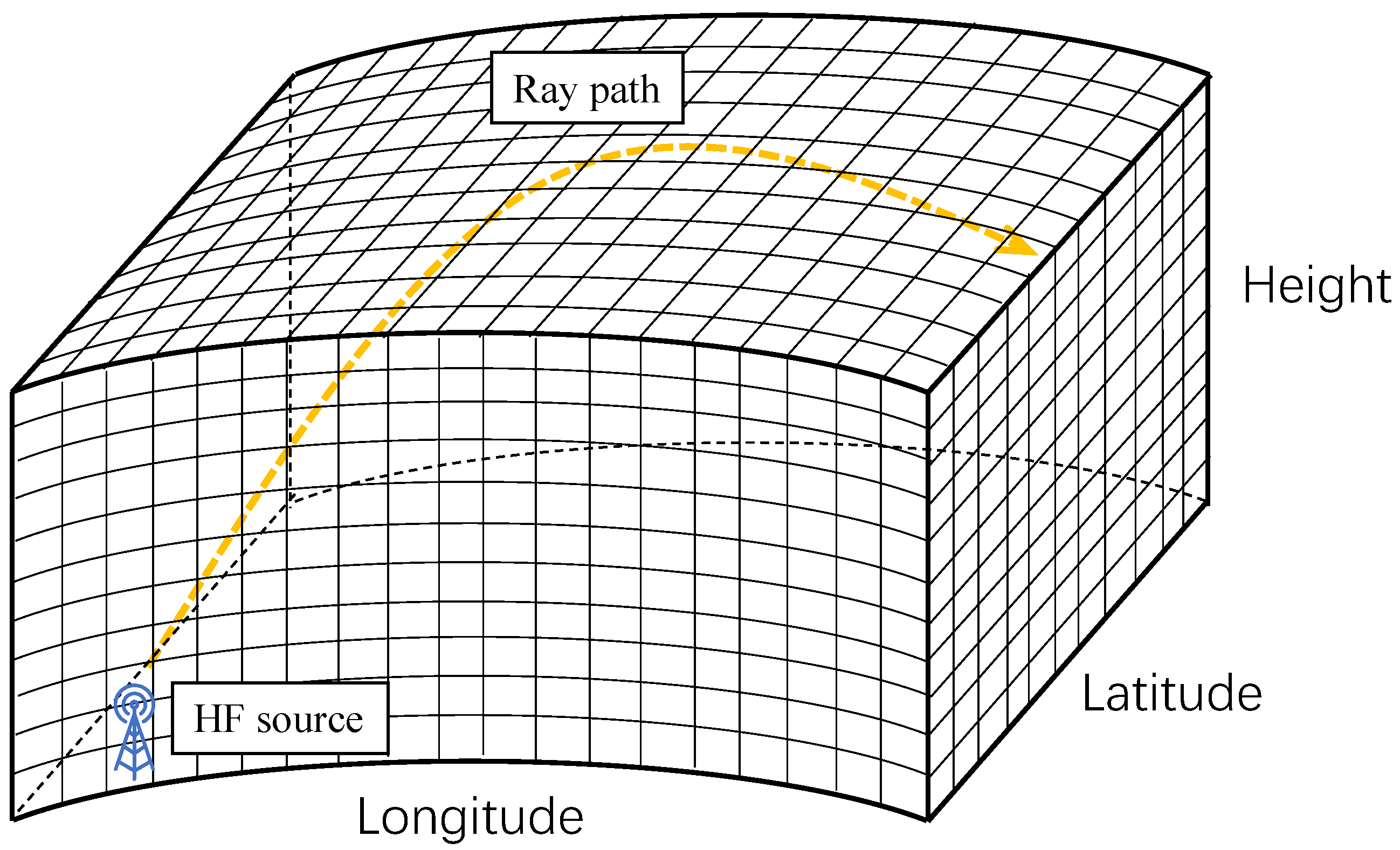
Appendix A. 3D Ionospheric Model


References
- McNamara, L.F. The Ionosphere: Communications, Surveillance, and Direction Finding; Krieger Publishing Company: Malabar, FL, USA, 1991. [Google Scholar]
- Rao, N.N.; Beckwith, R.I.; Ernst, E.W. Prediction of Differential Time-e-Delay Errors in HF Hyperbolic Position-Fixing Systems. IEEE Trans. Aerosp. Electron. Syst. 1974, 6, 765–769. [Google Scholar] [CrossRef]
- Fabrizio, G. Geolocation of HF skywave radar signals using multipath in an unknown ionosphere. In Proceedings of the 2014 IEEE Radar Conference, Cincinnati, OH, USA, 19–23 May 2014; pp. 422–425. [Google Scholar]
- Gholami, M.R.; Vaghefi, R.M.; Ström, E.G. RSS-based sensor localization in the presence of unknown channel Pparameters. IEEE Trans. Signal Process. 2013, 61, 3752–3759. [Google Scholar] [CrossRef] [Green Version]
- Vaghefi, R.M.; Schloemann, J.; Buehrer, R.M. NLOS mitigation in TOA-based localization using semidefinite programming. In Proceedings of the 2013 10th Workshop on Positioning, Navigation and Communication (WPNC), Dresden, Germany, 20–21 March 2013; pp. 1–6. [Google Scholar]
- Al-Qahtani, K.M.; Al-Ahmari, A.S.; Muqaibel, A.H.; Landolsi, M.A.; Johar, U.M. Improved residual weighting for NLOS mitigation in TDOA-based UWB positioning systems. In Proceedings of the 2014 21st International Conference on Telecommunications (ICT), Lisbon, Portugal, 4–7 May 2014; pp. 211–215. [Google Scholar]
- Yang, G.; Liu, T.; Zhou, A.; Jiang, C.; Hu, Y.; Zhao, Z.; Ni, B. A Novel Land-Based High-Frequency Geolocation System. IEEE Geosci. Remote Sens. Lett. 2021, 18, 48–52. [Google Scholar] [CrossRef]
- Xu, C.; Wang, Z.; Wang, Y.; Wang, Z.; Yu, L. Three Passive TDOA-AOA Receivers-Based Flying-UAV Positioning in Extreme Environments. IEEE Sens. J. 2020, 20, 9589–9595. [Google Scholar] [CrossRef]
- Stoica, P.; Sharman, K.C. Maximum likelihood methods for direction-of-arrival estimation. IEEE Trans. Acoust. Speech Signal Process. 1990, 38, 1132–1143. [Google Scholar] [CrossRef]
- Tan, Z.; Eldar, Y.C.; Nehorai, A. Direction of Arrival Estimation Using Co-Prime Arrays: A Super Resolution Viewpoint. IEEE Trans. Signal Process. 2014, 62, 5565–5576. [Google Scholar] [CrossRef] [Green Version]
- Shahbazpanahi, S.; Valaee, S.; Bastani, M.H. Distributed source localization using ESPRIT algorithm. IEEE Trans. Signal Process. 2001, 49, 2169–2178. [Google Scholar] [CrossRef] [Green Version]
- Xia, N.; Wei, W.; Li, J.; Zhang, X. Kalman particle filtering algorithm for symmetric alpha-stable distribution signals with application to high frequency time difference of arrival geolocation. IET Signal Process. 2016, 10, 619–625. [Google Scholar] [CrossRef]
- Jain, A.; Pagani, P.; Fleury, R.; Ney, M.M.; Pajusco, P. HF Source Geolocation Using an Operational TDoA Receiver Network: Experimental Results. IEEE Antennas Wirel. Propagat. Lett. 2018, 17, 1643–1647. [Google Scholar] [CrossRef]
- Hou, C.; Guo, K.; Fu, Y. The sky-wave radar detection performance computing based on the dynamic ionospheric model. Neurocomputing 2015, 151, 1305–1315. [Google Scholar]
- Wang, T.; Hong, X.; Liu, W.; So, A.M.-C.; Yang, K. Geolocation of Unknown Emitters Using Tdoa of Path Rays Through the Ionosphere by Multiple Coordinated Distant Receivers. In Proceedings of the 2018 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Calgary, AB, Canada, 15–20 April 2018; pp. 3509–3513. [Google Scholar]
- Huang, S.; Pun, Y.-M.; So, A.M.-C.; Yang, K. A Provably Convergent Projected Gradient-Type Algorithm for TDOA-Based Geolocation Under the Quasi-Parabolic Ionosphere Model. IEEE Signal Process. Lett. 2020, 27, 1335–1339. [Google Scholar] [CrossRef]
- Shikur, B.Y.; Weber, T. TDOA/AOD/AOA localization in NLOS environments. In Proceedings of the 2014 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Florence, Italy, 4–9 May 2014; pp. 6518–6522. [Google Scholar]
- Miao, H.; Yu, K.; Juntti, M.J. Positioning for NLOS propagation: Algorithm derivations and Cramer-Rao bounds. IEEE Trans. Veh. Technol. 2007, 56, 2568–2580. [Google Scholar] [CrossRef]
- Papakonstantinou, K.; Slock, D. Performance bounds and identifiability conditions for location estimation in NLoS dynamic environments. In Proceedings of the 2011 IEEE Statistical Signal Processing Workshop (SSP), Nice, France, 28–30 June 2011; pp. 189–192. [Google Scholar]
- Vaghefi, R.M.; Buehrer, R.M. Cooperative localization in NLOS environments using semidefinite programming. IEEE Commun. Lett. 2015, 19, 1382–1385. [Google Scholar] [CrossRef]
- Jain, A.; Pagani, P.; Fleury, R.; Ney, M.M.; Pajusco, P. Efficient time domain HF geolocation using multiple distributed receivers. In Proceedings of the 2017 11th European Conference on Antennas and Propagation (EUCAP), Paris, France, 19–24 March 2017; pp. 1852–1856. [Google Scholar]
- Vandenberghe, L.; Boyd, S. Semidefinite programming. SIAM Rev. 1996, 38, 49–95. [Google Scholar] [CrossRef] [Green Version]
- Yan, Z.; Zhang, L.; Rahman, T.; Su, D. Prediction of the HF Ionospheric Channel Stability Based on the Modified ITS Model. Trans. Antennas Propagat. 2013, 61, 3321–3333. [Google Scholar] [CrossRef]
- Vaghefi, R.M.; Gholami, M.R.; Buehrer, R.M.; Ström, E.G. Cooperative received signal strength-based sensor localization with unknown transmit powers. IEEE Trans. Signal Process. 2013, 61, 1382–1385. [Google Scholar] [CrossRef] [Green Version]
- Su, Z.; Shao, G.; Liu, H. Semidefinite programming for NLOS error mitigation in TDOA localization. IEEE Commun. Lett. 2018, 22, 1430–1433. [Google Scholar] [CrossRef]
- Grant, M.; Boyd, S. CVX: Matlab Software for Disciplined Convex Programming, Version 2.1. Available online: http://cvxr.com/cvx (accessed on 1 December 2018).
- Boyd, S.; Vandenberghe, L.; Faybusovich, L. Convex Optimization. IEEE Trans. Autom. Control 2006, 51, 1859. [Google Scholar]
- Huang, J.; Wan, Q. Analysis of TDOA and TDOA/SS based geolocation techniques in a non-line-of-sight environment. J. Commun. Netw. 2012, 14, 533–539. [Google Scholar] [CrossRef]
- Li, J.; Ma, G. Dual-frequency GPS single-point positioning error during the ionospheric irregularity. In Proceedings of the 2012 International Conference on Electromagnetics in Advanced Applications, Cape Town, South Africa, 2–7 September 2012; pp. 654–657. [Google Scholar]
- Kelso, J.M. Ray tracing in the ionosphere. Radio Sci. 1968, 3, 1–12. [Google Scholar] [CrossRef]
- Long, H.; Lixin, G.; Jiangting, L. The simulation of short wave propagation by ray-tracing method in sporadic E layer of ionosphere. In Proceedings of the 2014 3rd Asia-Pacific Conference on Antennas and Propagation, Harbin, China, 26–29 July 2014; pp. 724–727. [Google Scholar]
- Coleman, C.J. A ray tracing formulation and its application to some problems in over-the-horizon radar. Radio Sci. 1998, 33, 1187–1197. [Google Scholar] [CrossRef]



| MSE < 10 km | MSE < 30 km | MSE < 50 km | MSE < 70 km | MSE < 90 km | Average MSE | |
|---|---|---|---|---|---|---|
| 28.07 km | ||||||
| 59.92 km |
| MSE < 10 km | MSE < 30 km | MSE < 50 km | MSE < 70 km | MSE < 90 km | Average MSE | |
|---|---|---|---|---|---|---|
| 33.76 km | ||||||
| 70.90 km |
| 5 Receivers | 6 Receivers | 7 Receivers | 8 Receivers | 9 Receivers | |
|---|---|---|---|---|---|
| Running time (s) | 0.4841 | 0.6521 | 0.8829 | 1.1503 | 1.4001 |
| Harbin | Wuyishan | Shanghai | Kunming | Shenzhen | |
|---|---|---|---|---|---|
| TDOA (Convert to distance) | 1280 | 311 | 461 | 513 | 560 |
| Beijing | Chengdu | Shenzhen | Kunming | Shanxi | |
|---|---|---|---|---|---|
| TDOA (Convert to distance) | 612 | 1209 | 638 | 1369 | 619 |
| Time | Geolocation Error Min., Error Max., Average Error (km) | |||
|---|---|---|---|---|
| (UTC) | PROPOSED | KPF | TQP | |
| AM | 9:00–9:40 | 23.97, 180.11, 42.65 | 65.49, 312.59, 87.02 | 51.33, 264.23, 83.16 |
| FSK | 14:50–15:30 | 33.65, 234.37, 56.32 | 74.27, 356.43, 126.88 | 80.58, 422.84, 127.74 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, C.; Cai, H.; Gao, S.; Zhai, Q. An Improved TDOA Method for Land-Based Long-Range HF Skywave Source Geolocation and Experimental Results. Sensors 2023, 23, 507. https://doi.org/10.3390/s23010507
Xu C, Cai H, Gao S, Zhai Q. An Improved TDOA Method for Land-Based Long-Range HF Skywave Source Geolocation and Experimental Results. Sensors. 2023; 23(1):507. https://doi.org/10.3390/s23010507
Chicago/Turabian StyleXu, Chen, Hongtao Cai, Shunzu Gao, and Qingwei Zhai. 2023. "An Improved TDOA Method for Land-Based Long-Range HF Skywave Source Geolocation and Experimental Results" Sensors 23, no. 1: 507. https://doi.org/10.3390/s23010507
APA StyleXu, C., Cai, H., Gao, S., & Zhai, Q. (2023). An Improved TDOA Method for Land-Based Long-Range HF Skywave Source Geolocation and Experimental Results. Sensors, 23(1), 507. https://doi.org/10.3390/s23010507




