Heuristic Radio Access Network Subslicing with User Clustering and Bandwidth Subpartitioning
Abstract
:1. Introduction
1.1. Related Work
- Regarding slice performance evaluation, most studies have considered throughput and/or delay as the main metrics. However, goodput (application-level throughput) should be taken into account, because throughput alone does not provide details about overheads (packet headers and packet retransmissions).
- Slice performance evaluation does not consider resource utilization, which is needed to understand the number and size of subslices to achieve the best performance.
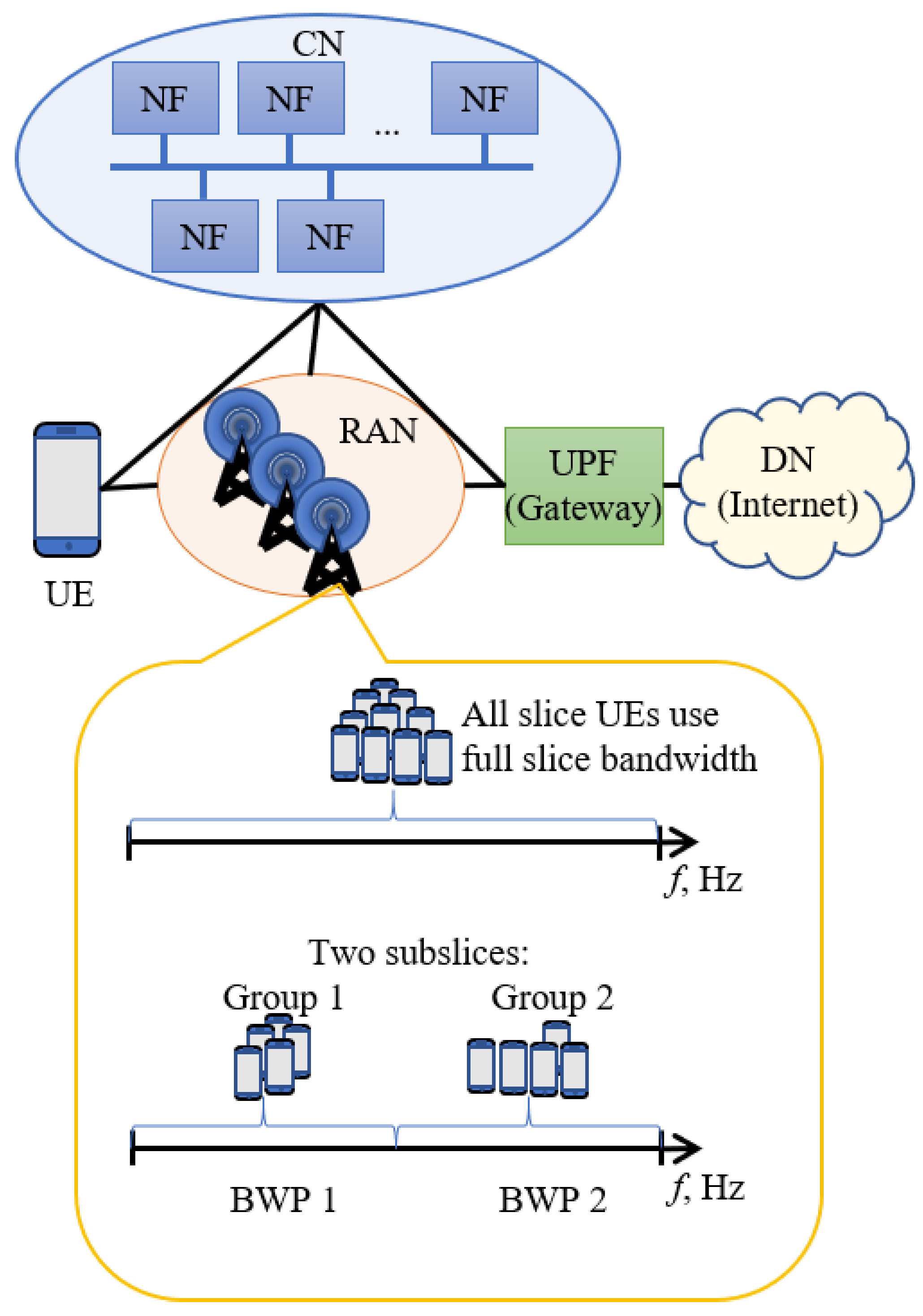
1.2. Motivation and Problem Description
- Input: 275 UEs, 50 MHz (275 RBs), number of subslices in a slice, slice performance data (utilization, throughput, goodput, BLER) when the slice is not subsliced.
- Decision: Select the number of subslices to create and select the subslicing method.
- Objective: Improve the slice performance (reduce the bandwidth utilization and increase the slice goodput).
1.3. Contributions
- Present the dependence of subslice performance on the subslice size.
- Propose a subslicing algorithm that prevents creating too-small subslices.
- Compare the slice performance, if it is subsliced using the proposed algorithm, equal UE grouping, or k-means UE clustering algorithms.
2. Subslice Performance Evaluation at Different Subslice Sizes
2.1. Subslicing
2.2. Subslice Simulation Setup
2.3. Subslice Simulation Results
3. Proposed User Clustering and Bandwidth-Allocation Algorithms for Enhanced Slice Performance
3.1. System Model
3.2. Proposed UE Clustering Algorithm
| Algorithm 1 Modified k-means cluster assignment step. |
|
| Algorithm 2 Proposed algorithm for UE clustering. |
|
3.3. Proposed Group Bandwidth-Allocation Algorithm
| Algorithm 3 Proposed RB allocation for UE groups. |
|
3.4. Proposed Subslicing Algorithm
4. Slice Performance Evaluation
4.1. Simulation Setup
4.2. Results
4.2.1. Slice Bandwidth Utilization
4.2.2. Slice Throughput and Goodput
4.2.3. Slice BLER
4.2.4. Slice Performance Improvement
4.2.5. Algorithm Performance
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- TS 28.530; Management and Orchestration; Concepts, Use Cases and Requirements. Technical Specification; 3GPP: Sophia Antipolis Cedex, France, 2020. Available online: https://www.3gpp.org/DynaReport/28530.htm (accessed on 7 September 2022).
- Kulmar, M.; Muursepp, I.; Alam, M.M. The Impact of RAN Slice Bandwidth Subpartitioning on Slice Performance. In Proceedings of the 2022 International Wireless Communications and Mobile Computing (IWCMC), Dubrovnik, Croatia, 30 May–3 June 2022; IEEE: Piscataway, NJ, USA, 2022; pp. 419–424. [Google Scholar] [CrossRef]
- TS 23.501; System Architecture for the 5G System (5GS); Stage 2. Technical Specification; 3GPP: Sophia Antipolis Cedex, France, 2023. Available online: https://www.3gpp.org/DynaReport/23501.htm (accessed on 10 January 2023).
- Mohammedali, N.A.; Kanakis, T.; Al-Sherbaz, A.; Agyeman, M.O. Performance Evaluation for End-to-End Slice Management in 5G/B5G Cellular Networks. In Proceedings of the 2022 International Conference on Software, Telecommunications and Computer Networks (SoftCOM), Split, Croatia, 22–24 September 2022; IEEE: Piscataway, NJ, USA, 2022; pp. 1–6. [Google Scholar] [CrossRef]
- Singh, S.K.; Salim, M.M.; Cha, J.; Pan, Y.; Park, J.H. Machine Learning-Based Network Sub-Slicing Framework in a Sustainable 5G Environment. Sustainability 2020, 12, 6250. [Google Scholar] [CrossRef]
- Hasegawa, G.; Hasegawa, S.; Arakawa, S.; Murata, M. UONA: User-Oriented Network slicing Architecture for beyond-5G networks. In Proceedings of the ICC 2021—IEEE International Conference on Communications, Montreal, QC, Canada, 14–23 June 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 1–6. [Google Scholar] [CrossRef]
- Ravindran, S.; Chaudhuri, S.; Bapat, J.; Das, D. Isolation-based Sub-Slices for Throughput Optimization in 5G Radio Access Network. In Proceedings of the 2019 IEEE International Conference on Electronics, Computing and Communication Technologies (CONECCT), Bangalore, India, 26–27 July 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 1–6. [Google Scholar] [CrossRef]
- Ravindran, S.; Chaudhuri, S.; Bapat, J.; Das, D. EESO: Energy Efficient System-resource Optimization of Multi-Sub-Slice-Connected User in 5G RAN. In Proceedings of the 2020 IEEE International Conference on Electronics, Computing and Communication Technologies (CONECCT), Bangalore, India, 2–4 July 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 1–6. [Google Scholar] [CrossRef]
- Ravindran, S.; Chaudhuri, S.; Bapat, J.; Das, D. Efficient Service Allocation Scheduling Algorithms for 5G User Equipments in Slice-in-Slice Networks. In Proceedings of the 2021 IEEE International Conference on Advanced Networks and Telecommunications Systems (ANTS), Hyderabad, India, 13–16 December 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 36–41. [Google Scholar] [CrossRef]
- Kuklinski, S.; Tomaszewski, L. Key Performance Indicators for 5G network slicing. In Proceedings of the 2019 IEEE Conference on Network Softwarization (NetSoft), Paris, France, 24–28 June 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 464–471. [Google Scholar] [CrossRef]
- Salhab, N.; Falou, S.E.; Rahim, R.; Ayoubi, S.E.E.; Langar, R. Optimization of the implementation of network slicing in 5G RAN. In Proceedings of the 2018 IEEE Middle East and North Africa Communications Conference (MENACOMM), Jounieh, Lebanon, 18–20 April 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 1–6. [Google Scholar] [CrossRef]
- Han, Y.; Tao, X.; Zhang, X.; Jia, S. Hierarchical Resource Allocation in Multi-Service Wireless Networks with Wireless Network Virtualization. IEEE Trans. Veh. Technol. 2020, 69, 11811–11827. [Google Scholar] [CrossRef]
- Adachi, F.; Takahashi, R.; Matsuo, H. Enhanced Interference Coordination and Radio Resource Management for 5G Advanced Ultra-dense RAN. In Proceedings of the 2020 IEEE 91st Vehicular Technology Conference (VTC2020-Spring), Antwerp, Belgium, 25–28 May 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 1–5. [Google Scholar] [CrossRef]
- Dghais, W.; Souilem, M.; Chi, H.R.; Radwan, A.; Taha, A.E.M. Dynamic Clustering for Power Effective Small Cell Deployment in HetNet 5G Networks. In Proceedings of the ICC 2020—2020 IEEE International Conference on Communications (ICC), Dublin, Ireland, 7–11 June 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 1–5. [Google Scholar] [CrossRef]
- Wang, H.; Zhao, H.; Wu, W.; Xiong, J.; Ma, D.; Wei, J. Deployment Algorithms of Flying Base Stations: 5G and Beyond With UAVs. IEEE Internet Things J. 2019, 6, 10009–10027. [Google Scholar] [CrossRef]
- Thantharate, A.; Paropkari, R.; Walunj, V.; Beard, C. DeepSlice: A Deep Learning Approach towards an Efficient and Reliable Network Slicing in 5G Networks. In Proceedings of the 2019 IEEE 10th Annual Ubiquitous Computing, Electronics & Mobile Communication Conference (UEMCON), New York, NY, USA, 10–12 October 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 0762–0767. [Google Scholar] [CrossRef]
- Addad, R.A.; Taleb, T.; Flinck, H.; Bagaa, M.; Dutra, D. Network Slice Mobility in Next Generation Mobile Systems: Challenges and Potential Solutions. IEEE Netw. 2020, 34, 84–93. [Google Scholar] [CrossRef]
- MacQueen, J. Some Methods for Classification and Analysis of MultiVariate Observations. In Proceedings of the Berkeley Symposium on Mathematical Statistics and Probability, Berkeley, CA, USA, 21 June–18 July 1965; pp. 281–297. [Google Scholar]
- Sinaga, K.P.; Yang, M.S. Unsupervised K-Means Clustering Algorithm. IEEE Access 2020, 8, 80716–80727. [Google Scholar] [CrossRef]
- Bradley, P.S.; Bennett, K.P.; Demiriz, A. Constrained k-Means Clustering; Technical Report; Microsoft publication MSR-TR-2000-65; 2000; p. 8. Available online: https://www.microsoft.com/en-us/research/publication/constrained-k-means-clustering/ (accessed on 27 May 2022).
- Malinen, M.I.; Fränti, P. Balanced k-means for clustering. In Structural, Syntactic, and Statistical Pattern Recognition; S+SSPR 2014. Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2014; Volume 8621, pp. 32–41. [Google Scholar] [CrossRef]
- TS 28.535; Management and Orchestration; Management Services for Communication Service Assurance; Requirements. Technical Specification; 3GPP: Sophia Antipolis Cedex, France, 2020. Available online: https://www.3gpp.org/DynaReport/28535.htm (accessed on 10 January 2023).
- Chang, C.Y.; Nikaein, N. RAN runtime slicing system for flexible and dynamic service execution environment. IEEE Access 2018, 6, 34018–34042. [Google Scholar] [CrossRef]
- MathWorks. NR Cell Performance Evaluation with Physical Layer Integration. 2022. Available online: https://se.mathworks.com/help/5g/ug/nr-cell-performance-evaluation-with-physical-layer-integration.html (accessed on 19 January 2022).
- GSMA. NG.116 Generic Network Slice Template v5.0; Technical Report; GSMA: London, UK, 2021; Available online: https://www.gsma.com/newsroom/wp-content/uploads//NG.116-v5.0.pdf (accessed on 6 September 2021).
- TS 38.214 NR; Physical Layer Procedures for Data. Technical Specification; 3GPP: Sophia Antipolis Cedex, France, 2021. Available online: https://www.3gpp.org/DynaReport/38214.htm (accessed on 16 August 2022).
- Fjodorov, A.; Masood, A.; Alam, M.M.; Parand, S. 5G Testbed Implementation and Measurement Campaign for Ground and Aerial Coverage. In Proceedings of the 2022 18th Biennial Baltic Electronics Conference (BEC), Tallinn, Estonia, 4–6 October 2022; IEEE: Piscataway, NJ, USA, 2022; pp. 1–6. [Google Scholar] [CrossRef]















| Paper | How Subslicing Is Performed | Benefits | Limitations |
|---|---|---|---|
| [7] | Three verticals each contain subgroups of services. UEs grouped by similar SLA values | Performance improvement achieved by subslicing: increased SNR and throughput. | The planned use of capacity varies between underload and half of the full load. The effect of the number of subslices on slice performance has not been evaluated. |
| [8] | A subslice is a logical group of services that is associated with a single UE. The UE can connect to multiple subslices. | The performance improvement achieved by subslicing: increased throughput and energy efficiency. | The planned use of capacity is variable between underload and close to full load. |
| [9] | One subslice can serve not only UEs with similar SLAs, but also a mixed set of UEs with different throughputs. | The performance improvement achieved by subslicing: increased throughput. | The planned use of capacity cannot be evaluated using the given data. |
| [5] | UEs are clustered by the similarity of their requirements. | Subslicing results in decreased bandwidth consumption, improved load balancing, improved latency and heterogeneity, and improved energy efficiency. | Planned underload, RAN simulated as Android UEs in Wi-Fi. The proposed subslicing method does not avoid creating subslices that are too small. |
| [6] | In the RAN subslice, the virtual cell covers multiple physical cells, and the UE by mobility allocates the virtual cell. | The latency and throughput can be improved because UE handover is performed faster. | Evaluation of just signalling for handover. The UE can select subslices without constraints on the subslice performance. |
| [4] | The slice with identifier SST contains all slices with the same SST and different SDs as subslices. | Performance improvement was achieved by subslicing. | The RAN was simulated as ideal. |
| This paper | The slice bandwidth is subpartitioned, slice UEs are grouped, and bandwidth subpartitions are allocated to UE groups. The number and sizes of subslices are determined with the aim of achieving better performance than without subslicing. | Slice performance can be improved by reducing bandwidth utilization and increasing goodput if the subslices are not too small. Simulations were performed using 5G-NR and close to the full capacity of the allocated bandwidth. UE requested rates are sufficient to utilize one RB per UE. | Simulations were performed under the assumptions that all UEs are similar to their requirements and capabilities. The proposed algorithm requires significant computational resources. |
| Parameter | Value | |
|---|---|---|
| Number of UEs in a subslice | {4–275} | |
| Number of RBs allocated to subslice | {4–275} | |
| Subslice modification for next step | Increase UEs by one and increase RBs by one | |
| Subcarrier spacing | 15 kHz | |
| UE rate requirements | UL 500 kbps, DL 667 kbps | |
| Subband size | ||
| Size of BWP in RBs | Subband size specified in TS 38.214 | Subband size used in simulations |
| 4–23 | - | 4 |
| 24–72 | 4, 8 | 8 |
| 73–144 | 8, 16 | 8 |
| 145–275 | 16, 32 | 16 |
| Parameter | Value |
|---|---|
| Carrier frequency | 3 GHz |
| Channel model (for both UL and DL) | CDL-C |
| PUSCH preparation time for UEs | 200 μs |
| Logical channels per UE | 1 |
| RLC entity type | UM bidirectional |
| Duplex mode | FDD |
| Scheduler strategy | Round Robin |
| Length of scheduling cycle | 1 frame |
| RB allocation limit UL | same as RBs for subslice |
| RB allocation limit DL | same as RBs for subslice |
| Simulation time | 1 s |
| Subslice simulation tool from MATLAB 5G Toolbox | NR Cell Performance Evaluation with Physical Layer Integration [24] R2021b |
| Zone | Subslice Size (RBs) | Average Utilization | Average Throughput | Average Goodput | Average BLER | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1500 B | 40 B | 1500 B | 40 B | 1500 B | 40 B | 1500 B | 40 B | ||||||||||
| UL | DL | UL | DL | UL | DL | UL | DL | UL | DL | UL | DL | UL | DL | UL | DL | ||
| 1 | 4–36 | 0.949 | 0.988 | 0.986 | 0.998 | 0.522 | 0.571 | 0.485 | 0.586 | 0.493 | 0.566 | 0.457 | 0.581 | 0.081 | 0.056 | 0.079 | 0.053 |
| 2 | 37–72 | 0.675 | 0.777 | 0.831 | 0.998 | 0.726 | 0.804 | 0.896 | 1.044 | 0.68 | 0.791 | 0.838 | 1.031 | 0.057 | 0.015 | 0.061 | 0.013 |
| 3 | 73–144 | 0.815 | 0.923 | 0.993 | 0.998 | 0.915 | 1.000 | 1.115 | 1.082 | 0.796 | 0.975 | 0.97 | 1.057 | 0.122 | 0.024 | 0.122 | 0.024 |
| 4 | 145–275 | 0.905 | 0.978 | 0.993 | 0.998 | 1.014 | 1.065 | 1.113 | 1.087 | 0.786 | 0.994 | 0.863 | 1.015 | 0.205 | 0.064 | 0.206 | 0.064 |
| Parameter | Value |
|---|---|
| Slice bandwidth | 275 RBs (49.5 MHz) |
| Subcarrier spacing | 15 kHz |
| Number of UEs is the slice | 275 |
| Number of subslices and minimum subslice sizes | 3, if 7, if 14, if 25, if 68, if |
| Parameter to cluster UEs | BLER |
| UE distance from gNB (m): all good-BLER UEs, all medium-BLER UEs, all poor-BLER UEs | . 1–275 1001–1275 6001–6275 |
| UE rate requirements | UL 500 kbps, DL 667 kbps |
| UE packet sizes | {1500 B, 40 B} |
| Algorithm | 3 Subslices | 7 Subslices | 14 Subslices | 25 Subslices | 68 subslices |
|---|---|---|---|---|---|
| Equal | 35.3 | 45 | 36.5 | 24.2 | −32.7 |
| K-means | 34.6 | 34.8 | 18.4 | −4.9 | N/A |
| Proposed | 34.8 | 44.3 | 35.5 | 24.3 | −33.8 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kulmar, M.; Müürsepp, I.; Alam, M.M. Heuristic Radio Access Network Subslicing with User Clustering and Bandwidth Subpartitioning. Sensors 2023, 23, 4613. https://doi.org/10.3390/s23104613
Kulmar M, Müürsepp I, Alam MM. Heuristic Radio Access Network Subslicing with User Clustering and Bandwidth Subpartitioning. Sensors. 2023; 23(10):4613. https://doi.org/10.3390/s23104613
Chicago/Turabian StyleKulmar, Marika, Ivo Müürsepp, and Muhammad Mahtab Alam. 2023. "Heuristic Radio Access Network Subslicing with User Clustering and Bandwidth Subpartitioning" Sensors 23, no. 10: 4613. https://doi.org/10.3390/s23104613
APA StyleKulmar, M., Müürsepp, I., & Alam, M. M. (2023). Heuristic Radio Access Network Subslicing with User Clustering and Bandwidth Subpartitioning. Sensors, 23(10), 4613. https://doi.org/10.3390/s23104613







