Backward THz Emission from Two-Color Laser Field-Induced Air Plasma Filament
Abstract
:1. Introduction
2. Theoretical and Experimental Basis
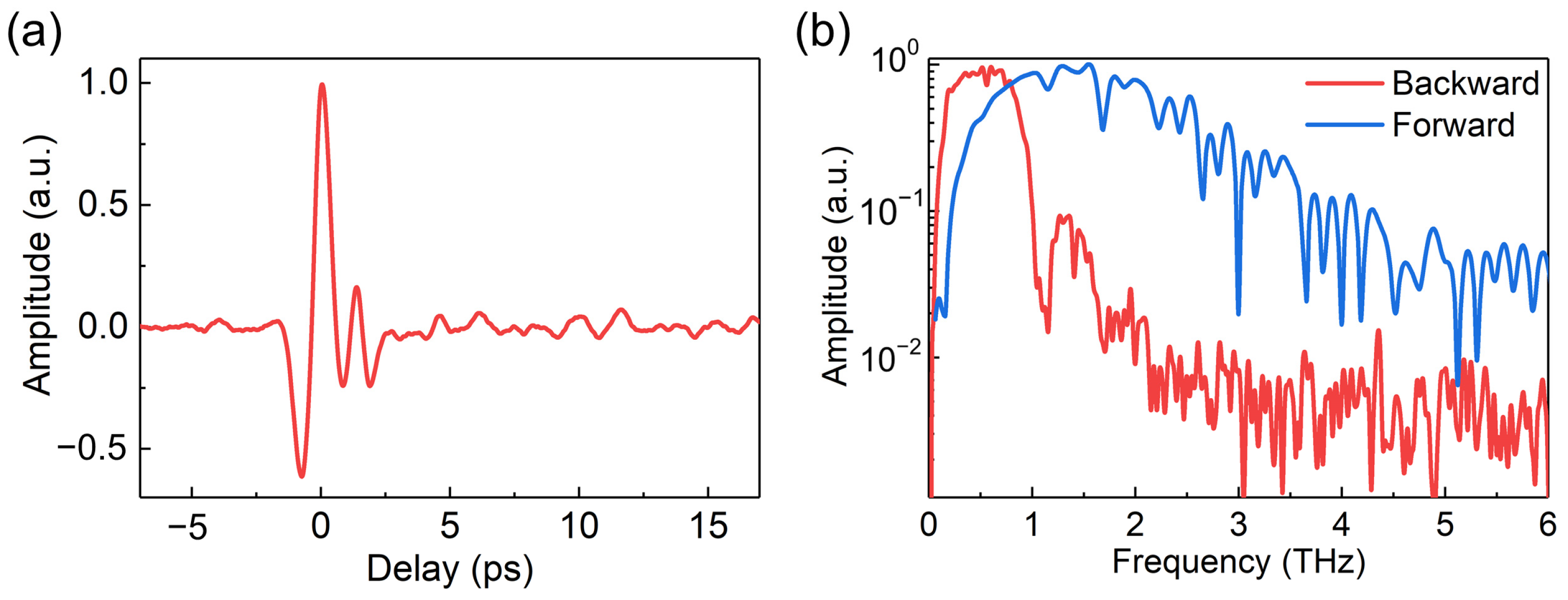
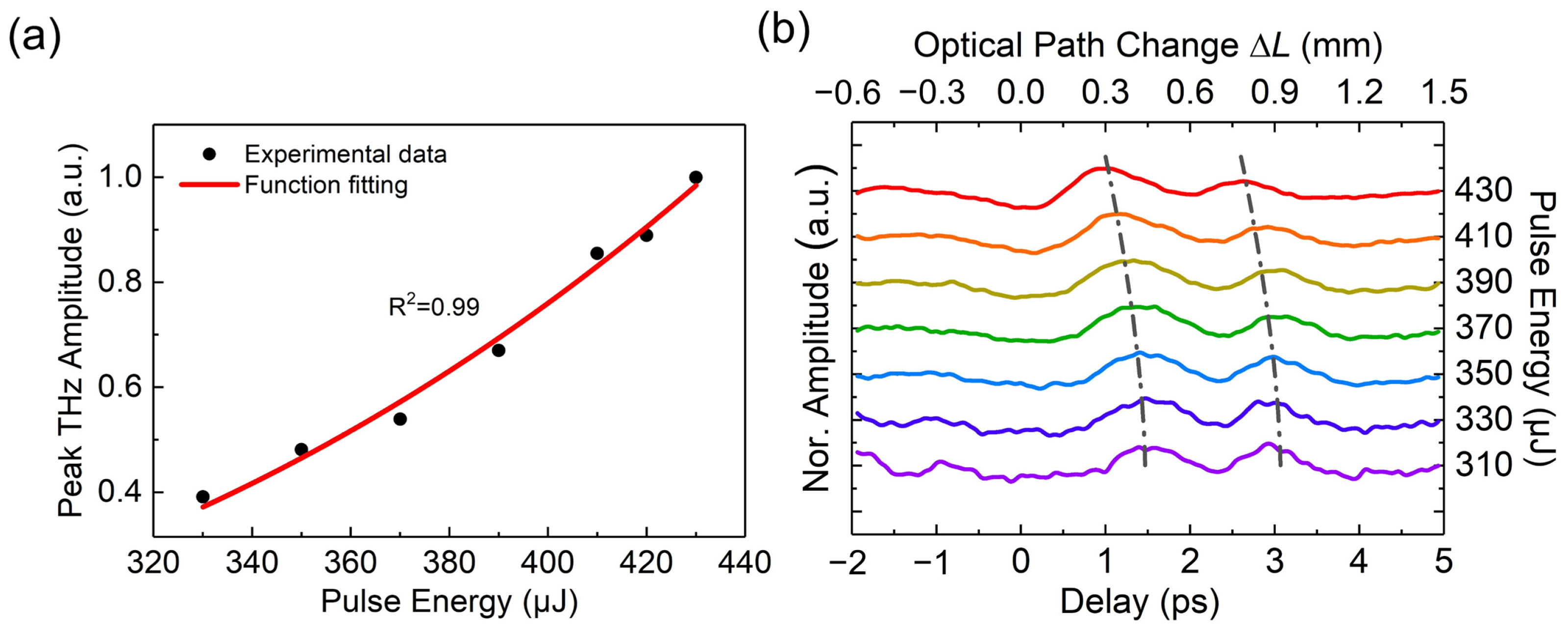
3. Results and Discussions
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Kim, K.Y.; Taylor, A.J.; Glownia, J.H.; Rodriguez, G. Coherent control of terahertz supercontinuum generation in ultrafast laser-gas interactions. Nat. Photonics 2008, 2, 605–609. [Google Scholar] [CrossRef]
- Mitrofanov, A.V.; Sidorov-Biryukov, D.A.; Nazarov, M.M.; Voronin, A.A.; Rozhko, M.V.; Shutov, A.D.; Ryabchuk, S.V.; Serebryannikov, E.E.; Fedotov, A.B.; Zheltikov, A.M. Ultraviolet-to-millimeter-band supercontinua driven by ultrashort mid-infrared laser pulses. Optica 2020, 7, 15–19. [Google Scholar] [CrossRef]
- Tonouchi, M. Cutting-edge terahertz technology. Nat. Photonics 2007, 1, 97–105. [Google Scholar] [CrossRef]
- Jepsen, P.U.; Cooke, D.G.; Koch, M. Terahertz spectroscopy and imaging—Modern techniques and applications. Laser Photonics Rev. 2011, 5, 124–166. [Google Scholar] [CrossRef]
- Xie, X.; Dai, J.; Zhang, X.C. Coherent control of THz wave generation in ambient air. Phys. Rev. Lett. 2006, 96, 075005. [Google Scholar] [CrossRef] [PubMed]
- Wen, H.; Lindenberg, A.M. Coherent terahertz polarization control through manipulation of electron trajectories. Phys. Rev. Lett. 2009, 103, 023902. [Google Scholar] [CrossRef]
- Zhang, Z.; Chen, Y.; Cui, S.; He, F.; Chen, M.; Zhang, Z.; Yu, J.; Chen, L.; Sheng, Z.; Zhang, J. Manipulation of polarizations for broadband terahertz waves emitted from laser plasma filaments. Nat. Photonics 2018, 12, 554–559. [Google Scholar] [CrossRef]
- Liu, S.J.; Fan, Z.Q.; Lu, C.H.; Gui, J.Y.; Luo, C.; Wang, S.X.; Liang, Q.Q.; Zhou, B.; Houard, A.; Mysyrowicz, A.; et al. Coherent control of boosted terahertz radiation from air plasma pumped by a femtosecond three-color sawtooth field. Phys. Rev. A 2020, 102, 063522. [Google Scholar] [CrossRef]
- Vaičaitis, V.; Balachninaitė, O.; Morgner, U.; Babushkin, I. Terahertz radiation generation by three-color laser pulses in air filament. J. Appl. Phys. 2019, 125, 173103. [Google Scholar] [CrossRef]
- Löffler, T.; Jacob, F.; Roskos, H.G. Generation of terahertz pulses by photoionization of electrically biased air. Appl. Phys. Lett. 2000, 77, 453–455. [Google Scholar] [CrossRef]
- Chen, Y.; Wang, T.-j.; Marceau, C.; Théberge, F.; Châteauneuf, M.; Dubois, J.; Kosareva, O.; Chin, S.L. Characterization of terahertz emission from a dc-biased filament in air. Appl. Phys. Lett. 2009, 95, 101101. [Google Scholar] [CrossRef]
- D’Amico, C.; Houard, A.; Franco, M.; Prade, B.; Mysyrowicz, A.; Couairon, A.; Tikhonchuk, V.T. Conical forward THz emission from femtosecond-laser-beam filamentation in air. Phys. Rev. Lett. 2007, 98, 235002. [Google Scholar] [CrossRef] [PubMed]
- Gorodetsky, A.; Koulouklidis, A.D.; Massaouti, M.; Tzortzakis, S. Physics of the conical broadband terahertz emission from two-color laser-induced plasma filaments. Phys. Rev. A 2014, 89, 033838. [Google Scholar] [CrossRef]
- Zhang, Z.; Chen, Y.; Chen, M.; Zhang, Z.; Yu, J.; Sheng, Z.; Zhang, J. Controllable Terahertz Radiation from a Linear-Dipole Array Formed by a Two-Color Laser Filament in Air. Phys. Rev. Lett. 2016, 117, 243901. [Google Scholar] [CrossRef] [PubMed]
- Koribut, A.V.; Rizaev, G.E.; Mokrousova, D.V.; Savinov, S.A.; Reutov, A.A.; Mityagin, Y.A.; Seleznev, L.V.; Ionin, A.A. Similarity of angular distribution for THz radiation emitted by laser filament plasma channels of different lengths. Opt. Lett. 2020, 45, 4009–4011. [Google Scholar] [CrossRef]
- Rizaev, G.E.; Seleznev, L.V.; Mokrousova, D.V.; Pushkarev, D.V.; Ionin, A.A. Terahertz emission pattern from a single-color filament plasma. Opt. Lett. 2022, 47, 5917–5920. [Google Scholar] [CrossRef]
- Panov, N.; Andreeva, V.; Kosareva, O.; Shkurinov, A.; Makarov, V.A.; Bergé, L.; Chin, S.L. Directionality of terahertz radiation emitted from an array of femtosecond filaments in gases. Laser Phys. Lett. 2014, 11, 125401. [Google Scholar] [CrossRef]
- Shkurinov, A.P.; Sinko, A.S.; Solyankin, P.M.; Borodin, A.V.; Esaulkov, M.N.; Annenkov, V.V.; Kotelnikov, I.A.; Timofeev, I.V.; Zhang, X.C. Impact of the dipole contribution on the terahertz emission of air-based plasma induced by tightly focused femtosecond laser pulses. Phys. Rev. E 2017, 95, 043209. [Google Scholar] [CrossRef]
- Jahangiri, F.; Hashida, M.; Nagashima, T.; Tokita, S.; Hangyo, M.; Sakabe, S. Intense terahertz emission from atomic cluster plasma produced by intense femtosecond laser pulses. Appl. Phys. Lett. 2011, 99, 261503. [Google Scholar] [CrossRef]
- Kohler, C.; Cabrera-Granado, E.; Babushkin, I.; Berge, L.; Herrmann, J.; Skupin, S. Directionality of terahertz emission from photoinduced gas plasmas. Opt. Lett. 2011, 36, 3166–3168. [Google Scholar] [CrossRef]
- Ushakov, A.A.; Panov, N.A.; Chizhov, P.A.; Shipilo, D.E.; Bukin, V.V.; Savel’ev, A.B.; Garnov, S.V.; Kosareva, O.G. Waveform, spectrum, and energy of backward terahertz emission from two-color femtosecond laser-induced microplasma. Appl. Phys. Lett. 2019, 114, 081102. [Google Scholar] [CrossRef]
- Cook, D.J.; Hochstrasser, R.M. Intense terahertz pulses by four-wave rectification in air. Opt. Lett. 2000, 25, 1210–1212. [Google Scholar] [CrossRef] [PubMed]
- Dai, J.M.; Zhang, X.C. Terahertz wave generation from thin metal films excited by asymmetrical optical fields. Opt. Lett. 2014, 39, 777–780. [Google Scholar] [CrossRef] [PubMed]
- Whalen, P.; Moloney, J.V.; Kolesik, M. Self-focusing collapse distance in ultrashort pulses and measurement of nonlinear index. Opt. Lett. 2011, 36, 2542–2544. [Google Scholar] [CrossRef]
- Liu, J.L.; Dai, J.M.; Chin, S.L.; Zhang, X.C. Broadband terahertz wave remote sensing using coherent manipulation of fluorescence from asymmetrically ionized gases. Nat. Photonics 2010, 4, 627–631. [Google Scholar] [CrossRef]
- Solyankin, P.M.; Nikolaeva, I.A.; Angeluts, A.A.; Shipilo, D.E.; Minaev, N.V.; Panov, N.A.; Balakin, A.V.; Zhu, Y.; Kosareva, O.G.; Shkurinov, A.P. THz generation from laser-induced breakdown in pressurized molecular gases: On the way to terahertz remote sensing of the atmospheres of Mars and Venus. New J.Phys. 2020, 22, 013039. [Google Scholar] [CrossRef]
- Dai, J.M.; Zhang, X.C. Terahertz wave generation from gas plasma using a phase compensator with attosecond phase-control accuracy. Appl. Phys. Lett. 2009, 94, 021117. [Google Scholar] [CrossRef]
- Wang, T.-J.; Chen, Y.; Marceau, C.; Théberge, F.; Châteauneuf, M.; Dubois, J.; Chin, S.L. High energy terahertz emission from two-color laser-induced filamentation in air with pump pulse duration control. Appl. Phys. Lett. 2009, 95, 131108. [Google Scholar] [CrossRef]
- Zhang, Z.; Panov, N.; Andreeva, V.; Zhang, Z.; Slepkov, A.; Shipilo, D.; Thomson, M.D.; Wang, T.-J.; Babushkin, I.; Demircan, A.; et al. Optimum chirp for efficient terahertz generation from two-color femtosecond pulses in air. Appl. Phys. Lett. 2018, 113, 241103. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, Y.; He, Y.; Liu, L.; Tian, Z.; Dai, J.; Zhang, X.-C. Backward THz Emission from Two-Color Laser Field-Induced Air Plasma Filament. Sensors 2023, 23, 4630. https://doi.org/10.3390/s23104630
Chen Y, He Y, Liu L, Tian Z, Dai J, Zhang X-C. Backward THz Emission from Two-Color Laser Field-Induced Air Plasma Filament. Sensors. 2023; 23(10):4630. https://doi.org/10.3390/s23104630
Chicago/Turabian StyleChen, Yuxuan, Yuhang He, Liyuan Liu, Zhen Tian, Jianming Dai, and Xi-Cheng Zhang. 2023. "Backward THz Emission from Two-Color Laser Field-Induced Air Plasma Filament" Sensors 23, no. 10: 4630. https://doi.org/10.3390/s23104630
APA StyleChen, Y., He, Y., Liu, L., Tian, Z., Dai, J., & Zhang, X.-C. (2023). Backward THz Emission from Two-Color Laser Field-Induced Air Plasma Filament. Sensors, 23(10), 4630. https://doi.org/10.3390/s23104630





