A Probabilistic Model of Human Activity Recognition with Loose Clothing †
Abstract
:1. Introduction
2. Related Work
3. Probabilistic Modeling Framework
3.1. Problem Definition
3.2. Probabilistic Model of Fabric Motion
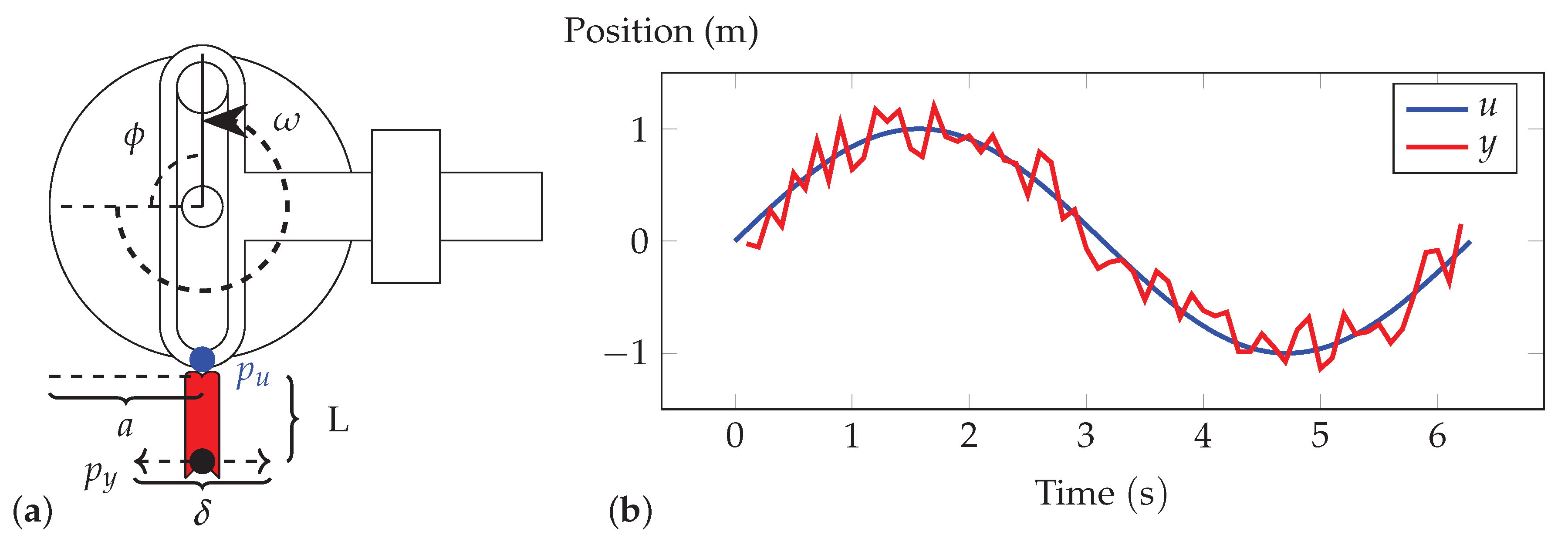
3.3. Example: Oscillatory Motion
4. Activity Recogntion Via Statistical Methods
4.1. Case Study 1: Simple Harmonic Motion
4.1.1. Materials and Methods
4.1.2. Results
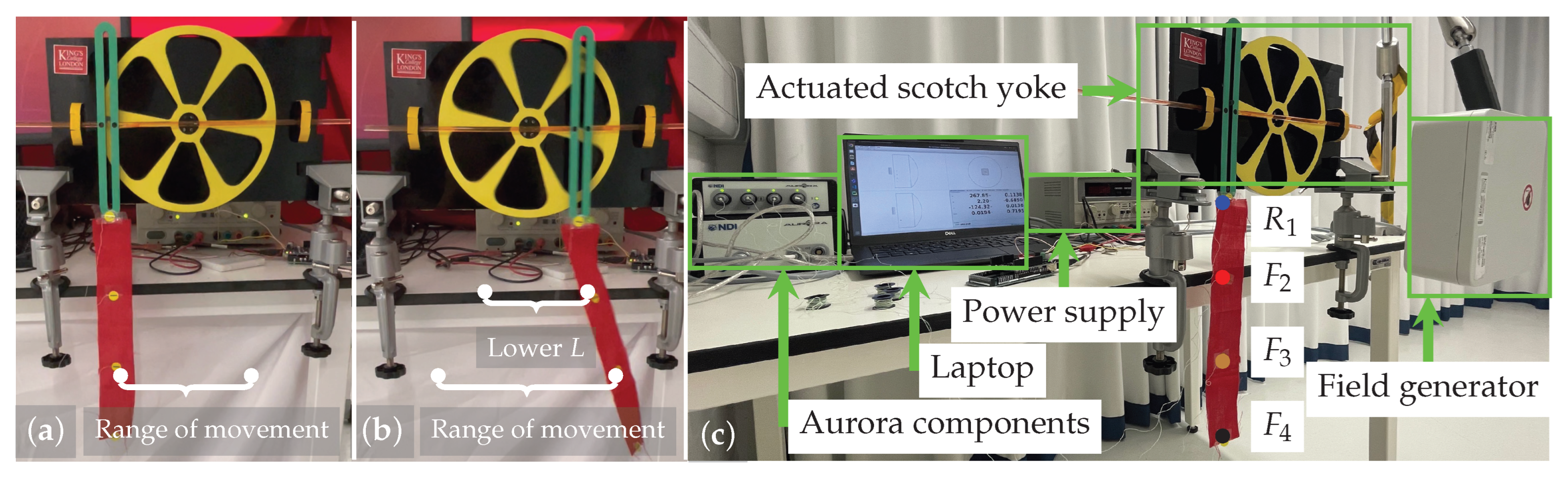
4.2. Case Study 2: Scotch Yoke
4.2.1. Materials and Methods
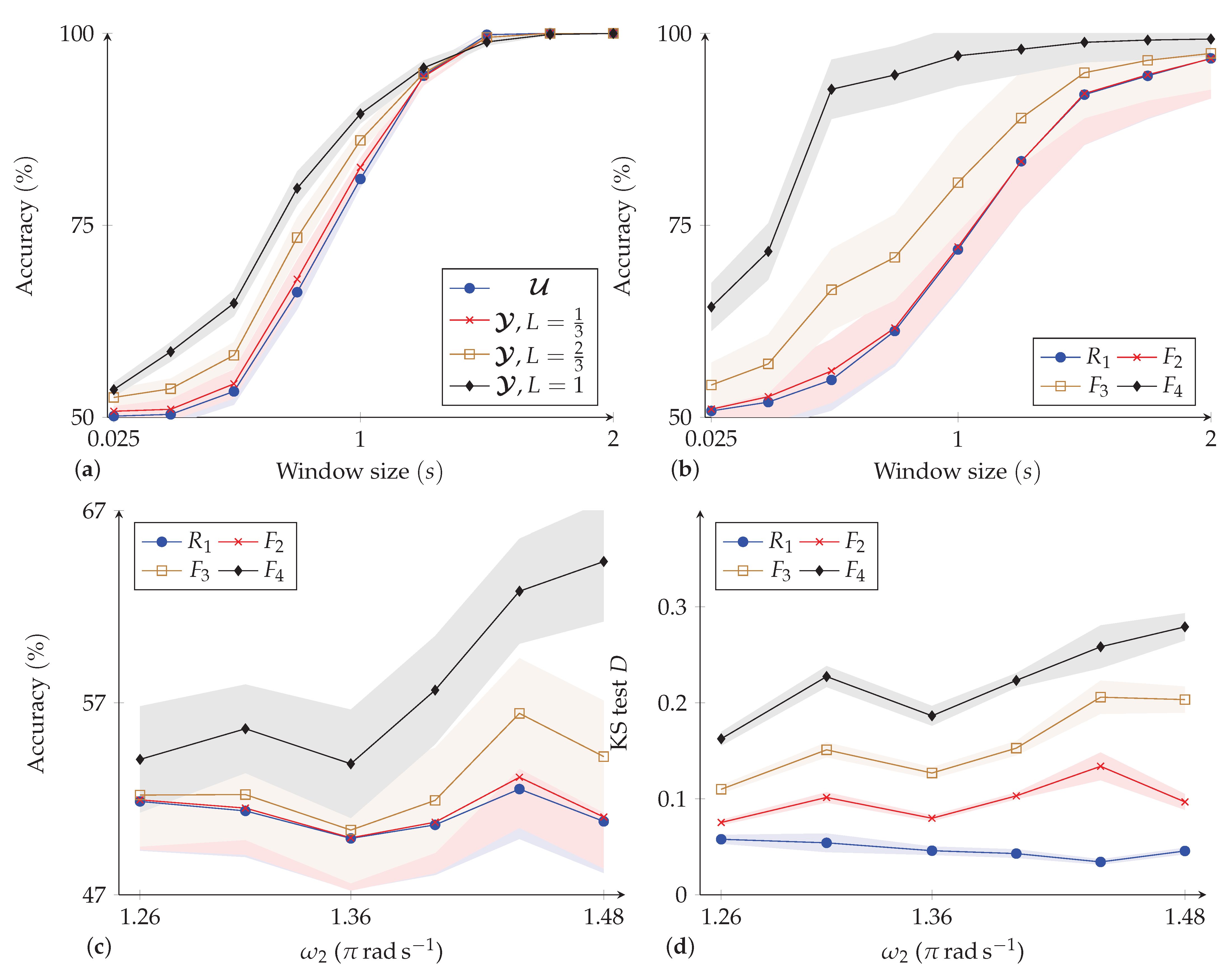
4.2.2. Results
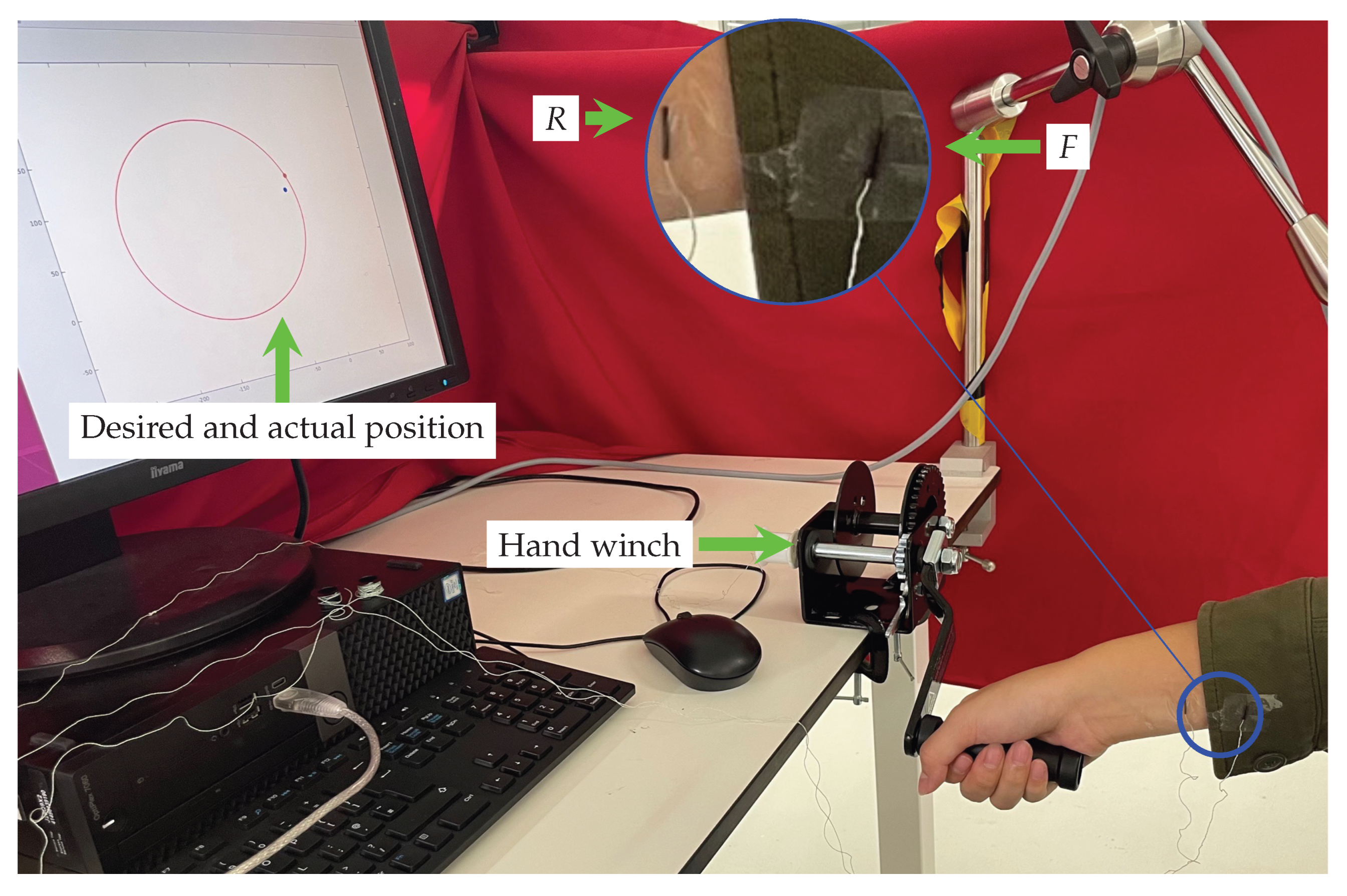
4.3. Case Study 3: Human Activity Recognition
4.3.1. Hypothesis
4.3.2. Experimental Procedure
4.3.3. Participants
4.3.4. Results
5. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
Appendix A.1. Simulation of Scotch Yoke
Appendix A.1.1. The PDF of Fabric Position
Appendix A.1.2. The CDF of Fabric Position
Appendix A.2. The Error of Yoke Movement Estimation
References
- Anagnostis, A.; Benos, L.; Tsaopoulos, D.; Tagarakis, A.; Tsolakis, N.; Bochtis, D. Human activity recognition through recurrent neural networks for human–robot interaction in agriculture. Appl. Sci. 2021, 11, 2188. [Google Scholar] [CrossRef]
- Meng, Z.; Zhang, M.; Guo, C.; Fan, Q.; Zhang, H.; Gao, N.; Zhang, Z. Recent progress in sensing and computing techniques for human activity recognition and motion analysis. Electronics 2020, 9, 1357. [Google Scholar] [CrossRef]
- Castano, L.M.; Flatau, A.B. Smart fabric sensors and e-textile technologies: A review. Smart Mater. Struct. 2014, 23, 053001. [Google Scholar] [CrossRef]
- Yang, K.; Isaia, B.; Brown, L.J.; Beeby, S. E-Textiles for Healthy Ageing. Sensors 2019, 19, 4463. [Google Scholar] [CrossRef] [PubMed]
- Slyper, R.; Hodgins, J.K. Action Capture with Accelerometers. In Proceedings of the Proceedings of the 2008 ACM SIGGRAPH/Eurographics symposium on computer animation, Dublin, Ireland, 7–9 July 2008; pp. 193–199. [Google Scholar]
- Michael, B.; Howard, M. Eliminating motion artifacts from fabric-mounted wearable sensors. In Proceedings of the 2014 IEEE-RAS International Conference on Humanoid Robots, Madrid, Spain, 18–20 November 2014; pp. 868–873. [Google Scholar]
- Michael, B.; Howard, M. Learning predictive movement models from fabric-mounted wearable sensors. IEEE Trans. Neural Syst. Rehabil. Eng. 2015, 24, 1395–1404. [Google Scholar] [CrossRef] [PubMed]
- Lorenz, M.; Bleser, G.; Akiyama, T.; Niikura, T.; Stricker, D.; Taetz, B. Towards Artefact Aware Human Motion Capture using Inertial Sensors Integrated into Loose Clothing. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), Philadelphia, PA, USA, 23–27 May 2022; pp. 1682–1688. [Google Scholar]
- Michael, B.; Howard, M. Activity recognition with wearable sensors on loose clothing. PLoS ONE 2017, 12, 10. [Google Scholar] [CrossRef] [PubMed]
- Jayasinghe, U.; Hwang, F.; Harwin, W.S. Comparing Clothing-Mounted Sensors with Wearable Sensors for Movement Analysis and Activity Classification. Sensors 2019, 20, 82. [Google Scholar] [CrossRef] [PubMed]
- Jayasinghe, U.; Hwang, F.; Harwin, W.S. Comparing loose clothing-mounted sensors with body-mounted sensors in the analysis of walking. Sensors 2022, 22, 6605. [Google Scholar] [CrossRef] [PubMed]
- Lara, O.D.; Labrador, M.A. A survey on human activity recognition using wearable sensors. IEEE Commun. Surv. Tutorials 2012, 15, 1192–1209. [Google Scholar] [CrossRef]
- Bello, H.; Zhou, B.; Suh, S.; Lukowicz, P. Mocapaci: Posture and gesture detection in loose garments using textile cables as capacitive antennas. In Proceedings of the 2021 International Symposium on Wearable Computers, Virtual, 21–26 September 2021; pp. 78–83. [Google Scholar]
- Cha, Y.; Kim, H.; Kim, D. Flexible piezoelectric sensor-based gait recognition. Sensors 2018, 18, 468. [Google Scholar] [CrossRef] [PubMed]
- Skach, S.; Stewart, R.; Healey, P.G. Smart arse: Posture classification with textile sensors in trousers. In Proceedings of the 20th ACM International Conference on Multimodal Interaction, Boulder, CO, USA, 16–20 October 2018; pp. 116–124. [Google Scholar]
- Lin, Q.; Peng, S.; Wu, Y.; Liu, J.; Hu, W.; Hassan, M.; Seneviratne, A.; Wang, C.H. E-jacket: Posture detection with loose-fitting garment using a novel strain sensor. In Proceedings of the 2020 19th ACM/IEEE International Conference on Information Processing in Sensor Networks (IPSN), Sydney, NSW, Australia, 21–24 April 2020; pp. 49–60. [Google Scholar]
- Jayasinghe, U.; Janko, B.; Hwang, F.; Harwin, W.S. Classification of static postures with wearable sensors mounted on loose clothing. Sci. Rep. 2023, 13, 131. [Google Scholar] [CrossRef] [PubMed]
- Tang, W.; Fu, C.; Xia, L.; Lyu, P.; Li, L.; Fu, Z.; Pan, H.; Zhang, C.; Xu, W. A flexible and sensitive strain sensor with three-dimensional reticular structure using biomass Juncus effusus for monitoring human motions. Chem. Eng. J. 2022, 438, 135600. [Google Scholar] [CrossRef]
- Lu, D.; Liao, S.; Chu, Y.; Cai, Y.; Wei, Q.; Chen, K.; Wang, Q. Highly durable and fast response fabric strain sensor for movement monitoring under extreme conditions. Adv. Fiber Mater. 2022, 5, 1–12. [Google Scholar] [CrossRef]
- Xu, D.; Ouyang, Z.; Dong, Y.; Yu, H.Y.; Zheng, S.; Li, S.; Tam, K.C. Robust, Breathable and Flexible Smart Textiles as Multifunctional Sensor and Heater for Personal Health Management. Adv. Fiber Mater. 2022, 5, 1–14. [Google Scholar] [CrossRef]
- Justel, A.; Peña, D.; Zamar, R. A multivariate Kolmogorov-Smirnov test of goodness of fit. Stat. Probab. Lett. 1997, 35, 251–259. [Google Scholar] [CrossRef]
- Shin, K.; Hammond, J. Fundamentals of Signal Processing for Sound and Vibration Engineers; John Wiley & Sons: Hoboken, NJ, USA, 2008. [Google Scholar]
- Chang, C.C.; Lin, C.J. LIBSVM: A library for support vector machines. TIST 2011, 2, 1–27. [Google Scholar] [CrossRef]
- Oldfield, R.C. The assessment and analysis of handedness: The Edinburgh inventory. Neuropsychologia 1971, 9, 97–113. [Google Scholar] [CrossRef] [PubMed]
- Koskimaki, H.; Huikari, V.; Siirtola, P.; Laurinen, P.; Roning, J. Activity recognition using a wrist-worn inertial measurement unit: A case study for industrial assembly lines. In Proceedings of the 2009 17th Mediterranean Conference on Control and Automation, Thessaloniki, Greece, 24–26 June 2009; pp. 401–405. [Google Scholar]
- Forkan, A.R.M.; Montori, F.; Georgakopoulos, D.; Jayaraman, P.P.; Yavari, A.; Morshed, A. An industrial IoT solution for evaluating workers’ performance via activity recognition. In Proceedings of the 2019 International Conference on Distributed Computing Systems, Dallas, TX, USA, 7–10 July 2019; pp. 1393–1403. [Google Scholar]
- Mai, J.; Yi, C.; Ding, Z. Human Activity Recognition of Exoskeleton Robot with Supervised Learning Techniques. 20 December 2021. Available online: https://doi.org/10.21203/rs.3.rs-1161576/v1 (accessed on 6 February 2023).
- Pitou, S.; Wu, F.; Shafti, A.; Michael, B.; Stopforth, R.; Howard, M. Embroidered electrodes for control of affordable myoelectric prostheses. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), Brisbane, QLD, Australia, 21–25 May 2018; pp. 1812–1817. [Google Scholar]
- Domínguez, A. A history of the convolution operation [Retrospectroscope]. IEEE Pulse 2015, 6, 38–49. [Google Scholar] [CrossRef] [PubMed]


| Reference | Sensor Type | Sensor Placement | Type of Clothes or Fabric | Activities | Method | Strength/Finding | Limitation |
|---|---|---|---|---|---|---|---|
| Jayasinghe et al. [10] | accelerometers | waist, thigh, ankle and clothes in similar position | slacks, skirt and frock | four daily activities | correlation coefficients decision tree | clothing and body worn sensor data are correlated | sensors are heavy |
| Jayasinghe et al. [11] | IMU | waist, thigh, lower shank and clothes in similar position | daily clothes | gait cycle | correlation coefficients | clothing worn sensor data have key points in the gait cycle | classification accuracy of the sensors has not been investigated |
| Jayasinghe et al. [17] | IMU | waist, thigh, ankle and clothes in similar position | daily clothes | 4 static and 2 dynamic activities | KNN | clothing worn sensor has good posture classification | the number of participants is limited |
| Michael et al. [9] | accelerometers | rigid pendulum and a piece of fabric attached | denim, jersey and roma | low and high swing speed | SVM, DRM | fabric sensors has higher accuracy of AR | lack theoretical model |
| Bello et al. [13] | capacitive | four antennas to cover the chest, shoulders, back and arms | loose blazer | 20 posture/gestures | conv2D | sensor is not affected from muscular strength | affected from conductors |
| Cha et al. [14] | piezoelectric | clothing near knee, hip | loose trousers | gait | rule-based algorithm | feasibility of gait detection | gender of participants is not balanced |
| Skach et al. [15] | pressure | clothing near thigh | loose trousers | 19 postures | random forest | sensor can detect human postures | the upper body has not been tested |
| Lin et al. [16] | strain | clothing near shoulder, elbow, waist and abdomen | loose jacket | daily activities, postures and slouch | CNN-LSTM | sensor can detect human postures | gender of participants is not balanced |
| Tang et al. [18] | strain | several positions on the body | juncus effusus fiber | several daily activities | gauge factor | sensitive stretchable | the maximum sensing range is limited |
| Lu et al. [19] | strain | human joints | conductive PSKF@rGO | exercise monitoring | gauge factor | useful under extreme conditions | the strain range is limited |
| Xu et al. [20] | strain | various human body parts | composite fiber | language recognition pulse diagnosis | gauge factor | sensitivity, stability and durability | the number of participants is limited |
| Our approach | magnetic | scotch yoke with a piece of fabric attached wrist and sleeve | woven cotton | various rotating frequencies | SVM |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shen, T.; Di Giulio, I.; Howard, M. A Probabilistic Model of Human Activity Recognition with Loose Clothing. Sensors 2023, 23, 4669. https://doi.org/10.3390/s23104669
Shen T, Di Giulio I, Howard M. A Probabilistic Model of Human Activity Recognition with Loose Clothing. Sensors. 2023; 23(10):4669. https://doi.org/10.3390/s23104669
Chicago/Turabian StyleShen, Tianchen, Irene Di Giulio, and Matthew Howard. 2023. "A Probabilistic Model of Human Activity Recognition with Loose Clothing" Sensors 23, no. 10: 4669. https://doi.org/10.3390/s23104669
APA StyleShen, T., Di Giulio, I., & Howard, M. (2023). A Probabilistic Model of Human Activity Recognition with Loose Clothing. Sensors, 23(10), 4669. https://doi.org/10.3390/s23104669






