Experimental Determination Influence of Flow Disturbances behind the Knife Gate Valve on the Indications of the Ultrasonic Flow Meter with Clamp-On Sensors on Pipelines
Abstract
:1. Introduction
- High measurement accuracy—high sensitivity and resolution;
- Non-invasiveness during operation;
- Non-contact;
- Service life—long-term operation;
- Independence from environmental conditions/system operation conditions;
- Low cost of investment and of operation.
2. Measurements
- With the valve placed in the position of closure of 1/3 of the knife gate valve’s height, one obtains P1/3 = 78.09% of the active flow area;
- With the valve placed in the position of closure of 1/2 of the knife gate valve’s height, one obtains P1/2 = 60.89% of the active flow area.
3. Results
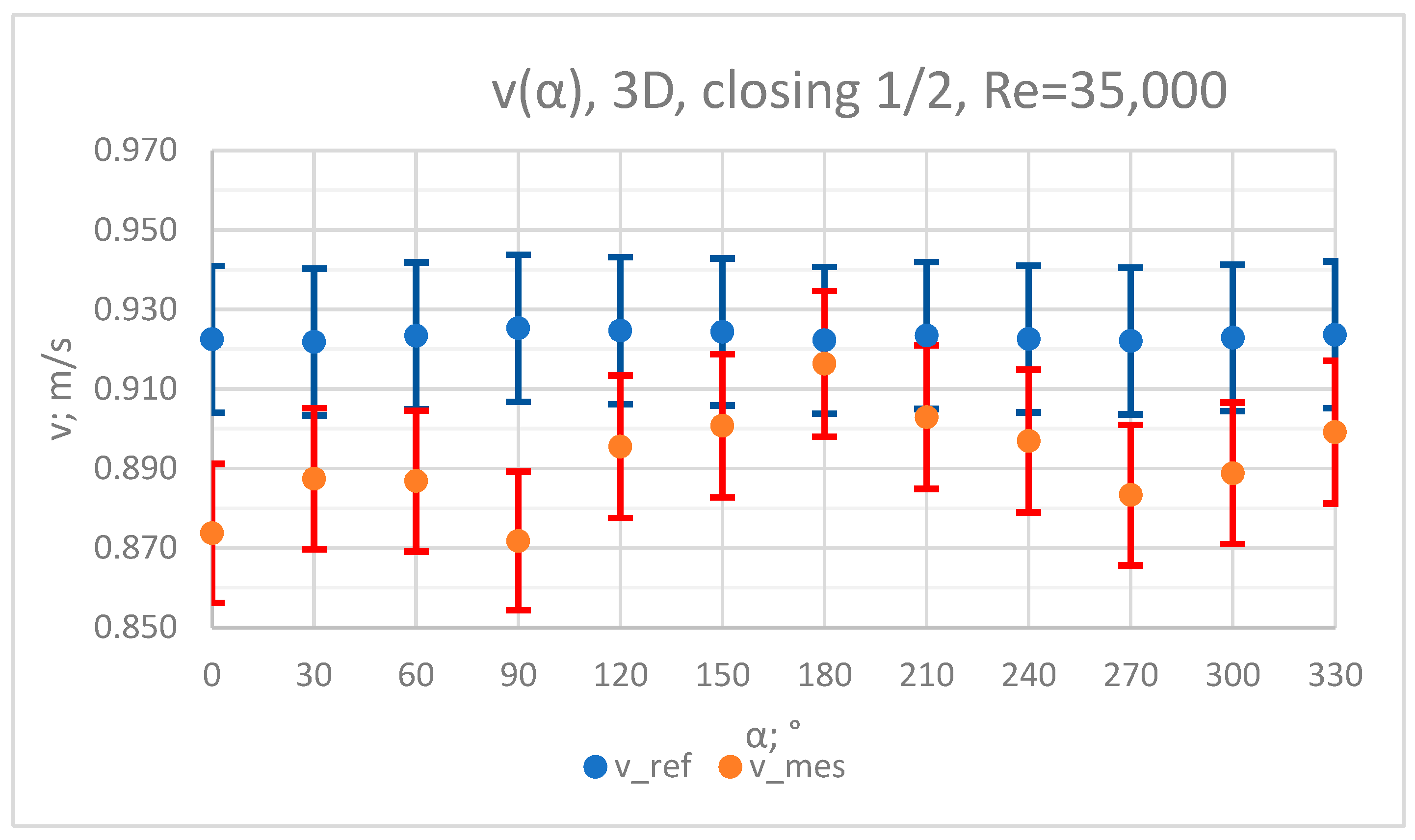
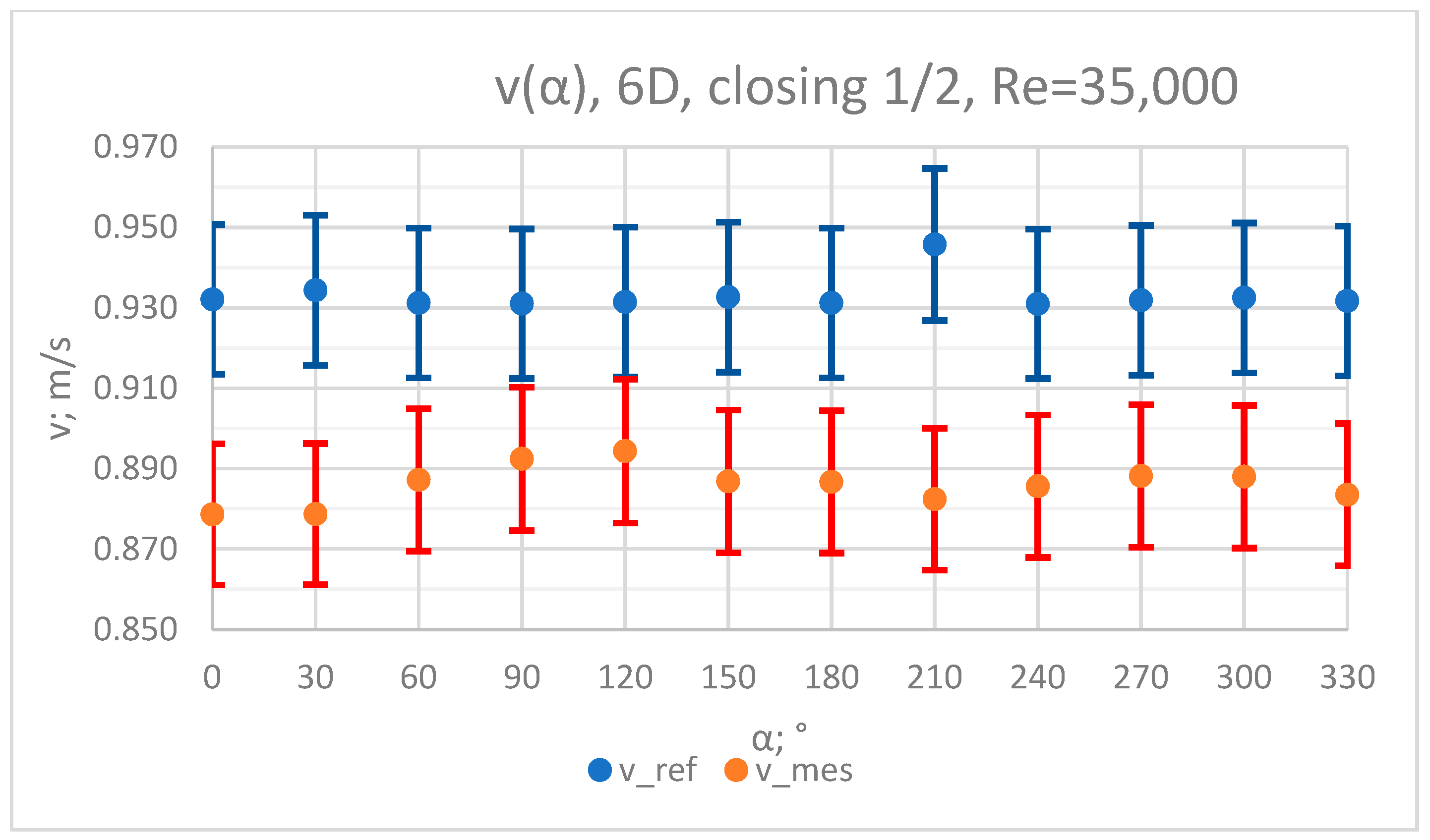
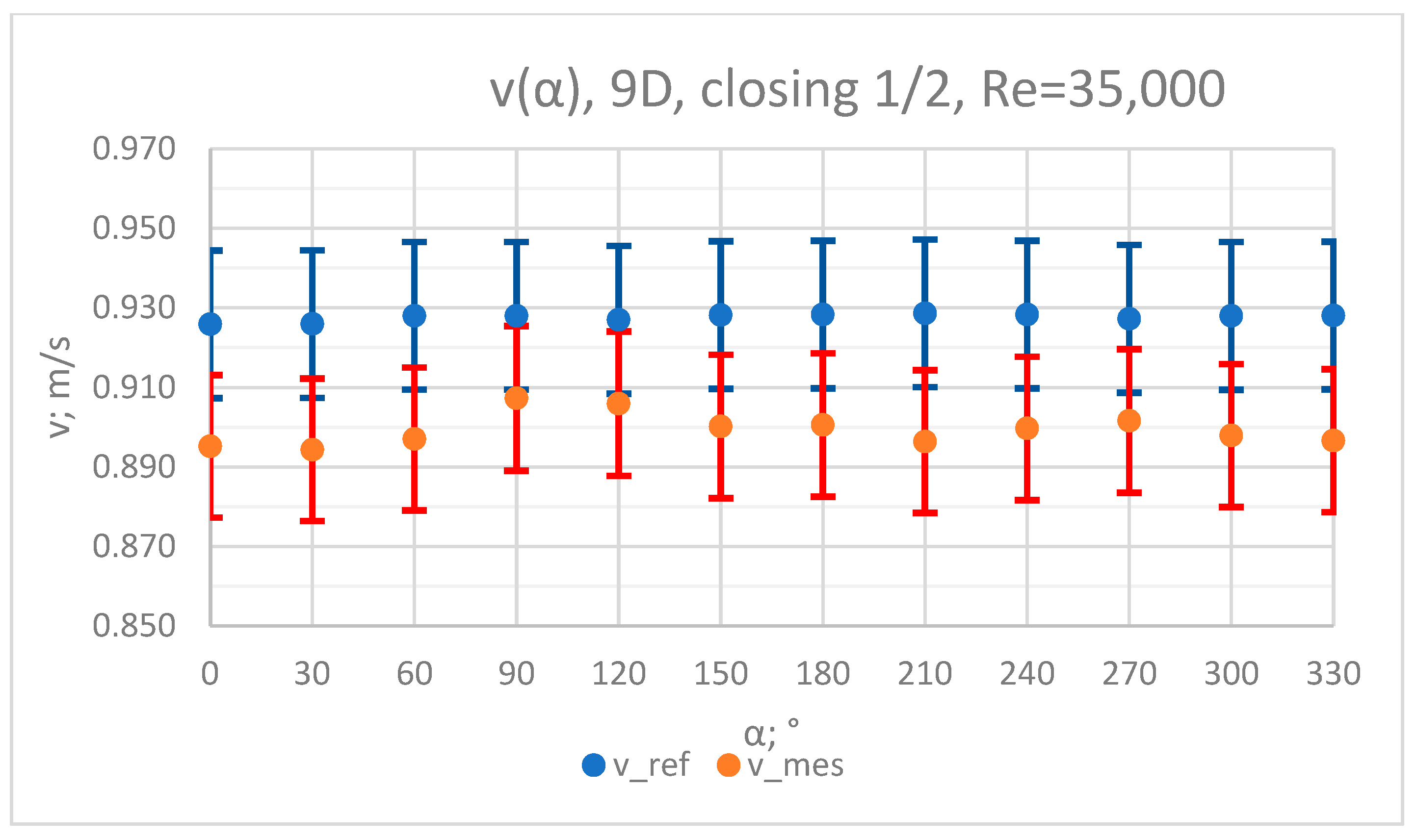
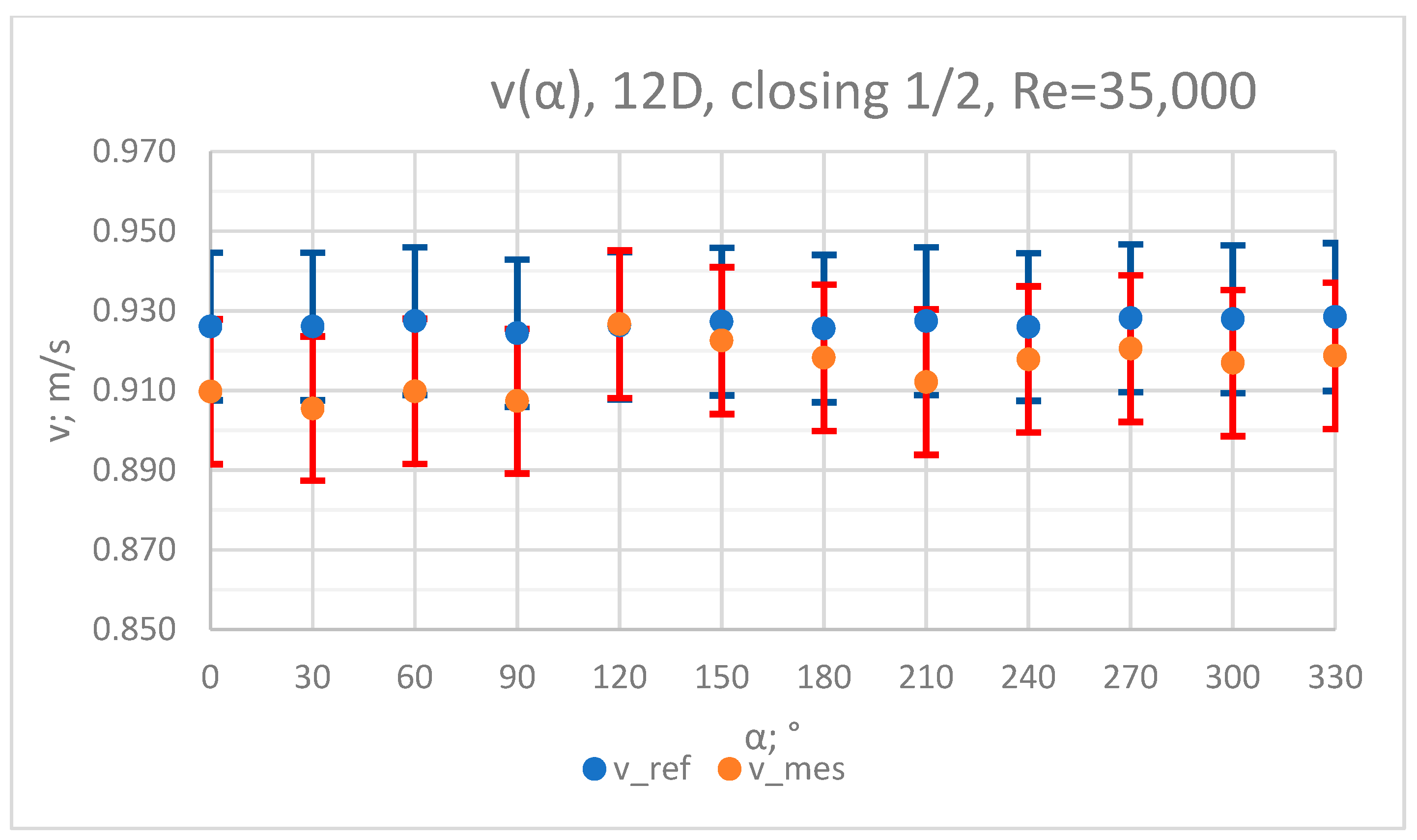
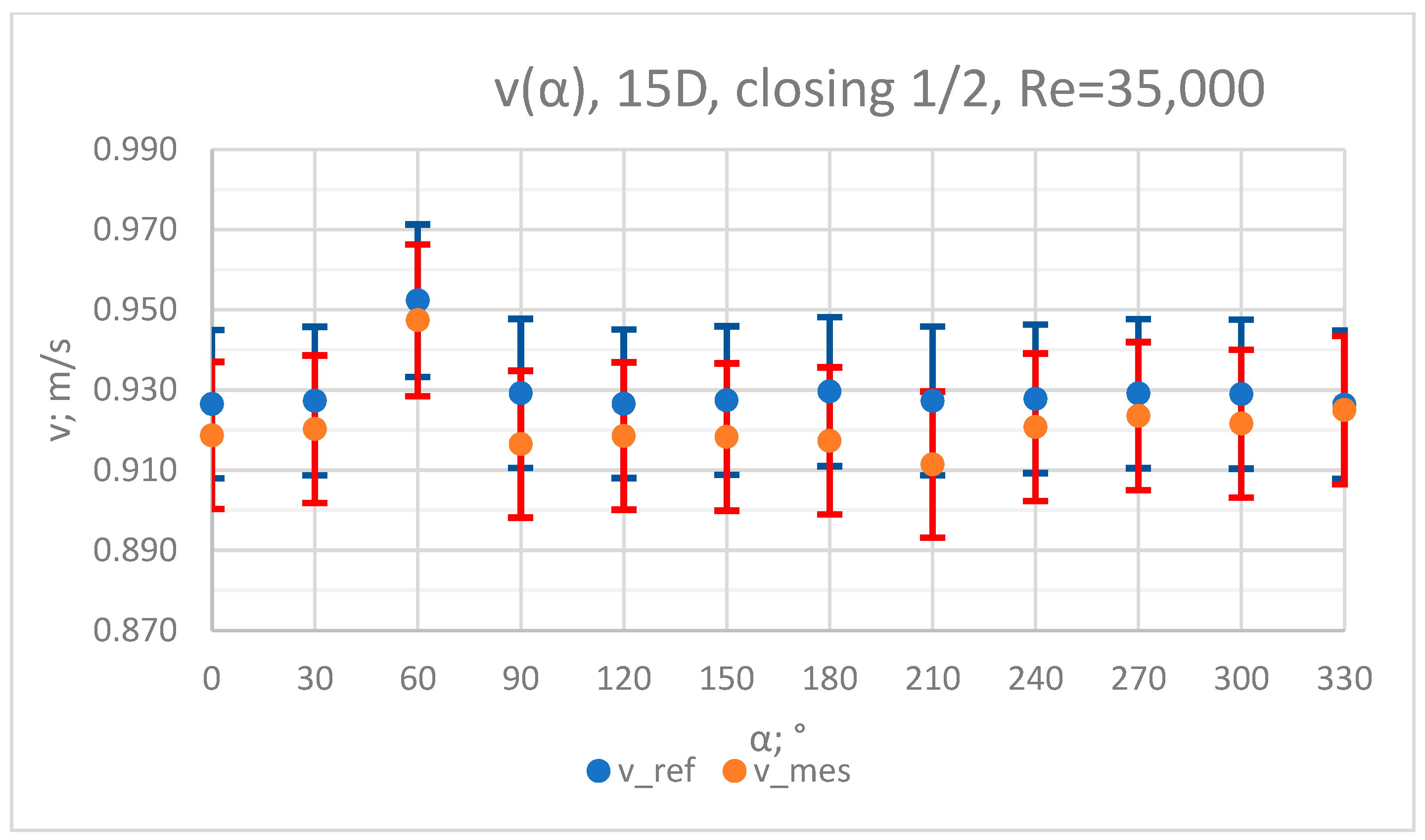
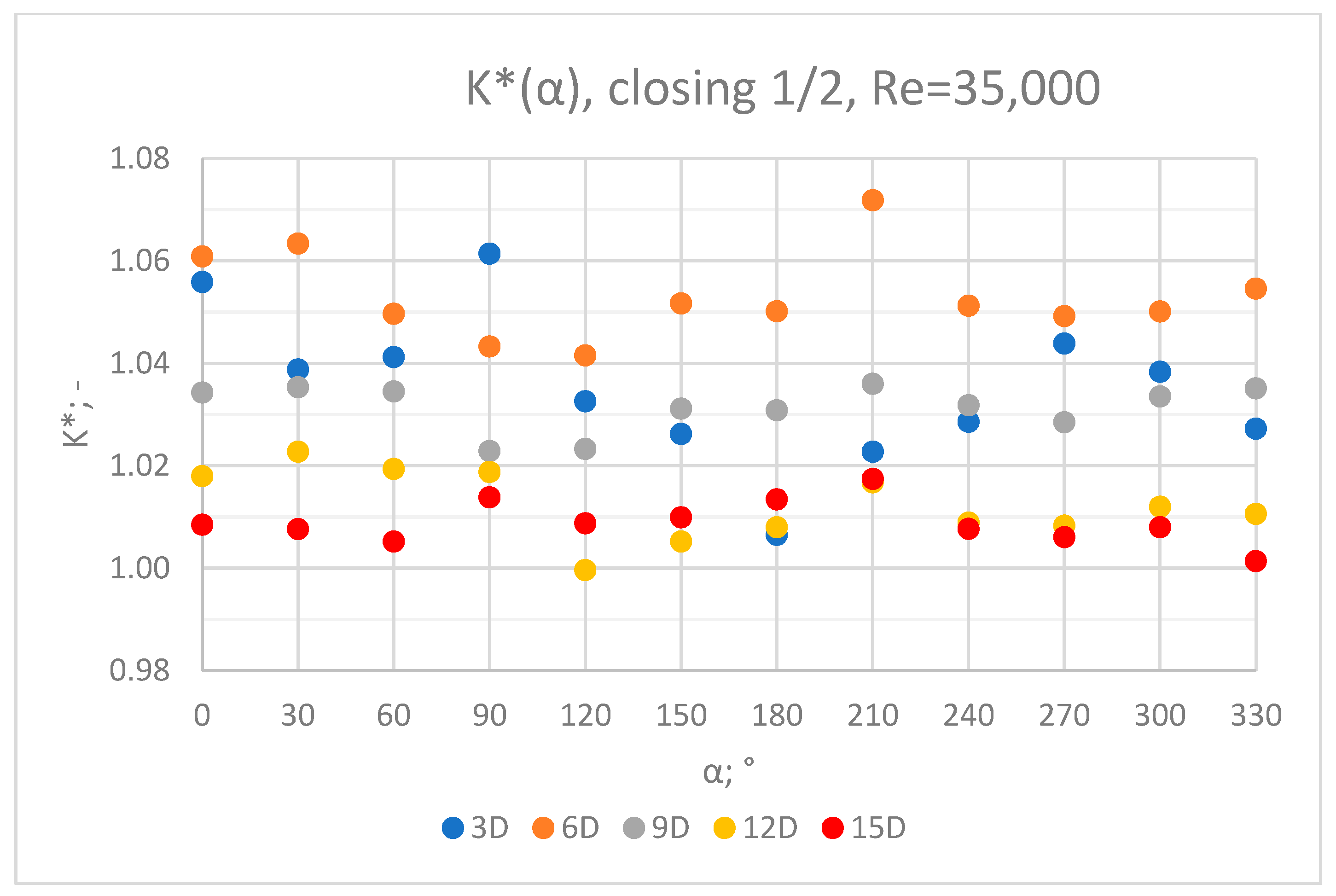
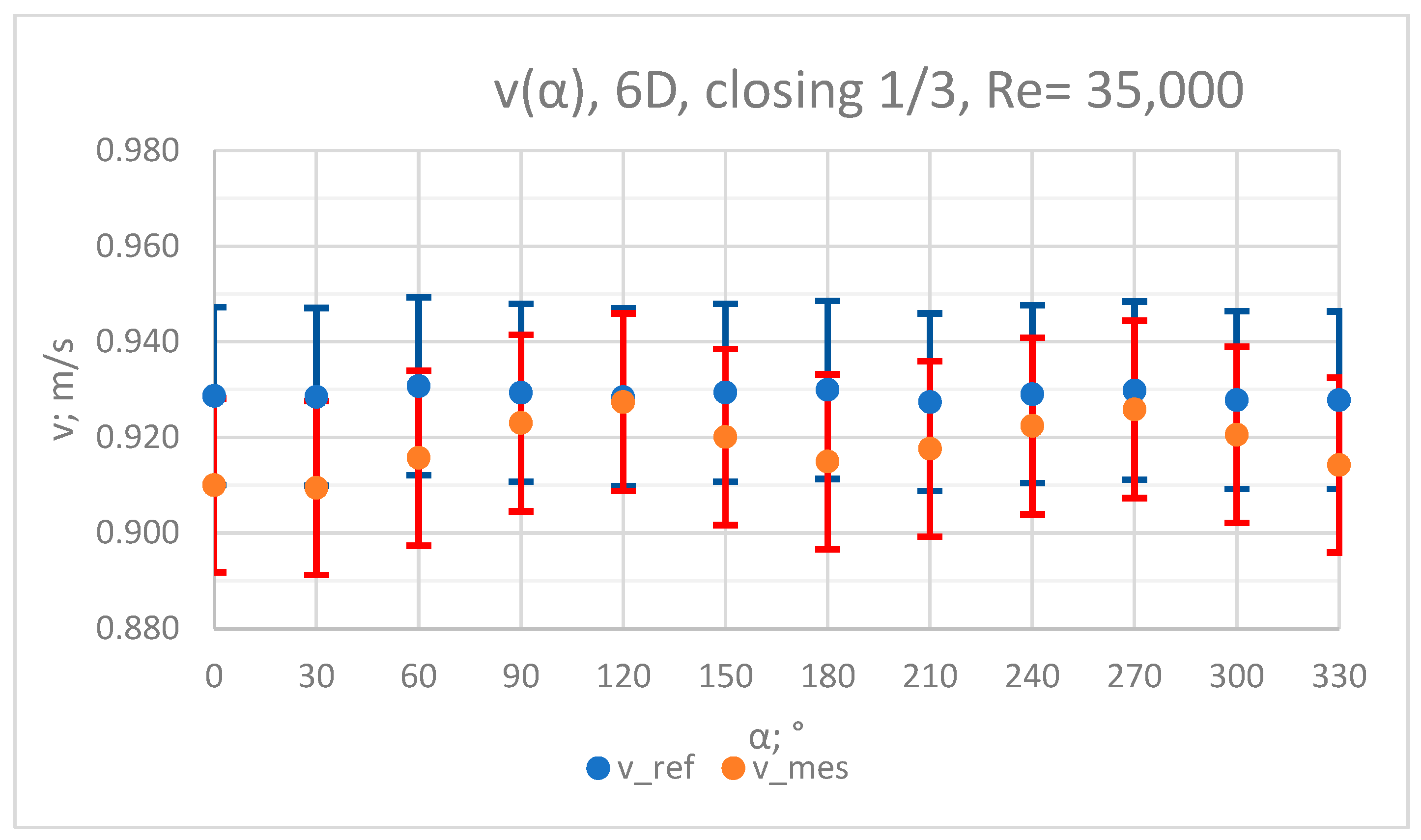
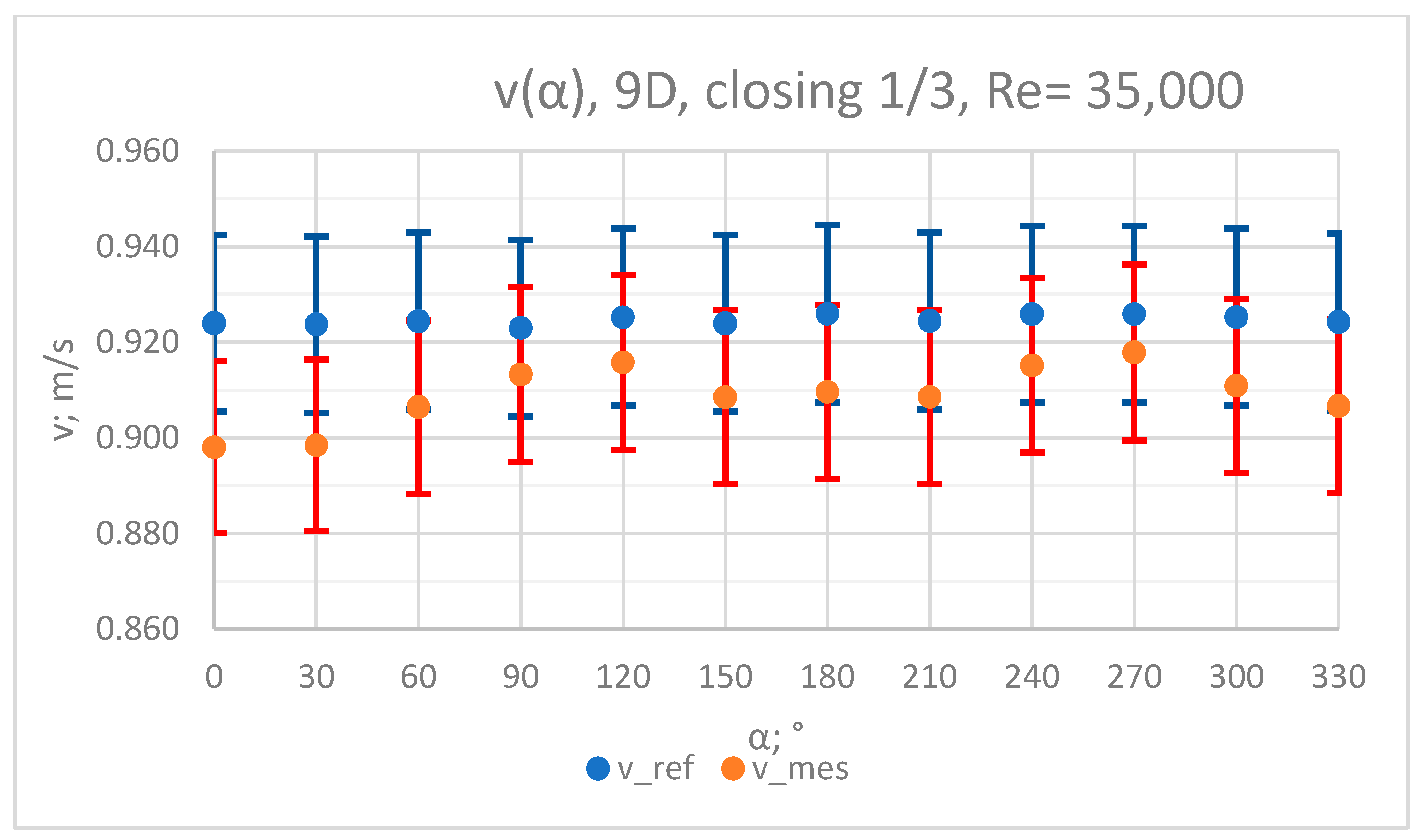
3.1. Measurement Results—½ Closure of the Knife Gate Valve’s Height, Re = 35,000
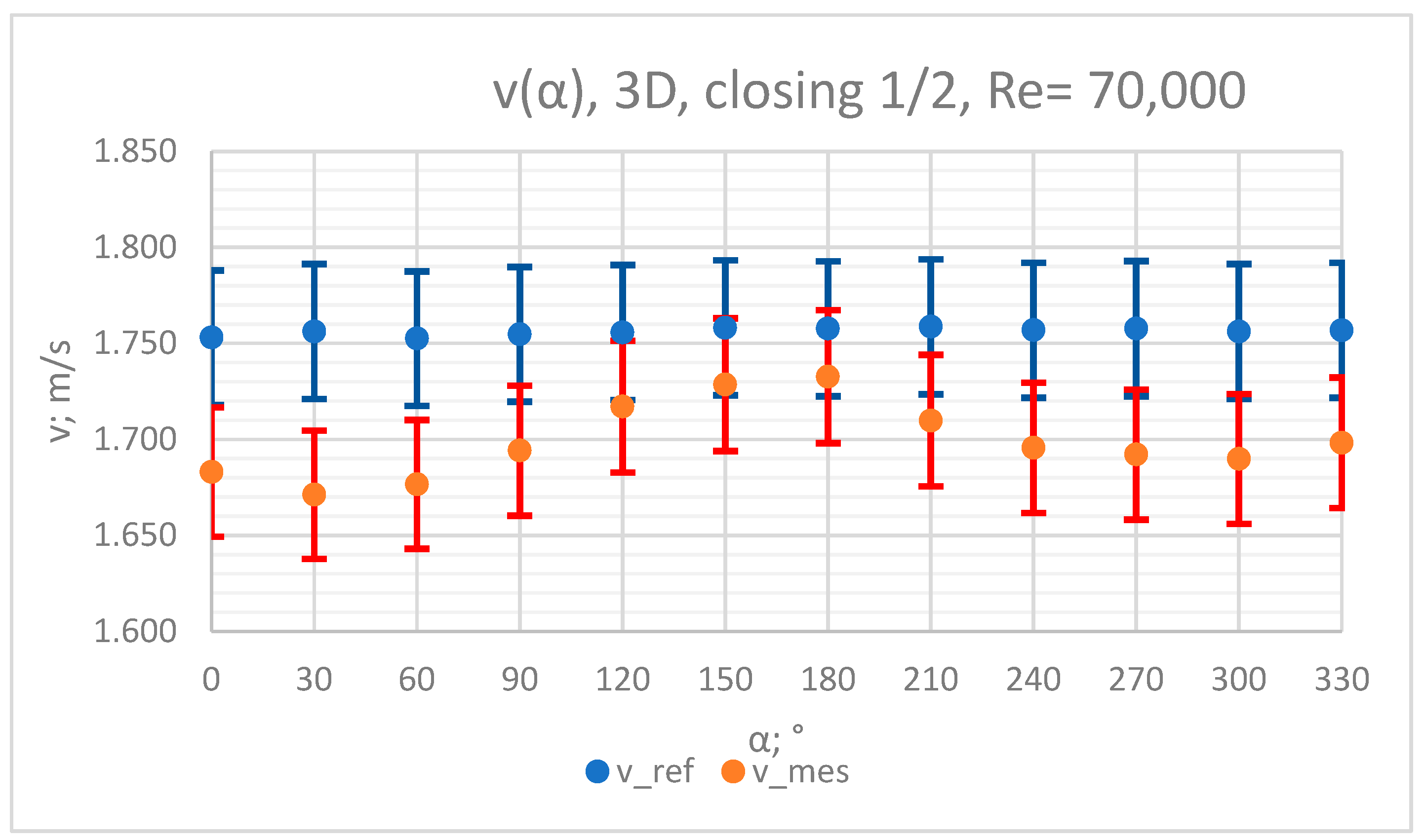
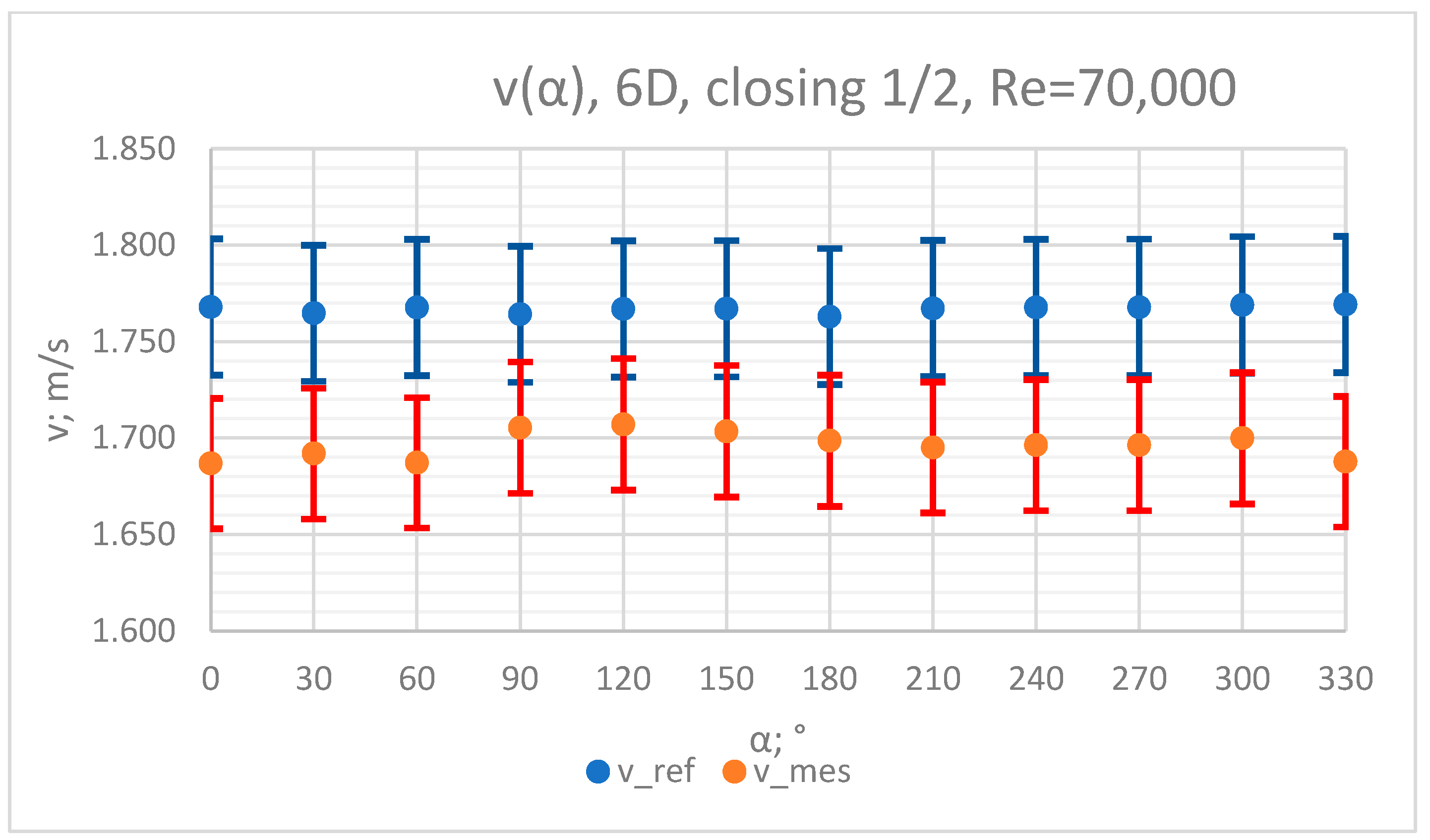
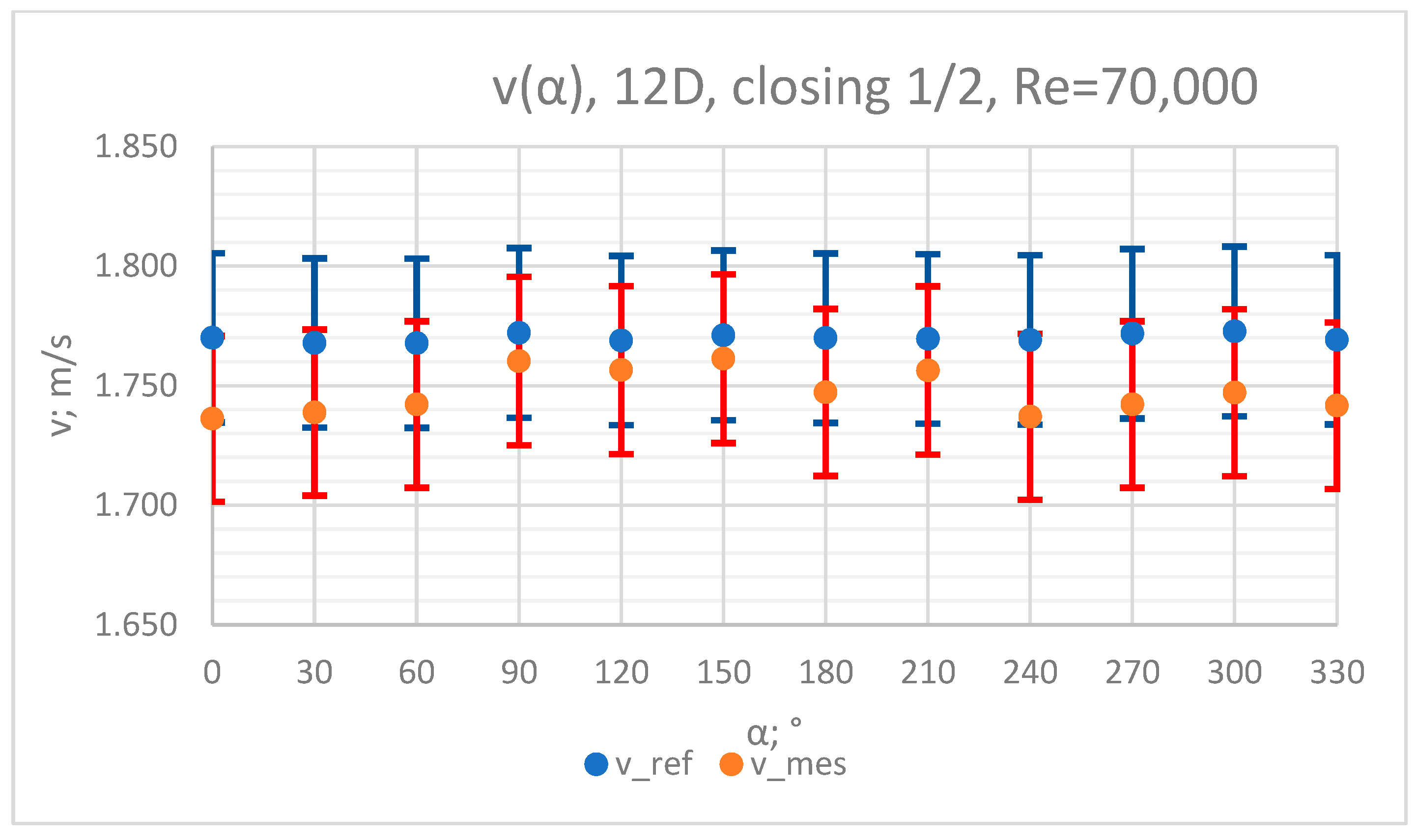
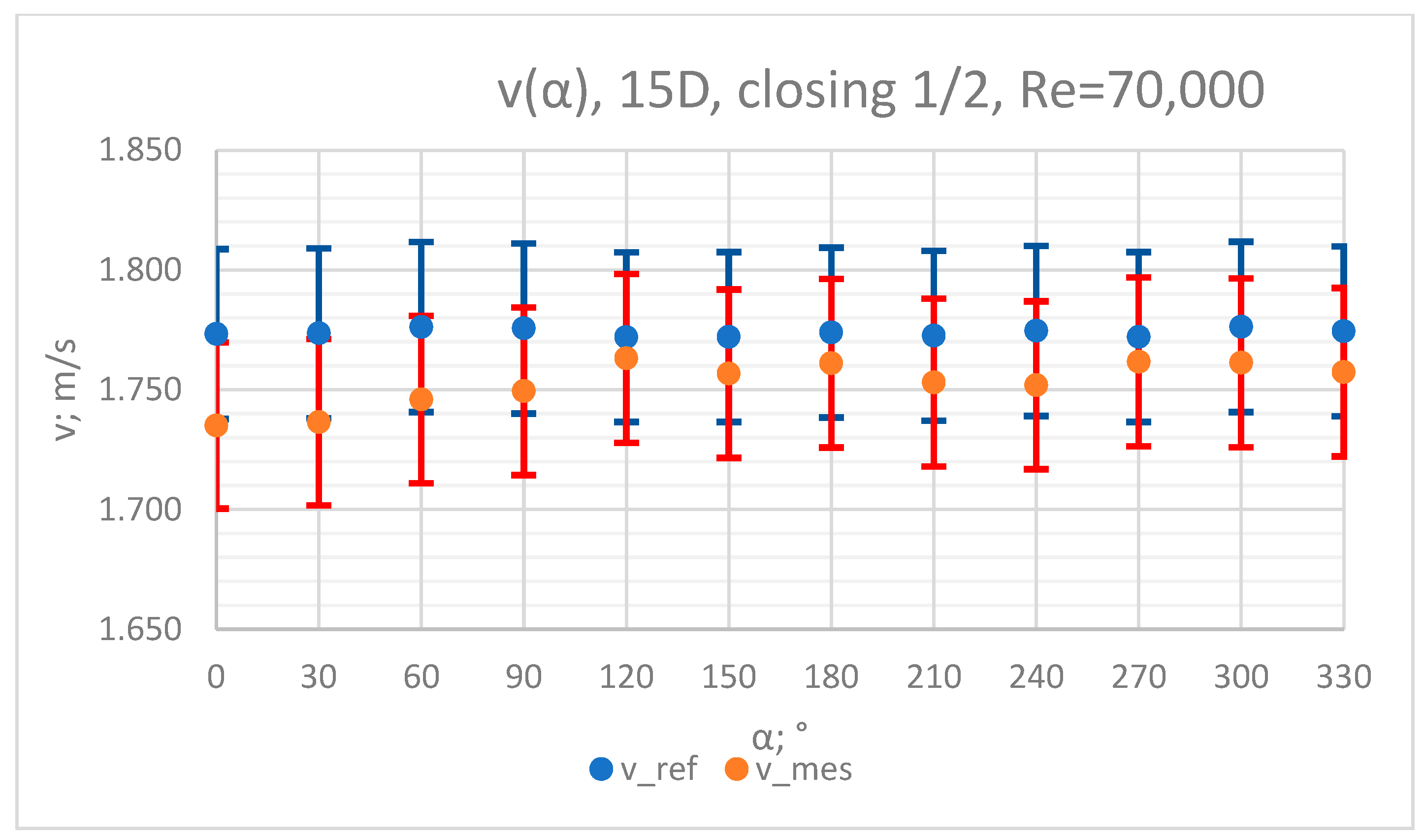
3.2. Measurement Results—½ of Closure of the Knife Gate Valve’s Height, Re = 70,000
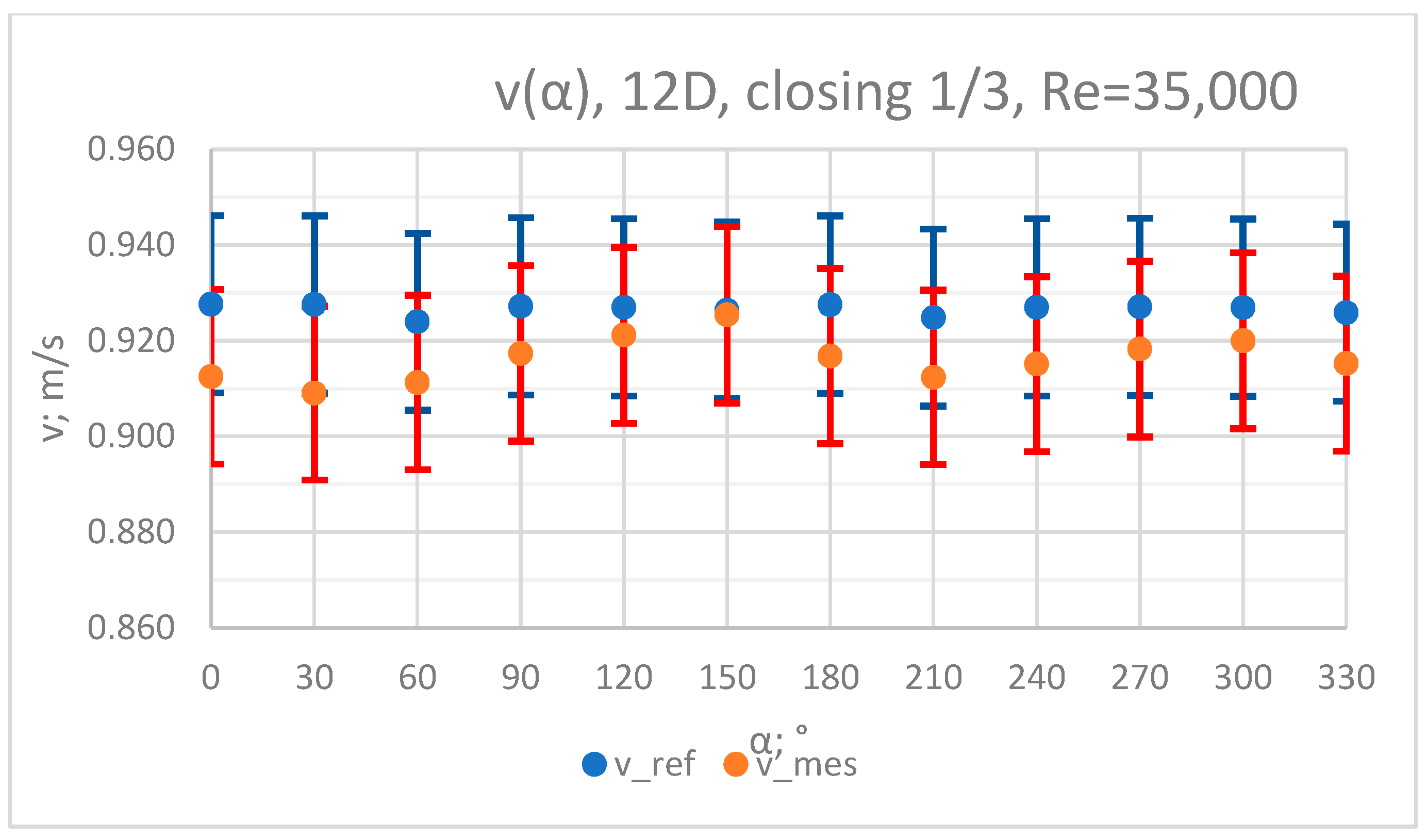
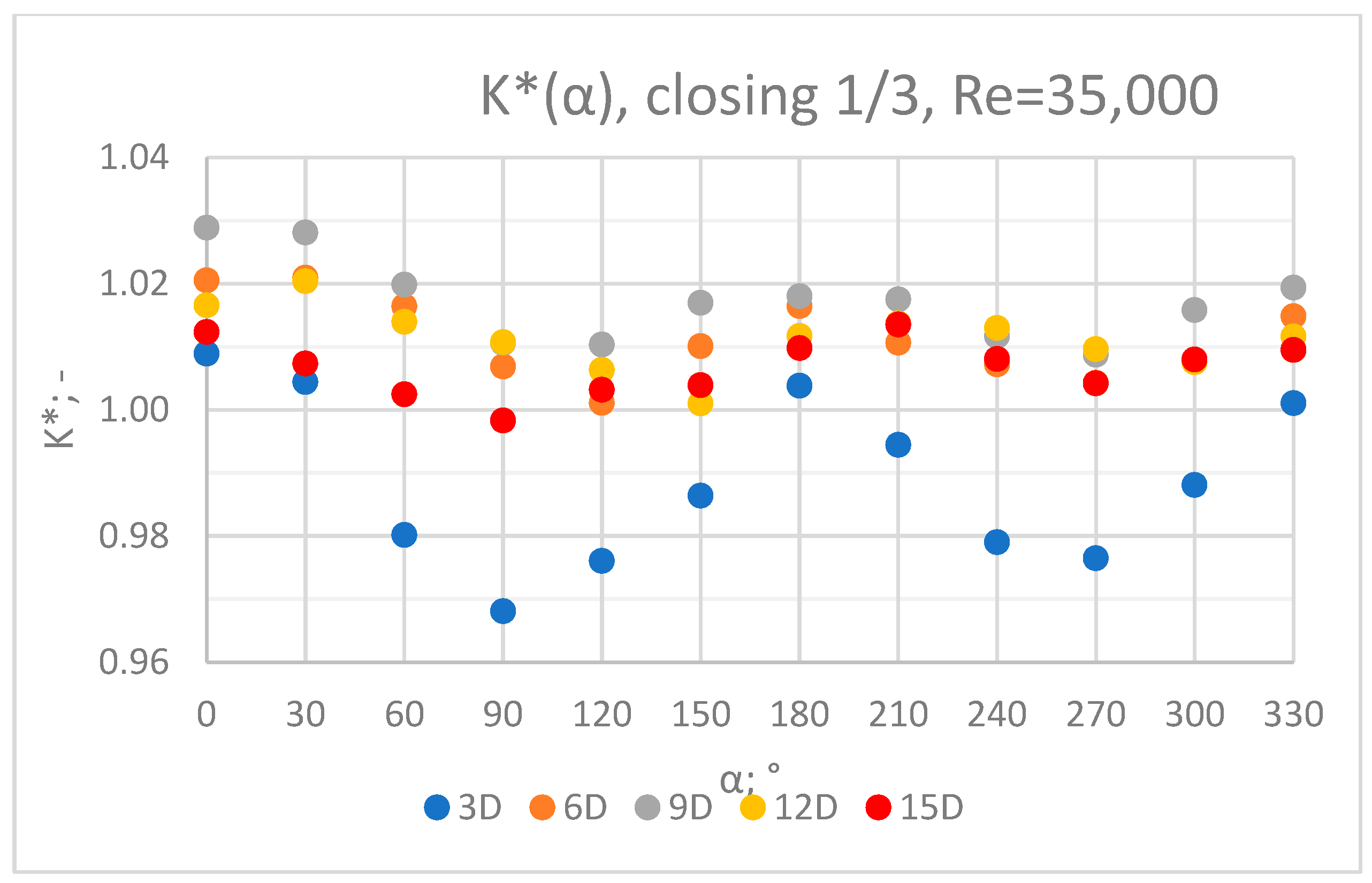
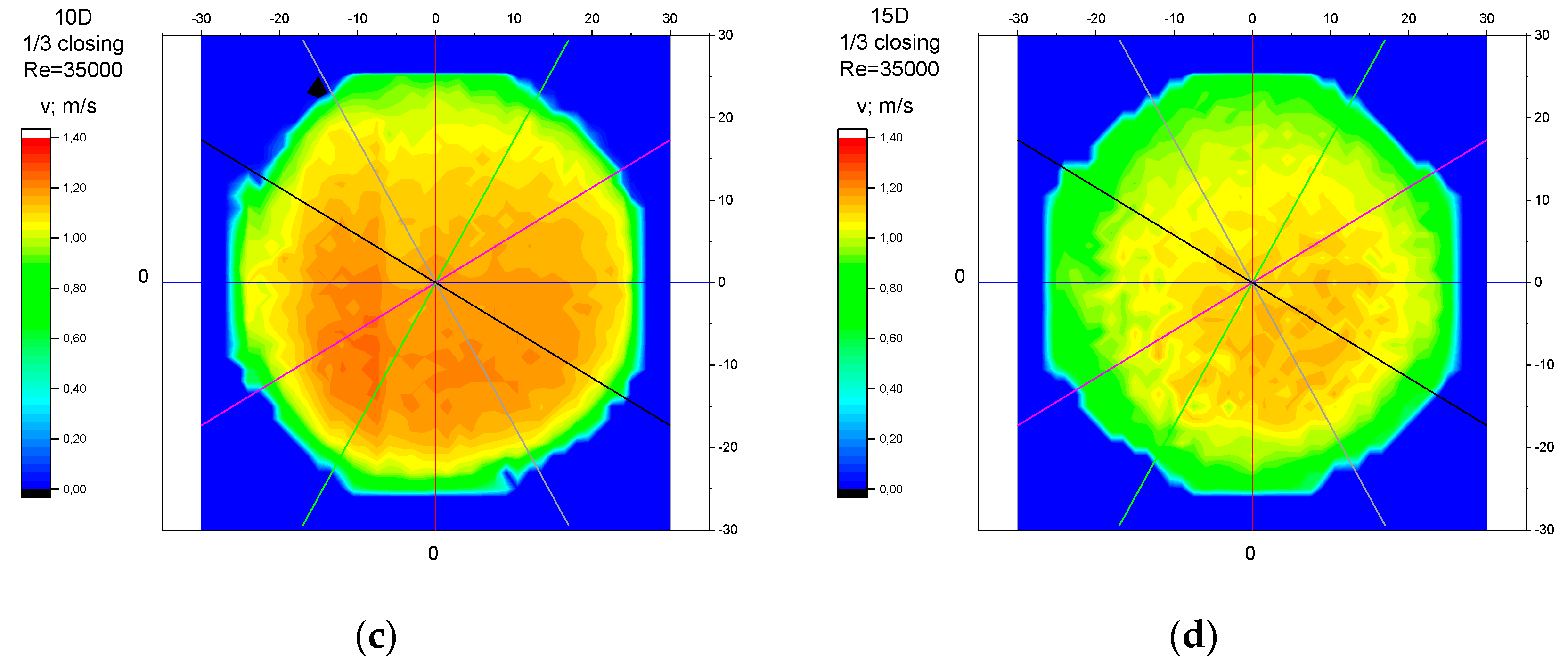
3.3. Measurement Results—1/3 of the Knife Gate Valve’s Height Closed, Re = 35,000
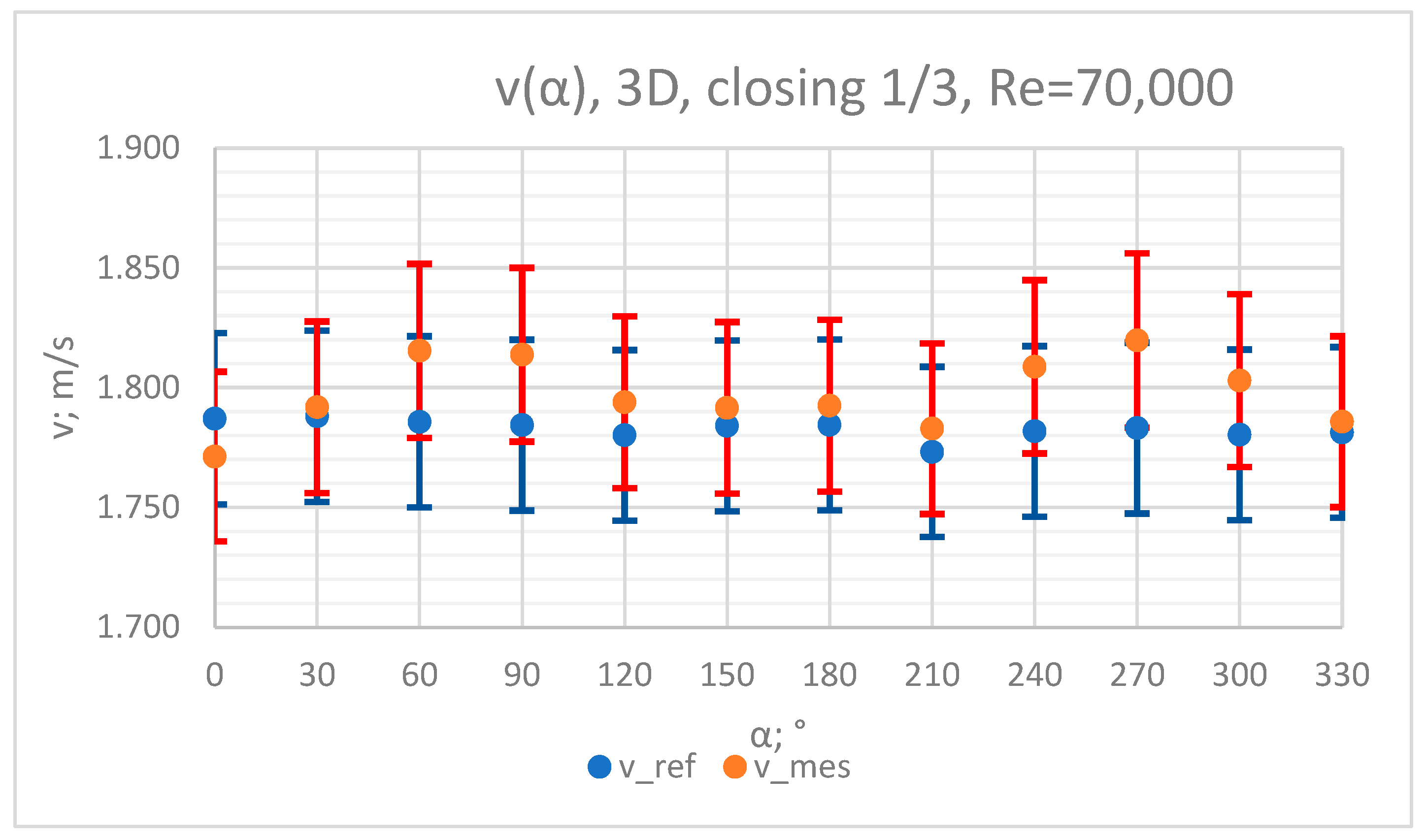
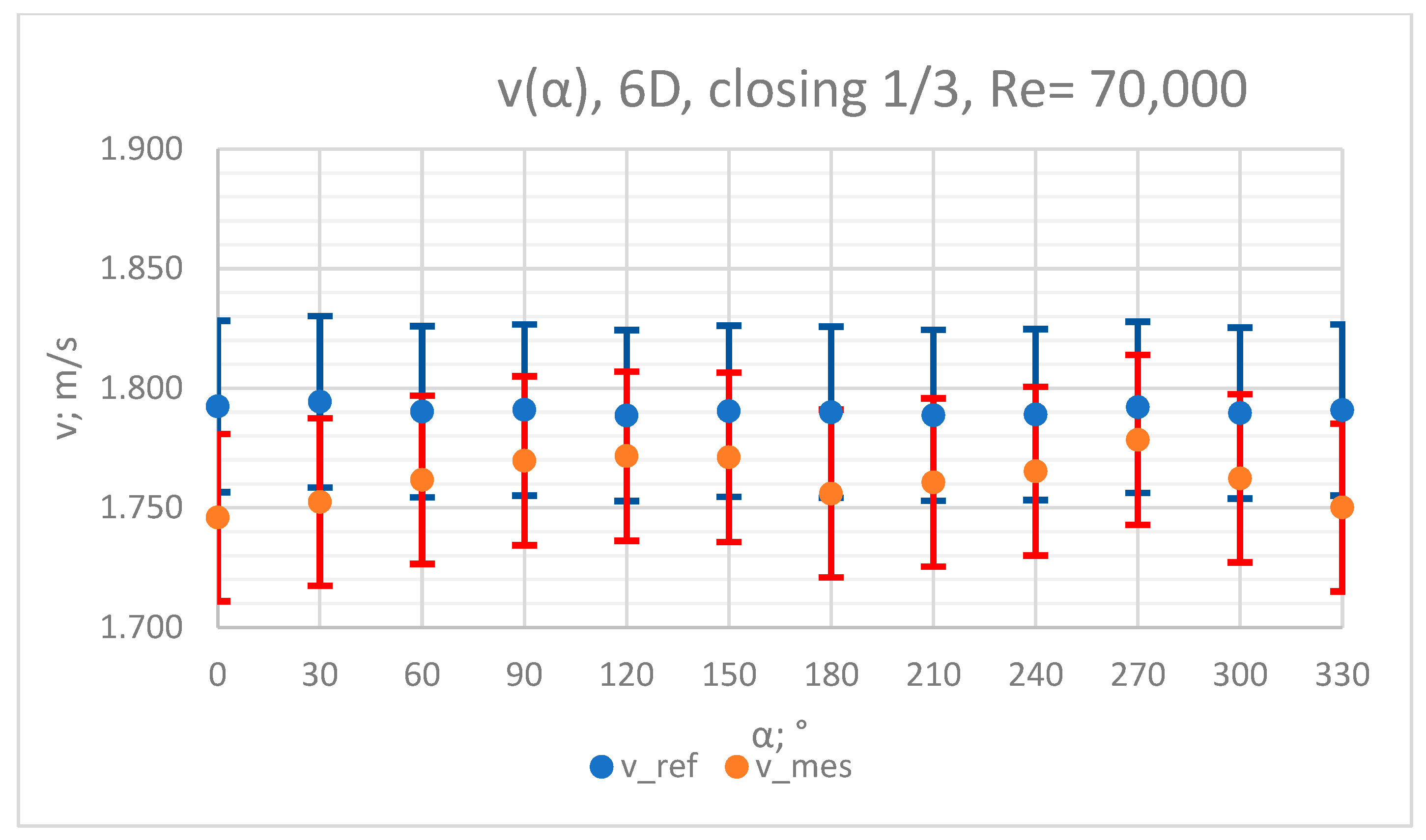
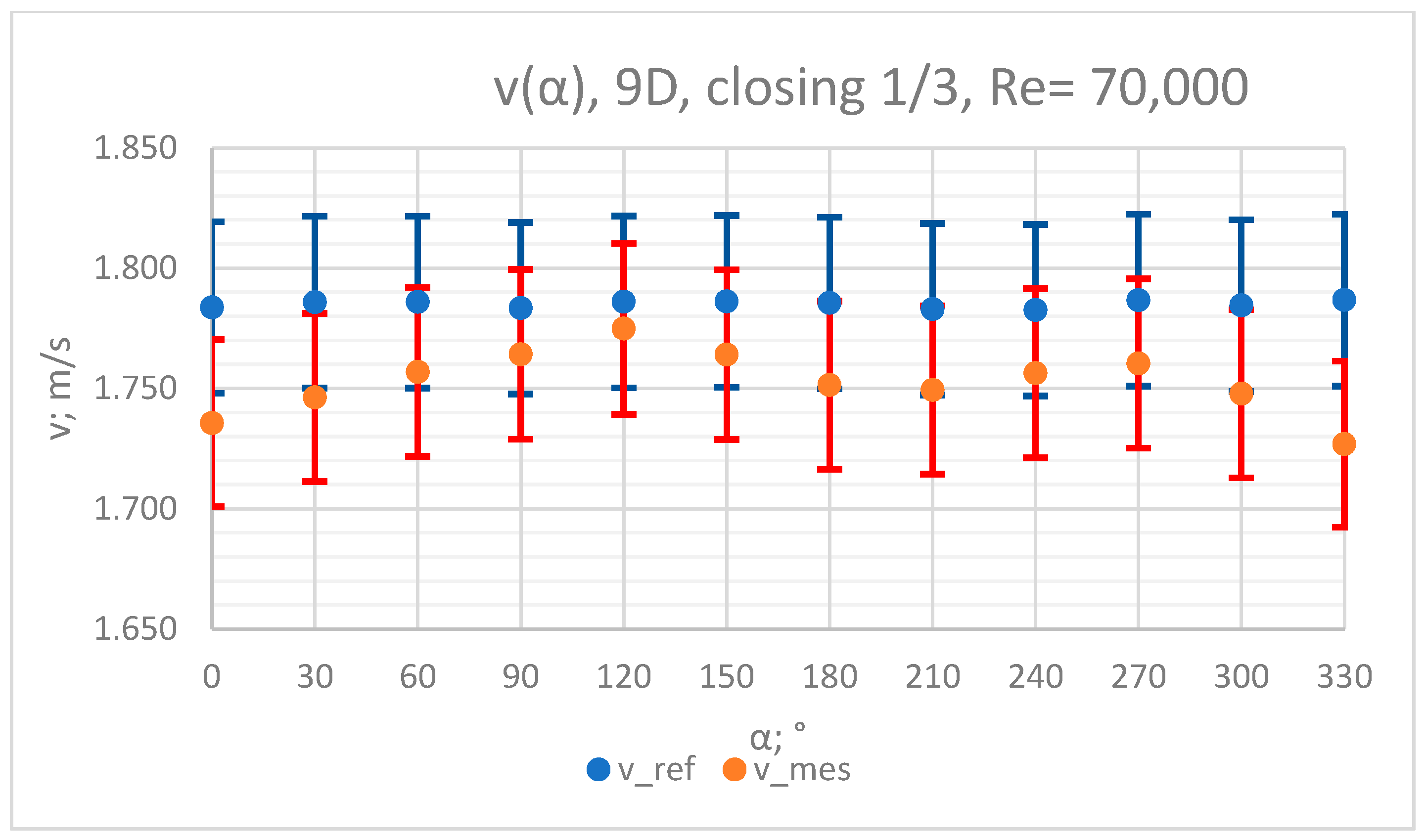
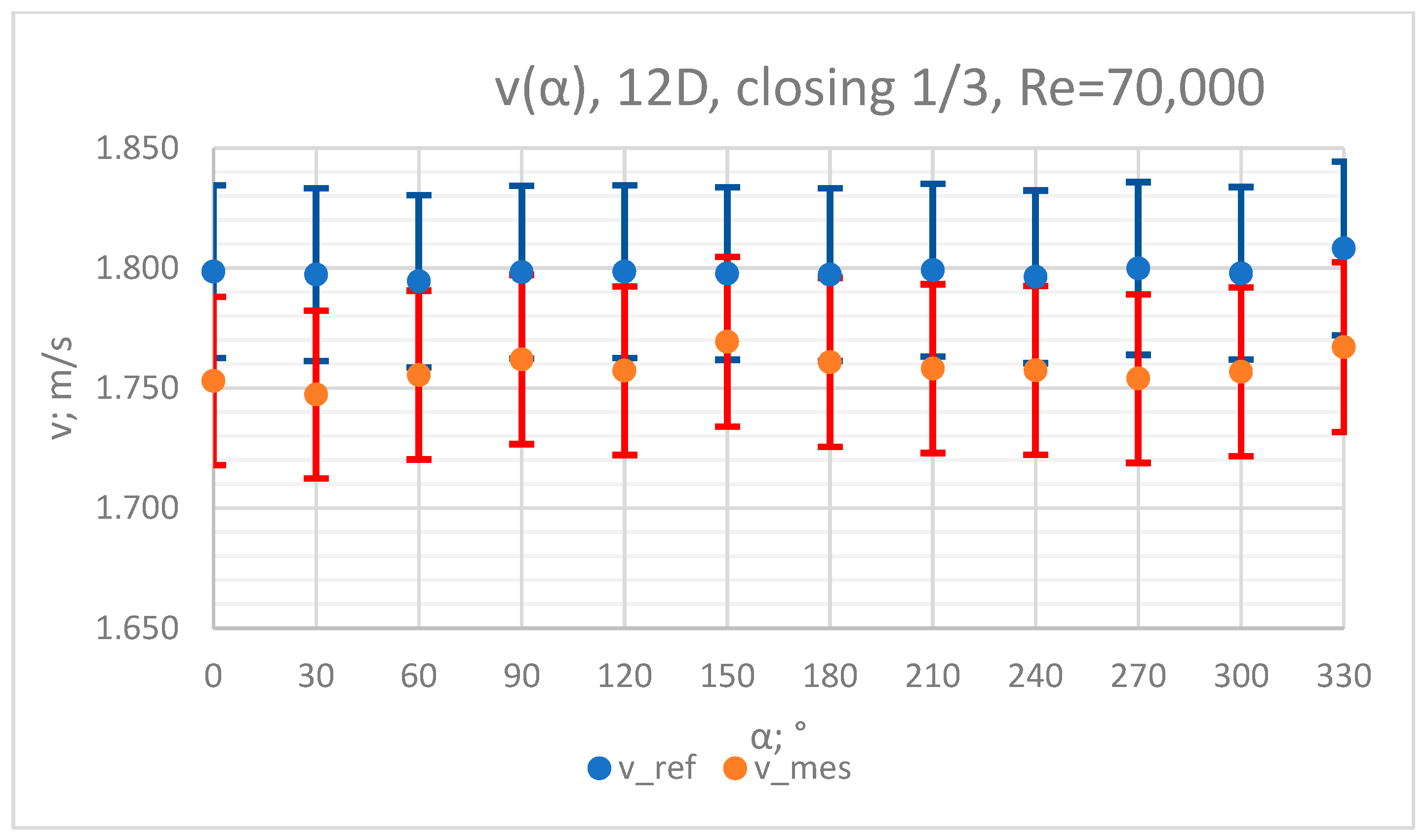
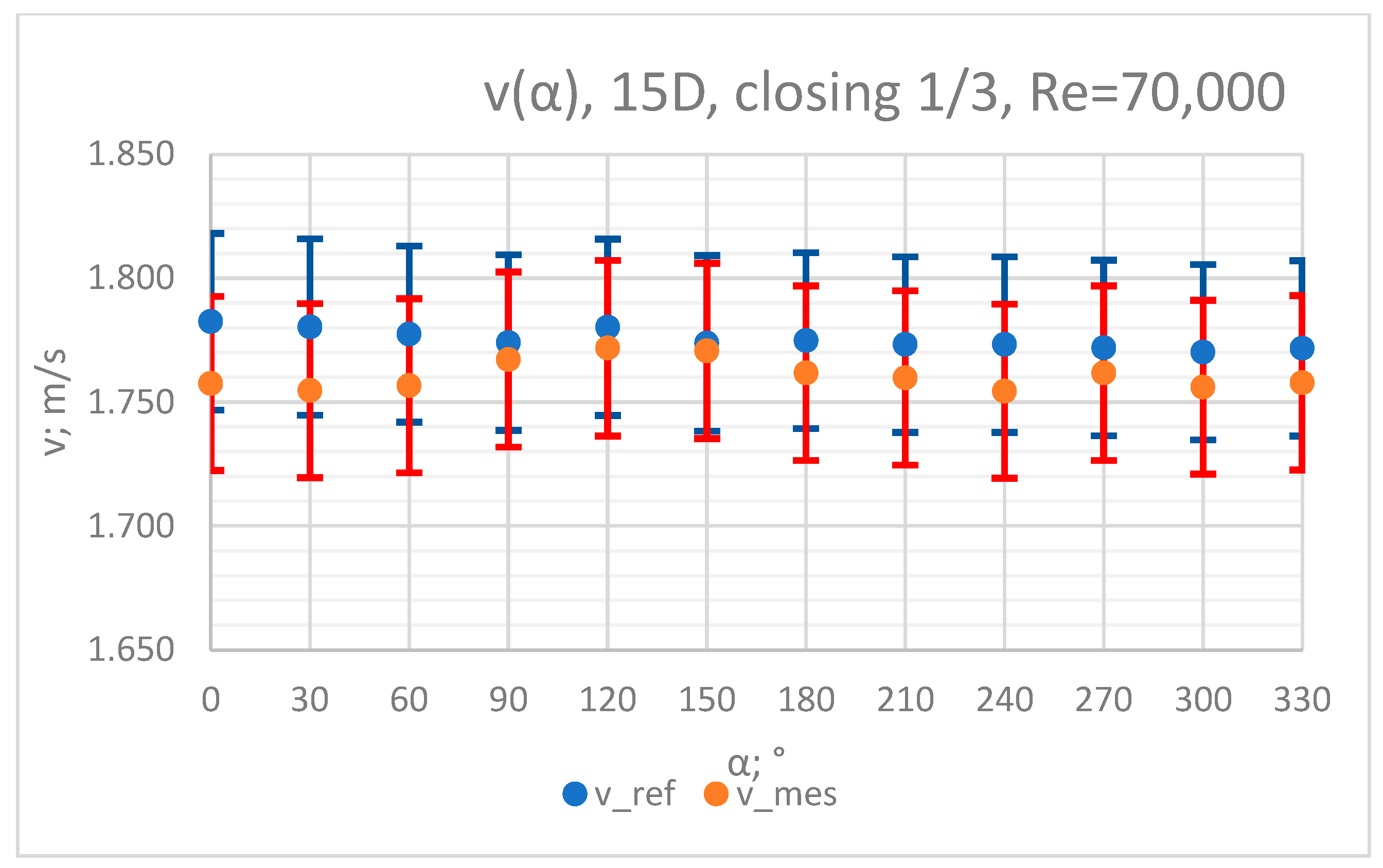
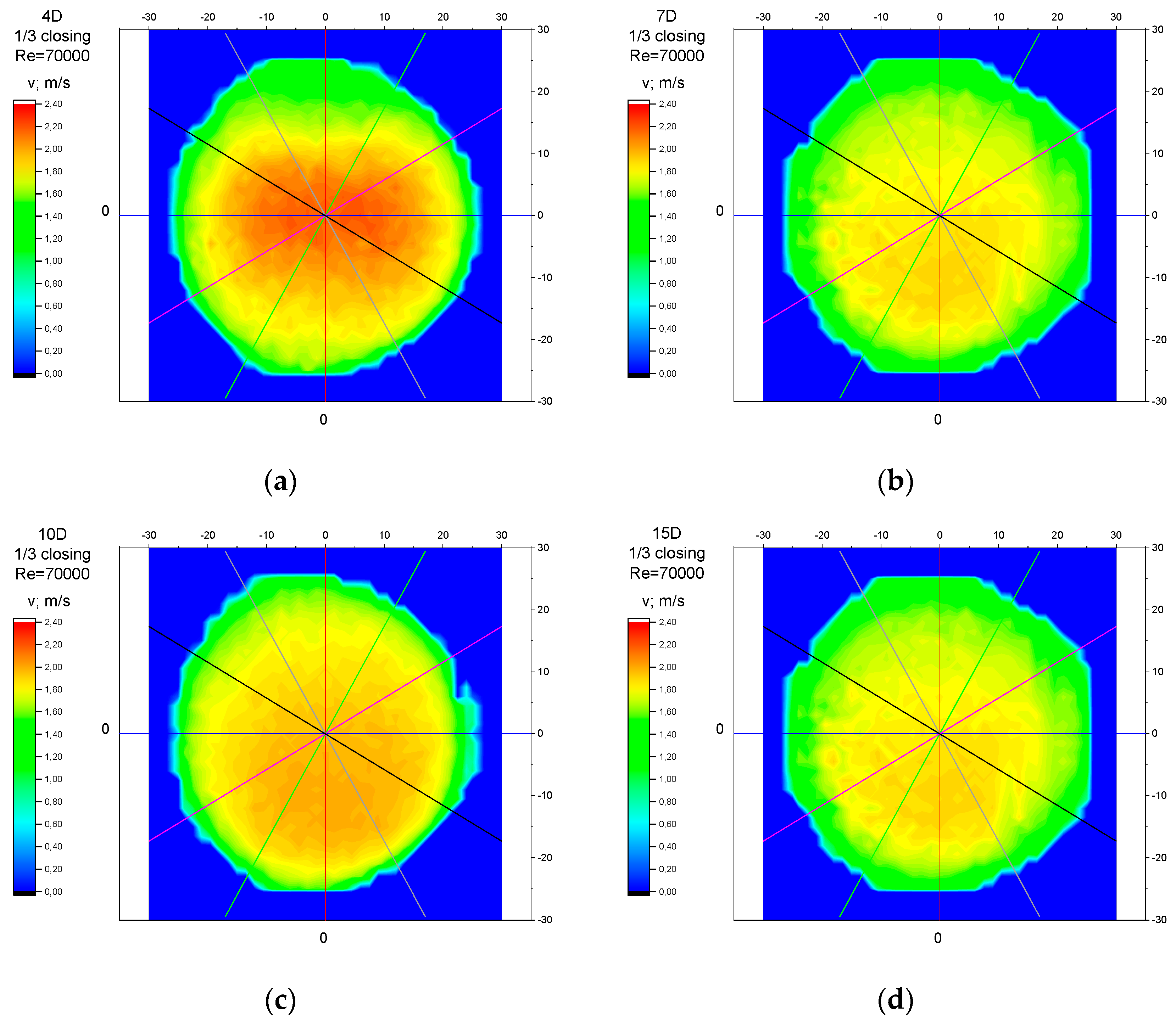
3.4. Measurement Results—1/3 of the Knife Gate Valve’s Height Closed, Re = 70,000
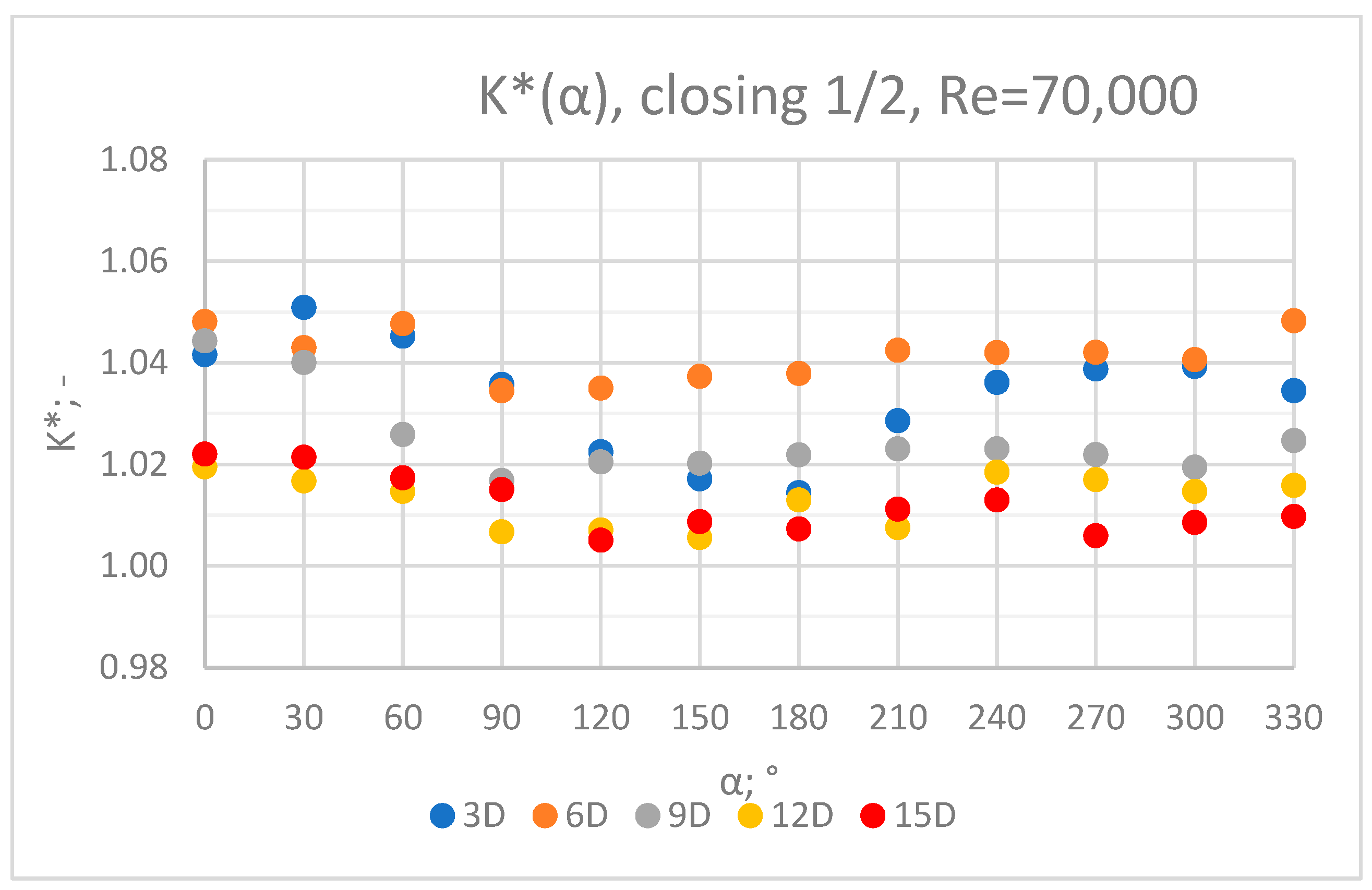
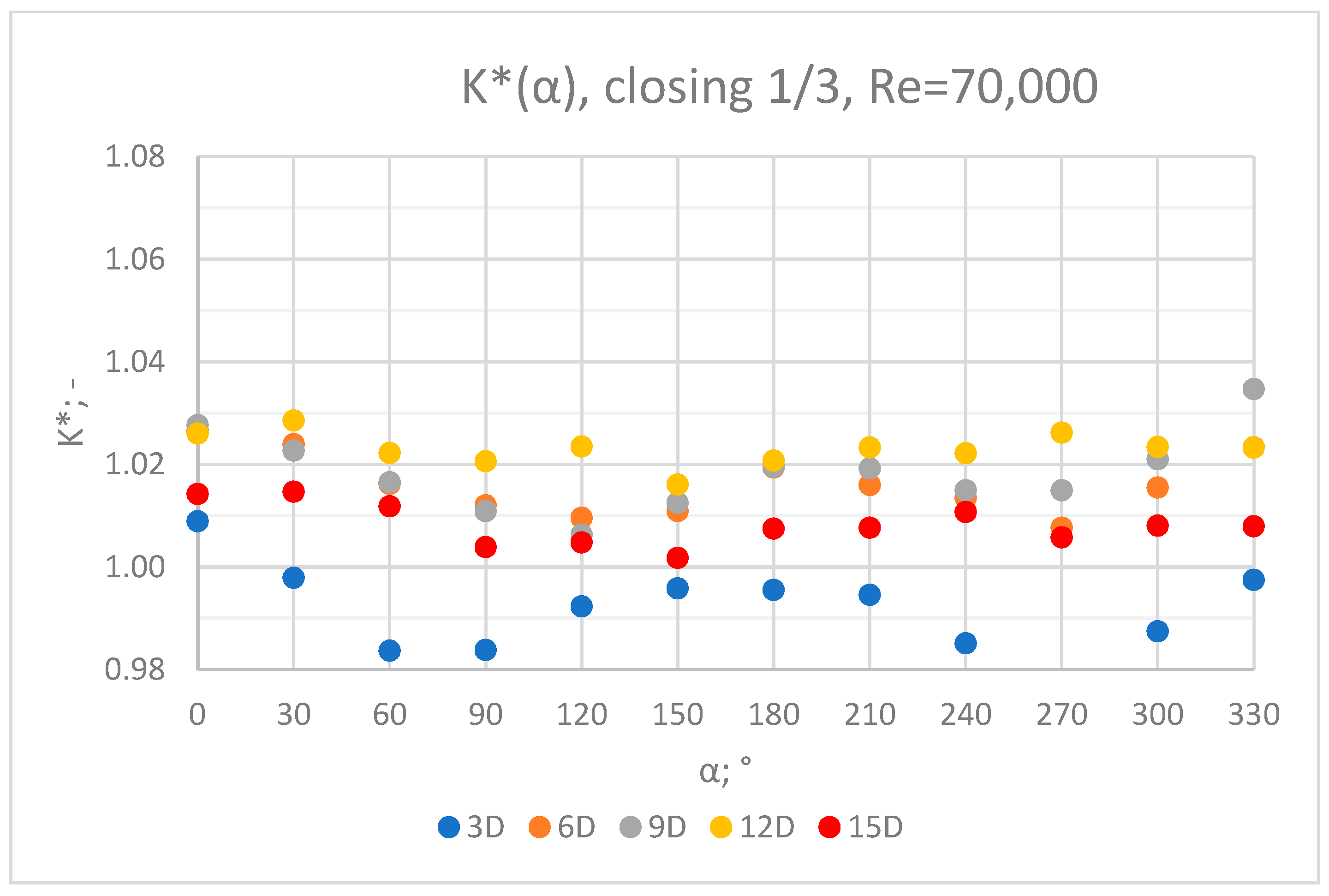
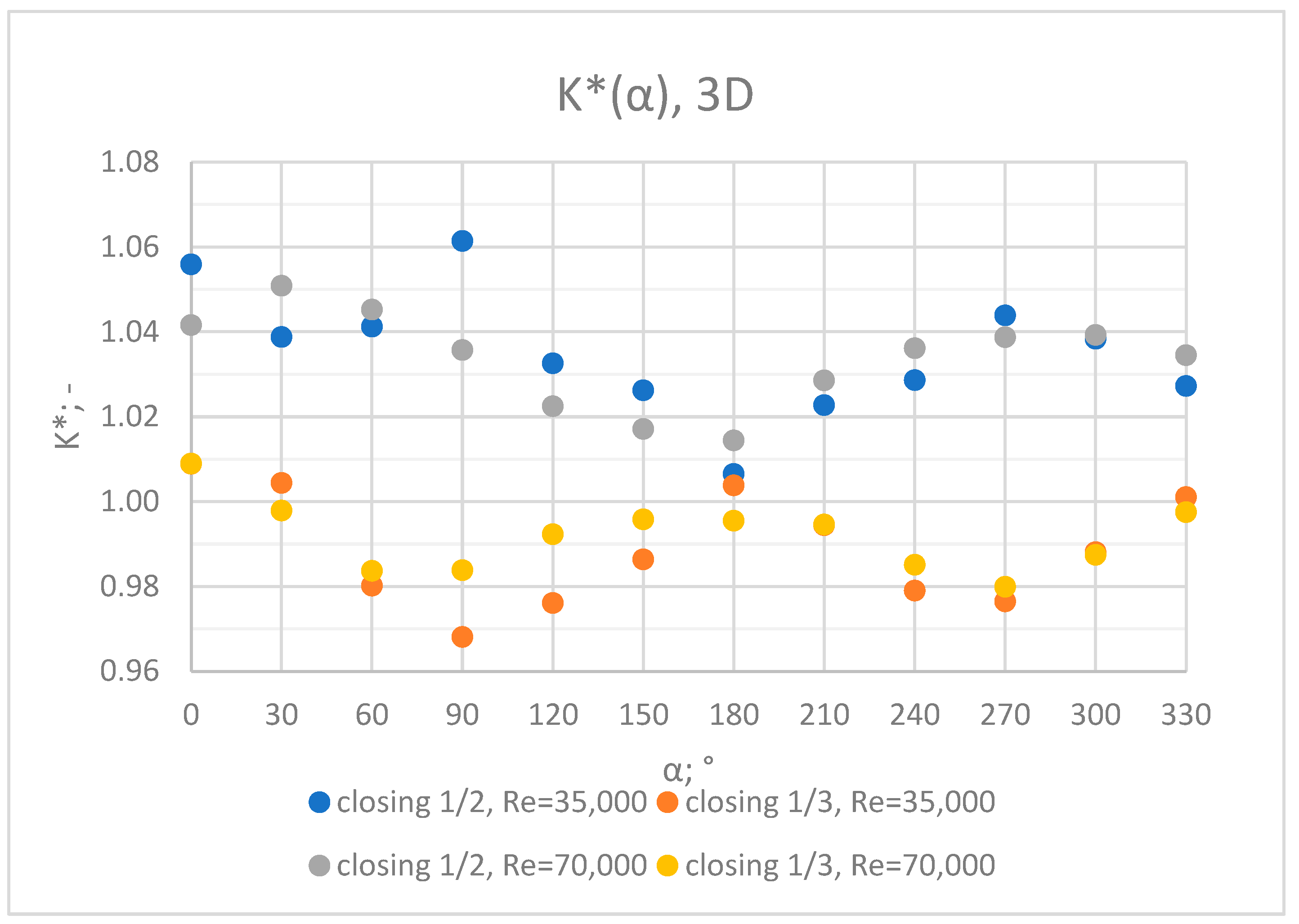
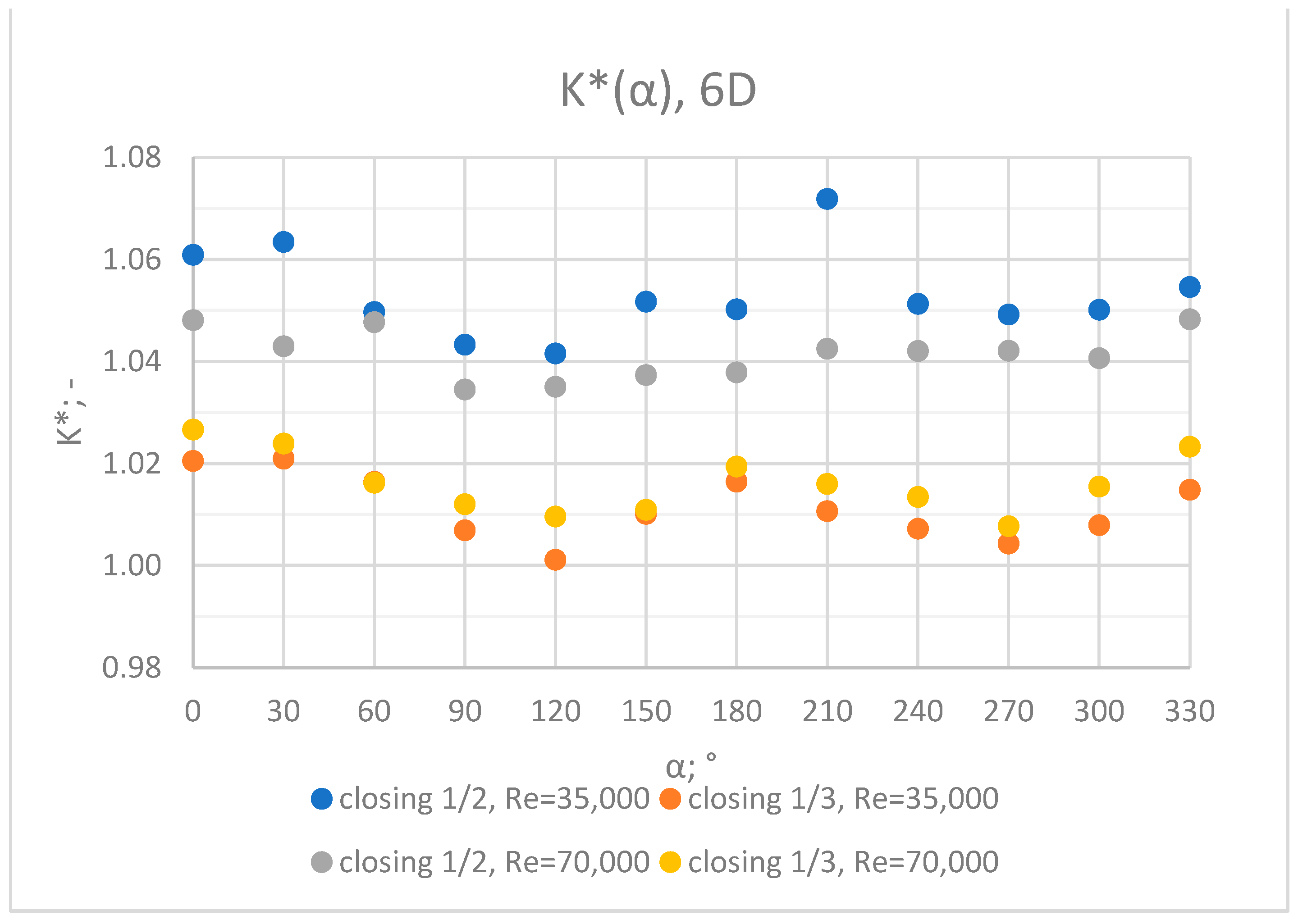
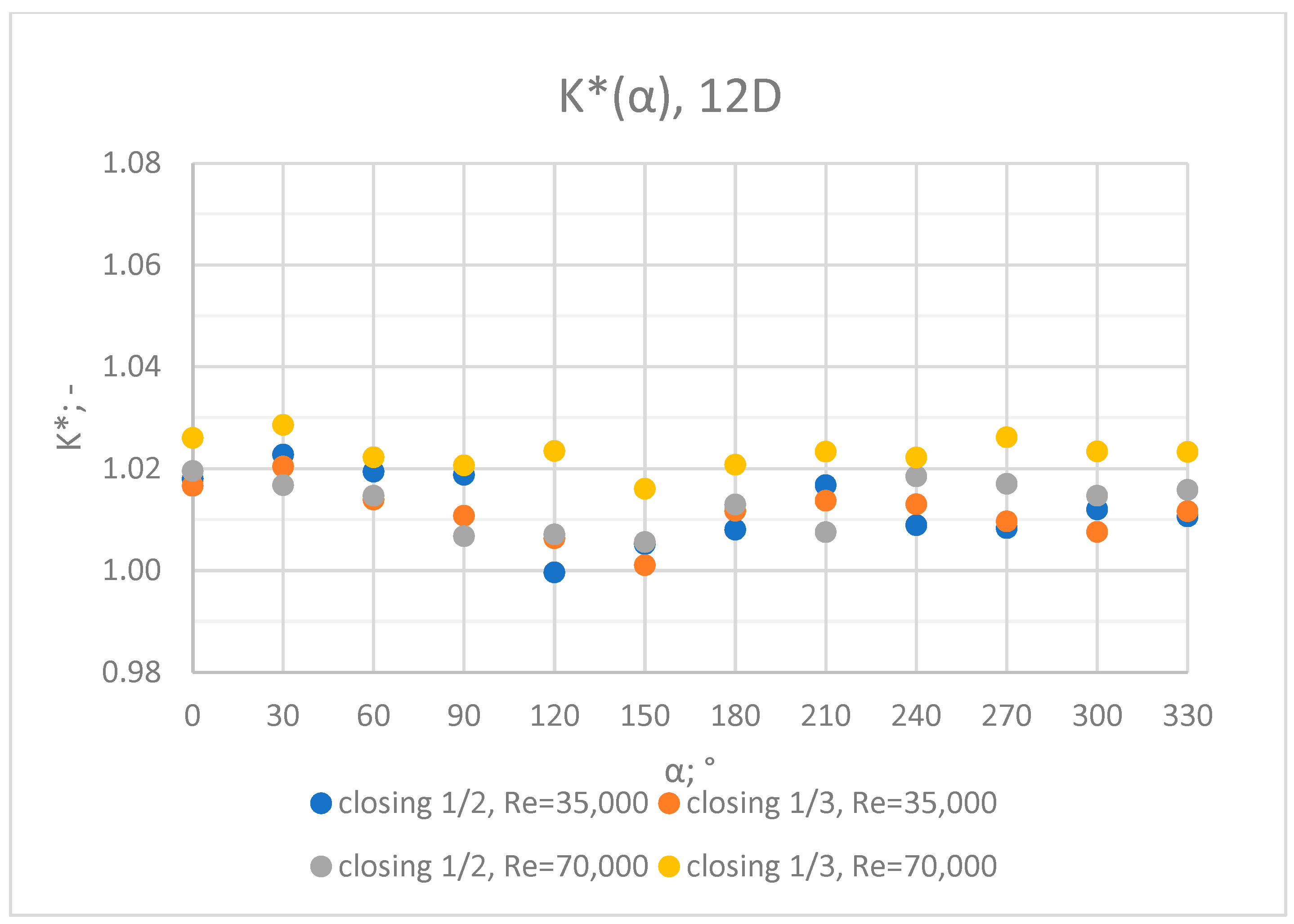
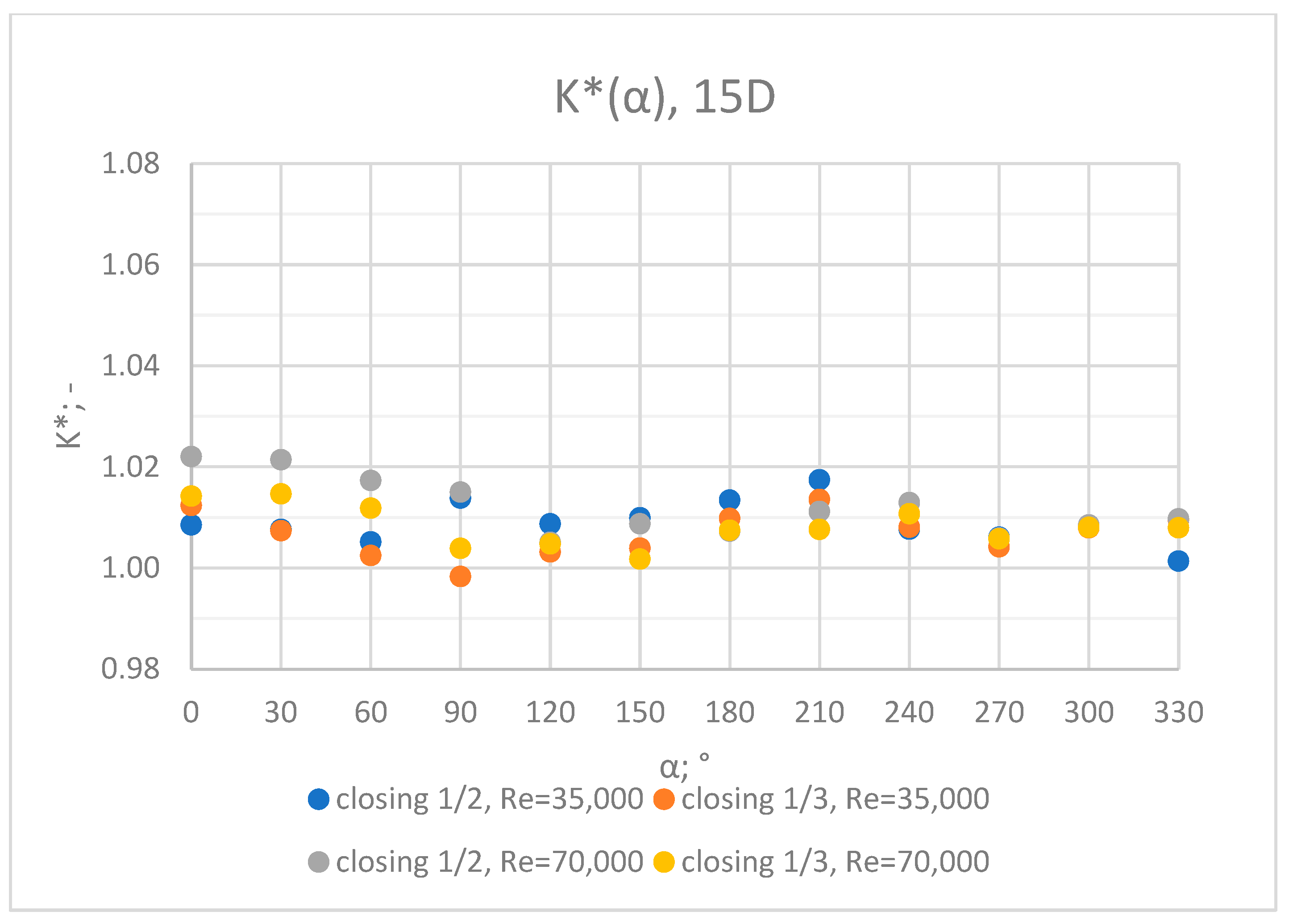
3.5. Comparison of Results from All of the Measurement Series
3.6. Treatment of Results of Laser Anemometry Test
4. Conclusions
- In the measurement series conducted for the ½ closure of the knife gate valve, much larger flow disturbances occurred than in the measurement series conducted for the 1/3 closure of the valve. These observations were also confirmed by the laser anemometry LDA tests. Graphic analysis of the velocity profiles showed an analogy in the flow disturbance structure for both levels of the closure of the valve.
- In the course of the correlation of the K* factor (α) for the series with Re = 35,000 and Re = 70,000, analogies can be noticed. It can be assumed that this correlation is universal for Reynolds numbers in the range of the turbulent flow.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviation
| Symbols | |
| C | velocity of ultrasonic wave, m/s |
| D | diameter of the pipeline, mm |
| …D | measurement cross sections at a distance |
| … | pipeline diameters from the knife gate valve, mm |
| K* | correction factor |
| l | path length of the ultrasonic wave, mm |
| L | distance between ultrasonic sensors, mm |
| qv | volume flow rate, m3/s |
| t | transit time of the ultrasonic wave, s |
| Δt | time difference between the flow upstream and downstream, s |
| Re | Reynolds number |
| V | flow velocity, m/s |
| vmes | velocity measured behind the knife gate valve, m/s |
| vref | velocity measured in front of the knife gate valve, m/s |
| α | angle of the ultrasonic heads setting, ° |
| uA | component of the type A uncertainty of the flow velocity measurement, m/s |
| uB | component of the type B uncertainty of the flow velocity measurement, m/s |
References
- ISO. Guide to the Expression of Uncertainty in Measurement; ISO: Geneva, Switzerland, 1995. [Google Scholar]
- JCGM 200:2012; International Vocabulary of Metrology—Basic and General Concepts and Associated Terms (VIM). 2012. Available online: https://www.bipm.org/documents/20126/2071204/JCGM_200_2012.pdf/f0e1ad45-d337-bbeb-53a6-15fe649d0ff1 (accessed on 1 May 2023).
- Joint Committee for Guides in Metrology. Evaluation of Measurement Data—Guide to the Expression of Uncertainty in Measurement; International Bureau of Weights and Measures (BIPM): Sèvres, France, 2008.
- JCGM 101:2008; Evaluation of Measurement Data—Supplement 1 to the Guide—Propagation of Distribution Using a Monte Carlo Method. 2008. Available online: https://www.bipm.org/documents/20126/2071204/JCGM_101_2008_E.pdf/325dcaad-c15a-407c-1105-8b7f322d651c (accessed on 8 May 2023).
- Joint Committee for Guides in Metrology. Evaluation of Measurement Data—Supplement 1 to the “Guide to the Expression of Uncertainty in Measurement”—Propagation of Distributions Using a Monte Carlo Method; International Bureau of Weights and Measures (BIPM): Sèvres, France, 2008. [Google Scholar]
- AlSaqoor, S.; Alahmer, A.; Andruszkiewicz, A.; Piechota, P.; Synowiec, P.; Beithu, N.; Wędrychowicz, W.; Wróblewska, E.; Jouhara, H. Ultrasonic technique for measuring the mean flow velocity behind a throttle: A metrological analysis. Therm. Sci. Eng. Prog. 2022, 34, 101402. [Google Scholar] [CrossRef]
- Synowiec, P.; Andruszkiewicz, A.; Wędrychowicz, W.; Piechota, P.; Wróblewska, E. Influence of flow disturbances behind the 90° bend on the indications of the ultrasonic flow meter with clamp-on sensors on pipelines. Sensors 2021, 21, 868. [Google Scholar] [CrossRef] [PubMed]
- Awad, A.S.; Abulghanam, Z.; Fayyad, S.M.; AlSaqoor, S.; Alahmer, A.; Aljabarin, N.; Piechota, P.; Andruszkiewicz, A.; Wędrychowicz, W.; Synowiec, P. Measuring the fluid flow velocity and its uncertainty using Monte Carlo method and ultrasonic technique. WSEAS Trans. Fluid Mech. 2020, 15, 172–182. [Google Scholar] [CrossRef]
- Piechota, P.; Synowiec, P.; Andruszkiewicz, A.; Wędrychowicz, W. Analysis of the accuracy of liquid flow measurements by the means of ultrasonic method in non-standard measurements conditions. In Methods and Techniques of Signal Processing in Physical Measurements; Hanus, R., Mazur, D., Kreischer, C., Eds.; Springer: Cham, Switzerland, 2019; pp. 275–285. [Google Scholar]
- Synowiec, P.; Andruszkiewicz, A.; Wędrychowicz, W.; Regucki, P. Badania możliwości pomiaru strumienia objętości czynnika dwufazowego przepływomierzem ultradźwiękowym. Prz. Elektrotechniczny 2015, 10, 181–184. [Google Scholar] [CrossRef]
- Salami, L.A. Errors in the velocity area method of measuring asymetric flows in circular pipes. Mod. Dev. Flow Meas. 1971, 10, 381–399. [Google Scholar]
- Moore, P.I.; Brown, G.J.; Stimpson, B.P. Ultrasonic transit-time flowmeters modelled with theoretical velocity profiles: Methodology. Measurement Sci. Technol. 2000, 11, 1802–1810. [Google Scholar] [CrossRef]
- Pistun, Y.; Roman, V.; Matiko, F. Investigating the Ultrasonic Flowmeter Error in Conditions of Distorted Flow Using Multipeaks Salami Functions. Errors Uncertain. 2019, 24, 14–19. [Google Scholar] [CrossRef]
- Waluś, S. Mathematical modelling of an ultrasonic flowmeter primary device. Arch. Acoust. 1998, 23, 429–442. [Google Scholar]
- Piechota, P.; Synowiec, P.; Andruszkiewicz, A.; Wędrychowicz, W. Selection of the relevant turbulence model in a CFD simulation of a flow disturbed by hydraulic elbow: Comparative analysis of the simulation with measurements results obtained by the ultrasonic flowmeter. J. Therm. Sci. 2018, 27, 413–420. [Google Scholar] [CrossRef]
- Ekambara, K.; Sanders, R.S.; Nandakumar, K.; Masliyah, J.H. Hydrodynamic Simulation of Horizontal Slurry Pipeline Flow Using ANSYS-CFX. Ind. Eng. Chem. Res. 2009, 48, 8159–8171. [Google Scholar] [CrossRef]
- Hu, L.; Fang, Z.; Qin, L.; Mao, K.; Chen, W.; Fu, X. Modelling of received ultrasonic signals based on variable frequency. Flow Meas. Instrum. 2019, 65, 141–149. [Google Scholar] [CrossRef]
- Papathanasiou, P.; Kissling, B.; Berberig, O.; Kumar, V.; Rohner, A.; Bezděk, M. Flow disturbance compensation calculated with flow simulations for ultrasonic clamp-on flowmeters with optimized path arrangement. Flow Meas. Instrum. 2022, 85, 102167. [Google Scholar] [CrossRef]
- Bopp, S.; Durst, F.; Holweg, J.; Weber, H. A laser—Doppler sensor for flowrate measurements. Flow Meas. Instrum. 1989, 1, 31–38. [Google Scholar] [CrossRef]
- Waluś, S. The use of the ultrasonic flowmeter in the conditions other than normal. Int. Conf. Flow Meas. Melb. 1985, 20–23, 171–176. [Google Scholar]
- Stoker, D.; Barfuss, S.; Johnson, M.C. Ultrasonic Flow Measurement for Pipe Installations with Non-Ideal Conditions. J. Irrig. Drain. Eng. 2012, 138, 993–998. [Google Scholar] [CrossRef]
- Sejong, C.; Byung-Ro, Y.; Woong, K.; Hyu-Sang, K. Assessment of combined V/Z clamp-on ultrasonic flow metering. J. Mech. Sci. Technol. 2014, 28, 2169–2177. [Google Scholar]
- Martins, R.S.; Andrade, J.R.; Ramos, R. On the effect of the mounting angle on single-path transit-time ultrasonic flow measurement of flare gas. J. Braz. Soc. Mech. Sci. Eng. 2020, 42, 13. [Google Scholar] [CrossRef]
- Kumar, K.; Farande, K.; Sahoo, G. Installation effects of a clamp-On transit time ultrasonic flow metery. Int. J. Fluid Mech. 2011, 2011, 489–498. [Google Scholar] [CrossRef]
- Zhang, H.; Guo, C.; Lin, J. Effects of Velocity Profiles on Measuring Accuracy of Transit-Time Ultrasonic Flowmeter. Appl. Sci. 2019, 9, 1648. [Google Scholar] [CrossRef]
- Sakhavi, N.; Nouri, N.M. Generalized velocity profile evaluation of multipath ultrasonic phased array flowmeter. Measurement 2021, 187, 110302. [Google Scholar] [CrossRef]
- Waluś, S. Some guidelines for ultrasonic flowmeter sensors installation for distorted velocity profiles. Mol. Quantum Acoust. 1998, 19, 91–102. [Google Scholar]
- Wada, S.; Furuichi, N. Influence of obstacle plates on flowrate measurement uncertainty based on ultrasonic Doppler velocity profile method. Flow Meas. Instrum. 2016, 48, 81–89. [Google Scholar] [CrossRef]
- Waluś, S. The Compensation of Sensitivity Changes and the Influence of Liquid Temperature in the Microprocessor-Based Multi-Path Ultrasonic Flowmeter; Wissenschaftliche Tage: Magdeburg, Germany, 1989; pp. 214–218. [Google Scholar]
- Tawackolian, K.; Büker, O.; Hogendoorn, J.; Lederer, T. Calibration of an ultrasonic flow meter for hot water. Flow Meas. Instrum. 2013, 30, 166–173. [Google Scholar] [CrossRef]
- Utsumi, H. An Ultrasonic Velocitymeter for Use of Calibration of Waste-Water Flowmeter. Fluid Control and Measurement, tom Volume 2, M. Harada, Red.; Pergamon Press: Tokyo, Japan, 1985; pp. 997–1002. [Google Scholar]
- Endress+Hauser, Manual Proline Prosonic Flow 93T HART-Portable Ultrasonic Flowmeter. Available online: https://portal.endress.com/wa001/dla/5000255/6790/000/02/BA00136DEN_1311.pdf (accessed on 20 January 2021).
- Micronics Ltd. User Manual of Portable Ultrasonic Flow Meter Micronics Portaflow PF330; Micronics Ltd.: Loudwater, UK, 2012. [Google Scholar]
- Guo, S.; Xiang, N.; Li, B.; Wang, F.; Zhao, N.; Zhang, T. Integration method of multipath ultrasonic flowmeter based on velocity distribution. Measurement 2023, 207, 112388. [Google Scholar] [CrossRef]
- Sakhavi, N.; Nouri, N.M. Performance of novel multipath ultrasonic phased array flowmeter using Gaussian quadrature integration. Appl. Acoust. 2022, 199, 109004. [Google Scholar] [CrossRef]
- Kurniadi, D.; Trisnobudi, A. A Multi-Path Ultrasonic Transit Time Flow Meter Using a Tomography Method for Gas Flow Velocity Profile Measurement. Part. Part. Syst. Charact. 2006, 23, 330–338. [Google Scholar] [CrossRef]
- Tang, X.-Y.; Yang, Q.; Sun, Y. Gas flow-rate measurement using a transit-time multi-path ultrasonic flow meter based on PSO-SVM. In Proceedings of the 2017 IEEE International Instrumentation and Measurement Technology Conference (I2MTC), Turin, Italy, 22–25 May 2017; pp. 1–6. [Google Scholar] [CrossRef]
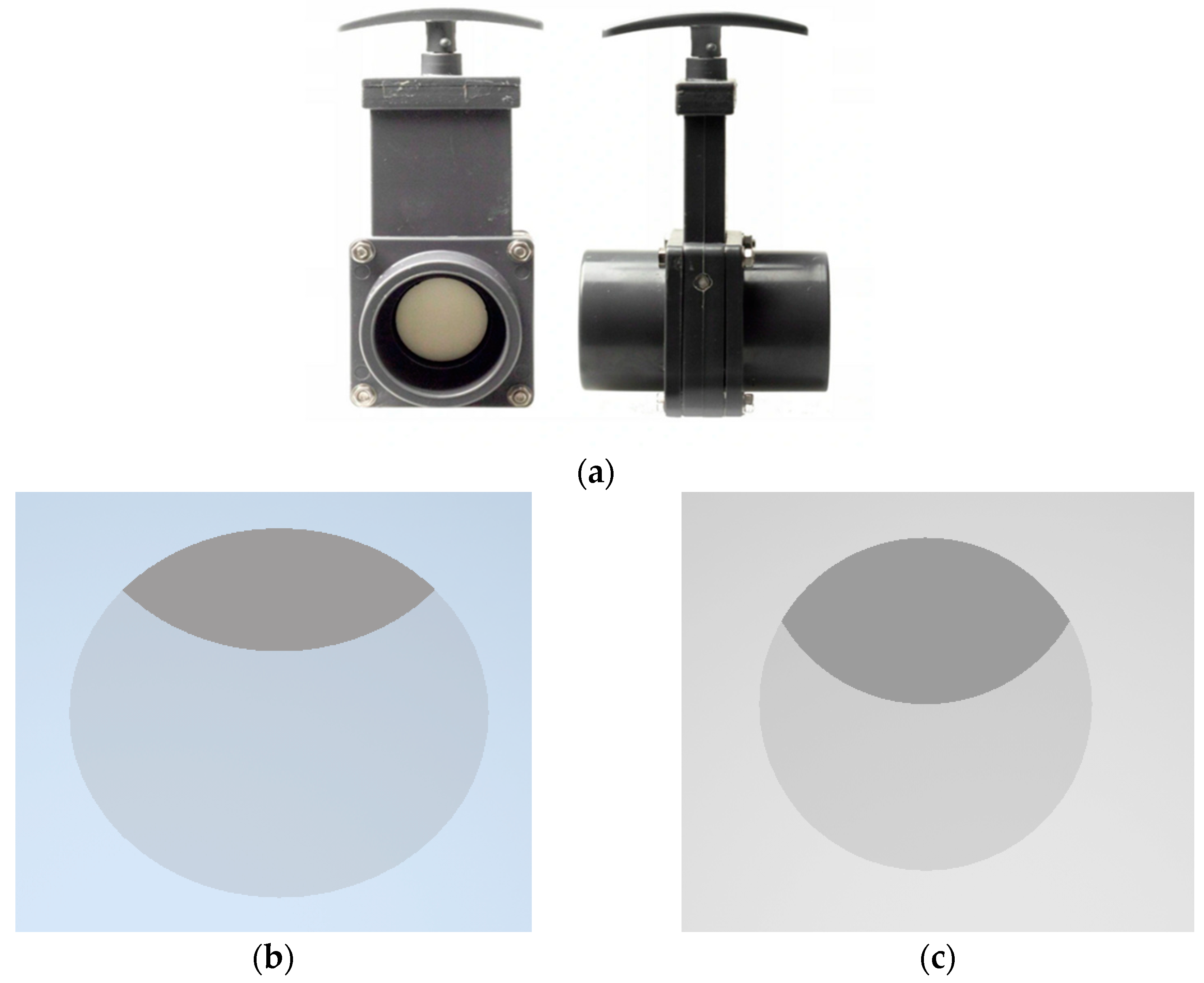
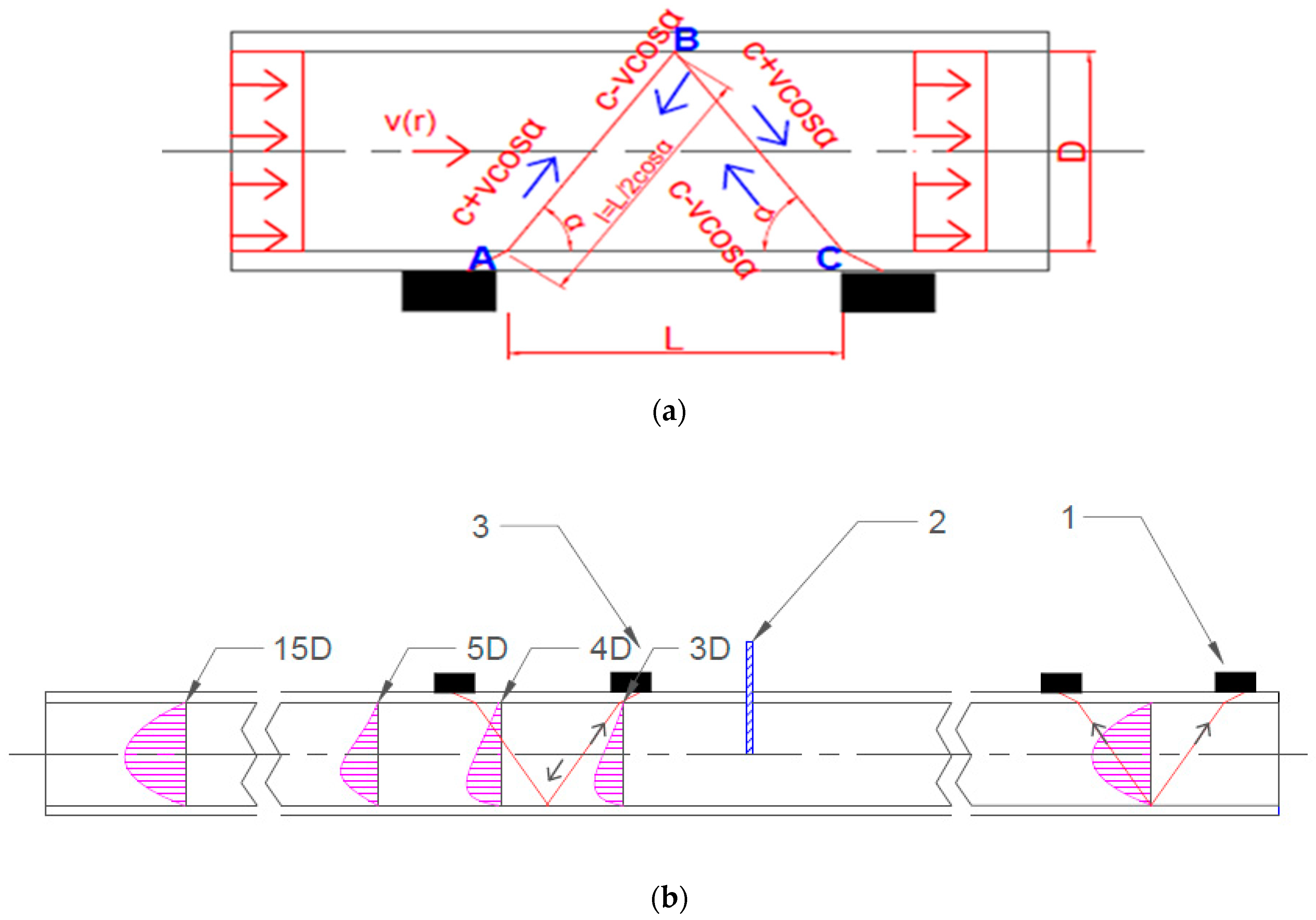
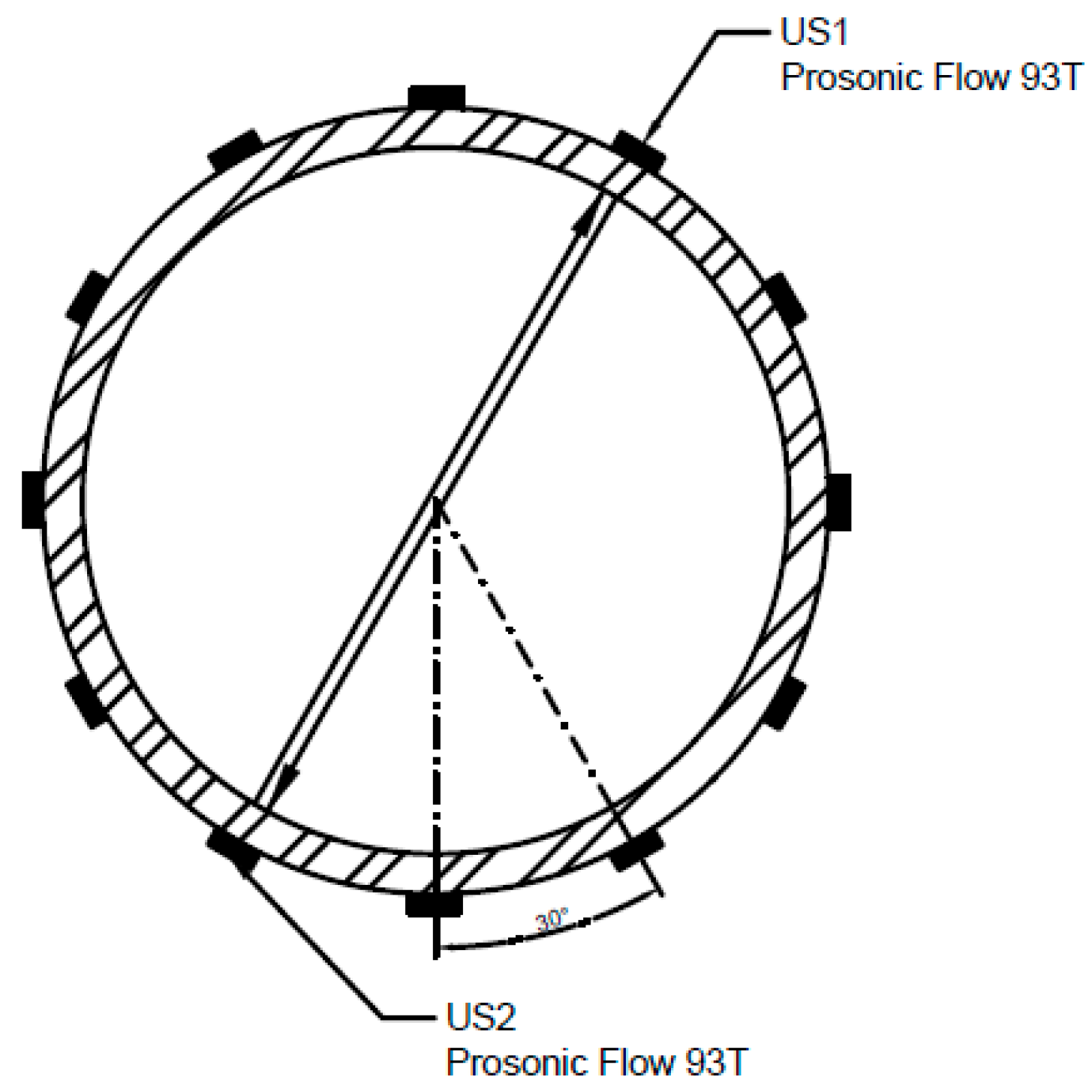







| Name of Parameter | Parameter |
|---|---|
| Nominal diameter of the pipeline | DN 50 |
| Measurement sections | 3D–15D |
| Velocities | ca. 0.3 m/s for Re = 35,000 |
| ca. 1.78 m/s for Re = 70,000 | |
| The ultrasound wave path | V |
| Sampling interval | 5 s |
| Distance between sensors | ca. 90 mm |
| Knife gate closing level | 1/3 valve height (ca. 22%) |
| 1/2 valve height (ca. 40%) |
| Device | Brand | Model | Specification | Maximum Permissible Error (MPE) |
|---|---|---|---|---|
| Ultrasonic flow meter | Microsonic | Porta Flow 330 | Transit-time measurement, clamp-on sensors | 0.5% to 2% of velocity reading for v > 0.2 m/s |
| Ultrasonic flow meter | Endress+Hausser | Prosonic Flow 93T | Transit-time measurement, clamp-on sensors | 0.5% to 2% of velocity reading for v > 0.3 m/s for Re > 10,000 |
| Laser Doppler anemometer | Dantec | One-channel laser Doppler anemometer data | Power of laser: 10 mW Light wavelength: 632.8 nm-red Light focal length: 160 mm Measuring volume: 75 μm × 630 μm | - |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Piechota, P.; Synowiec, P.; Andruszkiewicz, A.; Wędrychowicz, W.; Wróblewska, E.; Mrowiec, A. Experimental Determination Influence of Flow Disturbances behind the Knife Gate Valve on the Indications of the Ultrasonic Flow Meter with Clamp-On Sensors on Pipelines. Sensors 2023, 23, 4677. https://doi.org/10.3390/s23104677
Piechota P, Synowiec P, Andruszkiewicz A, Wędrychowicz W, Wróblewska E, Mrowiec A. Experimental Determination Influence of Flow Disturbances behind the Knife Gate Valve on the Indications of the Ultrasonic Flow Meter with Clamp-On Sensors on Pipelines. Sensors. 2023; 23(10):4677. https://doi.org/10.3390/s23104677
Chicago/Turabian StylePiechota, Piotr, Piotr Synowiec, Artur Andruszkiewicz, Wiesław Wędrychowicz, Elżbieta Wróblewska, and Andrzej Mrowiec. 2023. "Experimental Determination Influence of Flow Disturbances behind the Knife Gate Valve on the Indications of the Ultrasonic Flow Meter with Clamp-On Sensors on Pipelines" Sensors 23, no. 10: 4677. https://doi.org/10.3390/s23104677
APA StylePiechota, P., Synowiec, P., Andruszkiewicz, A., Wędrychowicz, W., Wróblewska, E., & Mrowiec, A. (2023). Experimental Determination Influence of Flow Disturbances behind the Knife Gate Valve on the Indications of the Ultrasonic Flow Meter with Clamp-On Sensors on Pipelines. Sensors, 23(10), 4677. https://doi.org/10.3390/s23104677








