A Hybrid Feature Selection and Multi-Label Driven Intelligent Fault Diagnosis Method for Gearbox
Abstract
:1. Introduction
2. Motivation and Literature Review
- A feature set construction method that efficiently handles a low signal-to-noise ratio and nonlinear signals using statistical feature extraction techniques;
- A feature selection framework that is applicable to multi-label data and can automatically search for the optimal subset from the original high-dimensional feature set;
- A physical interpretative fault diagnosis framework that can maximize the preservation of fault features.
3. Theoretical Basis of the Study
3.1. Feature Selection Models
3.1.1. Filter Models
- Fischer score:
- Information gain:
- Pearson correlation coefficient:
3.1.2. Wrapper Models
- Binary search:
- Sequential forward search:
- Sequential backward search:
3.2. Multi-Label Classification
3.2.1. Label Powerset
3.2.2. Multi-Label k-Nearest Neighbor Classifier
4. The Proposed Methodology
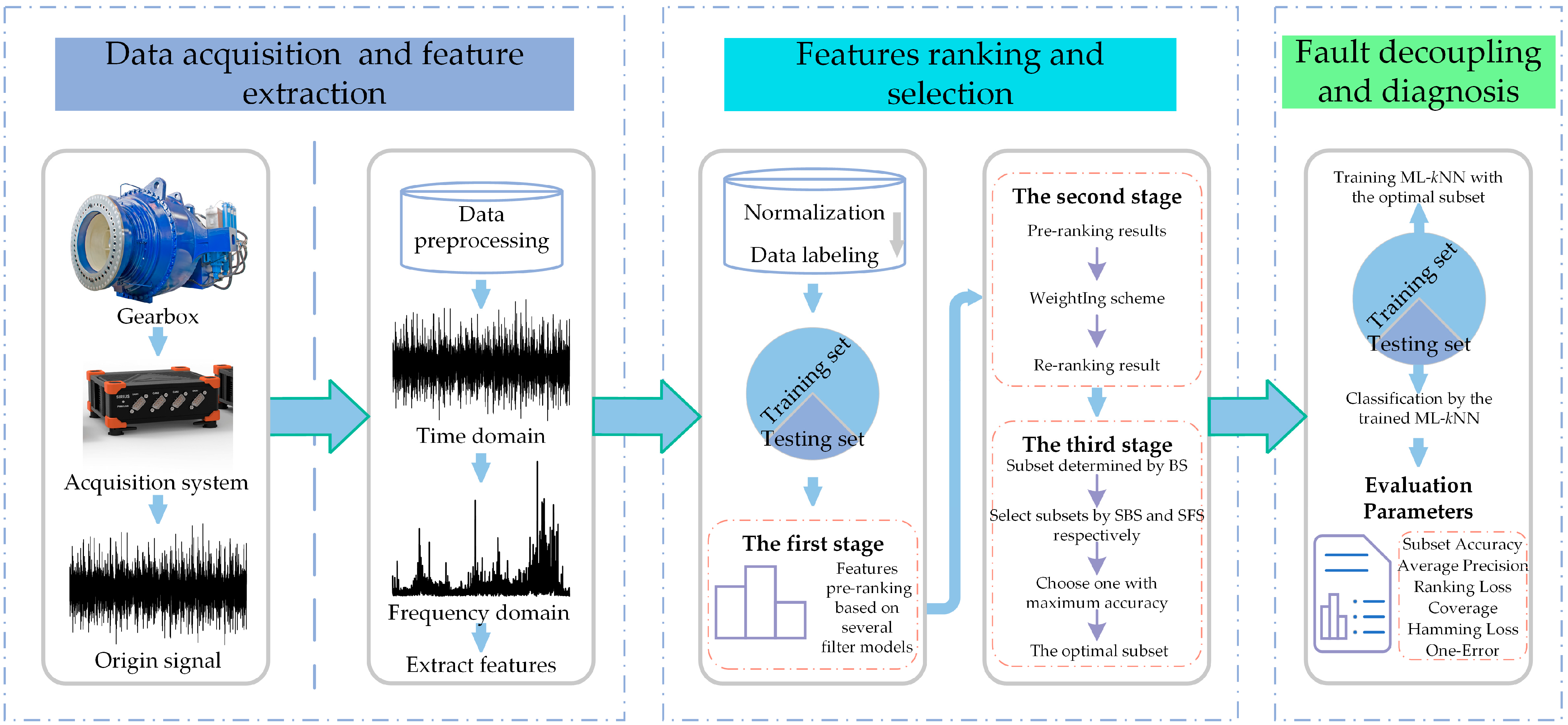
4.1. An Overview of the Proposed Feature Selection and Fault Decoupling Method
- Data acquisition and feature extraction: A data acquisition system is used to obtain the gearbox’s vibration signal. In order to more effectively remove disturbing components from the signal and highlight fault characteristic information, the raw signal is first pre-processed and then time domain statistical features and frequency domain statistical features are extracted from the raw and pre-processed signals, as shown in Section 4.2;
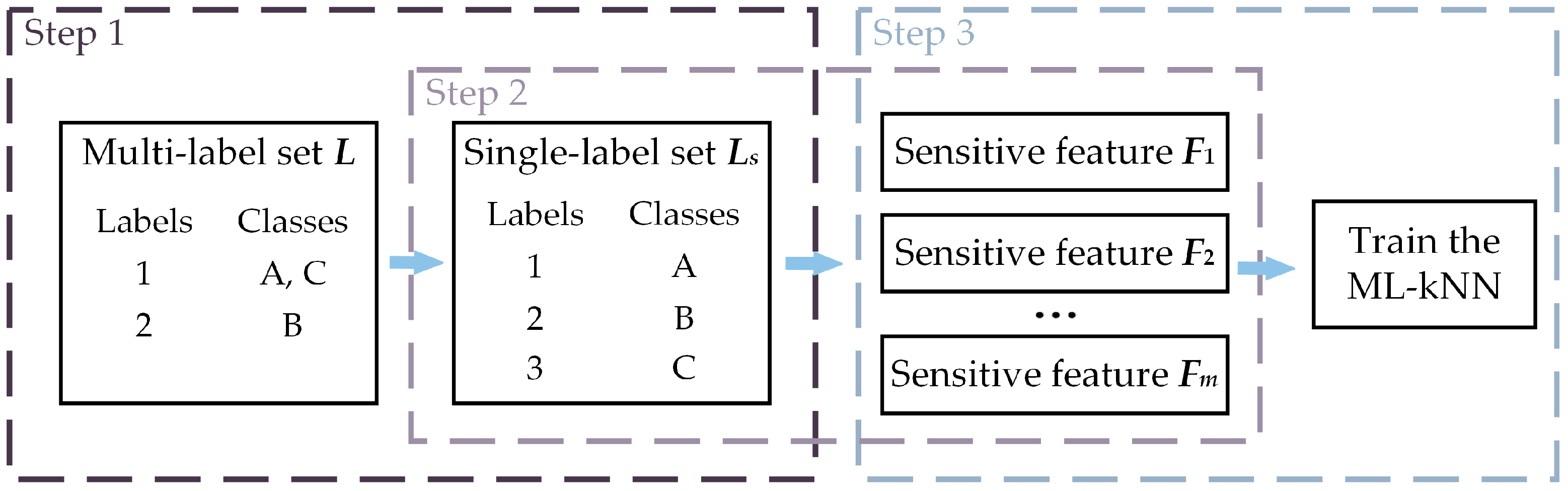
- Feature ranking and selection: In this paper, we will use the LP method to transform the multi-label data and perform feature selection before utilizing ML-kNN as a classifier to evaluate the effectiveness of feature selection. In other words, the PT method is merely utilized to achieve feature selection, and once feature selection for the original feature set has been finished, the original multi-label problem will be taken into account once more to achieve multi-label classification using the AA method. As a result, our proposed processing method consists of 3 primary steps, as shown in Figure 2. The LP method is used in step 1 to transform the multi-label set L into ingle-label set Ls. The proposed feature selection method, which is illustrated in Section 4.3, is used to search the most sensitive features from the origin feature set in step 2. In step 3, the quality of the optimal subset Lm is evaluated by ML-kNN.
- Fault decoupling and diagnosis: Using the index of the optimal features obtained through the training set, the corresponding optimal features are selected from the original high-dimensional feature set of the testing set. Finally, the fault decoupling results of the testing set are obtained by the trained ML-kNN classifier, which is trained by the training set.
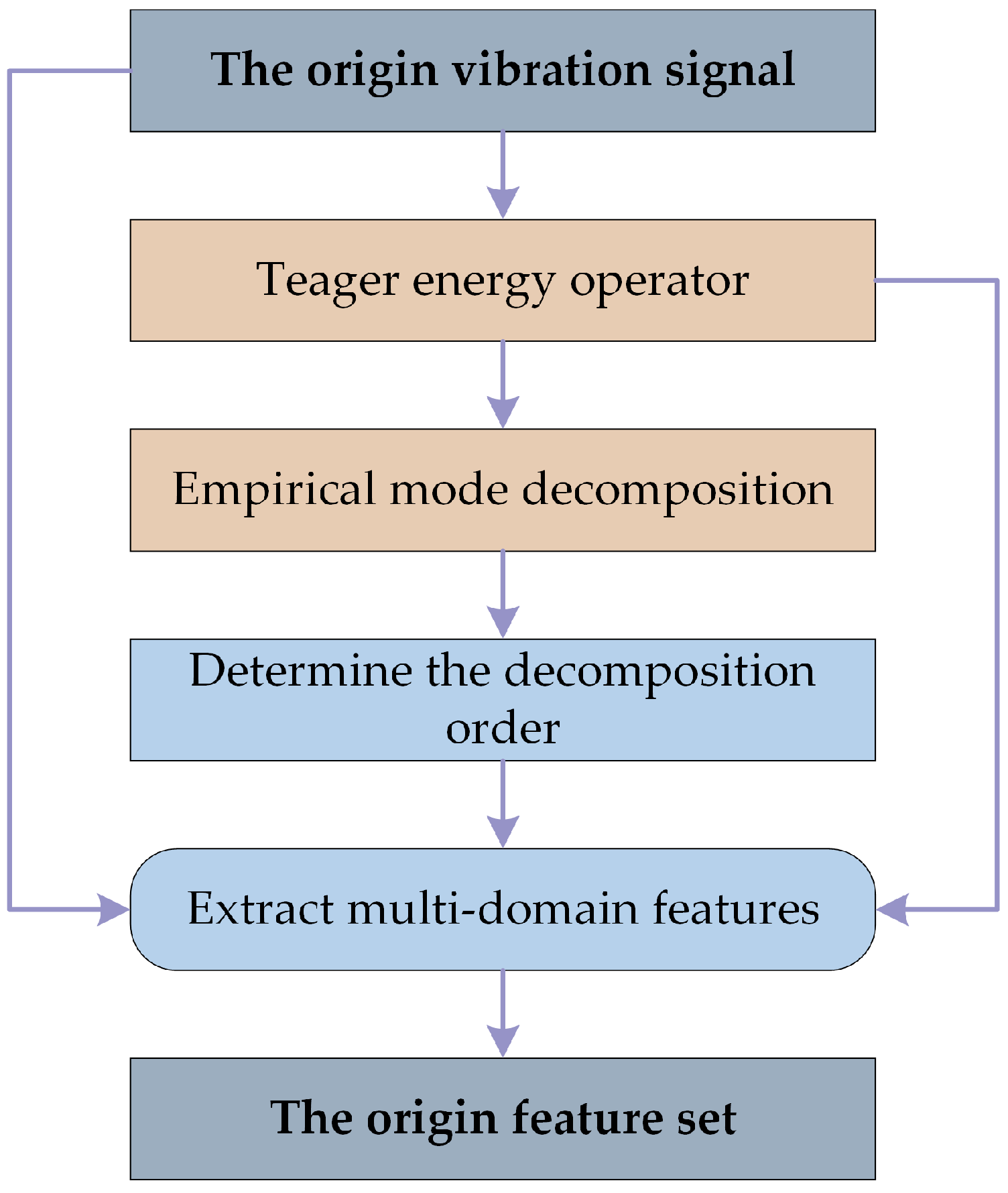
4.2. Original Feature Extraction of Vibration Signals
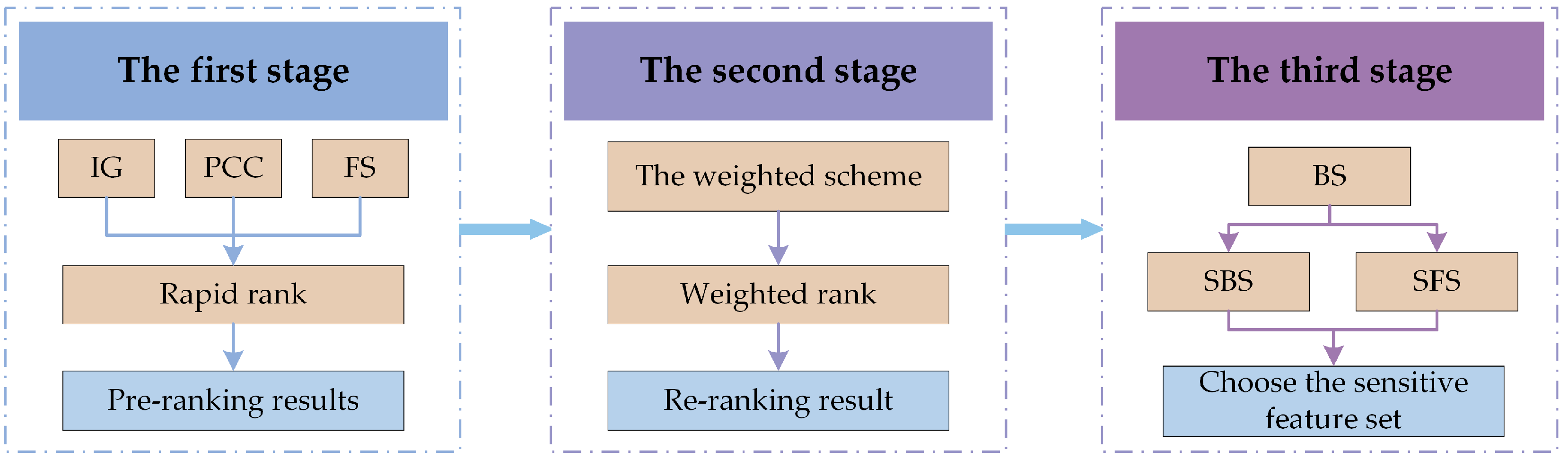
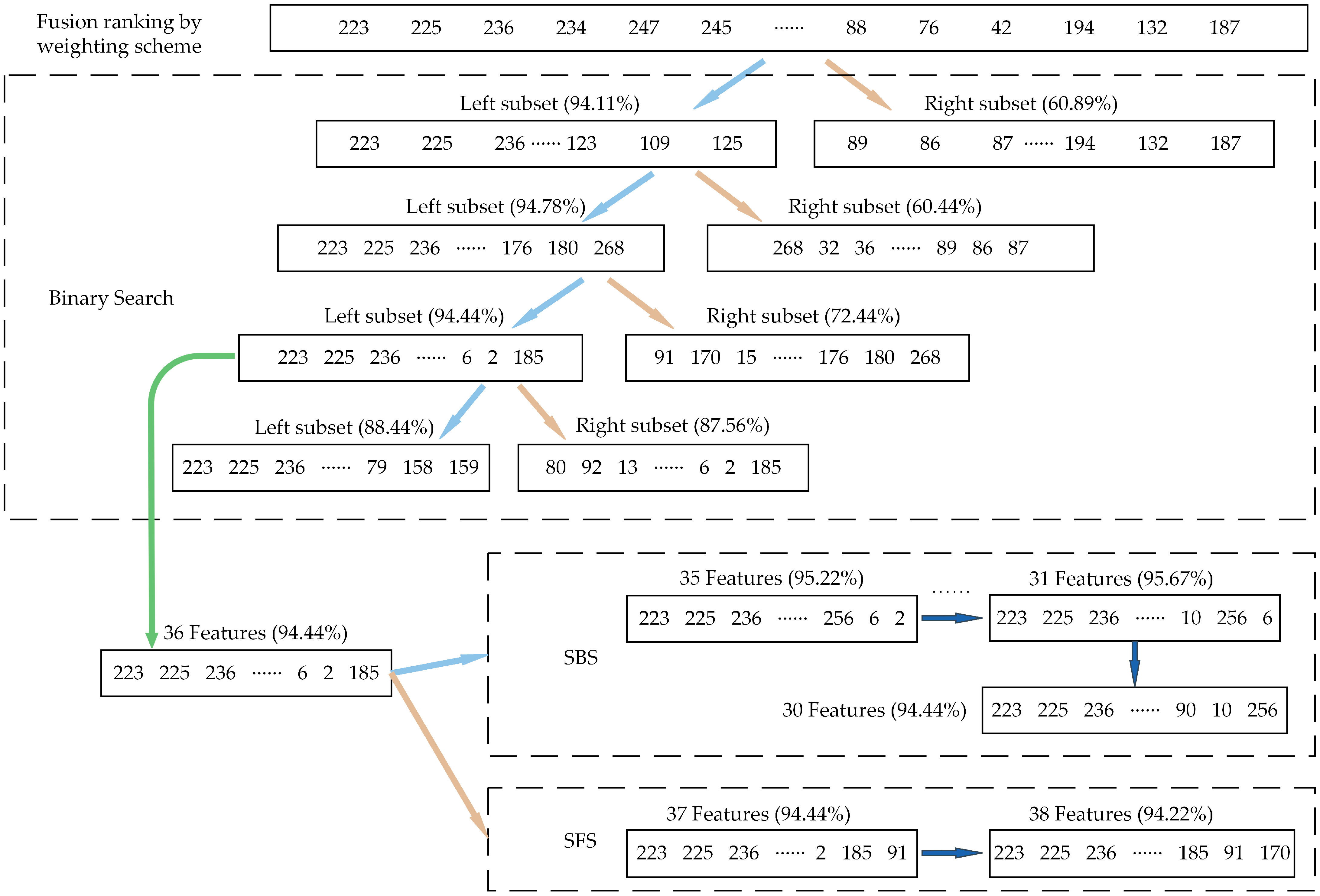
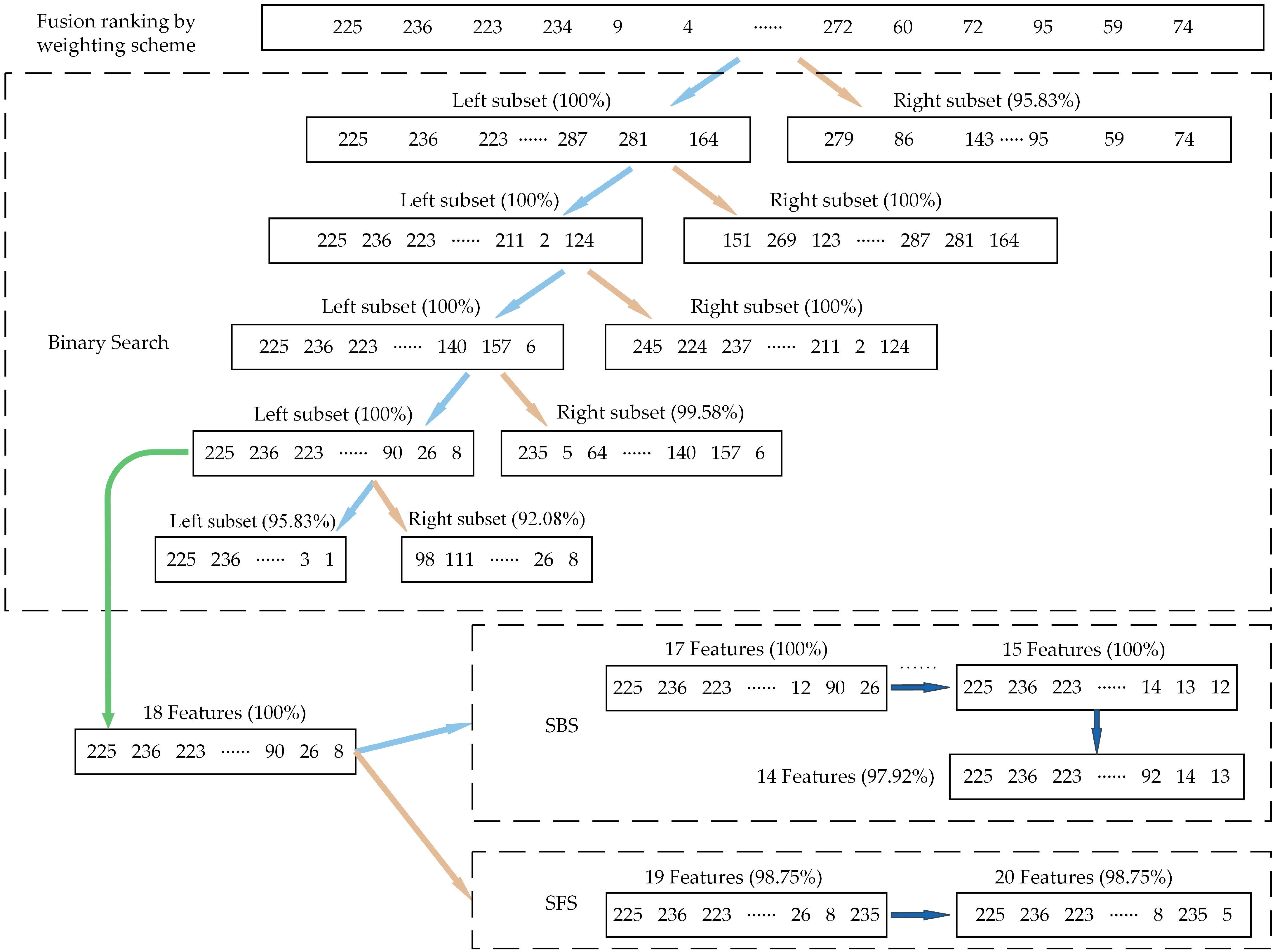
4.3. The Proposed 3-Stage Hybrid Feature Selection Framework
5. Experiments and Analyses
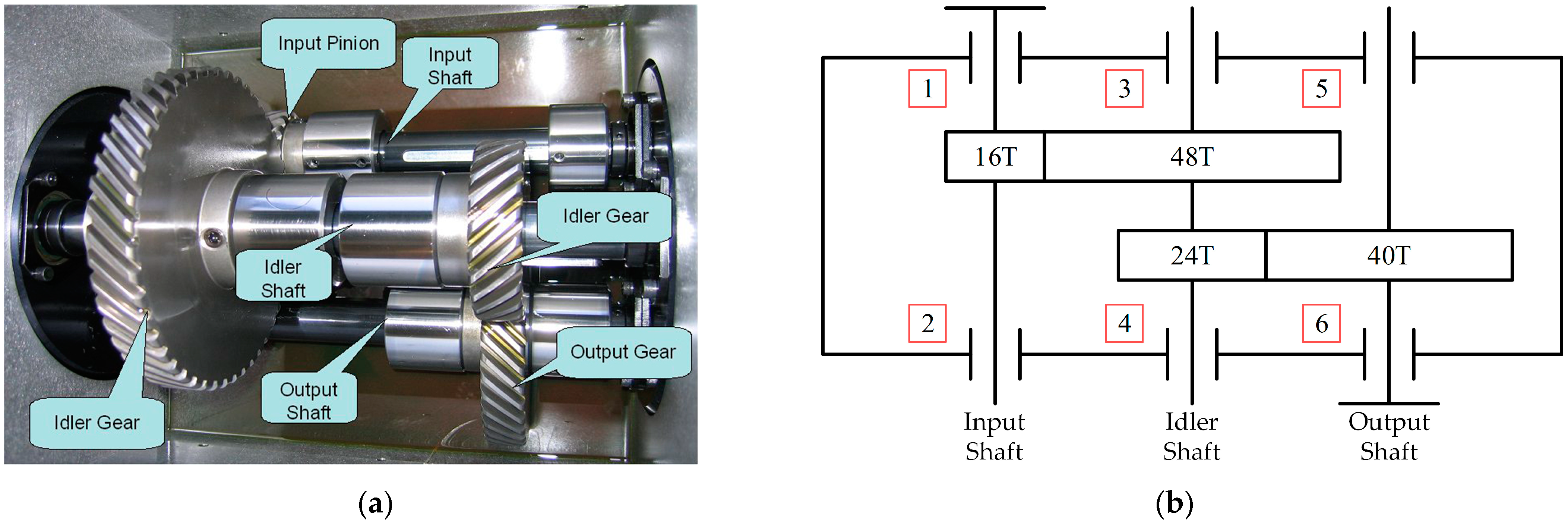
5.1. Experimental Apparatus and Data Acquisition
5.2. Experimental Results and Analysis
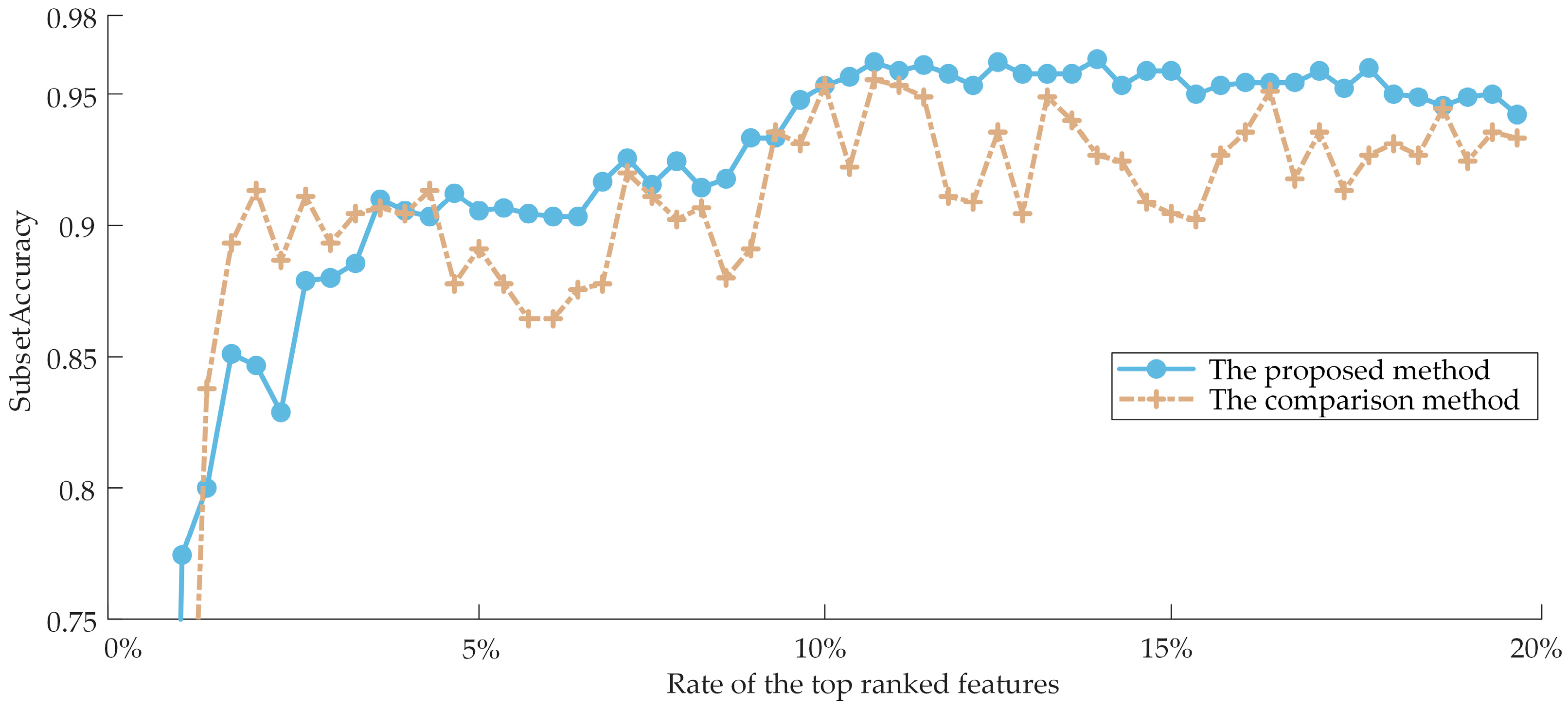
5.3. Comparison with Other Methods
5.4. Added Experiments
6. Conclusions and Future Works
- In order to describe the operating condition of the gearbox as comprehensively as possible, we propose to construct multi-domain feature sets. The Teager energy operator and the EMD algorithm are utilized in the proposed feature extraction stage to filter out disturbing components from the signal and highlight the fault feature information. Each vibration signal is thus given a high-dimensional feature vector that contains irrelevant and redundant features, and it is important to adaptively screen the most sensitive features using feature selection techniques;
- The original multi-label problem will be taken again into account to achieve multi-label classification by the AA method once the feature selection for the original feature set has been completed by employing the PT method. Consequently, the feature selection and fault decoupling framework proposed in this paper is more adaptable;
- The original high-dimensional feature set contained redundant and irrelevant features, which may have increased training time and decreased recognition accuracy. The ML-kNN is utilized as the classifier in the proposed feature selection method, and three Filter models are initially employed to pre-rank the features. To achieve a reranking result that takes into account feature irrelevance, redundancy, and inter-feature interaction factors, the pre-ranking results are fused using a weighting scheme. In order to optimize the subset for the classifier and attain the highest diagnostic accuracy, a search stage that could adaptively discover the optimal subset is constructed based on three heuristic search strategies;
- The proposed method does not entail complicated mapping, which is an intuitive and straightforward process. Therefore, this method has a good physical interpretation and helps to reveal the connection between faults and their related features, offering a new solution for diagnosing compound defects in gearboxes.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
| Time-Domain Feature | Frequency-Domain Feature | ||
|---|---|---|---|
References
- Yu, F.; Liu, Y.; Zhao, Q. Compound Fault Diagnosis of Gearbox Based on Wavelet Packet Transform and Sparse Representation Classification. In Proceedings of the 2020 Chinese Control and Decision Conference (CCDC), Hefei, China, 22–24 August 2020; pp. 1105–1109. [Google Scholar]
- Dibaj, A.; Ettefagh, M.M.; Hassannejad, R.; Ehghaghi, M.B. A hybrid fine-tuned VMD and CNN scheme for untrained compound fault diagnosis of rotating machinery with unequal-severity faults. Expert Syst. Appl. 2021, 167, 114094. [Google Scholar] [CrossRef]
- Huang, R.; Liao, Y.; Zhang, S.; Li, W. Deep Decoupling Convolutional Neural Network for Intelligent Compound Fault Diagnosis. IEEE Access 2019, 7, 1848–1858. [Google Scholar] [CrossRef]
- Okwuosa, C.N.; Hur, J.-W. A Filter-Based Feature-Engineering-Assisted SVC Fault Classification for SCIM at Minor-Load Conditions. Energies 2022, 15, 7597. [Google Scholar] [CrossRef]
- Zhang, X.; Zhang, Q.; Chen, M.; Sun, Y.; Qin, X.; Li, H. A two-stage feature selection and intelligent fault diagnosis method for rotating machinery using hybrid filter and wrapper method. Neurocomputing 2018, 275, 2426–2439. [Google Scholar] [CrossRef]
- Pan, L.; Zhao, L.; Song, A.; She, S.; Wang, S. Research on gear fault diagnosis based on feature fusion optimization and improved two hidden layer extreme learning machine. Measurement 2021, 177, 109317. [Google Scholar] [CrossRef]
- Wen, L.; Li, X.; Gao, L. A New Two-Level Hierarchical Diagnosis Network Based on Convolutional Neural Network. IEEE Trans. Instrum. Meas. 2020, 69, 330–338. [Google Scholar] [CrossRef]
- Akpudo, U.E.; Hur, J.-W. A Cost-Efficient MFCC-Based Fault Detection and Isolation Technology for Electromagnetic Pumps. Electronics 2021, 10, 439. [Google Scholar] [CrossRef]
- Lee, C.; Le, T.; Lin, Y. A Feature Selection Approach Hybrid Grey Wolf and Heap-Based Optimizer Applied in Bearing Fault Diagnosis. IEEE Access 2022, 10, 56691–56705. [Google Scholar] [CrossRef]
- Liu, H.; Zhou, M.; Liu, Q. An Embedded Feature Selection Method for Imbalanced Data Classification. IEEE/CAA J. Autom. Sin. 2019, 6, 703–715. [Google Scholar] [CrossRef]
- Chen, K.; Xue, B.; Zhang, M.; Zhou, F. An Evolutionary Multitasking-Based Feature Selection Method for High-Dimensional Classification. IEEE Trans. Cybern. 2022, 52, 7172–7186. [Google Scholar] [CrossRef]
- Lei, Y.; Jia, F.; Lin, J.; Xing, S.; Ding, S.X. An Intelligent Fault Diagnosis Method Using Unsupervised Feature Learning Towards Mechanical Big Data. IEEE Trans. Ind. Electron. 2016, 63, 3137–3147. [Google Scholar] [CrossRef]
- Dhamande, L.S.; Chaudhari, M.B. Compound gear-bearing fault feature extraction using statistical features based on time-frequency method. Measurement 2018, 125, 63–77. [Google Scholar] [CrossRef]
- Yan, X.; Jia, M. A novel optimized SVM classification algorithm with multi-domain feature and its application to fault diagnosis of rolling bearing. Neurocomputing 2018, 313, 47–64. [Google Scholar] [CrossRef]
- Zhao, X.; Jia, M. Fault diagnosis of rolling bearing based on feature reduction with global-local margin Fisher analysis. Neurocomputing 2018, 315, 447–464. [Google Scholar] [CrossRef]
- Wen, X.; Xu, Z. Wind turbine fault diagnosis based on ReliefF-PCA and DNN. Expert Syst. Appl. 2021, 178, 115016. [Google Scholar] [CrossRef]
- Zhou, Y.; Yan, S.; Ren, Y.; Liu, S. Rolling bearing fault diagnosis using transient-extracting transform and linear discriminant analysis. Measurement 2021, 178, 109298. [Google Scholar] [CrossRef]
- Qian, W.; Long, X.; Wang, Y.; Xie, Y. Multi-label feature selection based on label distribution and feature complementarity. Appl. Soft Comput. 2020, 90, 106167. [Google Scholar] [CrossRef]
- Malhi, A.; Gao, R.X. PCA-based feature selection scheme for machine defect classification. IEEE Trans. Instrum. Meas. 2004, 53, 1517–1525. [Google Scholar] [CrossRef]
- Cadenas, J.M.; Carmen Garrido, M.; Martinez, R. Feature subset selection Filter-Wrapper based on low quality data. Expert Syst. Appl. 2013, 40, 6241–6252. [Google Scholar] [CrossRef]
- Dokeroglu, T.; Deniz, A.; Kiziloz, H.E. A comprehensive survey on recent metaheuristics for feature selection. Neurocomputing 2022, 494, 269–296. [Google Scholar] [CrossRef]
- Li, X.; Ren, J. MICQ-IPSO: An effective two-stage hybrid feature selection algorithm for high-dimensional data. Neurocomputing 2022, 501, 328–342. [Google Scholar] [CrossRef]
- Patel, S.P.; Upadhyay, S.H. Euclidean distance based feature ranking and subset selection for bearing fault diagnosis. Expert Syst. Appl. 2020, 154, 113400. [Google Scholar] [CrossRef]
- Shi, J.; Yi, J.; Ren, Y.; Li, Y.; Zhong, Q.; Tang, H.; Chen, L. Fault diagnosis in a hydraulic directional valve using a two-stage multi-sensor information fusion. Measurement 2021, 179, 109460. [Google Scholar] [CrossRef]
- Ding, Y.; Fan, L.; Liu, X. Analysis of feature matrix in machine learning algorithms to predict energy consumption of public buildings. Energy Build. 2021, 249, 111208. [Google Scholar] [CrossRef]
- Wang, Y.; Feng, L. Hybrid feature selection using component co-occurrence based feature relevance measurement. Expert Syst. Appl. 2018, 102, 83–99. [Google Scholar] [CrossRef]
- Liang, K.; Dai, W.; Du, R. A Feature Selection Method Based on Improved Genetic Algorithm. In Proceedings of the 2020 Global Reliability and Prognostics and Health Management (PHM-Shanghai), Shanghai, China, 16–18 October 2020; pp. 1–5. [Google Scholar]
- Mochammad, S.; Kang, Y.; Noh, Y.; Park, S.; Ahn, B. Stable Hybrid Feature Selection Method for Compressor Fault Diagnosis. IEEE Access 2021, 9, 97415–97429. [Google Scholar] [CrossRef]
- Ganjei, M.A.; Boostani, R. A hybrid feature selection scheme for high-dimensional data. Eng. Appl. Artif. Intell. 2022, 113, 104894. [Google Scholar] [CrossRef]
- Ma, Y.; Cheng, J.; Wang, P.; Wang, J.; Yang, Y. Rotating machinery fault diagnosis based on multivariate multiscale fuzzy distribution entropy and Fisher score. Measurement 2021, 179, 109495. [Google Scholar] [CrossRef]
- Shannon, C.E. A Mathematical Theory of Communication. Bell Syst. Tech. J. 1948, 27, 623–656. [Google Scholar] [CrossRef]
- Omuya, E.O.; Okeyo, G.O.; Kimwele, M.W. Feature Selection for Classification using Principal Component Analysis and Information Gain. Expert Syst. Appl. 2021, 174, 114765. [Google Scholar] [CrossRef]
- Guyon, I.; Elisseeff, A. An introduction to variable and feature selection. J. Mach. Learn. Res. 2003, 3, 1157–1182. [Google Scholar]
- Mladenic, D. Feature selection for dimensionality reduction. In Subspace, Latent Structure and Feature Selection; Saunders, G., Grobelnik, M., Gunn, S., ShaweTaylor, J., Eds.; Lecture Notes in Computer Science; Springer Science+Business Media: Berlin/Heidelberg, Germany, 2006; Volume 3940, pp. 84–102. [Google Scholar]
- Liu, H.; Yu, L. Toward integrating feature selection algorithms for classification and clustering. IEEE Trans. Knowl. Data Eng. 2005, 17, 491–502. [Google Scholar]
- Moyano, J.M.; Gibaja, E.L.; Cios, K.J.; Ventura, S. Review of ensembles of multi-label classifiers: Models, experimental study and prospects. Inf. Fusion 2018, 44, 33–45. [Google Scholar] [CrossRef]
- Reyes, O.; Morell, C.; Ventura, S. Scalable extensions of the ReliefF algorithm for weighting and selecting features on the multi-label learning context. Neurocomputing 2015, 161, 168–182. [Google Scholar] [CrossRef]
- Newton, S.; Everton, A.C.; Maria, C.M.; Huei, D.L. A Comparison of Multi-label Feature Selection Methods using the Problem Transformation Approach. Electron. Notes Theor. Comput. Sci. 2013, 292, 135–151. [Google Scholar]
- Tsoumakas, G.; Katakis, I.; Vlahavas, I. Random k-Labelsets for Multilabel Classification. IEEE Trans. Knowl. Data Eng. 2011, 23, 1079–1089. [Google Scholar] [CrossRef]
- Maltoudoglou, L.; Paisios, A.; Lenc, L.; Martinek, J.; Kral, P.; Papadopoulos, H. Well-calibrated confidence measures for multi-label text classification with a large number of labels. Pattern Recognit. 2022, 122, 108271. [Google Scholar] [CrossRef]
- Zhang, M.; Zhou, Z. ML-KNN: A lazy learning approach to multi-label leaming. Pattern Recognit. 2007, 40, 2038–2048. [Google Scholar] [CrossRef]
- Van Tung, T.; AlThobiani, F.; Ball, A. An approach to fault diagnosis of reciprocating compressor valves using Teager-Kaiser energy operator and deep belief networks. Expert Syst. Appl. 2014, 41, 4113–4122. [Google Scholar]
- Robert, B.; Randall, J.A. Why EMD and similar decompositions are of little benefit for bearing diagnostics. Mech. Syst. Signal Process. 2023, 192, 110207. [Google Scholar]
- Lei, Y.; He, Z.; Zi, Y.; Hu, Q. Fault diagnosis of rotating machinery based on multiple ANFIS combination with GAS. Mech. Syst. Signal Process. 2007, 21, 2280–2294. [Google Scholar] [CrossRef]
- Zhang, K.; Li, Y.; Scarf, P.; Ball, A. Feature selection for high-dimensional machinery fault diagnosis data using multiple models and Radial Basis Function networks. Neurocomputing 2011, 74, 2941–2952. [Google Scholar] [CrossRef]
- Doquire, G.V.M. Feature Selection for Multi-label Classification Problems. In Proceedings of the International Work-Conference on Artificial Neural Networks, Torremolinos, Spain, 8–10 June 2011; pp. 9–16. [Google Scholar]
- Trochidis, K.; Tsoumakas, G.; Kalliris, G.; Vlahavas, I. Multi-label classification of music into emotions. In Proceedings of the 9th International Conference on Music Information Retrieval (ISMIR 2008), Philadelphia, PA, USA, 14–18 September 2008; pp. 325–330. [Google Scholar]
- PHM, Phm Data Challenge 2009 [DB]. 2009. Available online: https://www.phmsociety.org/competition/PHM/09 (accessed on 10 April 2009).






| Fault Types | S1 | S2 | S3 | S4 | S5 | S6 | S7 | S8 | S9 |
|---|---|---|---|---|---|---|---|---|---|
| Normal | √ | ||||||||
| Gear surface wear | √ | √ | |||||||
| Gear root crack | √ | √ | |||||||
| Gear missing tooth | √ | √ | |||||||
| Bearing inner race fault | √ | √ | |||||||
| Bearing outer race fault | √ | √ | √ |
| Order | FS | IG | PCC | Weighting Scheme |
|---|---|---|---|---|
| 1 | 223 | 146 | 240 | 223 |
| 2 | 225 | 159 | 229 | 225 |
| 3 | 236 | 172 | 251 | 236 |
| 4 | 234 | 185 | 262 | 234 |
| 5 | 247 | 236 | 273 | 247 |
| 6 | 106 | 223 | 172 | 245 |
| 7 | 245 | 234 | 146 | 235 |
| 8 | 107 | 198 | 185 | 226 |
| 9 | 1 | 211 | 159 | 107 |
| 10 | 226 | 225 | 228 | 1 |
| … | … | … | … | … |
| 285 | 34 | 141 | 261 | 42 |
| 286 | 99 | 143 | 139 | 194 |
| 287 | 194 | 121 | 239 | 132 |
| 288 | 88 | 128 | 106 | 187 |
| Computational Cost (s) | SA | AP | HL | RL | Cov | OE | |
|---|---|---|---|---|---|---|---|
| Origin feature set | 0.971 | 0.8622 | 0.9765 | 0.0278 | 0.0114 | 0.3878 | 0.0444 |
| Optimal subset | 0.469 | 0.9622 | 0.9841 | 0.0113 | 0.0084 | 0.3689 | 0.0300 |
| Method | Number of Optimal Features | Computational Cost (s) | SA | AP | HL | RL | Cov | OE |
|---|---|---|---|---|---|---|---|---|
| The proposed method | 31 | 0.469 | 0.9622 | 0.9841 | 0.0113 | 0.0084 | 0.3689 | 0.0300 |
| Method 1 | 45 | 0.489 | 0.9311 | 0.9730 | 0.0187 | 0.0124 | 0.3956 | 0.0500 |
| Method 2 | 44 | 0.489 | 0.9533 | 0.9765 | 0.0150 | 0.0096 | 0.3811 | 0.0467 |
| Method 3 | 57 | 0.517 | 0.9600 | 0.9843 | 0.0113 | 0.0088 | 0.3678 | 0.0278 |
| Case | Gear | Bearing | Shaft | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 16T | 48T | 24T | 40T | 1 | 2 | 3 | 4 | 5 | 6 | Input | Output | |
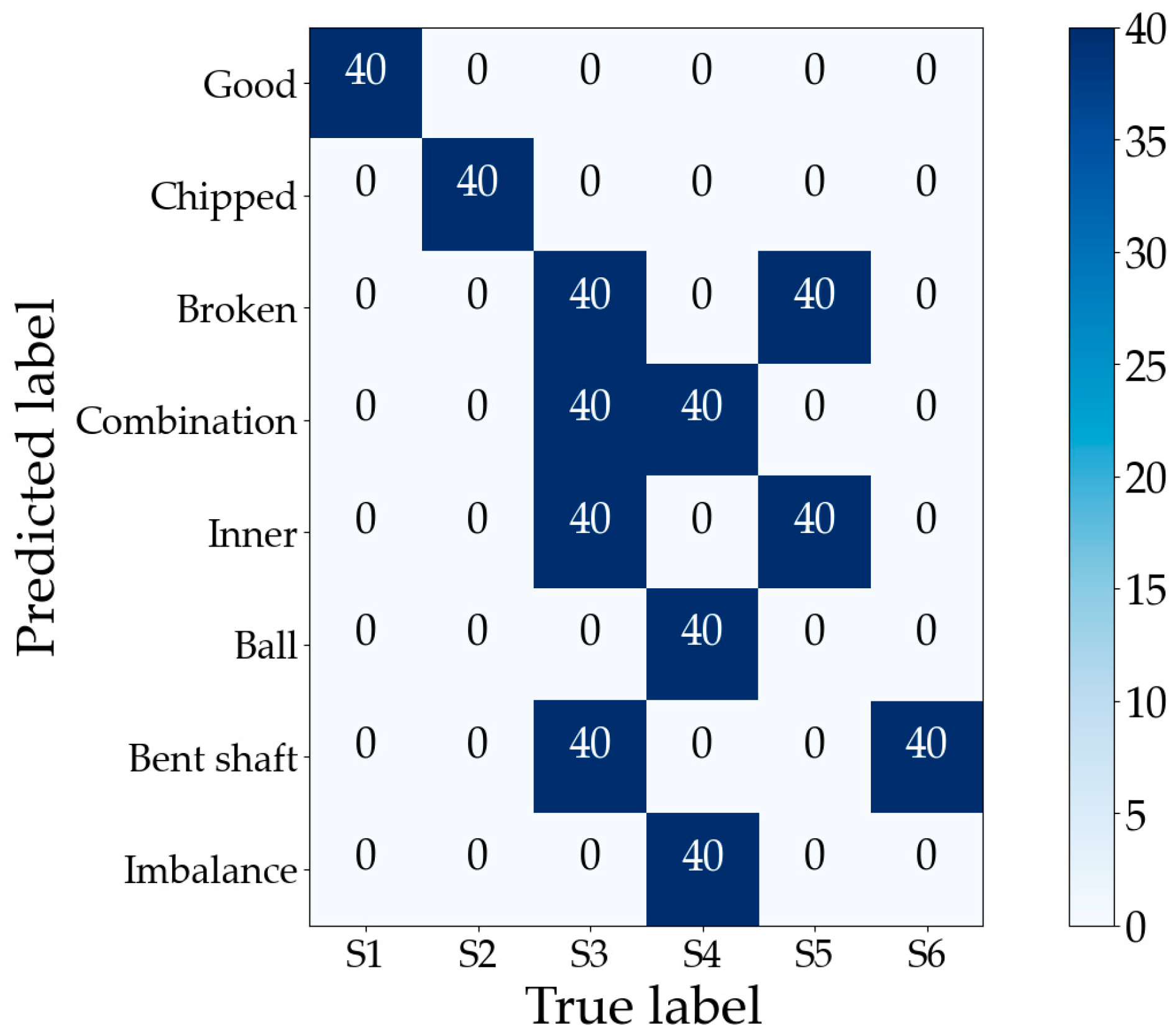
| S1 | Good | Good | Good | Good | Good | Good | Good | Good | Good | Good | Good | Good |
| S2 | Good | Good | Chipped | Good | Good | Good | Good | Good | Good | Good | Good | Good |
| S3 | Good | Good | Broken | Good | Good | Good | Good | Combination | Inner | Good | Bent shaft | Good |
| S4 | Good | Good | Good | Good | Good | Good | Good | Combination | Ball | Good | Imbalance | Good |
| S5 | Good | Good | Broken | Good | Good | Good | Good | Good | Inner | Good | Good | Good |
| S6 | Good | Good | Good | Good | Good | Good | Good | Good | Good | Good | Bent shaft | Good |
| Order | FS | IG | PCC | Weighting Scheme |
|---|---|---|---|---|
| 1 | 225 | 80 | 229 | 225 |
| 2 | 236 | 223 | 251 | 236 |
| 3 | 223 | 82 | 240 | 223 |
| 4 | 9 | 88 | 228 | 234 |
| 5 | 234 | 5 | 254 | 9 |
| 6 | 11 | 6 | 96 | 4 |
| 7 | 1 | 7 | 262 | 11 |
| 8 | 88 | 14 | 51 | 3 |
| 9 | 5 | 91 | 253 | 1 |
| 10 | 80 | 10 | 232 | 81 |
| … | … | … | … | … |
| 285 | 33 | 63 | 283 | 72 |
| 286 | 34 | 142 | 31 | 95 |
| 287 | 59 | 144 | 57 | 59 |
| 288 | 74 | 143 | 139 | 74 |
| Method | SA | AP | HL |
|---|---|---|---|
| The proposed method | 1.0000 | 1.0000 | 0.0000 |
| Method 1 | 0.9917 | 1.0000 | 0.0021 |
| Method 2 | 0.9875 | 1.0000 | 0.0031 |
| Method 3 | 0.9667 | 0.9861 | 0.0078 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, D.; Zhang, X.; Zhang, Z.; Jiang, H. A Hybrid Feature Selection and Multi-Label Driven Intelligent Fault Diagnosis Method for Gearbox. Sensors 2023, 23, 4792. https://doi.org/10.3390/s23104792
Liu D, Zhang X, Zhang Z, Jiang H. A Hybrid Feature Selection and Multi-Label Driven Intelligent Fault Diagnosis Method for Gearbox. Sensors. 2023; 23(10):4792. https://doi.org/10.3390/s23104792
Chicago/Turabian StyleLiu, Di, Xiangfeng Zhang, Zhiyu Zhang, and Hong Jiang. 2023. "A Hybrid Feature Selection and Multi-Label Driven Intelligent Fault Diagnosis Method for Gearbox" Sensors 23, no. 10: 4792. https://doi.org/10.3390/s23104792
APA StyleLiu, D., Zhang, X., Zhang, Z., & Jiang, H. (2023). A Hybrid Feature Selection and Multi-Label Driven Intelligent Fault Diagnosis Method for Gearbox. Sensors, 23(10), 4792. https://doi.org/10.3390/s23104792





