Deep-Reinforcement-Learning-Based Object Transportation Using Task Space Decomposition
Abstract
:1. Introduction
- We present a novel object transportation method using DRL and TSD.
- We propose a DRL-based object transportation training method within an SLE.
- A TSD approach is introduced that can be applied to arbitrary object transportation environments.
- We verify the proposed method by performing simulations in a variety of environments, such as a long corridor, a polygon, and a maze.
2. Related Work
3. Problem Description
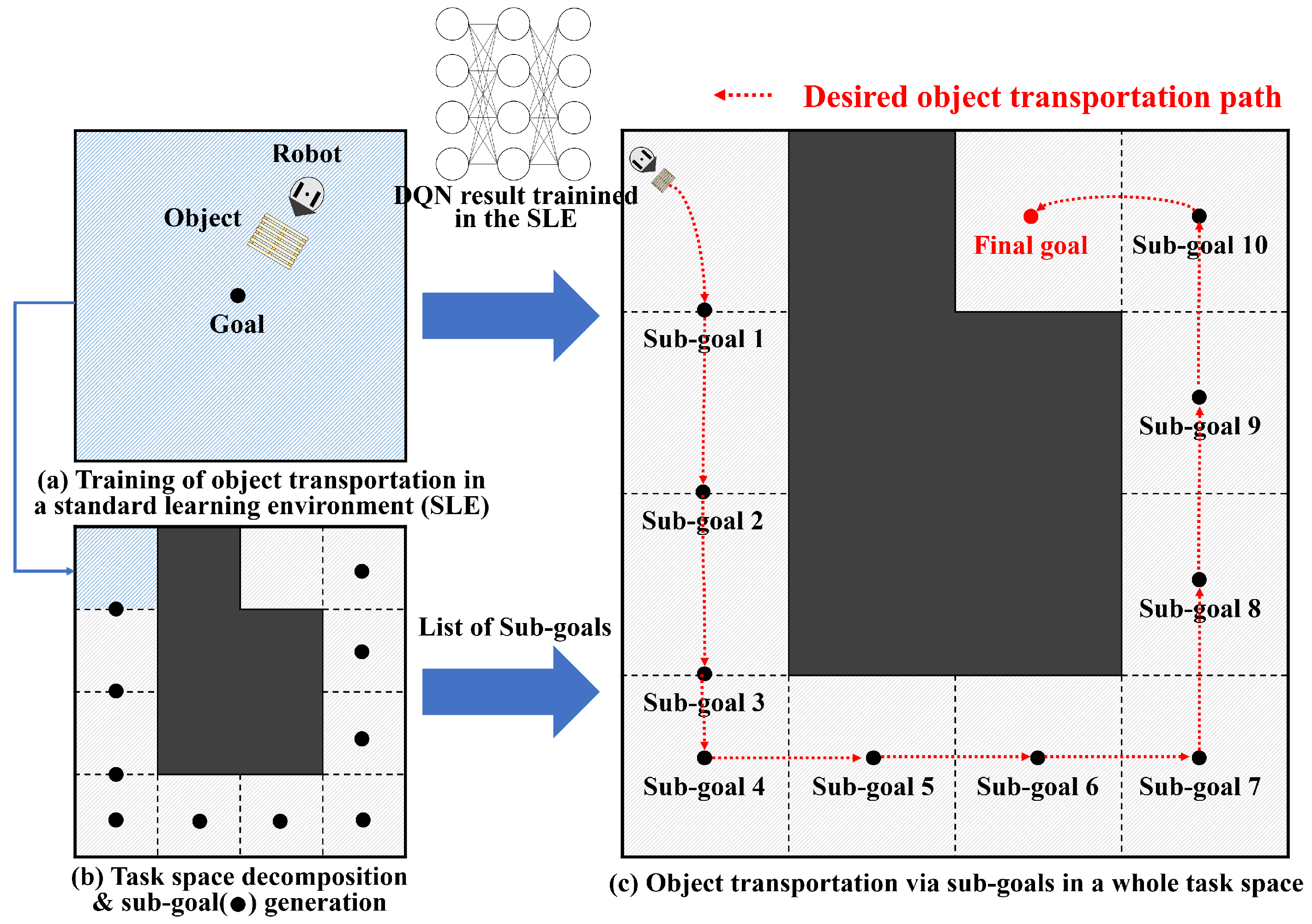
4. System Overview
5. Training in a Standard Learning Environment
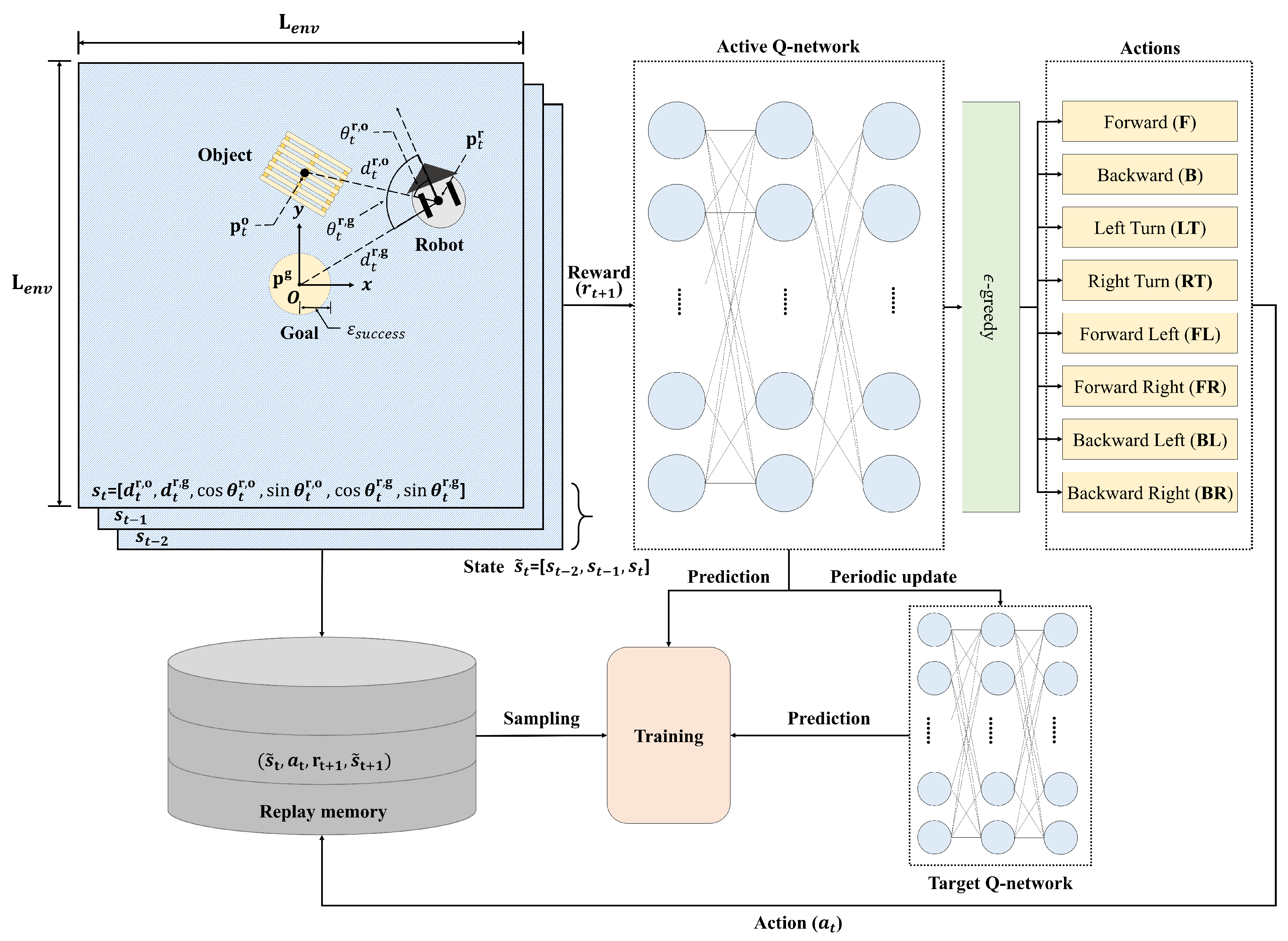
5.1. Markov Decision Process
5.2. Reinforcement Learning Framework for Object Transportation
5.3. Object Transportation Learning Using Deep Q-Network
| Algorithm 1: Training in a standard learning environment |
  |
6. Object Transportation Using a Task Space Decomposition Method
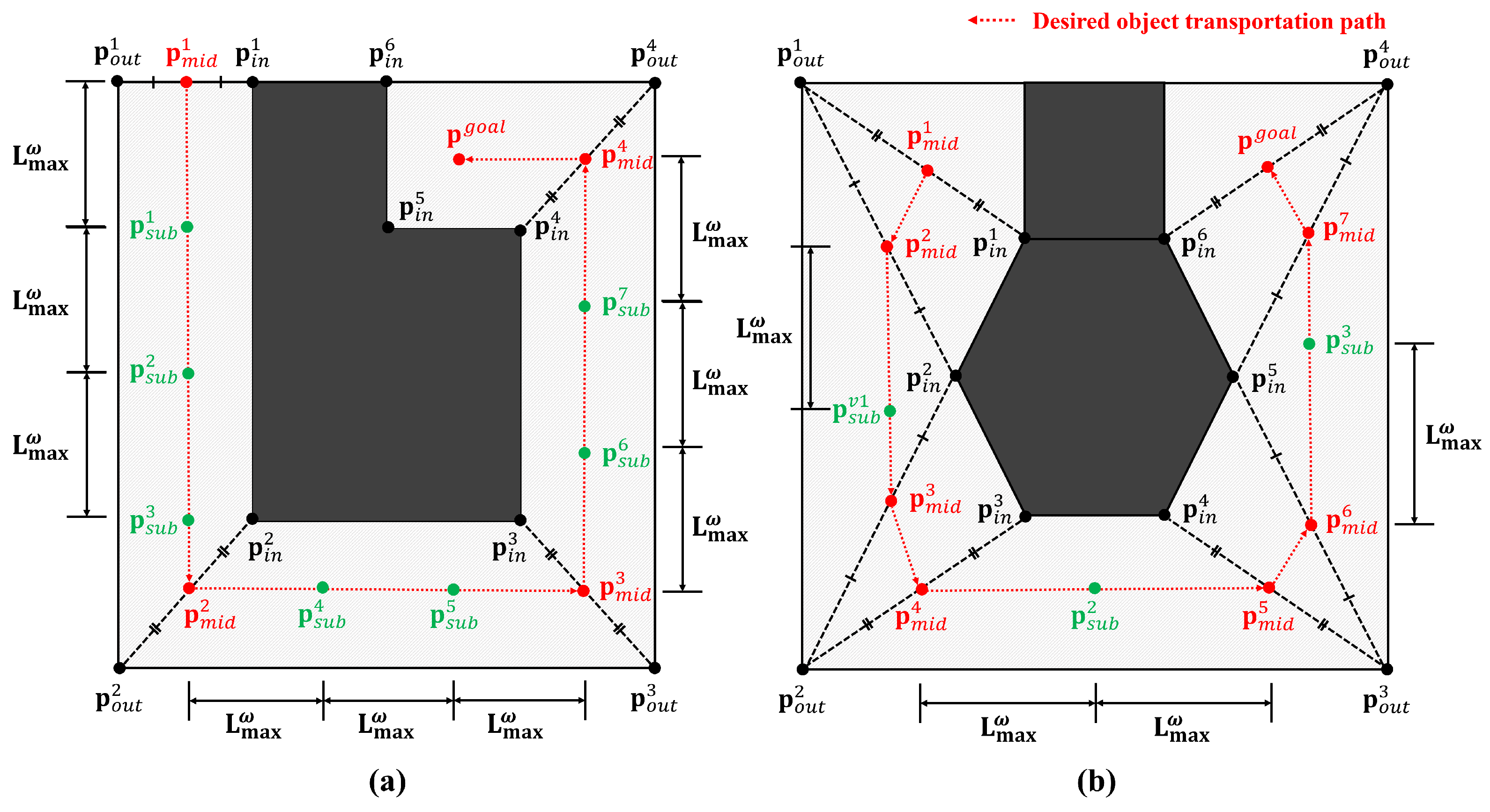
6.1. Midpoint Generation
| Algorithm 2: Midpoint generation |
 |
6.2. Task Space Decomposition
| Algorithm 3: Task space decomposition |
 |
6.3. Sub-Goal Generation and Object Transportation
| Algorithm 4: Sub-goal generation for object transportation |
 |
| Algorithm 5: Object transportation via sub-goals |
 |
7. Simulations
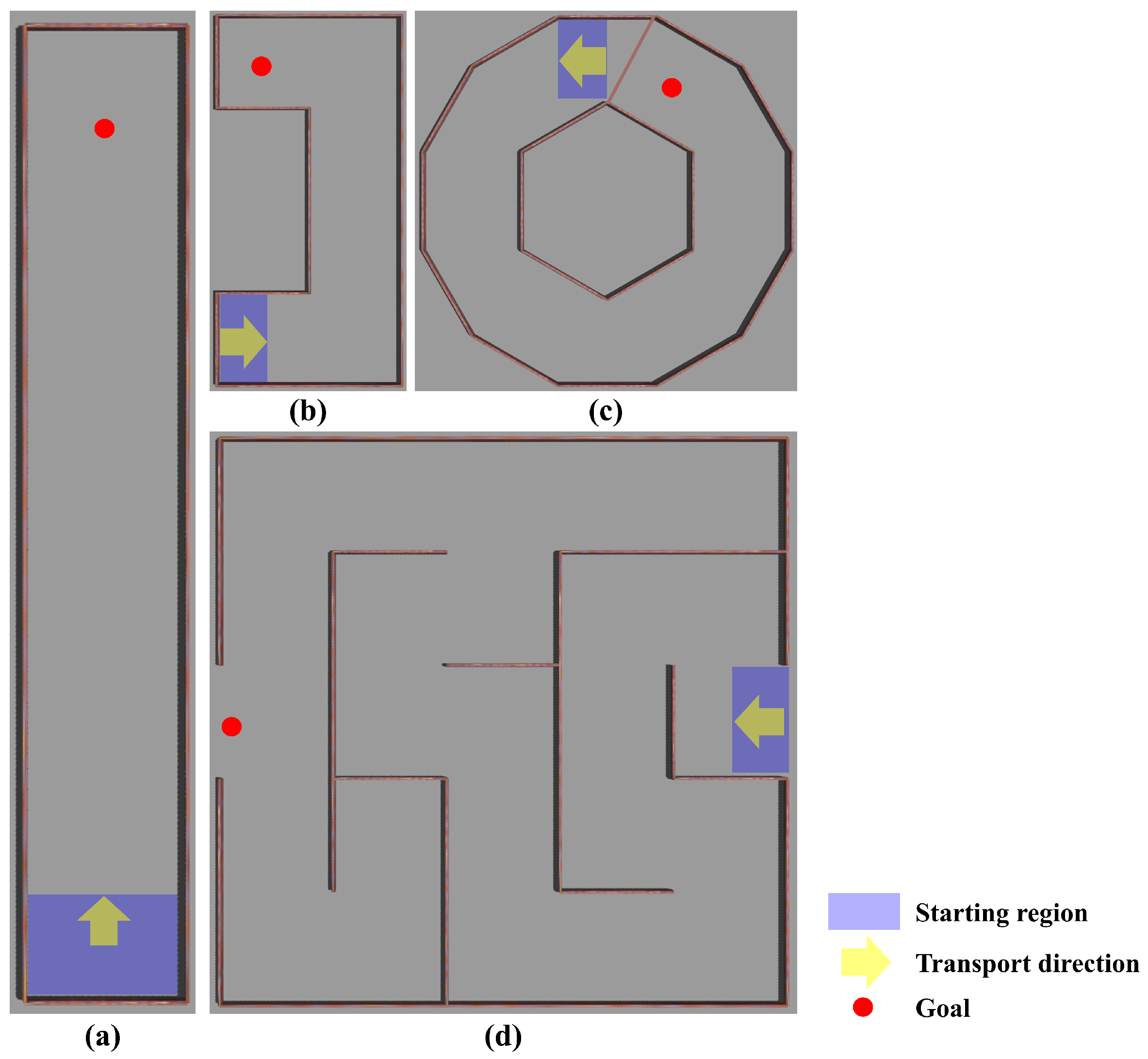
7.1. Simulation Environment
7.2. Training Results in Standard Learning Environments
7.3. Test Results in Various-Shaped Environments
8. Discussion
9. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| RL | Reinforcement learning |
| DRL | Deep reinforcement learning |
| SLE | Standard learning environment |
| TSD | Task space decomposition |
| DQN | Deep Q-network |
References
- Matsuo, I.; Shimizu, T.; Nakai, Y.; Kakimoto, M.; Sawasaki, Y.; Mori, Y.; Sugano, T.; Ikemoto, S.; Miyamoto, T. Q-bot: Heavy object carriage robot for in-house logistics based on universal vacuum gripper. Adv. Robot. 2020, 34, 173–188. [Google Scholar] [CrossRef]
- Koung, D.; Kermorgant, O.; Fantoni, I.; Belouaer, L. Cooperative multi-robot object transportation system based on hierarchical quadratic programming. IEEE Robot. Autom. Lett. 2021, 6, 6466–6472. [Google Scholar] [CrossRef]
- Hu, J.; Niu, H.; Carrasco, J.; Lennox, B.; Arvin, F. Voronoi-based multi-robot autonomous exploration in unknown environments via deep reinforcement learning. IEEE Trans. Veh. Technol. 2020, 69, 14413–14423. [Google Scholar] [CrossRef]
- Choi, D.; Kim, D. Intelligent multi-robot system for collaborative object transportation tasks in rough terrains. Electronics 2021, 10, 1499. [Google Scholar] [CrossRef]
- Eoh, G.; Choi, J.S.; Lee, B.H. Faulty robot rescue by multi-robot cooperation. Robotica 2013, 31, 1239. [Google Scholar] [CrossRef]
- Ordaz-Rivas, E.; Rodriguez-Liñan, A.; Torres-Treviño, L. Autonomous foraging with a pack of robots based on repulsion, attraction and influence. Auton. Robot. 2021, 45, 919–935. [Google Scholar] [CrossRef]
- Imtiaz, M.B.; Qiao, Y.; Lee, B. Prehensile and Non-Prehensile Robotic Pick-and-Place of Objects in Clutter Using Deep Reinforcement Learning. Sensors 2023, 23, 1513. [Google Scholar] [CrossRef]
- Appius, A.X.; Bauer, E.; Blöchlinger, M.; Kalra, A.; Oberson, R.; Raayatsanati, A.; Strauch, P.; Suresh, S.; von Salis, M.; Katzschmann, R.K. Raptor: Rapid aerial pickup and transport of objects by robots. In Proceedings of the 2022 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Kyoto, Japan, 23–27 October 2022; IEEE: Piscataway, NJ, USA, 2022; pp. 349–355. [Google Scholar]
- Gupta, A.; Eppner, C.; Levine, S.; Abbeel, P. Learning dexterous manipulation for a soft robotic hand from human demonstrations. In Proceedings of the 2016 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Daejeon, Republic of Korea, 9–14 October 2016; IEEE: Piscataway, NJ, USA, 2016; pp. 3786–3793. [Google Scholar]
- Ebel, H.; Eberhard, P. Non-prehensile cooperative object transportation with omnidirectional mobile robots: Organization, control, simulation, and experimentation. In Proceedings of the 2021 International Symposium on Multi-Robot and Multi-Agent Systems (MRS), Cambridge, UK, 4–5 November 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 1–10. [Google Scholar]
- Stüber, J.; Zito, C.; Stolkin, R. Let’s Push Things Forward: A Survey on Robot Pushing. Front. Robot. AI 2020, 7, 8. [Google Scholar] [CrossRef]
- De Berg, M.; Gerrits, D.H. Computing push plans for disk-shaped robots. Int. J. Comput. Geom. Appl. 2013, 23, 29–48. [Google Scholar] [CrossRef]
- Lamiraux, F.; Mirabel, J. Prehensile manipulation planning: Modeling, algorithms and implementation. IEEE Trans. Robot. 2021, 38, 2370–2388. [Google Scholar] [CrossRef]
- Pasricha, A.; Tung, Y.S.; Hayes, B.; Roncone, A. PokeRRT: Poking as a Skill and Failure Recovery Tactic for Planar Non-Prehensile Manipulation. IEEE Robot. Autom. Lett. 2022, 7, 4480–4487. [Google Scholar] [CrossRef]
- Lee, J.; Nam, C.; Park, J.; Kim, C. Tree search-based task and motion planning with prehensile and non-prehensile manipulation for obstacle rearrangement in clutter. In Proceedings of the 2021 IEEE International Conference on Robotics and Automation (ICRA), Xi’an, China, 30 May–5 June 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 8516–8522. [Google Scholar]
- Wu, J.; Sun, X.; Zeng, A.; Song, S.; Rusinkiewicz, S.; Funkhouser, T. Learning pneumatic non-prehensile manipulation with a mobile blower. IEEE Robot. Autom. Lett. 2022, 7, 8471–8478. [Google Scholar] [CrossRef]
- Eoh, G.; Park, T.H. Cooperative Object Transportation Using Curriculum-Based Deep Reinforcement Learning. Sensors 2021, 21, 4780. [Google Scholar] [CrossRef]
- Kalashnikov, D.; Irpan, A.; Pastor, P.; Ibarz, J.; Herzog, A.; Jang, E.; Quillen, D.; Holly, E.; Kalakrishnan, M.; Vanhoucke, V.; et al. Scalable deep reinforcement learning for vision-based robotic manipulation. In Proceedings of the Conference on Robot Learning, Zurich, Switzerland, 29–31 October 2018; pp. 651–673. [Google Scholar]
- Lowrey, K.; Kolev, S.; Dao, J.; Rajeswaran, A.; Todorov, E. Reinforcement learning for non-prehensile manipulation: Transfer from simulation to physical system. In Proceedings of the 2018 IEEE International Conference on Simulation, Modeling, and Programming for Autonomous Robots (SIMPAR), Brisbane, Australia, 16–19 May 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 35–42. [Google Scholar]
- Smith, D.R. The design of divide and conquer algorithms. Sci. Comput. Program. 1985, 5, 37–58. [Google Scholar] [CrossRef]
- Manko, S.V.; Diane, S.A.; Krivoshatskiy, A.E.; Margolin, I.D.; Slepynina, E.A. Adaptive control of a multi-robot system for transportation of large-sized objects based on reinforcement learning. In Proceedings of the 2018 IEEE Conference of Russian Young Researchers in Electrical and Electronic Engineering (EIConRus), Moscow and St. Petersburg, Russia, 29 January–1 February 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 923–927. [Google Scholar]
- Wang, Y.; De Silva, C.W. Multi-robot box-pushing: Single-agent q-learning vs. team q-learning. In Proceedings of the 2006 IEEE/RSJ International Conference on Intelligent Robots and Systems, Beijing, China, 9–13 October 2006; IEEE: Piscataway, NJ, USA, 2006; pp. 3694–3699. [Google Scholar]
- Rahimi, M.; Gibb, S.; Shen, Y.; La, H.M. A comparison of various approaches to reinforcement learning algorithms for multi-robot box pushing. In Proceedings of the International Conference on Engineering Research and Applications, Tokyo, Japan, 22–24 August 2018; Springer: Berlin/Heidelberg, Germany, 2018; pp. 16–30. [Google Scholar]
- Wang, Y.; de Silva, C.W. Sequential Q-Learning with Kalman Filtering for Multirobot Cooperative Transportation. IEEE/ASME Trans. Mechatron. 2009, 15, 261–268. [Google Scholar] [CrossRef]
- Mnih, V.; Kavukcuoglu, K.; Silver, D.; Rusu, A.A.; Veness, J.; Bellemare, M.G.; Graves, A.; Riedmiller, M.; Fidjeland, A.K.; Ostrovski, G.; et al. Human-level control through deep reinforcement learning. Nature 2015, 518, 529–533. [Google Scholar] [CrossRef]
- Silver, D.; Huang, A.; Maddison, C.J.; Guez, A.; Sifre, L.; Van Den Driessche, G.; Schrittwieser, J.; Antonoglou, I.; Panneershelvam, V.; Lanctot, M.; et al. Mastering the game of Go with deep neural networks and tree search. Nature 2016, 529, 484–489. [Google Scholar] [CrossRef]
- Zhang, L.; Sun, Y.; Barth, A.; Ma, O. Decentralized Control of Multi-Robot System in Cooperative Object Transportation Using Deep Reinforcement Learning. IEEE Access 2020, 8, 184109–184119. [Google Scholar] [CrossRef]
- Xiao, Y.; Hoffman, J.; Xia, T.; Amato, C. Learning Multi-Robot Decentralized Macro-Action-Based Policies via a Centralized Q-Net. In Proceedings of the 2020 IEEE International Conference on Robotics and Automation (ICRA), Paris, France, 31 May–31 August 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 10695–10701. [Google Scholar]
- Eoh, G.; Park, T.H. Automatic Curriculum Design for Object Transportation Based on Deep Reinforcement Learning. IEEE Access 2021, 9, 137281–137294. [Google Scholar] [CrossRef]
- Shibata, K.; Jimbo, T.; Matsubara, T. Deep reinforcement learning of event-triggered communication and consensus-based control for distributed cooperative transport. Robot. Auton. Syst. 2023, 159, 104307. [Google Scholar] [CrossRef]
- Yang, H.Y.; Wong, S.K. Agent-based cooperative animation for box-manipulation using reinforcement learning. Proc. ACM Comput. Graph. Interact. Tech. 2019, 2, 1–18. [Google Scholar] [CrossRef]
- Rybak, L.; Behera, L.; Averbukh, M.; Sapryka, A. Development of an algorithm for managing a multi-robot system for cargo transportation based on reinforcement learning in a virtual environment. In Proceedings of the IOP Conference Series: Materials Science and Engineering, Chennai, India, 16–17 September 2020; IOP Publishing: Bristol, UK, 2020; Volume 945, p. 012083. [Google Scholar]
- Kawano, H. Hierarchical sub-task decomposition for reinforcement learning of multi-robot delivery mission. In Proceedings of the 2013 IEEE International Conference on Robotics and Automation, Karlsruhe, Germany, 6–10 May 2013; IEEE: Piscataway, NJ, USA, 2013; pp. 828–835. [Google Scholar]
- Mesesan, G.; Roa, M.A.; Icer, E.; Althoff, M. Hierarchical path planner using workspace decomposition and parallel task-space rrts. In Proceedings of the 2018 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Madrid, Spain, 1–5 October 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 1–9. [Google Scholar]
- Zhang, X.; Yan, L.; Lam, T.L.; Vijayakumar, S. Task-space decomposed motion planning framework for multi-robot loco-manipulation. In Proceedings of the 2021 IEEE International Conference on Robotics and Automation (ICRA), Xi’an, China, 30 May–5 June 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 8158–8164. [Google Scholar]
- Fosong, E.; Rahman, A.; Carlucho, I.; Albrecht, S.V. Learning Complex Teamwork Tasks using a Sub-task Curriculum. arXiv 2023, arXiv:2302.04944. [Google Scholar]
- Watkins, C.J.; Dayan, P. Q-learning. Mach. Learn. 1992, 8, 279–292. [Google Scholar] [CrossRef]
- Yogeswaran, M.; Ponnambalam, S. Reinforcement learning: Exploration–exploitation dilemma in multi-agent foraging task. Opsearch 2012, 49, 223–236. [Google Scholar] [CrossRef]
- Lin, L.J. Self-improving reactive agents based on reinforcement learning, planning and teaching. Mach. Learn. 1992, 8, 293–321. [Google Scholar] [CrossRef]
- Takaya, K.; Asai, T.; Kroumov, V.; Smarandache, F. Simulation environment for mobile robots testing using ROS and Gazebo. In Proceedings of the 2016 20th International Conference on System Theory, Control and Computing (ICSTCC), Sinaia, Romania, 13–15 October 2016; IEEE: Piscataway, NJ, USA, 2016; pp. 96–101. [Google Scholar]
- Amsters, R.; Slaets, P. Turtlebot 3 as a robotics education platform. In Proceedings of the Robotics in Education: Current Research and Innovations 10, Vienna, Austria, 10–12 April 2019; Springer: Berlin/Heidelberg, Germany, 2020; pp. 170–181. [Google Scholar]



| Category | Description | Index | Value |
|---|---|---|---|
| Action (Equation (4)) | Rotational velocity | 1.0 rad/s | |
| Translational velocity | 0.3 m/s | ||
| Reward (Equation (5)) | Success reward | 1.0 | |
| Collision reward | −0.05 | ||
| Weight | 1.0 | ||
| 0.1 |
| Source | Description | Index | Value |
|---|---|---|---|
| Training (Algorithm 1) | Unit size of episode | 500 | |
| Length of one side of the SLE | 6/8/12 m | ||
| Number of attempts for calculating success rate | 30 | ||
| Step size for each episode | 1000 | ||
| Number of training iterations per episode | 200 | ||
| Update period of target Q-network | 32 | ||
| Threshold of the success rate | 0.98 | ||
| Q-Network (Figure 2) | Depth of Q-network | - | 4 |
| Width of each layer | - | 256 | |
| Activation function | - | ReLU | |
| Learning rate | 0.001 | ||
| Discount factor | 0.99 | ||
| Batch size | - | 512 | |
| Replay memory size | # of | ||
| Initial exploration probability in -greedy | - | 1.0 | |
| Final exploration probability in -greedy | - | 0.1 |
| Environment Size () | The Number of Success/Trial | Success Rate () | The Number of Training Episodes () |
|---|---|---|---|
| m | 100/100 | 100% | 2000 |
| m | 99/100 | 99% | 4000 |
| m | 100/100 | 100% | 8000 |
| Environment | The Number of Success/Trial (Success Rate) | Avg. Travelling Distance of an Object | Avg. Travelling Distance of a Robot |
|---|---|---|---|
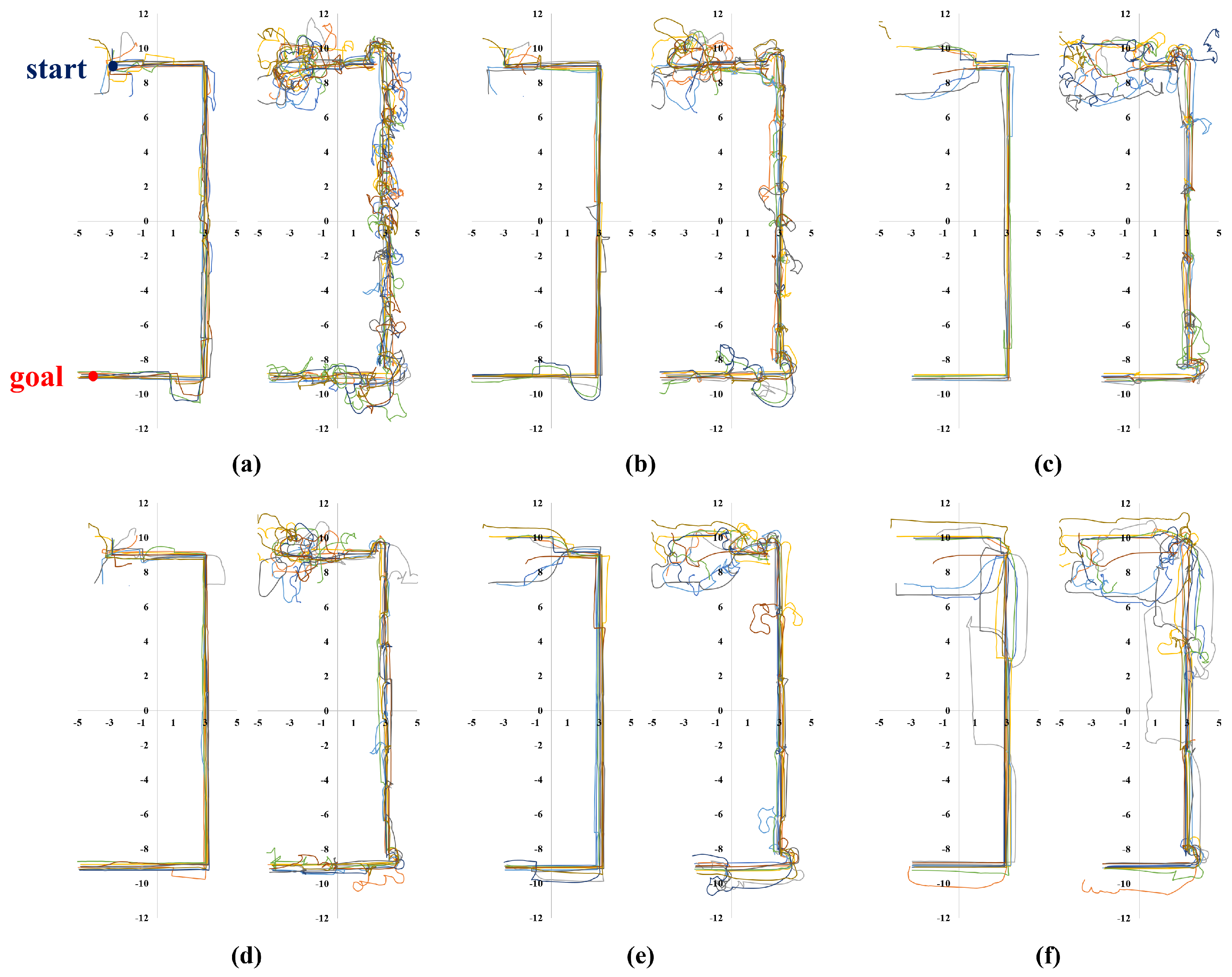
| Long corridor (Figure 5a) | 133/200 (0.67) | 23.59 m | 23.21 m |
| Simple polygon (Figure 5b) | 0/200 (0.0) | - | - |
| Complex polygon (Figure 5c) | 0/200 (0.0) | - | - |
| Maze (Figure 5d) | 0/200 (0.0) | - | - |
| Environment | Size of Standard Learning Environment () | Maximum Distance Traveled between Sub-Goals () | The Number of Success/Trial (Success Rate) | Avg. Travelling Distance of an Object | Avg. Travelling Distance of a Robot |
|---|---|---|---|---|---|
| Long corridor (Figure 5a) | 6 m × 6 m | 2 m | 127/200 (0.64) | 37.47 m | 36.42 m |
| 8 m × 8 m | 2 m | 143/200 (0.71) | 29.55 m | 28.86 m | |
| 4 m | 193/200 (0.96) | 26.94 m | 26.02 m | ||
| 12 m × 12 m | 2 m | 131/200 (0.66) | 27.82 m | 27.82 m | |
| 4 m | 183/200 (0.92) | 20.20 m | 19.75 m | ||
| 6 m | 200/200 (1.00) | 19.93 m | 19.33 m | ||
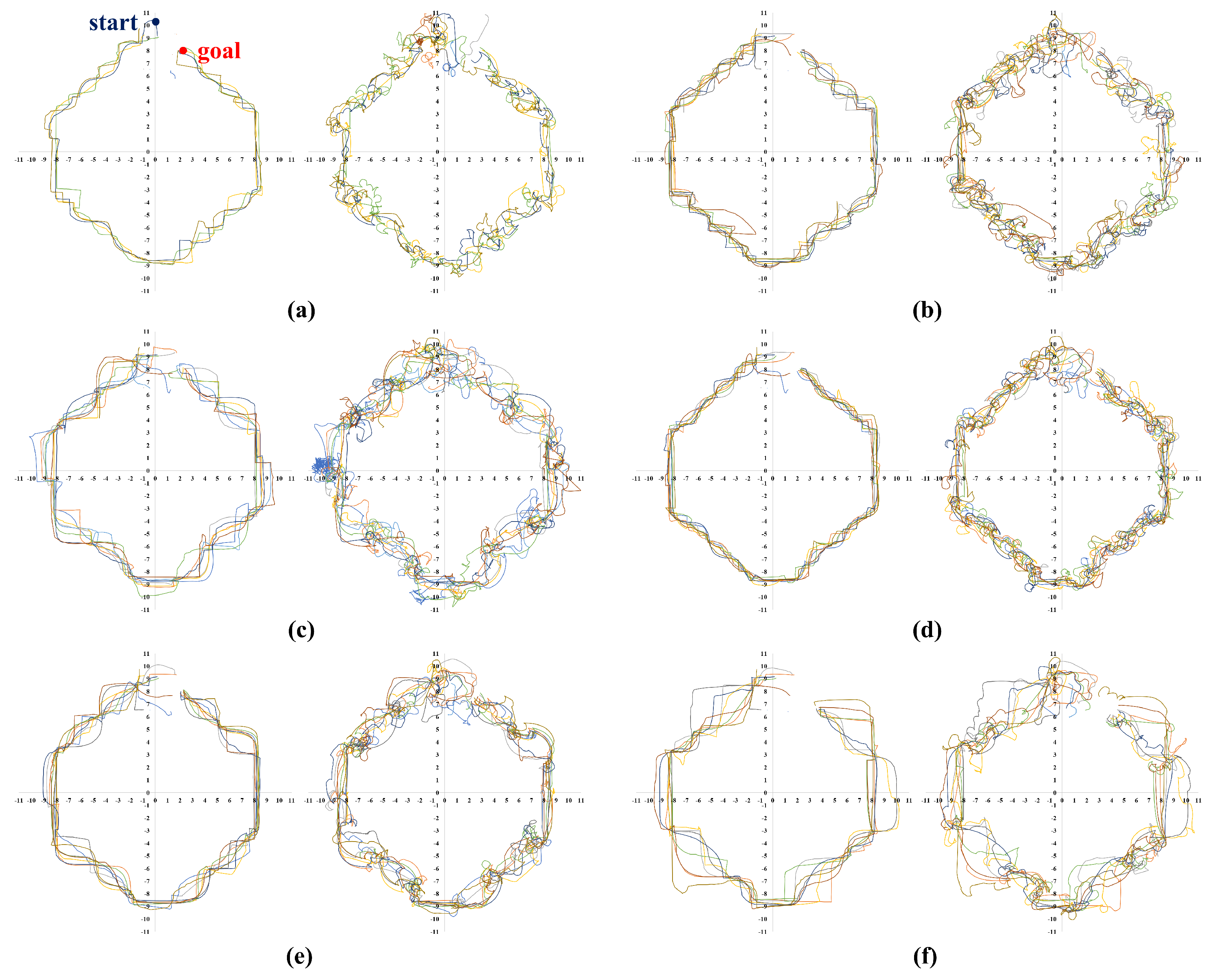
| Simple polygon (Figure 5b) | 6 m × 6 m | 2 m | 196/200 (0.98) | 27.45 m | 27.00 m |
| 8 m × 8 m | 2 m | 196/200 (0.98) | 22.61 m | 22.25 m | |
| 4 m | 146/200 (0.73) | 22.25 m | 22.39 m | ||
| 12 m × 12 m | 2 m | 190/200 (0.95) | 21.32 m | 21.11 m | |
| 4 m | 195/200 (0.97) | 17.15 m | 16.75 m | ||
| 6 m | 191/200 (0.95) | 18.08 m | 17.88 m | ||
| Complex polygon (Figure 5c) | 6 m×6 m | 2 m | 150/200 (0.75) | 59.97 m | 61.67 m |
| 8 m × 8 m | 2 m | 166/200 (0.83) | 59.53 m | 61.10 m | |
| 4 m | 166/200 (0.83) | 56.72 m | 57.46 m | ||
| 12 m × 12 m | 2 m | 179/200 (0.90) | 54.33 m | 55.47 m | |
| 4 m | 177/200 (0.89) | 47.75 m | 48.78 m | ||
| 6 m | 157/200 (0.79) | 56.71 m | 57.14 m | ||
| Maze (Figure 5d) | 6 m × 6 m | 2 m | 192/200 (0.96) | 151.06 m | 150.05 m |
| 8 m × 8 m | 2 m | 198/200 (0.99) | 125.18 m | 124.08 m | |
| 4 m | 135/200 (0.68) | 134.40 m | 133.41 m | ||
| 12 m × 12 m | 2 m | 200/200 (1.00) | 116.70 m | 115.58 m | |
| 4 m | 200/200 (1.00) | 102.38 m | 101.46 m | ||
| 6 m | 196/200 (0.98) | 98.57 m | 97.91 m |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Eoh, G. Deep-Reinforcement-Learning-Based Object Transportation Using Task Space Decomposition. Sensors 2023, 23, 4807. https://doi.org/10.3390/s23104807
Eoh G. Deep-Reinforcement-Learning-Based Object Transportation Using Task Space Decomposition. Sensors. 2023; 23(10):4807. https://doi.org/10.3390/s23104807
Chicago/Turabian StyleEoh, Gyuho. 2023. "Deep-Reinforcement-Learning-Based Object Transportation Using Task Space Decomposition" Sensors 23, no. 10: 4807. https://doi.org/10.3390/s23104807
APA StyleEoh, G. (2023). Deep-Reinforcement-Learning-Based Object Transportation Using Task Space Decomposition. Sensors, 23(10), 4807. https://doi.org/10.3390/s23104807





