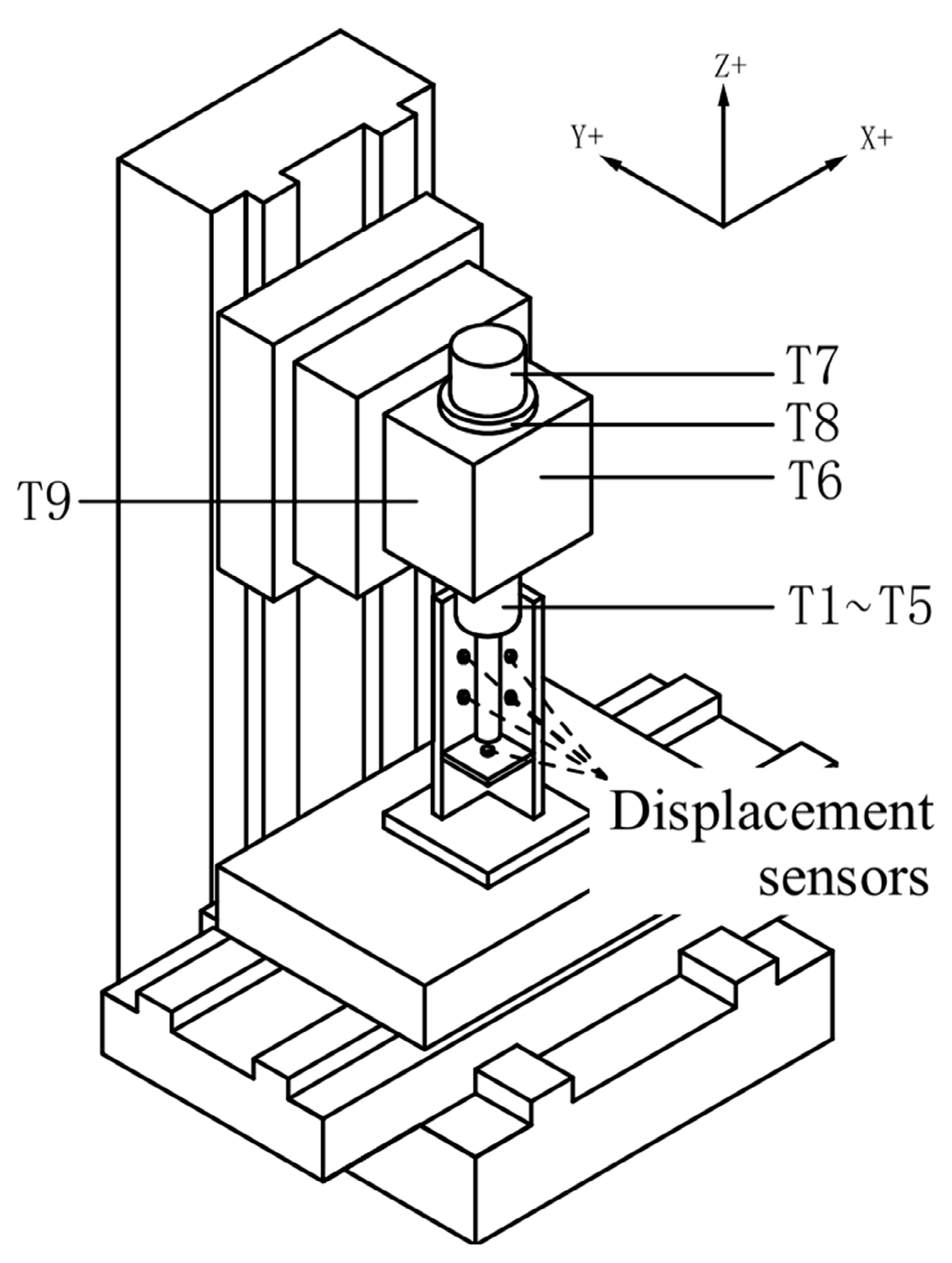
1. Introduction
Thermal error is one of the main factors affecting the accuracy of CNC machine tools [
1], which are gradually becoming dominant with the improvement of machine tool accuracy. In general, there are two main approaches to solving the problem of thermal errors. The first approach is to establish a simulation model based on some physical properties that can be used to simulate the thermal deformation of the structure [
2]. However, this approach suffers by determining consistent boundary conditions and building an exact physical model in practice. Alternatively, the second approach is to establish a mathematical model to predict thermal errors. This approach has been widely used in practice and has been the subject of a large amount of research [
1,
3]. In general, a mathematical thermal error modeling method includes two key steps. The first step is to select temperature variables for modeling and is called temperature-sensitive point (TSP) selection. The temperature variables refer to the values measured by temperature sensors at different positions of the machine tool. TSP selection can simplify the model structure or mitigate the collinearity between temperature variables. The idea of TSP selection is to first classify temperature variables into different clusters and then select the most important one from each cluster [
4]. This can effectively prevent the temperature variables from being strongly correlated, and the number of modeling temperature variables (MTVs) is reduced at the same time.
In the second step of a mathematical thermal error modeling method, establishing a thermal error prediction model is the key to achieving satisfactory prediction effects. Various algorithms have been applied to thermal error modeling, such as backpropagation neural network (NN) [
5], support vector machine [
6], multiple linear regression [
7,
8], state-space [
9], and Gaussian process regression (GPR) [
10]. Notably, the NN [
5] only consists of a single hidden layer whereas the deep learning method is more complicated with multiple hidden layers. In addition, ridge regression [
11] and principal component regression [
12] algorithms have been used to solve the collinearity between temperature variables. Recently, deep learning algorithms have been adopted for thermal error modeling to further improve prediction accuracy. For example, Fujishima et al. [
13] proposed a novel deep-learning thermal error compensation method in which the compensation weight can be changed adaptively according to the reliability of thermal displacement prediction. The deep learning convolutional NN algorithm [
14], bidirectional long short-term memory (LSTM) deep learning algorithm [
15], and stacked LSTM algorithm [
16] have all been used for thermal error modeling. Furthermore, several researchers have built hybrid thermal error models by combining different algorithms to take advantage of their respective features [
17,
18,
19,
20,
21]. More recently, digital twin technology was adopted by [
22] to solve the problem of thermal errors. The authors utilized the digital twin concept to propose a self-learning-empowered error control framework for the real-time thermal error prediction and control.
The above studies provide various solutions to thermal errors. However, thermal error models, especially for those based on the deep learning method, have several limitations, including a very complex structure, requiring a large amount of training data, and a lack of interpretability. As a result, these methods are difficult to deploy in practical engineering for thermal error compensation of machine tools. In other words, in addition to prediction accuracy, robustness [
23], and adaptability [
24], practicality should be considered as another important indicator to effectively solve the engineering problem of thermal error modeling and compensation. From this perspective, it is suggested that traditional regression algorithms are more suitable. While traditional regression algorithms have a simple model structure and good interpretability, the prediction effects of the regression algorithms in the existing literature are not as good as those of deep learning algorithms. Therefore, there is a research gap: the existing literature lacks a thermal error modeling method that has a simple structure, good interpretability, and comparable performance of prediction effects to deep learning algorithms.
To fill the research gap, a new method based on a regularized regression algorithm is proposed to enhance the prediction ability of the regression algorithm. In particular, the least absolute regression algorithm is first used for thermal error modeling. To improve the robustness of the established model, both L1 and L2 regularizations are used by shrinking the regression coefficients. Accordingly, the stability of the regression model is improved. In addition, the proposed modeling method can automatically select TSPs owing to the presence of L1 regularization. Further, multiple batches of experimental data are used for modeling to ensure the sufficiency of thermal error information, which is a key prerequisite for effective modeling. Through analysis, the optimal combination of the number of MTVs and the coefficients of different regularization terms can be obtained, which is further used for thermal error modeling by the regularized regression algorithm. In summary, there are two main contributions of the proposed thermal error modeling method: (1) the least absolute regression algorithm, integrated with L1 and L2 regularization, is able to automatically select TSPs and reduce the collinearity simultaneously, thereby enhancing the prediction ability; (2) the prediction effects of the proposed thermal error modeling method are better with the simple model structure, compared with the state-of-the-art algorithms, including complex deep-learning-based algorithms.
Section 2 introduces the thermal error measurement experiments. Afterward, the existing thermal error modeling algorithms are briefly described in
Section 3, including TSP selection and modeling algorithms. The proposed thermal error modeling method based on a regularized regression algorithm is introduced in
Section 4. The effects of the number of MTVs and the coefficients of regularization terms are systematically analyzed for the proposed modeling method in
Section 5. In
Section 6, the proposed modeling method is compared with the state-of-the-art algorithms and verified by actual compensation experiments. Finally, conclusions are drawn in
Section 7.
4. The Proposed Thermal Error Modeling Method
As has been noted, the existing thermal error modeling algorithms lack simple structure, good interpretability, and comparable performance of prediction effects to deep learning algorithms. To fill this gap, we propose a new method based on the regularized regression model in this section. Specifically, the regularized regression model is first formulated in
Section 4.1. Then, the solution to the regularized regression model is provided in
Section 4.2.
4.1. Thermal Error Modeling Based on Regularized Regression
The multiple linear regression thermal error
model concerning temperature variables
can be expressed as
where
represent the coefficients of the model.
is the random error obeying N(0,
), where
is the variance of the normal distribution.
According to the least-squares algorithm,
can be calculated by minimizing the objective function as shown below.
where
and
indicate an n-dimensional unit column vector.
Then the regression coefficients can be calculated in the closed-form equation as
As pointed out in the existing literature [
11], the least-squares algorithm is sensitive to outliers and collinearity between independent variables. The collinearity would lead to
and then the values of the main diagonal elements of
are large. As a result, the variance of the estimated regression coefficients
is large, as shown below.
To solve this problem, the ridge regression algorithm replaces the matrix
in Equation (4) with
. Then the coefficients can be estimated as
where
represents an n-dimensional identity matrix.
is called the ridge parameter.
From the optimization point of view, the object function of the ridge regression algorithm adds the L2 regularization term as a penalty term based on the least-squares algorithm, as shown below.
Further, the least absolute shrinkage and selection operator (LASSO) algorithm takes the L1 regularization term as the penalty term to select important variables involved in the model. Then the objective function is
In addition, the elastic-net regression (ENR) algorithm combines the L1 and L2 regularization to construct the penalty terms. The object function of the ENR algorithm is
where
and
are the coefficients of the L1 and L2 regularization terms, respectively.
It can be found from Equation (13) that the ENR algorithm includes the least-squares regression, ridge regression, and LASSO. When , Equation (13) is the objective function of the least-squares algorithm. When and , Equation (13) is the objective function of the ridge regression algorithm. When and , Equation (13) is the objective function of the LASSO algorithm.
Compared with the least-squares regression, the least-absolute regression has better robustness. The object function of the least-absolute algorithm is shown below.
Similarly, the L1 and L2 regularization can also be applied to Equation (14), then the objective function of Equation (14) can be updated as follows.
where
and
are the coefficients of the L1 and L2 regularization terms, respectively.
The regression coefficients can be estimated by solving Equation (15), which is called the least absolute elastic-net regression (LAENR) algorithm in this study. As a result, the LAENR algorithm can not only select important variables like LASSO regression but also inherits the stability of ridge regression. Furthermore, with the use of the least-absolute algorithm, the LAENR algorithm has better robustness.
To intuitively show the differences between the ridge regression, LASSO, ENR, and LAENR algorithms, the case of only two independent variables is taken as an example to illustrate the optimal solutions to Equations (11)–(13) and (15) (
Figure 5). In
Figure 5, the blue parts represent the original objective function of Equation (7). The green parts represent the regularization terms, which indicates that the regularization terms limit the value of the model coefficients. It can be observed that the optimal solutions of LASSO, ENR, and LAENR algorithms can easily fall on a coordinate axis. In this case, the coefficient of the independent variable on the other coordinate axis is zero. As a result, the variable selection is realized. The reason for this situation is the existence of L1 regularization, which restricts the feasible region of the optimal solution to a region with cusps. As a comparison, the ridge regression algorithm cannot select variables since the coefficients are close to zero but not equal to zero. The shape of the objective function changes from a paraboloid (LASSO and ENR) to a conical surface (LAENR), which demonstrates the difference between the least-squares and the least-absolute algorithms.
4.2. Solution to the Least-Absolute Regularized Regression
Solving Equation (15) is an unconstrained nonlinear multivariable minima problem. Since there is an operation to solve the absolute value of the objective function, there is no continuous first derivative. As a result, the analytical solution to this problem does not exist. Therefore, the quasi-Newton method [
28] is adopted to obtain the optimal solution quickly and reliably. In the Newton method, the minimum
of objective function
can be calculated by the iterative equation as shown below.
where
, which is called the Hessian matrix, and
is the index of the
th iteration.
, which represents the value of the gradient vector of
at point
.
The difference between the quasi-Newton and Newton methods is to solve the inverse of the Hessian matrix. In the quasi-Newton method, the inverse of the Hessian matrix is represented by an approximate positive definite symmetric matrix, thus avoiding the calculation of second-order partial derivatives. There are other methods to construct the inverse of the Hessian matrix, such as the Davidon–Fletcher–Powell method [
29]. In this study, the inverse of the Hessian matrix is constructed using the Broyden–Fletcher–Goldfarb–Shanno method, which is generally considered to be the most efficient. The iterative equation of the Hessian matrix is shown below.
where
,
.
Based on the above iterative calculation, the optimal solution to the problem of Equation (15) can be obtained. To minimize the influence of the local minimum problem and obtain the global optimal solution, a multi-start algorithm is adopted. The multi-start algorithm first generates many start points within the feasible region. Then the quasi-Newton method is used to solve Equation (15) at each start point. Finally, the global optimal solution is obtained from all the solutions corresponding to the start points.
Note that the temperature and thermal error data are normalized before modeling. The normalized method is shown below.
where
and
represent the mean of the
and
, respectively. The
and
are the standard deviations of
and
, respectively.
Then the thermal error prediction model after normalization can be established based on the above modeling method, as shown below.
where
are the coefficients of the model.
The model coefficients of the original data
can be obtained by the follow formula:
7. Conclusions
To address the growing complexity and lack of interpretability of thermal error modeling, this study proposes an effective and practical method based on regularized regression. The optimal number of MTVs and regularization coefficients are analyzed based on experimental data. The prediction models are established by experimental data under different experimental conditions. The proposed modeling method is compared with those of the ENR, ARX, LSTM, and GPR algorithms. The calculation results show that the proposed modeling method achieves the best prediction accuracy and robustness in all X, Y, and Z directions. Finally, the effectiveness of the proposed modeling method in real-world applications is proved by compensation experiments, which can control the thermal errors with .
For future research, the modeling method with other normalizations of temperature differences between experiments will be studied first. Second, in our verification experiments, the error drifted out of the tolerance bandwidth after a certain amount of time. To address this issue, the adaptability of the thermal error prediction model by online updating will be considered as an important future work to improve the ability to maintain prediction accuracy. Last, a universal modeling method applicable to most types of machine tools will be studied.