Channel Modeling and Characteristics Analysis under Different 3D Dynamic Trajectories for UAV-Assisted Emergency Communications
Abstract
:1. Introduction
- For this study, our proposed model took two approaches to realizing multi-trajectories. A Markov chain was introduced in the aerial part, by changing the azimuth and elevation angle of the UAV flight, to obtain a random trajectory. It could simulate the dive, climb, and level flight of the UAV in arbitrary 3D space. As most vehicles on the ground-Rx end do not make sharp turns, we used a smooth-turn (ST) mobility model to simulate the movement of the Rx end in two dimensions. Moreover, the trajectories of moving clusters were also considered, to mimic the movement of vehicles around the Rx.
- Based on the proposed channel model, typical AG channel characteristics of UAV communications during different trajectories of the Tx and the Rx were studied, including PDP, temporal ACF, spatial CCF, stationary interval, and RMS DS. By analyzing and studying the effect of multi-mobility multi-trajectories on statistical properties, the non-stationary characteristics of the UAV AG channel were analyzed and compared.
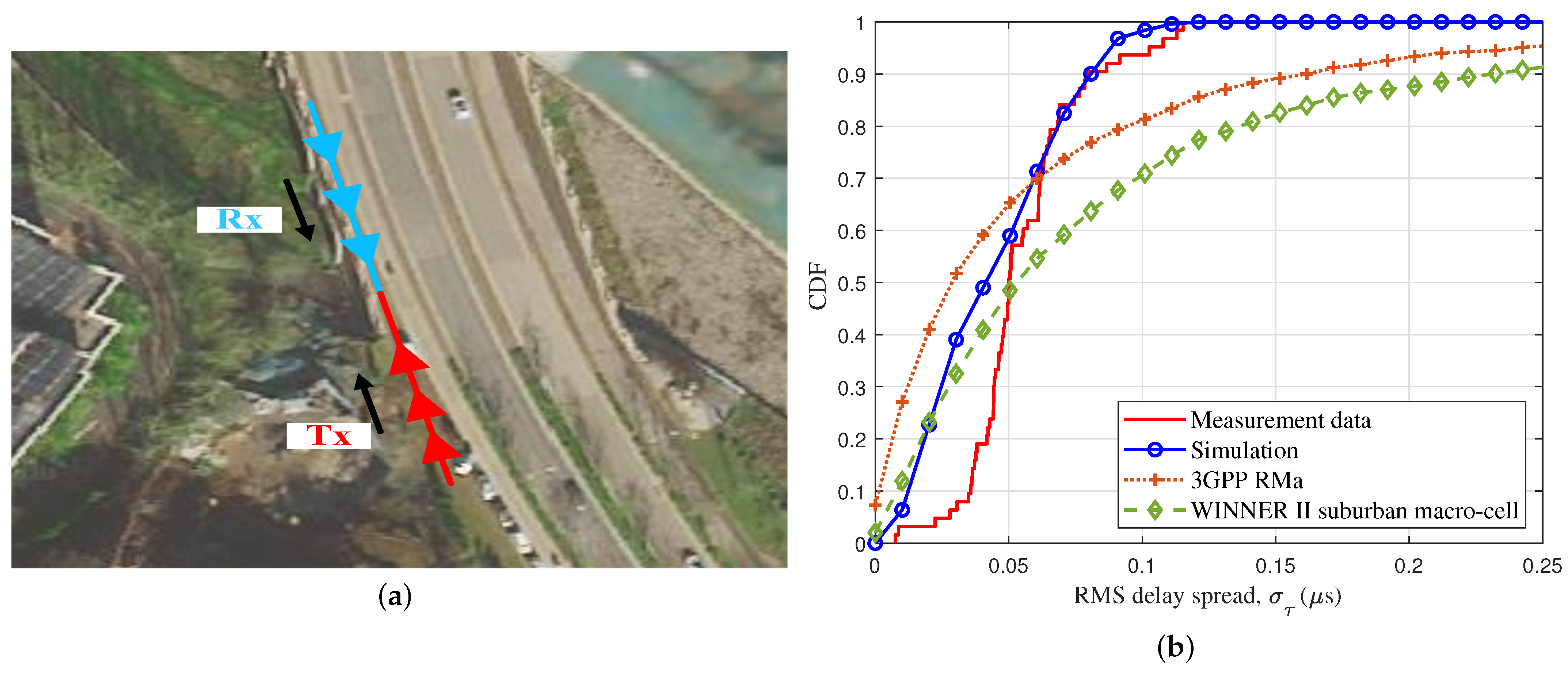
- Channel measurement of relevant scenarios was carried out. Some statistical properties of the proposed channel model were verified by actual measurement data, which demonstrated the accuracy of the proposed model.
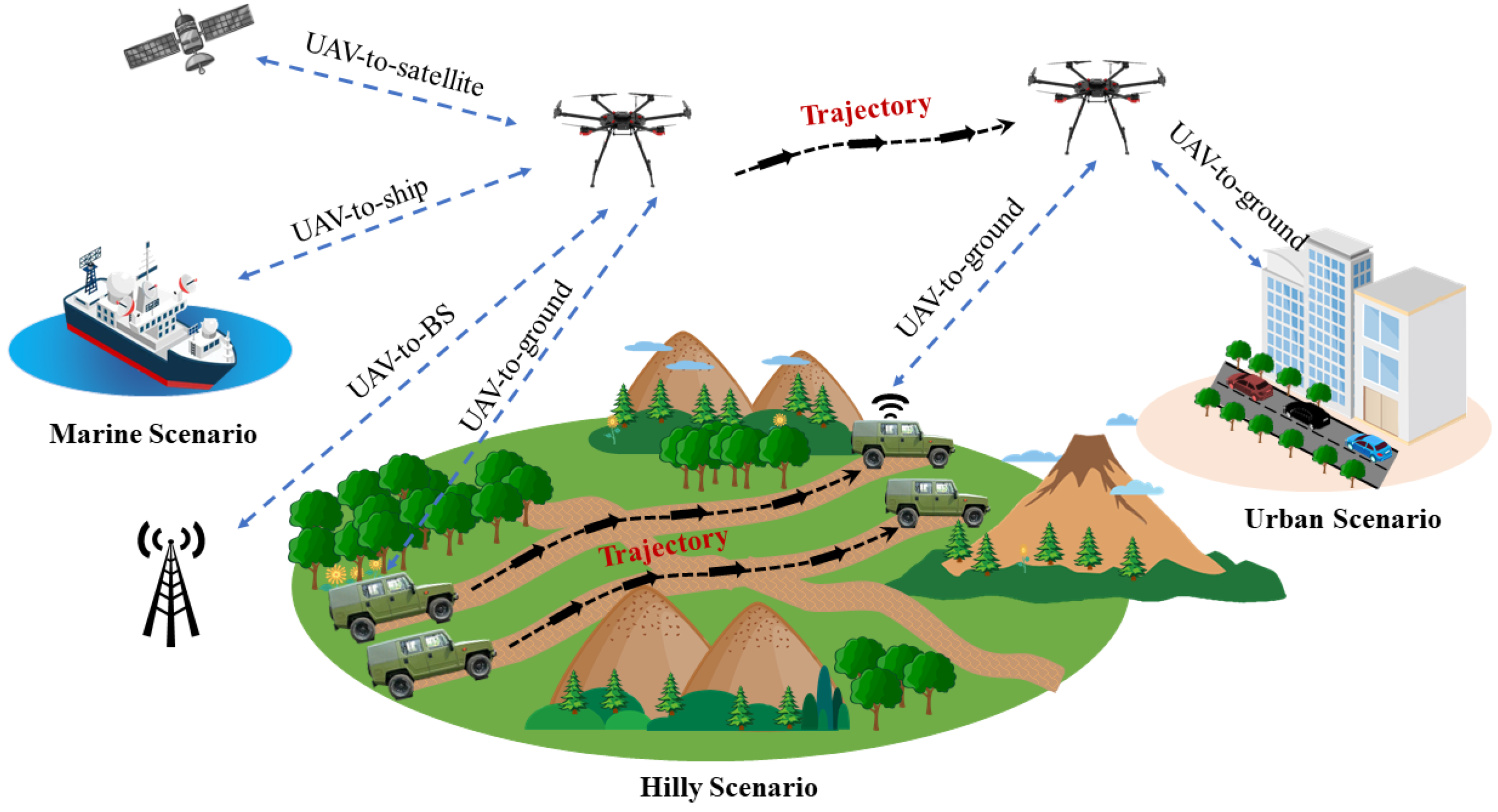
2. UAV-Assisted Communication Network with Multi-Mobility Multi-Trajectory Cases
3. UAV AG Communication Channel Modeling and Characterization
3.1. A UAV AG Multi-Mobility Multi-Trajectories Channel Model
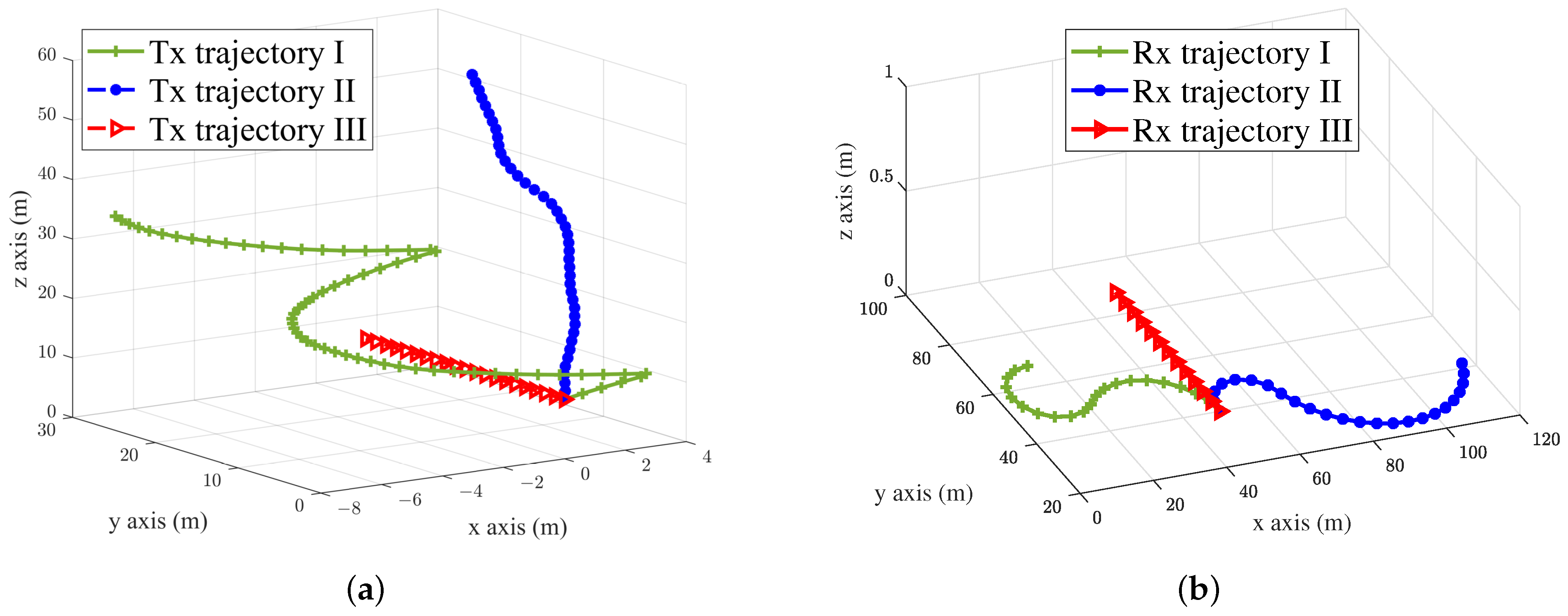
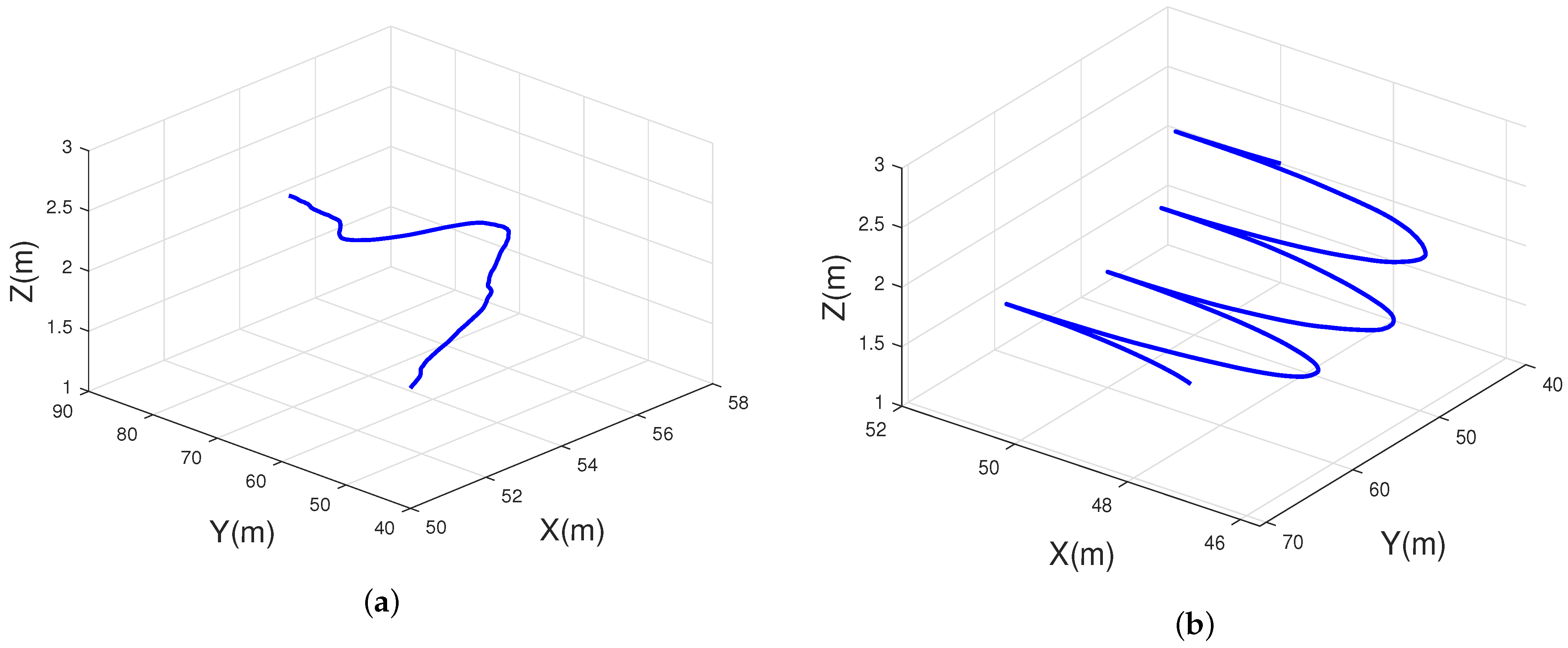
3.1.1. Generation of Tx Trajectories
3.1.2. Generation of Rx Trajectories
3.1.3. Generation of Cluster Trajectories
3.2. Typical Statistical Properties of Channel Model
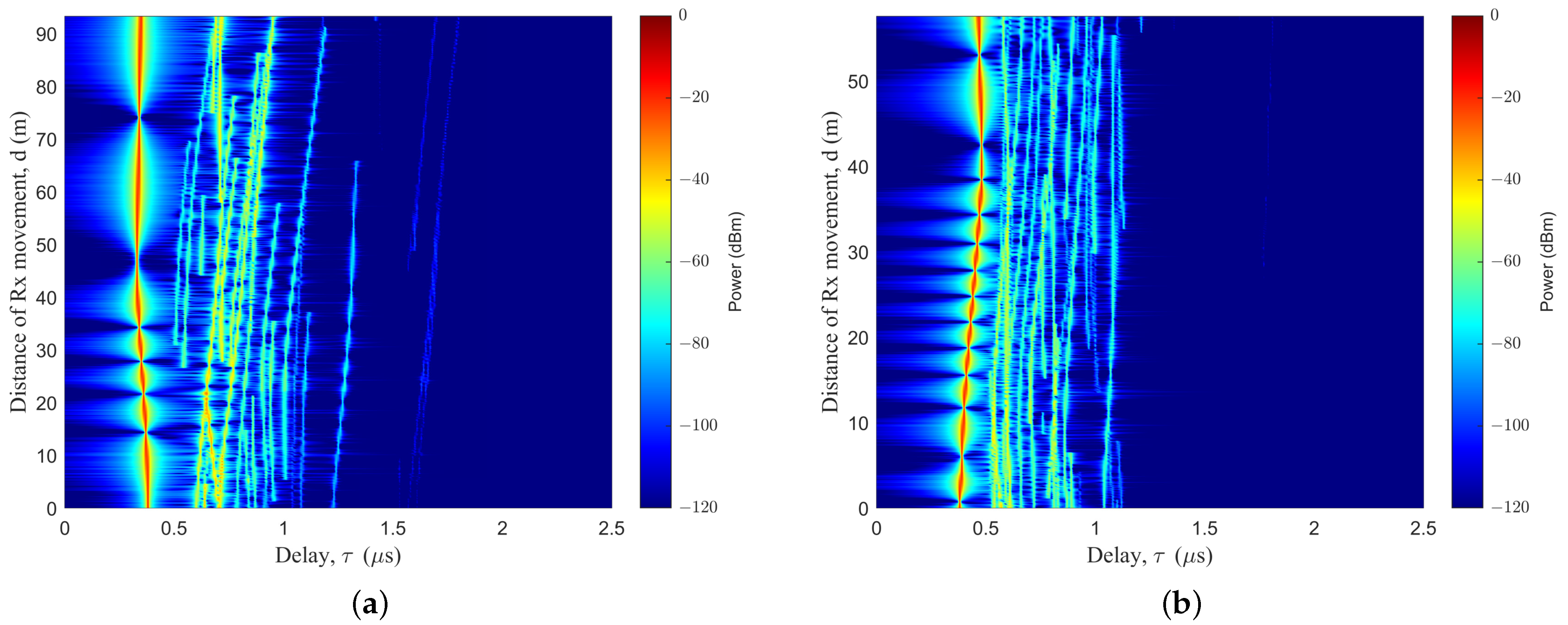
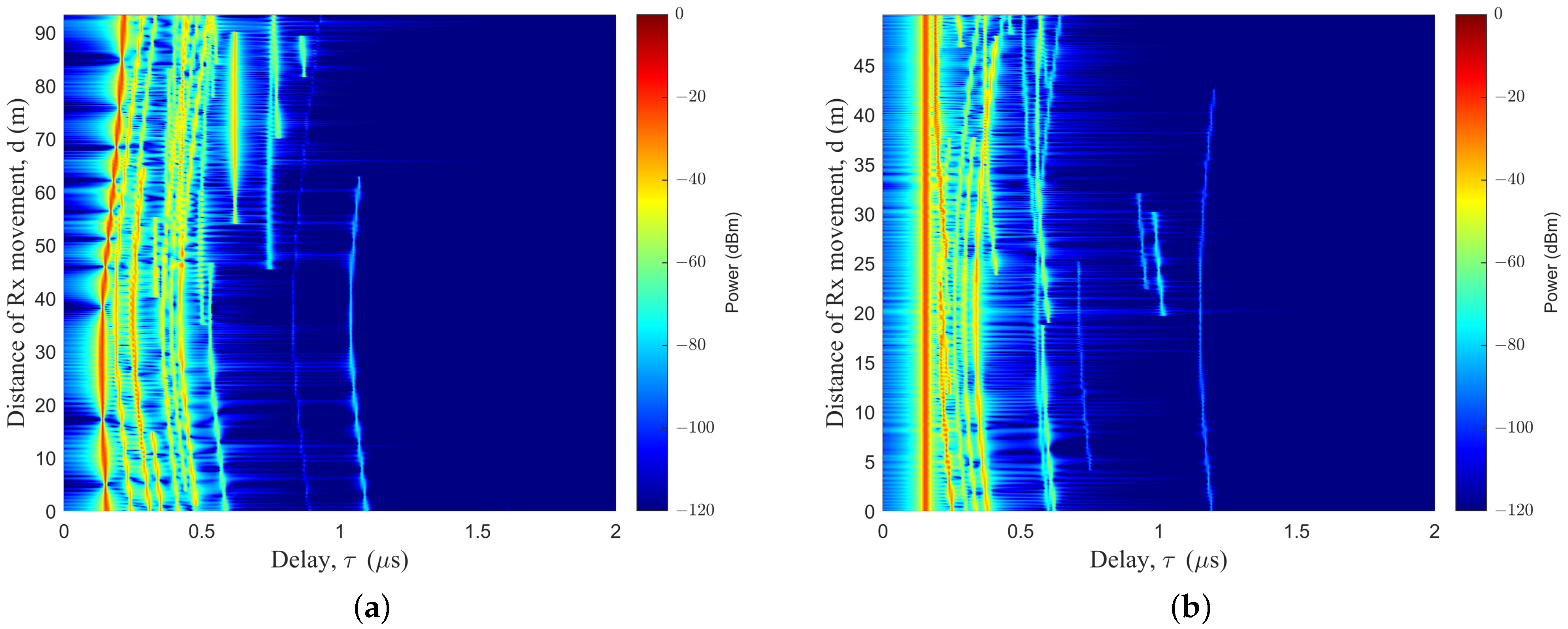
3.2.1. PDP
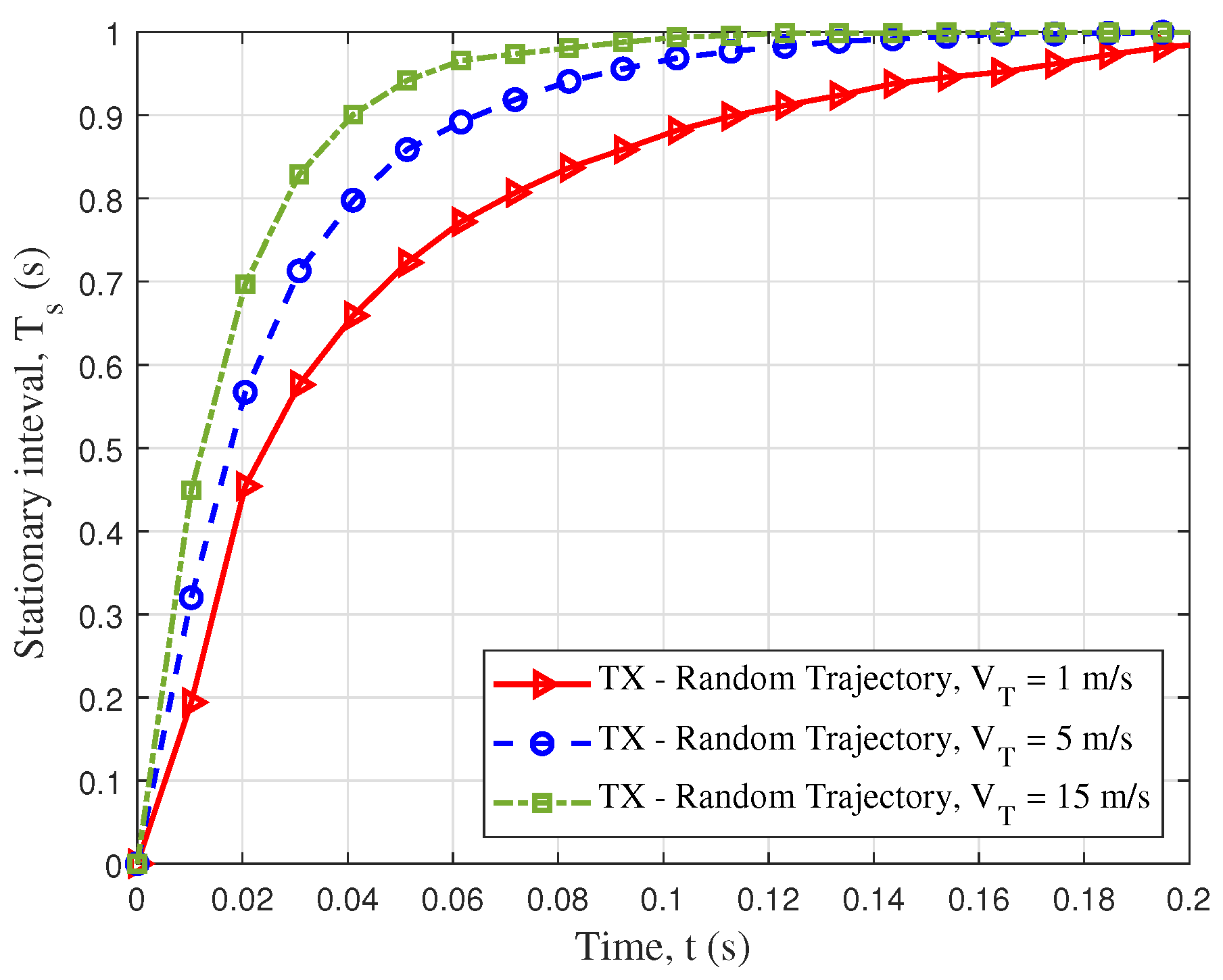
3.2.2. Stationary Interval
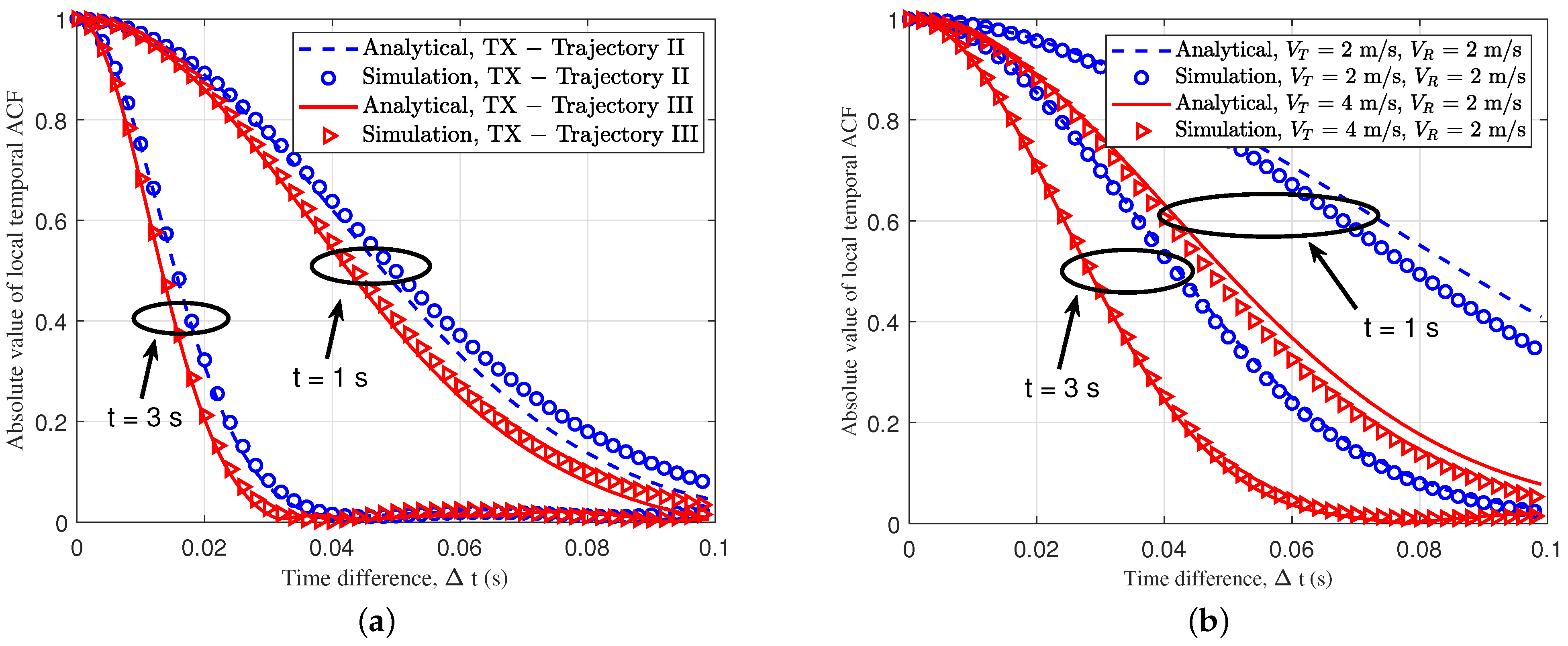
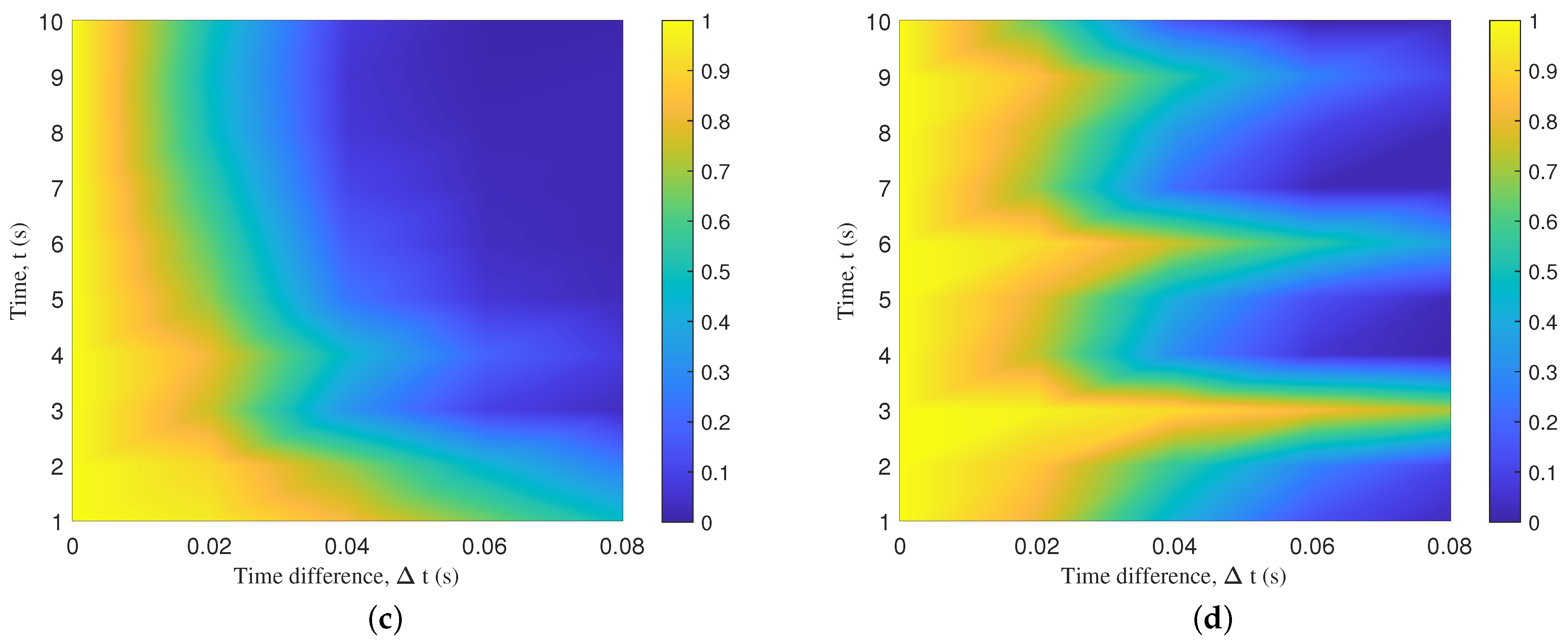
3.2.3. Temporal ACF and Spatial CCF
3.2.4. RMS DS
4. Numerical Results and Analysis
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Wang, C.X.; You, X.; Gao, X.; Zhu, X.; Li, Z.; Zhang, C.; Wang, H.; Huang, Y.; Chen, Y.; Haas, H.; et al. On the road to 6G: Visions, requirements, key technologies and Testbeds. IEEE Commun. Surv. Tutor. 2023, 25, 905–974. [Google Scholar] [CrossRef]
- Wang, Z.; Du, Y.; Wei, K.; Han, K.; Xu, X.; Wei, G.; Tong, W.; Zhu, P.; Ma, J.; Wang, J.; et al. Vision, application scenarios, and key technology trends for 6G mobile communications. Sci. China Inf. Sci. 2022, 65, 1–27. [Google Scholar] [CrossRef]
- Wang, C.X.; Bian, J.; Sun, J.; Zhang, W.; Zhang, M. A survey of 5G channel measurements and models. IEEE Commun. Surv. Tutor. 2018, 20, 3142–3168. [Google Scholar] [CrossRef]
- Mozaffari, M.; Saad, W.; Bennis, M.; Nam, Y.H.; Debbah, M. A tutorial on UAVs for wireless networks: Applications, challenges, and open problems. IEEE Commun. Surv. Tutor. 2019, 21, 2334–2360. [Google Scholar] [CrossRef] [Green Version]
- Wang, C.X.; Lv, Z.; Gao, X.; You, X.; Hao, Y.; Haas, H. Pervasive wireless channel modeling theory and applications to 6G GBSMs for all frequency bands and all scenarios. IEEE Trans. Veh. Technol. 2022, 71, 9159–9173. [Google Scholar] [CrossRef]
- Geraci, G.; Garcia-Rodriguez, A.; Azari, M.M.; Lozano, A.; Mezzavilla, M.; Chatzinotas, S.; Chen, Y.; Rangan, S.; Di Renzo, M. What will the future of UAV cellular communications be? A flight from 5G to 6G. IEEE Commun. Surv. Tutor. 2022, 24, 1304–1335. [Google Scholar] [CrossRef]
- Liu, Y.; Wang, C.X.; Huang, J.; Sun, J.; Zhang, W. Novel 3-D nonstationary mmWave massive MIMO channel models for 5G high-speed train wireless communications. IEEE Trans. Veh. Technol. 2018, 68, 2077–2086. [Google Scholar] [CrossRef]
- Zhou, T.; Zhang, H.; Ai, B.; Xue, C.; Liu, L. Deep-learning-based spatial–temporal channel prediction for smart high-speed railway communication networks. IEEE Trans. Wirel. Commun. 2022, 21, 5333–5345. [Google Scholar] [CrossRef]
- Guan, K.; Peng, B.; He, D.; Eckhardt, J.M.; Rey, S.; Ai, B.; Zhong, Z.; Kürner, T. Measurement, simulation, and characterization of train-to-infrastructure inside-station channel at the terahertz band. IEEE Trans. Terahertz Sci. Technol. 2019, 9, 291–306. [Google Scholar] [CrossRef]
- Guan, K.; He, D.; Ai, B.; Chen, Y.; Han, C.; Peng, B.; Zhong, Z.; Kuerner, T. Channel characterization and capacity analysis for THz communication enabled smart rail mobility. IEEE Trans. Veh. Technol. 2021, 70, 4065–4080. [Google Scholar] [CrossRef]
- Liu, Y.; Wang, C.X.; Chang, H.; He, Y.; Bian, J. A novel non-stationary 6G UAV channel model for maritime communications. IEEE J. Sel. Areas Commun. 2021, 39, 2992–3005. [Google Scholar] [CrossRef]
- Zhang, L.; Zhao, H.; Hou, S.; Zhao, Z.; Xu, H.; Wu, X.; Wu, Q.; Zhang, R. A survey on 5G millimeter wave communications for UAV-assisted wireless networks. IEEE Access 2019, 7, 117460–117504. [Google Scholar] [CrossRef]
- Yuan, B.; He, R.; Ai, B.; Chen, R.; Wang, G.; Ding, J.; Zhong, Z. A UAV-assisted search and localization strategy in non-line-of-sight scenarios. IEEE Int. Things J. 2022, 9, 23841–23851. [Google Scholar] [CrossRef]
- Zhu, Q.; Mao, K.; Song, M.; Chen, X.; Hua, B.; Zhong, W.; Ye, X. Map-based channel modeling and generation for U2V mmWave communication. IEEE Trans. Veh. Technol. 2022, 71, 8004–8015. [Google Scholar] [CrossRef]
- Liu, B.; Su, Z.; Xu, Q. Game theoretical secure wireless communication for UAV-assisted vehicular internet of things. China Commun. 2021, 18, 147–157. [Google Scholar] [CrossRef]
- Khawaja, W.; Guvenc, I.; Matolak, D.W.; Fiebig, U.C.; Schneckenburger, N. A survey of air-to-ground propagation channel modeling for unmanned aerial vehicles. IEEE Commun. Surv. Tutor. 2019, 21, 2361–2391. [Google Scholar] [CrossRef] [Green Version]
- He, R.; Ai, B.; Wang, G.; Yang, M.; Huang, C.; Zhong, Z. Wireless channel sparsity: Measurement, analysis, and exploitation in estimation. IEEE Wirel. Commun. 2021, 28, 113–119. [Google Scholar] [CrossRef]
- Yu, C.; Liu, Y.; Chang, H.; Zhang, J.; Zhang, M.; Poechmueller, P.; Wang, C. AG channel measurements and characteristics analysis in hilly scenarios for 6G UAV communications. China Commun. 2022, 19, 32–46. [Google Scholar] [CrossRef]
- Matolak, D.W.; Sun, R. Air–ground channel characterization for unmanned aircraft systems—Part I: Methods, measurements, and models for over-water settings. IEEE Trans. Veh. Technol. 2016, 66, 26–44. [Google Scholar] [CrossRef]
- Sun, R.; Matolak, D.W. Air–ground channel characterization for unmanned aircraft systems part II: Hilly and mountainous settings. IEEE Trans. Veh. Technol. 2016, 66, 1913–1925. [Google Scholar] [CrossRef]
- Matolak, D.W.; Sun, R. Air–ground channel characterization for unmanned aircraft systems—Part III: The suburban and near-urban environments. IEEE Trans. Veh. Technol. 2017, 66, 6607–6618. [Google Scholar] [CrossRef]
- Sun, R.; Matolak, D.W.; Rayess, W. Air-ground channel characterization for unmanned aircraft systems—Part IV: Airframe shadowing. IEEE Trans. Veh. Technol. 2017, 66, 7643–7652. [Google Scholar] [CrossRef]
- Cui, Z.; Briso-Rodriguez, C.; Guan, K.; Zhong, Z.; Quitin, F. Multi-frequency air-to-ground channel measurements and analysis for UAV communication systems. IEEE Access 2020, 8, 110565–110574. [Google Scholar] [CrossRef]
- Zhang, X.; He, R.; Yang, M.; Ai, B.; Wang, S.; Li, W.; Sun, W.; Li, L.; Huang, P.; Xue, Y. Measurements and modeling of large-scale channel characteristics in subway tunnels at 1.8 and 5.8 GHz. IEEE Antennas Wirel. Propag. Lett. 2023, 22, 561–565. [Google Scholar] [CrossRef]
- Yang, M.; Ai, B.; He, R.; Ma, Z.; Zhong, Z. Vehicle-to-vehicle channel characteristics in intersection environment. In Proceedings of the 2022 IEEE International Conference on Communications Workshops (ICC Workshops), Seoul, Republic of Korea, 16–20 May 2022; pp. 1124–1129. [Google Scholar]
- Wu, S.; Wang, C.X.; Alwakeel, M.M.; You, X. A general 3-D non-stationary 5G wireless channel model. IEEE Trans. Commun. 2017, 66, 3065–3078. [Google Scholar] [CrossRef]
- Chang, H.; Wang, C.X.; Liu, Y.; Huang, J.; Sun, J.; Zhang, W.; Gao, X. A novel nonstationary 6G UAV-to-ground wireless channel model with 3-D arbitrary trajectory changes. IEEE Int. Things J. 2021, 8, 9865–9877. [Google Scholar] [CrossRef]
- Jia, R.; Li, Y.; Cheng, X.; Ai, B. 3D geometry-based UAV-MIMO channel modeling and simulation. China Commun. 2018, 15, 64–74. [Google Scholar]
- Bai, L.; Huang, Z.; Cheng, X. A non-stationary model with time-space consistency for 6G massive MIMO mmWave UAV channels. IEEE Trans. Wirel. Commun. 2023, 22, 2048–2064. [Google Scholar] [CrossRef]
- Bian, J.; Wang, C.X.; Gao, X.; You, X.; Zhang, M. A general 3D non-stationary wireless channel model for 5G and beyond. IEEE Trans. Wirel. Commun. 2021, 20, 3211–3224. [Google Scholar] [CrossRef]
- Bian, J.; Wang, C.X.; Zhang, M.; Ge, X.; Gao, X. A 3-D non-stationary wideband MIMO channel model allowing for velocity variations of the mobile station. In Proceedings of the 2017 IEEE International Conference on Communications (ICC), Paris, France, 21–25 May 2017; pp. 1–6. [Google Scholar]
- Avazov, N.; Hicheri, R.; Muaaz, M.; Sanfilippo, F.; Pätzold, M. A trajectory-driven 3D non-stationary mm-wave MIMO channel model for a single moving point scatterer. IEEE Access 2021, 9, 115990–116001. [Google Scholar] [CrossRef]
- Jiang, H.; Zhang, Z.; Wang, C.X.; Zhang, J.; Dang, J.; Wu, L.; Zhang, H. A novel 3D UAV channel model for A2G communication environments using AoD and AoA estimation algorithms. IEEE Trans. Commun. 2020, 68, 7232–7246. [Google Scholar] [CrossRef]
- Serfozo, R. Basics of Applied Stochastic Processes, 1st ed.; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2009; ISBN 978-3-540-89331-8. [Google Scholar]
- Wan, Y.; Namuduri, K.; Zhou, Y.; Fu, S. A smooth-turn mobility model for airborne networks. IEEE Trans. Veh. Technol. 2013, 62, 3359–3370. [Google Scholar] [CrossRef]
- ResearchGate. WINNER II Channel Models. Available online: https://www.researchgate.net/publication/234055761_WINNER_II_channel_models (accessed on 1 May 2023).
- 3GPP. Study on Channel Model for Frequencies from 0.5 to 100 GHz; Technical Report (TR) 38.901, V16.1.0. 3GPP, Technical Report; 3GPP Mobile Competence Centre: Sophia Antipolis, France, 2017. [Google Scholar]


| Symbol | Definition |
|---|---|
| The number of clusters | |
| Rays number of the kth cluster | |
| Coordinates of the center of clusters | |
| Coordinates of the scattering points of the lth ray in the kth cluster | |
| AAoD and EAoD of the lth ray in the kth cluster | |
| AAoA and EAoA of the lth ray in the kth cluster | |
| AAoD and EAoD of the LoS ray | |
| AAoA and EAoA of the LoS ray | |
| Initial phases subject to uniform distribution in (0, 2] | |
| Cross-polarization power ratio | |
| Distance of the lth ray between Tx/Rx and clusters for the MB case | |
| Distance of the LoS path between the pth antenna and the qth antenna | |
| Coordinates of pth Tx or qth Rx antenna | |
| Coordinates of the single cluster for the SB case | |
| / | Distance of the lth ray between the Tx/Rx and the single cluster for the SB case |
| The speed vector of the Tx | |
| The speed vector of the Rx |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, J.; Liu, Y.; Huang, J.; Chang, H.; Zhang, Z.; Li, J. Channel Modeling and Characteristics Analysis under Different 3D Dynamic Trajectories for UAV-Assisted Emergency Communications. Sensors 2023, 23, 5372. https://doi.org/10.3390/s23125372
Zhang J, Liu Y, Huang J, Chang H, Zhang Z, Li J. Channel Modeling and Characteristics Analysis under Different 3D Dynamic Trajectories for UAV-Assisted Emergency Communications. Sensors. 2023; 23(12):5372. https://doi.org/10.3390/s23125372
Chicago/Turabian StyleZhang, Jingfan, Yu Liu, Jie Huang, Hengtai Chang, Zhaolei Zhang, and Jingquan Li. 2023. "Channel Modeling and Characteristics Analysis under Different 3D Dynamic Trajectories for UAV-Assisted Emergency Communications" Sensors 23, no. 12: 5372. https://doi.org/10.3390/s23125372
APA StyleZhang, J., Liu, Y., Huang, J., Chang, H., Zhang, Z., & Li, J. (2023). Channel Modeling and Characteristics Analysis under Different 3D Dynamic Trajectories for UAV-Assisted Emergency Communications. Sensors, 23(12), 5372. https://doi.org/10.3390/s23125372







