Load-Bearing Performance of Non-Prismatic RC Beams Wrapped with Carbon FRP Composites
Abstract
:1. Introduction
2. Experimental Program
2.1. Test Matrix
2.2. Details of Beams
2.3. Material Properties
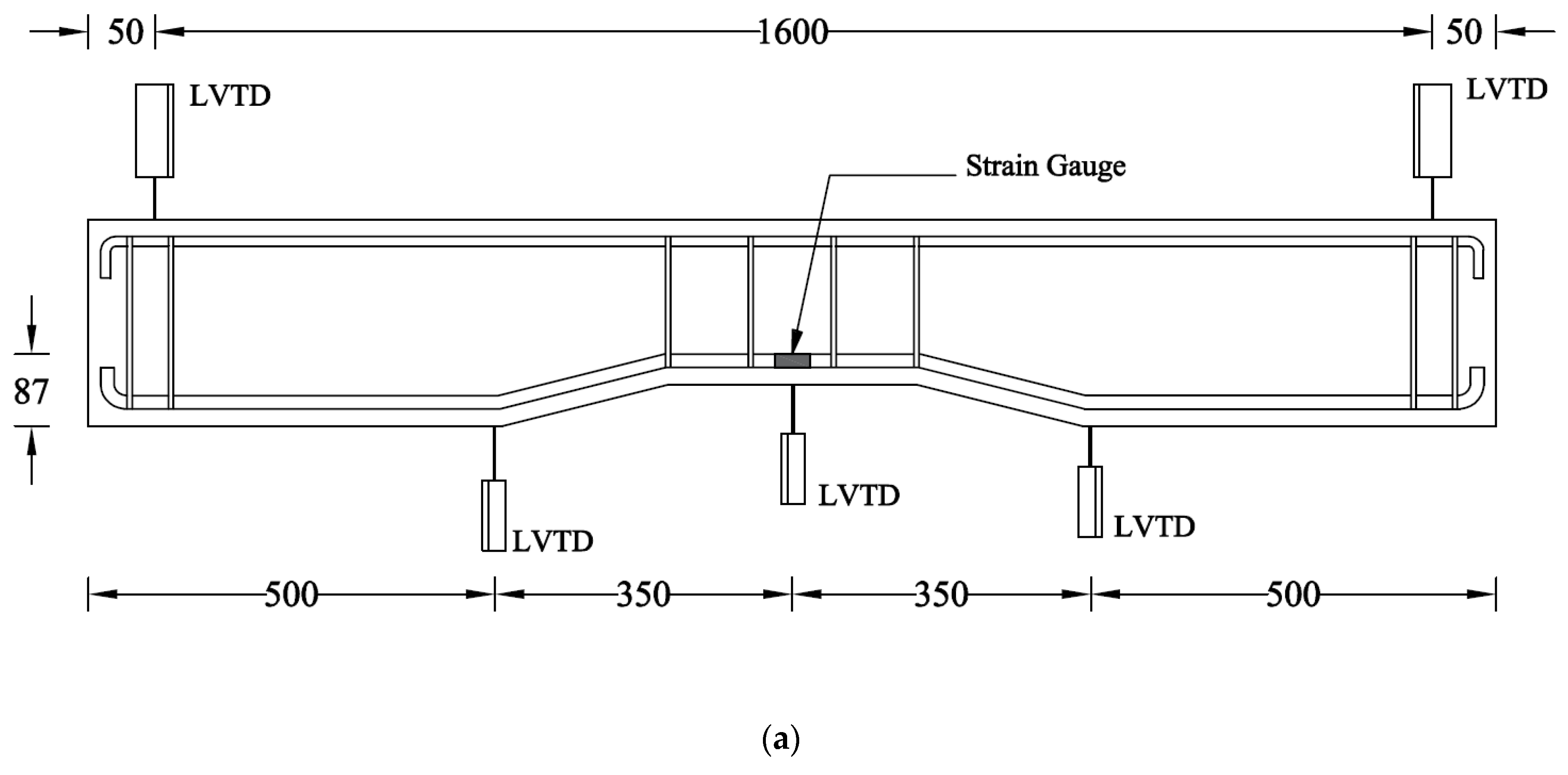
2.4. Strengthening, Test Setup, and Instrumentation
3. Experimental Results
3.1. Ultimate Failure Modes
3.2. Load–Displacement Curves
3.3. Peak Load and Deflection
3.4. Energy Dissipation Capacity
3.5. Support Deflections
3.6. Strain along Longitudinal Bars
4. Conclusions
- The study findings showed that control beams developed flexural cracks within the constant moment region, whereas solid section beams strengthened with CFRP strips and full wraps exhibited no shear cracks. However, strengthened hollow section beams displayed minor shear cracks in addition to main flexural cracks. The research provided important insights into the behavior and failure modes of non-prismatic beams, emphasizing the significance of considering the interaction between flexural and shear stresses when designing and reinforcing such structures with CFRP.
- It was also highlighted that the length of the non-prismatic section requires careful attention during CFRP confinement design. Some strengthened beams exhibited failure modes that involved CFRP delamination, emphasizing the need for a strong bond between CFRP and the concrete surface to fully utilize the potential of CFRP composites.
- The load–deflection curves of control beams demonstrated an abrupt drop in their capacities soon after achieving the peak load, which can be attributed to the predominant shear phenomenon observed from the cracking behavior. On the contrary, the strengthened beams demonstrated ductile behavior.
- The strengthened beams demonstrated 40% to 70% higher peak loads than control beams, whereas the ultimate deflection was increased up to 524.87% over that of the control beams. The improvement in the peak load was more prominent as the length of the non-prismatic section increased. A better improvement in ductility was achieved for the case of CFRP strips and short non-prismatic lengths, whereas the efficiency of CFRP strips was reduced as the length of the non-prismatic section increased.
- Steel bars in tension did not achieve yielding in all control beams, whereas the strengthened beams exhibited yielding that was reflected in their ductile load–deflection response. It is noteworthy that both CFRP strips and full wraps allowed the beams to surpass yield points of longitudinal reinforcement in tension.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Attarnejad, R.; Shahba, A. Application of Differential Transform Method in Free Vibration Analysis of Rotating Non-Prismatic Beams. World Appl. Sci. J. 2008, 5, 441–448. [Google Scholar]
- Dawood, M.; Nabbat, R. Flexural and Shear Strength of Non-Prismatic Reinforced High Strength Concrete Beams with Openings and Strengthened with NSM-CFPR Bars. Int. J. Civ. Eng. Technol. 2015, 6, 93–103. [Google Scholar]
- Han, L.H.; Li, W.; Bjorhovde, R. Developments and Advanced Applications of Concrete-Filled Steel Tubular (CFST) Structures: Members. J. Constr. Steel Res. 2014, 100, 211–228. [Google Scholar] [CrossRef]
- Alshimmeri, A.J.H.; Jaafar, E.K.; Shihab, L.A.; Al-Maliki, H.N.G.; Al-Balhawi, A.; Zhang, B. Structural Efficiency of Non-Prismatic Hollow Reinforced Concrete Beams Retrofitted with CFRP Sheets. Buildings 2022, 12, 109. [Google Scholar] [CrossRef]
- Alnauimi, A.S.; Bhatt, P. Direct Design of Hollow Reinforced Concrete Beams. Part II: Experimental Investigation. Struct. Concr. 2015, 5, 147–160. [Google Scholar] [CrossRef]
- Alnuaimi, A.S.; Al-Jabri, K.S.; Hago, A. Comparison between Solid and Hollow Reinforced Concrete Beams. Mater. Struct./Mater. Et Constr. 2008, 41, 269–286. [Google Scholar] [CrossRef]
- Balaji, G.; Vetturayasudharsanan, R. Experimental Investigation on Flexural Behaviour of RC Hollow Beams. Mater. Today Proc. 2020, 21, 351–356. [Google Scholar] [CrossRef]
- Hemzah, S.A.; Alyhya, W.S.; Hassan, S.A. Experimental Investigation for Structural Behaviour of Self-Compacting Reinforced Concrete Hollow Beams with in-Place Circular Openings Strengthened with CFRP Laminates. Structures 2020, 24, 99–106. [Google Scholar] [CrossRef]
- Abbass, A.; Abid, S.; Özakça, M. Experimental Investigation on the Effect of Steel Fibers on the Flexural Behavior and Ductility of High-Strength Concrete Hollow Beams. Adv. Civ. Eng. 2019, 2019, 8390345. [Google Scholar] [CrossRef]
- Zhou, M.; Shang, X.; Hassanein, M.F.; Zhou, L. The Differences in the Mechanical Performance of Prismatic and Non-Prismatic Beams with Corrugated Steel Webs: A Comparative Research. Thin-Walled Struct. 2019, 141, 402–410. [Google Scholar] [CrossRef]
- Vijayakumar, A.; Madhavi, T.C. Behaviour of Self Compacting Concrete with Hybrid Fibers in Hollow Beams. Mater. Today Proc. 2020, 46, 3212–3219. [Google Scholar] [CrossRef]
- El-kassas, A.I.; Hassan, H.M.; Arab, M.A.E.S. Effect of Longitudinal Opening on the Structural Behavior of Reinforced High-Strength Self-Compacted Concrete Deep Beams. Case Stud. Constr. Mater. 2020, 12, e00348. [Google Scholar] [CrossRef]
- Abbass, A.A.; Abid, S.R.; Arna’ot, F.H.; Al-Ameri, R.A.; Özakça, M. Flexural Response of Hollow High Strength Concrete Beams Considering Different Size Reductions. Structures 2020, 23, 69–86. [Google Scholar] [CrossRef]
- Elamary, A.S.; Sharaky, I.A.; Alqurashi, M. Flexural Behaviour of Hollow Concrete Beams under Three Points Loading: Experimental and Numerical Study. Structures 2021, 32, 1543–1552. [Google Scholar] [CrossRef]
- ACI 318-19: Building Code Requirements for Structural Concrete and Commentary; American Concrete Institute: Farmington Hills, MI, USA, 2019.
- BS5400-1; Steel, Concrete and Composite Bridges—Part 1: General Statement. British Standards Institution: London, UK, 1988.
- Al-Ahmed, A.H.A.; Al-Zuhairi, A.H.; Hasan, A.M. Behavior of Reinforced Concrete Tapered Beams. Structures 2022, 37, 1098–1118. [Google Scholar] [CrossRef]
- Tena-Colunga, A.; Archundia-Aranda, H.I.; González-Cuevas, Ó.M. Behavior of Reinforced Concrete Haunched Beams Subjected to Static Shear Loading. Eng. Struct. 2008, 30, 478–492. [Google Scholar] [CrossRef]
- Caldentey, A.P.; Padilla, P.; Muttoni, A.; Ruiz, M.F. Effect of Load Distribution and Variable Depth on Shear Resistance of Slender Beams without Stirrups. ACI Struct. J. 2012, 109, 595–604. [Google Scholar] [CrossRef] [Green Version]
- Qissab, M.A.; Salman, M.M. Shear Strength of Non-Prismatic Steel Fiber Reinforced Concrete Beams without Stirrups. Struct. Eng. Mech. 2018, 67, 358. [Google Scholar] [CrossRef]
- Mazzuca, P.; Firmo, J.P.; Correia, J.R.; Castilho, E. Influence of Elevated Temperatures on the Mechanical Properties of Glass Fibre Reinforced Polymer Laminates Produced by Vacuum Infusion. Constr. Build Mater. 2022, 345, 128340. [Google Scholar] [CrossRef]
- Xian, G.; Guo, R.; Li, C.; Hong, B. Mechanical Properties of Carbon/Glass Fiber Reinforced Polymer Plates with Sandwich Structure Exposed to Freezing-Thawing Environment: Effects of Water Immersion, Bending Loading and Fiber Hybrid Mode. Mech. Adv. Mater. Struct. 2022, 30, 814–834. [Google Scholar] [CrossRef]
- Alsuhaibani, E.; Yazdani, N.; Beneberu, E. Durability and Long-Term Performance Prediction of Carbon Fiber Reinforced Polymer Laminates. Polymers 2022, 14, 3207. [Google Scholar] [CrossRef] [PubMed]
- Xian, G.; Guo, R.; Li, C.; Wang, Y. Mechanical Performance Evolution and Life Prediction of Prestressed CFRP Plate Exposed to Hygrothermal and Freeze-Thaw Environments. Compos. Struct. 2022, 293, 115719. [Google Scholar] [CrossRef]
- Baggio, D.; Soudki, K.; Noël, M. Strengthening of Shear Critical RC Beams with Various FRP Systems. Constr. Build Mater. 2014, 66, 634–644. [Google Scholar] [CrossRef]
- Ameli, M.; Ronagh, H.R.; Dux, P.F. Behavior of FRP Strengthened Reinforced Concrete Beams under Torsion. J. Compos. Constr. 2007, 11, 192–200. [Google Scholar] [CrossRef]
- ASTM International ASTM E8/E8M-21; Standard Test Methods for Tension Testing of Metallic Materials. ASTM International: West Conshohocken, PA, USA, 2021.
- ASTM ASTM C39/C39M; 21 Standard Test Method for Compressive Strength of Cylindrical Concrete Specimens 1. Infinita Lab: Newark, CA, USA, 2021.






















| Group | Subgroup | Type of Beam | CFRP Shape | Type of Prismatic Section | Section |
|---|---|---|---|---|---|
| 1 | 1 | NP1-S-CON | - | Type-01 | Solid |
| NP1-S-CFRP-S | Strip | Type-01 | Solid | ||
| NP1-S-CFRP-F | Full Wrap | Type-01 | Solid | ||
| 2 | NP2-S-CON | - | Type-02 | Solid | |
| NP2-S-CFRP-S | Strip | Type-02 | Solid | ||
| NP2-S-CFRP-F | Full Wrap | Type-02 | Solid | ||
| 2 | 1 | NP1-H-CON | - | Type-01 | Hollow |
| NP1-H-CFRP-S | Strip | Type-01 | Hollow | ||
| NP1-H-CFRP-F | Full Wrap | Type-01 | Hollow | ||
| 2 | NP2-H-CON | - | Type-02 | Hollow | |
| NP2-H-CFRP-S | Strip | Type-02 | Hollow | ||
| NP2-H-CFRP-F | Full Wrap | Type-02 | Hollow |
| Type of Bar | Yield Strength (MPa) | Yield Strain (mm/mm) | Ultimate Strength (MPa) | Ultimate Strain (mm/mm) |
|---|---|---|---|---|
| RB-6 | 373 | 0.00184 | 494.7 | 0.1836 |
| DB-12 | 633 | 0.00394 | 761 | 0.1151 |
| DB-16 | 455 | 0.00241 | 614 | 0.0151 |
| Properties | Values | Units |
|---|---|---|
| Curing time | 7–10 | Hours |
| Compressive strength | 650 | kgf/cm2 |
| Tensile strength | 50 | MPa |
| Elongation at break | 2.5 | % |
| Flexural strength | 75 | MPa |
| Properties | Values | Units |
|---|---|---|
| Weight | 300 | g/m2 |
| Thickness | 0.167 | mm |
| Fiber density | 1.8 | g/cm3 |
| Tensile strength | 5214 | MPa |
| Elongation | 1.51 | % |
| Beam | Peak Load (kN) | Increase in Peak Load (%) | Ultimate Deflection (mm) | Increase in Ultimate Deflection (%) | Dissipated Energy (kN-mm) | Increase in Dissipated Energy (%) |
|---|---|---|---|---|---|---|
| NP1-S-CON | 70.47 | - | 15.63 | - | 955 | - |
| NP1-S-CFRP-S | 96.02 | 36.26 | 40.05 | 156.24 | 3313 | 246.50 |
| NP1-S-CFRP-F | 89.09 | 26.42 | 35.07 | 124.38 | 2300 | 140.84 |
| NP2-S-CON | 36.92 | - | 19.76 | - | 975 | - |
| NP2-S-CFRP-S | 62.99 | 70.61 | 30.00 | 51.82 | 1504 | 54.26 |
| NP2-S-CFRP-F | 62.02 | 67.98 | 34.11 | 72.62 | 1706 | 74.97 |
| NP1-H-CON | 65.25 | - | 9.97 | - | 447 | - |
| NP1-H-CFRP-S | 96.02 | 47.16 | 62.30 | 524.87 | 5462 | 1121.93 |
| NP1-H-CFRP-F | 91.85 | 40.77 | 43.90 | 340.32 | 3626 | 711.19 |
| NP2-H-CON | 36.25 | - | 22.50 | - | 820 | - |
| NP2-H-CFRP-S | 57.03 | 57.32 | 30.00 | 33.33 | 1131 | 37.93 |
| NP2-H-CFRP-F | 56.87 | 56.88 | 37.10 | 64.89 | 1752 | 113.66 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Suparp, S.; Ejaz, A.; Khan, K.; Hussain, Q.; Joyklad, P.; Saingam, P. Load-Bearing Performance of Non-Prismatic RC Beams Wrapped with Carbon FRP Composites. Sensors 2023, 23, 5409. https://doi.org/10.3390/s23125409
Suparp S, Ejaz A, Khan K, Hussain Q, Joyklad P, Saingam P. Load-Bearing Performance of Non-Prismatic RC Beams Wrapped with Carbon FRP Composites. Sensors. 2023; 23(12):5409. https://doi.org/10.3390/s23125409
Chicago/Turabian StyleSuparp, Suniti, Ali Ejaz, Kaffayatullah Khan, Qudeer Hussain, Panuwat Joyklad, and Panumas Saingam. 2023. "Load-Bearing Performance of Non-Prismatic RC Beams Wrapped with Carbon FRP Composites" Sensors 23, no. 12: 5409. https://doi.org/10.3390/s23125409
APA StyleSuparp, S., Ejaz, A., Khan, K., Hussain, Q., Joyklad, P., & Saingam, P. (2023). Load-Bearing Performance of Non-Prismatic RC Beams Wrapped with Carbon FRP Composites. Sensors, 23(12), 5409. https://doi.org/10.3390/s23125409






