Detection of Gas Pipeline Leakage Using Distributed Optical Fiber Sensors: Multi-Physics Analysis of Leakage-Fiber Coupling Mechanism in Soil Environment
Abstract
:1. Introduction
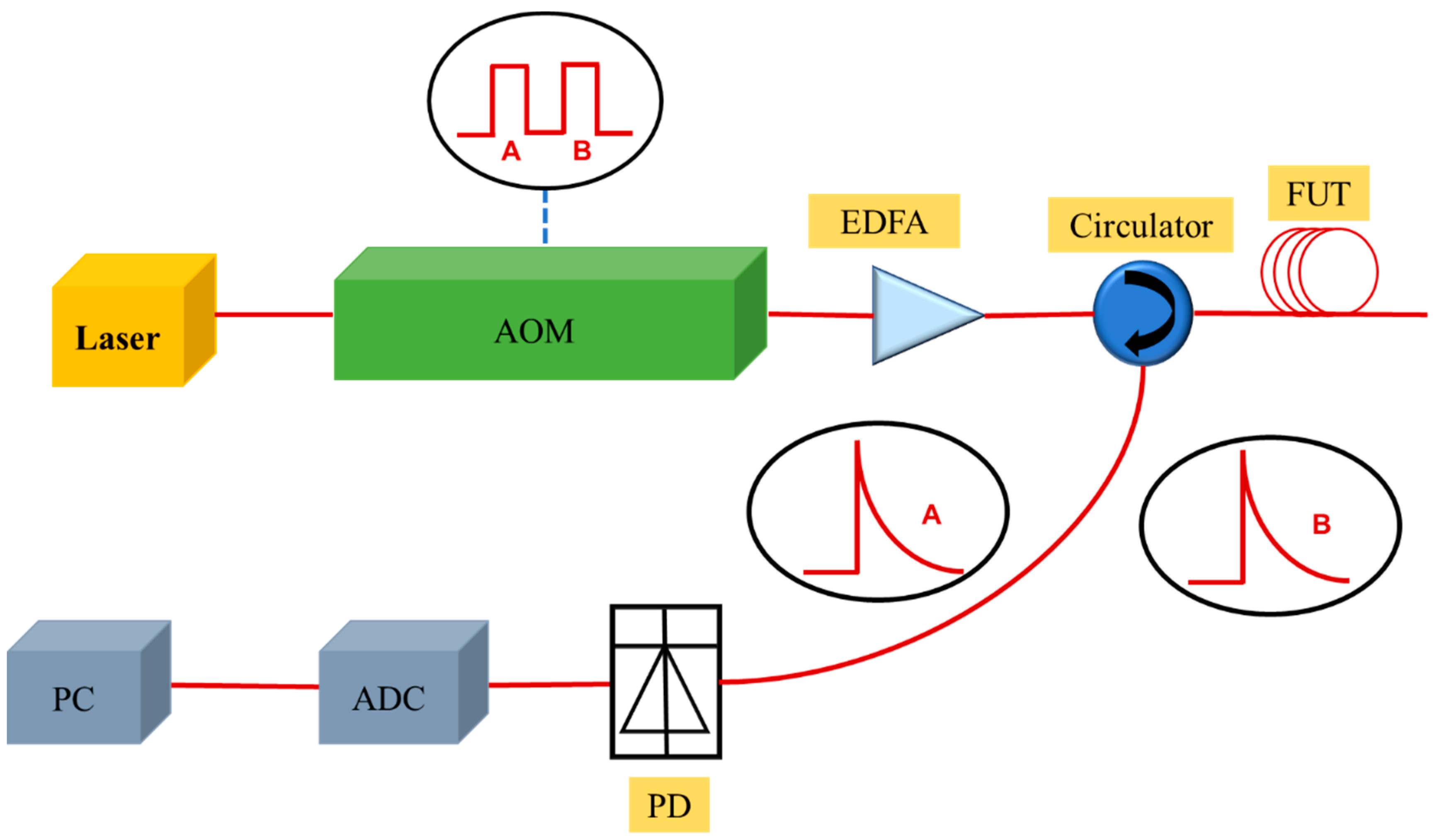
2. Principle of Distributed Optical Fiber Strain and Temperature Sensors
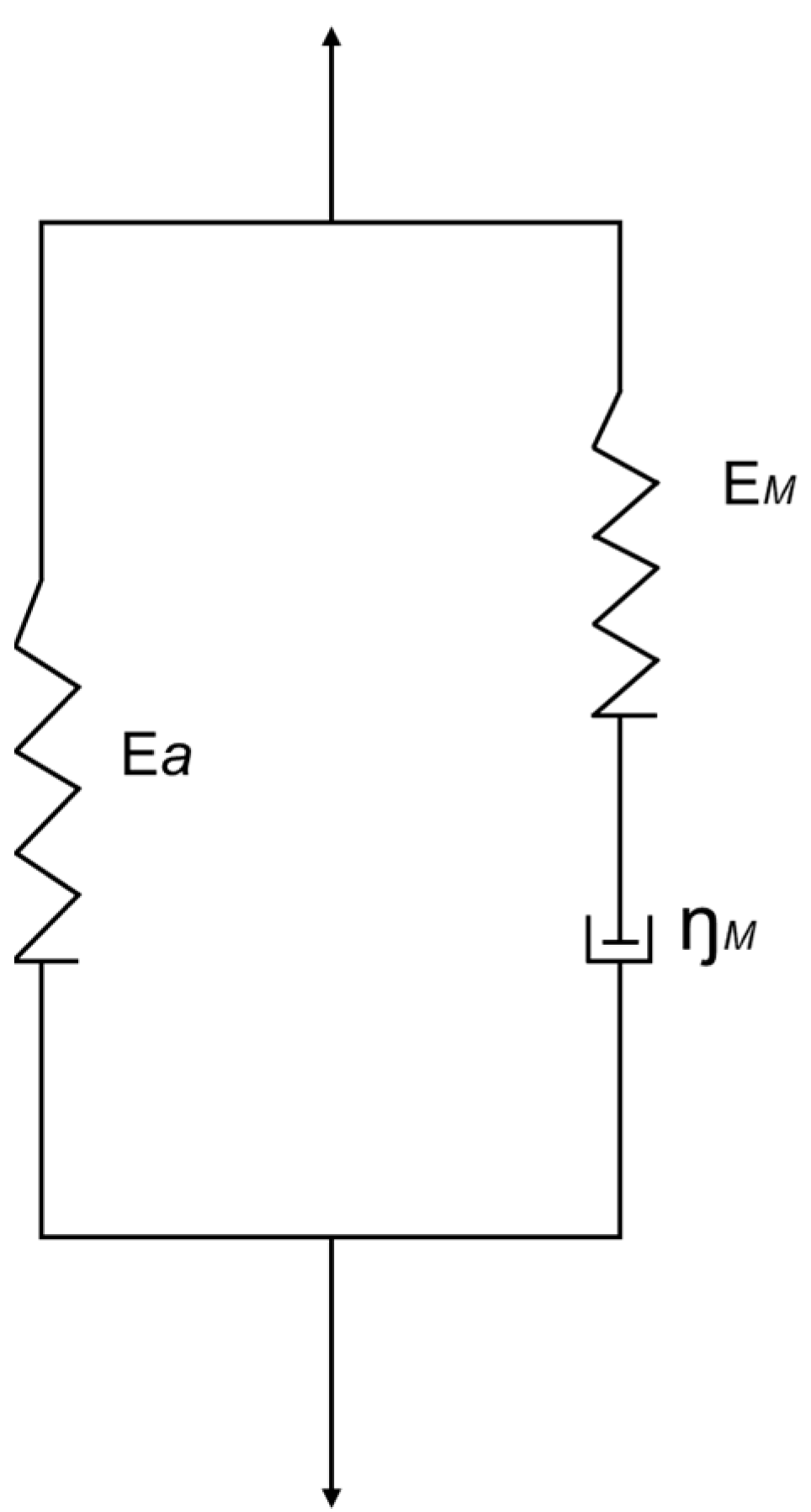
3. Analytical Model: Spherical Stress Wave Propagation
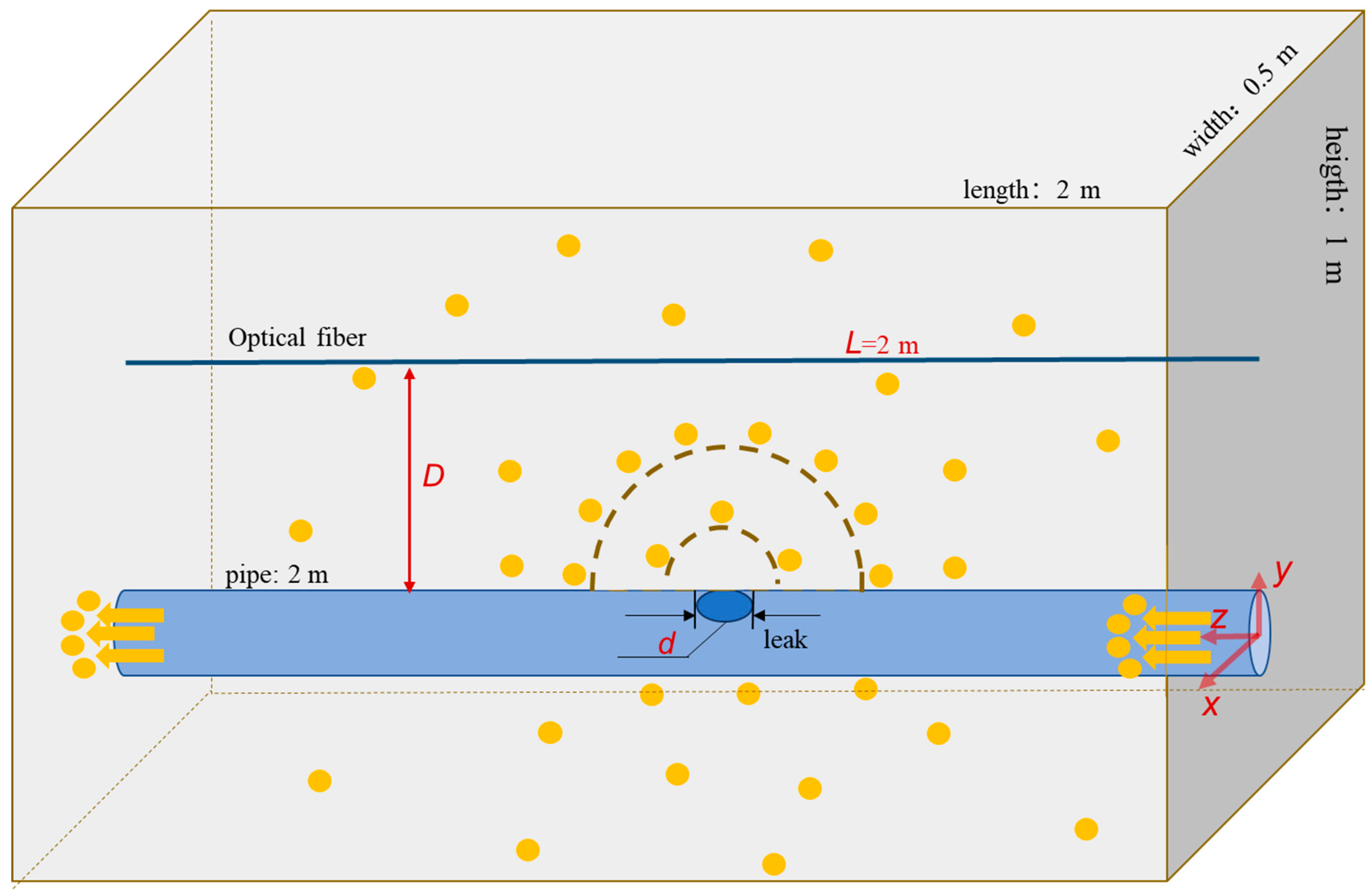
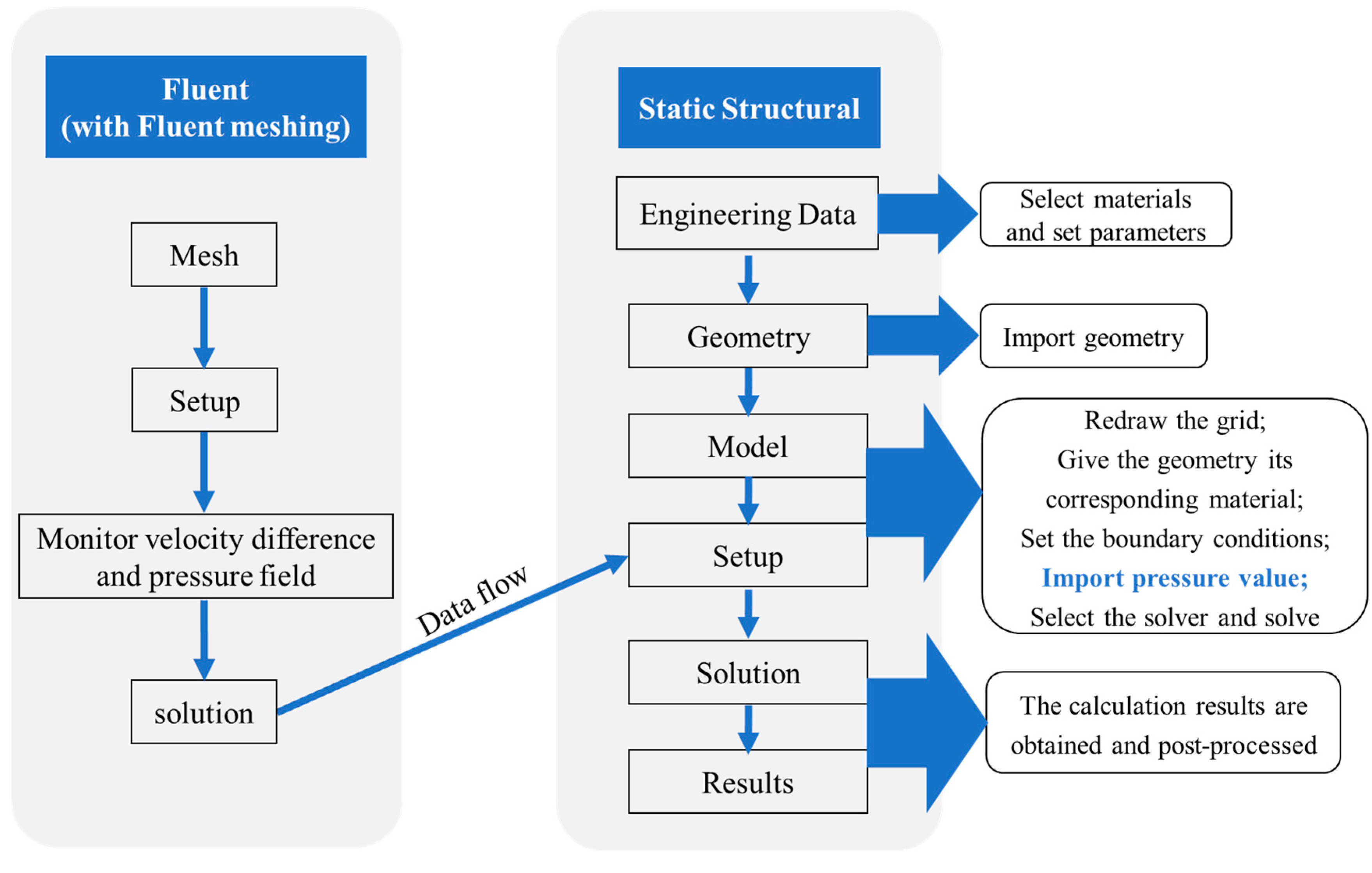
4. Numerical Model
4.1. Simulation Procedure
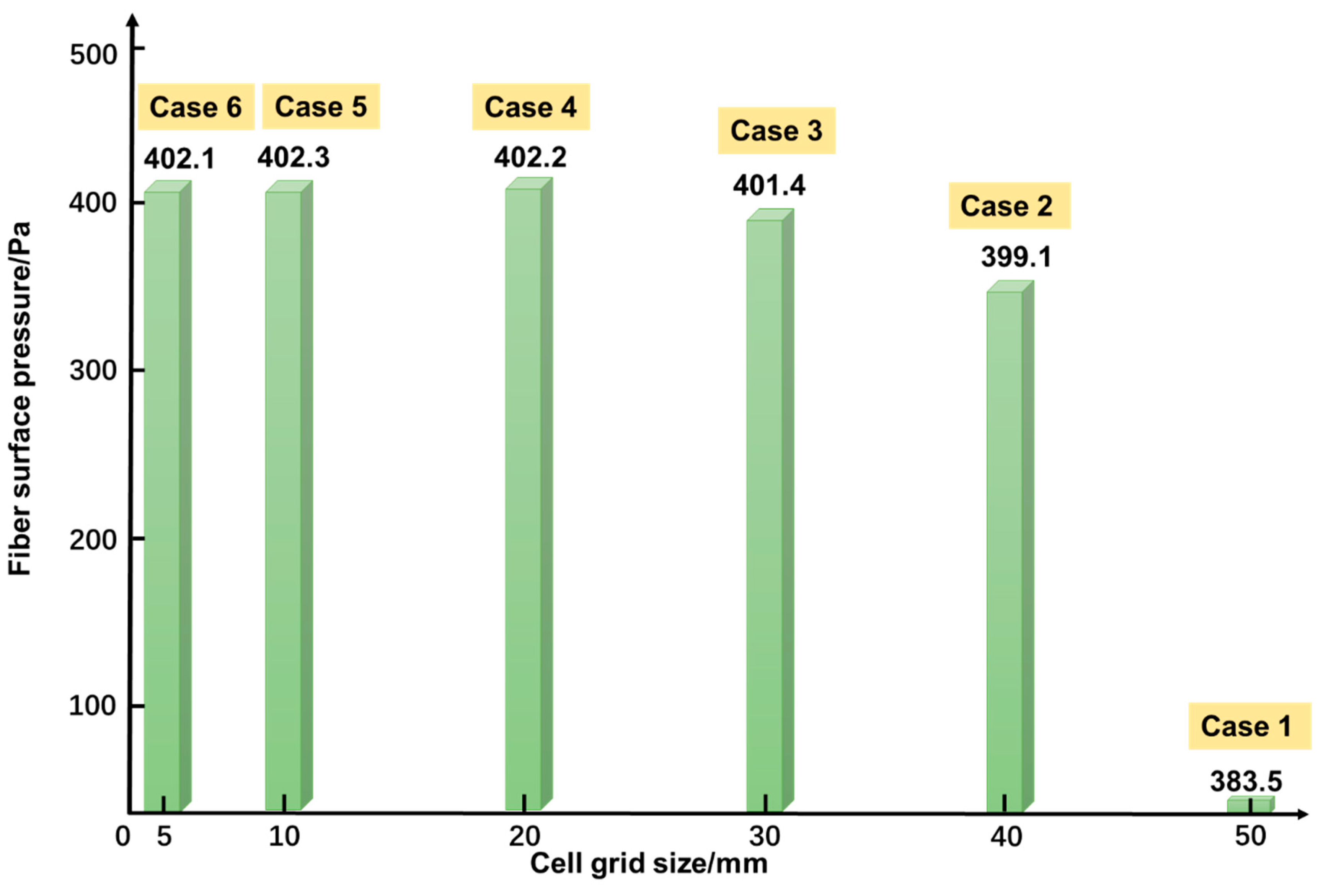
4.2. Verification of Grid Independence
5. Results and Discussion
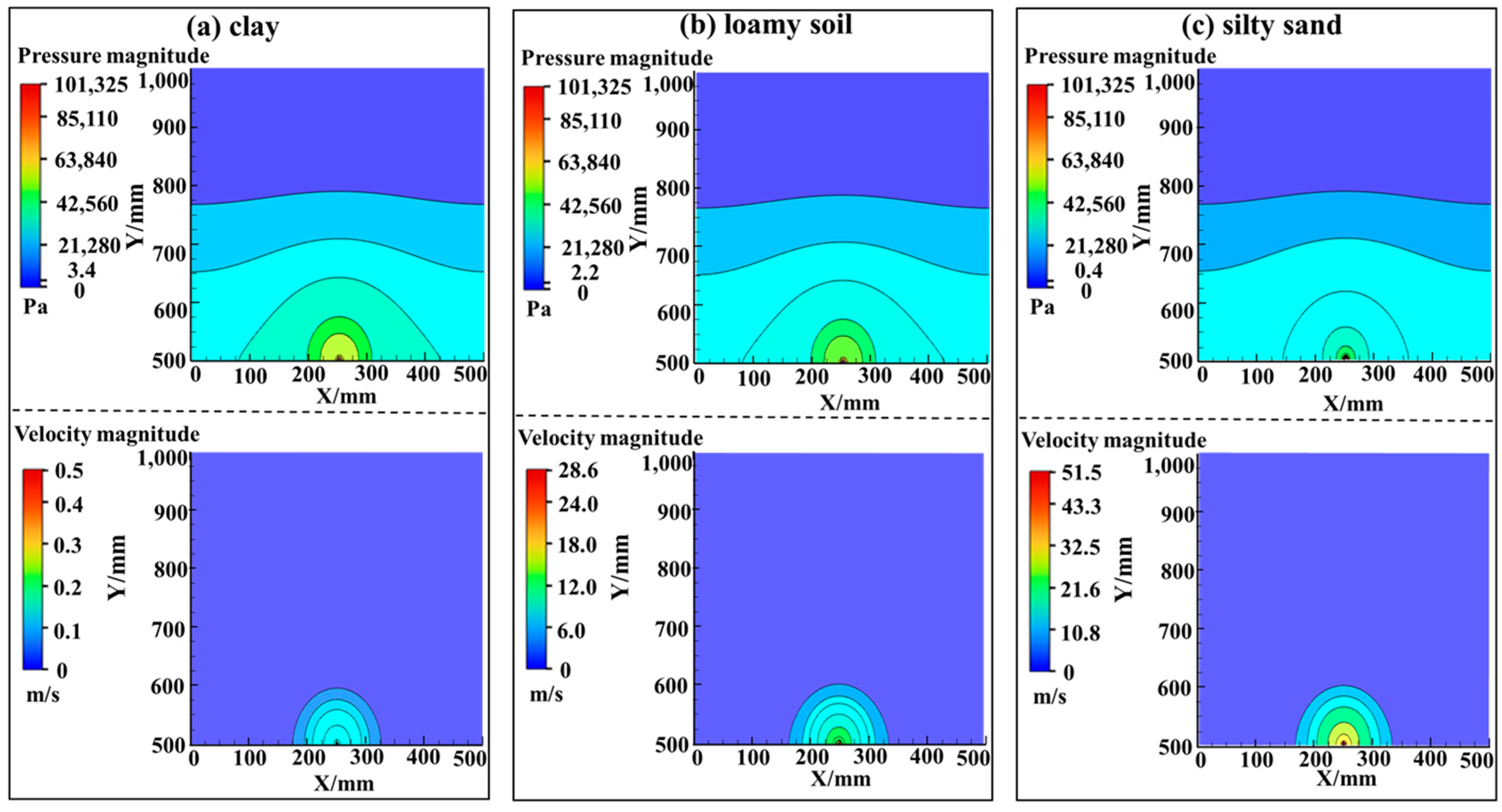
5.1. Gas Leakage Simulation
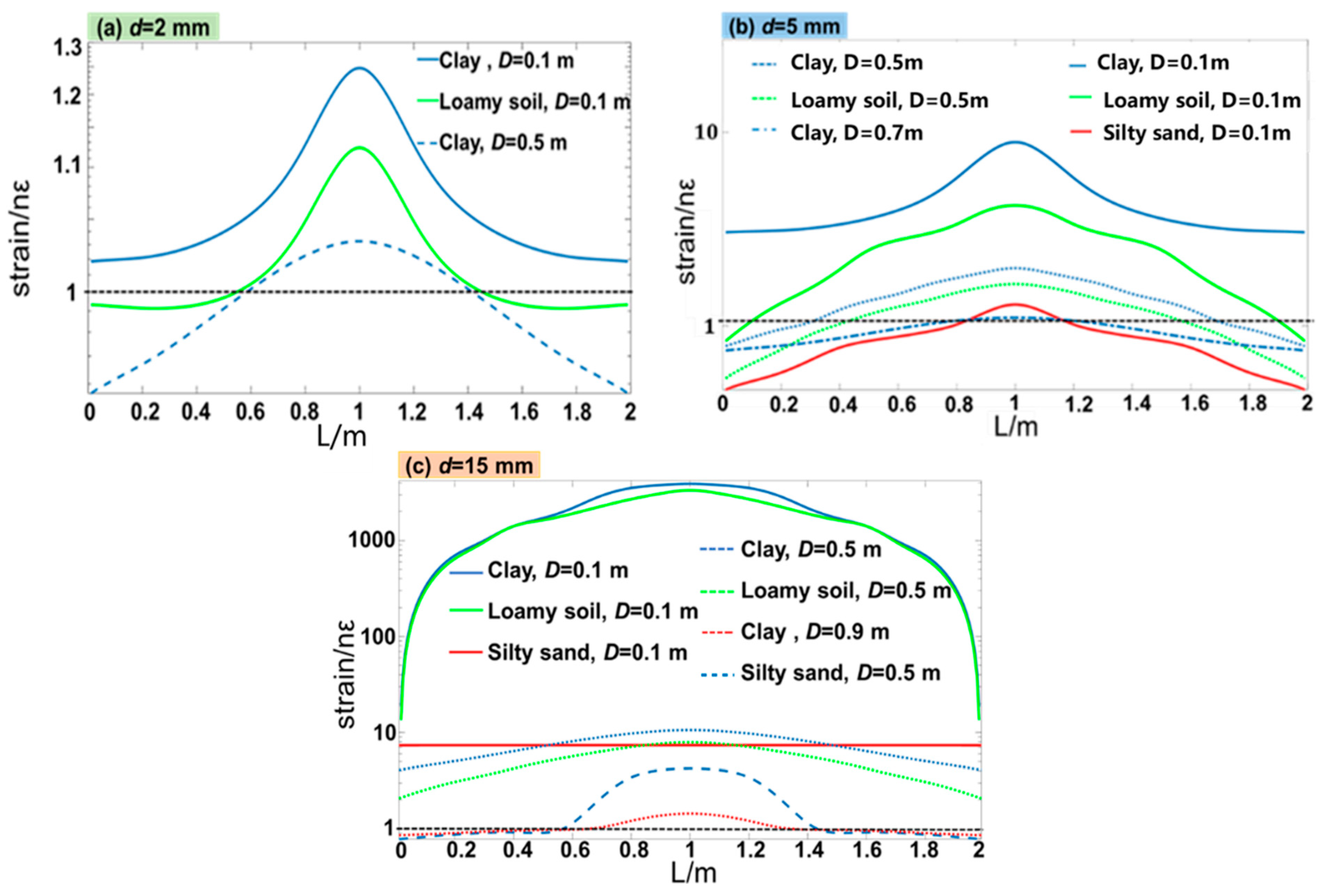
5.2. Leakage–Induced Static Strain on FUT
5.3. Leakage–Induced Transient Strain on FUT
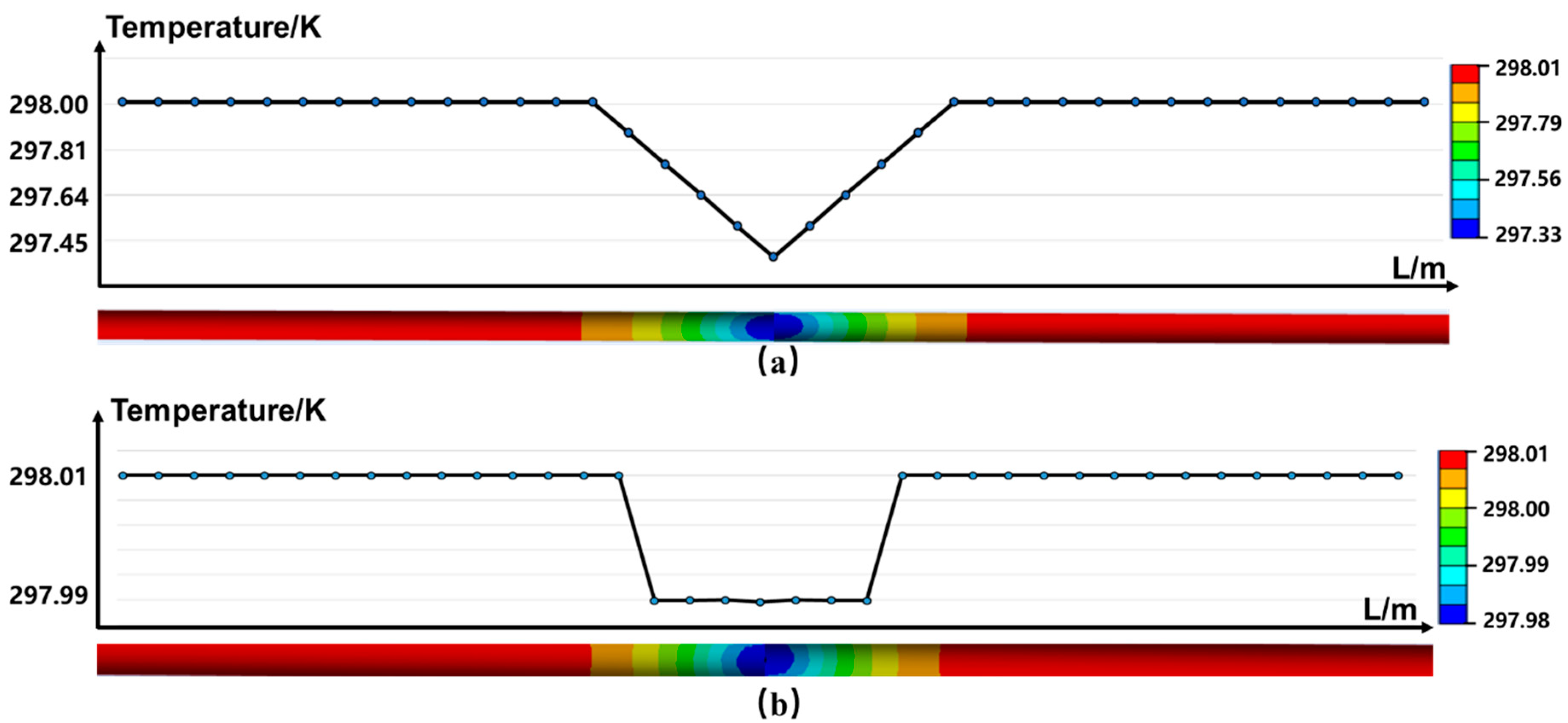
5.4. Leakage–Induced Temperature Variation along FUT
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Chang, H.; Tan, Y.; Wang, X.; Xiao, R.; Zhang, X. Simulation study on leakage diffusion along soil of urban directly buried gas pipeline. Gas Heat 2020, 40, 28–34. [Google Scholar]
- Wang, Y. Study on Thermal Oxygen Aging Life Prediction Method of Urban Gas Polyethylene Pipeline; Beijing Jiaotong University: Beijing, China, 2019. [Google Scholar]
- Wang, X.; Su, X.; Yang, W. A review of oil and gas pipeline leak detection technology. Nat. Gas Oil 2007, 25, 19–23. [Google Scholar]
- Gao, Y.; Piltan, F.; Kim, J.-M. A Hybrid Leak Localization Approach Using Acoustic Emission for Industrial Pipelines. Sensors 2022, 22, 3963. [Google Scholar] [CrossRef]
- Li, W.; Zhu, Y. Analysis of leakage detection and positioning methods for long-distance pipelines. Nat. Gas Ind. 2005, 25, 105–109. [Google Scholar]
- Wang, Z.; Zhang, L.; Xin, R.; Liang, W. Application of acoustic emission technology in pipeline leak detection. J. China Univ. Pet. 2007, 31, 87–90. [Google Scholar]
- Zhang, J.; Zhang, F.; Weiran, W.; Jiang, W.; Zhao, Z.; Zilong, G. Experimental study on leak detection of long-distance pipeline by acoustic wave method. Liaoning Chem. Ind. 2013, 42, 1431–1432. [Google Scholar]
- Lu, H.; Wu, X.; Iseley, T.; Matthews, J.; Peng, S. The current situation and enlightenment of foreign natural gas pipeline detection technology. Nat. Gas Ind. 2018, 38, 103–111. [Google Scholar]
- Shen, Y.; Shao, K.; Wu, J.; Huang, F.; Guo, Y. Research progress on gas optical detection technology and its application. Optoelectron. Eng. 2020, 47, 3–18. [Google Scholar]
- Ma, X.; Ceng, X.; Pu, R. Application of Smartball self-drifting leak detection system in oil pipelines. Oil Gas Storage Transp. 2010, 29, 839–840. [Google Scholar]
- Zhang, R. Design of Natural Gas Pipeline Leakage Detection Device Based on Pgc Demodulation of Optical Fiber Sensor; China Institute of Metrology: Yiwu, China, 2014. [Google Scholar]
- Yang, G. Research on Distributed Fiber Dynamic Strain Sensing Technology Based on Fiber Backscatter; Shanghai Jiao Tong University: Shanghai, China, 2020. [Google Scholar]
- Barrias, A.; Casas, J.R.; Villalba, S. A review of distributed optical fiber sensors for civil engineering applications. Sensors 2016, 16, 748. [Google Scholar] [CrossRef] [Green Version]
- Barrias, A.; Rodriguez, G.; Casas, J.R.; Villalba, S. Application of distributed optical fiber sensors for the health monitoring of two real structures in Barcelona. Struct. Infrastruct. Eng. 2018, 14, 967–985. [Google Scholar] [CrossRef]
- Deng, C.; Yu, W.; Luo, H.; Zhu, X.; Yang, X.; Li, J.; Liu, C. Application of distributed optical fiber sensing technologies to the monitoring of leakage and abnormal disturbance of oil pipeline. Fiber Opt. Sens. Opt. Commun. 2017, 10464, 615–623. [Google Scholar] [CrossRef]
- Abe, T.; Mitsunaga, Y.; Koga, H. A strain sensor using twisted optical fibers. J. Light. Technol. 1989, 7, 525–529. [Google Scholar] [CrossRef]
- Dan, Y.; Wu, Z.; Xu, X.; Chang, Z.; Ma, Y. Strain measurement method and application of distributed optical fiber sensor. Piezoelectric Sound Light 2015, 37, 485–488. [Google Scholar]
- Wang, J.; Wang, H.; Mei, C.; Tan, J.; Zhang, Q.; Bai, R. Distributed fiber optic leakage monitoring of natural gas pipelines with gas collection devices. Gas Heat 2022, 42, 39–42. [Google Scholar]
- Wang, J.-N.; Tang, J.-L. Feasibility of Fiber Bragg Grating and Long-Period Fiber Grating Sensors under Different Environmental Conditions. Sensors 2010, 10, 10105–10127. [Google Scholar] [CrossRef] [PubMed]
- Zheng, L.; Xianlong, J.; Wenguo, Q. Study on the parallel algorithm for finite element simulation of fluid-structure interaction. Chin. J. Comput. Mech. 2007, 24, 727–732. [Google Scholar]
- Bao, X.; Chen, L. Recent Progress in Distributed Fiber Optic Sensors. Sensors 2012, 12, 8601–8639. [Google Scholar] [CrossRef] [Green Version]
- Haiwen, C.; Qing, Y.; Zhaoyong, W.; Bin, L. Distributed Optical Fiber Acoustic Sensing Technology Based on Coherent Rayleigh Scattering. Laser Optoelectron. Prog. 2020, 57, 050001. [Google Scholar] [CrossRef]
- Liu, Y.; Li, H.; Gao, S.; Wang, J.; Fan, X.; Li, X.; Tian, Y.; Li, J. Application of distributed optical fiber sensing in large transformer temperature and winding deformation monitoring. Proc. CSEE 2022, 42, 6126–6135. [Google Scholar]
- Lu, P.; Lalam, N.; Badar, M.; Liu, B.; Chorpening, B.T.; Buric, M.P.; Ohodnicki, P. Distributed optical fiber sensing: Review and perspective. Appl. Phys. Rev. 2019, 6, 041302. [Google Scholar] [CrossRef]
- Masoudi, A.; Belal, M.; Newson, T.P. A distributed optical fibre dynamic strain sensor based on phase-OTDR. Meas. Sci. Technol. 2013, 24, 085204. [Google Scholar] [CrossRef]
- Song, W. Research on OTDR AUTOMATED Testing Related Technologies; Harbin Institute of Technology: Harbin, China, 2021. [Google Scholar]
- Yan, R.; Zhao, Z.; Gao, W.; Yang, L.; Wang, Y.; Hu, Y. Status quo, and prospect of urban gas pipeline leak detection technology. Gas Heat 2021, 41, 27–29. [Google Scholar]
- He, X.; Xie, S.; Liu, F.; Cao, S.; Gu, L.; Zheng, X.; Zhang, M. Multi-event waveform-retrieved distributed optical fiber acoustic sensor using dual-pulse heterodyne phase-sensitive OTDR. Opt. Lett. 2017, 42, 442–445. [Google Scholar] [CrossRef] [PubMed]
- He, X.; Zhang, M.; Gu, L.; Xie, S.; Liu, F.; Lu, H. Performance Improvement of Dual-Pulse Heterodyne Distributed Acoustic Sensor for Sound Detection. Sensors 2020, 20, 999. [Google Scholar] [CrossRef] [Green Version]
- Sun, M.; Yang, S.; Tang, Y.; Zhao, X.; Zhang, Z.; Zhuang, F. Distributed fiber optic temperature sensing system based on dynamic calibration of Raman scattered light. Acta Phys. Sin. Ch. Ed. 2022, 71, 1–15. [Google Scholar]
- Lu, Q.; Wang, Z. Study on the propagation characteristics of spherical stress waves in standard linear solid materials. J. Phys. 2015, 64, 352–358. [Google Scholar]
- Lai, H.; Wang, Z.; Yang, L.; Wang, L. Characteristic line analysis of linear viscoelastic spherical waves. Explos. Shock. 2013, 33, 1–10. [Google Scholar]
- Huo, L.; Yue, G.; Wang, B. Joule-Thomson effect during gas pressure relief. Coal Sci. Technol. 2017, 45, 127–133. [Google Scholar]
- Wang, J.; Wang, H. The effect of a natural gas pipeline leak on the temperature of the surrounding soil. Pet. Eng. Constr. 2020, 46, 5–8. [Google Scholar]
- Wang, J.; Wang, H.; Cui, K.; Rong, Z.; Zhang, G. Application of fiber optic temperature sensor in gas pipeline leak monitoring. Opt. Commun. Technol. 2021, 45, 19–22. [Google Scholar]
- Kasch, M.; Hurtig, E.; Grosswig, S.; Schubart, P. Leak detection and online surveying at underground gas pipelines using fibre optic temperature sensing. Oil Gas 1997, 23, 17–21. [Google Scholar]
- Zhou, Z.; Tan, J.; Zhang, J.; Huang, X.; Wu, D. High pressure buried gas pipeline leakage temperature drop testing and theory analysis. Numer. Heat Transfer Part A Appl. 2020, 78, 18–28. [Google Scholar] [CrossRef]
- Mao, W.; Zhang, L. Study on the calculation method of Joule-Thomson coefficient. Spec. Oil Gas Reserv. 2002, 9, 44–46. [Google Scholar]
- Peng, S.; Chen, J.; Yang, J. Calculation of natural gas insulation throttle temperature drop. Gas Heat 2006, 26, 1–4. [Google Scholar]
- Zhan, Y.; Cai, H.; Xiang, S.; Zhai, R.; Wang, X. Research on high-resolution fiber optic grating temperature sensors. Chin. J. Lasers 2005, 83–86. [Google Scholar]


| Density (kg/m3) | Young’s Modulus (GPa) | Poisson’s Ratio | Bulk Modulus (Pa) | Shear Modulus (Pa) | |
|---|---|---|---|---|---|
| Value | 2220 | 73 | 0.17 | 3.6869 × 1010 | 3.1197 × 1010 |
| Case | Number of Grids | Mesh Quality | Pressure on Fiber Surface (Pa) | Grid Cell Size/mm |
|---|---|---|---|---|
| 1 | 63,036 | 0.2 | 385.5 | 50 |
| 2 | 163,552 | 0.2 | 399.1 | 40 |
| 3 | 182,008 | 0.2 | 401.4 | 30 |
| 4 | 220,054 | 0.2 | 402.2 | 20 |
| 5 | 319,240 | 0.2 | 402.3 | 10 |
| 6 | 336,523 | 0.2 | 402.1 | 5 |
| Soil Type | Average Particle Diameter (mm) | Porosity (%) | Viscous Drag Coefficient (m–2) | Inertia Drag Coefficient (m–1) |
|---|---|---|---|---|
| Silty sand | 0.50 | 25 | 2.16 × 1010 | 3.36 × 105 |
| loam | 0.05 | 43 | 2.45 × 1011 | 5.02 × 105 |
| clay | 0.01 | 30 | 2.72 × 1013 | 9.07 × 106 |
| Type of Soil | α (m–1) |
|---|---|
| clay | 1.151 |
| loamy soil | 2.168 |
| silty sand | 3.919 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, S.; Xie, S.; Li, Y.; Yuan, M.; Qian, X. Detection of Gas Pipeline Leakage Using Distributed Optical Fiber Sensors: Multi-Physics Analysis of Leakage-Fiber Coupling Mechanism in Soil Environment. Sensors 2023, 23, 5430. https://doi.org/10.3390/s23125430
Zhang S, Xie S, Li Y, Yuan M, Qian X. Detection of Gas Pipeline Leakage Using Distributed Optical Fiber Sensors: Multi-Physics Analysis of Leakage-Fiber Coupling Mechanism in Soil Environment. Sensors. 2023; 23(12):5430. https://doi.org/10.3390/s23125430
Chicago/Turabian StyleZhang, Shuyu, Shangran Xie, Yuanzhi Li, Mengqi Yuan, and Xinming Qian. 2023. "Detection of Gas Pipeline Leakage Using Distributed Optical Fiber Sensors: Multi-Physics Analysis of Leakage-Fiber Coupling Mechanism in Soil Environment" Sensors 23, no. 12: 5430. https://doi.org/10.3390/s23125430
APA StyleZhang, S., Xie, S., Li, Y., Yuan, M., & Qian, X. (2023). Detection of Gas Pipeline Leakage Using Distributed Optical Fiber Sensors: Multi-Physics Analysis of Leakage-Fiber Coupling Mechanism in Soil Environment. Sensors, 23(12), 5430. https://doi.org/10.3390/s23125430





