A Joint Acoustic Emission Source Localization Method for Composite Materials
Abstract
:1. Introduction
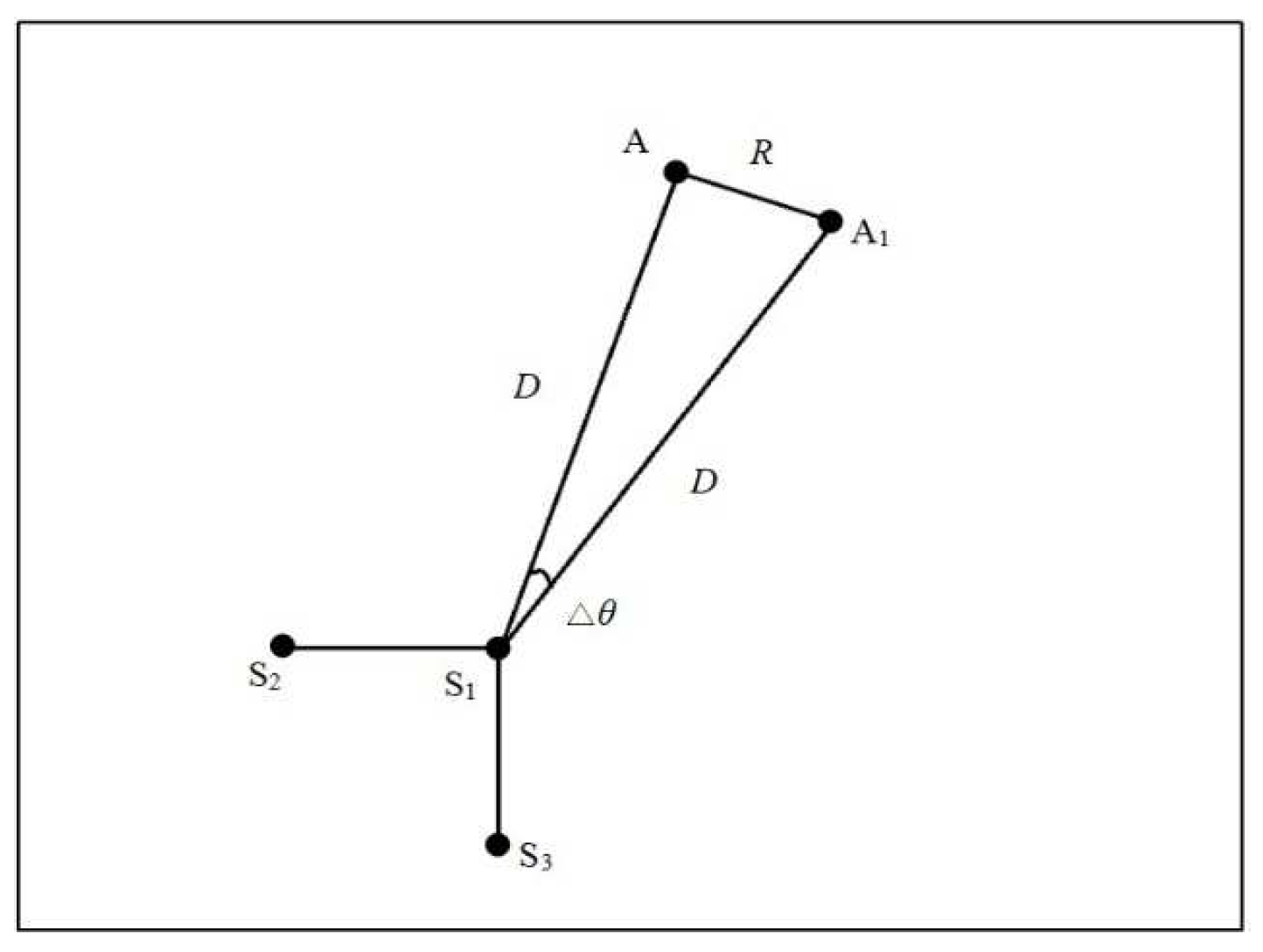
2. Principle and Performance Analysis of Time-Difference-Blind Localization Method
2.1. Principle of Time-Difference-Blind Localization Method
2.2. Test Object and Localization Results
2.3. Error Analysis
3. Principle and Performance Analysis of Beamforming Localization Method
4. Joint Localization of the Time-Difference-Blind Localization Method and Beamforming Method
4.1. Principle of the Joint Localization Method
- (1)
- Use the time-difference-blind localization method to locate the acoustic emission source with the collected data;
- (2)
- If the localization result of the time-difference-blind localization method is to the left (right) of the plate, bring the obtained data into the beamforming localization procedure. Change the area scanned in the program from the original whole plate to the left (right) half plate.
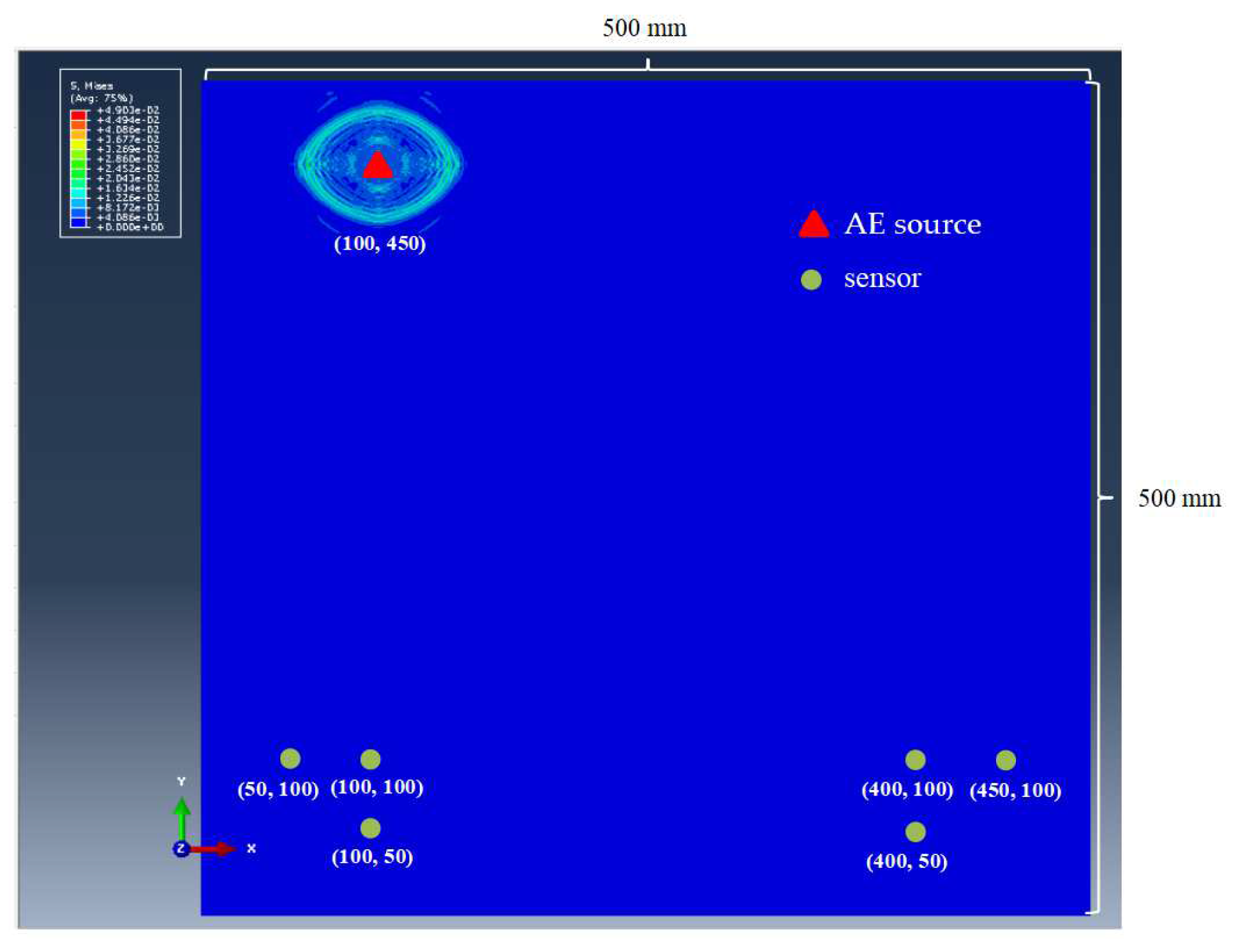
4.2. Simulation Verification
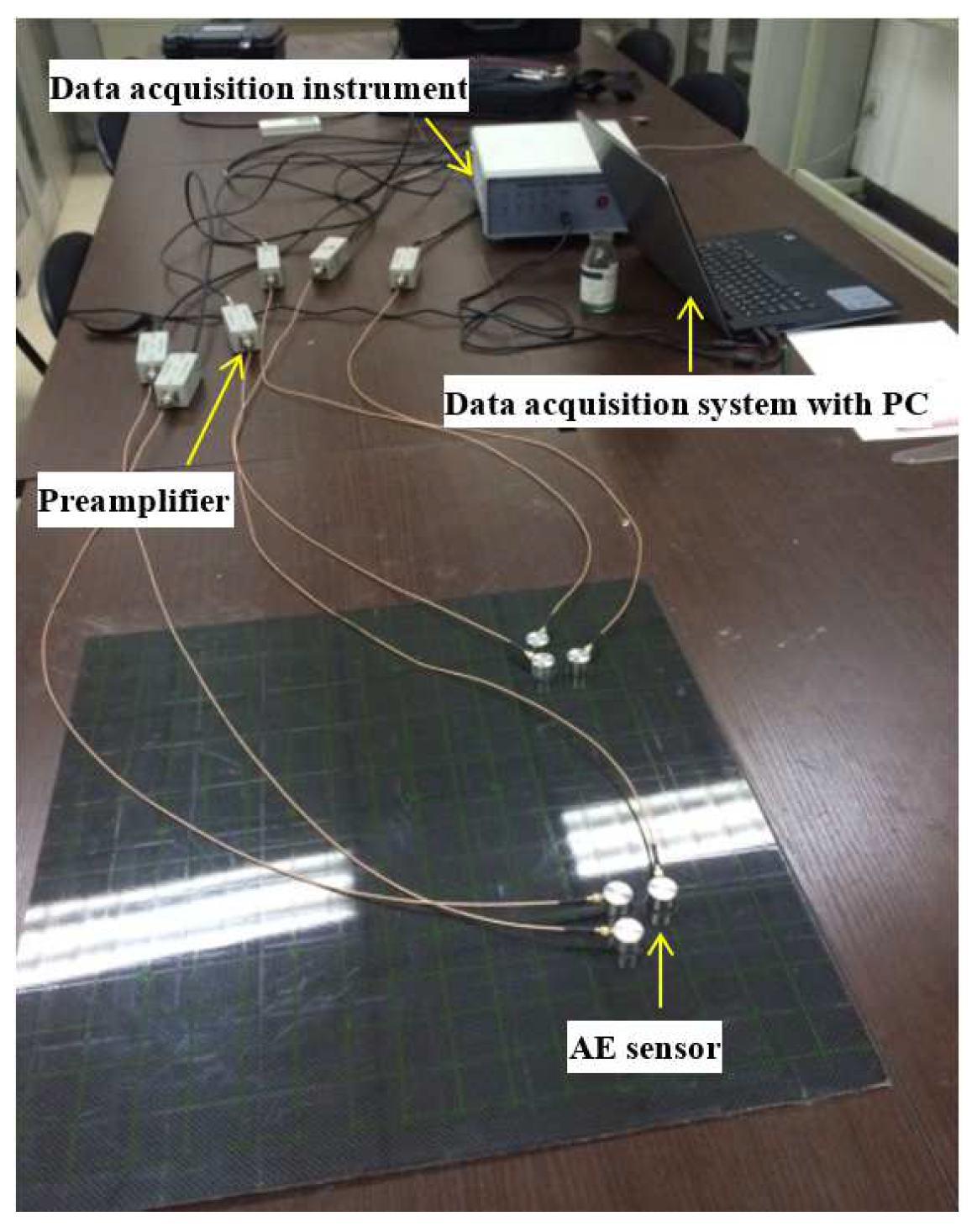
5. Experimental Verification
6. Conclusions
- (1)
- The assumption of the time-difference-blind localization method is that the position of the sound source is far enough from the sensors. However, the method shows difficulty in meeting its assumptions in use, resulting in large errors in localization results. Through analysis, it was found that the x-coordinate positioned by this method is accurate. Therefore, the approximate position of the acoustic emission source can be determined according to the abscissa of the localization result—for example, whether it is on the left or right of the composite material plate.
- (2)
- The beamforming localization method has high localization accuracy. However, the localization speed is very low since great quantities of points need to be scanned. The calculation speed is affected by the length of the calculation signal, the number of sensors, the localization accuracy (the higher the accuracy, the more points need to be scanned) and the size of the structure. Among these influencing factors, the signal length, number of sensors, localization accuracy and structural size are all rigid requirements, and it is difficult to change them for the speed of calculation.
- (3)
- Based on the advantages of the time-difference-blind localization method and beamforming localization method, the error of the joint localization method is smaller than the error of the time-difference-blind localization method, and the localization time is reduced by half compared with the beamforming localization method.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Rajak, D.K.; Pagar, D.D.; Menezes, P.L.; Linul, E. Fiber-reinforced polymer composites: Manufacturing, properties, and applications. Polymers 2019, 11, 1667. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Friedrich, K.; Almajid, A.A. Manufacturing aspects of advanced polymer composites for automotive applications. Appl. Compos. Mater. 2012, 20, 107–128. [Google Scholar] [CrossRef]
- Jensen, J.P.; Skelton, K. Wind turbine blade recycling: Experiences, challenges and possibilities in a circular economy. Renew. Sustain. Energy Rev. 2018, 97, 165–176. [Google Scholar] [CrossRef]
- Manalo, A.C.; Mendis, P.; Bai, Y.; Jachmann, B.; Sorbello, C.D. Fiber-reinforced polymer bars for concrete structures: State-of-the-practice in Australia. J. Compos. Constr. 2021, 25, 05020007. [Google Scholar] [CrossRef]
- Xu, X.; He, M.; Zhu, C.; Lin, Y.; Cao, C. A new calculation model of blasting damage degree—Based on fractal and tie rod damage theory. Eng. Fract. Mech. 2019, 220, 106619. [Google Scholar] [CrossRef]
- Rubino, F.; Nisticò, A.; Tucci, F.; Carlone, P. Marine application of fiber reinforced composites: A review. J. Mar. Sci. Eng. 2020, 8, 26. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Z.; Chen, M.; Li, S. Application and development of advanced composite materials for aircraft structures. In Proceedings of the Fourteenth National Conference on Composite Materials, Yichang, China, 15–17 October 2006. [Google Scholar]
- Crivelli, D.; Guagliano, M.; Monici, A. Development of an artificial neural network processing technique for the analysis of damage evolution in pultruded composites with acoustic emission. Compos. Part B Eng. 2014, 56, 948–959. [Google Scholar] [CrossRef] [Green Version]
- Surgeon, M.; Wevers, M. One sensor linear location of acoustic emission events using plate wave theories. Mater. Sci. Eng. A-Struct. Mater. Prop. Microstruct. Process. 1999, 265, 254–261. [Google Scholar] [CrossRef]
- Qiu, X.; Wang, Y.; Xu, J.; Xiao, S.; Li, C. Acoustic emission propagation characteristics and damage source localization of asphalt mixtures. Constr. Build. Mater. 2020, 252, 119086. [Google Scholar] [CrossRef]
- Veen, B.V.; Buckley, K.M. Beamforming: A versatile approach to spatial filtering. IEEE Assp Mag. 1988, 5, 4–24. [Google Scholar] [CrossRef]
- Mclaskey, G.C.; Glaser, S.D.; Grosse, C.U. Beamforming array techniques for acoustic emission monitoring of large concrete structures. J. Sound Vib. 2010, 329, 2384–2394. [Google Scholar] [CrossRef]
- He, T.; Pan, Q.; Liu, Y.; Liu, X.; Hu, D. Near-field beamforming analysis for acoustic emission source localization. Ultrasonics 2012, 52, 587–592. [Google Scholar] [CrossRef] [PubMed]
- Nakatani, H.; Hajzargarbashi, T.; Ito, K.; Kundu, T.; Takeda, N. Impact localization on a cylindrical plate by near-field beamforming analysis. In Sensors and Smart Structures Technologies for Civil, Mechanical, and Aerospace Systems, Proceedings of the SPIE’s 2012 Annual International Symposium on Smart Structures and Nondestructive Evaluation, San Diego, CA, USA, 12–15 March 2012; SPIE: Bellingham, WA, USA, 2012; p. 83450Y. [Google Scholar]
- He, T.; Xiao, D.; Pan, Q.; Liu, X.; Shan, Y. Analysis on accuracy improvement of rotor-stator rubbing localization based on acoustic emission beamforming method. Ultrasonics 2014, 54, 318–329. [Google Scholar] [CrossRef] [PubMed]
- He, T.; Tai, J.; Shan, Y.; Wang, X.; Liu, X. A fast acoustic emission beamforming localization method based on hilbert curve. Mech. Syst. Signal Process. 2019, 133, 106291. [Google Scholar] [CrossRef]
- Wang, X.; Liu, X.; He, T.; Tai, J.; Shan, Y. A novel joint localization method for acoustic emission source based on time difference of arrival and beamforming. Appl. Sci. 2020, 10, 8045. [Google Scholar] [CrossRef]
- He, T.; Xiao, D.H.; Liu, X.D.; Shan, Y.C. Research on acoustic emission source localization based on near field beamforming method. J. Vib. Eng. 2012, 025, 199–205. [Google Scholar]
- Tobias, A. Acoustic-emission source location in two dimensions by an array of three sensors. Non-Destruct. Test. 1976, 9, 9–12. [Google Scholar] [CrossRef]
- Ahadi, M.; Bakhtiar, M.S. Leak detection in water-filled plastic pipes through the application of tuned wavelet transforms to Acoustic Emission signals. Appl. Acoust. 2010, 71, 634–639. [Google Scholar] [CrossRef]
- Gorman, M.R. Plate wave acoustic emission. J. Acoust. Soc. Am. 1991, 90, 358–364. [Google Scholar] [CrossRef]
- Gangadharan, R.; Prasanna, G.; Bhat, M.R.; Murthy CR, L.; Gopalakrishnan, S. Acoustic emission source location in composite structure by Voronoi construction using geodesic curve evolution. J. Acoust. Soc. Am. 2009, 126, 2324–2330. [Google Scholar] [CrossRef]
- Gollob, S.; Kocur, G.K.; Schumacher, T.; Mhamdi, L.; Vogel, T. A novel multi-segment path analysis based on a heterogeneous velocity model for the localization of acoustic emission sources in complex propagation media. Ultrasonics 2017, 74, 48–61. [Google Scholar] [CrossRef] [PubMed]
- Madarshahian, R.; Ziehl, P.; Caicedo, J.M. Acoustic emission Bayesian source location: Onset time challenge. Mech. Syst. Signal Process. 2019, 123, 483–495. [Google Scholar] [CrossRef]
- Dong, L.; Zou, W.; Li, X.; Shu, W.; Wang, Z. Collaborative localization method using analytical and iterative solutions for microseismic/acoustic emission sources in the rockmass structure for underground mining. Eng. Fract. Mech. 2019, 210, 95–112. [Google Scholar] [CrossRef]
- Kundu, T.; Nakatani, H.; Takeda, N. Acoustic source localization in anisotropic plates. Ultrasonics 2012, 52, 740–746. [Google Scholar] [CrossRef] [PubMed]
- Yin, S.; Cui, Z.; Kundu, T. Acoustic source localization in anisotropic plates with “Z” shaped sensor clusters. Ultrasonics 2018, 84, 34–37. [Google Scholar] [CrossRef]
- Park, W.H.; Packo, P.; Kundu, T. Acoustic source localization in an anisotropic plate without knowing its material properties—A new approach. Ultrasonics 2017, 79, 9–17. [Google Scholar] [CrossRef] [Green Version]
- Sen, N.; Kundu, T. A new wave front shape-based approach for acoustic source localization in an anisotropic plate without knowing its material properties. Ultrasonics 2018, 87, 20–32. [Google Scholar] [CrossRef] [Green Version]
- Sen, N.; Gawroński, M.; Packo, P.; Uhl, T.; Kundu, T. Square-shaped sensor clusters for acoustic source localization in anisotropic plates by wave front shape-based approach. Mech. Syst. Signal Process. 2021, 153, 107489. [Google Scholar] [CrossRef]
- Xiao, D.; He, T.; Pan, Q.; Liu, X.; Wang, J.; Shan, Y. A novel acoustic emission beamforming method with two uniform linear arrays on plate-like structures. Ultrasonics 2014, 54, 737–745. [Google Scholar] [CrossRef]

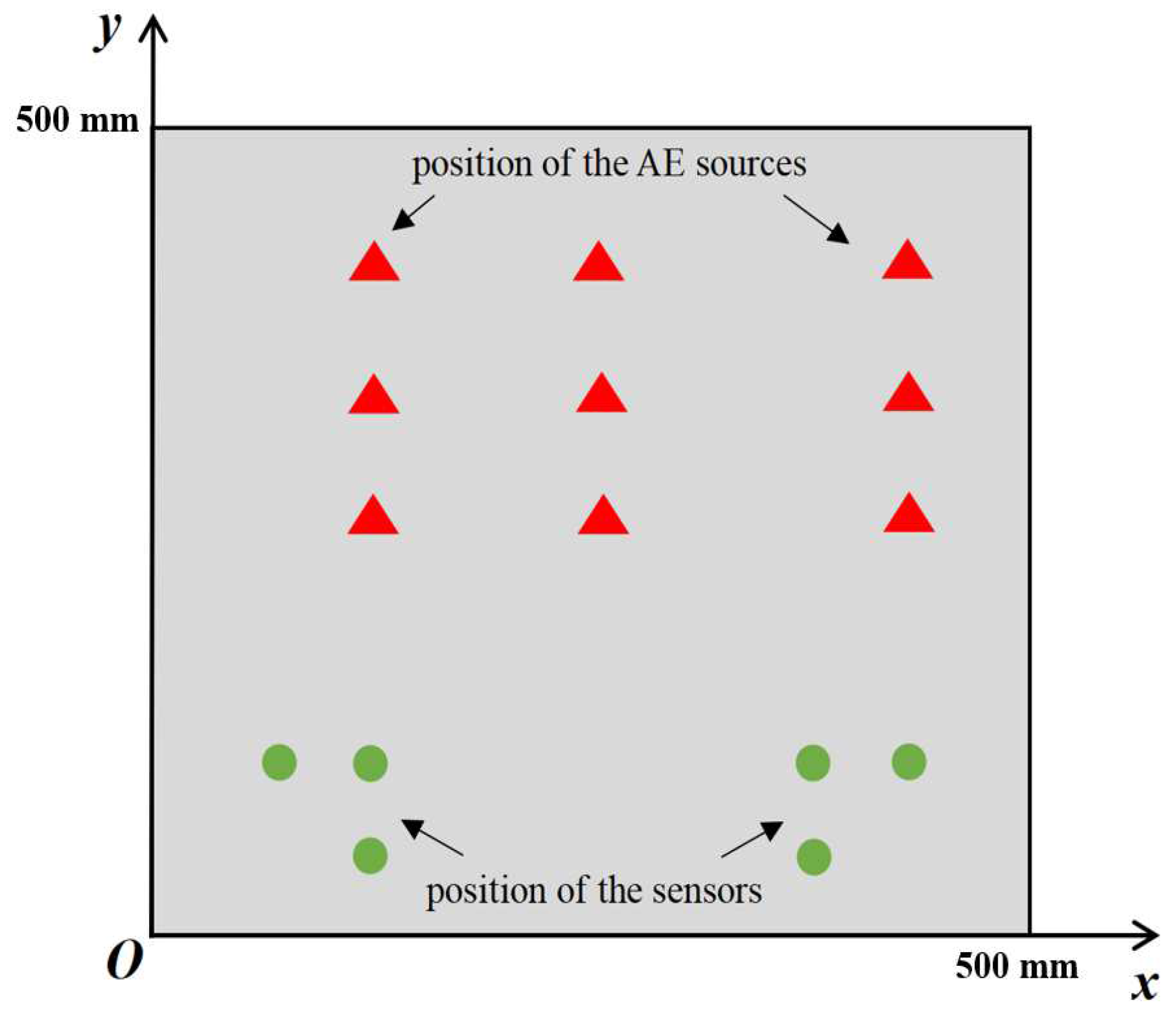
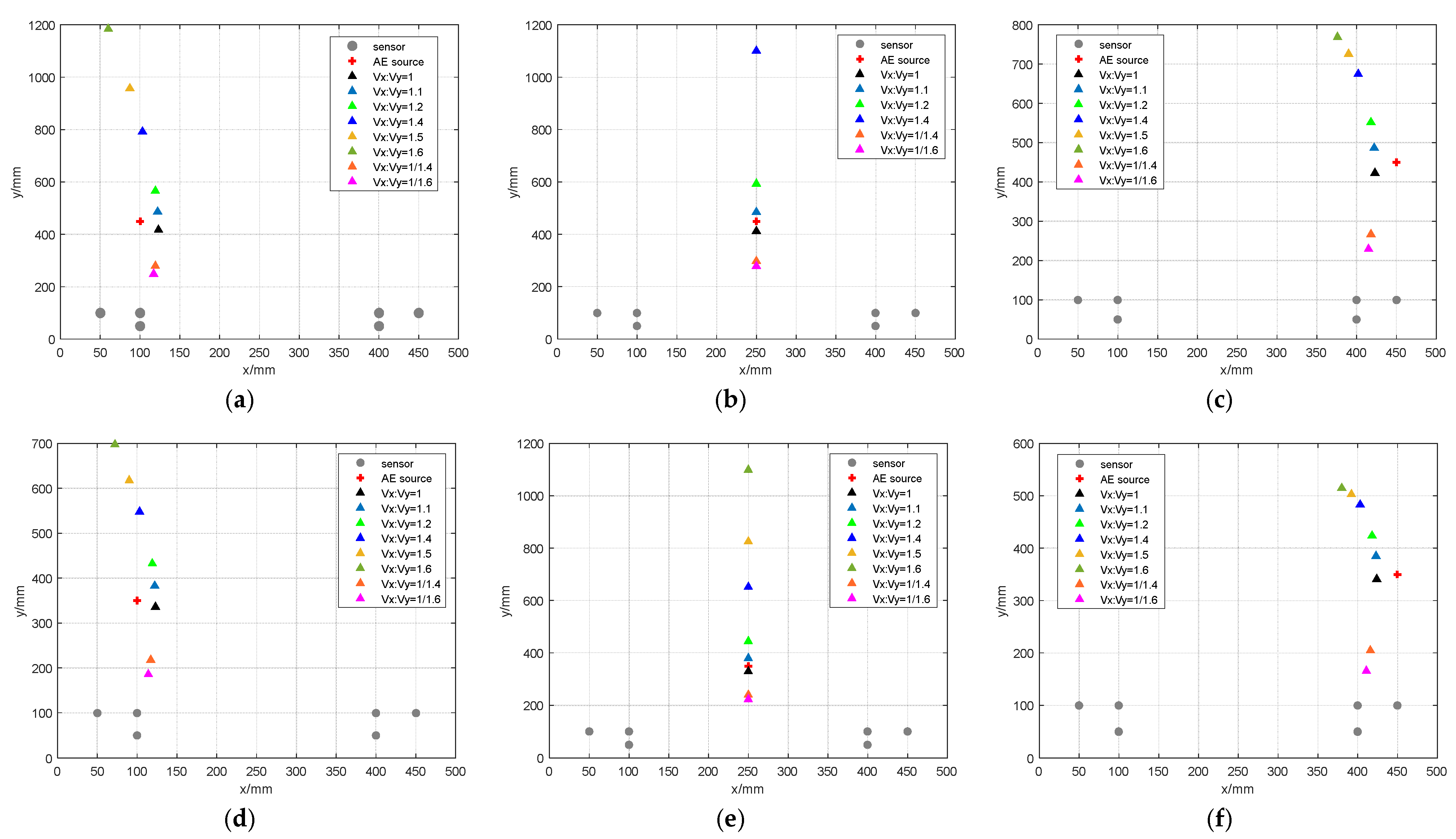
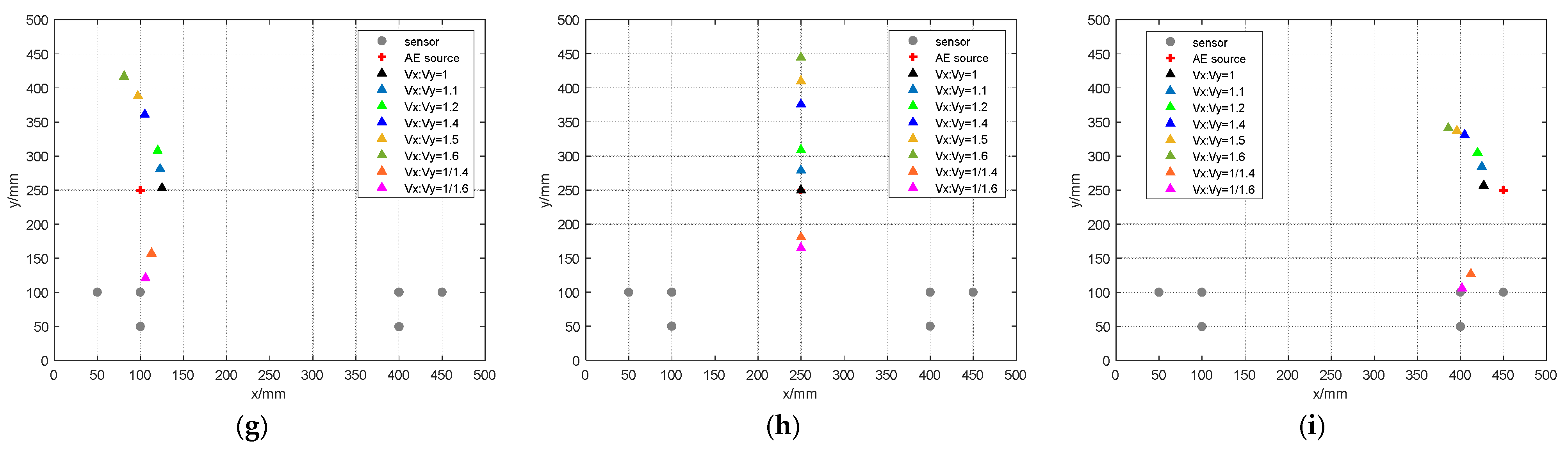

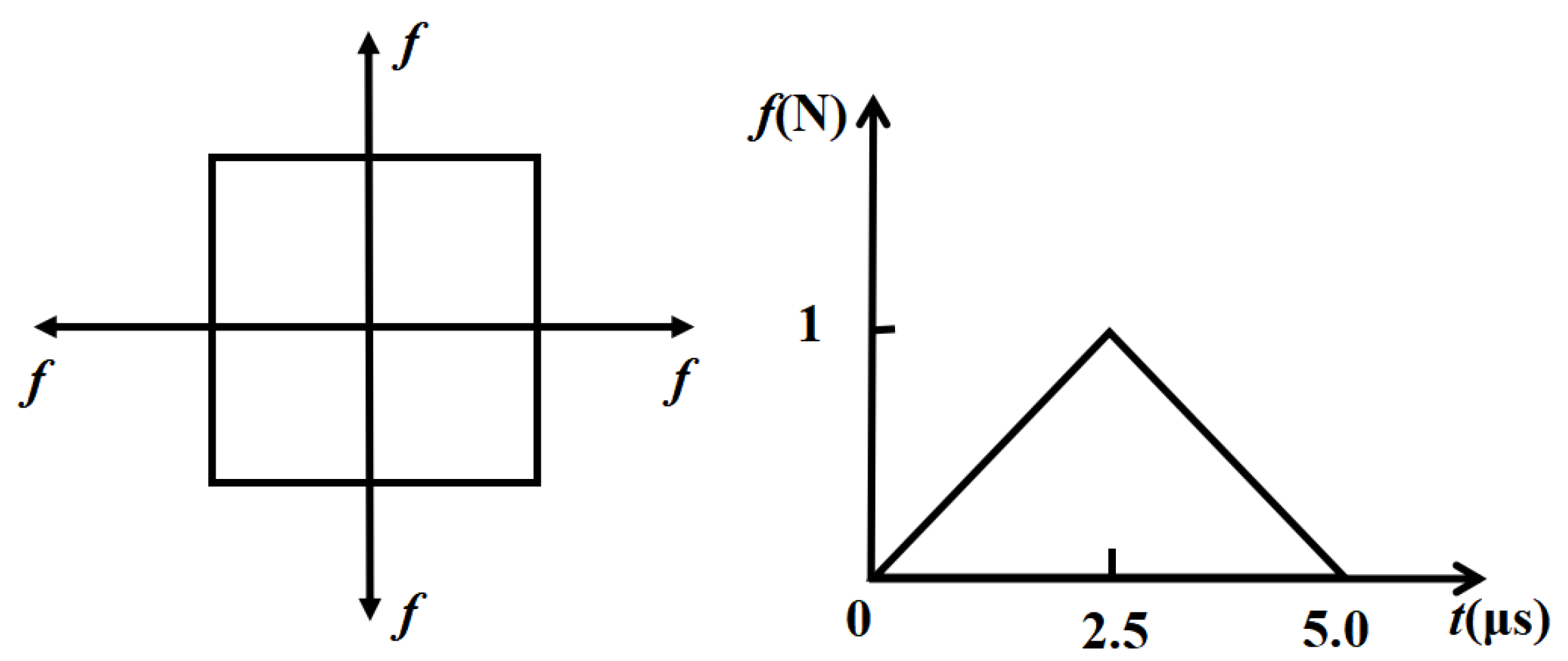

| Coordinate of AE Source/mm | Vx:Vy = 1 | Vx:Vy = 1.1 | ||||
| Locating Point/mm | Error of Coordinate/mm | Error of Distance/mm | Locating Point/mm | Error of Coordinate/mm | Error of Distance/mm | |
| (100, 250) | (125, 253) | (25, 3) | 25 | (123, 281) | (23, 31) | 39 |
| (250, 250) | (250, 250) | (0, 0) | 0 | (250, 279) | (0, 29) | 29 |
| (450, 250) | (427, 257) | (−23, 7) | 24 | (425, 284) | (−25, 34) | 42 |
| (100, 350) | (123, 336) | (23, −14) | 27 | (122, 383) | (22, 33) | 40 |
| (250, 350) | (250, 330) | (0, 30) | 30 | (250, 380) | (0, 30) | 30 |
| (450, 350) | (424, 341) | (−26, −9) | 28 | (423, 385) | (−27, 35) | 44 |
| (100, 450) | (123, 418) | (23, −32) | 39 | (122, 486) | (22, 36) | 42 |
| (250, 450) | (250, 412) | (0, −38) | 38 | (250, 485) | (0, 35) | 35 |
| (450, 450) | (423, 423) | (27, 27) | 38 | (422, 487) | (−28, 37) | 46 |
| Coordinate of AE Source/mm | Vx:Vy = 1.2 | Vx:Vy = 1.4 | ||||
| Locating Point/mm | Error of Coordinate/mm | Error of Distance/mm | Locating Point/mm | Error of Coordinate/mm | Error of Distance/mm | |
| (100, 250) | (120, 308) | (20, 58) | 61 | (105, 361) | (5, 111) | 111 |
| (250, 250) | (250, 309) | (0, 59) | 59 | (250, 376) | (0, 126) | 126 |
| (450, 250) | (420, 305) | (−30, 55) | 63 | (405, 331) | (−45, 81) | 93 |
| (100, 350) | (119, 433) | (19, 83) | 85 | (103, 548) | (3, 198) | 198 |
| (250, 350) | (250, 445) | (0, 95) | 95 | (250, 652) | (0, 302) | 302 |
| (450, 350) | (418, 424) | (−32, 74) | 81 | (403, 483) | (−47, 133) | 141 |
| (100, 450) | (119, 566) | (19, 116) | 118 | (103, 792) | (3, 342) | 342 |
| (250, 450) | (250, 593) | (0, 143) | 143 | (250, 1101) | (0, 651) | 651 |
| (450, 450) | (418, 552) | (−32, 102) | 107 | (402, 675) | (−48, 225) | 230 |
| Coordinate of AE Source/mm | Vx:Vy = 1.5 | Vx:Vy = 1.6 | ||||
| Locating Point/mm | Error of Coordinate/mm | Error of Distance/mm | Locating Point/mm | Error of Coordinate/mm | Error of Distance/mm | |
| (100, 250) | (97, 388) | (−3, 138) | 138 | (81, 417) | (−19, 167) | 168 |
| (250, 250) | (250, 410) | (0, 160) | 160 | (250, 445) | (0, 195) | 195 |
| (450, 250) | (396, 337) | (−54, 87) | 102 | (386, 341) | (−64, 91) | 111 |
| (100, 350) | (90, 618) | (−10, 268) | 268 | (72, 698) | (−28, 348) | 349 |
| (250, 350) | (250, 826) | (0, 476) | 476 | (250, 1099) | (0, 749) | 749 |
| (450, 350) | (392, 503) | (−58, 153) | 164 | (380, 515) | (−70, 165) | 179 |
| (100, 450) | (87, 957) | (−13, 507) | 507 | (60, 1185) | (−40, 635) | 636 |
| (250, 450) | (250, 1933) | (0, 1483) | 1483 | (250, 7663) | (0, 7213) | 7213 |
| (450, 450) | (390, 726) | (−60, 276) | 282 | (376, 769) | (−74, 319) | 327 |
| Coordinate of AE Source/mm | Vx:Vy = 1/1.4 | Vx:Vy = 1/1.6 | ||||
| Locating Point/mm | Error of Coordinate/mm | Error of Distance/mm | Locating Point/mm | Error of Coordinate/mm | Error of Distance/mm | |
| (100, 250) | (113, 157) | (13, −93) | 94 | (106, 121) | (6, −129) | 129 |
| (250, 250) | (250, 181) | (0, −69) | 69 | (250, 165) | (0, −85) | 85 |
| (450, 250) | (412, 127) | (−38, −123) | 129 | (402, 106) | (−48, −144) | 152 |
| (100, 350) | (117, 218) | (17, −132) | 133 | (114, 186) | (14, −164) | 165 |
| (250, 350) | (250, 240) | (0, −110) | 110 | (250, 223) | (0, −127) | 127 |
| (450, 350) | (416, 205) | (−34, −145) | 149 | (411, 166) | (−39, 184) | 188 |
| (100, 450) | (119, 280) | (19, −170) | 171 | (117, 249) | (17, −201) | 202 |
| (250, 450) | (250, 298) | (0, 152) | 152 | (250, 278) | (0, −172) | 172 |
| (450, 450) | (418, 267) | (−32, −183) | 186 | (415, 230) | (−35, −220) | 223 |
| Coordinate of AE Source/mm | Error/mm | |||
|---|---|---|---|---|
| Sensors Spacing | ||||
| 1 mm | 10 mm | 30 mm | 50 mm | |
| (100, 450) | 0.86 | 8.48 | 24.35 | 38.89 |
| (250, 450) | 0.90 | 8.75 | 24.47 | 38.15 |
| (450,450) | 0.81 | 8.00 | 23.39 | 37.94 |
| (100, 350) | 0.58 | 5.74 | 16.83 | 27.34 |
| (250, 350) | 0.48 | 4.62 | 12.88 | 20.02 |
| (450, 350) | 0.54 | 5.43 | 16.43 | 27.43 |
| (100, 250) | 0.51 | 5.1 | 15.19 | 24.88 |
| (250, 250) | 0 | 0 | 0 | 0 |
| (450, 250) | 0.45 | 4.59 | 14.27 | 24.51 |
| Coordinate of AE Source/mm | Time-Difference-Blind Localization Method | Beamforming Localization Method | Joint Localization Method | |||
|---|---|---|---|---|---|---|
| Locating Point/mm | Calculating Time/s | Locating Point/mm | Calculating Time/s | Locating Point/mm | Calculating Time/s | |
| (100, 450) | (120, 833) | 0.373936 | (100, 480) | 3.789047 | (100, 480) | 2.268460 |
| (250, 450) | (250, 787) | 0.796325 | (250, 150) | 3.897832 | (250, 150) | 2.745241 |
| (450, 450) | (421, 846) | 0.110530 | (450, 480) | 3.784312 | (450, 480) | 2.002686 |
| (100, 350) | (125, 649) | 0.107162 | (100, 370) | 3.712398 | (100, 370) | 1.963361 |
| (250, 350) | (250, 609) | 0.813859 | (250, 340) | 3.732149 | (250, 340) | 2.679934 |
| (450, 350) | (427, 692) | 0.118872 | (450, 360) | 3.873213 | (450, 360) | 2.055478 |
| (100, 250) | (130, 468) | 0.106911 | (120, 390) | 3.897124 | (120, 390) | 2.055473 |
| (250, 250) | (250, 442) | 0.840809 | (250, 250) | 3.984321 | (250, 250) | 2.832970 |
| (450, 250) | (434, 497) | 0.099531 | (470, 430) | 3.789047 | (470, 430) | 2.021392 |
| Coordinate of AE Source/mm | Time-Difference-Blind Localization Method | Beamforming Localization Method | Joint Localization Method | |||
|---|---|---|---|---|---|---|
| Error of Coordinate/mm | Error of Distance/mm | Error of Coordinate/mm | Error of Distance/mm | Error of Distance/mm | Error of Distance/mm | |
| (100, 450) | (20, 383) | 384 | (0, 30) | 30 | (0, 30) | 30 |
| (250, 450) | (0, 337) | 337 | (0, 300) | 300 | (0, 300) | 300 |
| (450, 450) | (29, 396) | 397 | (0, 30) | 30 | (0, 30) | 30 |
| (100, 350) | (25, 299) | 300 | (0, 20) | 20 | (0, 20) | 20 |
| (250, 350) | (0, 259) | 259 | (0, 10) | 10 | (0, 10) | 10 |
| (450, 350) | (23, 342) | 343 | (0, 10) | 10 | (0, 10) | 10 |
| (100, 250) | (30, 218) | 220 | (20, 140) | 141 | (20, 140) | 141 |
| (250, 250) | (0, 192) | 192 | (0, 0) | 0 | (0, 0) | 0 |
| (450, 250) | (16, 247) | 248 | (20, 180) | 181 | (20, 180) | 181 |
| Coordinate of AE Source /mm | Time-Difference-Blind Localization Method | Beamforming Localization Method | Joint Localization Method | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Locating Point/mm | Error of Coordinate/mm | Error of Distance/mm | Locating Point/mm | Error of Coordinate/mm | Error of Distance/mm | Locating Point/mm | Error of Coordinate/mm | Error of Distance/mm | |
| (100, 450) | (140, 298) | (40, 152) | 157 | (102, 477) | (2, 27) | 27 | (102, 477) | (2, 27) | 27 |
| (250, 450) | (237, 301) | (13, 149) | 150 | (253, 407) | (3, 43) | 43 | (253, 407) | (3, 43) | 43 |
| (450, 450) | (462, 418) | (12, 32) | 34 | (444, 466) | (6, 16) | 17 | (444, 466) | (6, 16) | 17 |
| (100, 350) | (138, 266) | (38, 84) | 92 | (100, 366) | (0, 16) | 16 | (100, 366) | (0, 16) | 16 |
| (250, 350) | (235, 256) | (15, 94) | 95 | (252, 347) | (2, 3) | 4 | (252, 347) | (2, 3) | 4 |
| (450, 350) | (463, 373) | (13, 23) | 26 | (449, 361) | (1, 11) | 11 | (449, 361) | (1, 11) | 11 |
| (100, 250) | (147, 238) | (47, 12) | 49 | (118, 395) | (18, 145) | 146 | (118, 395) | (18, 145) | 146 |
| (250, 250) | (234, 220) | (16, 30) | 34 | (250, 249) | (0, 1) | 1 | (250, 249) | (0, 1) | 1 |
| (450, 250) | (466, 302) | (16, 52) | 54 | (475, 442) | (25, 192) | 194 | (475, 442) | (25, 192) | 194 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, X.; Yin, F.; Wan, Z. A Joint Acoustic Emission Source Localization Method for Composite Materials. Sensors 2023, 23, 5473. https://doi.org/10.3390/s23125473
Wang X, Yin F, Wan Z. A Joint Acoustic Emission Source Localization Method for Composite Materials. Sensors. 2023; 23(12):5473. https://doi.org/10.3390/s23125473
Chicago/Turabian StyleWang, Xiaoran, Fang Yin, and Zhishuai Wan. 2023. "A Joint Acoustic Emission Source Localization Method for Composite Materials" Sensors 23, no. 12: 5473. https://doi.org/10.3390/s23125473
APA StyleWang, X., Yin, F., & Wan, Z. (2023). A Joint Acoustic Emission Source Localization Method for Composite Materials. Sensors, 23(12), 5473. https://doi.org/10.3390/s23125473





