The Unknown Abnormal Condition Monitoring Method for Pumped-Storage Hydroelectricity
Abstract
:1. Introduction
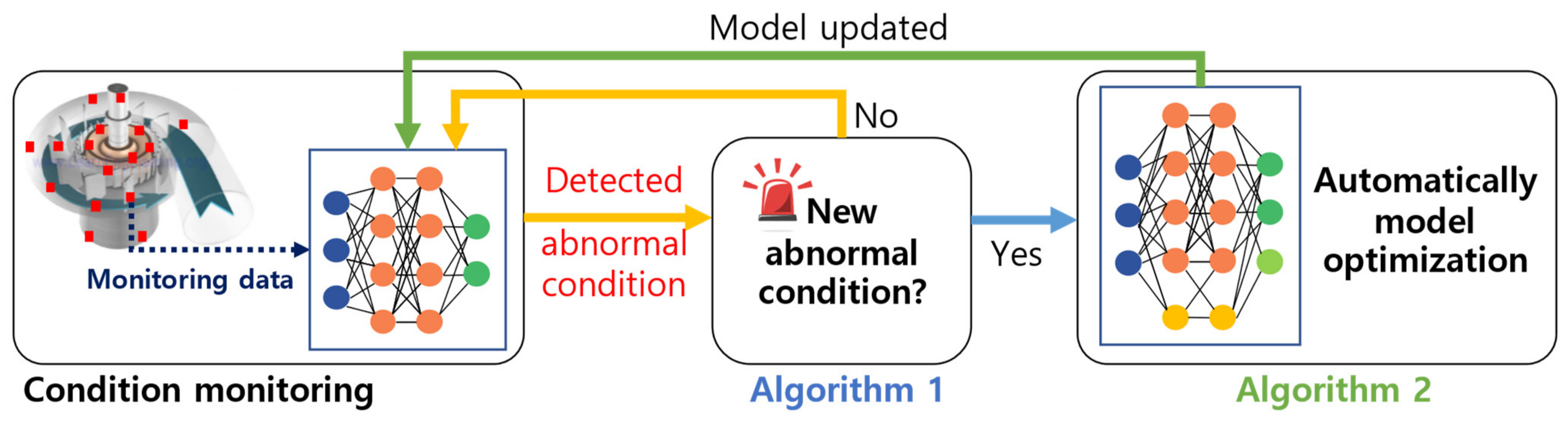
2. Pumped-Storage Hydroelectricity Condition-Monitoring Method
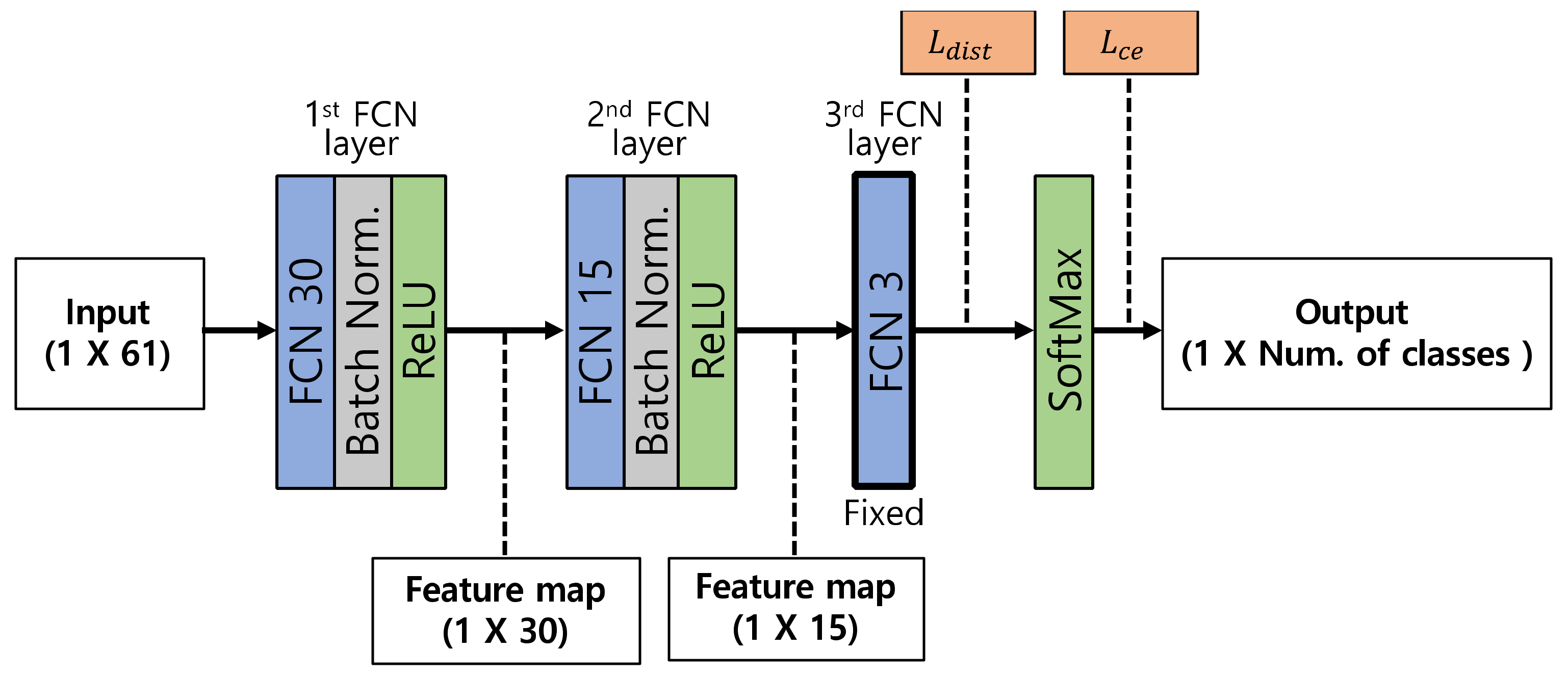
2.1. Base Model Configuration of ACDN
2.2. Algorithm 1: Open Set Recognition for Detecting New Abnormal Conditions
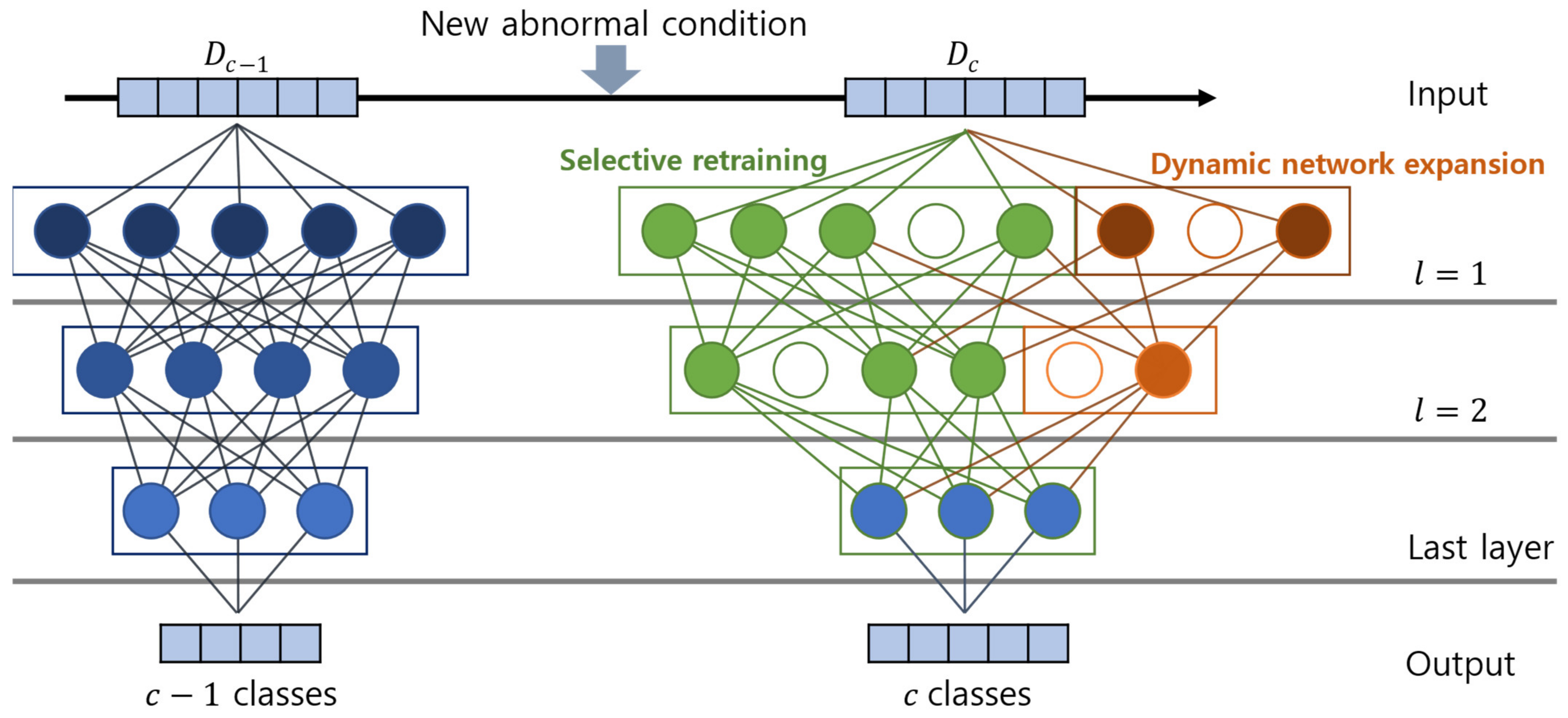
2.3. Algorithm 2: Model Optimization for Adding New Abnormal Condition
3. Experimental Verification of the Performance of the Proposed Method
3.1. Description of the Target PSH System and Its Condition-Monitoring System
3.2. Dataset
3.3. Comparison Models for Validation and Model Training
- DNN-MTL (reference model): base deep neural networks (DNN) are manually trained for each task separately. MTL indicates “Manually Task Learning.” Without class incrementation, this is the most conventional machine learning model for classification. This model is optimized to have the highest classification accuracy for the data of this study.
- DNN-fine—same architecture as DNN-MTL model, trained for initial tasks and the fine-tuning of the last layer under an increasing number of conditions.
- INN—increment neural network (INN) for each task consistently, based on incremental learning. The most widely used machine learning model for increasing the number of classes.
- ACDN—the proposed model.
- ACDN-1st—base ACDN, applies Algorithm 2 at only the first layer. The computing cost and time are lower than those of the ACDN.
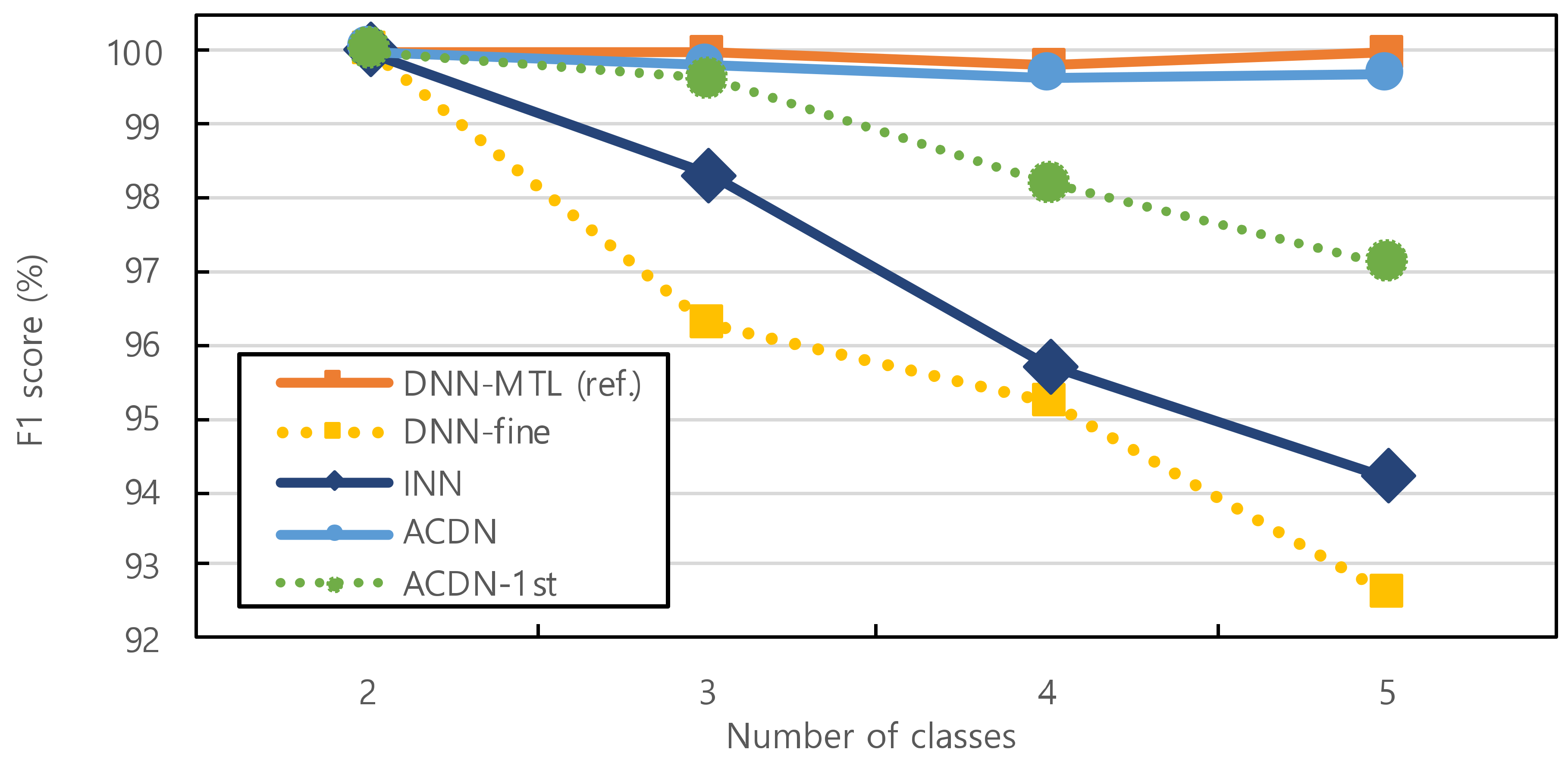
3.4. Performance Evaluation
4. Conclusions and Further Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Rehman, S.; Al-Hadhrami, L.M.; Alam, M.M. Pumped Hydro Energy Storage System: A Technological Review. Renew. Sustain. Energy Rev. 2015, 44, 586–598. [Google Scholar] [CrossRef]
- Yasuda, M.; Watanabe, S. How to Avoid Severe Incidents at Hydropower Plants. Int. J. Fluid Mach. Syst. 2017, 10, 296–306. [Google Scholar] [CrossRef]
- EPRI. Hydropower Technology Roundup Report: Accommodating Wear and Tear Effects on Hydroelectric Facilities Operating to Provide Ancillary Services; EPRI: Palo Alto, CA, USA, 2001. [Google Scholar]
- KEPCO. KHNP Annual Reports for Hydropower Plants (1996–2006); KEPCO: Naju-si, Republic of Korea, 2006. [Google Scholar]
- Dorji, U.; Analysis, R.G.-E.F. Hydro Turbine Failure Mechanisms: An Overview. Eng. Fail. Anal. 2014, 44, 136–147. [Google Scholar] [CrossRef]
- Bianchini, A.; Rossi, J.; Antipodi, L. A Procedure for Condition-Based Maintenance and Diagnostics of Submersible Well Pumps through Vibration Monitoring. Int. J. Syst. Assur. Eng. Manag. 2018, 9, 999–1013. [Google Scholar] [CrossRef]
- Valero, C.; Egusquiza, M.; Egusquiza, E.; Presas, A.; Id, D.V.; Bossio, M. Extension of Operating Range in Pump-Turbines. Influence of Head and Load. Energies 2017, 10, 2178. [Google Scholar] [CrossRef] [Green Version]
- Egusquiza, E.; Valero, C.; Valentin, D.; Measurement, A.P. Condition Monitoring of Pump-Turbines. New Challenges. Measurement 2015, 67, 151–163. [Google Scholar] [CrossRef] [Green Version]
- Zhao, W.; Egusquiza, M.; Valero, C.; Valentín, D.; Measurement, A.P. On the Use of Artificial Neural Networks for Condition Monitoring of Pump-Turbines with Extended Operation. Measurement 2020, 163, 107952. [Google Scholar] [CrossRef]
- Mustata, S.C.; Dracea, D.; Tronac, A.S.; Sarbu, N.; Constantin, E. Diagnosis and Vibration Diminishing in Pump Operation. Procedia Eng. 2015, 100, 970–976. [Google Scholar] [CrossRef]
- Li, H.; Xu, B.; Riasi, A.; Szulc, P.; Chen, D.; M’zoughi, F.; Skjelbred, H.I.; Kong, J.; Tazraei, P. Performance Evaluation in Enabling Safety for a Hydropower Generation System. Renew. Energy 2019, 143, 1628–1642. [Google Scholar] [CrossRef]
- Calvo-Bascones, P.; Sanz-Bobi, M.A.; Welte, T.M. Anomaly Detection Method Based on the Deep Knowledge behind Behavior Patterns in Industrial Components. Application to a Hydropower Plant. Comput. Ind. 2021, 125, 103376. [Google Scholar] [CrossRef]
- Selak, L.; Butala, P.; Industry, A.S.-C. Condition Monitoring and Fault Diagnostics for Hydropower Plants. Comput. Ind. 2014, 65, 924–936. [Google Scholar] [CrossRef]
- Betti, A.; Crisostomi, E.; Paolinelli, G.; Piazzi, A.; Ruffini, F.; Tucci, M. Condition Monitoring and Predictive Maintenance Methodologies for Hydropower Plants Equipment. Renew. Energy 2021, 171, 246–253. [Google Scholar] [CrossRef]
- Liu, X.; Tian, Y.; Lei, X.; Liu, M.; Wen, X.; Huang, H.; Wang, H. Deep Forest Based Intelligent Fault Diagnosis of Hydraulic Turbine. J. Mech. Sci. Technol. 2019, 33, 2049–2058. [Google Scholar] [CrossRef]
- Wen, W.; Wu, C.; Wang, Y.; Chen, Y.; Li, H. Learning Structured Sparsity in Deep Neural Networks. Adv. Neural Inf. Process. Syst. 2016, 29, 1–9. [Google Scholar]
- Alvarez, J.M.; Salzmann, M. Learning the Number of Neurons in Deep Networks. Adv. Neural Inf. Process Syst. 2016, 29, 2270–2278. [Google Scholar]
- KHNP. Casebook of Annual Reports for Hydropower Plants (2012–2018); KHNP: Gyeongju-si, Republic of Korea, 2018. [Google Scholar]
- Paszke, A.; Gross, S.; Massa, F.; Lerer, A.; Bradbury Google, J.; Chanan, G.; Killeen, T.; Lin, Z.; Gimelshein, N.; Antiga, L.; et al. PyTorch: An Imperative Style, High-Performance Deep Learning Library. Adv. Neural Inf. Process. Syst. 2019, 32, 1–12. [Google Scholar]
- Kingma, D.P.; Ba, J.L. Adam: A Method for Stochastic Optimization. In Proceedings of the 3rd International Conference on Learning Representations, ICLR 2015—Conference Track Proceedings, San Diego, CA, USA, 7–9 May 2015; Volume 1, pp. 448–456. [Google Scholar]
- Bergstra, J.; Ca, J.B.; Ca, Y.B. Random Search for Hyper-Parameter Optimization Yoshua Bengio. J. Mach. Learn. Res. 2012, 13, 281–305. [Google Scholar]
- Bendale, A.; Boult, T.E. Towards Open Set Deep Networks. In Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 1563–1572. [Google Scholar] [CrossRef]



| Facility | Typical Abnormal Conditions |
|---|---|
| Runner Draft tube | -Steel wear and leaking -Fatigue stress and cracks |
| Guide vane | -Efficiency degradation -Operating error-Loosening of bolts and bearing damage |
| Shaft | -Misalignment -Over-vibration -Distortion and fatigue |
| Generator | -Low insulation resistance -Shortening and sequence failure -Over-vibration -Overheating and thermal stress |
| Physical Quantities | Sensor Type | Number of Sensors |
|---|---|---|
| Temperature (°C) | Resistance temperature detector | 44 |
| Vibration (mm/s) | Eddy current proximity sensor | 9 |
| Displacement (µm) | Laser displacement sensor | 6 |
| Rotation speed (RPM) | Switch sensor | 1 |
| Guide vane opening rate (%) | Customized sensor | 1 |
| Operation State | Condition | Datapoints | Configuration of an Abnormal Condition |
|---|---|---|---|
| Pump state | Normal | 6,856,351 | - |
| Abnormal #1 | 13,351 | Crashing noise from rupturing residual air in hydropower turbine | |
| Abnormal #2 | 488 | Operating error due to the malfunction of a guide vane | |
| Turbine state | Normal | 6,993,007 | - |
| Abnormal #3 | 384 | Sequential failure at high output power of a generator | |
| Abnormal #4 | 3978 | High vibration from cracks at welding points of a hydropower turbine |
| Operation State | Condition | Actual Datapoints | Balanced Datapoints |
|---|---|---|---|
| Pump state | Normal | 6,856,351 | 1152 |
| Abnormal #1 | 13,351 | 384 | |
| Abnormal #2 | 488 | 384 | |
| Turbine state | Normal | 6,993,007 | 1152 |
| Abnormal #3 | 384 | 384 | |
| Abnormal #4 | 3978 | 384 |
| Number of Trained Classes | F1 Score (%) | |||||
|---|---|---|---|---|---|---|
| SoftMax (θ = 0.7) | Openmax | ACDN (Proposed) | ||||
| 3 DP * | Total | 3 DP * | Total | 3 DP * | Total | |
| 2 | 76.67 | 87.42 | 91.32 | 97.24 | 100 | 100 |
| 3 | 65.21 | 82.51 | 87.63 | 95.52 | 98.63 | 99.57 |
| 4 | 52.88 | 75.16 | 85.44 | 93.18 | 95.89 | 99.53 |
| Number of Classes | 2 | 3 | 4 | 5 |
|---|---|---|---|---|
| Precision | 100 | 99.74 | 99.47 | 99.48 |
| Recall | 100 | 100 | 100 | 100 |
| F1 score | 100 | 99.87 | 99.73 | 99.74 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, J.; Kim, K.; Sohn, H. The Unknown Abnormal Condition Monitoring Method for Pumped-Storage Hydroelectricity. Sensors 2023, 23, 6336. https://doi.org/10.3390/s23146336
Lee J, Kim K, Sohn H. The Unknown Abnormal Condition Monitoring Method for Pumped-Storage Hydroelectricity. Sensors. 2023; 23(14):6336. https://doi.org/10.3390/s23146336
Chicago/Turabian StyleLee, Jun, Kiyoung Kim, and Hoon Sohn. 2023. "The Unknown Abnormal Condition Monitoring Method for Pumped-Storage Hydroelectricity" Sensors 23, no. 14: 6336. https://doi.org/10.3390/s23146336
APA StyleLee, J., Kim, K., & Sohn, H. (2023). The Unknown Abnormal Condition Monitoring Method for Pumped-Storage Hydroelectricity. Sensors, 23(14), 6336. https://doi.org/10.3390/s23146336







