Affine Iterative Closest Point Algorithm Based on Color Information and Correntropy for Precise Point Set Registration
Abstract
:1. Introduction
- We introduce color information into affine point cloud registration, which can increase the robustness of the algorithm.
- we introduce the robust correntropy metric to address outliers and noises in the point clouds for more accurate registration.
2. A Review of the Traditional Affine ICP Algorithm
3. Precise Affine Registration with Correntropy and Color Information
3.1. Problem Statement
3.2. Precise Affine Registration with Color Information and Correntropy
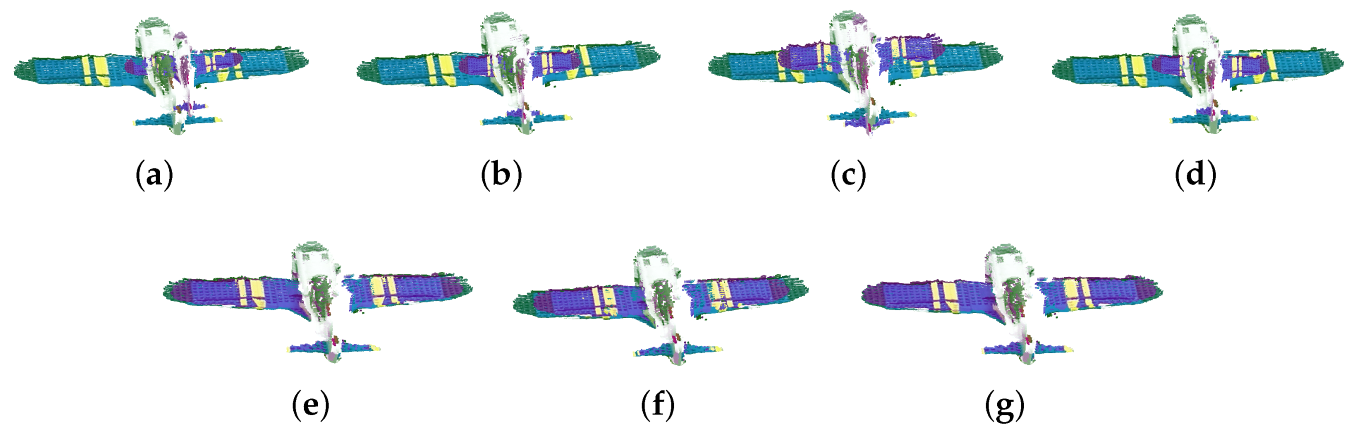
4. Experimental Results
4.1. Simulation Experiment
4.2. Indoor Scenes Experiment
4.3. Experiments with Real Data
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Liang, L.X. Precise iterative closest point algorithm for RGB-D data registration with noise and outliers. Neurocomputing 2020, 399, 361–368. [Google Scholar] [CrossRef]
- Yang, Y.; Fan, D.; Du, S.; Wang, M.; Chen, B.; Gao, Y. Point set registration with similarity and affine transformations based on bidirectional KMPE loss. IEEE Trans. Cybern. 2021, 51, 1678–1689. [Google Scholar] [CrossRef] [PubMed]
- Du, S.; Guo, Y.; Sanroma, G.; Ni, D.; Wu, G.; Shen, D. Building dynamic population graph for accurate correspondence detection. Med. Image Anal. 2015, 26, 256–267. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhang, H.; Zeng, D.; Zhang, H.; Wang, J.; Liang, Z.; Ma, J. Applications of nonlocal means algorithm in low-dose X-ray CT image processing and reconstruction: A review. Med. Phys. 2017, 44, 1168–1185. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Li, Y.; Zhang, H.; Bermudez, C.; Chen, Y.; Landman, B.; Vorobeychik, Y. Anatomical context protects deep learning from adversarial perturbations in medical imaging. Neurocomputing 2020, 379, 370–378. [Google Scholar] [CrossRef] [PubMed]
- Buenaventura, J.R.S.; Kobayashi, J.T.; Valles, L.M.P.; Goma, J.C.D.; Balan, A.K.D. Classification of varietal type of philippine rice grains using image processing through multi-View 3D reconstruction. In Proceedings of the 2nd International Conference on Computing and Big Data, Taichung, Taiwan, 18–20 October 2019; pp. 140–144. [Google Scholar]
- Rebecq, H.; Gallego, G.; Mueggler, E.; Scaramuzza, D. EMVS: Event-based multi-view stereo—3D reconstruction with an event camera in real-time. Int. J. Comput. Vis. 2018, 126, 1394–1414. [Google Scholar] [CrossRef] [Green Version]
- Khot, T.; Agrawal, S.; Tulsiani, S.; Mertz, C.; Lucey, S.; Hebert, M. Learning unsupervised multi-view stereopsis via robust photometric consistency. arXiv 2019, arXiv:1905.02706. [Google Scholar]
- Chu, Y.; Lin, H.; Yang, L.; Diao, Y.; Zhang, D.; Zhang, S.; Fan, X.; Shen, C.; Xu, B.; Yan, D. Discriminative globality-locality preserving extreme learning machine for image classification. Neurocomputing 2020, 387, 13–21. [Google Scholar] [CrossRef]
- Mescheder, L.; Oechsle, M.; Niemeyer, M.; Nowozin, S.; Geiger, A. Occupancy networks: Learning 3D reconstruction in function space. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 16–20 June 2019; pp. 4460–4470. [Google Scholar]
- Lin, C.; Kumar, A. Contactless and partial 3D fingerprint recognition using multi-view deep representation. Pattern Recognit. 2018, 83, 314–327. [Google Scholar] [CrossRef]
- Cadena, C.; Carlone, L.; Carrillo, H.; Latif, Y.; Scaramuzza, D.; Neira, J.; Reid, I.; Leonard, J.J. Past, present, and future of simultaneous localization and mapping: Toward the robust-perception age. IEEE Trans. Robot. 2016, 32, 1309–1332. [Google Scholar] [CrossRef] [Green Version]
- Wan, T.; Du, S.; Cui, W.; Yao, R.; Ge, Y.; Li, C.; Gao, Y.; Zheng, N. RGB-D point cloud registration based on salient object detection. IEEE Trans. Neural Netw. Learn. Syst. 2022, 33, 3547–3559. [Google Scholar] [CrossRef]
- Yousif, K.; Taguchi, Y.; Ramalingam, S. MonoRGBD-SLAM: Simultaneous localization and mapping using both monocular and RGBD cameras. In Proceedings of the IEEE International Conference on Robotics and Automation, Singapore, 29 May–3 June 2017; pp. 4495–4502. [Google Scholar]
- Besl, P.J.; McKay, N.D. Method for registration of 3-D shapes. Proceedings of Sensor Fusion IV: Control Paradigms and Data Structures, Boston, MA, USA, 14–15 November 1992; Volume 1611, pp. 586–606. [Google Scholar]
- Blais, G.; Levine, M.D. Registering multiview range data to create 3D computer objects. IEEE Trans. Pattern Anal. Mach. Intell. 1995, 17, 820–824. [Google Scholar] [CrossRef] [Green Version]
- Fitzgibbon, A.W. Robust registration of 2D and 3D point sets. Image Vis. Comput. 2003, 21, 1145–1153. [Google Scholar] [CrossRef]
- Sharp, G.C.; Lee, S.W.; Wehe, D.K. ICP registration using invariant features. IEEE Trans. Pattern Anal. Mach. Intell. 2002, 24, 90–102. [Google Scholar] [CrossRef] [Green Version]
- Chetverikov, D.; Stepanov, D.; Krsek, P. Robust Euclidean alignment of 3-D point sets: The trimmed iterative closest point algorithm. Image Vis. Comput. 2005, 23, 299–309. [Google Scholar] [CrossRef]
- Phillips, J.M.; Liu, R.; Tomasi, C. Outlier robust ICP for minimizing fractional RMSD. In Proceedings of the IEEE International Conference on 3-D Digital Imaging and Modeling (3DIM), Montreal, QC, Canada, 21–23 August 2007; pp. 427–434. [Google Scholar]
- Myronenko, A.; Song, X. Point set registration: Coherent point drift. IEEE Trans. Pattern Anal. Mach. Intell. 2010, 32, 2262–2275. [Google Scholar] [CrossRef] [Green Version]
- Yang, X.; Sheng, Y.; Sevigny, L.; Valin, P. Robust multisensor image registration with partial distance merits. In Proceedings of the Third International Conference on Information Fusion, Paris, France, 10–13 July 2000; Volume 11, pp. MOD3/23–MOD3/29. [Google Scholar]
- Du, S.; Liu, J.; Zhang, C.; Zhu, J.; Li, K. Probability iterative closest point algorithm for m-D point set registration with noise. Neurocomputing 2015, 157, 187–198. [Google Scholar] [CrossRef]
- Yu, H.; Qin, Z.; Hou, J.; Saleh, M.; Li, D.; Busam, B.; Ilic, S. Rotation-invariant transformer for point cloud matching. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Vancouver, BC, Canada, 18–22 June 2023; pp. 5384–5393. [Google Scholar]
- Gu, X.; Tang, C.; Yuan, W.; Dai, Z.; Zhu, S.; Tan, P. RCP: Recurrent closest point for point cloud. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LO, USA, 19–24 June 2022; pp. 8216–8226. [Google Scholar]
- Hu, P.; Ho, E.S.; Munteanu, A. AlignBodyNet: Deep learning-based alignment of non-overlapping partial body point clouds from a single depth camera. IEEE Trans. Instrum. Meas. 2020, 72, 2502609. [Google Scholar] [CrossRef]
- Sun, L.; Zhang, Z.; Zhong, R.; Chen, D.; Zhang, L.; Zhu, L.; Wang, Q.; Wang, G.; Zou, J.; Wang, Y. A weakly supervised graph deep learning framework for point cloud registration. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5702012. [Google Scholar] [CrossRef]
- Zeng, A.; Song, S.; Nießner, M.; Fisher, M.; Xiao, J.; Funkhouser, T. 3dmatch: Learning local geometric descriptors from rgb-d reconstructions. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 1802–1811. [Google Scholar]
- Yew, Z.J.; Lee, G.H. RPM-Net: Robust point matching using learned features. In Proceedings of the IEEE/CVF conference on computer vision and pattern recognition, Virtual, 14–19 June 2020; pp. 11824–11833. [Google Scholar]
- Wang, Y.; Solomon, J.M. Deep closest point: Learning representations for point cloud registration. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Seoul, Republic of Korea, 27 October–2 November 2019; pp. 3523–3532. [Google Scholar]
- Bari, A.S.M.H.; Gavrilova, M.L. OMNet: Learning overlapping mask for partial-to-partial point cloud registration. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Vitural, 11–17 October 2021; pp. 3133–3141. [Google Scholar]
- Xu, H.; Ye, N.; Liu, S.; Zeng, B.; Liu, S. FINet: Dual branches feature interaction for partial-to-partial point cloud registration. In Proceedings of the Thirty-Sixth AAAI Conference on Artificial Intelligence, Virtual Event, 22 February–1 March 2022; pp. 1–14. [Google Scholar]
- Qin, Z.; Yu, H.; Wang, C.; Peng, Y.; Xu, K. Geometric transformer for fast and robust point cloud registration. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LO, USA, 19–24 June 2022; pp. 11143–11152. [Google Scholar]
- Feldmar, J.; Rigid, N.A. Affine and locally affine registration of free-form surfaces. Int. J. Comput. Vis. 1996, 18, 99–119. [Google Scholar] [CrossRef] [Green Version]
- Amberg, B.; Romdhani, S.; Vetter, T. Optimal step nonrigid ICP algorithms for surface registration. Proceedings of IEEE International Conference on Computer Vision and Pattern Recognition, Minneapolis, MN, USA, 17–22 June 2007; pp. 1–8. [Google Scholar]
- Du, S.Y.; Zheng, N.N.; Meng, G.F.; Yuan, Z.J. Affine registration of point sets using ICP and ICA. IEEE Signal Process. Lett. 2008, 15, 689–692. [Google Scholar]
- Wan, T.; Du, S.; Xu, Y.; Xu, G.; Li, Z.; Chen, B.; Gao, Y. RGB-D point cloud registration via infrared and color camera. Multimed. Tools Appl. 2019, 78, 33223–33246. [Google Scholar] [CrossRef]
- Men, H.; Gebre, B.; Pochiraju, K. Color point cloud registration with 4D ICP algorithm. Proceedings of IEEE International Conference on Robotics and Automation, Shanghai, China, 9–13 May 2011; pp. 1511–1516. [Google Scholar]
- Korn, M.; Holzkothen, M.; Pauli, J. Color supported generalized-ICP. In Proceedings of the International Conference on Computer Vision Theory and Applications, Lisbon, Portugal, 5–8 January 2014; Volume 3, pp. 592–599. [Google Scholar]
- Du, S.; Zheng, N.; Ying, S.; Liu, J. Affine iterative closest point algorithm for point set registration. Pattern Recognit. Lett. 2010, 31, 791–799. [Google Scholar] [CrossRef]
- Cui, W.; Liu, J.; Du, S.; Liu, Y.; Wan, T.; Han, M.; Mou, Q.; Yang, J.; Gou, Y. Individual retrieval based on oral cavity point cloud data and correntropy-based registration algorithm. IET Image Process. 2020, 14, 2675–2681. [Google Scholar] [CrossRef]
- Cui, W.; Du, S.; Wan, T.; Yao, R.; Liu, Y.; Han, M.; Mou, Q.; Gou, Y.; Zheng, N. Robust and precise isotropic scaling registration algorithm using bi-directional distance and correntropy. Pattern Recognit. Lett. 2020, 138, 298–304. [Google Scholar] [CrossRef]
- Wang, H.; Xie, L. Convergence analysis of a least squared algorithm of linear switched identification. J. Control. Decis. 2020, 7, 379–396. [Google Scholar] [CrossRef]
- Ram, P.; Sinha, K. Revisiting kd-tree for Nearest Neighbor Search. In Proceedings of the 25th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Anchorage, AK, USA, 4–8 August 2019; pp. 1378–1388. [Google Scholar]
- Hou, W.; Li, D.; Xu, C.; Zhang, H.; Li, T. An advanced k nearest neighbor classification algorithm based on KD-tree. In Proceedings of the International Conference of Safety Produce Informatization, Chongqing, China, 10–12 December 2018; pp. 902–905. [Google Scholar]
- Yin, L.; Andrews, J.; Heaton, T. Reducing process delays for real-time earthquake parameter estimation—An application of KD tree to large databases for Earthquake Early Warning. Comput. Geosci. 2018, 114, 22–29. [Google Scholar] [CrossRef]
- Du, S.; Zhang, C.; Wu, Z.; Liu, J.; Xue, J. Robust isotropic scaling ICP algorithm with bidirectional distance and bounded rotation angle. Neurocomputing 2016, 215, 160–168. [Google Scholar] [CrossRef]
- Du, S.; Bi, B.; Xu, G.; Zhu, J.; Zhang, X. Robust non-rigid point set registration via building tree dynamically. Multimed. Tools Appl. 2017, 76, 12065–12081. [Google Scholar] [CrossRef]
- Wu, Z.; Chen, H.; Du, S.; Fu, M.; Zhou, N.; Zheng, N. Correntropy based scale ICP algorithm for robust point set registration. Pattern Recognit. 2019, 93, 14–24. [Google Scholar] [CrossRef]
- Dong, J.; Cai, Z.; Du, S. Improvement of affine iterative closest point algorithm for partial registration. IET Comput. Vis. 2016, 11, 135–144. [Google Scholar] [CrossRef]
- Du, S.; Xu, G.; Zhang, S.; Zhang, X.; Gao, Y.; Chen, B. Robust rigid registration algorithm based on pointwise correspondence and correntropy. Pattern Recognit. Lett. 2020, 132, 91–98. [Google Scholar] [CrossRef]
- Chen, H.; Zhang, X.; Du, S.; Wu, Z.; Zheng, N. A correntropy-based affine iterative closest point algorithm for robust point set registration. IEEE/CAA J. Autom. Sin. 2019, 6, 981–991. [Google Scholar] [CrossRef]
- Wang, L.; Huynh, D.Q.; Koniusz, P. A comparative review of recent Kinect-based action recognition algorithms. IEEE Trans. Image Process. 2019, 29, 15–28. [Google Scholar] [CrossRef] [Green Version]
- Su, Y.; Gao, W.; Liu, Z.; Sun, S.; Fu, Y. Hybrid marker-based object tracking using Kinect v2. IEEE Trans. Instrum. Meas. 2020, 69, 6436–6445. [Google Scholar] [CrossRef]
- Bari, A.S.M.H.; Gavrilova, M.L. Artificial neural network based gait recognition using Kinect sensor. IEEE Access 2019, 7, 162708–162722. [Google Scholar] [CrossRef]









| M D |
| . |
| via Equation (6). |
| Data | Error | ICP | SICP | CICP | AICP | ACICP | Geo | Ours |
|---|---|---|---|---|---|---|---|---|
| 1 | 4.2404 | 2.4567 | 4.2396 | 0.8909 | 0.4171 | 4.1203 | 0.0027 | |
| 0.0047 | 0.0063 | 0.0046 | 0.0076 | 0.0024 | 0.0049 | 0.0001 | ||
| 2 | 2.3110 | 2.7573 | 2.3110 | 9.1136 | 185.5356 | 2.2430 | 0.0017 | |
| 0.0046 | 0.2191 | 0.0046 | 3.7153 | 73.5416 | 0.0045 | 0.0017 | ||
| 3 | 2.4192 | 2.3792 | 2.4047 | 0.5648 | 1.3316 | 2.3182 | 0.0002 | |
| 0.0405 | 0.1401 | 0.0338 | 0.0533 | 0.7607 | 0.0389 | 9.9 × | ||
| 4 | 2.3729 | 2.3284 | 2.3424 | 2.7484 | 1.4589 | 2.2894 | 0.0002 | |
| 0.0187 | 0.1071 | 0.0070 | 2.8215 | 1.1970 | 0.0172 | 0.0001 |
| Data | Error | ICP | SICP | CICP | AICP | ACICP | Geo | Ours |
|---|---|---|---|---|---|---|---|---|
| 1 | 2.4466 | 2.0499 | 2.4452 | 0.0188 | 0.4177 | 2.4424 | 0.0131 | |
| 0.0055 | 0.0048 | 0.0005 | 0.0076 | 0.0002 | 0.0047 | 0.0003 | ||
| 2 | 4.2451 | 1.5872 | 4.1448 | 0.0257 | 9.2455 | 4.3012 | 0.0248 | |
| 0.0089 | 0.0252 | 0.0086 | 0.0006 | 0.2515 | 0.0078 | 0.0004 | ||
| 3 | 2.4497 | 1.8683 | 2.4526 | 0.0767 | 0.0728 | 2.3342 | 0.0542 | |
| 0.0010 | 0.0021 | 0.0012 | 0.0003 | 0.0002 | 0.0009 | 0.0002 | ||
| 4 | 4.0085 | 1.8849 | 4.0209 | 0.0893 | 0.0979 | 4.0143 | 0.0570 | |
| 0.0027 | 0.0245 | 0.0032 | 0.0007 | 0.0010 | 0.0031 | 0.0007 |
| The Error of Data 1 | The Error of Data 2 | |
|---|---|---|
| ICP | 1.7 × | 2.0 × |
| SICP | 1.7 × | 2.0 × |
| CICP | 8.9 × | 3.4 × |
| AICP | 3.1 × | 1.5 × |
| ACICP | 8.8 × | 1.1 × |
| Ours | 8.2 × | 6.7 × |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liang, L.; Pei, H. Affine Iterative Closest Point Algorithm Based on Color Information and Correntropy for Precise Point Set Registration. Sensors 2023, 23, 6475. https://doi.org/10.3390/s23146475
Liang L, Pei H. Affine Iterative Closest Point Algorithm Based on Color Information and Correntropy for Precise Point Set Registration. Sensors. 2023; 23(14):6475. https://doi.org/10.3390/s23146475
Chicago/Turabian StyleLiang, Lexian, and Hailong Pei. 2023. "Affine Iterative Closest Point Algorithm Based on Color Information and Correntropy for Precise Point Set Registration" Sensors 23, no. 14: 6475. https://doi.org/10.3390/s23146475
APA StyleLiang, L., & Pei, H. (2023). Affine Iterative Closest Point Algorithm Based on Color Information and Correntropy for Precise Point Set Registration. Sensors, 23(14), 6475. https://doi.org/10.3390/s23146475





